2015年北京东城高三一模数学(文科)试题及答案
北京市东城区示范校2015届高三上学期综合能力测试数学(文)试卷及答案

北京市东城区普通高中示范校2015届上学期高三年级综合能力测试数学试卷(文科)本试卷分第I 卷和第II 卷两部分,共150分。
考试时长120分钟。
第I 卷(选择题 共40分)一、选择题。
(本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项)1. 已知集合{}22|<<-∈=x R x A ,{}034|2≥+-∈=x x R x B ,则=⋂B A ( )A. ]1,2(-B. ()1,2-C. ()2,2-D. ()),3[2,∞+⋃∞-2. 已知复数i a z 21+=,i z 212-=,若21z z 是纯虚数,则实数a 的值为( )A. 2-B. 1C. 2D. 43. “3π=x ”是“21cos =x ”成立的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 下图是一算法的程序框图,若此程序运行结果为55=s ,则在判断框中应填入关于k 的判断条件是( )A. 11≤kB. 10≤kC. 9≤kD. 8≤k5. 已知一个棱锥的三视图如下,根据图中标出的尺寸(单位:cm ),可得这个棱锥的侧面积是( )A. 24cmB. 212cmC. 2248cm +D. 232244cm ++6. 已知()a x x f x ++=2||2有唯一的零点,则实数a 的值为( )A. -3B. -2C. -1D. 07. 如图,直线2-=x y 与圆03422=+-+x y x 及抛物线x y 82=依次交于A 、B 、C 、D 四点,则=+||||CD AB ( )A. 13B. 14C. 15D. 168. 已知()⎪⎩⎪⎨⎧>+--≤+-=,0,32,0,3422x x x x x x x f 不等式()()x a f a x f ->+2在[]1,+a a 上恒成立,则实数a 的取值范围是( ) A. ()2,-∞-B. ()0,∞-C. ()2,0D. ()0,2-第II 卷(非选择题 共110分)二、填空题。
数学_2015年北京市东城区普通示范校高考数学模拟试卷(文科)(含答案)

2015年北京市东城区普通示范校高考数学模拟试卷(文科)一、选择题.(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1. 已知集合A={x∈R|−3<x<2},B={x∈R|x2−4x+3≥0},则A∩B=()A (−3, 1]B (−3, 1)C [1, 2)D (−∞, 2)∪[3, +∞)2. 已知复数z1=a+2i,z2=1−2i,若z1z2是纯虚数,则实数a的值为()A −2B 1C 2D 43. “α=π3”是“cosα=12”的()A 必要不充分条件B 充分不必要条件C 充分必要条件D 既不充分也不必要条件4. 如图是一算法的程序框图,若此程序运行结果为s=55,则在判断框中应填入关于k的判断条件是()A k≤11B k≤10C k≤9D k≤85. 已知一个棱锥的三视图如下,根据图中标出的尺寸(单位:cm),可得这个棱锥的侧面积是()A 4cm2B 12cm2C 8+4√2cm2D 4+4√2+2√3cm26. 已知f(x)=2|x|+x2+a有唯一的零点,则实数a的值为()A −3B −2C −1D 07. 已知直线y=x−2与圆x2+y2−4x+3=0及抛物线y2=8x的四个交点从上到下依次为A、B、C、D四点,则|AB|+|CD|=()A 12B 14C 16D 188. 已知f(x)={x 2−4x+3,x≤0−x2−2x+3,x>0,不等式f(x+a)>f(2a−x)在[a, a+1]上恒成立,则实数a的取值范围是()A (−∞, −2)B (−∞, 0)C (0, 2)D (−2, 0)二、填空题.(本大题共6小题,每小题5分,共30分)9. 不等式组{x −y +1≥0x +y ≥1x ≤1表示的平面区域的面积为________.10. 设平面向量a →=(1, 2),b →=(−2, y),若a →⊥b →,则|2a →−b →|=________.11. 在等差数列{a n }中,a 1=3,a 4=2,则a 4+a 7+...a 3n+1等于________.12. 直线x −√3y −4=0被圆(x −2)2+y 2=4截得的弦长为________.13. 已知0<x <π,且sin2x =−725,则sin(π4−x)的值为________. 14. 已知数集A ={a 1, a 2, a 3, a 4, a 5}(0≤a 1<a 2<a 3<a 4<a 5)具有性质p :对任意i ,j ∈Z ,其中1≤i ≤j ≤5,均有(a j −a i )∈A ,若a 5=60,则a 3=________.三、解答题.(本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程)15. 设数列{a n }的前n 项和为S n ,且S n =2a n −1(n =1, 2,…).(Ⅰ)求数列{a n }的通项公式;(Ⅱ)若数列{b n }满足b n+1=a n +b n (n =1, 2,…),b 1=2,求数列{b n }的通项公式.16. 在△ABC 中,a ,b ,c 分别是角A ,B ,C 的对边,满足c =1,cosBsinC −(a −sinB)cosC =0.(1)求C 的大小;(2)求a 2+b 2的最大值,并求取得最大值时角A ,B 的值.17. 如图,将矩形ABCD 沿对角线BD 把△ABD 折起,使A 点移到A 1点,且A 1在平面BCD 上的射影O 恰好在CD 上.(Ⅰ)求证:BC ⊥A 1D ;(Ⅱ)求证:平面A 1CD ⊥平面A 1BC ;(Ⅲ)若AB =10,BC =6,求三棱锥A 1−BCD 的体积.18. 设a ∈R ,已知函数f(x)=ax 3−3x 2.(Ⅰ)当a =1时,求函数f(x)的单调区间;(Ⅱ)若对任意的x ∈[1, 3],有f(x)+f′(x)≤0恒成立,求实数a 的取值范围.19. 已知椭圆W:x 22m+10+y 2m 2−2=1的左焦点为F(m, 0),过点M(−3, 0)作一条斜率大于0的直线l 与W 交于不同的两点A 、B ,延长BF 交W 于点C .(Ⅰ)求椭圆W 的离心率;(Ⅱ)求证:点A 与点C 关于x 轴对称.20. 已知定义在(1, +∞)上的函数f(x)=x −lnx −2,g(x)=xlnx +x .(1)求证:f(x)存在唯一的零点,且零点属于(3, 4);(2)若k∈Z,且g(x)>k(x−1)对任意的x>1恒成立,求k的最大值.2015年北京市东城区普通示范校高考数学模拟试卷(文科)答案1. A2. D3. B4. B5. D6. C7. B8. A9. 110. 511. n(5−n)212. 2√313. −4514. 3015.(I)因为S n=2a n−1(n=1, 2,…),则S n−1=2a n−1−1(n=2, 3,…),所以当n≥2时,a n=S n−S n−1=2a n−2a n−1,整理得a n=2a n−1,由S n=2a n−1,令n=1,得a1=2a1−1,解得a1=1.所以{a n}是首项为1,公比为2的等比数列,可得a n=2n−1(II)因为a n=2n−1,由b n+1=a n+b n(n=1, 2,…),得b n+1−b n=2n−1,由累加得b n=b1+(b2−b1)+(b3−b2)+...+(b n−b n−1)=2+1−2n−11−2=2n−1+1,(n≥2),当n=1时也满足,所以b n=2n−1+1.16. cosBsinC−(a−sinB)cosC=0,即有sinBcosC+cosBsinC=acosC,即sin(B+C)=acosC,即sinA=acosC.由正弦定理可知:asinA =csinC=1cosC,由于c=1,则sinC=cosC,即tanC=1,C是三角形内角,∴ C=π4.由余弦定理可知:c2=a2+b2−2abcosC,得1=a2+b2−√2ab,又ab≤a 2+b22,∴ (1−√22)(a2+b2)≤1,即a2+b2≤2+√2.当且仅当a=b即A=B=3π8时,a2+b2取到最大值为2+√2.17.(I)证明:因为A1在平面BCD上的射影O在CD上,所以A1O⊥平面BCD.又BC⊂平面BCD,所以BC⊥A1O.又BC⊥CO,CO∩A1O=O,CO⊂平面A1CD,A1O⊂平面A1CD,所以BC⊥平面A1CD.又A1D⊂平面A1CD,所以BC⊥A1D.(II)证明:因为矩形ABCD,所以A1D⊥A1B.由(I)知BC⊥A1D.又BC∩A1B=B,BC⊂平面A1BC,A1B⊂平面A1BC,所以A1D⊥平面A1BC.又A1D⊂平面A1CD,所以平面A1BC⊥平面A1CD.(III)因为A1D⊥平面A1BC,所以A1D⊥A1C.因为CD=10,A1D=6,所以A1C=8.所以V A1−BCD =V D−A1BC=13×12×6×8×6=48.18.(I)当a=1时,f(x)=x3−3x2,则f′(x)=3x2−6x,由f′(x)>0,得x<0,或x>2,由f′(x)<0,得0<x<2,所以f(x)的单调递增区间为(−∞, 0),(2, +∞),单调递减区间为(0, 2).(II)依题意,对∀x∈[1, 3],ax3−3x2+3ax2−6x≤0,这等价于,不等式a≤3x 2+6xx3+3x2=3x+6x2+3x对x∈[1, 3]恒成立.令ℎ(x)=3x+6x2+3x(x∈[1,3]),则ℎ(x)=3(x 2+4x+6)(x2+3x)2=−3[(x+2)2+2](x2+3x)2<0,所以ℎ(x)在区间[1, 3]上是减函数,所以ℎ(x)的最小值为ℎ(3)=56.所以a ≤56,即实数a 的取值范围为(−∞,56]. 19.(I)由题意(2m +10)−(m 2−2)=m 2(m <0),解得m =−2.所以椭圆W:x 26+y 22=1. 离心率e =ca =2√6=√63.(II)设直线l 的方程为y =k(x +3).联立{y =k(x +3)x 26+y 22=1得(1+3k 2)x 2+18k 2x +27k 2−6=0.由直线l 与椭圆W 交于A 、B 两点,可知△=(18k 2)2−4(1+3k 2)(27k 2−6)>0,解得k 2<23.设点A ,B 的坐标分别为(x 1, y 1),(x 2, y 2),则x 1+x 2=−18k 21+3k 2,x 1x 2=27k 2−61+3k 2,y 1=k(x 1+3),y 2=k(x 2+3). 因为F(−2, 0),设点A 关于x 轴的对称点为C′,则C′(x 1, −y 1), 所以FC ′→=(x 1+2,−y 1),FB →=(x 2+2,y 2).又因为(x 1+2)y 2−(x 2+2)(−y 1)=(x 1+2)k(x 2+3)+(x 2+2)k(x 1+3)=k[2x 1x 2+5(x 1+x 2)+12]=k[54k 2−121+3k 2+−90k 21+3k 2+12]=k(54k 2−12−90k 2+12+36k 2)1+3k 2=0,所以B ,F ,C′共线,从而C 与C′重合,故点A 与点C 关于x 轴对称.20. 证明:令f(x)=0,得:x −2=lnx ,画出函数y =x −2,y =lnx 的图象,如图示:∴ f(x)存在唯一的零点,又f(3)=1−ln3<0,f(4)=2−ln4=2(1−ln2)>0,∴ 零点属于(3, 4);由g(x)>k(x −1)对任意的x >1恒成立,得:k <xlnx+xx−1,(x >1),令ℎ(x)=xlnx+xx−1,(x >1),则ℎ′(x)=x−lnx−2(x−1)2=f(x)(x−1)2,设f(x0)=0,则由(1)得:3<x0<4,∴ ℎ(x)在(1, x0)递减,在(x0, +∞)递增,而3<ℎ(3)=31n3+32<4,83<ℎ(4)=41n4+43<4,∴ ℎ(x0)<4,∴ k的最大值是3.。
数学_2015年北京市东城区高考数学一模试卷(理科)(含答案)

2015年北京市东城区高考数学一模试卷(理科)一、选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1. 已知全集U =R ,集合A ={x|−1≤x ≤2},B ={x|x <−3, 或x >4},那么A ∩(∁U B)=( )A {x|−1≤x ≤4}B {x|−3≤x ≤2}C {x|−1≤x ≤2}D {x|−3≤x ≤4} 2. 复数a+i2−i 为纯虚数,则实数a =( ) A −2 B −12 C 2 D 123. 在区间[0, 2]上随机取一个实数x ,若事件“3x −m <0”发生的概率为16,则实数m =( )A 1B 12C 13D 164. 已知点M 的极坐标为(5,2π3),那么将点M 的极坐标化成直角坐标为( )A (−5√32,−52) B (−5√32,52) C (52,5√32) D (−52,5√32) 5. “x <1”是“log 12x >0”的( )A 充分而不必要条件B 必要而不充分条件C 充分必要条件D 既不充分也不必要条件6. 某学校开设“蓝天工程博览课程”,组织6个年级的学生外出参观包括甲博物馆在内的6个博物馆,每个年级任选一个博物馆参观,则有且只有两个年级选择甲博物馆的方案有( )A A 62×A 54种B A 62×54种C C 62×A 54种D C 62×54种7. 一个几何体的三视图如图所示,图中直角三角形的直角边长均为1,则该几何体体积为( )A 16 B √26 C √36 D 128. 已知函数f(x)=2mx 2−2(4−m)x +1,g(x)=mx ,若对于任一实数x ,f(x)与g(x)至少有一个为正数,则实数m 的取值范围是( ) A (0, 2) B (0, 8) C (2, 8) D (−∞, 0)二、填空题(共6小题,每小题5分,共30分)9. 设等差数列{a n }的前n 项和为S n ,若S 2=8,S 4=12,则{a n }的公差d =________. 10. 曲线y =sinx(0≤x ≤π)与x 轴围成的封闭区域的面积为________.11. 如图,在△ABC 中,∠A =60∘,AB =2AC =8,过C 作△ABC 外接圆的切线CD ,BD ⊥CD 于D ,BD 与外接圆交于点E ,则DE =________.12. 已知F 1,F 2分别为椭圆x 2a 2+y 2b 2=1(a >b >0)的左、右焦点,P 为椭圆上一点,且PF 2垂直于x 轴.若|F 1F 2|=2|PF 2|,则该椭圆的离心率为________.13. 已知函数f(x)是R 上的减函数,且y =f(x −2)的图象关于点(2, 0)成中心对称.若u ,v 满足不等式组{f(u)+f(v −1)≤0f(u −v −1)≥0,则u 2+v 2的最小值为________12 .14. 已知x ∈R ,定义:A(x)表示不小于x 的最小整数.如A(√3)=2,A(−1.2)=−1.若A(2x +1)=3,则x 的取值范围是________;若x >0且A (2x ⋅A(x))=5,则x 的取值范围是________.三、解答题(共6小题,共80分.解答应写出文字说明,演算步骤或证明过程) 15. 在△ABC 中,b =2,cosC =34,△ABC 的面积为√74.(Ⅰ)求a 的值; (Ⅱ)求sin2A 值.16. 某地区有800名学员参加交通法规考试,考试成绩的频率分布直方图如图所示.其中成绩分组区间是:[75, 80),[80, 85),[85, 90),[90, 95),[95, 100].规定90分及其以上为合格. (Ⅰ)求图中a 的值(Ⅱ)根据频率分布直方图估计该地区学员交通法规考试合格的概率;(Ⅲ)若三个人参加交通法规考试,用X 表示这三人中考试合格的人数,求X 的分布列与数学期望.17. 如图,在三棱锥P −ABC 中,PA ⊥底面ABC ,AB ⊥BC ,AB =PA =BC =2.D ,E 分别为AB ,AC 的中点,过DE 的平面与PB ,PC 相交于点M ,N (M 与P ,B 不重合,N 与P ,C 不重合).(Ⅰ)求证:MN // BC;(Ⅱ)求直线AC与平面PBC所成角的大小;(Ⅲ)若直线EM与直线AP所成角的余弦值3√14时,求MC的长.14+lnx,a∈R.18. 已知函数f(x)=x+ax(Ⅰ)若f(x)在x=1处取得极值,求a的值;(Ⅱ)若f(x)在区间(1, 2)上单调递增,求a的取值范围;(Ⅲ)讨论函数g(x)=f′(x)−x的零点个数.19. 在平面直角坐标系中xOy中,动点E到定点(1, 0)的距离与它到直线x=−1的距离相等.(Ⅰ)求动点E的轨迹C的方程;(Ⅱ)设动直线l:y=kx+b与曲线C相切于点P,与直线x=−1相交于点Q.证明:以PQ为直径的圆恒过x轴上某定点.20. 在无穷数列{a n}中,a1=1,对于任意n∈N∗,都有a n∈N∗,且a n<a n+1.设集合A m ={n|a n≤m, m∈N∗},将集合A m中的元素的最大值记为b m,即b m是数列{a n}中满足不等式a n≤m的所有项的项数的最大值,我们称数列{b n}为数列{a n}的伴随数列.例如:数列{a n}是1,3,4,…,它的伴随数列{b n}是1,1,2,3,….(Ⅰ)设数列{a n}是1,4,5,…,请写出{a n}的伴随数列{b n}的前5项;(Ⅱ)设a n=3n−1(n∈N∗),求数列{a n}的伴随数列{b n}的前20项和;(Ⅲ)设a n=3n−2(n∈N∗),求数列{a n}的伴随数列{b n}前n项和S n.2015年北京市东城区高考数学一模试卷(理科)答案1. C2. D3. A4. D5. B6. D7. A8. B9. −110. 211. 212. √5−1213. 1214. (12, 1],(1, 54]15. (1)△ABC中,∵ b=2,cosC=34,∴ sinC=√74,∴ △ABC的面积为√74=12ab⋅sinC=12a⋅2⋅√74.a=(1)(2)由余弦定理可得c2=a2+b2−2ab⋅cosC=1+4−3=2,∴ c=√2.再由正弦定理可得asinA =csinC,即1sinA=√2√74,∴ sinA=√148.由于a不是最大边,故A为锐角,故cosA=5√28,∴ sin2A=2sinAcosA=2×√148⋅5√28=5√716.16. (I)由直方图知.(0.01+0.02+0.06+0.07+a)×5=(1)解得a=0.(04)(2)设事件A为“某名学员交通考试合格”.由直方图知,P(A)=(0.06+0.02)×5=0.(4)(III)以题意得出X的取值为0,1,2,(3)P(X=0)=(1−0.4)3=0.2(16)P(X=1)=C31×0.4×(0.6)2=0.4(32)P(X=2)=C32×(0.4)2×(0.6)=0.2(88)P(X=3)=C33×(0.4)3=0.06(4)所以X的分布列为E(X)=0×0.216+1×0.432×2×0.288+3×0.064=1.(2) 17. (1)证明:∵ D,E分别为AB,AC的中点;∴ DE // BC,BC⊂平面PBC,DE⊄平面PBC;∴ DE // 平面PBC,平面DENM∩平面PBC=MN;∴ DE // MN;∴ MN // BC;(2)如图,在平面PAB内作BZ // PA,则根据:PA ⊥底面ABC ,及AB ⊥BC 即知,BC ,BA ,BZ 两两垂直;∴ 以B 为坐标原点,BC ,BA ,BZ 所在直线为x ,y ,z 轴建立如图所示空间直角坐标系,则: B(0, 0, 0),C(2, 0, 0),A(0, 2, 0),P(0, 2, 2); ∴ BC →=(2,0,0),BP →=(0,2,2),AC →=(2,−2,0); 设平面PBC 的法向量为n →=(x 1,y 1,z 1); 则由{n →⋅BC →=0n →⋅BP →=0得: {2x 1=02y 1+2z 1=0 ,令z 1=1,得x 1=0,y 1=−1; ∴ n →=(0,−1,1);设直线AC 和平面PBC 所成角为α,则: sinα=|cos <AC →,n →>|=|AC →⋅n→|AC →||n →||=22√2⋅√2=12; 又α∈[0,π2]; ∴ α=π6;即直线AC 和平面PBC 所成角为π6;(Ⅲ)设M(0, y, z),M 在棱PB 上,则:BM →=λBP →,(0<λ<1); ∴ (0, y, z)=λ(0, 2, 2);∴ M(0, 2λ, 2λ),E(1, 1, 0);∴ EM →=(−1,2λ−1,2λ),AP →=(0,0,2); 因为直线EM 与直线AP 所成角的余弦值3√1414; 设直线EM 和直线AP 所成角为θ; 所以cosθ=|EM →⋅AP →|EM →||AP →||=4λ√8λ2−4λ+2⋅2=3√1414; ∴ 8λ2−18λ+9=0; 解得λ=34,或λ=32(舍去);∴ M(0, 32,32 );∴ MC=√4+94+94=√342.18. (1)函数f(x)=x+ax+lnx(x>0),f′(x)=1−ax2+1x=x2+x−ax2,f(x)在x=1处取得极小值,即有f′(1)=0,解得a=2,经检验,a=2时,f(x)在x=1处取得极小值.则有a=2;(2)f′(x)=1−ax2+1x=x2+x−ax2,x>0,f(x)在区间(1, 2)上单调递增,即为f′(x)≥0在区间(1, 2)上恒成立,即a≤x2+x在区间(1, 2)上恒成立,由x2+x∈(2, 6),则a≤2;(Ⅲ)g(x)=f′(x)−x=1−ax2+1x−x,x>0,令g(x)=0,则a=−x3+x2+x,令ℎ(x)=−x3+x2+x,x>0,则ℎ′(x)=−3x2+2x+1=−(3x+1)(x−1),当x∈(0, 1),ℎ′(x)>0,ℎ(x)在(0, 1)递增;当x∈(1, +∞),ℎ′(x)<0,ℎ(x)在(1, +∞)递减.即有ℎ(x)的最大值为ℎ(1)=1,则当a>1时,函数g(x)无零点;当a=1或a≤0时,函数g(x)有一个零点;当0<a<1时,函数g(x)有两个零点.19. (1)设动点E的坐标为(x, y),由抛物线定义知,动点E的轨迹是以(1, 0)为焦点,x=−1为准线的抛物线,∴ 动点E的轨迹C的方程为:y2=4x;(2)证明:设直线l的方程为:y=kx+b(k≠0),由{y2=4xy=kx+b,消去x得:ky2−4y+4b=(0)∵ 直线l与抛物线相切,∴ △=16−16kb=0,即b=1k.∴ 直线l的方程为y=kx+1k.令x=−1,得y=−k+1k,∴ Q(−1, −k+1k),设切点坐标P(x 0, y 0),则ky 02−4y 0+4k=0,解得:P(1k2,2k),设M(m, 0),则MQ →⋅MP →=(1k 2−m)(−1−m)+2k (−k +1k ) =−1k 2+m −m k 2+m 2+2k 2−2 =(m −1)(1k 2−m −2). 当m =1时,MQ →⋅MP →=0.∴ 以PQ 为直径的圆恒过x 轴上定点M(1, 0).20. (I )由{a n }伴随数列{b n }的定义可得前5项为1,1,1,2,(3) (II)由a n =3n−1≤m ,可得n ≤1+log 3m ,m ∈N ∗, ∴ 当1≤m ≤2时,m ∈N ∗,b 1=b 2=1;当3≤m ≤8时,m ∈N ∗,b 3=b 4=...=b 8=2; 当9≤m ≤20时,m ∈N ∗,b 9=b 10= (3)∴ 数列{a n }的伴随数列{b n }的前20项和=1×2+2×6+3×12=50; (III)由a n =3n −2≤m ,解得n ≤m+23,∵ 不等式a n ≤m 成立的最大值为b m ,∴ b 1=b 2=b 3=1,b 4=b 5=b 6=2,…,b 3n−2+b 3n−1+b 3n =t(t ∈N ∗), ∴ 当n =3t −2时,(t ∈N ∗),S n =3×1+(t−1)2(t −1)+t =3t 2−t 2=16(n +1)(n +2);当n =3t −1时,(t ∈N ∗),S n =3×1+(t−1)2(t −1)+2t =3t 2+t 2=16(n +1)(n +2);当n =3t 时,(t ∈N ∗),S n =3×1+t 2×t =3(t 2+t)2=16n(n +3).∴ S n ={(n+1)(n+2)6,(n =3t −23t −1)n(n+3)6,(n =3t)(t ∈N ∗).。
北京市东城区普通校2015届高三11月联考数学

北京市东城区普通校2015届高三11月联考数学(理)试题 命题校:北京市第五十中学分校 2014年11月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷一、 选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 集合2{6},{30}A x x B x x x =∈≤=∈->N|R|,则A B =A.}5,4,3{B.}6,5,4{C.}63/{≤<x xD. }63/{<≤x x2. 复数11i+在复平面上对应的点的坐标是 A . ),(11 B .),(11- C .)(1,1-- D .)(1,1- 3. 已知{}n a 为等差数列,其前n 项和为n S ,若36a =,312S =,则公差d 等于A. 1B.53C. 2D. 3 4.”1“>x 是”1“2>x 的 A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 5. 已知角α的终边经过点53cos 且)4,(-=-αm P ,则m 的值为 A. 3 B. -3 C. 3± D. 5第Ⅱ卷二、 填空题:本大题共6小题,每小题5分,共30分。
11. 已知命题022,:0200≤++∈∃x x R x P ,那么该命题的否定是_____________.12. 已知53),sin ,2(=∈αππα,则)4tan(πα+=_____________. 13. 若等比数列}{n a 满足40,205342=+=+a a a a ,,则公比=q _________;前n 项和=n S _______________________.14.函数)22,0)(sin(2)(πϕπωϕω<<->+=x x f 的 部分图象如图所示,则ω=______________;ϕ=____________________.15. 若函数⎪⎩⎪⎨⎧≥<<≤≤=232121022x x x x x f ,,,)(,则)3(f =_______________,函数的的值域是 .16. 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数)(x f 的图像恰好通过)(*∈N n n 个整点,则称函数)(x f 为n 阶整点函数,有下列函数:① xx f 2sin )(= ② 3)(x x g = ③ x x h )31()(= ④x x ln )(=ϕ其中,是一阶整点函数的是_____________________.东城区普通校2014-2015学年第一学期联考试卷答案高三数学(理科)命题校:北京市第五十中学分校 2014年11月第Ⅰ卷三、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5答案 B D C A A第Ⅱ卷四、填空题:本大题共6小题,每小题5分,共30分.。
【真题】2015-2016年北京市东城区高三(上)期末数学试卷(文科)与答案

2015-2016学年北京市东城区高三(上)期末数学试卷(文科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合A={1,2,m},B={3,4}.若A∩B={3},则实数m=()A.1 B.2 C.3 D.42.(5分)在复平面内,复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)已知向量=(1,2),=(﹣2,x).若+与﹣平行,则实数x的值是()A.4 B.﹣1 C.﹣44.(5分)经过圆x2+y2﹣2x+2y=0的圆心且与直线2x﹣y=0平行的直线方程是()A.2x﹣y﹣3=0 B.2x﹣y﹣1=0 C.2x﹣y+3=0 D.x+2y+1=05.(5分)给出下列函数:①y=log2x;②y=x2;③y=2|x|④.其中图象关于y轴对称的是()A.①②B.②③C.①③D.②④6.(5分)“sin2α﹣cos2α=1”是“α=”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.(5分)某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是,则在空白的处理框处应填入的关系式可以是()A.y=x3 B.y=3x C.y=3x D.8.(5分)已知函数f(x)=a﹣x2(1≤x≤2)与g(x)=x+1的图象上存在关于x 轴对称的点,则实数a的取值范围是()A.B.[1,2]C.D.[﹣1,1]二、填空题共6小题,每小题5分,共30分.9.(5分)双曲线的离心率为.10.(5分)在△ABC中,角A,B,C所对边分别为a,b,c,且,B=45°,面积S=2,则a=;b=.11.(5分)100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则模块测试成绩落在[50,70)中的学生人数是.12.(5分)设某几何体的三视图如图,则该几何体的体积为13.(5分)已知点P(x,y)的坐标满足条件点O为坐标原点,那么|OP|的最大值等于.14.(5分)纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以A0,A1,A2,B1,B2,…等标记来表示纸张的幅面规格.复印纸幅面规格只采用A系列和B系列,其中An(n∈N,n≤8)系列的幅面规格为:①A0,A1,A2,…,A8所有规格的纸张的幅宽(以x表示)和长度(以y表示)的比例关系都为;②将A0纸张沿长度方向对开成两等分,便成为A1规格,A1纸张沿长度方向对开成两等分,便成为A2规格,…,如此对开至A8规格.现有A0,A1,A2,…,A8纸各一张.若A4纸的宽度为2dm,则A0纸的面积为dm2;这9张纸的面积之和等于dm2.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知等差数列{a n}的前n项和为S n,且满足a1=2,S3=12.(I)求数列{a n}的通项公式;,S k成等比数列,求正整数k的值.(II)若a3,a k+116.(13分)已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的部分对应值如下表:(Ⅰ)求f(x)的解析式;(Ⅱ)求函数g(x)=f(x)+2sinx的最大值和最小值.17.(13分)某中学从高三男生中随机抽取100名学生的身高,将数据整理,得到的频率分布表如下所示.(Ⅰ)求出频率分布表中①和②位置上相应的数据;(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行体能测试,求第3,4,5组每组各抽取多少名学生进行测试?(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求:第4组中至少有一名学生被抽中的概率.组号分组频数频率第1组[160,165)50.050第2组[165,170)①0.350第3组[170,175)30②第4组[175,180)200.200第5组[180,185]100.100合计100 1.0018.(13分)如图,在四棱锥E﹣ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.(Ⅰ)求证:平面ACE⊥平面CDE;(Ⅱ)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出的值;若不存在,说明理由.19.(14分)已知函数f(x)=x﹣ae x,a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线的方程;(Ⅱ)若曲线y=f(x)与x轴有且只有一个交点,求a的取值范围;(Ⅲ)设函数g(x)=x3,请写出曲线y=f(x)与y=g(x)最多有几个交点.(直接写出结论即可)20.(14分)已知椭圆C:=1(a>b>0)过点,且满足a+b=3.(Ⅰ)求椭圆C的方程;(Ⅱ)斜率为的直线交椭圆C于两个不同点A,B,点M的坐标为(2,1),设直线MA与MB的斜率分别为k1,k2.①若直线过椭圆C的左顶点,求此时k 1,k2的值;②试探究k1+k2是否为定值?并说明理由.2015-2016学年北京市东城区高三(上)期末数学试卷(文科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知集合A={1,2,m},B={3,4}.若A∩B={3},则实数m=()A.1 B.2 C.3 D.4【解答】解:∵集合A={1,2,m},B={3,4},A∩B={3},∴m=3,故选:C.2.(5分)在复平面内,复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵=,∴复数对应的点的坐标为(﹣1,﹣2),位于第三象限.故选:C.3.(5分)已知向量=(1,2),=(﹣2,x).若+与﹣平行,则实数x的值是()A.4 B.﹣1 C.﹣4【解答】解:+=(﹣1,2+x).﹣=(3,2﹣x),∵+与﹣平行,∴3(2+x)+(2﹣x)=0,解得x=﹣4.4.(5分)经过圆x2+y2﹣2x+2y=0的圆心且与直线2x﹣y=0平行的直线方程是()A.2x﹣y﹣3=0 B.2x﹣y﹣1=0 C.2x﹣y+3=0 D.x+2y+1=0【解答】解:圆x2+y2﹣2x+2y=0的圆心(1,﹣1),与直线2x﹣y=0平行的直线的斜率为:2,所求直线方程为:y+1=2(x﹣1).∴2x﹣y﹣3=0.故选:A.5.(5分)给出下列函数:①y=log2x;②y=x2;③y=2|x|④.其中图象关于y轴对称的是()A.①②B.②③C.①③D.②④【解答】解:①y=log2x的定义域为(0,+∞),定义域关于原点不对称,则函数为非奇非偶函数;②y=x2;是偶函数,图象关于y轴对称,满足条件.③y=2|x|是偶函数,图象关于y轴对称,满足条件.④是奇函数,图象关于y轴不对称,不满足条件,故选:B.6.(5分)“sin2α﹣cos2α=1”是“α=”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:sin2α﹣cos2α=1,化为=,∴=或,k∈Z.当k=0时,可得α=或.∴“sin2α﹣cos2α=1”是“α=”必要不充分条件,7.(5分)某程序框图如图所示,当输入的x的值为5时,输出的y值恰好是,则在空白的处理框处应填入的关系式可以是()A.y=x3 B.y=3x C.y=3x D.【解答】解:由题意,执行程序框图,有x=5不满足条件x≤0,有x=x﹣2=3不满足条件x≤0,有x=x﹣2=1不满足条件x≤0,有x=x﹣2=﹣1满足条件x≤0,此时经相应关系式计算得y=,检验4个选项,有A,y=(﹣1)3=﹣1,不正确.B,y=3×(﹣1)=﹣3,C,y=3﹣1=,D,y==﹣.故选:C.8.(5分)已知函数f(x)=a﹣x2(1≤x≤2)与g(x)=x+1的图象上存在关于x轴对称的点,则实数a的取值范围是()A.B.[1,2]C.D.[﹣1,1]【解答】解:若函数f(x)=a﹣x2(1≤x≤2)与g(x)=x+1的图象上存在关于x轴对称的点,则方程a﹣x2=﹣(x+1)⇔a=x2﹣x﹣1在区间[1,2]上有解,令g(x)=x2﹣x﹣1,1≤x≤2,由g(x)=x2﹣x﹣1的图象是开口朝上,且以直线x=为对称轴的抛物线,故当x=1时,g(x)取最小值﹣1,当x=2时,函数取最大值1,故a∈[﹣1,1],故选:D.二、填空题共6小题,每小题5分,共30分.9.(5分)双曲线的离心率为.【解答】解:因为双曲线,所以a=4,b=3,所以c=,所以双曲线的离心率为:e=.故答案为:.10.(5分)在△ABC中,角A,B,C所对边分别为a,b,c,且,B=45°,面积S=2,则a=1;b=5.【解答】解:由题意可得S=acsinB=×a×4×=2,解得a=1,由余弦定理可得b2=a2+c2﹣2acsinB,=1+32﹣2×1×4×=25,解得b=5.故答案为:1;5.11.(5分)100名学生某次数学测试成绩(单位:分)的频率分布直方图如图所示,则模块测试成绩落在[50,70)中的学生人数是25.【解答】解:根据频率分布直方图中频率和为1,得;10(2a+3a+7a+6a+2a)=1,解得a=;∴模块测试成绩落在[50,70)中的频率是10(2a+3a)=50a=50×=,∴对应的学生人数是100×=25.故答案为:25.12.(5分)设某几何体的三视图如图,则该几何体的体积为4【解答】解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,棱锥的底面面积S==6,棱锥的高h=2,故棱锥的体积V==4,故答案为:4.13.(5分)已知点P(x,y)的坐标满足条件点O为坐标原点,那么|OP|的最大值等于.【解答】解:作出不等式组对应的平面区域如右图所示,则OB的距离最大,由,即,即B(1,3),则.故答案为:.14.(5分)纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以A0,A1,A2,B1,B2,…等标记来表示纸张的幅面规格.复印纸幅面规格只采用A系列和B系列,其中An(n∈N,n≤8)系列的幅面规格为:①A0,A1,A2,…,A8所有规格的纸张的幅宽(以x表示)和长度(以y表示)的比例关系都为;②将A0纸张沿长度方向对开成两等分,便成为A1规格,A1纸张沿长度方向对开成两等分,便成为A2规格,…,如此对开至A8规格.现有A0,A1,A2,…,A8纸各一张.若A4纸的宽度为2dm,则A0纸的面积为64dm2;这9张纸的面积之和等于dm2.【解答】解:可设A i纸张的长度为y i,i=0,1, (8)由A4纸的宽度为2dm,且纸张的幅宽和长度的比例关系都为,可得y4=2,由题意可得y0=2•24=32,即有A0纸的面积为32×2=64dm2;由A0,A1,A2,…,A8纸9张纸的面积构成一个以64为首项,为公比的等比数列,可得这9张纸的面积之和为=dm2.故答案为:64,.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知等差数列{a n}的前n项和为S n,且满足a1=2,S3=12.(I)求数列{a n}的通项公式;(II)若a3,a k,S k成等比数列,求正整数k的值.+1【解答】(共13分)解:(Ⅰ)设数列{a n}的公差为d,由题意知a2+a3=10,即2a1+3d=10,由a1=2,解得d=2.所以a n=2+2(n﹣1)=2n,即a n=2n,n∈N*.…(6分)(Ⅱ)由(Ⅰ)可得,所以.又a3=2×3=6,a k+1=2(k+1),由已知可得,即(2k+2)2=6(k2+k),整理得k2﹣k﹣2=0,k∈N*.解得k=﹣1(舍去)或k=2.故k=2.…(13分)16.(13分)已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)在一个周期内的部分对应值如下表:(Ⅰ)求f(x)的解析式;(Ⅱ)求函数g(x)=f(x)+2sinx的最大值和最小值.【解答】解:(Ⅰ)由表格可知,f(x)的周期,所以.又由sin(2×0+φ)=1,且0<φ<2π,所以.所以.…(6分)(Ⅱ)g(x)=f(x)+2sinx=cos2x+2sinx=1﹣2sin2x+2sinx=.由sinx∈[﹣1,1],所以当时,g(x)有最大值;当sinx=﹣1时,g(x)有最小值﹣3.…(13分)17.(13分)某中学从高三男生中随机抽取100名学生的身高,将数据整理,得到的频率分布表如下所示.(Ⅰ)求出频率分布表中①和②位置上相应的数据;(Ⅱ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样抽取6名学生进行体能测试,求第3,4,5组每组各抽取多少名学生进行测试?(Ⅲ)在(Ⅱ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求:第4组中至少有一名学生被抽中的概率.组号分组频数频率第1组[160,165)50.050第2组[165,170)①0.350第3组[170,175)30②第4组[175,180)200.200第5组[180,185]100.100合计100 1.00【解答】(共13分)(Ⅰ)由题可知,第2组的频数为0.35×100=35人,第3组的频率为.解:即①处的数据为35,②处的数据为0.300.…(3分)(Ⅱ)因为第3,4,5组共有60名学生,所以利用分层抽样,在60名学生中抽取6名学生,每组分别为:第3组:人;第4组:人;第5组:人.所以第3,4,5组分别抽取3人,2人,人.…(6分)(Ⅲ)设第3组的3位同学为A1,A2,A3,第4组的2位同学为B1,B2,第5组的位同学为C1,则从6位同学中抽两位同学有15种可能,分别为:(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),(A3,C1),(B1,B2),(B1,C1),(B2,C1).其中第4组的两位同学至少有一位同学被选中的有:(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,C1),(B2,C1),(B1,B2)9种可能.所以第4组的两位同学至少有一位同学被选中的概率P=.…(13分)18.(13分)如图,在四棱锥E﹣ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=3AB.(Ⅰ)求证:平面ACE⊥平面CDE;(Ⅱ)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出的值;若不存在,说明理由.【解答】(共13分)证明:(Ⅰ)因为CD⊥平面ADE,AE⊂平面ADE,所以CD⊥AE.又因为AE⊥DE,CD∩DE=D,所以AE⊥平面CDE.又因为AE⊂平面ACE,所以平面ACE⊥平面CDE.…(7分)(Ⅱ)在线段DE上存在一点F,且,使AF∥平面BCE.设F为线段DE上一点,且.过点F作FM∥CD交CE于M,则.因为CD⊥平面ADE,AB⊥平面ADE,所以CD∥AB.又FM∥CD,所以FM∥AB.因为CD=3AB,所以FM=AB.所以四边形ABMF是平行四边形.所以AF∥BM.又因为AF⊄平面BCE,BM⊂平面BCE,所以AF∥平面BCE.…(13分)19.(14分)已知函数f(x)=x﹣ae x,a∈R.(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线的方程;(Ⅱ)若曲线y=f(x)与x轴有且只有一个交点,求a的取值范围;(Ⅲ)设函数g(x)=x3,请写出曲线y=f(x)与y=g(x)最多有几个交点.(直接写出结论即可)【解答】解:(Ⅰ)当a=1时,f(x)=x﹣e x,f′(x)=1﹣e x.当x=0时,y=﹣1,又f′(0)=0,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=﹣1;(Ⅱ)由f(x)=x﹣ae x,得f′(x)=1﹣ae x.当a≤0时,f'(x)>0,此时f(x)在R上单调递增;当x=a时,f(a)=a﹣ae a=a(1﹣e a)≤0,当x=1时,f(1)=1﹣ae>0,所以当a≤0时,曲线y=f(x)与x轴有且只有一个交点;当a>0时,令f'(x)=0,得x=﹣lna.f(x)与f'(x)在区间(﹣∞,+∞)上的情况如下:若曲线y=f(x)与x轴有且只有一个交点,则有f(﹣lna)=0,即﹣lna﹣a e﹣lna=0.解得.综上所述,当a≤0或时,曲线y=f(x)与x轴有且只有一个交点;(Ⅲ)曲线f(x)=x﹣ae x与曲线g(x)=x3最多有3个交点.20.(14分)已知椭圆C:=1(a>b>0)过点,且满足a+b=3.(Ⅰ)求椭圆C的方程;(Ⅱ)斜率为的直线交椭圆C于两个不同点A,B,点M的坐标为(2,1),设直线MA与MB的斜率分别为k1,k2.①若直线过椭圆C的左顶点,求此时k1,k2的值;②试探究k1+k2是否为定值?并说明理由.【解答】(共14分)解:(Ⅰ)由椭圆过点,则.又,故.所以椭圆C的方程为.…(4分)(Ⅱ)①若直线过椭圆的左顶点,则直线的方程是,由解得或故,.…(8分)②k1+k2为定值,且k1+k2=0.设直线的方程为.由消y ,得x 2+2mx +2m 2﹣4=0.当△=4m 2﹣8m 2+16>0,即﹣2<m <2时,直线与椭圆交于两点. 设A (x 1,y 1).B (x 2,y 2),则x 1+x 2=﹣2m ,.又,,故=.又,,所以(y 1﹣1)(x 2﹣2)+(y 2﹣1)(x 1﹣2)==x 1x 2+(m ﹣2)(x 1+x 2)﹣4(m ﹣1)=2m 2﹣4+(m ﹣2)(﹣2m )﹣4(m ﹣1)=0. 故k 1+k 2=0.…(14分)赠送—高中数学知识点二次函数(1)一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容,这部分知识在初中代数中虽有所涉及,但尚不够系统和完整,且解决的方法偏重于二次方程根的判别式和根与系数关系定理(韦达定理)的运用,下面结合二次函数图象的性质,系统地来分析一元二次方程实根的分布.设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ,且12x x ≤.令2()f x ax bx c =++,从以下四个方面来分析此类问题:①开口方向:a ②对称轴位置:2bx a=-③判别式:∆ ④端点函数值符号. ①k <x 1≤x 2 ⇔②x 1≤x 2<k ⇔③x 1<k <x 2 ⇔ af (k )<0)(<k f xy1x 2x 0>a O∙kx y1x 2x O∙k<a 0)(>k f④k 1<x 1≤x 2<k 2 ⇔xy1x 2x 0>a O ∙∙1k2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O∙<a 1k ∙2k 0)(1<k f 0)(2<k f ab x 2-=⑤有且仅有一个根x 1(或x 2)满足k 1<x 1(或x 2)<k 2 ⇔f (k 1)f (k 2)<0,并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合⑥k 1<x 1<k 2≤p 1<x 2<p 2 ⇔ 此结论可直接由⑤推出.(5)二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值设()f x 在区间[,]p q 上的最大值为M ,最小值为m ,令01()2x p q =+. (Ⅰ)当0a >时(开口向上) ①若2b p a -<,则()m f p = ②若2b p q a ≤-≤,则()2b m f a =- ③若2b q a->,则()m f q =①若02b x a -≤,则()M f q = ②02b x a->,则()M f p =(Ⅱ)当0a <时(开口向下) ①若2b p a -<,则()M f p = ②若2b p q a ≤-≤,则()2b M f a =- ③若2b q a->,则()M f q =①若02b x a -≤,则()mf q = ②02b x a->,则()m f p =. xxxx>O-=f (p) f (q)()2b f a-0x x>O -=f(p) f(q)()2b f a-0x xf xfxx<O-=f (p)f(q)()2b f a-x x<O-=f (p)f (q)()2b f a-x。
北京市东城区普通校2015届高三11月联考数学

北京市东城区普通校2015届高三11月联考数学(理)试题 命题校:北京市第五十中学分校 2014年11月本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷一、 选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 集合2{6},{30}A x x B x x x =∈≤=∈->N|R|,则A B =A.}5,4,3{B.}6,5,4{C.}63/{≤<x xD. }63/{<≤x x2. 复数11i+在复平面上对应的点的坐标是 A . ),(11 B .),(11- C .)(1,1-- D .)(1,1- 3. 已知{}n a 为等差数列,其前n 项和为n S ,若36a =,312S =,则公差d 等于A. 1B.53C. 2D. 3 4.”1“>x 是”1“2>x 的 A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 5. 已知角α的终边经过点53cos 且)4,(-=-αm P ,则m 的值为 A. 3 B. -3 C. 3± D. 5第Ⅱ卷二、 填空题:本大题共6小题,每小题5分,共30分。
11. 已知命题022,:0200≤++∈∃x x R x P ,那么该命题的否定是_____________.12. 已知53),sin ,2(=∈αππα,则)4tan(πα+=_____________. 13. 若等比数列}{n a 满足40,205342=+=+a a a a ,,则公比=q _________; 前n 项和=n S _______________________.14.函数)22,0)(sin(2)(πϕπωϕω<<->+=x x f 的 部分图象如图所示,则ω=______________;ϕ=____________________.15. 若函数⎪⎩⎪⎨⎧≥<<≤≤=232121022x x x x x f ,,,)(,则)3(f =_______________,函数的的值域是 .16. 在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数)(x f 的图像恰好通过)(*∈N n n 个整点,则称函数)(x f 为n 阶整点函数,有下列函数:① xx f 2sin )(= ② 3)(x x g = ③ x x h )31()(= ④x x ln )(=ϕ其中,是一阶整点函数的是_____________________.东城区普通校2014-2015学年第一学期联考试卷答案高三数学(理科)命题校:北京市第五十中学分校 2014年11月第Ⅰ卷三、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,只有一项是符合题目要求的.题号 1 2 3 4 5答案 B D C A A第Ⅱ卷四、填空题:本大题共6小题,每小题5分,共30分.。
2015-2016东城区第一学期期末数学文科答案定稿

东城区2015-2016学年第一学期期末教学统一检测高三数学参考答案及评分标准 (文科)一、选择题(本大题共8小题,每小题5分,共40分)(1) C (2)C (3)D (4)A (5)B (6)B (7)C (8)D 二、填空题(本大题共6小题,每小题5分,共30分) (9)54(10)1 5 (11)25 (12)4(13)(14) 注:两个空的填空题第一个空填对得3分,第二个空填对得2分. 三、解答题(本大题共6小题,共80分) (15)(共13分)解:(Ⅰ)设数列{}n a 的公差为d ,由题意知2310a a +=,即12+310a d =,由12a = ,解得2d =.所以22(1)2n a n n =+-=,即2n a n = ,n *∈N . ………………………………6分 (Ⅱ)由(Ⅰ)可得2(22)2n n nS n n +==+,所以2k S k k =+. 又3236a =⨯=,12(1)k a k +=+,由已知可得213k k a a S +=,即22(22)6()k k k +=+,整理得 220k k --=,*k ∈N . 解得1k =-(舍去)或2k =.故2k =. ………………………………13分(16)(共13分)解:(Ⅰ)由表格可知,()f x 的周期()22T ππ=--=π, 所以22ωπ==π. 又由()sin 201ϕ⨯+=,且02ϕ<<π,所以2ϕπ=. 所以()sin(2)cos 22f x x x π=+=. ………………………………6分 (Ⅱ)2()()2sin cos 22sin 12sin 2sin g x f x x x x x x =+=+=-+2132(sin )22x =--+. 由sin [1,1]x ∈-,所以当1sin 2x =时,()g x 有最大值32; 当sin 1x =-时,()g x 有最小值3-. ………………………………13分(17)(共13分)解:(Ⅰ)由题可知,第2组的频数为0.3510035⨯=人,第3组的频率为300.300100=. 即①处的数据为35,②处的数据为0.300. ………………………………3分(Ⅱ)因为第3,4,5组共有60名学生,所以利用分层抽样,在60名学生中抽取6名学生,每组分别为:第3组:306360⨯=人;第4组:206260⨯=人;第5组:106160⨯=人. 所以第3,4,5组分别抽取3人,2人,1人. ………………………………6分 (Ⅲ)设第3组的3位同学为1A ,2A ,3A ,第4组的2位同学为1B ,2B ,第5组的1位同学为1C ,则从6位同学中抽两位同学有15种可能,分别为: 12(,)A A ,13(,)A A ,11(,)A B ,12(,)A B ,11(,)A C ,23(,)A A ,21(,)A B ,22(,)A B ,21(,)A C ,31(,)A B ,32(,)A B ,31(,)A C ,12(,)B B ,11(,)B C ,21(,)B C .其中第4组的两位同学至少有一位同学被选中的有: 11(,)A B ,12(,)A B ,21(,)A B ,22(,)A B ,31(,)A B ,32(,)A B ,11(,)B C ,21(,)B C ,12(,)B B 9种可能.所以第4组的两位同学至少有一位同学被选中的概率P =93155=. ………………………13分 (18)(共13分)证明:(Ⅰ)因为CD ⊥平面ADE ,AE ⊂平面ADE ,所以CD AE ⊥. 又因为AE DE ⊥,CDDE D =,所以AE ⊥平面CDE .又因为AE ⊂平面ACE ,所以平面ACE ⊥平面CDE . ………………………………7分(Ⅱ)在线段DE 上存在一点F ,且13EF ED =,使AF 平面BCE .设F 为线段DE 上一点, 且13EF ED =. 过点F 作FMCD 交CE 于M ,则13FM CD =.因为CD ⊥平面ADE ,AB ⊥平面ADE , 所以CDAB .又FM CD ,所以FMAB .因为3CD AB =,所以FM AB =. 所以四边形ABMF 是平行四边形. 所以AFBM .又因为AF ⊄平面BCE ,BM ⊂平面BCE , 所以AF平面BCE . ………………………………13分(19)(共14分)解:(Ⅰ)当1a =时,()e xf x x =-,()1e xf x '=-.当0x =时,1y =-,又(0)0f '=,所以曲线()y f x =在点(0,(0))f 处的切线方程为1y =-. ………………………………4分(Ⅱ)由()e xf x x a =-,得()1e xf x a '=-.当0a ≤时,()0f x '>,此时()f x 在R 上单调递增.当x a =时,()e (1e )0a af a a a a =-=-≤,当1x =时,(1)1e >0f a =-,所以当0a ≤时,曲线()y f x =与x 轴有且只有一个交点; …………………8分 当0a >时,令()0f x '=,得ln x a =-.()f x 与()f x '在区间(,)-∞+∞上的情况如下:ABCED FM若曲线()y f x =与x 轴有且只有一个交点,则有(ln )0f a -=,即ln ln e0aa a ---=.解得1ea =.综上所述,当0a ≤或1ea =时,曲线()y f x =与x 轴有且只有一个交点. …………………12分 (Ⅲ)曲线()e xfx x a =-与曲线3()g x x =最多有3个交点. …………………14分(20)(共14分)解:(Ⅰ)由椭圆过点(0,则b =又a b += 故a =所以椭圆C 的方程为12822=+y x . ………………………………4分(Ⅱ)① 若直线过椭圆的左顶点,则直线的方程是1:2l y x =由2212182y x x y ⎧=+⎪⎪⎨⎪+=⎪⎩解得110x y =⎧⎪⎨=⎪⎩,或220.x y ⎧=-⎪⎨=⎪⎩ 故2121--=k ,2122-=k . ………………………………8分 ②21k k + 为定值,且021=+k k . 设直线的方程为m x y +=21. 由2212182y x m x y ⎧=+⎪⎪⎨⎪+=⎪⎩,消y ,得042222=-++m mx x . 当0168422>+-=∆m m ,即22<<-m 时,直线与椭圆交于两点.设),(11y x A .),(22y x B ,则122x x m +=-,42221-=m x x .又21111--=x y k ,21222--=x y k , 故2121221121--+--=+x y x y k k =)2)(2()2)(1()2)(1(211221----+--x x x y x y . 又m x y +=1121,m x y +=2221, 所以)2)(1()2)(1(1221--+--x y x y )2)(121()2)(121(1221--++--+=x m x x m x)1(4))(2(2121--+-+=m x x m x x 0)1(4)2)(2(422=----+-=m m m m .故021=+k k . ………………………………14分。
2015年北京市高考数学试卷(文科)(解析版)
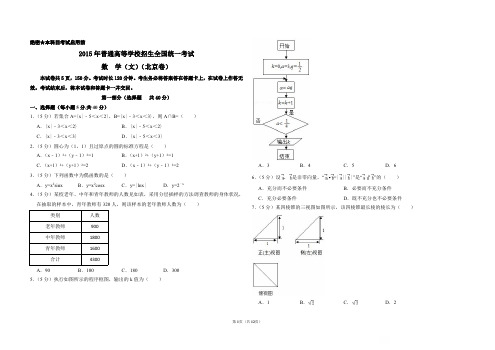
C.充分必要条件
D.既不充分也不必要条件
在抽取的样本中,青年教师有 320 人,则该样本的老年教师人数为( )
7.(5 分)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
类别
人数
老年教师
900
中年教师
1800
青年教师
1600
合计
4300
A.90
B.100
C.180
5.(5 分)执行如图所示的程序框图,输出的 k 值为(
2.(5 分)圆心为(1,1)且过原点的圆的标准方程是( )
A.(x﹣1)2+(y﹣1)2=1
B.(x+1)2+(y+1)2=1
C.(x+1)2+(y+1)2=2
D.(x﹣1)2+(y﹣1)2=2
【考点】J1:圆的标准方程. 菁优网版 权所有
【专题】11:计算题;5B:直线与圆. 【分析】利用两点间距离公式求出半径,由此能求出圆的方程. 【解答】解:由题意知圆半径 r= , ∴圆的方程为(x﹣1)2+(y﹣1)2=2. 故选:D. 【点评】本题考查圆的方程的求法,解题时要认真审题,注意圆的方程的求法,是基础题.
(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大?
19.(13 分)设函数 f(x)= ﹣klnx,k>0. (1)求 f(x)的单调区间和极值; (2)证明:若 f(x)存在零点,则 f(x)在区间(1, ]上仅有一个零点.
20.(14 分)已知椭圆 C:x2+3y2=3,过点 D(1,0)且不过点 E(2,1)的直线与椭圆 C 交于 A, B 两点,直线 AE 与直线 x=3 交于点 M.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年北京东城高三一模数学(文科)试题及答案
北京市东城区2014-2015学年度第二学期综合练习(一)
高三数学 (文科)
本试卷共5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
一、选择题(共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题
目要求的一项)
(1)在复平面内,复数12i z =-对应的点的坐标为
(A )(1,2) (B )(2,1)
(C ) (1,2)- (D )(2,1)-
(2)双曲线2
21
4x y -=的渐近线方程为
(A )
12y x =± (B )3y x =± (C )2y x =± (D )5y x =±
(3)记函数)(x f 的导函数为)(x f ',若()f x 对应的曲线在点))(,(00x f x 处的切线方程为
1y x =-+,则
(A )0()=2f x '
(B )0()=1f x ' (C )0)(0='x f (D )0()=1f x '-
(4)已知命题p :直线a ,b 不相交,命题q :直线a ,b 为异
面直线,则p 是q 的
(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D )既不充分也不必要条件
(5)在区间[0,2]上随机取一个实数x ,则事件“310x -<”发生
的概率为
(A )1
2 (B )13
(C )1
4
(D )16
(6)执行如图所示的程序框图,若输出的b 的值为4,
则图中判断框内①处应填
(A )2 (B )3
(C )4 (D )5
(7)设集合
1,(,) 1.x y D x y x y ⎧⎫+≥⎧⎪⎪=⎨⎨⎬-≤⎩⎪⎪⎩⎭,则下列命题中正确的是 (A )(,)x y ∀D ∈,20x y -≤
(B )(,)x y ∀D ∈,22x y +≥- (C )(,)x y ∀D ∈,2x ≥ (D )(,)x y ∃D ∈,1y ≤-
(8)某学校餐厅每天供应500名学生用餐,每星期一有A ,B 两种菜可供选择.调查资料表明,凡是在星期一选A 种菜的学生,下星期一会有20%改选B 种菜;而选B 种菜的学生,下星期一会有30%改选A 种菜.用
n a ,n b 分别表示在第n 个星期的星期一选A 种菜和选B 种菜的学生人数,若1300a =,则+1n a 与n a 的关系可以表示为
(A )111502n n a a +=+ (B )112003n n a a +=+
(C )113005n n a a +=+ (D )121805n n a a +=+
第Ⅱ卷(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分。
(9)已知集合{}1A =,{}1,21B m =--,若A ≠⊂B ,则实数m 的值为 .
(10)将函数
()sin(2)3f x x π=+的图象向右平移6π个单位后所得图象对应的解析式为 .
(11)在矩形ABCD 中,AB =(1,3)-,(,2)AC k =-,则实数k = .
(12)已知函数()f x 的对应关系如下表所示,数列{}n a 满足1
3a =,1()n n a f a +=,则4a = ,
2015a = . x
1 2 3 ()f x
3
2 1 (13)函数()f x 是定义在R 上的偶函数,且满足(2)()f x f x +=.当[0x ∈,1]时,
()2f x x =.若在区间[2-,3]上方程+2()0ax a f x -=恰有四个不相等的实数根,则实数a 的取值范围是________.
(14)C 是曲线
21(10)y x x =--≤≤上一点,CD 垂直于y 轴,D 是垂足,点A 的坐标是1,0-().设CAO θ∠=(其中O 表示原点),将AC CD +表示成关于θ的函数()f θ,则()f θ= ,()f θ的最大值为 .
三、解答题(共6小题,共80分。
解答应写出文字说明,演算步骤或证明过程)
(15)(本小题共13分)
下面的茎叶图记录了甲、乙两组各5名学生在一次英语听力测试中的成绩(单位:分).
甲组
乙组 9
0 9 x 2
1 5 y 8 7
4 2 4 已知甲组数据的中位数为13,乙组数据的平均数是16.8.
(Ⅰ)求x ,y 的值; (Ⅱ)从成绩不低于10分且不超过20分的学生中任意抽取3名,求恰有2名学生在乙组的概率.
(16)(本小题共13分)
在△ABC 中,sin 3cos 2A A +=.
(Ⅰ)求A 的大小;
(Ⅱ)现给出三个条件:①2a =; ②45B =;③3c b =.
试从中选出两个可以确定△ABC 的条件,写出你的选择并以此为依据求△ABC 的面积 (只需写出一个选定方案即可,选多种方案以第一种方案记分) .
(17)(本小题共14分)
如图甲,⊙O 的直径2AB =,圆上两点,C D 在直径AB 的两侧,且CBA ∠3DAB π
=∠=.沿直径AB 将半圆ACB 所在平面折起,使两
个半圆所在的平面互相垂直(如图乙).F 为BC 的中点,E 为AO 的
中点.
(Ⅰ)求证 :CB DE ⊥;
(Ⅱ)求三棱锥C BOD -的体积;
(Ⅲ)在劣弧BD 上是否存在一点G ,使得FG ∥平面ACD ?若存
在,试确定点G 的位置;
若不存在,请说明理由.
(18)(本小题共14分) 已知1x =是函数()2ln b f x
x x x
=+
+的一个极值点. (Ⅰ)求实数b 的值;
(Ⅱ)求()f x 的单调递减区间; (Ⅲ)设函数3()()g x f x x
=-
,试问过点2(,5)可作多少条直线与曲线()y g x =相切?请说明理由.
(19)(本小题共13分)
图乙
已知椭圆C :()222210x y a b a b
+=>>的左、右焦点分别为1F ,2F ,离心率为12,M 为椭圆上任意一点且△12MF F 的周长等于6.
(Ⅰ)求椭圆C 的方程;
(Ⅱ)以M 为圆心,1MF 为半径作圆M ,当圆M 与直线 l 4x =:有公共点时,求△
12MF F 面积的最大值.
(20)(本小题共13分)
已知等差数列{}n a 中错误!未找到引用源。
,1
5a =,2474a a =,数列{}n b 前n 项和为n S ,且2(1)n n S b =-n *∈N ().
(Ⅰ)求数列{}n a 和{}n b 的通项公式;
(Ⅱ)设数列
,,n n n a n c b n ⎧=⎨⎩为奇数为偶数,,求{}n c 错误!未找到引用源。
的前n 项和n T ; (Ⅲ)把数列{}n a 和{}n b 的公共项从小到大排成新数列{}n d ,试写出1d ,2d ,并证明{}n d 为等比数列.。
