假设检验汇总表
新课标高中数学知识点总结汇总表

新课标高中数学知识点总结汇总表一、函数与导数1. 函数基础- 函数的概念与表示法- 函数的性质:定义域、值域、单调性、奇偶性、周期性- 函数的运算:四则运算、复合函数、反函数、基本初等函数(幂函数、指数函数、对数函数、三角函数)2. 极限与连续- 极限的定义与性质- 无穷小与无穷大- 极限的运算法则- 函数的连续性与间断点3. 导数与微分- 导数的定义与几何意义- 导数的运算法则- 高阶导数- 隐函数与参数方程的导数- 微分的概念与应用4. 导数的应用- 函数的极值与最值问题- 曲线的切线与法线- 罗尔定理、拉格朗日中值定理、柯西中值定理- 泰勒公式与麦克劳林公式5. 不定积分- 积分的概念与性质- 基本积分表- 积分的运算法则- 特殊积分技巧:换元法、分部积分法二、平面向量与立体几何1. 平面向量- 向量的基本概念与运算- 向量的几何意义与线性运算- 向量的数量积与向量积- 平面向量的坐标表示与运算2. 立体几何- 空间几何体的性质与计算- 直线与平面的方程- 空间向量及其运算- 立体图形的表面积与体积三、解析几何1. 圆锥曲线- 圆的方程- 椭圆、双曲线、抛物线的方程与性质 - 圆锥曲线的切线与法线- 圆锥曲线的应用问题2. 参数方程与极坐标- 参数方程的概念与应用- 极坐标系与直角坐标系的转换- 简单曲线的极坐标方程四、概率与统计1. 概率论基础- 随机事件与概率的定义- 条件概率与独立事件- 全概率公式与贝叶斯公式- 随机变量与分布函数2. 统计学基础- 统计量的概念:均值、方差、标准差、中位数、众数 - 抽样与估计- 假设检验- 线性回归分析五、数学分析进阶1. 定积分- 定积分的概念与性质- 微积分基本定理- 定积分的计算方法- 定积分的应用:面积、体积、弧长、工作量2. 级数- 数项级数的概念与性质- 正项级数与收敛性判别法- 交错级数与绝对收敛- 幂级数与泰勒级数3. 多元函数微分学- 多元函数的偏导数与全微分- 多元函数的极值与最优化问题- 多重积分的概念与计算4. 常微分方程- 微分方程的基本概念- 可分离变量的微分方程- 一阶线性微分方程- 二阶常系数线性微分方程以上是新课标高中数学的主要知识点汇总,涵盖了函数、几何、概率统计以及数学分析等领域的核心内容。
假设检验汇总
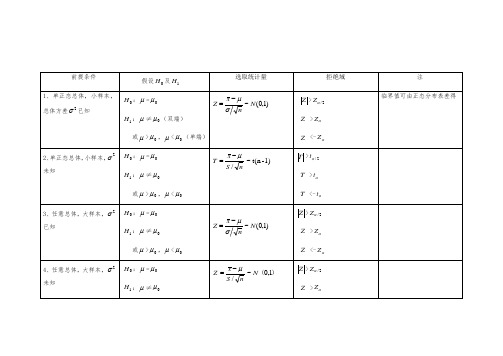
前提条件
假设 及
选取统计量
拒绝域
注
1、单正态总体,小样本,总体方差 已知
: =
: ≠ (双端)
或 > , < (单端)
>
>
<-
临界值可由正态分布表差得
2、单正态总体,小样本, 未知
: =
: ≠
或 > , <
>
>
<-
3、任意总体,大样本, 已知
: =
: ≠
或 > , <
>
>
<-
4、任意总体,大样本, 未知
选取统计量
拒绝域
注
1、双正态总体
、 已知
小样本
: =
: ≠
或 > , <
>
>
<-
拒绝域对应备择假设
2、双正态总体
、 未知
小样本,方差齐性
( = )
: =
: ≠
或 > , <
式中
>
>
<-
3、任意总体,大样本
、 未知
: =
: ≠
或 > , <
>
>
<-
4、二项总体,大样本
总体成数 - 的假设检验
: =
: ≠
: =
: ≠
或 > , <
>
>
<-
5、二分总体,大样本,总体成数 的假设检验
: =
: ≠
或 > , <
>
>
假设检验表-leycon
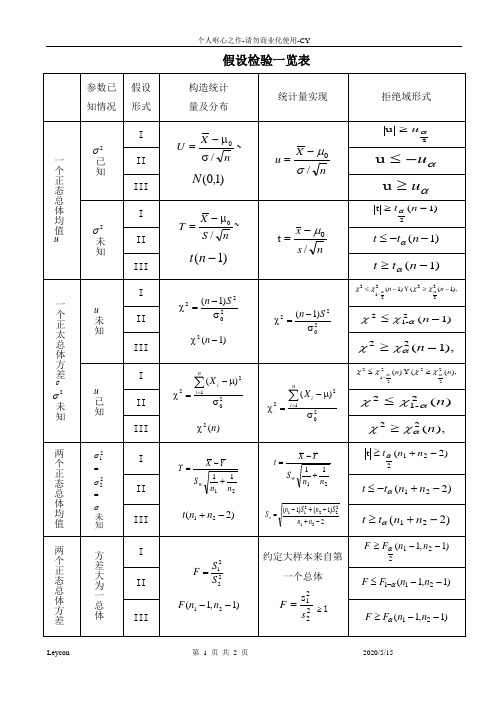
u u
t t (n 1)
2
未 知
2
T
II III I
~
t
x 0 s/ n
t t (n 1)
t (n 1)
(n 1)S 2 2 0
2
t t ( n 1)
2 2 2 (n 1) ( 2 (n 1), 1 2 2
一 个 正 太 总 体 方 差
u 未 知
II III I
2
2 (n 1)
n
(n 1)S 2 0
2
2 2 1- ( n 1)
2 2 (n 1),
未 知
2
u 已 知
II III
2
(X
i 1
i
)
2
2 2
1
2
2 (n) ( 2 (n), 2
2
方 差 大 为 一 总 体
S2 F 12 S2
F (n1 1, n2 1)
约定大样本来自第 一个总体
F F1 (n1 1, n2 1)
F
2 s1 2 1 s2
F F (n1 1, n2 1)
第 1 页 共 2 页
2012/12/27
个人呕心之作-请勿商业化使用-CY
u u
u u
2
U
X 0 S/ n
~ N (0,1)
u
x 0 s/ n
u u
代 替
u u
U X Y
2 2 S1 S 2 n1 n 2
u u
u x y
2 2 s1 s 2 n1 n2
正态分布总体的区间估计与假设检验汇总表
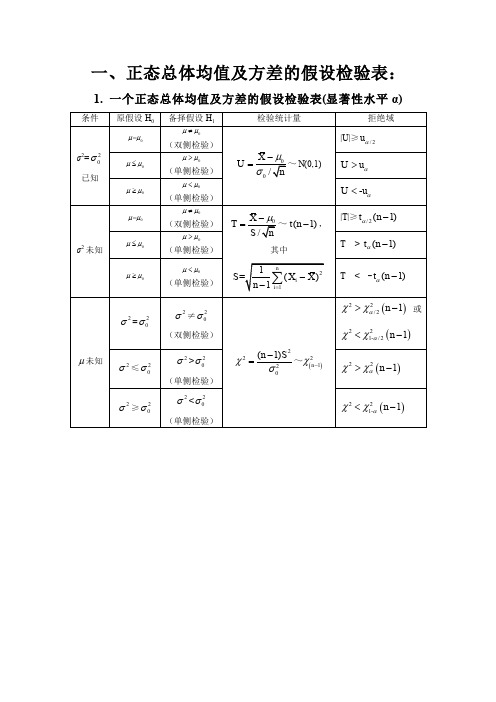
(单侧检验)
2
(n
1)S 2
2 0
~2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
(单侧检验)
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
,
2 2
已知
1 =2 1 2 1 2
1 2
1 2
(单侧检验)
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1,2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
(双侧检验)
2 1
>
2 2
(单侧检验)
F
S12 S22
~
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ~ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
~2n1
(n 2 /
1)S 2
质量检验报告汇总表
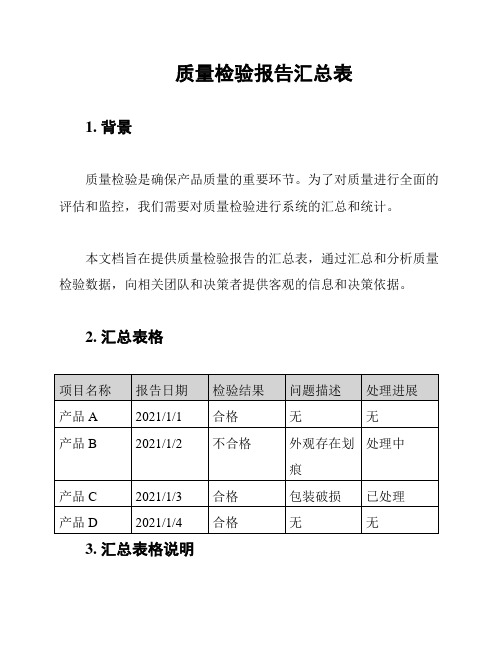
质量检验报告汇总表1. 背景质量检验是确保产品质量的重要环节。
为了对质量进行全面的评估和监控,我们需要对质量检验进行系统的汇总和统计。
本文档旨在提供质量检验报告的汇总表,通过汇总和分析质量检验数据,向相关团队和决策者提供客观的信息和决策依据。
2. 汇总表格3. 汇总表格说明- 项目名称:记录所检验的产品或相关项目的名称。
项目名称:记录所检验的产品或相关项目的名称。
- 报告日期:指该次检验报告的日期。
报告日期:指该次检验报告的日期。
- 检验结果:指该次检验的结果,可以是“合格”、“不合格”等。
检验结果:指该次检验的结果,可以是“合格”、“不合格”等。
- 问题描述:若检验结果为“不合格”或存在问题,记录问题描述,例如外观划痕、包装破损等。
问题描述:若检验结果为“不合格”或存在问题,记录问题描述,例如外观划痕、包装破损等。
- 处理进展:记录对存在问题的处理进展,可以是“无”(没有问题)、“处理中”、“已处理”等。
处理进展:记录对存在问题的处理进展,可以是“无”(没有问题)、“处理中”、“已处理”等。
4. 使用指南4.1 产品质量评估通过查看汇总表格中的检验结果,可以直观地了解产品的质量状况。
对于“合格”产品,可以放心地进行下一步处理或销售;而对于“不合格”产品,则需要及时处理和修复相关问题,确保产品质量符合标准。
4.2 问题处理跟踪通过查看汇总表格中的问题描述和处理进展,可以追踪和记录存在问题的处理情况。
团队成员或负责人可以根据表格中的信息,及时采取措施解决问题,确保质量问题能够被有效解决和追踪。
5. 结论通过质量检验报告汇总表,我们能够全面了解产品的质量状况,并及时跟踪和处理存在的问题。
这有助于提高产品质量、增强客户满意度,并为决策者提供参考,为质量管理提供有效支持。
请团队成员和决策者密切关注汇总表格,并及时进行问题处理和改进操作,以提升产品质量和效率。
如有任何问题或需要进一步的信息,请随时联系相关负责人。
3试验三、用Excel进行假设检验

H0:新肥料比对照每亩增收不到5kg,最多5kg,即
H 0:μd 5 ;对HA : 新肥料比对照每亩可增收5kg以上,即
显著水平 α 0.05 。 测验计算:d (6.8 6.2 5.9) / 9 50.5/ 9 5.61(公斤/亩 )
6.82 6.22 5.92 (50.5) 2 / 9 sd 0.70(公 斤 /亩 ) 9 (9 1)
160 200 160 200
170
270 180 250 270
即喷矮壮素的株高较未喷的为矮,
作一尾测验。 显著水平 =0.05。
170
150 210
290
270 230 170
测验计算: y 1=176.3cm SS1=3787.5
2 故有 se
y 2 =233.3cm
SS2=18400
给予不同处理,则所得观察值为成对数据。 在分析试验结果时,只要假设两样本的总体差数的平均 数 d 1 2 0,而不必假定两样本的总体方差 12 和 2 相同。
2
设两个样本的观察值分别为y1和 y2 ,共配成n对,各个对 的差数为 d =y1-y2,差数的平均数为 d y1 y 2 ,则差数平 均数的标准误 s
t 双尾临界
2.306004
作业:
课本例题:例题5-2(P78);例题5-4(P80);
例题5-5(P81);例题5-7(P83)。 2、课后习题(P111):习题5.5 实验报告: 实验报告五、课后习题(P111):习题5.6; 实验报告六、课后习题(P111):习题5.7;
428 440 t 1.08 11.136
查附表4,v=4+4=8时, t0.05=2.306。
统计工具箱中的假设检验表
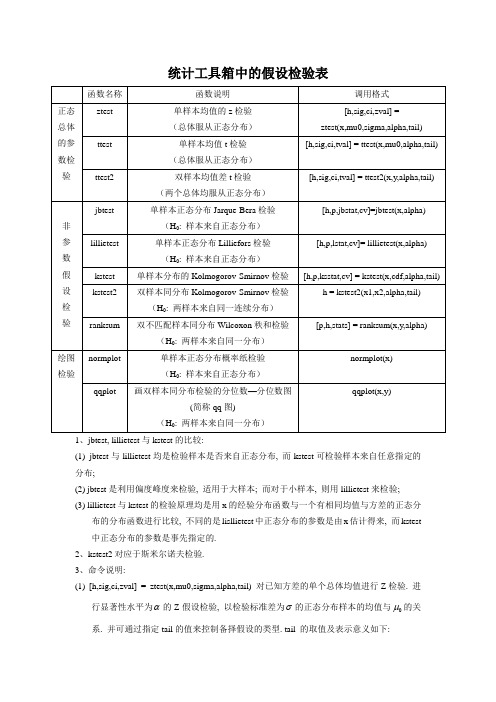
统计工具箱中的假设检验表1、jbtest, lillietest与kstest的比较:(1) jbtest与lillietest均是检验样本是否来自正态分布, 而kstest可检验样本来自任意指定的分布;(2) jbtest是利用偏度峰度来检验, 适用于大样本; 而对于小样本, 则用lillietest来检验;(3) lillietest与kstest的检验原理均是用x的经验分布函数与一个有相同均值与方差的正态分布的分布函数进行比较, 不同的是lisllietest中正态分布的参数是由x估计得来, 而kstest 中正态分布的参数是事先指定的.2、kstest2对应于斯米尔诺夫检验.3、命令说明:(1) [h,sig,ci,zval] = ztest(x,mu0,sigma,alpha,tail) 对已知方差的单个总体均值进行Z检验. 进行显著性水平为α的Z假设检验, 以检验标准差为σ的正态分布样本的均值与0μ的关系. 并可通过指定tail的值来控制备择假设的类型. tail 的取值及表示意义如下:tail=0 备择假设为0μμ≠ (缺省值);tail=1备择假设为0μμ>;tail= -1备择假设为0μμ<.(原假设则为00:H μμ≥) ·输出变量含义:h ——如果h=0, 则接受0H ; 如果h=1, 则拒绝0H 而接受备择假设1H ;sig ——Z 的观察值在00:H μμ=下较大或统计意义上较大的概率值;ci ——方差2σ未知时均值μ的1α-的置信区间.zval ——Z 统计量x Z=的观测值. ·单边检验对应单侧区间估计.(2) [h,sig,ci,tval] = ttest(x,mu0,alpha,tail) 格式调用中无“tval ”这个输出变量, 但可加上此项.tval ——包含两个结果: tstat 表示t 统计量x t=; df 表示t 分布的自由度. (3) [h,p,jbstat,cv] = jbtest(x,alpha) 对“单个总体服从正态分布(未指定均值和方差)”假设进行显著水平为α的Jarque-Bera 检验. 此检验基于x 的偏度与峰度. 对于真实的正态分布, 样本偏度应接近于0, 样本峰度应接近于3. Jarque-Bera 检验通过2χ统计量来判定样本偏度和峰度是否与它们的期望值显著不同.·输出变量含义:h ——如果h=0, 则接受“0H : 认为x 来自正态总体”; 如果h=1, 则接受备择假设“1H :认为x 不是来自正态总体”;p ——检验的概率p-值;jbstat ——检验统计量的值;cv ——判断是否拒绝原假设的关键值.(4) [h,p,ksstat,cv] = kstest(x,cdf,alpha,tail) 对“x 的总体服从由两列矩阵cdf 指定的分布G ”假设进行显著水平为α的Kolmogorov-Smirnov 检验. 矩阵cdf 的第一列包含可能的x 值, 第二列包含相应的理论累积分布函数值G(x0). 在可能的情况下, 应定义cdf 使每一列包含x 中的值. 如果cdf=[ ], kstest( )将使用标准正态分布.(5) [h,p,ksstat] = kstest2(x1,x2,,alpha,tail) 对“两个样本来自同一连续分布”假设进行显著水平为α的Kolmogorov-Smirnov 检验. 对于大容量的样本来说, p-值将很精确, 一般来说,当样本容量N 1和N 2满足1212(*)/()4N N N N +≥时, p-值即可认为是精确的.(6) normplot(x) 绘出x 中数据的正态检验概率图. 如果x 是一个矩阵, 则对每一列绘出一条线. 图中样本数据用符号‘+’来表示, 叠加在数据上的实线是数据的第一个与第三个四分位点之间的连线 (为样本顺序统计量的鲁棒线性拟合). 这条线延伸到样本数据的两端, 以便估计数据的线性度. 如果数据是来自一个正态分布, 则‘+’线近似地在一直线上. 一般地, 中间的点离直线位置的偏差不能过大, 两头的点的偏差可以允许大一些. 当中间的点离直线位置偏差太大时, 就认为x 来自其它分布.(7) qqplot(x,y) 绘出两样本的分位数-分位数图. 图中样本数据用符号‘+’来表示, 叠加在数据上的实线是各分布的第一个与第三个四分位点之间的连线 (为两个样本顺序统计量的鲁棒线性拟合). 这条线延伸到样本数据的两端以便估计数据的线性度. 如果两个样本来源于同一个分布, 则‘+’线近似地在一直线上.qqplot(x) 绘出样本x 的分位数-正态分布的理论分位数图. 如x 为正态分布, 则‘+’线近似地在一直线上.。
(06)第6章 假设检验(T6)PPT课件

6 - 14
7/16/2020
统计学
STATISTICS (第六版)
双侧检验与单侧检验
(假设的形式)
以总体均值的检验为例
假设
双侧检验
单侧检验 左侧检验 右侧检验
原假设 H0 : =0 H0 : 0 H0 : 0
备择假设 H1 : ≠0 H1 : <0 H1 : >0
已经成了一种 37.1 36.2 36.3 37.5 36.9
共识。下面是 一个研究人员
37.0
36.7
36.9
37.0
37.1
测量的50个健 36.6 37.2 36.4 36.6 37.3
康成年人的体 36.1 37.1 37.0 36.6 36.9
温数据
36.7 37.2 36.3 37.1 36.7
2. 所表达的含义是总体参数发生了变化或变量之间 有某种关系或总体分布于某种理论分布有差异
3. 备择假设通常用于表达研究者自己倾向于支持的 看法,然后就是想办法收集证据拒绝原假设,以 支持备择假设
alternative 4. 总是有符号 , 或 H1 : 某一数值 H1 : 某一数值 H1 : <某一数值
36.8 37.0 37.0 36.1 37.0
6-6
7/16/2020
统计学
STATISTICS (第六版)
正常人的平均体温是37oC吗?
➢ 根据样本数据计算的平均值是36.8oC ,标准差 为0.36oC
➢ 根据参数估计方法得到的健康成年人平均体温的 95%的置信区间为(36.7,36.9)。研究人员发现 这个区间内并没有包括37oC
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
m
2 2
{u u (m n 2)}
n
{ u u1 2}
{t t1 (n 1)} {t t (n 1)}t 检验ຫໍສະໝຸດ 1 2 但未知
1 2 0 1 2 0
xy t ~ t (m n 2) 1 1 Sw m n
{u u1 }
已 知
0 0 0
n
~ N (0,1)
{u u }
{ u u1 2}
{t t1 (n 1)} {t t (n 1)}
t 检验
2
未 知
0 0
{ t t1 2 (n 1)}
二、关于两个正态总体均值差的假设检验问题可汇总成如下的表: 检验名称 条件 原假设 H 0 备择假设 H 1 检验统计量及其分布 拒绝域
2
(n 1)S 2
2 0
~ 2 (n 1)
2 2 (n 1)
2 21 ( n 1) 或 2 2 (n 1) 2 2
2 2 0
2 2 0
四、关于两个正态总体方差比的假设检验问题可汇总成如下的表: 条件 原假设 H 0
{ t t1 2 (n 1)}
三、关于单个正态总体方差的假设检验问题可汇总成如下的表: 条件 原假设 H 0
2 2 0
2 2 0
备择假设 H 1
2 2 0
2 2 0
检验统计量及其分布
拒绝域
已 知
2
( xi )
i 1 2 0
n
2 12 2
2 12 2
FF
1
2
(m 1, n 1) 或 F F (m 1, n 1)
2
一、
关于单个正态总体均值的假设检验问题可汇总成如下的表: 条件 原假设 H 0 备择假设 H 1 检验统计量及其分布 拒绝域
检验名称
0
u 检验
2
0 0 0 0 0 0
t x 0 s n ~ t (n 1) u x 0
1 2 0
u 检验
1 2 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2 0
u
1 , 2
已知
xy
{u u1 (m n 2)}
~ N (0,1)
1 2 0 1 2 0 1 2 0
2 12 2
备择假设 H 1
2 12 2
检验统计量及其分布
n ( x i 1 )
i 1 n m
拒绝域
2
F F1 (m, n) F F (m, n)
1 2 已知
2 1
2 1
2 0
2 2
2 1
2 2
F
2 1
2 2
m ( y i 2 )
2
2 21 (n)
~ 2 (n)
2 2 (n)
2 21 ( n) 或 2 2 ( n) 2 2
2
2 0
2
2 0
未 知
2 2 0 2 2 0
2 2 0 2 2 0
2 21 (n 1)
i 1
2
FF
1
2
(m, n) 或 F F (m, n)
2
2 12 2
2 12 2
F F1 (m 1, n 1)
2 Sx F 2 ~ F (m 1, n 1) Sy
1 2 未知
2 1
2 0
2 1
2 2
F F (m 1, n 1)
