下数学平行四边形中的动点问题
平行线动点问题的解题技巧
平行线动点问题的解题技巧平行线动点问题是初中数学中常见的一种几何题型，也是高中数学中的重要考点之一。
这类问题常涉及到平行四边形、三角形等图形，需要运用多种定理和方法进行解题。
本文将从以下几个方面详细介绍平行线动点问题的解题技巧。
一、基本概念在介绍解题技巧之前，我们首先需要了解一些基本概念。
平行线指在同一个平面内不相交的两条直线，它们的斜率相等；动点指随着某种规律不断运动的点。
在平行线动点问题中，我们通常需要确定某个动点在运动过程中所处的位置或满足什么条件时两直线之间的距离最短等。
二、解题思路对于平行线动点问题，我们可以采用以下步骤进行分析和求解：1.画图：根据题目所给条件画出图形，并标出所需求的点或长度。
2.列出已知和未知量：根据图形标注出已知量和未知量，并列出方程或条件式。
3.确定关系式：利用几何定理或代数方法推导出各个量之间的关系式。
4.代入求解：将已知量代入关系式中，求解未知量。
三、常用定理和方法1.平行线的性质：平行线在同一平面内，它们的斜率相等。
2.三角形内角和定理：任何一个三角形的三个内角之和等于180度。
3.全等三角形的性质：两个全等的三角形对应边长相等，对应角度相等。
4.相似三角形的性质：两个相似的三角形对应边长成比例，对应角度相等。
5.勾股定理：直角三角形斜边上的正方形面积等于两腰上各自正方形面积之和。
6.垂线定理：在平面直角坐标系中，点(x,y)到直线Ax+By+C=0的距离为|Ax+By+C|/√(A²+B²)。
7.向量法求解：通过向量法求解可以简化计算过程。
利用向量叉积可判断两条线段是否相交，在一些特殊情况下可以极大地减少计算时间。
四、实例分析下面我们以一个具体例子来说明平行线动点问题的解题技巧：已知ABCD为矩形，P、Q分别在AB、CD上滑动，并且AP=PQ=QB。
若M为AC与QP交点，求证：BM=2AM。
解题思路：1.画图：如图所示，画出矩形ABCD和动点P、Q的运动轨迹。
特殊平行四边形动点问题解题技巧
特殊平行四边形动点问题解题技巧《特殊平行四边形动点问题解题技巧：和动点斗志斗勇的日子》嘿，大家好呀！今天咱就来唠唠特殊平行四边形动点问题解题技巧这档子事儿。
咱就说，遇到这种动点问题啊，就像是和一个调皮的小精灵在玩捉迷藏。
它一会儿在这儿，一会儿又跑那儿去了，让人是又好气又好笑。
但咱可不能被它给吓住，得和它斗智斗勇才行。
首先呢，咱得有双“火眼金睛”，能快速地找出题目中的关键信息。
比如这个动点的运动轨迹是啥呀，是沿着边跑，还是在对角线上蹦跶。
这就像是找到了小精灵的行动路线，心里就有底了。
然后呢，咱得学会“以静制动”。
别管它怎么动，咱就把它当成静止的来分析。
比如说，在某个时刻，它在这个位置，那这个时候的图形有啥特点，跟其他条件一结合，能得出啥结论。
嘿，就这么一分析，好像那小精灵也不那么调皮了。
还有啊，要多画画图。
有时候光靠脑子想是不行滴，得动手画出来。
看着那图形在笔下一点点呈现，感觉就像在掌控整个局面一样。
而且呀，多画几种不同时刻的图，说不定就能找到规律，那小精灵的小把戏也就不攻自破啦。
再说说解题的时候，那可得思路清晰啊。
把各种条件、结论像串珠子一样串起来，可不能乱了套。
这就好比在给小精灵设陷阱，让它乖乖地掉进咱的圈套里。
咱还得有点“大胆假设”的精神。
碰到难题别退缩，大胆地去猜测一下，说不定还就猜中了呢。
就算没猜中，那也没啥损失呀，就当给大脑做个热身运动了。
总之，面对特殊平行四边形动点问题，咱可不能怕。
就把它当成一场有趣的挑战，和那个调皮的小精灵好好过过招。
只要咱掌握了这些解题技巧，再加上一点点细心、耐心和恒心，那小精灵最后还不得乖乖就范。
所以呀，大家都别怕，大胆地去和动点战斗吧！让我们在解题的海洋里畅游，享受那份攻克难题后的喜悦和成就感！加油哦，朋友们！。
四边形中的动点问题(带答案)
四边形中的动点问题（带答案）四边形中的动点问题1、如图，把矩形ABCD沿 EF翻折，点B恰好落在AD边的B'处，若AE= 2, DE= 6,Z EFB= 60°, 则矩形ABCD勺面积是 _____________________2、如图，在四边形ABCD中对角线ACL BD 垂足为0,点E, F, G, H分别为边AD AB, BC CD 的中点•若AC= 8, BD= 6,则四边形EFGH的面积为3、如图，正方形ABCD勺边长为4,点P在DC 边上，且DP= 1,点Q是AC上一动点，则D® PQ 的最小值为 _____________________4、如图，在Rt△ ABC中，/ B= 90°,AC= 60 cm Z A= 60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D, E 运动的时间是t s(0 < t < 15) •过点D作DF 丄BC于点F,连接DE EF.(1)求证：AE= DF;(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△ DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm射线AG// BC,点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t. (1)连接EF当EF经过AC边的中点D时，(1)求证：△ ADE^A CDF：6、在菱形ABCD中，/ B=60°,点E在射线BC上运动，/ EAF=60，点F在射线CD上(1)当点E在线段BC上时(如图1)( 1)求证：EC+CF=A； (2) 当点E在BC的延长线上时(如图2),线段EC CFAB有怎样的相等关系？写出你的猜想，不需证明图1 027、如图，在菱形ABC［中, AB=2 / DAB=60 , 点E 是AD边的中点.点M是AB边上一动点（不与点A重合）,延长ME交射线CD于点N 连接MD AN（1）求证：四边形AMDI是平行四边形；（2）填空：①当AM的值为时，四边形AMD是矩形；②当AM的值为时，四边形AMD是菱形.D8 如图，△ ABC中，点0是边AC上一个动点，过0作直线MN BC 设MN交/ BCA的平分线于点E, 交/ BCA 的外角平分线于点F.(1)探究：线段0E与OF的数量关系并加以证明；(2)当点0运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形？(3)当点0在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由.9、如图，已知菱形ABC［中, / ABC=60 , AB=8 过线段BD上的一个动点P (不与B、D重合)分别向直线AB AD作垂线，垂足分别为E、F.(1)BD的长是______ ;(2)连接PC当PE+PF+P(取得最小值时，此时PB的长是_______10、如图，/ MON=9°,矩形ABCD勺顶点A B 分别在边OM ON上，当B在边ON上运动时，A随之在OMk运动，矩形ABCD勺形状保持不变，其中AB=2 BC=1运动过程中，点D到点O的最大距离为 __________________ .11、如图，已知矩形ABCD AD=4 CD=10 P是AB上一动点，M N E分别是PD PC CD的中点.(1)求证：四边形PMEI是平行四边形；(2)请直接写出当AP为何值时，四边形PMEN 是菱形；(3)四边形PMEf有可能是矩形吗？若有可能,求出AP的长；若不可能，请说明理由.12、如图，在平行四边形ABCD中，对角线BD=12cm AC=16cm AC BD相交于点0,若E, F 是AC上两动点，分别从A, C两点以相同的速度向C、A 运动，其速度为0.5cm/s。
四边形中的动点问题(带答案)
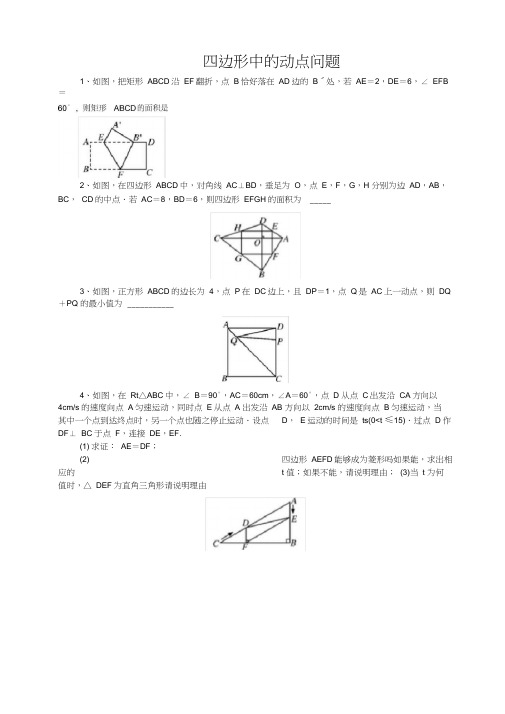
四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠ EFB ＝2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H 分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH的面积为 _____3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ ＋PQ 的最小值为___________4、如图，在Rt△ABC中，∠ B＝90°，AC＝60cm，∠A＝60°，点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动，同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts(0<t ≤15)．过点 D 作DF⊥ BC于点F，连接DE，EF.(1) 求证：AE＝DF；(2) 四边形AEFD能够成为菱形吗如果能，求出相应的t 值；如果不能，请说明理由；(3)当t 为何值时，△ DEF为直角三角形请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点 A 出发沿射线AG以1cm/s 的速度运动，同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动，设运动时间为t.（1）连接EF，当EF经过AC边的中点 D 时，（1）求证：△ ADE≌△ CDF；：（2）当t 为____ s 时，四边形ACFE是菱形；6、在菱形ABCD中，∠ B=60°，点E在射线BC上运动，∠ EAF=60°，点 F 在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点 E 在BC的延长线上时（如图2），线段EC、CF、AB 有怎样的相等关系写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠ DAB=60°，点E是AD边的中点．点M 是AB边上一动点不与点 A 重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN 是平行四边形；（2）填空：①当AM 的值为____ 时，四边形AMDN 是矩形；②当AM 的值为____ 时，四边形AMDN 是菱形．8、如图，△ ABC中，点O 是边AC上一个动点，过O 作直线MN ∥BC，设MN 交∠ BCA的平分线于点E，交∠ BCA 的外角平分线于点F．（1）探究：线段OE与OF 的数量关系并加以证明；（2）当点O 运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形（3）当点O 在边AC上运动时，四边形BCFE会是菱形吗若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD 作垂线，垂足分别为E、F．（1）BD的长是___ ；（2）连接PC，当PE+PF+PC取得最小值时，此时PB 的长是__10、如图，∠ MON=90°，矩形ABCD的顶点A、B分别在边OM，ON 上，当B在边ON 上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O 的最大距离为_____ ．11、如图，已知矩形ABCD，AD=4，CD=10，P 是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN 是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN 是菱形；（3）四边形PMEN有可能是矩形吗若有可能，求出AP 的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A 运动，其速度为／s。
平行四边形动点问题方法总结
平行四边形动点问题方法总结大家好，今天我们来聊聊平行四边形动点问题。
这个问题可大可小，有时候我们在生活中也会碰到这样的问题。
比如说，你拿着一个碗，碗口朝下放在地上，然后用一根棍子在碗里搅动，碗里的水会形成一个漩涡。
这个现象背后就隐藏着平行四边形动点问题。
那么，我们怎么解决这个问题呢？接下来，我就要给大家普及一下解决平行四边形动点问题的三大法宝：三角形法则、相似三角形法则和向量法。
我们来说说三角形法则。
三角形法则是解决平行四边形动点问题的基本方法。
它的核心思想是利用三角形的三个顶点和三条边的关系，将平行四边形分解成若干个三角形，然后分别求解这些三角形的问题，最后将结果合并起来得到原问题的解。
这个方法简单易懂，而且非常实用。
但是，有时候三角形法则并不能直接解决问题，这时候我们就需要用到第二个法宝：相似三角形法则。
相似三角形法则是解决平行四边形动点问题的另一个重要方法。
它的核心思想是利用相似三角形的性质，将平行四边形分解成若干个相似的三角形，然后分别求解这些三角形的问题，最后将结果合并起来得到原问题的解。
这个方法比三角形法则更加灵活，可以处理更多的问题类型。
但是，相似三角形法则也有它的局限性，有些问题无法用相似三角形法则解决。
这时候，我们就需要用到第三个法宝：向量法。
向量法是解决平行四边形动点问题的最高级方法。
它的核心思想是利用向量的概念，将平行四边形分解成若干个向量，然后分别求解这些向量的问题，最后将结果合并起来得到原问题的解。
这个方法非常强大，可以处理各种复杂的问题类型。
而且，向量法还有一个优点，就是它可以避免一些几何陷阱，让你在解决问题的过程中更加得心应手。
解决平行四边形动点问题有三大法宝：三角形法则、相似三角形法则和向量法。
这三大法宝各有优缺点，我们需要根据具体的问题类型来选择合适的方法。
如果你觉得这些方法还是太难了，也不用担心，我们还有很多其他的方法可以用来解决这个问题。
比如说，你可以尝试画图、列方程、用公式等等。
平行四边形中的动点问题
图形中的点、线运动，构成了数学中的一个 新问题----动态几何。它通常分为三种类型： 动点问题、动线问题、动形问题。在解这类问 题时，要充分发挥空间想象的能力，不要被 “动”所迷惑，而是要在“动”中求“静”， 化“动”为“静”，抓住它运动中的某一瞬间， 寻找确定的关系式，就能找到解决问题的途径。
本节课重点来探究动态几何中的第一种类 型----平行四边形中的动点问题。
平行四边形中的 动点问题
如图，在四边形ABCD中，AD∥BC，AD＝6，BC＝16，E是BC 的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向 点D运动；点Q同时以每秒2个单位长度的速度从点C出发， 沿CB向点B运动．点P停止运动时，点Q也随之停止运动．当 运动时间t为多少秒时，以点P，Q，E，D为顶点的四边形是 平行四边形？
A
D
M N
B
C
如图，梯形ABCD中AD//BC， ∠B=90 °AB=14cm，AD=15cm,BC=21cm，点M从A 点开始，沿AD边向D运动，速度为1cm/s，点N 从点C开始沿CB边向点B运动，速度为2cm/s， 设四边形MNCD的面积为S。（1）写出面积S 与时间t之间的函数关系式。
（2）t为何值时，四边形MNCD是平行四边形？ （3） t为何值时，四边形MNCD是等腰梯形？
（3）运动几s时，四边形APQB和四边形PDCQ的面积相等．
6-t t
2t
9-2t
如图，菱形ABCD中，E、F分别是AB、 AD边上的动点，且AE=AF. (1)在运动过程中，△CEF始终是等腰三角 形吗？
(2) △CEF能否运动成等边三角形？若能， 请说明理由。若不能，还需对四边形ABCD 添加怎样的限定条件？
ED
A
人教版八年级下册数学《平行四边形》动点问题带答案
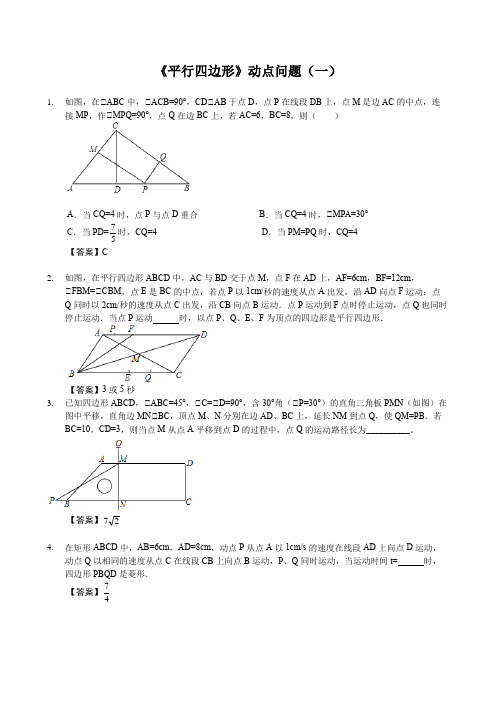
《平行四边形》动点问题（一） 1. 如图，在△ABC 中，△ACB=90°，CD△AB 于点D ，点P 在线段DB 上，点M 是边AC 的中点，连接MP ，作△MPQ=90°，点Q 在边BC 上，若AC=6，BC=8，则（ ）A ．当CQ=4时，点P 与点D 重合B ．当CQ=4时，△MPA=30°C ．当PD=57时，CQ=4 D ．当PM=PQ 时，CQ=4 【答案】C2. 如图，在平行四边形ABCD 中，AC 与BD 交于点M ，点F 在AD 上，AF=6cm ，BF=12cm ，△FBM=△CBM ，点E 是BC 的中点，若点P 以1cm/秒的速度从点A 出发，沿AD 向点F 运动；点Q 同时以2cm/秒的速度从点C 出发，沿CB 向点B 运动．点P 运动到F 点时停止运动，点Q 也同时停止运动．当点P 运动 时，以点P 、Q 、E 、F 为顶点的四边形是平行四边形．【答案】3或5秒3. 已知四边形ABCD ，△ABC=45°，△C=△D=90°，含30°角（△P=30°）的直角三角板PMN （如图）在图中平移，直角边MN△BC ，顶点M 、N 分别在边AD 、BC 上，延长NM 到点Q ，使QM=PB ．若BC=10，CD=3，则当点M 从点A 平移到点D 的过程中，点Q 的运动路径长为__________。
【答案】27△当P点有8个时，x=22-2；△当△PEF是等边三角形时，P点有4个A．△△B．△△C．△△D．△△【答案】B6.如图，在△ABCD中，AB=8cm，BC=16cm，△A=60°．点E从点D出发沿DA边运动到点A，点F从点B出发沿BC边向点C运动，点E运动速度为2cm/s，点F的运动速度为1cm/s，它们同时出发，同时停止运动，经过s时，EF=AB．7.如图，一根竹竿AB，斜靠在竖直的墙上，P是AB中点，A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置，则在竹竿AB滑动过程中OP（）A．下滑时，OP增大B．上升时，OP减小C．无论怎样滑动，OP不变D．只要滑动，OP就变化【答案】C8.如图，E是△ABCD边AD上动点，连接CE作△ECDN，过A点作AM△EN，交EN延长线于点M，作矩形AMEF，动点E从A出发，沿着AD方向运动到终点D，在整个运动变化的过程中，记△ECDN的面积为S2，矩形AMEF的面积为S1，则S1+S2大小变化情况是（）A．一直在减小B．一直不变C．先减小后增大D．先增大后减小【答案】C9. 如图，在矩形OAHC 中，OC=8，OA=12，B 为CH 中点，连接AB ．动点M 从点O 出发沿OA 边向点A 运动，动点N 从点A 出发沿AB 边向点B 运动，两个动点同时出发，速度都是每秒1个单位长度，连接CM ，CN ，MN ，设运动时间为t （秒）（0＜t ＜10）．则t= 时，△CMN 为直角三角形．【答案】27或424141 10. 如图，已知矩形ABCD ，AB=8，AD=4，E 为CD 边上一点，CE=5，点P 从B 点出发，以每秒1个单位的速度沿着BA 边向终点A 运动，连接PE ，设点P 运动的时间为t 秒，则当t 的值为 时，△PAE 是以PE 为腰的等腰三角形．动点．若点P 从点F 出发，沿F→A→D→C 的路线运动，当△FPE=30°时，FP 的长为__________。
初二数学《平行四边形中的动点问题》(附练习及答案)
四边形中的动点问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或直线上运动的一类开放性题目。
解决这类问题关键是动中求静,灵活运用有关数学知识。
数学思想：分类思想、函数思想、方程思想、数形结合思想、转化思想，其注重对几何图形运动变化能力的考查。
这类类问题从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。
选择基本的几何图形，让学生经历探索的过程，以能力立意，考查自主探究能力，促进培养学生解决问题的能力。
解决这类问题首先要在动点的运动过程中观察图形的变化情况，需要画出图形在不同位置的情况，才能做好计算推理的过程；其次在变化中找到不变量的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
动点问题题型方法归纳：动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。
）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就四边形中的动点问题的常见题型作简单介绍，解题方法、关键给以点拨。
1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB ＝60°，则矩形ABCD的面积是_____________2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH 的面积为________（第1题）（第2题）（第3题）3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ＋PQ的最小值为____________4、如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t s(0 < t ≤15)．过点D作DF⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以1cm/s 的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t（s）；（1）连接EF，当EF经过AC边的中点D时，求证：△ADE≌△CDF；（2）求当t为何值时，四边形ACFE是菱形；（3）是否存在某一时刻t，使以A、F、C、E为顶点的四边形内角出现直角？若存在，求出t的值；若不存在，请说明理由．6、在菱形ABCD中，∠B=60°，点E在射线BC上运动，∠EAF=60°，点F在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点E在BC的延长线上时（如图2），线段EC、CF、AB有怎样的相等关系？写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN是平行四边形；（2）填空：①当AM的值为______时，四边形AMDN是矩形；②当AM的值为______时，四边形AMDN是菱形．8、如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D重合）分别向直线AB、AD作垂线，垂足分别为E、F．（1）BD的长是______；（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______（第9题）（第10题）10、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为______．11、如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD 的中点．（1）求证：四边形PMEN是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN是菱形；（3）四边形PMEN有可能是矩形吗？若有可能，求AP的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm／s。
有关平行四边形的动点问题
有关平行四边形的动点问题
平行四边形是由两组相邻的平行线和它们之间的四条线段组成的四边形。
在平行四边形中，我们可以考虑一个点在它沿着一个方向移动的同时，沿着另一个方向的轨迹。
这个点被称为“动点”。
如果动点沿着平行四边形的一条边上移动，那么它所相应的高度和底边也会相应地改变。
因此，如果我们将平行四边形分成许多小长方形，并在这些小长方形的顶点处放置动点，则可以形成一条光滑的曲线。
这个曲线被称为平行四边形的“径线”。
如果动点同时沿着两个方向移动，则可以得到一个新的曲线，称为“余弦曲线”。
这个曲线看起来像是一个上下波动的曲线，与平行四边形的一条对角线平行。
有趣的是，这两个曲线都是周期性的，其周期等于平行四边形的面积除以它沿着这个方向的速度。
因此，我们可以通过这些曲线来计算平行四边形的面积和周长。
通过研究这些平行四边形的动点问题，我们能够深入了解其内在的几何性质和性质之间的相互关系。
这不仅有助于帮助我们更好地理解平行四边形，还可以为其他更复杂的几何形状和问题提供有用的洞见和启示。
平行四边形的动点问题
平行四边形的动点问题1. 平行四边形是指具有两对相对平行的边的四边形。
在这个问题中，我们关注一个动点在平行四边形内移动的情况。
2. 首先，让我们定义平行四边形的四个顶点为A、B、C和D，并假设它们按顺时针方向排列。
我们还假设动点记为P，并且它可以在平行四边形内的任意位置移动。
3. 问题的第一部分是，如果动点P从A点出发，按一定路径移动，最后回到A点，那么它经过的路径会是什么样子4. 要回答这个问题，我们需要注意到平行四边形的两对相对边分别是AB和CD，以及AD和BC。
因此，如果动点P从A点出发并回到A 点，它必定会经过平行四边形的另外两个顶点，即C和B。
5. 为了更具体地描述动点P的路径，我们可以进一步假设动点P沿着直线AC移动到顶点C，然后沿着直线CB移动到顶点B，最后沿着直线BA移动回到顶点A。
这样，动点P所经过的路径形成了一个三角形ABC。
6. 需要注意的是，这个路径并不是唯一的。
动点P可以按任意方式从A到C，再从C到B，最后从B到A。
但无论路径如何，最终的路径都是一个三角形ABC。
7. 接下来，让我们来看问题的第二部分。
如果动点P从一个顶点出发，按一定路径移动，最后回到另一个顶点，那么它经过的路径会是什么样子8. 在这种情况下，我们可以假设动点P从顶点A出发，并沿着直线AC移动到顶点C。
然后，它会继续按照平行四边形的形状，沿着直线CB移动到顶点B，并最终沿着直线BA返回到顶点A。
9. 与第一部分类似，这个路径也不是唯一的。
动点P可以从任意顶点出发，按照相应的顺序经过其他两个顶点，最后回到初始的顶点。
10. 总结起来，平行四边形的动点问题涉及动点在平行四边形内移动的路径问题。
无论是从一个顶点出发回到同一个顶点，还是从一个顶点出发回到另一个顶点，最终路径都可以看作是一个三角形。
11. 这个问题的解答可以帮助我们更好地理解平行四边形的形状和特性，以及动点在平行四边形内移动时的可能路径。
它也为我们提供了一种思考和探索几何问题的方式。
平行四边形动点问题方法总结
平行四边形动点问题方法总结1. 引言：为什么我们要关注平行四边形动点问题？嘿，朋友们！今天我们来聊聊一个看似枯燥却又很有趣的数学话题——平行四边形动点问题。
别急着打哈欠，咱们慢慢来，这可是个让你从头到脚都充满成就感的数学冒险哦。
平行四边形动点问题，听名字就知道，讲的是在平行四边形里，某个点在移动时，会发生什么奇妙的事情。
这不仅仅是数学题，更像是一场迷人的舞蹈。
你知道吗？这些问题其实很接地气，因为它们涉及到很多我们生活中常见的现象，比如房子四角是直角的，家具摆放的角度等等。
2. 方法一：坐标法——从数学角度看平行四边形的奇妙。
2.1 说到解决这类问题，坐标法可是个不可或缺的好帮手。
咱们首先给平行四边形的四个顶点分配坐标，比如A、B、C、D分别是(0, 0)、(a, 0)、(b, c)、(d, e)。
坐标法就是把平行四边形里的每个点都用坐标表示出来，这样一来，不管点怎么动，我们都能通过数学公式来搞定。
2.2 你可以把平行四边形当成一个平面上的大布景，点A、B、C、D就是布景上的关键位置。
然后，动点就是在这个布景上游走的小演员。
比如，如果你要找出某个点P 的轨迹，只需要把P的坐标带入公式，就能知道P跑到哪儿去了。
坐标法简直是数学里的瑞士军刀，万能又省事。
3. 方法二：向量法——用矢量的眼光看世界。
3.1 向量法是另一个很酷的方法。
想象一下，向量就像是一把利刃，把复杂的数学问题一刀切成简单易懂的形状。
比如，平行四边形的对角线是彼此平行的，那么它们之间的向量关系就能告诉我们很多有用的秘密。
如果我们把动点P的运动看作一个向量变化，我们就能用向量运算来分析它的行为。
3.2 向量法的好处在于，它能帮我们迅速搞清楚平行四边形中各个点的相对位置和移动规律。
用这个方法，你可以非常方便地计算出点P在平行四边形内的各种可能位置，也能找到一些隐含的规律，比如点P可能会在平行四边形的对角线附近来回移动。
数学就像个魔术师，向量法让我们能透过表面看到更多的奥秘。
第十八章平行四边形四边形中的动点问题(教案)人教版八年级数学下册
（五）总结回顾（用时5分钟）
今天的学习，我们了解了平行四边形中动点问题的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对动点问题的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
五、教学反思
在今天的教学中，我发现同学们对平行四边形内动点问题的探究表现得非常积极。他们对于动点的运动规律和性质有了初步的认识，也尝试着将这些知识应用到实际问题中。我觉得这是一个很好的开始，但也发现了一些需要改进的地方。
首先，理论讲授部分，我发现有些同学对动点问题的基本概念掌握不够扎实。可能是我讲解得不够细致，也可能是同学们对这些概念还不够熟悉。在以后的教学中，我需要更加注意这一点，尽量用简单易懂的语言和丰富的例子来帮助他们理解。
3.重点难点解析：在讲授过程中，我会特别强调动点的运动规律和利用平行四边形性质解题这两个重点。对于难点部分，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与动点问题相关的实际问题。
2.实行四边形中的运动规律和性质。
-难点二：在实际问题中，学生可能不知道如何选择合适的定理和性质来解决动点问题。教师应指导学生通过分析问题结构，识别关键信息，进而选择恰当的几何定理进行求解。
-难点三：针对不同动点问题，如路径最短、面积最大等，学生可能不知如何下手。教师应教授学生分类讨论和优化的方法，帮助学生理清思路，找到解题突破口。
4.培养合作意识和团队精神，在小组讨论和探究过程中，学会倾听、交流、表达和协作，共同解决问题。
人教版初二数学8年级下册 第18章(平行四边形)动点问题专项训练(含答案)
人教版数学八年级下期第十八章平行四边形动点问题训练1.如图，P为正方形ABCD的边BC上一动点（P与B、C不重合），点Q在CD边上，且BP=CQ，连接AP、BQ交于点E，将△BQC沿BQ所在的直线对着得到△BQN，延长QN交BA的延长线于点M．（1）求证：AP⊥BQ；（2）当P在BC何处时，点N是MQ的中点．（3）若AB=3，P是BC的三等分点，求QM的长；2.如图，四边形ABCD是正方形，点E是边BC的动点，连接AE，以AE为边在AE的右上侧作Rt△AEF，使得∠AEF=90°，AE=EF，再过点F作FG⊥BC，交BC的延长于点G．（1）求证：∠BAE=∠GEF；（2）求证：CG=FG；（3）填空：若正方形ABCD的边长是2，当点E从点B运动到点C的过程中，点F也随之运动，则点F运动的痕迹的长是______．3.如图，点P是正方形ABCD（在小学，同学们学习过：正方形四边相等，四个角都是直角）对角线AC上一动点，点E在射线BC上，且PB=PE，连结PD，O为AC 中点．（1）如图①，当点P在线段AO上时，猜想PE与PD的关系，并说明理由；（2）如图②，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由．4.如图，已知菱形ABCD中，∠BAD=60°，点E、F分别是AB、AD上两个动点，若AE=DF，连接BF与DE相交于点G，连接CG，（1）求∠BGE的大小；（2）求证：GC平分∠BGD．5.如图，在平行四边形ABCD中，AB=10，AD=16，∠A=60°，P是射线AD上一点，连接PB，沿PB将△APB折叠，得△A'PB．（1）如图1所示，当∠DPA'=10°时，∠A'PB=______度；（2）如图2所示，当PA'⊥BC时，求线段PA的长度；（3）当点P为AD中点时，点F是边AB上不与点A，B重合的一个动点，将△APF 沿PF折叠，得到△A'PF，连接BA'，求△BA'F周长的最小值．6.如图，边长为8的正方形ABCD的対角线AC，BD交于点O，M是AB边上一动点，ME⊥AO，MF⊥BO．（1）求证：四边形OEMF为矩形；（2）连接EF，求EF的最小值．7.如图，在正方形ABCD中，点E是AD边上的一个动点，连接BE，以BE为斜边在正方形ABCD内部构造等腰直角三角形BEF，连接CF．（1）求证：∠DEF+∠CBF=90°；，求△BEF的面积；（2）若AB=3，△BCF的面积为32（3）求证：DE=2CF．8.如图，在菱形ABCD中，AB＝2，∠DAB＝60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．（1）求证：△NDE≌△MAE；（2）求证：四边形AMDN是平行四边形；（3）当AM的值为何值时，四边形AMDN是矩形？请说明理由．9.如图，已知四边形ABCD为正方形，AB=42，点E为对角线AC上一动点，连接DE、过点E作EF⊥DE．交BC点F，以DE、EF为邻边作矩形DEFC，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．10.如图,已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≅△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.11.如图，已知矩形ABCD中，AB＝5，AD＝2＋13．菱形EFGH的顶点H在边AD上，且AH＝2，顶点G、E分别是边DC、AB上的动点，连结CF．（1）当四边形EFGH为正方形时，直接写出DG的长；（2）若△FCG的面积等于3，求DG的长；（3）试探究点G运动至什么位置时，△FCG的面积取得最小值.12.如图，P为正方形ABCD的边AD上的一个动点，AE⊥BP，CF⊥BP，垂足分别为点E，F，已知AD=4，试说明AE2+CF2的值是一个常数．13.如图，在△ABC中，CA＝CB，∠ACB=90°，AB＝5，点D是边AB上的一个动点，连接CD，过C点在上方作CE⊥CD，且CE=CD，点P是DE的中点.(1)如图①，连接AP，判断线段AP与线段DE的数量关系并说明理由；(2)如图②，连接CP并延长交AB边所在直线于点Q，若AQ＝2，求BD的长.14.如图,D、E分别是△ABC的边AB、AC的中点,O是△ABC内一动点,F、G分别是OB、OC的中点.判断四边形DEGF的形状,并说明理由.15.在正方形ABCD中，如图1，点E是AB边上的一个动点（点E与点A、B不重合），连接CE，过点B作BF⊥CE于点G，交AD于点F.（1）求证：△ABF≌△BCE.（2）如图2，当点E运动到AB中点时，连接DG，若AB=2，求DG的长.16.如图，在矩形ABCD中，BC=4，AB=10，E为CD边上的一点，DE=7，动点P从点A出发，以每秒1个单位的速度沿着边AB向终点B运动，连接PE．设每秒运动的时间为t秒．（1）求BE的长；（2）当t为多少秒时，△BPE是直角三角形．参考答案1.（1）证明：∵四边形ABCD是正方形，∴∠ABC=∠C=90°，AB=BC，在△ABP和△BCQ中，AB=BC∠ABC=∠CBP=CQ，∴△ABP≌△BCQ（SAS），∴∠BAP=∠CBQ，∵∠BAP+∠APB=90°，∴∠CBQ+∠APB=90°，∴∠BEP=90°，∴AP⊥BQ；（2）解：由折叠的性质得：NQ=CQ，∠BNQ=∠C=90°，∠NBQ=∠CBQ，∴∠BNM=90°，∵点N是MQ的中点，∴NQ=MN，由（1）得：MQ=MB，∴MN=12MB，∴∠MBN=30°，∴∠CBN=60°，∴∠NBQ=∠CBQ=30°，∴CQ=33BC，∴BP=CQ=33BC，即BP=33BC时，点N是MQ的中点．（3）解：∵四边形ABCD是正方形，AB=3，P是BC的三等分点，∴BP=2CP，或CP=2BP，①当BP=2CP时，BP=2，由折叠的性质得：NQ=CQ=BP=2，BN=BC=3，∵∠NQB=∠CQB=∠ABQ，∴MQ=MB，设MQ=MB=x，则MN=x-2，在Rt△MBN中，MB2=BN2+MN2，即x 2=32+（x -2）2，解得：x =134，即MQ =134；②当CP =2BP 时，BP =1，由折叠的性质得：NQ =CQ =BP =1，BN =BC =3，∵∠NQB =∠CQB =∠ABQ ，∴MQ =MB ，设MQ =MB =x ，则MN =x -1，在Rt △MBN 中，MB 2=BN 2+MN 2，即x 2=32+（x -1）2，解得：x =5，即MQ =5；综上所述，若AB =3，P 是BC 的三等分点，QM 的长为134或5．2.解：（1）∵∠AEF =90°，∴∠AEB +∠FEG =90°，∵四边形ABCD 是正方形，∴∠B =90°，∴∠AEB +∠BAE =90°，∴∠BAE =∠GEF ，（2）在△ABE 和△EGF 中，∠ABE =∠EGF ∠BAE =∠GEF AE =EF，∴△ABE ≌△EGF （AAS ），∴BE =GF ，AB =EG ，∴BE =CG ，∴CG =FG ；（3）223.解:（1）当点P在线段AO上时PE=PD且PE⊥PD.理由：当点P在线段AO上时,在△ABP和△ADP中AB=AD∠BAP=∠DAP=45∘AP=AP∴△ABP≌△ADP,∴BP=DP,∵PB=PE,∴PE=PD,如图，过点P作PM⊥CD于点M,作PN⊥BC于点N,∵AC平分∠BCD，∴PM=PN，在Rt△PNE与Rt△PMD中,∵PD=PE,PM=PN∴Rt△PNE≌Rt△PMD,∴∠DPM=∠EP N,易得∠MPN=90∘,∴∠DPE=90∘,故PE⊥PD,PE与PD的数量关系和位置关系分别为:PE=PD,PE⊥PD;（2）当点P在线段OC上时，（1）中的猜想成立；如图2,当点P在线段OC上时，∵四边形ABCD是正方形，AC为对角线，∴BA=DA，∠BAP=∠DAP=45°，又PA=PA，∴△BAP≌△DAP(SAS)，∴PB=PD，又∵PB=PE，∴PE=PD，①当点E与点C重合时，PE⊥PD；②当点E在BC的延长线上时，如图2所示，∵△BAP≌△DAP，∴∠ABP=∠ADP，∠CDP=∠CBP，∵PB=PE，∴∠CBP=∠PEC，故∠PEC=∠PDC，∵∠1=∠2，∴∠DPE=∠DCE=90°，∴PE⊥PD，综上所述：PE⊥PD，当点P在线段OC上时，（1）中的猜想成立；4.解：（1）∵四边形ABCD是菱形∴AD=AB，∠BAD=60°∴△ADB是等边三角形∴AD=AB=BD，∠DAB=∠ADB=∠ABD∵AE=DF，∠DAB=∠ADB=60°，AD=BD∴△ADE≌△DBF（SAS）∴∠ADE=∠DBF又∠BGE=∠BDE+∠DBF=∠BDE+∠ADE=∠ADB∴∠BGE=∠ADB=60°（2）如图，过点C作CN⊥BF于点N，过点C作CM⊥ED于点M，由（1）得∠ADE=∠DBF∴∠CBF=60°+∠DBF=60°+∠ADE=∠DEB又∠DEB=∠MDC∴∠CBF=∠CDM∵BC=CD，∠CBF=∠CDM，∠CMD=∠CNG=90°∴Rt△CBN≌Rt△CDM（AAS）∴CN=CM，且CN⊥BF，CM⊥ED∴点C在∠BGD的平分线上即GC平分∠BGD5.856.（1）证明：∵ME⊥AO，MF⊥BO，∴∠MEO=90°，∠MFO=90°，∵正方形ABCD的対角线AC，BD交于点O，∴∠EOF=90°，∴四边形OEMF为矩形；（2）解：∵边长为8的正方形ABCD的対角线AC，BD交于点O，∴利用勾股定理可以得到OA=OB=42，当M在AB的中点时，EF有最小值，最小值=OE2+OF2=(22)2+(22)2=4.7.证明：（1）过点F作MN⊥AD于点M，交BC于点N，∴∠MEF+∠EFM=90°，∵∠EFB=90°，∴∠BFN +∠EFM =90°，∴∠MEF =∠BFN ，在正方形ABCD 中，AD ∥BC ．∴MN ⊥BC ，∴∠FBN +∠BFN =90°，∴∠FBN +∠MEF =90°，即∠DEF +∠CBF =90°；证法二：在正方形ABCD 中，AD ∥BC ，∴∠DEB +∠CBE =180°，即∠DEF +∠BEF +∠EBF +∠CBF =180°，∵∠EFB =90°，∴∠BEF +∠EBF =90°，∴∠DEF +∠CBF =90°；（2）由（1）得MN ⊥AD ，∴正方形ABCD 的性质得四边形MNCD 是矩形，∴MN =CD =AB =3，在△BFN 与△FEM 中，由（1）得∠MEF =∠BFN ，∠EMF =∠FNB =90°，∵△BEF 为等腰直角三角形，∴BF =EF ，在△BFN 与△FEM 中，∠EMF =∠FNB ∠MEF =∠BFN BF =EF，∴△BFN ≌△FEM （AAS ），∵BC =AB =3，∴S △BCF =12BC ⋅FN =32FN =32，∴FN =1．∴BN =FM =MN -FN =2，在Rt △BFN 中，EF =BN 2+FN 2=12+22=5，∴S △BEF =12BF 2=12×(5)2=52；（3）在△BFN与△FEM中由（2）△BFN≌△FEM，MD=NC，∴BN=FM，EM=FN，∵MN=AB=BC，∴FM+FN=BN+NC，∴FN=NC=MD=EM，∴∠FCN=45°，DE=2MD=2CN，CF，在Rt△FNC中，CN=22∴DE=2×2CF=2CF．28.（1）证明：∵四边形ABCD是菱形，∴ND∥AM，∴∠NDE=∠MAE，∵点E是AD中点，∴DE=AE，在△NDE和△MAE中，∠NDE=∠MAEDE=AE，∠DEN=∠AEM∴△NDE≌△MAE（ASA）；（2）∵△NDE≌△MAE，∴ND=MA，∴四边形AMDN是平行四边形；（3）解：当AM=1时，四边形AMDN是矩形．理由如下：∵四边形ABCD是菱形，∴AD=AB=2，∵四边形AMDN是矩形，∴DM⊥AB，即∠DMA=90°，∵∠DAB=60°，∴∠ADM=30°，∴AM=12AD=1．9.解：（1）如图所示，过E作EM⊥BC于M点，过E作EN⊥CD于N点，∵正方形ABCD，∴∠BCD=90°，∠ECN=45°，∴∠EMC=∠ENC=∠BCD=90°，且NE=NC，∴四边形EMCN为正方形，∵四边形DEFG是矩形，∴EM=EN，∠DEN+∠NEF=∠MEF+∠NEF=90°，∴∠DEN=∠MEF，又∠DNE=∠FME=90°，在△DEN和△FEM中，∠DNE=∠FME EN=EM∠DEN=∠FEM，∴△DEN≌△FEM（ASA），∴ED=EF，∴矩形DEFG为正方形，（2）CE+CG的值为定值，理由如下：∵矩形DEFG为正方形，∴DE=DG，∠EDC+∠CDG=90°，∵四边形ABCD是正方形，∵AD=DC，∠ADE+∠EDC=90°，∴∠ADE=∠CDG，在△ADE和△CDG中，AD=CD∠ADE=∠CDG DE=DG，∴△ADE≌△CDG（SAS），∴AE=CG，∴AC=AE+CE=2AB=2×42=8，∴CE+CG=8是定值．10. (1)∵点F,H分别是BC,CE的中点,∴FH //BE ,FH =12BE ,∴∠CFH =∠CBG .又∵点G 是BE 的中点,∴FH =BG .又∵BF =FC ,∴△BGF ≅△FHC .(2)连接EF ,GH .当四边形EGFH 是正方形时,可知EF ⊥GH且EF =GH .∵在△BEC 中,点G ,H 分别是BE ,EC 的中点,∴GH =12BC =12AD =12a ,且GH //BC ,∴EF ⊥BC .又∵AD //BC ,AB ⊥BC ,∴AB =EF =GH =12a ,∴S 矩形ABCD =AB ⋅AD =12a ⋅a =12a 211.解：（1）∵四边形EFGH 为正方形，∴HG =HE ，∠ADG =∠HAE =90°，∵∠DHG +∠AHE =90°，∠DHG +∠DGH =90°，∴∠DGH =∠AHE ，∴△DGH ≌△AHE （AAS ），∴DG =AH =2；（2）如图，作FM⊥DC，M为垂足，连结GE．∵AB∥CD，∴∠AEG＝∠MGE，∵HE∥GF，∴∠HEG＝∠FGE，∴∠AEG-∠HEG＝∠MGE-∠FGE，即∠AEH＝∠MGF，又∠A＝∠M＝90°，HE＝FG，∴△AHE≌△MFG，∴FM＝HA＝2，即无论菱形EFGH如何变化，点F到直线CD的距离恒等于2，∴S▵FCG=1×2⋅GC=3，2解得GC＝3，∴DG＝2；（3）设DG＝x，则CG＝5-x，由（2）可知，S△FCG＝5-x．要使△FCG的面积最小，须使x最大，∵在Rt△DHG中，DH=13，∴当GH取得最大时，x最大当点E与点B重合时，HE最大，此时，HE=22+52=29，则GH=HE=29，在Rt△DHG中，x=(29)2−(13)2=4，∴当DG＝4时，△FCG的面积取得最小值．12.解：∵四边形ABCD是正方形，∴∠AEB=∠BFC=90°，AB=BC，又∵∠ABE+∠FBC=∠BCF+∠FBC，∴∠ABE=∠BCF，在△ABE和△BCF中，AB=BC∠ABE=∠BCF∴△ABE≌△BCF（AAS），∠AEB=∠BFC∴AE=BF，∴AE2+CF2=BF2+CF2=BC2=AD2=16为常数．13.解：（1）AP=1DE，理由如下：2连接AE.∵CE⊥CD，∴∠ACE+∠ACD=90°，∵∠ACB=90°，∴∠BCD+∠ACD=90°，∴∠ACE=∠BCD，在△BCD和△ACE中，CE=CD∠ACE=∠BCD，AC=BC∴△BCD≌△ACE（SAS），∴∠EAC=∠B=45°，∴∠EAD=90°，∵P为DE中点，DE.∴AP=12（2）①当Q在边AB上时，连接AE，EQ.∵P 为DE 中点，CE =CD ，∴PC 垂直平分DE ，∴DQ =QD ，∵AB =5，AQ =2，∴BD =3，设BD =AE =x ，则QD =EQ =3-x ，在Rt △AEQ 中，AE 2+AQ 2=QE 2，即x 2+22=(3-x )2解得x =56;当Q 在BA 延长线上时，连接AE ，EQ ，如图，设BD =AE =x ，同理可得AE 2+AQ 2=QE 2，即x 2+22=(7-x )2解得x =4514.综上可得BD =56或4514.14.解析 四边形DEGF 是平行四边形.理由:∵D 、E 分别是△ABC 的边AB 、AC 的中点,∴DE =12BC ,DE //BC ,∵F、G分别是OB、OC的中点,BC,FG//BC,∴FG=12∴DE=FG,DE//FG,∴四边形DEGF是平行四边形15.（1）证明：∵BF⊥CE，∴∠CGB=90°，∴∠GCB+∠GBC=90°，又∵四边形ABCD为正方形，∴∠GBA+∠GBC=90°，∴∠GCB=∠FBA，又∵BC=AB，∠FAB=∠EBC=90°，在△ABF与△BCE中，∠GCB=∠FBABC=AB，∠EBC=∠FAB∴△ABF≌△BCE（SAS）；（2）解：过点D作DH⊥CE于点H，∵E为AB中点，∴EB=1，∵AB=2，∴BC=2，∴CE=BC2+EB2=22+12=5，在Rt △CEB 中，由CE •BG =EB •BC 得BG =EB ⋅BC CE =1×25=255，∴CG =455，∵∠DCE +∠BCE =∠BCE +∠CBF =90°，∴∠DCE =∠CBF ，又∵DC =BC =2，∠CHD =∠CGB =90°，在△CHD 与△BGC 中，∠CHD =∠CGB =90°∠DCE =∠CBF DC =BC，∴△CHD ≌△BGC （AAS ）∴CH =BG =255，∴GH =CG -CH =255=CH ，∵DH =DH ，∠CHD =∠GHD =90°，在△DGH 与△DCH 中，GH =CH ∠GHD =∠CHD DH =DH，∴△DGH ≌△DCH （SAS ），∴DG =DC =2．16.解：（1）在矩形ABCD 中，∠C =∠B =90°，CD =AB =10，在Rt △BCE 中，CE =CD -ED =10-7=3，根据勾股定理得，BE =BC 2+CE 2=42+32=5，（2）①当以P 为直角顶点时，即∠BPE =90°，则∠C =∠B =∠BPE =90°，∴四边形CBPE 是矩形，∴BP =CE =3，即10-t =3，∴t =7，②当以E 为直角顶点时，即∠BEP =90°，由勾股定理得，BE 2+PE 2=BP 2，过点P 作PF ⊥CD 于F ，则PF=AD=4，DF=AP，设AP=t，则EF=7-t，BP=10-t，PE2=42+（7-t）2，∴52+42+（7-t）2=（10-t）2，，解得，t=53∴当t=7或5秒时，△BPE是直角三角形．3。
平行四边形中的动点问题专题复习【精品】
平行四边形中的动点问题【教材母题】课本68页第13题例：如图，在四边形ABCD 中，AD ∥BC ，∠B ＝90°，AB ＝8cm ，AD ＝24cm ，BC ＝26cm ，点P 从点A 出发，以1cm/s 的速度向点D 运动；点Q 从点C 同时出发，以3cm/s 的速度向点B 运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．从运动开始，使PQ//CD 和PQ=CD ，分别需经过多少时间？为什么？解：设点P ，Q 运动的时间为ts （3260≤≤t ）． 则AP=t,PD=24-t;CQ=3t,BQ=26-3t.（1）当PQ//CD 时，∵AD ∥BC ，∴四边形PQCD 为平行四边形 ∴PD ＝CQ∴24－t ＝3t ．∴t ＝6．∴当t 为6s 时，PQ//CD ．（2）当PQ=CD 时第一种情况：如图，PQ=CD，四边形PQCD为平行四边形由PD=CQ知24－t＝3t，∴t＝6．第二种情况：如图，分别过点P，D作BC边的垂线PE，DF，垂足为E，F．∵ AD∥BC，∴∠B＝∠A＝∠DFB＝90°，∴四边形ABFD是矩形∴AD＝BF=24.∴CF＝BC－BF＝2.同理可得四边形PEFD是矩形∴PE=DF,PD=EF=24-t∵PQ=CD，∠PEQ=∠DFC=90°∴△PQE≌△DCF∴QE=CF=2∴QC- EF=QE+FC=4∴3t-(24-t)=4, t=7∴当t为6s,或7s时，PQ＝CD．变式1：设点P ，Q 运动的时间为t s ，当t 取何值时,ABQP 是矩形?解：当四边形ABQP 为矩形时，AP=BQ即t ＝26－3t ，解得t ＝6.5．∴当t 为6.5 s 时，四边形ABQP 是矩形．变式2：设点P ，Q 运动的时间为t s ，是否存在t ，使得△DQC 是等腰三角形？若存在，请求出t 值；若不存在，请说明理由．解：CD 的长度为172第一种情况：当CQ ＝CD 时，即3t ＝172，∴t ＝3172． 第二种情况：当DQ ＝DC 时，过点D 作DH ⊥CQ 于H,∵ AD ∥BC∴∠B ＝∠A ＝∠DFB ＝90°，∴四边形ABHD 是矩形∴AD ＝BH=24．∴CH ＝BC －BH ＝2∵DQ=DC,DH ⊥CQ∴CQ=2CH=4∴3t=4，t=34第三种情况：当QD ＝QC 时过点D 作DH ⊥CQ 于H ，∵DH ＝8，CH ＝2，DC ＝172，QC ＝QD ＝3t ，∴QH ＝|3t －2|在Rt △DQH 中，DH 2+QH 2=DQ 2∴()()2223238t t =-+解得t ＝317 综上，当t ＝3172s ，34s 或317s 时，△DQC 是等腰三角形．专项一：平行四边形中的动点问题1.如图所示，在四边形ABCD中，AD∥BC，且AD＞BC，BC＝6cm，动点P，Q分别从A，C同时出发，P以1cm/s的速度由A向D运动，Q 以2cm/s的速度由C向B运动，则2 s后四边形ABQP为平行四边形．2.如图，在等边△ABC中，BC＝6cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s 的速度运动．如果点E，F同时出发，设运动时间为t（s），当t＝2或 6时，以A，C，E，F为顶点的四边形是平行四边形．3.如图，在平面直角坐标系中，点A，B的坐标分别为A(0，a)，B(b，a)，且a，b满足(a－3)2＋|b－6|＝0.现将线段AB向下平移3个单位长度，再向左平移2个单位长度，得到线段CD，点A，B的对应点分别为点C，D.连接AC，BD.(1)如图1，求点C，D的坐标及四边形ABDC的面积；(2)在y轴上是否存在一点M，使三角形MCD的面积与四边形ABDC的面积相等？若存在，求出点M的坐标，若不存在，试说明理由；(3)如图2，点P是直线BD上的一个动点，连接PA，PO，当点P在直线BD上移动时(不与B，D重合)，直接写出∠BAP，∠DOP，∠APO 之间满足的数量关系．解：(1)∵(a－3)2＋|b－6|＝0，∴a－3＝0，b－6＝0，解得a＝3，b＝6.∴A(0，3)，B(6，3)．。
北师大版数学八年级下册_易错15_平行四边形中的动点问题(解析版)-八下期末突破易错挑战满分
2020-2021学年八年级数学下册期末突破易错挑战满分（北师大版）易错15 平行四边形中的动点问题【典型例题】1．（2020·浙江八年级期末）如图，在四边形ABCD 中，//,90,16cm,12cm,21cm AD BC B AD AB BC ∠====．动点P 从点B 出发，沿射线BC 的方向以每秒2cm 的速度运动到C 点返回，动点Q 从点A 出发，在线段AD 上以每秒1cm 的速度向点D 运动，点P ，Q 分别从点B ，A 同时出发，当点Q 运动到点D 时，点P 随之停止运动，设运动时间为t （秒）．（1）当010.5t <<时，若四边形PQDC 是平行四边形，求出满足要求的t 的值；（2）当010.5t <<时，若以C ，D ，Q ，P 为顶点的四边形面积为260cm ，求相应的t 的值； （3）当10.516t ≤<时，若以C ，D ，Q ，P 为顶点的四边形面积为260cm ，求相应的t 的值．【答案】（1）t =5；（2）t =9；（3）t =15【分析】（1）由平行四边形的性质得出DQ =CP ，当0＜t ＜10.5时，P 、Q 分别沿AD 、BC 运动，由题意得出方程，解方程即可；（2）当0＜t ＜10.5时，P 、Q 分别沿AD 、BC 运动，由梯形面积公式得出方程，解方程即可； （3）当10.5≤t ＜16时，点P 到达C 点返回，由梯形面积公式得出方程，解方程即可．【详解】解：（1）∵四边形PQDC 是平行四边形，∵DQ =CP ，当0＜t ＜10.5时，P 、Q 分别沿AD 、BC 运动，如图1所示：∵DQ=AD-AQ=16-t，CP=21-2t∵16-t=21-2t解得：t=5；即当t=5秒时，四边形PQDC是平行四边形；（2）当0＜t＜10.5时，P、Q分别沿AD、BC运动，如图1所示：CP=21-2t，DQ=16-t，若以C，D，Q，P为顶点的四边形面积为60cm2，则12（DQ+CP）×AB=60，即12（16-t+21-2t）×12=60，解得：t=9；即当0＜t＜10.5时，若以C，D，Q，P为顶点的四边形面积为60cm2，t的值为9秒；（3）当10.5≤t＜16时，如图2所示，点P到达C点返回，CP=2t-21，DQ=16-t，则同（2）得：12（DQ+CP）×AB=60，即12（16-t+2t-21）×12=60，解得：t=15．即当10.5≤t＜16时，若以C，D，Q，P为顶点的四边形面积为60cm2，t的值为15秒．【点睛】本题是四边形综合题目，考查了直角梯形的性质、平行四边形的判定与性质、梯形的面积等知识，熟练掌握直角梯形的性质和平行四边形的判定与性质是解题的关键．【专题训练】一、选择题1．（2021·全国九年级专题练习）如图，在四边形ABCD 中，//AD BC ，且AD BC ，6cm BC ．动点P ，Q 分别从A ，C 同时出发，P 以1cm/s 的速度由A 向D 运动．Q 以2cm /s 的速度由C 向B 运动，______s 时四边形ABQP 为平行四边形．A ．1B ．1.5C ．2D ．2.5【答案】C【分析】 由运动时间为x 秒，则AP =x ，QC =2x ，而四边形ABQP 是平行四边形，所以AP =BQ ，则得方程x =6-2x 求解．【详解】解：∵运动时间为x 秒，∵AP =x ，QC =2x ，∵四边形ABQP 是平行四边形，∵AP=BQ，∵x=6-2x，∵x=2．答：2秒后四边形ABQP是平行四边形．故选：C．【点睛】本题考查了平行四边形的判定与性质．此题根据路程=速度×时间，得出AP、QC的长，然后根据已知条件列方程求解．2．（2021·新乡市·河南师大附中九年级其他模拟）如图，直线m经过点B且平行于AC，点P为直线m上的一动点，连接PC，P A，随着点P在直线m上移动，则下列说法中一定正确的是（）A．ABC与PCA全等B．ABC与PCA的周长相等C．ABC与PCA的面积相等D．四边形ACBP是平行四边形【答案】C【分析】由全等三角形和平行四边形的判定，以及同底等高三角形的面积相等，可以得出正确的选项．【详解】解：选项A，因为点A，B，C是定点，而点P是直线m上的动点，所以ABC与PCA不一定全等，故A错误；选项B，ABC的周长是定值，而PCA的周长随着点P位置的变化而变化，所以B错误；选项C，由于ABC与PCA都可以看作是以AC为底边的三角形，且直线m平行于AC，可由平行线间的距离处处相等知道ABC与PCA属于同底等高的三角形，故二者面积相等，所以选项C正确；选项D，由于P是动点，点A，B，C，是定点，所以BP不总是等于AC，而平行四边形的对边应该相等，所以选项D错误．故选：C．【点睛】本题是考查全等三角形和平行四边形的判定，以及同底等高三角形的面积相等的，属于中等难度的题目．3．（2020·浙江温州市·实验中学八年级期中）已知∵ABCD ，点E 是边BC 上的动点，以AE 为边构造∵AEFG ，使点D 在边FG 上，当点E 由B 往C 运动的过程中，∵AEFG 面积变化情况是（ ）A ．一直增大B ．保持不变C ．先增大后减小D ．先减小后增大【答案】B【分析】 延长BE ，与GF 的延长线交于点P ，先证明四边形ADPE 是平行四边形，再证明∵AGD ∵∵EFP ，得出平行四边形AGFE 的面积等于平行四边形ADPE 的面积，又AD ∵BP ，根据两平行线之间的距离处处相等得出平行四边形ABCD 的面积等于平行四边形ADPE 的面积，进而得出平行四边形ABCD 的面积等于平行四边形AEFG 面积．所以根据图示进行判断即可．【详解】解：设∵ABE ，∵ECH ，∵HFD ，∵DGA 的面积分别为S 1、S 2、S 3、S 4，延长BE ，与GF 的延长线交于点P ．∵四边形ABCD 是平行四边形，∵AD ∵BP ，∵ADG ＝∵P ．∵四边形AEFG 是平行四边形，∵AG ∵EF ，AE ∵DP ，AG ＝EF ，∵∵G ＝∵EFP ．∵AD ∵BP ，AE ∵DP ，∵四边形ADPE 是平行四边形．在∵AGD 与∵EFP 中，，AG EF ⎧⎪⎨⎪=⎩∠G=∠EFG ∠ADG=∠P∵∵AGD ∵∵EFP （AAS ），∵S 4＝S ∵EFP ，∵S4+S四边形AEFD＝S∵EFP+S四边形AEFD，即S∵AEFG＝S∵ADPE，又∵∵ADPE与∵ADCB的一条边AD重合，且AD边上的高相等，∵S∵ABCD＝S∵ADPE，∵平行四边形ABCD的面积＝平行四边形AEFG的面积．故∵AEFG面积不变，故选：B．【点睛】本题考查了平行四边形面积变化情况，解题的关键是根据两平行线之间的距离处处相等得出平行四边形ABCD的面积等于平行四边形ADPE的面积，进而得出平行四边形ABCD的面积等于平行四边形AEFG面积．4．（2019·山东济宁市·八年级期中）如图，在平行四边形ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∵FBM＝∵CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动：点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动，点P运动到F点时停止运动，点Q 也时停止运动，当点P运动（）秒时，以点P、Q、E、F为顶点的四边形是平行四边形．A．2B．3C．3或5D．4或5【答案】C【解析】【分析】由平行四边形的性质可得AD∵BC，AD=BC，由平行线的性质可得BF=DF=12cm，可得AD=AF+DF=18cm=BC，由平行四边形的性质可得PF=EQ，列出方程可求解．【详解】解：∵四边形ABCD是平行四边形∵AD∵BC，AD＝BC∵∵ADB＝∵MBC，且∵FBM＝∵MBC ∵ADB＝∵FBM∵BF＝DF＝12cm∵AD＝AF+DF＝18cm＝BC，∵点E是BC的中点∵EC＝12BC＝9cm，∵以点P、Q、E、F为顶点的四边形是平行四边形∵PF＝EQ∵6﹣t＝9﹣2t，或6﹣t＝2t﹣9∵t＝3或5故选C．【点睛】本题考查平行四边形的判定，利用方程思想解决问题是解本题的关键．5．（2019·四川绵阳市·中考模拟）如图，∵ABCD中，AB＝3，AD＝5，AC∵AB，E、F为线段BD上两动点（不与端点重合）且EF＝12BD连接AE，CF，当点EF运动时，对AE+CF的描述正确的是（）A．等于定值5B．有最大值13C D【答案】D【解析】【分析】由平行四边形的性质得出OB＝OD，OA＝OC，得出OB＝EF＝OD，BE＝OF，OE＝DF，由勾股定理求出AC 4，OB BE ＝OE 时，AE +CF 的值最小，E 为OB 的中点，由直角三角形的性质得出AE ＝12OB ，同理：CF ＝12OD ，即可得出结果 【详解】 解：∵四边形ABCD 是平行四边形，∵OB ＝OD ，OA ＝OC ，∵EF ＝12BD ， ∵OB ＝EF ＝OD ，∵BE ＝OF ，OE ＝DF ，∵AB ＝3，AD ＝5，AC ∵AB ，∵AC 4，∵OA ＝2，∵OB当BE ＝OE 时，AE +CF 的值最小，E 为OB 的中点，∵AE ＝12OB ， 同理：CF ＝12OD ，∵AE +CF ＝OB即AE +CF故选：D ．【点睛】本题考查了平行四边形的性质、直角三角形的性质、勾股定理等知识；熟练掌握平行四边形的性质和勾股定理是解题的关键．6．（2020·河北沧州市·九年级其他模拟）如图，在四边形ABCD 中，//AD BC ，6AD =，16BC =，E 是BC 的中点．点P 以每秒1个单位长度的速度从点A 出发，沿AD 向点D 运动；点Q 同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动．若以点,,,P Q E D为顶点的四边形是平行四边形，则点P运动的时间为（）A．1B．72C．2或72D．1或72【答案】D【分析】要使得以P、Q、E、D为顶点的四边形是平行四边形，已知//AD BC，即要使PD=EQ即可，设点P的运动时间为t (0≤t≤6) 秒，分别表示出PD，EQ的长度，根据PD=EQ列方程求解即可．【详解】设点P的运动时间为t (0≤t≤6) 秒，则AP=t，CQ=3t，由E是BC的中点可得：BE=EC=8，要使得以P、Q、E、D为顶点的四边形是平行四边形，已知//AD BC，即要使PD=EQ即可．（1）如图：点Q位于点E右侧时，PD=6－t，CQ=3t，EQ=8－3t，6－t =8－3t，t=1（秒）；（2）如图：点Q位于点E左侧时，PD=6－t，CQ=3t，EQ=3t－8，6－t =3t－8，t=72（秒）．综上所述：P的运动时间为1或72秒．故选：D．【点睛】本题主要考查平行四边形的判定方法以及一元一次方程的应用，熟记平行四边形的判定方法，根据对应边相等列方程是解题关键．7．（2017·江苏苏州市·）如图①，在∵ABCD中，∵B=120°，动点P从点B出发，沿BC、CD、DA运动至点A停止．设点P运动的路程为xcm，∵P AB的面积为ycm2，y关于x的函数的图象如图②所示，则图②中H 点的横坐标为（）A．11B．14C．8D．8+【答案】B【解析】试题分析：作CM∵AB于M，如图所示：当点P 在CD 上运动时，∵P AB 的面积不变，由图②得：BC ＝4cm ，∵∵ABC ＝120°，∵∵CBM ＝60°，∵CM ＝4∵∵ABC 的面积＝12AB •CM ＝12AB × ∵AB ＝6cm ， ∵OH ＝4＋6＋4＝14，∵点H 的横坐标为14．故选B ．点睛：本题考查了平行四边形的性质、动点问题的函数图象．解决本题的关键是利用函数图象和三角形面积确定AB 的长．8．（2020·山东济南市·八年级期末）如图，平行四边形ABCD 绕点A 逆时针旋转30°，得到平行四边形AB ′C ′D ′（点B ′与点B 是对应点，点C ′与点C 是对应点，点D ′与点D 是对应点），点B ′恰好落在BC 边上，则∵C 的度数等于（ ）A ．100°B ．105°C ．115°D ．120°【答案】B【解析】 分析：根据旋转的性质得出AB =AB ′，∵BAB ′=30°，进而得出∵B 的度数，再利用平行四边形的性质得出∵C 的详解：∵平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），∵AB=AB′，∵BAB′=30°，∵∵B=∵AB′B=（180°﹣30°）÷2=75°，∵∵C=180°﹣75°=105°．故选B．点睛：本题主要考查了旋转的性质以及平行四边形的性质，根据已知得出∵B=∵AB′B=75°是解题的关键．二、填空题9．（2019·山西运城市·八年级期末）如图,在四边形ABCD中,AD∵BC,且AD>BC,BC=6cm,动点P,Q分别从A,C 同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C向B运动(Q运动到B时两点同时停止运动),则________后四边形ABQP为平行四边形.【答案】2s【解析】【分析】设运动时间为t秒，则AP=t，QC=2t，根据四边形ABQP是平行四边形，得AP=BQ，则得方程t=6-2t即可求解．【详解】如图，设t秒后，四边形APQB为平行四边形，则AP=t，QC=2t，BQ=6-2t，∵AD∵BC，∵AP∵BQ，当AP=BQ时，四边形ABQP是平行四边形，∵t=6-2t，∵t=2，当t=2时，AP=BQ=2＜BC＜AD，符合．综上所述，2秒后四边形ABQP是平行四边形．故答案为2s．此题主要考查的是平行四边形的判定，熟练掌握平行四边形的判定方法是关键．10．（2019·武汉二中广雅中学八年级月考）如图，在四边形ABCD 中，AD ∵BC ，∵A ＝90°，AD ＝18cm ，BC ＝30cm ．点E 从点D 出发，以1cm /s 的速度向点A 运动：点F 从点C 同时出发，以2cm /s 的速度向点B 运动，规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动的时间为t 秒，M 为BC 上一点且CM ＝13cm ，t ＝_____s 秒时，以D 、M 、E 、F 为顶点的四边形是平行四边形．【答案】133或13 【分析】由题意得出DE ＝t ，CF ＝2t ，当点F 在点M 的右边；当点F 在点M 的左边；以D 、M 、E 、F 为顶点的四边形是平行四边形时，DE ＝MF ，分别得出方程，解方程即可．【详解】解：由题意得：DE ＝t ，CF ＝2t ，∵AD ∵BC ，当点F 在点M 的右边MF ＝13﹣2t ，以D 、M 、E 、F 为顶点的四边形是平行四边形时，DE ＝MF ， 即t ＝13﹣2t ，解得：t ＝133； 当点F 在点M 的左边MF ＝2t ﹣13，以D 、M 、E 、F 为顶点的四边形是平行四边形时，DE ＝MF ， 即t ＝2t ﹣13，解得：t ＝13；综上所述，t ＝133s 或13s 时，以D 、M 、E 、F 为顶点的四边形是平行四边形． 故答案为：133或13 【点睛】本题考查的是四边形的动点问题，主要涉及的知识是平行四边形的判定，运用了方程思想来求解． 11．（2020·广东九年级专题练习）如图，四边形ABCD 中，//AD BC ，8AD cm =，12BC cm =，M 是BC上一点，且9BM cm =，点E 从点A 出发以1/cm s 的速度向点D 运动，点F 从点C 出发，以3/cm s 的速度向点B 运动，当其中一点到达终点，另一点也随之停止，设运动时间为t ，则当以A 、M 、E 、F 为顶点的四边形是平行四边形时，t =__________．【答案】34或32. 【分析】 分两种情形列出方程即可解决问题【详解】①当点F 在线段BM 上，AE FM =时，以A 、M 、E 、F 为顶点的四边形是平行四边形， 则有9312t t =+-，解得32t =， ②当F 在线段CM 上，AE FM =时，以A 、M 、E 、F 为顶点的四边形是平行四边形，则有1293t t =--，解得3t 4=， 综上所述，3t 4=或32s 时，以A 、M 、E 、F 为顶点的四边形是平行四边形． 故答案为：34或32【点睛】本题考查平行四边形的判定和性质等知识，解题的关键是学会构建方程解决问题，学会用分类讨论的思想思考问题．12．（2020·辽宁营口市·八年级期末）如图，平行四边形ABCD 中，AB =8cm ，AD =12cm ，点P 在AD 边上以每秒1cm 的速度从点A 向点D 运动，点Q 在BC 边上，以每秒4cm 的速度从点C 出发，在CB 间往返运动，两个点同时出发，当点P 到达点D 时停止（同时点Q 也停止），在运动以后，以P 、D 、Q 、B 四点组成平行四边形的次数有______次．【解析】∵四边形ABCD是平行四边形，∵BC=AD=12,AD∵BC，∵四边形PDQB是平行四边形，∵PD=BQ，∵P的速度是1cm/秒，∵两点运动的时间为12÷1=12s，∵Q运动的路程为12×4=48cm，∵在BC上运动的次数为48÷12=4次．第一次PD=QB时，12−t=12−4t，解得t=0，不合题意，舍去；第二次PD=QB时，Q从B到C的过程中，12−t=4t−12，解得t=4.8；第三次PD=QB时，Q运动一个来回后从C到B，12−t=36−4t，解得t=8；第四次PD=QB时，Q在BC上运动3次后从B到C，12−t=4t−36，解得t=9.6.∵在运动以后，以P、D. Q、B四点组成平行四边形的次数有3次，故答案为3.点睛：本题考查了平行四边形的判定．注意能求出符合条件的所有情况是解此题的关键，注意掌握分类讨论思想的应用．13．（2020·浙江杭州市·八年级期中）如图，在四边形ABCD中，AD∵BC，AD=4，BC=12，点E是BC的中点．点P、Q分别是边AD、BC上的两点，其中点P以每秒1个单位长度的速度从点A运动到点D后再返回点A，同时点Q以每秒2个单位长度的速度从点C出发向点B运动．当其中一点到达终点时停止运动．当运动时间t为_____秒时，以点A、P，Q，E为顶点的四边形是平行四边形．【答案】2或14 3.【分析】分别从当Q运动到E和B之间与当Q运动到E和C之间去分析, 根据平行四边形的性质, 可得方程, 继而【详解】 解：E 是BC 的中点,∴BE =CE =12BC =12⨯12=6, ①当Q 运动到E 和C 之间, 设运动时间为t , 则AP =t , DP =AD -AP =4-t , CQ =2t ,EQ =CE -CQ =6-2t∴t =6-2t ,解得: t =2;②当Q 运动到E 和B 之间,设运动时间为t ,则AP =t , DP =AD -AP =4-t , CQ =2t ,EQ =CQ -CE =2t -6,∴t =2t -6,解得: t =6（舍），③P 点当D 后再返回点A 时候，Q 运动到E 和B 之间,设运动时间为t ，则AP =4-（t -4）=8-t , EQ =2t -6，∴8-t =2t -6，14t=3, ∴当运动时间t 为2、143秒时,以点P ,Q ,E ，A 为顶点的四边形是平行四边形． 故答案为: 2或143. 【点睛】 本题主要考查平行四边形的性质及解一元一次方程.14．（2021·全国八年级课时练习）如图，在Rt ABC 中，90B =∠，5AB =，12BC =，点D 是BC 边上一动点，以AC 为对角线的所有平行四边形ADCE 中，对角线DE 最小的值是_____．【答案】5【分析】由平行四边形的对角线互相平分可知，OD OE =，OA OC =，根据垂线段最短可知，当OD 取最小值时，DE 最短，此时OD BC ，由三角形中位线定理即可求出答案．【详解】在Rt ABC 中，90B =∠，∴BC AB ⊥，四边形ADCE 是平行四边形，∴OD OE =，OA OC =，∴当OD 取最小值时，DE 最短，此时OD BC ，∴OD 是ABC 的中位线， ∴1522OD AB ==，∴25DE OD ==．故答案为：5．【点睛】本题考查了平行四边形的性质，三角形中位线定理以及垂线段最短，熟练掌握平行四边形的性质是解题的关键．15．（2020·成都市·四川电子科大实验中学九年级期中）如图，四边形ABCD 是平行四边形，4AB =，12BC =，60ABC ∠=︒，点E 、F 是AD 边上的动点，且2EF =，则四边形BEFC 周长的最小值为______．【答案】14+【分析】根据题意，将点B 沿BC 向右平移2个单位长度得到点B '，作点B '关于AD 的对称点B ''，连接CB ''，交AD 于点F ，在AD 上截取2EF =，连接BE ，B F '，此时四边形BEFC 的周长为B C EF BC ''++，则当点C 、F 、B ''三点共线时，四边形BEFC 的周长最小，进而计算即可得解．【详解】如下图，将点B 沿BC 向右平移2个单位长度得到点B '，作点B '关于AD 的对称点B ''，连接CB ''，交AD于点F ，在AD 上截取2EF =，连接BE ，B F '，∵BE B F '=，B F B F '''=，此时四边形BEFC 的周长为BE EF FC BC B F EF FC BC B C EF BC ''''+++=+++=++， 当点C 、F 、B ''三点共线时，四边形BEFC 的周长最小，4AB =，2BB '=，60ABC ∠=︒，B B '''∴经过点A ，AB '∴=B B '''∴=12BC =，10B C '∴=，B C ''∴=，14B C EF BC ''∴++=+，四边形BEFC 周长的最小值为14+故答案为：14+【点睛】本题主要考查了四边形周长的最小值问题，涉及到含30的直角三角形的性质，勾股定理等，熟练掌握相关轴对称作图方法以及线段长的求解方法是解决本题的关键．16．（2019·四川省成都市七中育才学校八年级期中）如图，在ABC 中，45BAC ∠=︒，8AB AC ==，P 为AB 边上一动点，以A P 、PC 为边作平行四边形PAQC ，则对角线PQ 的最小值为__________．【答案】【分析】以P A，PC为邻边作平行四边形P AQC，由平行四边形的性质可知O是AC中点，PQ最短也就是PO最短，所以应该过O作A B的垂线PO，然后根据等腰直角三角形的性质即可求出PQ的最小值．【详解】解：∵四边形APCQ是平行四边形，∵AO=CO，OP=OQ，∵PQ最短也就是PO最短，∵过点O作OP´∵AB于P´，∵∵BAC=45°∵∵AP´O是等腰直角三角形，∵AO=12AC=4，∵OP AO ∵PQ的最小值=2OP´=故答案为：【点睛】本题考查平行四边形的性质和垂线段最短．找到最短线段是解决本题的关键．17．（2020·河南南阳市·八年级期中）如图，在∵ABCD中，AB＝，BC＝10，∵A＝45°，点E是边AD上一动点，将∵AEB沿直线BE折叠，得到∵FEB，设BF与AD交于点M，当BF与∵ABCD的一边垂直时，DM 的长为_____．【答案】4或7【分析】如图1，当BF∵AD时，如图2，当BF∵AB时，根据折叠的性质和等腰直角三角形的判定和性质即可得到结论．【详解】解：如图1，当BF∵AD时，∵∵AMB＝90°，∵将∵AEB沿BE翻折，得到∵FEB，∵∵A＝∵F＝45°，∵∵ABM＝45°，∵AB＝，∵AM＝BM＝＝3，2∵平行四边形ABCD，BC＝AD＝10，∵DM＝AD﹣AM＝10﹣3＝7；如图2，当BF∵AB时，∵将∵AEB沿BE翻折，得到∵FEB，∵∵A＝∵EFB＝45°，∵∵ABF＝90°，此时F与点M重合，∵AB＝BF＝，∵AF＝6，∵DM＝10﹣6＝4．综合以上可得DM的长为4或7．故答案为：4或7．【点睛】本题主要考查平行四边形的判定与性质，解题的关键是熟知平行四边形的性质及折叠的特点．三、解答题18．（2020·淮阳第一高级中学初中部八年级期末）如图，正方形ABCD的边长为6cm，点E在AB边上，且2AE cm=，动点M从点C开始，以2/cm s的速度沿折线C－B－E移动，动点N同时由点D开始，以1/cm s 的速度沿边DC移动，几秒钟时四边形EMND是平行四边形？【答案】103秒【分析】根据平行四边形的性质可知当EM平行且等于DN时，四边形EMDN为平行四边形，所以可设经过t（t≥3）秒后，EM等于DN，据此列出方程求解即可．【详解】解：设t（t≥3）秒时四边形EMND为平行四边形．由题意知，此时点M 运动到BE 上，则26BM t =-，DN t =，()426ME t =--，由ME DN =可得，()426t t --=， 解得，103t =． 所以103秒时四边形EMND 为平行四边形． 【点睛】本题主要考查了平行四边形的性质，根据平行四边形的对边相等列出方程是解决此题的关键．19．（2020·内蒙古通辽市·九年级月考）在四边形ABCD 中，//,90,8,2426AD BC B AB cm AD cm BC cm ∠=︒===,；点P 从点A 出发，以1/cm s 的速度向点D 运动；点Q 从点C 同时出发，以3/cm s 的速度向点B 运动． 规定其中一个动点到达端点时另一个动点也停止运动．从运动开始． 何时图中会出现平行四边形？点P Q 、最近距离为多少cm ？【答案】6s 或6.5s ；8PQ =．【分析】设经过t s 时，AP =BQ ，结合题意此时四边形ABQP 为平行四边形．根据平行四边形的性质列方程即可得到结论，当PD =CQ 时，四边形PQCD 为平行四边形，利用平行四边形的性质列方程求解，P ，Q 两点之间最短时，,PQ BC ⊥从而可得答案．【详解】解：当四边形ABQP 为平行四边形时，,AP BQ ∴=,263,AP t BQ t ==-263,t t ∴=-6.5,t =当四边形PQCD 为平行四边形时，,PD CQ ∴=24,3,PD t CQ t =-=243,t t ∴-=6,t ∴=综上：当 6.5t s =或6t s =的时候出现平行四边形．,P Q 两点最短时，,PQ BC ⊥此时四边形ABQP 为矩形，所以,P Q 之间的最短距离为8．【点睛】本题考查的是平行四边形的判定与性质，掌握平行四边形的判定与性质是解题的关键．20．（2016·江苏扬州市·八年级月考）如图所示，在直角梯形ABCD 中，AD //BC ，∵A ＝90°，AB ＝12，BC ＝21，AD =16．动点P 从点B 出发，沿射线BC 的方向以每秒2个单位长的速度运动，动点Q 同时从点A 出发，在线段AD 上以每秒1个单位长的速度向点D 运动，当其中一个动点到达端点时另一个动点也随之停止运动．设运动的时间为t （秒）．（1）设∵DPQ 的面积为S ，用含有t 的代数式表示S ．（2）当t 为何值时，四边形PCDQ 是平行四边形？【答案】S=96－6t；t=5.【解析】试题分析：（1）首先将QD的长度用含t的代数式来表示，然后得出三角形的面积与t之间的关系；（2）根据平行四边形的判定定理得出OD=PC，列出关于t的一元一次方程，求出t的值．试题解析：（1）根据题意得：AQ=t，则QD="16-t"∵S=12（16－t）×12=96－6t（2）∵AD∵BC∵当QD=PC时，四边形PCDQ是平行四边形∵BP=2t∵PC=21-2t∵16-t=21-2t∵t="5"答：当t为5秒时，四边形PCDQ是平行四边形考点：（1）平行四边形的性质；（2）一次函数；（3）动点问题．21．（2019·广东实验中学附属天河学校八年级月考）如图，等边∵ABC的边长为8，动点M从点B出发，沿B→A→C→B的方向以3的速度运动，动点N从点C出发，沿C→A→B→C方向以2的速度运动．（1）若动点M、N同时出发，经过几秒钟两点第一次相遇？（2）若动点M、N同时出发，且其中一点到达终点时，另一点即停止运动．那么运动到第几秒钟时，点A、M、N以及∵ABC的边上一点D恰能构成一个平行四边形？求出时间t并请指出此时点D的具体位置．【答案】（1）165秒；（2）运动了85秒或245秒时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=245或325．【分析】（1）设经过t秒钟两点第一次相遇，然后根据点M运动的路程+点N运动的路程=AB+CA列方程求解即可；（2）首先根据题意画出图形：如图②，当0≤t≤83时，DM+DN=AN+CN=8；当83＜t≤4时，此时A、M、N三点在同一直线上，不能构成平行四边形；4＜t≤163时，MB+NC=AN+CN=8；当163＜t≤8时，∵BNM为等边三角形，由BN=BM可求得t的值．【详解】解：（1）设经过t秒钟两点第一次相遇，由题意得：3t+2t=16，解得：t=165，所以，经过165秒钟两点第一次相遇；（2）①当0≤t≤83时，点M、N、D的位置如图2所示：∵四边形ANDM为平行四边形，∵DM=AN，DM//AN．DN//AB ∵∵MDB=∵C=60°，∵NDC=∵B=60°∵∵NDC=∵C．∵ND=NC∵DM+DN=AN+NC=AC+BN=8，即：3t+2t=8，t=85，此时点D在BC上，且BD=245（或CD=165），②当83＜t≤4时，此时A、M、N三点在同一直线上，不能构成平行四边形；③4＜t≤163时，点M、N、D的位置如图所1示：∵四边形ANDM为平行四边形，∵DN=AM，AM∵DN．∵∵NDB=∵ACB=60°∵∵ABC为等腰三角形，∵∵B=60°．∵∵MDB=∵B．∵MD=MB．∵MB+NC=AN+CN=8，3t-8+2t-8=8，解得：t=245，此时点D在BC上，且BD=325（或CD=85），④当165＜t≤8时，点M、N、D的位置如图3所示：则BN=16-2t，BM=24-3t，由题意可知：∵BNM为等边三角形，∵BN=BM，即：2t-8=3t-16，解得t=8，此时M、N重合，不能构成平行四边形．答：运动了85秒或245秒时，A、M、N、D四点能够成平行四边形，此时点D在BC上，且BD=245或325．【点睛】本题主要考查的是平行四边形的性质和等边三角形的性质，利用平行四边形的性质和等边三角形的性质求得相关线段的长度，然后列方程求解是解题的关键．22．（2021·安徽九年级一模）如图，在□ ABCD中，点P在对角线AC上一动点，过点P作PM//DC，且PM=DC，连接BM，CM，AP，BD．（1）求证：∵ADP∵∵BCM；（2）若P A=12PC，设∵ABP的面积为S，四边形BPCM的面积为T，求ST的值．【答案】（1）证明见解析；（2）13【分析】 （1）根据四边形ABCD 是平行四边形，得到AD =BC ，∵ADC +∵BCD =180︒，由PM //DC ，且PM =DC ，证得四边形PMCD 是平行四边形，得到PD =CM ，∵PDC +∵DCM =180︒，推出∵ADP =∵BCM ，即可证得结论； （2）作BH ∵AC 于H ，DG ∵AC 于G ，根据四边形ABCD 是平行四边形，得到∵ABC ∵∵CDA ，BH =DG ，求得2BCP ABP S S =，ADP ABP S S =，利用∵ADP ∵∵BCM ，得到ADP BCM S =S ，即可求出答案．【详解】（1）证明：∵四边形ABCD 是平行四边形，∵AD =BC ，∵ADC +∵BCD =180︒，∵PM //DC ，且PM =DC ，∵四边形PMCD 是平行四边形，∵PD =CM ，∵PDC +∵DCM =180︒，∵∵ADP =∵BCM ，∵∵ADP ∵∵BCM ；（2）解：作BH ∵AC 于H ，DG ∵AC 于G ，∵四边形ABCD 是平行四边形，∵∵ABC ∵∵CDA ，∵BH =DG ， ∵12ABP BCP SAP S CP ==，即2BCP ABP S S =，12112ABP ADP AP BH SS AP DG ⋅⋅==⋅⋅，即ADP ABP S S =，∵∵ADP ∵∵BCM ，∵ADP BCM S =S ， ∵S T =13ABP BCP ADP S S S =+．【点睛】此题考查平行四边形的性质，全等三角形的判定及性质，同底等高或同高的三角形的面积关系，证明∵ADP ∵∵BCM 并利用其全等的性质解决问题是解题的关键．23．（2020·吉林长春市·八年级期末）如图①，在ABCD □中，AB =3，AD =6．动点P 沿AD 边以每秒12个单位长度的速度从点A 向终点D 运动．设点P 运动的时间为()0t t >秒．（1）线段PD 的长为_________（用含t 的代数式表示）．（2）当CP 平分∵BCD 时，求t 的值．（3）如图②，另一动点Q 以每秒2个单位长度的速度从点C 出发，在CB 上往返运动．P 、Q 两点同时出发，当点P 停止运动时，点Q 也随之停止运动。
动点问题教学设计
人教版八年级下册数学第十八章平行四边形教学设计课题：四边形中的动点问题董晨浩一、内容及其分析1、内容：四边形中的动点问题.2、分析：“动点问题”是指题设图形中存在一个或多个动点，他们在线段、射线、或弧线上运动一类的开放性题目。
解决这一类问题的关键是动中求静，灵活运用有关的数学知识解决问题。
注重对几何图形运动变化能力的考察，从变化的角度和运动变化来研究四边形、函数，图像等图形。
通过对称、动点的运动等研究手段和方法来探索与发现图形性质及图形变化。
本节课选择基本图形为四边形，让学生经历探索的过程的能力立意，考查自主探究的能力，促进培养学生解决问题的能力。
综上所述本节课的难点：如何在动态问题中提炼出静态几何图形和数量关系。
二、教学目标及其分析根据教材的地位及作用，结合课程标准，从学生的学情出发。
我们将本节课的教学目标确定为：①知识与技能目标复习平行四边形、特殊平行四边形的相关知识、性质与判定；能初步应用特殊四边形的性质、判定、勾股定理等知识点综合解决动点问题的能力.②过程与方法目标（1）使学生经历探究“化动为静”、“以静制动”的过程.（2）在解决四边形动点问题的过程中，体会数形结合、转化、方程、函数、分类讨论的思想方法.③情感、态度与价值观目标在解决由变式逐层推进的问题时，培养学生的思维能力，养成主动探究的习惯，同时培养学生的合作意识和交流能力，体会探索发现的乐趣，增强学习数学的自信心。
2.分析：图形在动点运动过程中，观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程，在变化中找到不变的性质是解决数学重点和探究题型的基本思路，这也是动态几何数学问题中最研究的核心的数学素养，解决本节课的问题和达成目标的关键。
三、教学问题诊断分析动态几何的特点是问题背景是特殊图形、考查的问题也是特殊图形，所以要把握好一般与特殊的关系，分析过程中要特别关注图形的特性，特殊角、特殊图形的性质、图形的特殊位置。
八年级数学下册动点问题构成平行四边形解题技巧(一)
八年级数学下册动点问题构成平行四边形解题技巧(一)八年级数学下册动点问题构成平行四边形解题技巧什么是动点问题？动点问题是数学中经常遇到的一类问题，它通常涉及到平行四边形的性质和特点。
解决动点问题需要一定的技巧和方法。
动点问题解题技巧以下是一些解决八年级数学下册动点问题的技巧：•确定动点的位置和性质在解决动点问题时，首先要确定动点的位置和性质。
根据问题所给条件，我们可以确定动点在平行四边形内部、边界上还是延长线上。
这些信息有助于我们确定动点的坐标。
•确定平行四边形的特点平行四边形有一些独特的性质，利用这些性质可以解决动点问题。
例如，平行四边形的对角线相互平分，对角线长相等等。
通过确定平行四边形的特点，我们可以推断出关于动点的一些性质。
•运用向量法或坐标法求解在解决动点问题时，我们可以运用向量法或坐标法来求解。
向量法常用于证明或推导问题，而坐标法常用于具体计算。
具体选择使用哪种方法要根据问题的特点和要求来决定。
•画图辅助解题绘制图形是解决动点问题的重要步骤。
通过画图，我们可以更好地理解问题，并帮助我们找到解题的思路。
画图时，注意要准确绘制出平行四边形的形状和各个元素的位置关系。
•通过推理和运算得出答案在完成前面步骤后，我们可以通过推理和运算来得出最终的答案。
根据题目所要求的内容，进行逻辑推理和数学运算，得出问题的解答。
总结解决八年级数学下册动点问题需要我们熟悉平行四边形的性质和特点，并掌握相应的解题技巧。
通过确定动点的位置和性质、确定平行四边形的特点、运用向量法或坐标法、画图辅助解题以及通过推理和运算得出答案，我们可以有效地解决动点问题。
希望以上技巧能帮助到你解决八年级数学下册动点问题，在数学学习中取得更好的成绩！对于八年级数学下册动点问题构成平行四边形解题，下面给出了更具体的步骤和实例来帮助你更好地理解和应用这些技巧。
1.确定动点的位置和性质首先，从题目中找出关于动点的相关信息，然后根据这些信息来确定动点的位置和性质。
动点问题1：平行四边形及等腰梯形问题
由x 3x 20,
得x5
2 DN x 25 20 此时: 不符合题意．
故点Q与点M不能重合． x 21 1 综上所述，
（2）由（1）知，点Q只能在点M的左侧， ①当点P在点N的左侧时， P N
Q M ②当点P在点N的右侧时， P N
Q
M
（2）由（1）知，点Q 只能在点M的左侧， ①当点P在点N的左侧时， 2 由 20 ( x 3x) 20 (2 x x ) ， 解得：x1 0(舍去)，x2 2 ． 此时x=2时四边形PQMN是平行四边形． ②当点P在点N的右侧时， 由 20 ( x 3x) (2 x x2 ) 20 ， 解得：x1 10(舍去) ，x2 4 ． 此时x=4时四边形NQMP是平行四边形． 综上所述，当 x 2 或x 4时，以P，Q，M， N为顶点的四边形是平行四边形
例题：如图，在梯形ABCD中，AD∥BC，AD=4， DC=5，BC=11，梯形的高为4，动点M从B点出发 沿线段BC以每秒1个单位长度的速度向终点C运 动；动点N同时从C点出发沿CDA以每秒2单位长 度的速度向终点A运动．若M，N两点同时出发， 当其中一点到达端点时，另一点也随之停止运 动，设运动的时间为t秒． （1）t为何值时，四边形ABMN为平行四边形； （2）t为何值时，四边形CDNM为等腰梯形．
2.如图，在梯形ABCD中，AD∥BC，∠B=90°， AB=14cm，AD=18cm，• BC=21cm，点P从点A开始沿 AD边向点D以1cm/s的移动，点Q• 从点C• 开始沿CB• 边向点B• 以2cm/s的速度移动．如果P，Q分别从A， C同时出发，设移动时间为t秒， 求t为何值 时，• 梯形PQCD是等腰梯形？Biblioteka ①当点P在点N的左侧时 P N
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
动点问题练习题1．（宁夏回族自治区）已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．1、线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积； （2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．2．如图，在四边形ABCD中，3545AD BC AD DC AB B ====︒∥，，，．动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动；动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动．设运动的时间为t 秒． （1）求BC 的长．（2）当MN AB ∥时，求t 的值．（3）试探究：t 为何值时，MNC △为等腰三角形．CP Q BA M N CB1． 如图，在平面直角坐标系中，在四边形OABC 中，OA ∥BC ，点A 的坐标为(6，0)，点B 的 坐标为(4，3)，点C 在y 轴的正半轴上．动点M 在OA 上运动，从O 点出发到A 点；动点N 在AB 上运动，从A 点出发到B 点．两个动点同时出发，速度都是每秒1个单位长度，当其中一个点到达终点时，另一个点也随即停止，设两个点的运动时间为t (秒)． (1)求线段AB 的长；当t 为何值时，MN ∥OC ？(2)设△CMN 的面积为S ，求S 与t 之间的函数解析式， 并指出自变量t 的取值范围；S 是否有最小值？若有最小值，最小值是多少？(3)连接AC ，那么是否存在这样的t ，使MN 与AC 互相垂直？ 若存在，求出这时的t 值；若不存在，请说明理由．2．（河北卷）如图，在Rt △ABC 中，∠C ＝90°，AC ＝12，BC ＝16，动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动，动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动．P ，Q 分别从点A ，C 同时出发，当其中一点到达端点时，另一点也随之停止运动．在运动过程中，△PCQ 关于直线PQ 对称的图形是△PDQ ．设运动时间为t （秒）． （1）设四边形PCQD 的面积为y ，求y 与t 的函数关系式； （2）t 为何值时，四边形PQBA 是梯形？（3）是否存在时刻t ，使得PD ∥AB ？若存在，求出t 的值；若不存在，请说明理由；（4）通过观察、画图或折纸等方法，猜想是否存在时刻t ，使得PD ⊥AB ？若存在，请估计t 的值在括号中的哪个时间段内（0≤t ≤1；1＜t ≤2；2＜t ≤3；3＜t ≤4）；若不存在，请简要说明理由．3．（山东济宁）如图，A 、B 分别为x 轴和y 轴正半轴上的点。
OA 、OB的长分别是方程x 2－14x ＋48＝0的两根(OA ＞OB)，直线BC 平分∠ABO 交x 轴于C 点，P 为BC 上一动点，P 点以每秒1个单位的速度从B 点开始沿BC 方向移动。
(1)设△APB 和△OPB 的面积分别为S 1、S 2，求S 1∶S 2的值； (2)求直线BC 的解析式；(3)设PA －PO ＝m ，P 点的移动时间为t 。
①当0＜t≤m 的取值范围； ②当t＞m 的取值范围如何(只要求写出结论)？AP CEDBCAQP 4．在ABC ∆中，,4,5,D BC CD 3cm,C Rt AC cm BC cm ∠=∠==点在上，且以＝现有两个动点P 、Q 分别从点A 和点B 同时出发，其中点P 以1cm/s 的速度，沿AC 向终点C 移动；点Q 以1.25cm/s 的速度沿BC 向终点C 移动。
过点P 作PE ∥BC 交AD 于点E ，连结EQ 。
设动点运动时间为x 秒。
（1）用含x 的代数式表示AE 、DE 的长度；（2）当点Q 在BD （不包括点B 、D ）上移动时，设EDQ ∆的面积为2()y cm ，求y 与月份x 的函数关系式，并写出自变量x 的取值范围； （3）当x 为何值时，EDQ ∆为直角三角形。
5.（金华）如图1，在平面直角坐标系中，已知点(043)A ，，点B 在x 正半轴上，且30ABO =∠．动点P 在线段AB 上从点A 向点B 3设运动时间为t 秒．在x 轴上取两点M N ，作等边PMN △．（1）求直线AB 的解析式；（2）求等边PMN △的边长（用t 的代数式表示），并求出当等边PMN △的顶点M 运动到与原点O 重合时t 的值；（3）如果取OB 的中点D ，以OD 为边在Rt AOB △内部作如图2所示的矩形ODCE ，点C 在线段AB 上．设等边PMN △和矩形ODCE 重叠部分的面积为S ，请求出当02t ≤≤秒时S 与t 的函数关系式，并求出S 的最大值．6．（相似）两块完全相同的直角三角板ABC 和DEF 如图1所示放置，点C 、F 重合，且BC 、DF 在（图1） y A P M O N B x （图2）yA CO D B xEPDA 一条直线上，其中AC =DF =4，BC =EF =3．固定Rt △ABC 不动，让Rt △DEF 沿CB 向左平移，直到点F 和点B 重合为止．设FC =x ，两个三角形重叠阴影部分的面积为y ． （1）如图2，求当x =21时，y 的值是多少？ （2）如图3，当点E 移动到AB 上时，求x 、y 的值； （3）求y 与x 之间的函数关系式；8.（重庆课改卷）如图1所示，一张三角形纸片ABC ，∠ACB=90°，AC=8，BC=6.沿斜边AB 的中线CD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形（如图2所示）.将纸片11AC D ∆沿直线2D B （AB ）方向平移（点12,,,A D D B 始终在同一直线上），当点1D 于点B 重合时，停止平移.在平移过程中，11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.（1）当11AC D ∆平移到如图3所示的位置时，猜想图中的1D E 与2D F 的数量关系，并证明你的猜想；（2）设平移距离21D D 为x ，11AC D ∆与22BC D ∆重叠部分面积为y ，请写出y 与x 的函数关系式，以及自变量的取值范围；（3）对于（2）中的结论是否存在这样的x 的值；使得重叠部分的面积等于原ABC ∆面积的14？若不存在，请说明理由.1． 四边形ABCD 中，AD ∥BC ，∠B=90°，AD=24cm ，AB=8cm ，BC=26cm ，CB D A 图1PEF AD 1B1D 2C 2图3C 2D 2C 1BD 1A 图2动点P 从点A 开始，沿AD 边，以1厘米/秒的速度向点D 运动；动点Q 从点C 开始，沿CB 边，以3厘米/秒的速度向B 点运动。
已知P 、Q 两点分别从A 、C 同时出发，，当其中一点到达端点时，另一点也随之停止运动。
假设运动时间为t 秒，问： （1）t 为何值时，四边形PQCD 是平行四边形？（2）在某个时刻，四边形PQCD 可能是菱形吗？为什么？ （3）t 为何值时，四边形PQCD 是直角梯形？ （4）t 为何值时，四边形PQCD 是等腰梯形？2. 如右图，在矩形ABCD 中，AB=20cm ，BC=4cm ，点P 从A 开始沿折线A —B —C —D 以4cm/s 的速度运动，点Q 从C 开始沿CD 边1cm/s 的速度移动，如果点P 、Q 分别从A 、C 同时 出发，当其中一点到达点D 时，另一点也随之停止运动，设运动 时间为t (s)，t 为何值时，四边形APQD 也为矩形？3. 如图，在等腰梯形ABCD 中，AB ∥DC ，cm BC AD 5==,AB =12 cm,CD =6cm , 点P 从A 开 始沿AB 边向B 以每秒3cm 的速度移动，点Q 从C 开始沿CD 边向D 以每秒1cm 的速度移动， 如果点P 、Q 分别从A 、C 同时出发，当其中一点到达终点时运动停止。
设运动时间为t 秒。
（1）求证：当t=23时，四边形APQD 是平行四边形； （2）PQ 是否可能平分对角线BD ？若能，求出当t 为何值时PQ 平分BD ；若不能，请说明理由； （3）若△DPQ 是以PQ 为腰的等腰三角形，求t 的值。
ABCD PA F DPE B Q CO N M E FC A4. 如图所示，△ABC 中，点O 是AC 边上的一个动点，过O 作直线MN ∠BCA ∠BCA 6=2AE BC ∠B 如图所示，有四个动点P 、Q 、E 、F 分别从正方形ABCD 的四个顶点出发，沿着AB 、BC 、CD 、DA 以同样的速度向B 、C 、D 、A 各点移动。
（1）试判断四边形PQEF 是正方形并证明。
（2）PE 是否总过某一定点，并说明理由。
（3）四边形PQEF 的顶点位于何处时，其面积最小，最大？各是多少？7. 已知在梯形ABCD 中，AD ∥BC ，AB = DC ，对角线AC 和BD 相交于点O ，E 是BC 边上一个动点（E 点不与B 、C 两点重合），EF ∥BD 交AC 于点F ，EG ∥AC 交BD 于点G . ⑴求证：四边形EFOG 的周长等于2 OB ；⑵请你将上述题目的条件“梯形ABCD 中，AD ∥BC ，AB = DC ”改为另一种四边形，其他条件不变，使得结论“四边形EFOG 的周长等于2 OB ”仍成立，并将改编后的题目画出图形，写出已知、求证、不必证明.如图，直角梯形ABCD 中，AD ∥BC ，∠ABC＝90°，已知AD ＝AB ＝3，BC ＝4，动点P 从B 点出发，沿线段BC 向点C 作匀速运动；动点Q 从点D 出发，沿线段DA 向点A 作匀速运动．过Q 点垂直于AD 的射线交AC 于点M ，交BC 于点N ．P 、Q 两点同时出发，速度都为每秒1个单位长度．当Q 点运动到A 点，P 、Q 两点同时停止运动．设点Q 运动的时间为t 秒．（1）求NC ，MC 的长(用t 的代数式表示)；（2）当t 为何值时，四边形PCDQ 构成平行四边形？（3）是否存在某一时刻，使射线QN 恰好将△ABC 的面积和周长同时平分？若存在，求出此时t 的值；若不存在，请说明理由；（4）探究：t 为何值时，△PMC 为等腰三角形？图10G FO D A10.如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动．设点P的运动时间为t（s），解答下列问题：（1）当t为何值时，△PBQ是直角三角形?（2）设四边形APQC的面积为y（cm2），求y与t的关系式；是否存在某一时刻t，使四边形APQC的面积是△ABC面积的23？如果存在，求出相应的t值；不存在，说明理由；（3）设PQ的长为x（cm），试确定y与x之间的关系式．CB。