2014-2015学年第一学期八年级数学第一次月考试题
广州市八年级上数学月考试题

6.如图 1,△ABC≌△EDF,DF=BC,AB=ED,
AF=20,EC=10,则 AE 的长是(
)
(A)5 (B)8 (C)10
(D)15
E
A
D F
C
图1
B
7.在△ABC 和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍
不一定能保证△ABC≌△A′B′C′,则补充的这个条件是:( )
A、BC=B′C′ B、∠A=∠A′ C、AC=A′C′ D、∠C=∠C′
8.根据下列条件,能判定△ABC≌△A′B′C′的是:( )
A、 AB=A′B′,BC=B′C,∠A=∠A′ B、 ∠A=∠A′,∠B=∠C′,AC= A′C′ C、 ∠A=∠A′,∠B=∠B′,∠C=∠C′
D
C
O
D、AB=A′B′,BC=B′C′ AC= A′C′ A
2014-2015 学年度八年级数学第一学期月考试卷
班级
姓名
考号
一、选择题(每小题 2 分,共 20 分)
1.以下面各组线段为边,能组成三角形的是( ).
A.1cm,2cm,4cm B.8cm,6cm,4cm
C.12cm,5cm,6cm D.2cm,3cm,6cm
2.正多边形的一个内角等于 144°,则该多边形是正(
5.如图, 外角 CAE 等于120 , B = 40 ,则 C 的度数是______ .
第5题
第6题
6.如图 AB // CD , CE 平分 ACD 交 AB 于 E ,A = 118 ,则 AEC 等于______ 度.
7.如图(5),已知 AB=DC,AD=BC,E、F 是 DB 上两点且 BF=DE,
即 AB=
2014-2015学年九年级第一次月考数学试题

2014-2015学年九年级第一次月考数学试题一.选择题:(每题3分)1.(2005·甘肃兰州)已知m 方程012=--x x 的一个根,则代数式m m -2的值等于( )A.—1B.0C.1D.22.(2005·广东深圳)方程x x 22=的解为( )A.x =2B. x 1=2-,x 2=0C. x 1=2,x 2=0D. x =03.解方程)15(3)15(2-=-x x 的适当方法是( )A 、开平方法B 、配方法C 、公式法D 、因式分解法4.从正方形的铁皮上,截去2cm 宽的一条长方形,余下的面积是48cm 2,则原来的正方形铁皮的面积是( )A.9cm 2B.68cm 2C.8cm 2D.64cm 25.若方程013)2(||=+++mx x m m 是关于x 的一元二次方程,则( )A .2±=mB .m=2C .m= —2D .2±≠m6. 函数y=x 2-2x+3的图象的顶点坐标是( )A. (1,-4)B.(-1,2)C. (1,2)D.(0,3)7.一元二次方程0624)2(2=-+--m mx x m 有两个相等的实数根,则m 等于 ( )A. 6-B. 1C. 2D. 6-或18. 已知二次函数y=ax 2+bx+c 的图象如图所示,则下列结论中,正确的是( )A. ab>0,c>0B. ab>0,c<0C. ab<0,c>0D. ab<0,c<09.如果关于x 的方程ax 2+x –1= 0有实数根,则a 的取值范围是( )A .a >–14B .a ≥–14C .a ≥–14 且a ≠0D .a >–14且a ≠0 10.对于抛物线21(5)33y x =--+,下列说法正确的是( ) (A )开口向下,顶点坐标(53),(B )开口向上,顶点坐标(53), (C )开口向下,顶点坐标(53)-,(D )开口向上,顶点坐标(53)-,二、填空题(每题3分)11.二次函数23y x bx =++的对称轴是2x =,则 b =_______.12.一元二次方程22310x x -+=的二次项系数为 ,一次项系数为 ,常数项为 ;13.抛物线2y ax bx c =++过点(10)A ,,(30)B ,,则此抛物线的对称轴是直线x = .14.一元二次方程20(0)ax bx c a ++=≠的求根公式为 ; 15.抛物线y=x 2+bx+c, 经过A (-1,0),B(3,0)两点,则这条抛物线的解析式为_____________16.当代数式532++x x 的值等于7时,代数式2932-+x x 的值是 ;17.关于x 的一元二次方程02)12(2=--+x m mx 的根的判别式的值等于4,则 =m ;18.目前甲型H1N1流感病毒在全球已有蔓延趋势,世界卫生组织提出各国要严加防控,因为曾经有一种流感病毒,若一人患了流感,经过两轮传染后共有81人患流感.如果设每轮传染中平均一个人传染x 个人,那么可列方程为 .19.若一个三角形的三边长均满足方程2680x x -+=,则此三角形的周长为 ;20.参加一次同学聚会,每两人都握一次手,所有人共握了45次,若设共有x 人参加同学聚会。
2014-2015年八年级数学上第一次月考试卷含答案

八年级上册数学第一次月考试卷2014、9 一.选择题(共10小题,每小题3分)1.下列学习用具中,其形状不是轴对称图形的是()A.B.C.D.2.下列各组数可能是一个三角形的边长的是()A.1,2,4 B.4,5,9 C.4,6,8 D.5,5,113.在△ABC中,∠B=40°,∠C=80°,则∠A的度数为()A.30°B.40°C.50°D.60°4.在数学课上,同学们在练习画边AC上的高时,有一部分同学画出下列四种图形,请你判断一下,正确的是()A B C D5.下列命题为假命题的是()A.有两条边和一个角对应相等的两个三角形全等;B.对顶角相等C.等腰三角形的两个底角相等; D.两直线平行,内错角相等6.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,在下列结论中,不正确的是()A.∠EAB=∠FAC;B.BC=EF;C.∠BAC=∠CAF;D.∠AFE=∠ACB7.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是()A.∠BCA=∠F B.∠B=∠E C.BC∥EF D.∠A=∠EDF8.一个等腰三角形两边的长分别为4和9,那么这个三角形的周长是()A.13 B.17 C.22 D.17或229.如图,在△ABC中,已知∠B和∠C的平分线相交于点D,过点D作EF∥BC 交AB、AC于点E、F,若△AEF的周长为9,BC=6,则△ABC的周长为()A.18 B.17 C.16 D.1510.小明用19根火柴首尾顺次相接,恰好摆成一个三角形,若要求这个三角形是等腰三角形,则不同的摆法有()A.1种B.4种C.5种D.9种二.填空题(共8小题,每小题3分)11.如图,在△ABC中,∠A=45°,∠B=60°,则外角∠ACD=________度.12.已知△ABC中,AB=AC=2,∠A=60度,则△ABC的周长为_______.13.命题“等腰三角形的两个底角相等.”的逆命题是________________________.14.如图,已知AC=DB,再添加一个适当的条件___________,使△ABC≌△DCB.(只需填写满足要求的一个条件即可).15.如图,已知AE∥BD,∠1=130°,∠2=30°,则∠C=________度.16.如图,AD⊥BC于点D,D为BC的中点,连接AB,∠ABC的平分线交AD 于点O,连结OC,若∠AOC=125°,则∠ABC=_________.17.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为_______.18.如图,已知:∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为_________.第11题图第14题图第15题图第16题图11、___________12、__________13、__________14、___________15、___________16、__________17、__________18、___________三、解答题19、(8分)在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面给出的图中画出4个这样的△DEF。
八年级数学第一次月考质量分析报告
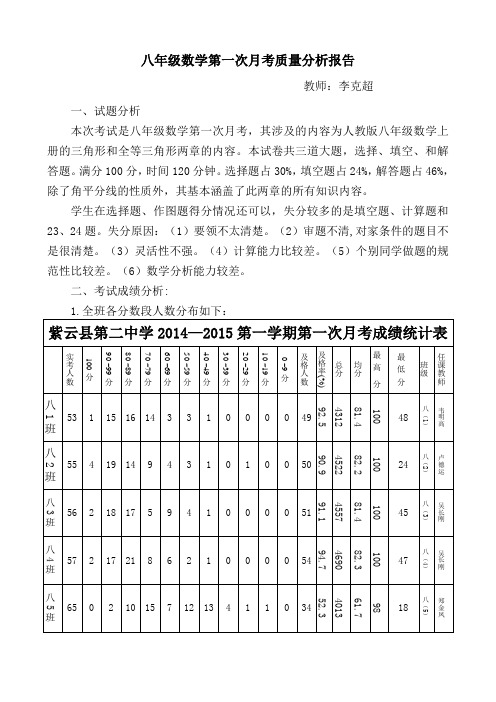
100 81.4 4312 (%) 92.5
1
八
53 1 15 16 14 3 3 1 0 0 0 0 49
班
48
1
八 (
韦 明
)高
2
八
55 4 19 14 9 4 3 1 0 1 0 0 50
班
100 82.2 4522 90.9
八卢
24 ( 德
)运
2
3
八 56 2 18 17 5 9 4 1 0 0 0 0 51
三、教与学存在的问题 ①学生层面: 对前面(1)(2)(3)(4)(5)(6)班来说还好点,各种表现都较好, 老师也教得很认真负责,但是及格率也还远没有到达 100%,希望实验班的老师 再改进方法,争取更优,你们要再接再厉,努力塑造二中品牌。
对于平行班来说: 1.学生的基础差,严重影响了学生的学习积极性。 2.学生的基础知识掌握不牢,综合分析问题、解决问题的能力差。 3. 整体素质偏低。学生的优秀率、及格率整体偏低。尖子生不突出,换句 话说,这种班级没有尖子生,后进生数量多,严重影响教学质量。 4. 学生整体学习风气不浓,不能做到主动学习和提前学习,大部分同学都 是在教师的监督下进行,并且个别同学缺乏数学学习的兴趣。无心向学的学生 较多,马虎应付学习的学生多,导致学习成绩不好。一部分学生不仅自己不好 好学习,而且还影响其他人,严重影响了良好班风和学风的形成。 5.学生的学习习惯较差。具体表现在:时间抓得不紧,不会合理安排和利 用;布置的作业好多学生不认真写,有的抄作业应付;课后没有养成及时复习 的习惯,对课堂知识的理解和掌握不到位,直接影响到后续知识的学习,导致 知识漏洞越来越大。 ②教师层面: 1.结合平时课堂的反映及考试成绩比较,在课堂上有以下几个问题:一是 课堂无计划性,包括知识目标、能力目标、时间搭配、教学进度、学生的个体 差异不能很好的规划。二是对基础知识课堂落实不到位,缺乏学生良好习惯的 培养。三是课堂练习的实效性差。 2.教师角色转化不到位。教学方式没有发生实际性的变化。仍然把重心放 在教上,忽视了练习的过程,学生被动学习。 3.课后辅导抓得不扎实。 4.教学理念和教学方法有待改进 在新课改的形势下,不主动学习,自身的教学理念和教学方法跟不上新课 改的要求,教学理念和教学方法陈旧。课堂上不能很好地调动学生的积极性, 课堂气氛不活跃、枯燥,导致学生对学习产生厌倦情绪,不想学,怕学,课堂 效率低下。 四、结合本次考试质量分析特提出以下努力措施: 1、转变教学理念,适应课程改革 要提高学生素质,首先要转变教学理念,。认真学习和研究《课程标准》 是转变教学理念的主要途径。在教学过程中,要改变教学方式, 关注学生的学
2014-2015学年滕州市八年级上第一次月考数学试题【北师大版】

一.单选题(3*10=30)1. 在△ABC 中,A B C ∠∠∠,,的对边分别为a b c ,,,且2()()a b a b c +-=,则( ).(A )A ∠为直角 (B )C ∠为直角(C )B ∠为直角 (D )不是直角三角形2.△ABC 中,∠A ,∠B ,∠C 的对边分别记为a ,b ,c ,由下列条件不能判定△ABC 为直角三角形的是( )A .∠A +∠B =∠C B .∠A ∶∠B ∶∠C =1∶2∶3C .222a c b =-D .a ∶b ∶c =3∶4∶63.如图所示,以Rt△ABC 的三条边为直径分别向外作半圆,设以BC 为直径的半圆的面积记作S 1,以AC 为直径的半圆的面积记作S 2,以AB 为直径的半圆的面积记作S 3,则S 1、S 2、S 3之间的关系正确的是( )A .S 1+S 2>S 3B .S 1+S 2<S 3C .S 1+S 2=S 3D .无法确定4.由于台风的影响,一棵树在离地面6 m 处折断(如图),树顶落在离树干底部8 m 处,则这棵树在折断前(不包括树根)长度是( )A .8 mB .10 mC .16 mD .18 m5.如果a 有算术平方根,那么a 一定是( )(A )正数 (B )0 (C )非负数 (D )非正数6.已知△ABC 的三边长分别为5,13,12,则△A BC 的面积为( )A .30B .60C .78D .不能确定7.将一个直角三角形两直角边同时扩大到原来的两倍,则斜边扩大到原来的( )A .4倍B .2倍C .不变D .无法确定8、已知x 、y 为正数,且|x 2-4|+(y 2-3)2=0,如果以x 、y 为直角边长作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为()A .5B .25C .7D .159.下列各组数中互为相反数的是( )(A )2-与2)2(- (B )2-与38- (C )2-与21- (D )2与2- 10.若将三个数3-,7,11表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )(A )3- (B )7 (C )11 (D ) 无法确定二、填空题(3*10=30)11.已知等腰三角形的一条腰长为5,底边长是6,则它底边上的高为________.12.在△ABC 中,∠C =90°,若AB =5,则AB 2+AC 2+BC 2=________.13.如图:一个圆柱的底面周长为16cm ,高为6cm ,BC 是上底面的直径,一只蚂蚁从点A 出发,沿着圆柱的侧面爬行到点C ,则蚂蚁爬行的最短路程为 cm .14.2)81(-的算术平方根是 ,271的立方根是 。
2014-2015年第一次月考八年级数学试题

2014-2015年第一次月考八年级数学试题(时间:120分钟 总分:150分)注意:本卷所有试题答案都要填在答卷相应位置一、选择题(每小题3分,共30分) 1.16的平方根是( )A .4B .±4C .±2D .2 2.下列说法正确的是( )A .负数没有立方根B .如果一个数有立方根,那么它一定有平方根C .一个数有两个立方根D .一个数的立方根与被开方数同号3.如图,数轴上点P 表示的数可能是( )A .7B .7-C .2.3-D .10-4.在实数 121121112272241053.、、、π、、、-中,无理数的个数为( ) A .1个 B .2个 C .3个 D .4个 5.下列运算中, 正确的个数是( ) ①1251144251=;②74322=+;③981±=;④73433-=- A .1个 B .2个 C .3个 D .4个 6.下列各式计算正确的是( )A .()222b a b a -=-B .()0248≠=÷a a a aC .523632a a a =⋅D .()632a a =- 7.下列计算中可采用平方差公式的是( )A .()()z x y x -+B .()()y x y x 22++-C .()()y x y x +--33D .()()a b b a 3232-+8.若一个正数的两个平方根分别是1-a 和3-a ,则a 的值为 ( )A .-2B .2C .1D .4 9.若()M y xy x y x ++-=-22242,则M 为( )A .xyB .-xyC .3xyD .-3xy10.若改动多项式22129y xy x ++中的某一项,使它变成完全平方式,则改动的办法是( )A .只能改动第一项B .只能改动第二项C .只能改动第三项D .可以改动三项中的任意一项二、填空题(每小题3分,共30分) 11.5的相反数为 . 12.比较大小:215- 21(用“>”、“<”“=”填空) 13.无理数105-的整数部分为 . 14.已知233+-+-=x x y ,则xy = .15.从边长为a 的大正方形纸板中挖去一个边长为b 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为 .16.若2=m a ,3=n a ,则n m a 2+的值为 .17.若32-x 与321y -互为相反数,则y x 2-的值为 . 18.如果11=-x x ,那么221xx += . 19.已知实数a 满足0332=++a a a ,那么=++-32a a . 20.已知204=x ,205=y ,则xy y x -+2的值为 .2014年秋初2013级第一次月考数学答题卷(时间:120分钟 总分:150分)一、选择题(每小题3分,共30分)题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题(每小题3分,共30分)11、 12、 13、 14、 15、 16、 17、 18、 19、 20、 三、解答题(共90分) 21.直接写出计算结果(每小题3分,共18分)① ()()()=-÷-⋅-643a a a ②()=-23xy③ =+--)32(32x x x ④()=--22b a⑤()()=-+y x y x 44 ⑥()()=+-56x x22.计算(每小题4分,共24分) (1)()16912823+-+- (2) ()3223xy z x -⋅(3) ()()y x y x 232+- (4) ()()2222x y y x --+(5) ()()1212++-+b a b a (6)⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+8422112112112112123.解方程(每小题4分,共8分)(1) ()01253=--x (2) ()()()45312=-+-+x x x 24.(5分)先化简,再求值:()()()1132+--+a a a ,其中3=a .25.(5分)先化简,再求值:()()()2422223y y x x y x y x +---+,其中201411=-=y x ,.26.(5分)已知03=-++b b a ,求b a -的值.27.(5分)已知12-+y x 的算术平方根是4,1+-y x 的立方根是3,求y 、x 的值.28.(6分)若()()n x x m x +-+32的积中不含32x x 、项,求n m 和的值.29.(6分)如图,大小两个正方形边长分别为a 、b . (1)用含a 、b 的代数式阴影部分的面积S ; (2)如果5,7==+ab b a ,求阴影部分的面积. 30.(8分)图①是一个长为2m ,宽为2n 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)图②中的阴影部分的正方形边长为 ;(2)观察图②,三个代数式()()mn n m n m ,,22-+之间的等量关系是 ;(3)观察图③,你能得到怎样的代数恒等式呢? ; (4)试画出一个几何图形,使它的面积能表示()()22232n mn m n m n m ++=++.(画在虚线框内)。
八年级数学

. .2014-2015学年第一学期八年级数学月考试题(总分120分)一. 选择题(共8题,24分)1、在下列各数:-0.333…, 4, 5, π-, 3π, 3.1415, 2.010101…(相邻两个1之间有1个0),76.0123456…(小数部分由相继的正整数组成). 中是无理数的有 ( )A.3个B.4个C. 5个D. 6个 2、下列各式中,正确的是( ) A .()222-=- B .()932=- C .39±= D .39±=±3、25的平方根是( )A 、5B 、5-C 、5±D 、5± 4.下列说法正确的是( )A .一个有理数的平方根有两个,它们互为相反数B .负数没有立方根C .无理数都是开不尽的方根数D .无理数都是无限小数 5、如果一个数的立方根是这个数本身,那么这个数是( ) A 、1 B 、1- C 、1± D 、0,1±6、一直角三角形的三边分别为2、3、x ,那么以x 为边长的正方形的面积为( )A 、13B 、5C 、13或5D 、无法确定7、4的平方的倒数的算术平方根是( )A .4B .18C .-14D .148.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )72425207152024257252024257202415(A)(B)(C)(D)班级 姓名 考密 封 线 内 不 要 答 卷………………………………………………装………………………………订………………………………线………………………………………………二.填空题(共8题,24分)9.如果a 的平方根等于2±,那么_____=a ;10.64 __ ____11-4.2(填 >或< 号)12.若a 、b 互为相反数,c 、d 互为倒数,则______3=++cd b a 。
八上压轴题(201429)

点评:(1)本题中的 2 倍角的问题,可以转化为∠BDC=∠BAC 然后利用“8”字型即可推导 出来;(2)证明角平分线的问题有两种途径,既可以直接证角相等,也可以转证线段相等。本 题可以利用第二种方法证明;(3)线段的和差问题,可以直接思考“截长补短”法。本题可以 根据经验猜想∠BAC 应该是一个特殊角——60°。
考点: 专题: 分析:
全等三角形的判定与性质;坐标与图形性质;三角形的面积;等腰三角形的性质. 几何综合题.
菁优网版 权所有
(1)根据点 B、C 的坐标判断出 y 轴是 BC 的垂直平分线,再根据线段垂直平分线上的点到线段两端点的距离相 可得 AB=AC, PB=PC, 根据等边对等角可得∠ABC=∠ACB, ∠PBC=∠PCB, 然后利用“角边角”证明△BCF 和△C 全等,根据全等三角形对应边相等可得 BE=CF; (2)连接 OF,先求出△AOB 的面积,再根据等高的三角形的面积的比等于底边的比求出△BOF 和△AOF 的面 再根据三角形的面积列式求出点 F 的横坐标与纵坐标的长度,从而得解; (3)设∠BAC=α,根据三角形的面积求出 BE=BA,根据等边对等角可得∠BEA=∠BAE=α,根据等腰三角形三 合一的性质和直角三角形两锐角互余求出∠ACB,再根据三角形的内角和定理求出α<90°,根据三角形的一个外 大于任何一个与它不相邻的内角可得∠AEB>∠ACB, 然后求出α>60°, 然后分α=60°和 90°时求出 m 的值即可得 (1)证明:∵B(﹣3,0),C(3,0), ∴OB=OC, ∴y 轴是 BC 的垂直平分线, 又∵点 A 在 y 轴正半轴上,点 P 在线段 OA 上, ∴AB=AC,PB=PC, ∴∠ABC=∠ACB,∠PBC=∠PCB,
解答:
(1)证明:∵
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014-2015学年第一学期八年级数学第一次月考试题
一、选择题 (每题3分)
1. 如图1,在①AB=AC ②A D=AE ③∠B=∠C ④BD=CE 四个条件中,能证明△ABD 与△ACE 全等的条件顺序是( )
A. ① ② ③
B. ② ③ ④
C. ① ② ④
D. ③ ② ④
D
C
B A
E
(3图) 2. 下列条件中,能让△ABC ≌△DFE
的条件是(
)
A. AB=DE ,∠A=∠D , BC=EF;
B. AB=BC ,∠B=∠E , BE=EF;
C. AB=EF ,∠A=∠D , AC=DF;
D. BC=EF ,∠C=∠F , AC=DF.
3. 如图,CD ⊥AB,BE ⊥AC,垂足为D 、E ,BE 、CD 相交于O 点,∠1=∠2,图中全等的三角形共有( )
A.1对
B.2对
C. 3对
D.4对
4. 两个直角三角形全等的条件是( )
A.一个锐角对应相等 ;
B.一条对边对应相等;C .两直角边对应相等;D.两个角对应相等
5. 如图所示,表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ) A.1处 B.2处 C.3处
D.4处
(7图)
(5图)
6. 在△ABC 和△A ′B ′C ′中,AB =A ′B ′,∠B=∠B ′,补充条件后仍不一定能保证△ABC ≌△A ′B ′C ′,
则补充的这个条件是:( )
A 、BC=
B ′
C ′ B 、∠A=∠A ′ C 、AC=A ′C ′
D 、∠C=∠C ′
7. 如图,OA=OC ,OB=OD ,则图中全等三角形共有( )
D
C B
A
2
1O
E
A
A 、2对
B 、3对
C 、4对
D 、5对
8. 两个三角形有两个角对应相等,正确的说法是( )
A 、两个三角形全等
B 、如果一对等角的角平分线相等,两三角形就全等
C 、两个三角形一定不全等
D 、如果还有一个角相等,两三角形就全等
9. 已知△ABC 在直角坐标系中的位置如图所示,如果△A'B'C' 与△ABC 关于y 轴对称,那么点A 的对应
点A'的坐标为( ).
A .(-4,2)
B .(-4,-2)
C .(4,-2)
D .(4,2)
10. 在△ABC 中,∠B 的平分线与∠C 的平分线相交于O ,且∠BOC=130°,则∠A=[ ]
A 50°
B 60°
C 80°
D 100°
二、填空题 (每题3分)
11. 如图,已知AB =AD ,需要条件_________可得△ABC ≌△ADC ,根据是________.
12. 已知线段AB ,直线CD ⊥AB 于O ,AO =OB ,若点M 在直线CD 上,则MA =____,若NA =NB ,则N 在________
上.
13. 如图,已知∠CAB=∠DBA , 要使△ABC ≌△BAD,只要增加的一个条件是________ (只写一个)。
D
C
B
A
(14图)
14. 如图,AE=AD, ∠B=∠C,BE=6,AD=4,则AC=______ .
D
C
A
E
15. 如图,已知∠DCE=∠A=90°,BE ⊥AC 于B,且DC=EC,BE=8cm,则AD+AB=_____ .
D
C
B A
16. 在ABC △中∠BAC 和∠ABC 的平分线相交于P ,若P 到AB 的距离为10,则它到边AC 和BC 的距离和
为 .
17. 如图,已知AE ∥BF , ∠E =∠F ,要使△ADE ≌△BCF ,可添加的条件是__________.
18. 在直角△ABC 中,∠C =90°,AD 平分∠BAC 交BC 于点D ,若CD =4,则点D 到斜边AB 的距离等于
_______________。
19. 若P 关于x 轴的对称点为()1,21+-+a b a P ,关于y 轴对称的点为()2,42+-b b P
,则P 点的坐标为 。
20. 如图,在ABC 和△FDE 中,AD=FC ,AB=EF ,当添加条件 时,就可得到△ABC ≌△FED 。
(只需填
写一个正确条件即可)
F
E
三、证明题 (21—22每题6分,23—26每题7分)
21. 如图,已知AB CD =,AE DF =,CE BF =.
求证:AF DE =.
22. 如图,已知12∠=∠,34∠=∠. 求证:BE CD =.
B
23. 如图,已知A F E B ,,,四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =. 求证:ACF BDE △≌△.
24. 如图,在ABC △中,点E 在BC 上,点D 在AE 上.
已知ABD ACD BDE CDE ∠=∠∠=∠,.求证:BD CD =.
B E
C
A F
D E B C
25. 如图,AB=AC,AD=AG,AE ⊥BG 交BG 的延长线于E ,AF ⊥CD 交CD 的延长线于F.求证:AE=AF.
D
F C
A E G
26. 如图,给出五个等量关系:①AD BC = ②AC BD = ③CE DE = ④D C ∠=∠ ⑤
DAB CBA ∠=∠.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出
一种情况),并加以证明.
A B
参考答案:
一、选择题
1. C
2. D ;
3. D
4. C
5. D
6. C
7. C
8. B
9. D 10. C
二、填空题
11. BC =DC ,SSS . 12. MB , 直线CD 13. AC=BD(答案不唯一) 14. 10
15. 8cm 16. 20, 17. AD=BC 18. 4,提示利用角平分线的性质。
19. ( -9,-3) 提示:()1,21+-+a b a P 与 ()2,42+-b b P 两坐标互为相反数。
20. BC=ED 或∠A ∠F 或AB ∥EF 或∠B=∠E=RT ∠等
三、证明题
21.
BF CE =BF EF CE EF ∴+=+BE CF ∴=又AB CD =,AE DF =,根据“SSS ”证
ABE DCF △≌△.B C ∴∠=∠,又A B C =,BF CE =,根据S A S 证
ABF DCE △≌△AF DE ∴=.
22. 34∠=∠,AD AE ∴=, 又1324∠+∠=∠+∠ 即ADC AEB ∠=∠,
又A A ∠=∠根据ASA 证ABE ACD △≌△, BE CD ∴=.
23. 证明:
AC CE ⊥,BD DF ⊥(已知)
90ACE BDF ∴∠=∠=(垂直的定义)
在Rt ACE △和Rt BDF △中,
()
()AE BF AC BD =⎧⎨
=⎩
已知已知 Rt HL ACE Rt BDF ∴△≌△()
A B ∴∠=∠(全等三角形的对应角相等)
()AE BF =已知
AE EF BF EF ∴-=-(等式性质) 即AF BE =
()()()AF BE ACF BDE A B AC BD =⎧⎪
∠=∠⎨⎪=⎩已证在和中已证已知△△,
SAS ACF BDE ∴△≌△().
24. 提示:证明:ABD ACD △≌△.
25. Rt △ABE ≌ Rt △ECD(AAS)
26. 情况一:已知:AD BC AC BD ==,
求证:CE DE =(或D C ∠=∠或DAB CBA ∠=∠) 情况二:已知:D C DAB CBA ∠=∠∠=∠,
求证:AD BC =(或AC BD =或CE DE =)。
