2.6闭环传递函数
3.2 闭环系统的传递函数

G0 (s ) = G (s )
p
0 .2 3s + 1.25
q y
4 G0 (s ) = s + 1.25
v
e
4 s + 1.25
§3.2 闭环系统的传递函数
2.关系:闭环传函的分母 = 开环传函+1
练习:系统结构图如图,试求Wyr (s ) 和 Wyf (s )
G (s ) 消去E(s )得: Y (s ) Y (s ) G (s ) Wyx (s ) = = X ( s ) 1 + G ( s )H ( s )
1 消去Y(s )得: E (s ) = X (s ) 1 + G (s )H (s ) E (s ) 1 = ∴ Wex (s ) = X (s ) 1 + G (s )H (s )
§3.2 闭环系统的传递函数
一、闭环系统的传函
X (s ) E (s ) G (s ) H (s )
1、基本概念: 1)前向通道:从偏差(e)到输出(y)的通道 2)反馈通道: 从输出(y)到偏差(e)的通道 2、闭环系统的传函W(s)
Y (s ) X (s ) E (s )
G (s )
Y (s )
Y (s ) X (s ) = 0,Wyp (s ) = = 1 + Gc (s )G p (s )F (s ) P(s )
Y2 (s ) = W yp (s ) × P(s )
G p (s )
∴Y (s ) = Y1 (s ) + Y2 (s )
= W yx (s ) ⋅ X (s ) + Wyp (s ) ⋅ P(s )
= 1 +G c (s )G p (s )F (s ) G c (s )G p (s ) ⋅ X (s ) + 1 +G c (s )G p (s )F (s ) G p (s ) ⋅ P(s )
《过程控制》课后习题答案
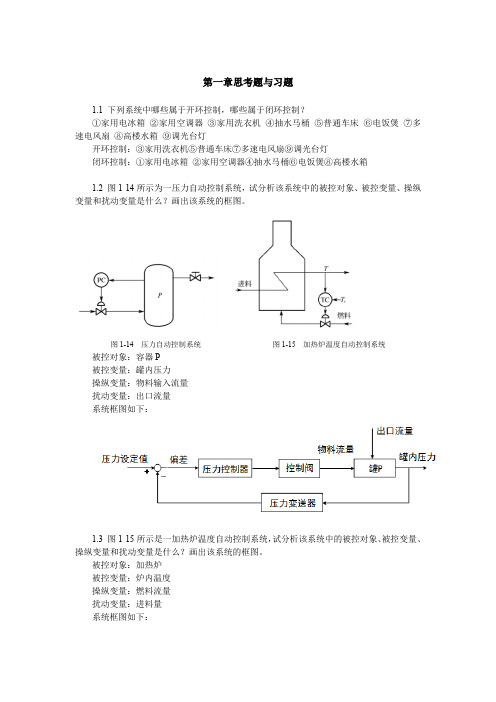
第一章思考题与习题1.1 下列系统中哪些属于开环控制,哪些属于闭环控制?①家用电冰箱②家用空调器③家用洗衣机④抽水马桶⑤普通车床⑥电饭煲⑦多速电风扇⑧高楼水箱⑨调光台灯开环控制:③家用洗衣机⑤普通车床⑦多速电风扇⑨调光台灯闭环控制:①家用电冰箱②家用空调器④抽水马桶⑥电饭煲⑧高楼水箱1.2 图1-14所示为一压力自动控制系统,试分析该系统中的被控对象、被控变量、操纵变量和扰动变量是什么?画出该系统的框图。
图1-14 压力自动控制系统图1-15 加热炉温度自动控制系统被控对象:容器P被控变量:罐内压力操纵变量:物料输入流量扰动变量:出口流量系统框图如下:1.3 图1-15所示是一加热炉温度自动控制系统,试分析该系统中的被控对象、被控变量、操纵变量和扰动变量是什么?画出该系统的框图。
被控对象:加热炉被控变量:炉内温度操纵变量:燃料流量扰动变量:进料量系统框图如下:1.4 按设定值的不同情况,过程控制系统分为哪几类?过程控制系统分为三类:定值控制系统、随动控制系统和程序控制系统。
1.5 什么是过程控制系统的过渡过程?有哪几种基本形式?过程控制系统从一个平衡状态过渡到另一个平衡状态的过程称为过程控制系统的过渡过程。
控制系统过渡过程有五种基本形式:发散振荡、单调发散、等幅振荡、衰减振荡和单调衰减。
1.6 某换热器的温度控制系统在单位阶跃干扰作用下的过渡过程曲线如图1-16所示。
试分别求出最大偏差、余差、衰减比、振荡周期和调整时间(设定值为200℃)。
图1-16 题1.6图最大偏差:30℃余差:5℃衰减比:5:1振荡周期:15min调整时间:22min第二章思考题与习题2.1 求取图2-55所示电路的传递函数,图中物理量角标i代表输入,o代表输出。
a)b)图2-55 习题2.1图a)(由分压公式求取)上式中,,。
b)上式中,,2.2 惯性环节在什么条件下可近似为比例环节?又在什么条件下可近似为积分环节?惯性环节在T很小的时候可近似为比例环节;T很大的时候条可近似为积分环节。
控制工程基础_课后答案
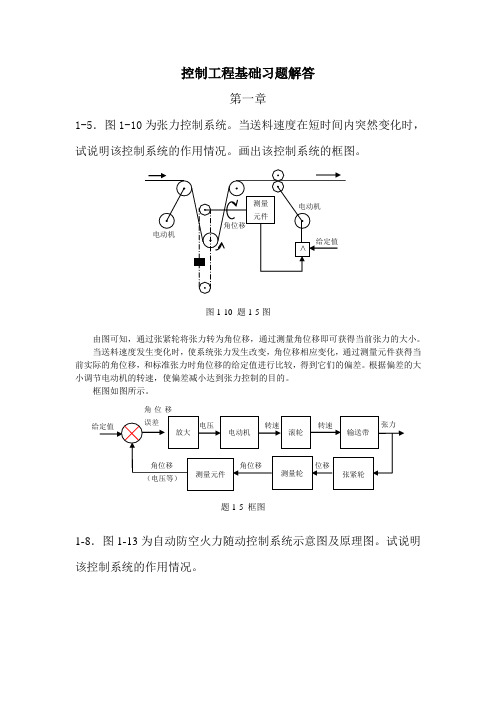
控制工程基础习题解答第一章1-5.图1-10为张力控制系统。
当送料速度在短时间内突然变化时,试说明该控制系统的作用情况。
画出该控制系统的框图。
由图可知,通过张紧轮将张力转为角位移,通过测量角位移即可获得当前张力的大小。
当送料速度发生变化时,使系统张力发生改变,角位移相应变化,通过测量元件获得当前实际的角位移,和标准张力时角位移的给定值进行比较,得到它们的偏差。
根据偏差的大小调节电动机的转速,使偏差减小达到张力控制的目的。
框图如图所示。
1-8.图1-13为自动防空火力随动控制系统示意图及原理图。
试说明该控制系统的作用情况。
题1-5 框图电动机给定值角位移误差张力-转速位移张紧轮滚轮输送带转速测量轮测量元件角位移角位移(电压等)放大电压测量 元件>电动机角位移给定值电动机图1-10 题1-5图该系统由两个自动控制系统串联而成:跟踪控制系统和瞄准控制系统,由跟踪控制系统获得目标的方位角和仰角,经过计算机进行弹道计算后给出火炮瞄准命令作为瞄准系统的给定值,瞄准系统控制火炮的水平旋转和垂直旋转实现瞄准。
跟踪控制系统根据敏感元件的输出获得对目标的跟踪误差,由此调整视线方向,保持敏感元件的最大输出,使视线始终对准目标,实现自动跟踪的功能。
瞄准系统分别由仰角伺服控制系统和方向角伺服控制系统并联组成,根据计算机给出的火炮瞄准命令,和仰角测量装置或水平方向角测量装置获得的火炮实际方位角比较,获得瞄准误差,通过定位伺服机构调整火炮瞄准的角度,实现火炮自动瞄准的功能。
控制工程基础习题解答第二章2-2.试求下列函数的拉氏变换,假定当t<0时,f(t)=0。
(3). ()t et f t10cos 5.0-=解:()[][]()1005.05.010cos 25.0+++==-s s t e L t f L t(5). ()⎪⎭⎫⎝⎛+=35sin πt t f 图1-13 题1-8图敏感 元件定位伺服机构 (方位和仰角)计算机指挥仪目标 方向跟踪环路跟踪 误差瞄准环路火炮方向火炮瞄准命令--视线瞄准 误差伺服机构(控制绕垂直轴转动)伺服机构(控制仰角)视线敏感元件计算机指挥仪解:()[]()252355cos 235sin 2135sin 2++=⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+=s s t t L t L t f L π2-6.试求下列函数的拉氏反变换。
闭环传递函数

闭环系统的调试与调优
初始化参数
1
根据系统要求设置初始参数
现场调试
2
对系统进行实时现场调试
数据采集
3
采集系统运行关键指标数据
性能优化
4
对采集数据进行分析优化系统
闭环系统调试与调优是关键步骤,需要仔细规划并逐步执行。首先根据系统要求合理设置初始参数,确保系统能正常运行。接下来对系统进行现 场实时调试,收集运行数据。最后通过对采集数据的分析,优化系统性能,达到最佳效果。
闭环系统的控制策略
控制策略制定
基于闭环系统的特点和性能目标,制定合理的控制策略,如PID控制、模型预测控制、自适应 控制等。
控制参数优化
对控制参数进行精细调整和优化,确保系统稳定性、动态性能和抗干扰能力。
控制策略鲁棒性
考虑模型不确定性和环境干扰,设计具有良好鲁棒性的控制策略,增强系统的抗干扰能力。
闭环系统的混合控制
复杂系统集成
混合控制通过融合不同控制策略,如 PID、自适应、鲁棒等,解决复杂系统的控制难题,提高 系统性能。
控制算法优化
混合控制通过不同算法的优势互补,如模型预测控制与神经网络控制,达到更优的控制效果。
系统性能平衡
混合控制通过调整各种控制策略的权重,平衡系统的稳定性、响应速度和鲁棒性等性能指标。
稳定性分析
进行鲁棒性分析需要对闭 环系统的稳定性进行仔细 评估。通过小扰动分析、 Lyapunov函数法等方法, 确保系统具有足够的稳定 裕度。
性能指标分析
除了稳定性,还需要分析 闭环系统的动态响应、跟 踪精度、抗干扰能力等性 能指标,确保满足设计要 求。考虑参数变化和干扰 情况下的指标变化趋势。
鲁棒控制设计
闭环系统的最优控制
采样系统的典型结构图闭环脉冲传递函数

a)
1 S2
1( a
1 S
1 S
) a
查表得:
Z( GP( s)) S
Tz ( z 1)2
1( a
z
z 1
z
z e aT
)
∴ 有零阶保持器的开环系统脉冲传递 函数为:
G( z) (1 z1 )Z( GP( s)) S
西南民族大学
例二、设离散系统如图所示,其中
1
a
G1( s) S , G2( s) S a
第六章
离散系统
黄勤珍
西南民族大学
※ 6 — 1 线性离散系统
一、信号采样和复现
1、在采样控制系统中,把连续信号转变为 脉冲系列的过程 — 采样过程(采样)
实现采样的装置 — 采样器(开关)T 表示采 样周期(S) ,fs = 1/T (采样频率) (1/S) , 表示采样角频率。
ws
2fs
2
G1( z)
Z( ) S
z1
a
az
G2( z)
Z( S
) a
z
e aT
G(
z)
G1(
z)G2 (
z)
(
z
az 2 1)( z
e aT
)
az 3 C( z) G( z)R( z) ( z 1)2( z eaT )
西南民族大学
系统b:
a G1( s)G2( s) S( S a) G( z) G1G2( z) Z[ a ]
Z 域(朱利稳定判据)且满足:
D(1) > 0 , D(-1)
2.4.3 闭环系统的结构图和传递函数
•
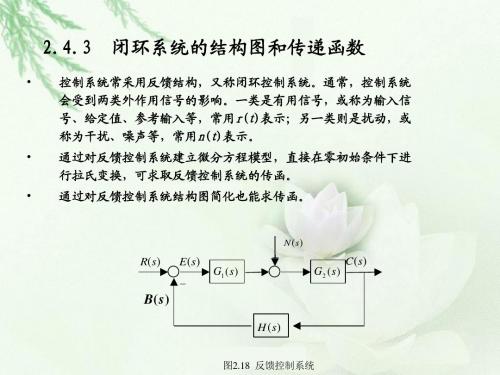
闭环系统的结构图和传递函数
控制系统常采用反馈结构,又称闭环控制系统。通常,控制系统 会受到两类外作用信号的影响。一类是有用信号,或称为输入信 号、给定值、参考输入等,常用r(t)表示;另一类则是扰动,或 称为干扰、噪声等,常用n(t)表示。 通过对反馈控制系统建立微分方程模型,直接在零初始条件下进 行拉氏变换,可求取反馈控制系统的传函。 通过对反馈控制系统结构图简化也能求传函。
N ( s)
R(s)
E ( s)
பைடு நூலகம்
G1 ( s )
G2 ( s )
C ( s)
B( s )
H ( s)
图2.18 反馈控制系统
系统的开环传递函数 上图中将反馈的输出通路断开,反馈信号 对于参考输入信号的传递函数称为开环 传递函数。这时前向通路传递函数与反 馈通路传递函数的乘积为该系统的开环 传递函数。
• •
N ( s)
R(s)
E ( s)
G1 ( s )
G2 ( s )
C ( s)
B( s )
H ( s)
图2.18 反馈控制系统
N ( s)
R(s)
E ( s)
G1 ( s )
G2 ( s )
C ( s)
B( s )
H ( s)
图2.18 反馈控制系统
前向通道传递函数 前向通道是指从输入端 到输出端的通道
闭环系统的特征方程
• 上面导出闭环传递函数及误差传递函数虽然各不相同,但是他们 的分母却是一样的。均为:1 G1 s G2 s H s
这是闭环控制系统各种传递函数都具有的的规律性,称其为特征多项式
令
控制系统的传递函数及信号流图和梅逊公式
1 Ln LrLsLt
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
例2-7 试用梅逊公式求系统的闭环传递函数 C(S)
R(S)
图2-45 例2-7图
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
解: P1 G1G2G3.
路 开通路—通路与任一节点相交不多于一次
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
闭通路—通路的终点也是通路的起点,并且与任何其它节 点相交不多于一次
6)前向通路—从输入节点到输出节点的通路上,通过任何节 点不多于一次,此通路自然保护区为前向通路
7)回路—就是闭环通路 8)不接触回路—如果一些回路间没有任何公共节点 9)前向通路增益—在前向通路中多支路增益的乘积。 10)回路增益—回路中多支路增益的乘积。
《自动控制理论》
§2.6 信号流图和梅逊公式的应用
信号流图的性质 (1)信号流图只适用于线性系统。 (2)支路表示一个信号对另一个信号的函数关系;信 号只能沿着支路上的箭头指向传递 (3)在节点上可以把所有输入支路的信号叠加,并把 相加后的信号传送到所有的输出支路。
(4)具有输入和输出支路的混合节点,通过增加一个具 有单位增益的支路,可以把它作为输出节点来处理。 (5)对于一个给定的系统,其信号流图不是唯一的, 这是由于描述的方程可以表示为不同的形式。
参考输入误差的传递函数为
CR(s) ER(s)G1(s)G2(s)
CR(s)
G1( s )G 2( s )
R(s) 1 G1(s)G2(s)H (s)
ER(s)G1(s)G2(s)
闭环传递函数

微分方程为: T dy(t) y(t) u(t) dt
开环传函为: G(s) 1
Ts
闭环传函为: (s) 1
T为系统的时间常数,
Ts 1
1/T为开环增益.
2019年8月28日4时34分
17
3.2 一阶系统的时域分析
1)单位阶跃响应 单位阶跃输入 u(t) 1(t)的像函数为 U(s) 1
2019年8月28日4时34分
26
3.2 一阶系统的时域分析
例3.2.1一阶系统Fra bibliotek结构图如图所示,若kt=0.1,
试求系统的调节时间ts,如果要求ts 0.1秒。试求
反馈系数应取多大?
R(s)
C(s)
100/s
kt
2019年8月28日4时34分
27
3.2 一阶系统的时域分析
解 系统的闭环传递函数
故kt 0.3
2019年8月28日4时34分
28
3.2 一阶系统的时域分析
思考题和选做题:
(1)当一阶对象的模型为 k 时,分别求其输出
Ts 1
响应所得的结果是否符合前面的证明和结论?试着
解释为什么有这样的结果?
(2)当输入信号为 u(t) 1 t2 时, 1 的输出响应是
2
Ts 1
什么?能否根据这个结果利用上面思考题直接写出
3、线性系统的时域分析
3.1 典型输入信号与时域性能指标 3.2 一阶系统的时域分析 3.3 二阶系统的时域分析 3.4 高阶系统的时域分析 3.5 系统模型的时域测定法
2019年8月28日4时34分
1
本章学习要点
• 掌握典型输入信号和时域性能指标 • 掌握一阶系统的时域分析方法 • 掌握二阶系统的时域分析方法 • 了解高阶系统的主导极点及其时域分析方
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3).给定信号作用下的误差传递函数
R(s) B(s) E(s)
_
H(s) G2(s) G1(s)
e (s) =
E (s) 1 1 R(s) 1 G1 (s) G 2 (s) H(s) 1+ GK (s)
E (s) 1 R(s) 1 Gk (s)
系统总的输出C(s)为输入和误差同时作用下的结果。
C (s) (s) R(s) n (s) N(s)
当
G1 (s) G 2 (s) G 2 (s) R(s) N (s) 1 Gk (s) 1 Gk (s)
C (s) R (s) H (s)
G1 (s)G2 (s) R(s) 1和G2 (s)N(s)>>1
例题 1 求 C(s)/R1(s),C(s)/R2(s)
a 1 R1(s) b c -f -h R2(s) l d -g 1 e 1 C(s)
解:当R1(s)作用时,R2(s)=0
a R1(s) 1 b c -f -h d -g 1 e 1 C(s)
p1 bcde,p2 ade,p3 bc,p4 a。
闭环传递函数具有相同的分母[1+Gk(s)], 因为具有相同的信号流图特征式,
La G1G2 ( H)
1 L a 1 G1G2 H 1+Gk (s)
1+Gk (s) 0
称为闭环系统特征方程式
注意:叠加原理求系统输出量C(s)和E(s),先求各种情况下的C(s)和 E(s),然后叠加。
4).扰动信号N(s)作用的误差传递函数
N(s)
E(s)
+
误差函数:偏差信号与扰动信号之比。
en (s)
G2(s) G1(s)
-H(s)
G (s) H(s) E (s) 2 N (s) 1 Gk (s)
G2 (k) H(s) N (s) 1 Gk (s)
En (s) en (s) N (s)
C (s)
G1 (s) G 2 (s) R(s) 1 Gk (s) 注意:负反馈分母去+,正反馈-
2).扰动信号N(s)作用的闭环传递函数 令R(s)=0
N(s) C(s)
G2(s) G1(s)
H(s)
系统闭环传递函数
n (s) = G2 (s) G2 (s) C(s) = N(s) 1+G1 (s)G2 (s)H(s) 1+GK (s)
表明一定条件下,输出只取决输入信号和反馈信号,不受扰动影响,较好抗干 扰能力。
系统总的输出E(s)为输入和误差同时作用下的结果。
E (s) e (s) R(s) en (s) N(s) G (k) H(s) 1 R(s) 2 N (s) 1 Gk (s) 1 Gk (s)lຫໍສະໝຸດ d -ge1
C(s)
1
p1 le, p2 lehbc, p3 leha
a b c -f -h R2(s) 1 d -g 1 e 1
1 1 cf , 2 1, 3 1
C(s)
L1 eg, L2 cf , L3 bcdeh, L4 adeh
a R1(s) 1 b c -f -h d -g 1 e 1 C(s)
L1 eg,L2 cf ,L3 bcdeh,L4 adeh。
L
a
b
=L1 + L2 + L3 + L4 = -(eg +cf +bcdeh+adeh)
c
L L
egcf
1 La Lb Lc 1 eg cf bcdef adeh egcf
若单位反馈,H(s)=1,
(s) =
Gk (s) G1 (s)G2 (s) C(s) = R(s) 1+G1 (s)G2 (s)H(s) 1+GK (s)
(s)
e (s) =
1 1+GK (s)
若已知单位反馈的闭环函数
Gk (s) =
(s) 1+ (s)
e (s) = 1 (s)
2.6 闭环系统的传递函数
1、闭环系统的开环传递函数
N(s) R(s)
E(s)
_
G1(s)
+
G2(s)
C(s)
B(s) H(s)
闭环控制系统的典型结构
闭环系统的开环传递函数是指:反馈信号与偏差的拉氏变换之比,
Gk (s) B(s) C (s) H(s) E (s) G1 (s) G 2 (s) H(s) G1 (s) G 2 (s) H(s) E (s) E (s) E (s)
C (s) le(1 cf ha hbc) R2 (s) 1 cf eg bcdeh adeh cefg
2、闭环系统的闭环传递函数
1).给定信号R(s)作用闭环传递函数
取扰动为零,N(s)=0,
R(s) E(s)
_
B(s)
G1(s) H(s)
G2(s)
C(s)
闭环系统传递函数:
(s) = G1 (s)G2 (s) G (s)G2 (s) C(s) = 1 R(s) 1+G1 (s)G2 (s)H(s) 1+GK (s)
1 1, 2 1, 3 1 eg, 4 1 eg
C (s) bcde ade a bc aeg bceg R1 (s) 1 eg cf bcdeh adeh egcf
当R2(s)作用时,R1(s)=0
b
a c -f -h
R2(s)
