常用几何截面与结构力学常用公式表
结构力学公式大全e
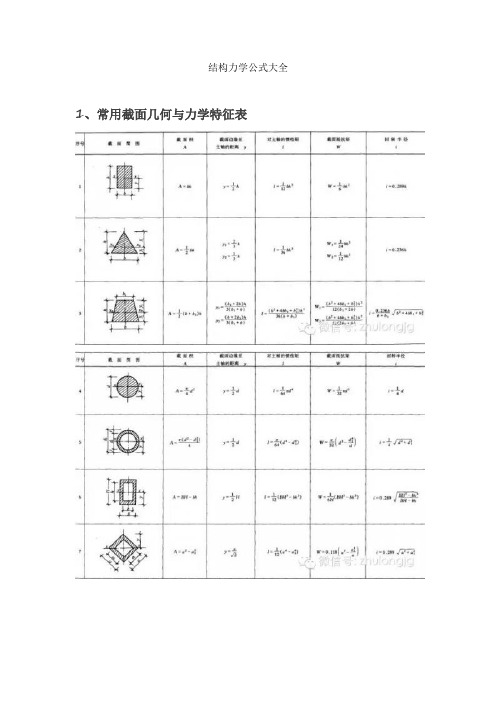
结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴〔形心轴〕的截面惯性矩〔mm4〕。
根本计算公式如下:2.W称为截面抵抗矩〔mm3〕,它表示截面抵抗弯曲变形能力的大小,根本计算公式如下:3.i称截面回转半径〔mm〕,其根本计算公式如下:4.上列各式中,A为截面面积〔mm2〕,y为截面边缘到主轴〔形心轴〕的距离〔mm〕,I为对主轴〔形心轴〕的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=〔-0.125×11.76×52〕+〔-0.188×29.4×5〕=〔-36.75〕+〔-27.64〕=-64.39kN·mVB左=〔-0.625×11.76×5〕+〔-0.688×29.4〕[例2] 三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
常用几何截面与结构力学常用公式表

常用几何截面与结构力学常用公式表| 2| 3注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
单跨梁的内力及变形表(1)简支梁的反力、剪力、弯矩、挠度(2)悬臂梁的反力、剪力、弯矩和挠度(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度(4)两端固定梁的反力、剪力、弯矩和挠度(5)外伸梁的反力、剪力、弯矩和挠度等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;w =表中系数×ql4/(100EI)。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;w =表中系数×Fl3/(100EI)。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] M B支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mV B左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
常用截面几何性质计算公式JX

常用截面几何性质计算公式JX1.矩形截面:矩形截面是一种常见的结构截面形式。
假设矩形截面宽度为b,高度为h,则其面积可以通过以下公式计算:A=b*h质心位置可以通过以下公式计算:x=b/2y=h/2惯性矩可以通过以下公式计算:Ix=(b*h^3)/12Iy=(h*b^3)/12截面模数可以通过以下公式计算:Wx=(b*h^2)/6Wy=(h*b^2)/62.圆形截面:圆形截面是另一种常见的结构截面形式。
假设圆形截面的半径为r,则其面积可以通过以下公式计算:A=π*r^2质心位置在圆心上,即x=0,y=0。
惯性矩可以通过以下公式计算:Ix=(π*r^4)/4Iy=(π*r^4)/4截面模数可以通过以下公式计算:Wx=(π*r^3)/4Wy=(π*r^3)/43.等边三角形截面:等边三角形截面是一个等边三角形形状的结构截面。
假设等边三角形截面的边长为a,则其面积可以通过以下公式计算:A = (sqrt(3) * a^2) / 4质心位置可以通过以下公式计算:x=a/2y = (sqrt(3) * a) / 6惯性矩可以通过以下公式计算:Ix = (a^4 * sqrt(3)) / 48Iy=(a^4)/48截面模数可以通过以下公式计算:Wx = (a^3 * sqrt(3)) / 12Wy=(a^3)/12以上是常见的几种截面几何性质的计算公式,通过这些公式可以方便地计算结构截面的重要性质,为结构设计和分析提供参考。
在实际应用中,还需要根据具体的截面形状和尺寸选择相应的公式进行计算。
结构力学公式大全(完整资料).doc
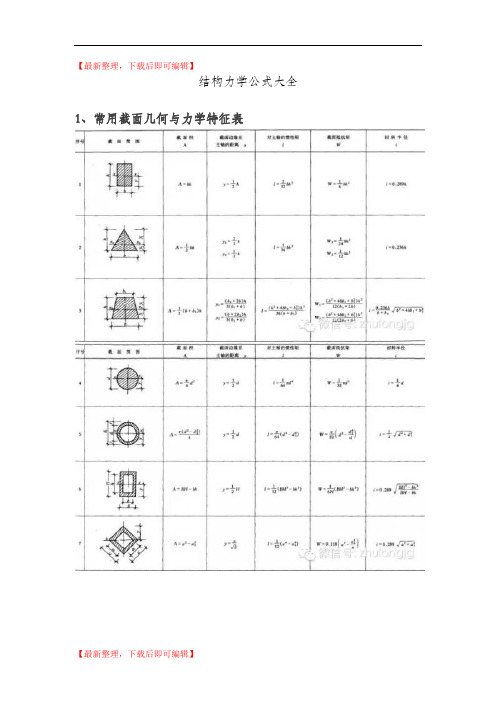
【最新整理,下载后即可编辑】结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全
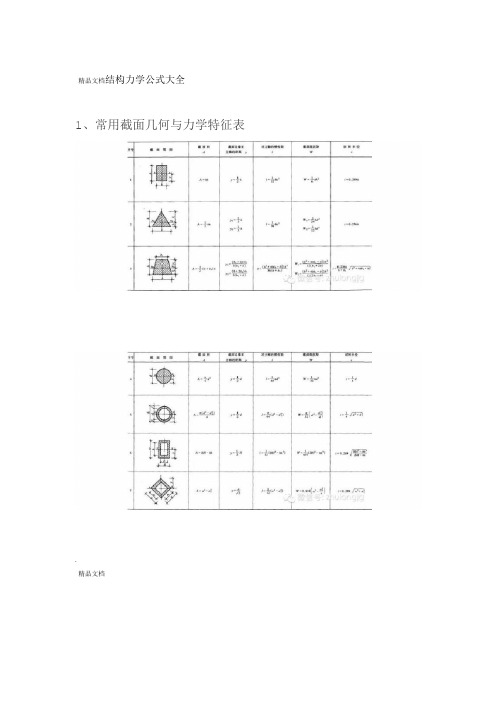
精品文档结构力学公式大全1、常用截面几何与力学特征表.精品文档.精品文档.精品文档)。
基本计算公式如mm4.I称为截面对主轴(形心轴)的截面惯性矩(1注:下:),它表示截面抵抗弯曲变形能力的大小,基本mm3W称为截面抵抗矩(2.计算公式如下:mm),其基本计算公式如下:3.i称截面回转半径(为截面边缘到主轴(形心轴)的距y为截面面积(mm2),.上列各式中,4A I为对主轴(形心轴)的惯性矩。
mm离(),.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
52、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度2.1 .精品文档.精品文档.精品文档2.2 悬臂梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.4 两端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.5 外伸梁的反力、剪力、弯矩和挠度.精品文档.精品文档.精品文档.等截面连续梁的内力及变形表3 3.1 二跨等跨梁的内力和挠度系数.精品文档;。
qlql2;V=表中系数×注:1.在均布荷载作用下:M=表中系数×;。
;V =表中系数×F 2.在集中荷载作用下:M=表中系数×Fl,每跨各有一集11.76kN/m,均布荷载q=例1] 已知二跨等跨梁l=5m [ =29.4kN,求中间支座的最大弯矩和剪力。
中荷载F 5))+(-0.188×29.4××解[] MB 支=(-0.125×11.7652m64.39kN·36.75)+(-27.64)=-=(-29.40.688×)0.625 VB左=(-×11.76×5)+(-56.98kN)+(-20.23)=-=(-36.75,求边跨最大跨中11.76kN/m6m,均布荷载q==2] [例已知三跨等跨梁l 弯矩。
常用截面几何特性计算公式

常用截面几何特性计算公式截面几何特性是指用于描述一个截面的形状和大小的参数,常用的包括面积、惯性矩、截面模量、截面半径等。
这些参数在工程中非常重要,因为它们能够直接影响截面的受力性能。
下面将介绍一些常用的截面几何特性计算公式。
1.截面面积计算公式:截面面积是指截面内部所有点的面积总和。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面面积:A=b*h,其中b为矩形的宽度,h为矩形的高度。
-圆形截面面积:A=π*r^2,其中r为圆的半径。
-等边三角形截面面积:A=(s^2*√3)/4,其中s为三角形的边长。
-梯形截面面积:A=(a+b)*h/2,其中a和b为梯形的上底和下底长度,h为梯形的高度。
2.截面惯性矩计算公式:惯性矩是描述截面抵御扭转和弯曲的能力的参数。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面惯性矩:I=(b*h^3)/12,其中b为矩形的宽度,h为矩形的高度。
-圆形截面惯性矩:I=π*r^4/4,其中r为圆的半径。
-等边三角形截面惯性矩:I=(s^4*√3)/64,其中s为三角形的边长。
-梯形截面惯性矩:I=[(b1*h1^3)+(b2*h2^3)]/12,其中b1和b2为梯形的上底和下底长度,h1和h2为梯形的高度。
3.截面模量计算公式:截面模量是描述截面抵御弯曲的能力的参数。
对于一些常见的截面形状,可以使用以下公式进行计算:-矩形截面模量:S=(b*h^2)/6,其中b为矩形的宽度,h为矩形的高度。
-圆形截面模量:S=π*r^3/3,其中r为圆的半径。
-等边三角形截面模量:S=(s^3*√3)/36,其中s为三角形的边长。
-梯形截面模量:S=[(b1*h1^2)+(b2*h2^2)]/6,其中b1和b2为梯形的上底和下底长度,h1和h2为梯形的高度。
4.截面半径计算公式:截面半径是描述截面的曲率半径的参数,通常用于弯曲性能的评估。
-矩形截面半径:r=h/2,其中h为矩形的高度。
常用截面几何特性计算公式

常用截面几何特性计算公式截面几何特性是指用来描述截面形状和大小的一些参数,可以用来进行结构设计和分析。
常用的截面几何特性包括面积、周长、惯性矩、截面模量等。
下面将详细介绍常用的截面几何特性计算公式。
1.面积(A):截面的面积是指该截面所围成的平面区域的大小,用来描述截面的大小。
常见的截面面积计算公式有:-矩形截面:A=b*h,其中b为矩形的宽度,h为矩形的高度。
-圆形截面:A=π*r^2,其中π约等于3.14,r为圆的半径。
-梯形截面:A=(a+b)*h/2,其中a和b为梯形的上底和下底长度,h为梯形的高度。
2.周长(P):截面的周长是指该截面围成的边界线的总长度,用来描述截面的形状。
常见的截面周长计算公式有:-矩形截面:P=2*(b+h),其中b为矩形的宽度,h为矩形的高度。
-圆形截面:P=2*π*r,其中π约等于3.14,r为圆的半径。
-梯形截面:P=a+b+2*L,其中a和b为梯形的上底和下底长度,L为梯形的斜边长度。
3.惯性矩(I):惯性矩是描述截面抵抗弯曲或扭转作用的能力,常用于计算截面的弯矩和扭矩。
惯性矩有I_x和I_y两个方向,分别表示关于x轴和y轴的惯性矩。
常见的截面惯性矩计算公式有:-矩形截面:I_x=(b*h^3)/12,I_y=(h*b^3)/12,其中b为矩形的宽度,h为矩形的高度。
-圆形截面:I_x=I_y=(π*r^4)/4,其中π约等于3.14,r为圆的半径。
-梯形截面:I_x=(b*h^3)/36*(3*a+b),I_y=(h*b^3)/36*(a+3*b),其中a和b为梯形的上底和下底长度,h为梯形的高度。
4.截面模量(W):截面模量是一种描述截面承受弯曲时变形能力的特性,常用于计算截面的弯曲应力和挠度。
截面模量有W_x和W_y两个方向,分别表示关于x轴和y轴的截面模量。
-矩形截面:W_x=(b*h^2)/6,W_y=(h*b^2)/6,其中b为矩形的宽度,h为矩形的高度。
十六种结构力学公式

十六种结构力学公式十六种结构力学公式是在工程结构领域中广泛应用的力学公式。
结构力学公式是结构工程的基础,是工程师在进行结构工程设计和分析时必须了解和掌握的基本技能。
结构工程是建筑工程中的一个分支,主要关注建筑物或其他结构的设计、分析和建造。
结构工程需要对建筑物或其他结构的结构、力学和物理性质有深入的了解,才能确保建筑物或其他结构的结构安全和稳定。
以下是十六种结构力学公式的详细介绍。
1. 颜氏公式颜氏公式是一种用于计算杆件在受力下的位移的公式,也称为斯特鲁夫定理。
该公式使用杆件的模量、长度、截面积和载荷来计算底部的杆件位移。
2. 韦尔斯公式韦尔斯公式是一种用于计算梁在受力下的最大弯曲应力的公式。
该公式使用梁的长度、截面积、载荷和弹性模量来计算梁上的最大弯曲应力。
3. 安普洛公式安普洛公式是一种用于计算板在受力下的最大弯曲应力的公式,也称为克莱温公式。
该公式使用板的长度、宽度、厚度、载荷和弹性模量来计算板上的最大弯曲应力。
4. 克利通公式克利通公式是一种用于计算光杆在受力下的临界载荷的公式。
该公式使用光杆的长度、截面积和弹性模量来计算光杆的临界载荷。
5. 邓肯公式邓肯公式是一种用于计算杆件在受力下的临界载荷的公式。
该公式使用杆件的长度、截面积、弹性模量和有效长度系数来计算杆件的临界载荷。
6. eul公式欧拉公式是一种用于计算杆件在不同长度、截面积、模量和载荷条件下的临界载荷的公式。
该公式使用杆件的长度、截面积、弹性模量和材料的泊松比来计算杆件的临界载荷。
7. 比客定律比客定律是一种用于计算异性截面梁的转角和剪力的公式,也称为截面定理。
该定律使用梁的截面积和重心位置来计算梁的剪力和转角。
8. 最小势能定理最小势能定理是一种用于计算结构势能最小的方法,也称为虚功原理。
该定理使用结构从起始到结束所消耗的能量,即适用于弹性结构中弹性应力根据微小位移所产生的功。
9. 莫尔定理莫尔定理是一种用于计算板的振动特性的定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用截面几何与力学特征表
| 1
| 2
| 3
| 4
| 5
| 6
| 7
注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:
2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:
3.i称截面回转半径(mm),其基本计算公式如下:
4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
单跨梁的内力及变形表(1)简支梁的反力、剪力、弯矩、挠度
| 8
| 9
| 10
(2)悬臂梁的反力、剪力、弯矩和挠度
| 11
| 12
(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度
| 13
| 14
| 15
(4)两端固定梁的反力、剪力、弯矩和挠度
| 16
| 17
| 18
(5)外伸梁的反力、剪力、弯矩和挠度
| 19
| 20
| 21
| 22
等截面连续梁的内力及变形表二跨等跨梁的内力和挠度系数
| 23 注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;w =表中系数×ql4/(100EI)。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;w =表中系数×Fl3/(100EI)。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最
大弯矩和剪力。
[解] M B支=(-0.125×11.76×52)+(-0.188×29.4×5)
=(-36.75)+(-27.64)=-64.39kN·m
V B左=(-0.625×11.76×5)+(-0.688×29.4)
=(-36.75)+(-20.23)=-56.98kN
[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
不等跨连续梁的内力系数1)二不等跨梁的内力系数
| 24 注:1.M=表中系数×ql21;V=表中系数×ql1;
2.(M max)、(V max)表示它为相应跨内的最大内力。
2)三不等跨梁内力系数
| 25 注:1.M=表中系数×ql21;V=表中系数×ql1;
2.(M max)、(V max)为荷载在最不利布置时的最大内力。
“┌┐”形刚架内力计算表(一)
| 26
| 27
“┌┐”形刚架内力计算表(二)
| 28
| 29
“”形刚架的内力计算表
| 30
| 31
| 32。
