matlab(四连杆优化设计)
matlab四连杆优化设计

机械优化设计在matlab中的应用东南大学机械工程学院**一优化设计目的:在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论证从中提取最佳方案。
最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方案的科学。
由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管理等,并取得了显著的经济效益和社会效益。
二优化设计步骤:1. 机械优化设计的全过程一般可以分为如下几个步骤:1)建立优化设计的数学模型;2)选择适当的优化方法;3)编写计算机程序;4)准备必要的初始数据并伤及计算;5)对计算机求得的结果进行必要的分析。
其中建立优化设计数学模型是首要的和关键的一步,它是取得正确结果的前提。
优化方法的选取取决于数学模型的特点,例如优化问题规模的大小,目标函数和约束函数的性态以及计算精度等。
在比较各种可供选用的优化方法时,需要考虑的一个重要因素是计算机执行这些程序所花费的时间和费用,也即计算效率。
2. 建立数学模型的基本原则与步骤①设计变量的确定;设计变量是指在优化设计的过程中,不断进行修改,调整,一直处于变化的参数称为设计变量。
设计变量的全体实际上是一组变量,可用一个列向量表示:②目标函数的建立;选择目标函数是整个优化设计过程中最重要的决策之一。
当对某以设计性能有特定的要求,而这个要求有很难满足时,则针对这一性能进行优化会得到满意的效果。
目标函数是设计变量的函数,是一项设计所追求的指标的数学反映,因此它能够用来评价设计的优劣。
目标函数的一般表达式为:f (X )= I (勺卞比衍产斗一話J ,要根据实际的设计要求来设计目标函数。
在可行域中,任意设计点满足全部约束条件,称为可行解,但不是最优解,而优化设 计就是要求出目标函数在可行域的最优解。
二实例分析(机械优化设计P241页例8-5)设计一曲柄摇杆机构如图,要求:曲柄11从曲萨笄叭产%+ 9"时・操秆】3的转角屐佳再現巳知的运动规律:2X ((p-<p 0) ft 2壮=%+亦且已知分析:1) 设计变量的确定决定机构尺寸的各杆长度,以及当摇杆按已知运动规律开始运行时,曲柄所载的位置角应列为设计变量,即:JI. . ,srTX= “勺勺勺牝=I 】S h »屮oI = 1 考虑到机构的杆长按比例变化时,不会改变其运动规律,因此在计算时常取,而其他杆长则按比例取为 L 的倍数。
第三章 四连杆之MATLAB程式
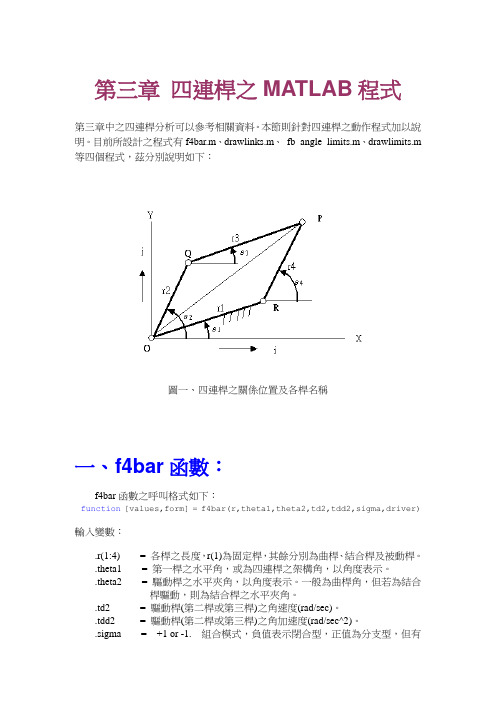
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式,茲分別說明如下:圖一、四連桿之關係位置及各桿名稱一、f4bar函數:f4bar函數之呼叫格式如下:function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數:.r(1:4) = 各桿之長度,r(1)為固定桿,其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角,或為四連桿之架構角,以角度表示。
.theta2 = 驅動桿之水平夾角,以角度表示。
一般為曲桿角,但若為結合桿驅動,則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式,負值表示閉合型,正值為分支型,但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數:.form = 組合狀態,0 :表示無法組合;1:可以正確組合.values = 輸出矩陣,其大小為 4 X 7,各行之資料分配如下:其中第一行之連桿位置向量,屬於單桿的位置向量。
第二行為各桿之水平夾角,第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量,第五行為向量,第六行為絕對量,第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中,以abs()這一個函數指令即可求得,而以函數angle()則可求得其夾角,雖然第二行與第七行之輸出亦有相對應之夾角。
例一:為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中,有框線者表示其為輸入值。
基于MATLAB的平面四连杆机构优化设计

基于 MATLAB 的四连杆机构的优化设计
陈伟斌
(汕头大学,工学院)
[摘要] 对平面四连杆机构进行数学建模,要求实现预期的传递函数运动轨迹。利用 MATLAB 强大的运算功能,快速精确地计 算出优化结果。再利用 MATLAB 编写程序检验得出的运动轨迹是否达到期望目标。 [关键词] 连杆、轨迹、优化设计、MATLAB。
Optimized design for four bar linkage mechanism of crushing machine based on MATLAB
Terry Chen (Shantou University, Engineering College)
[Abstract] Analyze the model of four bar linkage mechanism and try to satisfy the movement locus that we excepted. With the strong functions of MATLAB, we can calculate and get the best result quickly. Then write a program to simulate the movement locus of the output and examine whether it satisfy our requirement. [Key Words] Linkage, Movement locus , Optimized Design, MATLAB
l 2, l 3 两 个 独 立 变 量 。 设
l 2 x1; l 3 x 2; 可以得出本题是二维优化问题。
有志,有恒,有识,有为
基于matlab的平面四连杆机构设计以及该机构的运动分析参考模板

基于matlab的平面四连杆机构设计以及该机构的运动仿真分析摘要四连杆机构因其结构方便灵活,能够传递动力并实现多种运动形式而被广泛应用于各个领域,因此对其进行运动分析具有重要的意义。
传统的分析方法主要应用几何综合法和解析综合法,几何综合法简单直观,但是精确度较低;解析法精确度较高,但是计算工作量大。
随着计算机辅助数值解法的发展,特别是MATLAB软件的引入,解析法已经得到了广泛的应用。
对于四连杆的运动分析,若应用MATLAB 则需要大量的编程,因此我们引入proe软件,我们不仅可以在此软件中建立实物图,而且还可以对其进行运动仿真并对其运动分析。
在设计四连杆时,我们利用解析综合法建立数学模型,再根据数学模型在MATLAB中编程可以求得其他杆件的长度。
针对范例中所求得的各连杆的长度,我们在proe软件中画出其三维图(如图4)并在proe软件中进行仿真分析得出CB,的角加速度的变化,从而得到CB,两接触处所受到的力是成周期性变化的,可以看出CB,两点处的疲劳断裂,我们提B,两点处极易疲劳断裂,针对C出了在设计四连杆中的一些建议。
关键字:解析法 MATLAB 软件 proe 软件 运动仿真建立用解析法设计平面四杆机构模型对于问题中所给出的连架杆AB 的三个位置与连架杆CD 的三个位置相对应,即三组对应位置为:332211,,,,,ψϕψϕψϕ,其中他们对应的值分别为: 52,45,82,90,112,135,为了便于写代数式,可作出AB 与CD 对应的关系,其图如下:图—2 AB 与CD 三个位置对应的关系通过上图我们可以通过建立平面直角坐标系并利用解析法来求解,其直角坐标系图如下:φααi θi φi图—3 平面机构直角坐标系通过建立直角坐标系OXY ,如上图所示,其中0α与0φ为AB 杆与CD 杆的初始角,各杆件的长度分别用矢量d c b a ,,,,表示,将各矢量分别在X 轴与Y 轴上投影的方程为⎩⎨⎧=++=+)sin(*)sin(*)sin(*)cos(*)cos(*)cos(*φθαφθαc b a c d b a在上述的方程中我们可以消除θ,从而可以得到α与φ之间的关系如下:)cos(2)cos(2)cos(2)(2222αφαφab ac cd b d c a +-=+-++ (1) 为便于化简以及matlab 编程我们可以令:⎪⎪⎪⎩⎪⎪⎪⎨⎧==-++=c d H a d H ac b d c a H 32222212 (2) 通过将(2)式代入(1)式中则可以化简得到如下等式: )cos()cos()cos(321αφαφH H H +-=+ (3)我们可以通过(3)式将两连架杆对应的位置带入(3)式中,我们可以得到如下方程:⎪⎩⎪⎨⎧+-=++-=++-=+)cos()cos()cos()cos()cos()cos()cos()cos()cos(333332123222211311121ϕψϕψϕψϕψϕψϕψH H H H H H H H H (4) 联立(4)方程组我们可以求得321,,H H H ,再根据(2)中的条件以及所给定的机架d 的长度,我们可以求出其它杆件的长度为:⎪⎪⎪⎩⎪⎪⎪⎨⎧-++===1222322acH d c a b H d c H d a (5)四连杆设计范例:在日常生活中,我们经常看到消防门总能自动关上,其实它是利用四连杆机构与弹簧组成的。
基于Matlab软件的挑梁四连杆机构优化设计 (1)

基于Matlab软件的挑梁四连杆机构优化设计 (1)第31卷第09期2010年09月煤矿机械V01.3IN。
09SeI,.2010CoalMineMachinery基于Matlab软件的挑梁四连杆机构优化设计孙鹏飞.孟海岗.孙博,田家宝(三一重型装备有限公司支护研究院,沈阳110027)摘要:利用解析法设计四连杆机构,借助现代计算机软件强大的运算功能.可以快速实现四连杆机构相关参数的确定.简化设计过程。
简要介绍了基于Matlab软件液压支架挑梁四连杆设计方法,实例表明,应用此方法可缩短设计周期.并达到结构优化的目的。
关键词:液压支架:四连杆;优化设计DesignofFour-barSUN、中图分类号:THl22文献标志码:A文章编号:1003—0794(2010)09—0014—03OptimalMechanismsBasedonMatlabSoftwarePeng-Fei,MENGHai-gang,SUNBo,TIANJia-bao(DepartmentofHydraulicSupport,SanyHeavyEquipmentCo.,Ltd.,Shenyangl10027,China)Abstract:Four—barmechanismsparameterscanquicklyconfirmbymodemcomputer’Sstrongfunctiontoshortendesign’Sprocess.Afour-barmechanismsoptimaldesign’Smethodwasintroduced,theapplicationresultshowsthatthemethodcanreducedesign’Stimeandobtainoptimaldesign’Saim.Keywords:hydraulicsupport;four-barmechanisms;optimaldesign11.1设计原理几何分析为挑梁与水平方向夹角,妒。
基于MATLAB给定连杆预定位置的四杆机构设计

第14卷第2期2019年6月Vol.14No.2Jun.2019陕西工业职业技术学院学报Journal of Shaanxi Polytechnic Institute基于MATLAB给定连杆预定位置的四杆机构设计韩二豹(陕西工业职业技术学院土木工程学院,陕西咸阳712000)摘要:连杆机构是一种典型的机械机构,运动设计是一个比较复杂和困难的问题,给定连杆预定位置的四杆机构的设计常用的设计方法主要为解析法。
本文以MATLAB语言为基础,利用计算机对给定连杆预定位置的四杆机构进行设计。
结果表明,此方法设计过程简洁,结果合理,准确,效率高。
关键词:四杆机构;MATLAB;预定位置中图分类号:TB121文献标识码:A文章编号=9459-2019(2)-0006-03A MATLAB-based Design of Four-bar Linkage with PresetPosition of Connecting RodHan Erbao(School of Civil Engineering,Shaanxi Polytechnic Institute,Xianyang Shaanxi712000,China)Abstract:Connecting rod is a typical mechanical linkage and its motion design is complex and ually, analytical method is the main method used in the design of four一bar linkage with preset position of connecting rod. In the study,a MATLAB一based design of four bar mechanism was made to link the preset position given by com・puter.The results show that the design process is simple Key words:Four bar linkage;MATLAB;Preset positiono引言MATLAB是一种高级技术语言和发展环境,特提供了一个人机交互的系统环境,并以矩阵作为基础的数据结构,节省编程时间,语法简单、容易掌握、调试方便,可以设置调试断点、快速查找程序错误等优点,可以将使用者从繁重重复的计算中解脱出来,已经被大家认可和广泛使用,充分展现其高效、直观、简单的特点⑷。
基于MATLAB的液压支架四连杆机构优化设计

l k g t cu efo o t z d d sg tte n e w n w se — aro b t tT n g t e r a e w i h fc n e to o . i a e sr t r r m p i e e in me h e d o s i g o t itd p i r i Cn e a d mih c e s e g t o n cin rd n u mi f f d o 1 i o t z d d sg y tm u si td a t ca e in a d l r ey s o e e e in p r d a d i rv d d sg r cso . ' s pi e e in s s h mi e s b t u e ri i d sg n a g l h  ̄ n d d s e o n mp o e e in p e i n t i f l g i i Ke r s p w r d s p ot o rb rl k g t cu e p i z d d sg y wo d : o e e u p r ;f u — a i a e s u t r ;o t n r mie e in;
Op i ie De i n o ur ba nk g t u t e o we e up r s d n Ⅳ【 tm z d sg f r Fo - r Li a e S r c ur fPo r d S po tBa e o ATLAB
WANG Ja — u in g o
量。液压 支架 四连杆机构优化设计 系统代替 了人工设计 ,大大缩短 了设计周期杆机构 ;优化设计 [ 中图分类 号]T 3 54 D5 .1 [ 文献标识码 ]A [ 文章编号] 10 -25 (0 0 207 -3 0 66 2 2 1 )0 - 00 0
运用MATLAB解决四杆机构问题

MATLAB 解题1.设有如图所示四杆机构,其中→R 4为机架(常矢),→R1为主动杆,→R3为从动杆,→R 2为连杆。
设在某一工作位置时各杆的角速度和角加速度分别取如下值:ω1=20 rad/s, ε1= 0;ω2=8.5 rad/s, ε2=-10 rad /s 2;ω3=13 rad/s, ε3=-160rad /s 2.试根据上述要求确定该机构尺寸比。
根据图(2),回路闭合方程可写为:→R 1 +→R 2 +→R 3=-→R 4 回路闭合方程对时间求导一次,利用(6)式,可得: 图2 ω1→R 1 +ω2→R 2 +ω3→R 3 = 0回路闭合方程对时间求导两次,利用(7)式,可得c 1→R 1 + c 2 →R 2 + c 3→R 3 = 0其中 c 1=ε1+j ω12 , c 2=ε2+j ω22, c 3=ε3+j ω32解关于→R 1 ,→R 2 和→R 3的线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→→→001111321321321R R R c c c ωωω→R 4 (13) 可得 →R 1=DDx →R 4, →R 2=DDy →R 4 , →R 3=DDz →R 4注意到上述解中含有相同的分母D,它是一个复数,不妨记为D =k<j α|,被它除的效果是把各杆的长度都缩小k 倍,同时方向都顺时针旋转α角,相当于机构不动,坐标轴逆时针旋转α角。
设计机构时,重要的是机构的形状与尺寸比例。
基于这种考虑,可设→R 4 / D =1,则有→R 1=D x =32320111c c ωω-=1230-j497.3 ; →R 2= D y =311030111c c ωω-=-3200-j1820 ; →R 3= D z =001112121c c ωω-=200+j1955 . 于是:→R 4 = -(→R 1 +→R 2+→R 3) = 1770+j362.3在坐标系上作出上述各杆矢量图,根据各杆矢量图作出机构的闭合矢量图,再根据实际需要选定某一杆长度,其它各杆长度按图比例相似放大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
grad =
*
)
%函数在最优点处梯度信息
hessian =
…
>>
5)结果分析
① 采用 fmincon 求解的最优值: =[; ]; ;
采用算法:中型算法(mediun-scale)。
%函数在最优点处海塞矩阵
~
这与课本给出的最优解: =[;], =相比,计算精度更高,最优解的数值更精确,故计 算准确度高。 ② 用 matlab 绘制输入——输出曲线关系图
<
上图中(单位为“度”)蓝色的线代表曲柄摇杆机构的实际输出角与输入角的关系,红色的 线代表理想输出角与输入角的关系。 可以看出:
}
实际输出和理论输出曲线之间存在线性误差,其最大线性误差为 ,误差在允许的范围 之内,故结果的可信度也较大,运用 matlab 优化工具箱计算所得结果正确。
小结
通过结合实际问题的分析,计算,求解,更加深入地了解和掌握机械优化设计的过 程和步骤,比较重要的步骤是数学模型的建立,以及设计变量的选取,以及数学模型的 尺度变换,根据机构实际工作需要,建立目标函数的约束条件等等,当数学模型建好以 后,剩下的工作可以再 matlab 里面完成,而 matlab 里面的优化工具箱,给用户提供了 多种优化函数,使用者只需要将数学模型按要求编写成子程序嵌入已有的优化程序即 可。
⑵精度的控制:为了得到更加精确地解,需要设置优化函数的控制精度,函数本身默认精 度为 1e-4,精度比较低,通过 options 的设置将精度提高到 1e-9,这样得到的结果更精确。
&
以上两点通过设置options参数即可: options=optimset('largescale','off','display','off','Algorithm','active-set','TolF un',1e-9);
在设计过程中也遇到一些困难,比如说在在用 matlab 计算时,计算机已知处于 busy 状态,得不到函数的最优解,最后反复的检查,终于找的了其原因,是由于初始点选择 不恰当引起的,如果初始点选择得好,可以节省计算时间和计算空间,故初始点的选取 比较重要。
:
!
、
&
、
附录
1. 编写目标函数 M 文件:
,'TolFun',1e-9); %采用中型算法,设计精度为1e-9
[x,fval,exitflag,output]=fmincon(@myfun,x0,A,b,[],[],lb,[],@constrain,o
ptions)
%调用fmincon函数
机械优化设计在 matlab 中的应用
东南大学机械工程学院**
一 优化设计目的:
在生活和工作中,人们对于同一个问题往往会提出多个解决方案,并通过各方面的论 证从中提取最佳方案。最优化方法就是专门研究如何从多个方案中科学合理地提取出最佳方 案的科学。由于优化问题无所不在,目前最优化方法的应用和研究已经深入到了生产和科研 的各个领域,如土木工程、机械工程、化学工程、运输调度、生产控制、经济规划、经济管 理等,并取得了显著的经济效益和社会效益。
二 优化设计步骤:
1.机械优化设计的全过程一般可以分为如下几个步骤: 1)建立优化设计的数学模型;
'
2)选择适当的优化方法; 3)编写计算机程序; 4)准备必要的初始数据并伤及计算; 5)对计算机求得的结果进行必要的分析。 其中建立优化设计数学模型是首要的和关键的一步,它是取得正确结果的前提。优化方 法的选取取决于数学模型的特点,例如优化问题规模的大小,目标函数和约束函数的性态以 及计算精度等。在比较各种可供选用的优化方法时,需要考虑的一个重要因素是计算机执行 这些程序所花费的时间和费用,也即计算效率。 2.建立数学模型的基本原则与步骤 ① 设计变量的确定; 设计变量是指在优化设计的过程中,不断进行修改,调整,一直处于变化的参数称为 设计变量。设计变量的全体实际上是一组变量,可用一个列向量表示:
3)约束条件的确定
① 曲柄摇杆机构应满足曲柄存在条件,可得
¥
②曲柄摇杆机构的传动角
可得
'
把约束条件简化( )
=5
=
=
,
【
其中 满足条件,故最后一共有两个设计变量(
4)优化计算
),7 个约束条件。
)
!
① 此问题的图解见上图,有 7 个约束条件构成了改优化模型的可行域,而最优解在可行域 内。
②优化方法选择: 该问题属于一般的约束非线性最优化类型,可以使用 matlab 优化工具箱里面的
式中
—期望输出角,
;
m — 输入角等分数;
—实际输出角,由下图得:
<
a) 0≤ <
b)
(3) 式中
{
将输入角分成 30 等分,并用近似公式计算,可得目标函数的表达式:
f(x)= 由题意知,传动角的变化范围是
,
,则上式中变量的最后形式可以写成:
将 带入(4) (5)得:
·
为当
时的理想输出角,其值在题目中已经给出:
所有的程序编好以后,在命令窗口输入:youhua 得到的 matlab 的运行结果如下: >> youhua
x=
>
%最优解
fval =
*
%目标函数最优点的值
exitflag = 5
%标志值,’5’表示重要方向导数小于规定的容许范 围并且约束违背小于
output =
`
iterations: 12
%迭代次数
message: [1x780 char]
%跳出信息
lambda =
lower: [2x1 double] upper: [2x1 double] eqlin: [0x1 double]
\
eqnonlin: [0x1 double] ineqlin: [5x1 double]
ineqnonlin: [2x1 double]
funcCount: 40
%函数的评价次数
lssteplength: 1
stepsize:
algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'
%采用的
中型算法
firstorderopt:
%一阶最优性条件
constrviolation:
—
d(i)=acos((r^2+24)/(10*r));
if a(i)<=pi
e(i)=pi-c(i)-d(i);
%计算摇杆输出的实际值
else if a(i)<=2*pi
e(i)=pi-c(i)+d(i);
end
end
a(1)=a0;
f=f+((b(i)-e(i))^2)*(a(i)-a(i-1));
function f=myfun(x)
f=0;
%函数f赋初值
a0=acos(((1+x(1))^2-x(2)^2+25)/(10*(1+x(1)))); %初始计算点曲柄和摇杆的角度
b0=acos(((1+x(1))^2-x(2)^2-25)/(10*x(2)));
i=2;
while(i<=31)
%设置迭代次数为30次
a(i)=a0+(pi/2)*(i/30);
% 计算曲柄各分度的角度值
b(i)=b0+2*(a(i)-a0)^2/(3*pi);
% 计算摇杆各分度的角度值
r=sqrt(26-10*cos(a(i)));
c(i)=acos((r^2+x(2)^2-x(1)^2)/(2*x(2)*r));
三 实例分析 (机械优化设计 P241 页例 8-5)
设计一曲柄摇杆机构如图,要求:
曲柄 从
且
已
知
范围内变化。
分析:
1) ' 2) 设计变量的确定
决定机构尺寸的各杆长度,以及当摇杆按已知运动规律开始运行时,曲柄所载的位置角 应列为设计变量,即:
X=
=
考虑到机构的杆长按比例变化时,不会改变其运动规律,因此在计算时常取 ,而其他杆长则按比例取为 的倍数。若取曲柄的初始位置角为极位角,则 及相应摇杆 位置角 均为杆长的函数,几何图形关系如右图,其关系式为:
lb=[1;1];
%设计变量的下界
x0=[4;2];
%迭代初始点
A=[-1,0;0,-1;-1,-1;1,-1;-1,1];
%线性不等式约束
b=[-1;-1;-6;4;4];
options=optimset('largescale','off','display','off','Algohm','active-set'
‘fmincon’函数进行求解。 ⑴ fmincon 里面算法的选择:fmincon 里面一共提供了‘largescale’,‘ 'medium-scale’
两 种 算 法 , 由 于 此 问 题 只 有 两 个 设 计 变 量 , 维 数 较 低 , 故 采 用 ‘ medium-scale ’ 算 法 。 ‘medium-scale’算法是采用 SQP,算法中 Hessian 阵可以通过 BFGS 迭代,初始 Hessian 阵任给。注意 BFGS 公式中 q 项是需要计算目标函数梯度得到的。所以 Hessian 矩阵的近似 计算是需要用到有限差分法。在采用‘'medium-scale’算法时,需提供其设计变量的初始 点 的信息,而初始点的选择也将影响计算得收敛性和收敛速度,如果初始点选择得不恰 当,可能最后函数不能收敛,得不到计算结果。
