六年级总复习几何图形练习题(史上最全)
几何图形六年级

几何图形题型一:格点图形的面积计算(毕克定理) 1、正方形格点多边形的面积计算公式:(毕克定理)正方形格点多边形的面积=内点个数+界点个数÷2-1,如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么,正方形格点面积可以表示为:S =N +12L -1。
2、三角形格点多边形及其面积计算公式每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形,规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形。
三角形格点多边形的面积计算公式:(毕克定理)三角形格点多边形的面积=(内点个数+界点个数÷2-1)×2,如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么,三角形格点面积可以表示为:S =(N +12L -1)×2。
注意:1.毕克定理对任何格点图形都适用。
要区分面积是几个单位。
2.在数格点时要细心。
3.严格区分正方形格点多边形和三角形格点多边形。
正方形格点图形的面积[模型例题1.]如图是用橡皮筋在钉板上围成的一个三角形,计算它的面积是多少。
(每相邻两个小钉之间的距离都等于1个长度单位)分析 直接套用正方形格点多边形面积公式“正方形格点多边形的面积=内点个数+界点个数÷2-1”即可解答。
解:5+3÷2-1=5.5 答:三角形的面积为5.5。
[模型例题2.]如图所示,在边长为1厘米的正方形格点中,图形“”的面积是多少平方厘米?分析直接套用正方形格点多边形面积公式“正方形格点多边形的面积=内点个数+界点个数÷2-1”即可解答。
解:6+10÷2-1=10(平方厘米)答:图形“”的面积是10平方厘米。
三角形格点图形的面积[模型例题3.]下图中有28个点,其中每相邻的三点“∵”或“∴”所形成的三角形都是面积为1的等边三角形,试计算△ABC的面积。
分析直接套用三角形格点多边形面积公式“三角形格点多边形的面积=(内点个数+界点个数÷2-1)×2”即可解答。
六年级总复习几何图形练习题(史上最全)
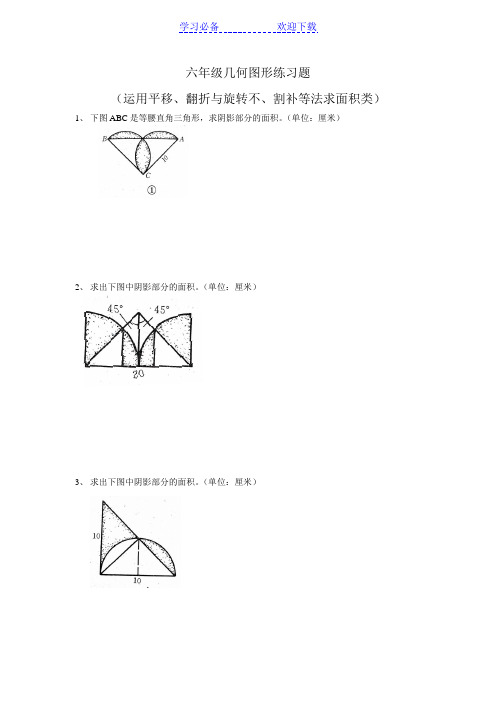
六年级几何图形练习题(运用平移、翻折与旋转不、割补等法求面积类)1、下图ABC是等腰直角三角形,求阴影部分的面积。
(单位:厘米)2、求出下图中阴影部分的面积。
(单位:厘米)3、求出下图中阴影部分的面积。
(单位:厘米)4、求出下图中阴影部分的面积。
(单位:厘米)5、在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E和F为圆心,以扇形半径之半为半径,画两个半圆交于D。
求图中阴影部分的面积(如下图)。
6、求出下图阴影部分的面积。
(单位:厘米)7、求出下图阴影部分的面积。
(单位:厘米)8、下图,直径AB=20厘米,阴影Ⅰ的面积比阴影Ⅱ的面积大7平方厘米,求BC的长。
9、如下图,四个圆的直径均为4厘米,求阴影部分面积。
(单位:厘米)10、下图中各小圆的半径为1,求该图中阴影部分的面积。
11、已知右图中两个正方形的边长分别是3厘米和6厘米,求阴影部分的面积。
12、下图的中的正方形的边长是2厘米,以圆弧为分界线的Ⅰ、Ⅱ两部的面积的差是多少平方厘米?( =3.14)12、如下图,已知直角三角形的面积是12平方厘米,求阴影部分的面积。
13、如下图,O为圆心CO垂直于AB,三角形ABC的面积是45平方厘米,以C为圆心,CA为半径画弧将圆分成两部分,求阴影部分的面积。
14、如下图扇形的半径OA=OB=6厘米。
角AOB等于45°,AC垂直OB于C点,那么图中阴影部分面积是多少平方厘米?(π=3.14)15、下图中,图①是一个直径为3厘米的半圆,AB是直径,让A点不动,整个半圆逆时针旋转60°角,此时B 点移动到B′(如图②)。
那么,图中阴影部分的面积是多少平方厘米?(π=3.14)16、求下列图形的阴影部分。
17、下图中长方形的面积是45平方米,求阴影部分的面积。
18、把一块1.35公顷的长方形田地划分成两部分(如下图),其中三角形田地比梯形田地少0.81公顷,三角形的底是60米。
最新六年级总复习几何图形练习题

1、 六年级总复习几何图形练习题2.在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E 和F 为圆心,以扇形半径之半为半径,画两个半圆交于D.求图中阴影部分的面积(如下图).3.如上图扇形的半径OA=OB=6厘米.角AOB 等于45°,AC 垂直OB 于C 点,那么图中阴影部分面积是多少平方厘米?( =3.14) 20、如下图,已知直角三角形ABC 中,AB 边上的高是4.8厘米,求阴影部分的面积.21、如上图,把一个圆剪成一个近似的长方形,已知长方形的周长是33.12厘米,求阴影部分面积.22、如下图,求阴影部分面积.(单位:厘米)23、求下列各图的阴影部分面积.(单位:厘米)31、求下面立体图形的体积.(单位:cm )32、如果,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒深15厘米.把酒瓶塞紧靠后,使其瓶口向下倒立,这时酒深19厘米,酒瓶容积是多少毫升?33、一个瓶子,它的瓶身呈圆柱形(不计瓶颈),如图,已知瓶内装有1.6升的水,当瓶子正放时瓶内水面高为12厘米,当瓶子倒立时瓶内空余部分高3厘米,求瓶子的容积.34、一个饮料瓶,它的瓶身呈圆柱形(不计瓶颈),如下图所示,已知它的容积为1200立方厘米,当瓶子正放时瓶内水面高为18厘米,倒放时瓶内空余部分高6厘米,瓶内装有多少立方厘米的饮料?36、下图中三角形ABC 的高是5厘米,三角形的面积是30平方厘米,求阴影部分的面积.37、如右图是四个半径均为1厘米的圆,求阴影部分的面积.339、已知直径AB=AD=20厘米,∠CAB的度数为45度,求图中阴影部分的面积(π取3.14)一、填空(34分)1.上海在北京的南偏东约30°的方向上,那么北京在上海的()偏()约()的方向上.2. 图形的变换方式有平移、()、().3. 观察钟面,(1)指针从12 绕点O顺时针方向旋转90°到().(2)指针从8绕点O顺时针方向旋转()°到10. 4.相交于同一个顶点的三条棱的长度分别叫做长方体的()、()、().正方体是()、()、()都相等的长方体,也叫().5.长方体和正方体都有()个面、()条棱、()个顶点.6.一个长方体长10厘米,宽9厘米,高5厘米,它的上、下面的面积分别是()平方厘米,前、后面的面积分别是()平方厘米,左、右面的面积分别是()平方厘米.它的表面积是()平方厘米,体积是()立方厘米.7.一个棱长是6分米的正方体,它的占地面积是()平方分米,表面积是()平方分米,体积是()立方分米.8.要做一个长5厘米,宽4厘米,高3厘米的长方体框架,至少需要( )厘米的铁丝.9.用36厘米的铁丝正好围成一个正方体框架,这个正方体框架的棱长是()厘米.要在它的外面贴一层红纸,至少需要()平方厘米的红纸.11.至少要()个小正方体才能拼成一个大正方体.12.一个正方体的棱长扩大3倍,那么它的表面积(),体积().二、判断(10分)1. 半圆的周长就是圆周长的一半.()2.棱长是6厘米的正方体的体积和表面积相等.()3.长方体的6个面中,至少有4个面是长方形.()4.一个物体的体积是1m³,这个物体的形状一定是正方体.()5.把一个正方体切成两部分,它的体积和表面积都不变.()6木箱的体积就是木箱的容积.()8.长方体和正方体的底面积相等,高也相等,它们的体积一定相等.()9.钟表的指针从12绕O逆时针旋转90°到3.()10.体积相等的两个正方体,它们的表面积也一定相等.()三、选择(16分)1.下列图形中,不一定是轴对称的图形是().A 正方形B三角形 C 圆 D 线段3.一个长方体水箱的容积是150升,这个水箱底面是一个边长为5分米的正方形,则水箱的高是()(水箱厚度忽略不计)A 30分米B 10分米C 4分米D 6分米4.汽车公路上行驶是()现象,风车的运动是()现象 A 平移 B 旋转C移动D转动5.两个长方体拼成一个正方体后,它的体积(),表面积().A 变大,变大B 变小,变小C 不变,变大D不变,变小6.我们在画长方体时一般只画出三个面,这是因为长方体().A 只有三个面 B 只能看到三个面C 最多只能看到三个面7.一个棱长为8分米的正方体鱼缸,水面距缸口3分米,则鱼缸里装水().A 320升B 192升C 512升D 24升8.把一个长方体切成两个正方体,表面积增加了60平方分米,已知原长方体长3米,则它的体积是().A 180立方分米B 900立方分米C 1800立方分米D 90立方分米四、按要求画图(6分)1. 画出下图关于直线的轴对称图形.2.画出下图绕点A顺时针旋转90°的图形.3. 画出下图绕点O逆时针旋转90°的图形,并将原图向右平移4格.5.王叔叔要做一个棱长为3分米的无盖鱼缸,至少需要多少平方分米的玻璃?这个鱼缸最多可装水多少升?(玻璃的厚度忽略不计)1.农民要挖一个长30米,宽20米,深3.5米的养鱼池,要挖土多少立方米?如果要在池底和四周抹水泥,抹水泥的面积是多少平方米?。
六年级几何练习册(带答案)

:
.
:
;
A. ;
B. ;
答案 A
解析 连接 ,则
考点
几何 四边形
C. ; ,
D. ; .
风筝模型
七、圆与扇形
【练习25】
如图,两个阴影扇形的半径和圆心角已经标注在图中,那么两个扇形的周长之和为
,面积之和为
.(保留 )
答案 (1)
(2)
解析 扇形的周长之和为 扇形的面积之和为
考点
几何 圆与扇形 圆与扇形基本概念运用 扇形的基本公式
【练习33】
计算下面圆柱的表面积和体积(单位:cm)
(1)图中圆柱的表面积是
cm2,体积是
cm3;
(2)图中圆柱的表面积是
cm2,体积是
cm3;
答案 (1) (2)
(3)
(4)
解析 (1)表面积 cm2,体积
cm3;(2)表面积
cm2,体积
考点
几何 圆柱与圆锥 圆柱与圆锥基本概念运用 圆柱的表面积与体积综合
cm3.
【练习34】 计算下面各圆锥体积(单位:厘米)( 取 )
答案 25.12立方厘米; 37.68立方厘米
解析
;
.
考点
几何 圆柱与圆锥 圆柱与圆锥基本概念运用 圆锥的基本公式
【练习35】 如图,圆锥形容器中装有水 升,水面高度是圆锥高度的一半,这个容器最多能装水
升.
答案
解析 半径变为原来的 倍,高度变为原来的 倍,根据圆锥的体积公式:
出,可得
.
考点
几何 四边形 蝴蝶模型 基本梯形蝴蝶模型
【练习12】 如图,梯形
面积为 ,四边形
面积为 ,问阴影部分面积为多少?
小学六年级数学中所有图形与几何的知识合集+练习题(有答案)

(一)图形的认识、测量量的计量一、长度单位是用来测量物体的长度的。
常用的长度单位三、面积单位是用来测量物体的表面或平面图形的大小的。
常用面积单位:平方千米、公顷、平方米、平方分米、平方厘米。
四、测量和计算土地面积,通常用公顷作单位。
边长100米的正方形土地,面积是1公顷。
五、测量和计算大面积的土地,通常用平方千米作单位。
边长1000米的正方形土地,面积是1平方千米。
六、面积单位:(100)平面图形【认识、周长、面积】一、用直尺把两点连接起来,就得到一条线段;把线段的一端无限延长,可以得到一条射线;把线段的两端无限延长,可以得到一条直线。
线段、射线都是直线上的一部分。
线段有两个端点,长度是有限的;射线只有一个端点,直线没有端点,射线和直线都是无限长的。
二、从一点引出两条射线,就组成了一个角。
角的大小与两边叉开的大小有关,与边的长短无关。
角的大小的计量单位是(°)。
三、角的分类:小于90度的角是锐角;等于90度的角是直角;大于90度小于180度的角是钝角;等于180度的角是平角;等于360度的角是周角。
四、相交成直角的两条直线互相垂直;在同一平面不相交的两条直线互相平行。
五、三角形是由三条线段围成的图形。
围成三角形的每条线段叫做三角形的边,每两条线段的交点叫做三角形的顶点。
六、三角形按角分,可以分为锐角三角形、直角三角形和钝角三角形。
按边分,可以分为等边三角形、等腰三角形和任意三角形。
七、三角形的内角和等于180度。
八、在一个三角形中,任意两边之和大于第三边。
九、在一个三角形中,最多只有一个直角或最多只有一个钝角。
十、四边形是由四条边围成的图形。
常见的特殊四边形有:平行四边形、长方形、正方形、梯形。
十一、圆是一种曲线图形。
圆上的任意一点到圆心的距离都相等,这个距离就是圆的半径的长。
通过圆心并且两端都在圆的线段叫做圆的直径。
十二、有一些图形,把它沿着一条直线对折,直线两侧的图形能够完全重合,这样的图形就是轴对称图形。
总复习——图形与几何一课一练(含答案)北师大版六年级数学上册

总复习——图形与几何一课一练(含答案)北师大版六年级数学上册学校:___________姓名:___________班级:___________考号:___________一、填空题1.一个时钟的分针长8cm,经过5小时分针针尖走过的路程是( )cm。
2.一个圆的半径增加2cm,直径增加( )cm,周长增加( )cm。
3.一个扇形的半径是10厘米,圆心角的度数为90度,扇形的面积是( )。
4.如图,直径2分米的圆贴着直角三角形的边在外侧滚动一周,回到起点时,圆心经过的路线长( )分米。
5.在一个周长是20dm的正方形木板内裁剪一个最大的圆,这个圆的半径是( )dm,面积是( )2dm,剩下的边角料是( )dm²。
6.一个立体图形从上面看是,从正面看是,搭成这样的图形需要( )个小正方体。
二、选择题7.傍晚,4名身高相同的同学站在路灯两侧(如图所示),在灯光的照射下,()的影子最长。
A.小芳B.小亮C.小明8.甲圆滚动6周的距离,乙圆要滚动5周,甲、乙两圆的直径比是().A.6︰5B.5︰6C.36︰259.下列四个语句中,正确的个数有().①能同时被2和3整除的数都是偶数②一个三角形中至少有一个角大于或等于60o ③凡是等腰三角形必定是锐角三角形④没有公约数的两个数是互质数A.1个B.2个C.3个10.如图,从上面看到的形状是()。
A.B.C.三、判断题11.圆周率是圆的周长除以它直径的商,是一个固定值。
( )12.圆是轴对称图形,它有很多条对称轴。
( )13.两个半圆一定能拼成一个整圆。
( )14.时针从9时顺时针旋转90度后,时针指向12时.( )15.周长相等的两个圆,它们的面积也一定相等,。
(判断对错)16.左图中,两个阴影部分的周长和面积都相等。
( )四、图形计算17.计算阴影部分的面积。
五、解答题18.一种压路机的前轮直径是1.5m,如果要压路282.6m,这台压路机的前轮大约要转动多少圈?19.A、B、C代表《西游记》中唐僧的三个徒弟,他们的关系可用下图表示.“C→B”表示C是B的师兄.回答下面的问题:①A和C的关系是什么?A和B的关系是什么?②你知道A、B、C分别代表谁吗?20.张老师每天骑自行车上下班,自行车的外轮直径大约是66cm,平均每分转150周,他从家到学校需要20分,他家到学校的路程大约是多少米?(得数保留整数)21.一辆大巴的车轮半径是45cm,车身长13m,现在要通过一座长1400m的隧道,这辆大巴的车轮至少要转多少圈车身才能完全通过隧道?22.学校在直径4米的圆形水池外铺一条1米宽的小路(如图),小路的面积是多少平方米?(π取3.14)23.姐弟两人在一个直径是100m的圆形广场外围,同时同地向相反方向行走,姐姐每分走16m,弟弟每分走15.4m,两人第二次相遇时离出发点多少米?参考答案:1.251.22. 4 12.563.78.5平方厘米4.18.28【分析】如图:绿色部分是圆心经过的路线,相当于这个三角形的三条边加上一个半径是1分米的圆的周长,根据三角形的周长公式和圆周长公式,用3+4+5+3.14×1×2即可求出圆心经过的路线长度。
小学六年级数学几何图形练习题及答案
小学六年级数学几何图形练习题及答案本文将为小学六年级的学生提供一些数学几何图形的练习题及答案,帮助他们巩固和提高几何图形的认知和理解能力。
以下是一些常见的几何图形及其练习题:一、直线、线段、射线1. 完成下图:画出两条不同的线段,并用字母标记它们。
答案:答案因为文字发不了图片二、点、面、角1. 下图中的阴影部分是什么?答案:阴影部分是一个三角形。
三、正方形1. 下图中的图形是什么?答案:下图中的图形是一个正方形。
2. 画出一个边长为5cm的正方形。
答案:答案因为文字发不了图片四、长方形1. 下图中哪个图形是长方形?答案:图形B是长方形。
2. 画出一个长6cm、宽3cm的长方形。
答案:答案因为文字发不了图片五、圆形1. 下图中哪个图形是圆形?答案:图形A是圆形。
2. 画出一个直径为8cm的圆。
答案:答案因为文字发不了图片六、三角形1. 画出一个任意形状的三角形。
答案:答案因为文字发不了图片2. 判断下列各形状是否是三角形:(1)正方形 (2)长方形 (3)梯形答案:(1)正方形不是三角形 (2)长方形不是三角形 (3)梯形是三角形七、梯形1. 下图中哪个图形是梯形?答案:图形C是梯形。
2. 画出一个上底为4cm,下底为8cm,高为3cm的梯形。
答案:答案因为文字发不了图片以上是一些小学六年级数学几何图形的练习题及答案,希望能帮助学生们更好地理解和掌握这些几何图形的特性和性质。
学习数学要多做题多练习,通过实际操作加深对知识的理解,才能在数学学习中取得好成绩。
祝愿学生们能够在几何图形的学习中取得更进一步的进展!。
六年级总复习几何图形练习题4
1、六年级总复习几何图形练习题42.在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E和F为圆心,以扇形半径之半为半径,画两个半圆交于D。
求图中阴影部分的面积(如下图)。
3.如上图扇形的半径OA=OB=6厘米。
角AOB等于45°,AC垂直OB于C点,那么图中阴影部分面积是多少平方厘米?( =3.14)20、如下图,已知直角三角形ABC中,AB边上的高是4.8厘米,求阴影部分的面积。
21、如上图,把一个圆剪成一个近似的长方形,已知长方形的周长是33.12厘米,求阴影部分面积。
22、如下图,求阴影部分面积。
(单位:厘米)23、求下列各图的阴影部分面积。
(单位:厘米)31、求下面立体图形的体积。
(单位:cm)32、如果,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒深15厘米。
把酒瓶塞紧靠后,使其瓶口向下倒立,这时酒深19厘米,酒瓶容积是多少毫升?33、一个瓶子,它的瓶身呈圆柱形(不计瓶颈),如图,已知瓶内装有1.6升的水,当瓶子正放时瓶内水面高为12厘米,当瓶子倒立时瓶内空余部分高3厘米,求瓶子的容积。
34、一个饮料瓶,它的瓶身呈圆柱形(不计瓶颈),如下图所示,已知它的容积为1200立方厘米,当瓶子正放时瓶内水面高为18厘米,倒放时瓶内空余部分高6厘米,瓶内装有多少立方厘米的饮料?36、下图中三角形ABC的高是5厘米,三角形的面积是30平方厘米,求阴影部分的面积。
37、如右图是四个半径均为1厘米的圆,求阴影部分的面积。
339、已知直径AB=AD=20厘米,∠CAB的度数为45度,求图中阴影部分的面积(π取3.14)一、填空(34分)1.上海在北京的南偏东约30°的方向上,那么北京在上海的()偏()约()的方向上。
2. 图形的变换方式有平移、()、()。
3. 观察钟面,(1)指针从12 绕点O顺时针方向旋转90°到()。
(2)指针从8绕点O顺时针方向旋转()°到10。
(完整版)六年级数学图形与几何练习题
六年级数学图形与几何练习题(满分80)一填空(15分)1、3小时20分=()小时9公顷200平方米=()公顷2、棱长是1分米的正方体,把它切成棱长1厘米的小正方体,摆成一排长()米。
3、一个棱长总和是48分米的长方体,长、宽、高的比是5:4:3,表面积是(),体积是()。
4、把一个正方体平均分成两个小长方体,其中一个长方体的表面积是原来正方体表面积的()。
5、把一个长20厘米、宽15厘米的长方形按1:5缩小后,长是()厘米,宽是()厘米,面积缩小到原来的()。
6、王丽坐在教室最后一排的最后一列上,她的位置可以表示为(6,8),这个班中共有( )名学生。
7、把高10厘米的圆柱分成16等份,拼成近似长方体,表面积增加了80平方厘米,圆柱的体积是()立方厘米。
8、两个圆的半径分别是3厘米和5厘米,它们周长的比是(),面积的比是()。
9、一个棱长4分米的正方体铁块,熔铸成底面积是32平方分米的圆锥,圆锥的高是()2倍。
( )7、如果一个圆柱的底面直径和高相等,那么把圆柱的侧面沿高展开是一个正方形。
()8、一条直线上的两点把这条直线分成两条射线和一条线段,所以射线比直线短。
( )9、.圆有无数条对称轴,而半圆只有一条对称轴。
( )10、教室里小华的位置用数对表示是(2,3),他的同桌可以用数对(2,4)表示。
( )三、选择1、一架飞机从某机场向南偏东50°方向飞行了1000米,返回时飞机要向( )A 、南偏东50°方向飞行1000米B 、 西偏北50°方向飞行1000米C 、南偏西50°方向飞行1000米D 、 北偏西50°方向飞行1000米2、把一段圆钢削成一个最大的圆锥,削去部分重4千克,这段圆钢原来重( )千克。
A 、24 B 、6 C 、 12 D 、 83、在一个等腰三角形中,已知两条边分别长8厘米和4厘米,这个等腰三角形的周长是( )厘米。
A 、12B 、 16C 、 20D 、 16或204、一个等腰梯形周长是48厘米,面积96平方厘米,高是8厘米,腰长( )厘米。
(完整版)小学六年级几何图形练习题
几何图形练习题
1、一条小河的一边有两个点A 和点B 。
从A 点出发,到小河里挑水,再到B 点。
怎么走最近?请你画出挑水的路线,并说明。
3、如图,三角形ABC 的面积是120平方厘米,AE=DE , DC=2
1
BC 。
求阴影部分的面积。
4、用篱笆围一块梯形范围的苗圃(如图),一面利用围墙不用篱笆, 这样共用去篱笆45米。
这块苗圃的面积是多少?
5、如图,在三角形ABC 中,D 、E 是两个将BC 边平均分成三份的两个点,F 为AB 的中点,如果三角形DEF 的面积是12平方厘米,则三角形ABC 的面积是多少?
D
C
6、有一个平行四边形的周长是80厘米,它的相邻两条边上的高是12厘米和8厘米。
求这个平行四边形的面积。
7、右图三角形ECD中EC=12厘米,CD=8厘米,并且它们的面积
是长方形ABCF的2倍,那么三角形ADF的面积是()。
8、如果三角形的两条边分别是4cm和7cm,那么第三条边的
取值范围是(),取整厘米数可以是()。
9、一个直角三角形三条边分别是6厘米、8厘米和10厘米,那么,它的斜边上的高是()。
10、2002年在北京召开了国际数学家大会,大会的会标如右图所示,它是由四个相同的直角三角形拼成的,直角三角形两条直角边边长分别是2和3.问:大正方形的面积是多少?
D B
11、有一条小河,河道原来面宽15米,底宽2米,深3米。
挖后面宽不变,底宽3米,深4米,求横截面中阴影部分的面积。
一条是长方形,一条是平行四边形。
那么,草地部分的面积是多少?
10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级几何图形练习题
(运用平移、翻折与旋转不、割补等法求面积类)1、下图ABC是等腰直角三角形,求阴影部分的面积。
(单位:厘米)
2、求出下图中阴影部分的面积。
(单位:厘米)
3、求出下图中阴影部分的面积。
(单位:厘米)
4、求出下图中阴影部分的面积。
(单位:厘米)
5、在半径为10厘米,圆心角为90°的扇形中,分别以两条半径的中点E和F为圆心,以
扇形半径之半为半径,画两个半圆交于D。
求图中阴影部分的面积(如下图)。
6、求出下图阴影部分的面积。
(单位:厘米)
7、求出下图阴影部分的面积。
(单位:厘米)
8、下图,直径AB=20厘米,阴影Ⅰ的面积比阴影Ⅱ的面积大7平方厘米,求BC的长。
9、如下图,四个圆的直径均为4厘米,求阴影部分面积。
(单位:厘米)
10、下图中各小圆的半径为1,求该图中阴影部分的面积。
11、已知右图中两个正方形的边长分别是3厘米和6厘米,求阴影部分的面积。
12、下图的中的正方形的边长是2厘米,以圆弧为分界线的Ⅰ、Ⅱ两部的面积的差是多少平方厘米?( =3.14)
12、如下图,已知直角三角形的面积是12平方厘米,求阴影部分的面积。
13、如下图,O为圆心CO垂直于AB,三角形ABC的面积是45平方厘米,以C为圆
心,CA为半径画弧将圆分成两部分,求阴影部分的面积。
14、如下图扇形的半径OA=OB=6厘米。
角AOB等于45°,AC垂直OB于C点,那么
图中阴影部分面积是多少平方厘米?(π=3.14)
15、下图中,图①是一个直径为3厘米的半圆,AB是直径,让A点不动,整个半圆逆
时针旋转60°角,此时B 点移动到B′(如图②)。
那么,图中阴影部分的面积是多少平方厘米?(π=3.14)
16、求下列图形的阴影部分。
17、下图中长方形的面积是45平方米,求阴影部分的面积。
18、把一块1.35公顷的长方形田地划分成两部分(如下图),其中三角形田地比梯形田地少0.81公顷,三角形的底是60米。
这块长方形地的长和宽各是多少米?
19、如下图,半圆的直径是10厘米,阴影部分甲比乙的面积少1.25平方厘米,求三角形△ABC的边OA的长。
20、如下图,已知直角三角形ABC中,AB边上的高是4.8厘米,求阴影部分的面积。
21、如下图,把一个圆剪成一个近似的长方形,已知长方形的周长是33.12厘米,求阴影部分面积。
22、如下图,求阴影部分面积。
(单位:厘米)
23、求下列各图的阴影部分面积。
(单位:厘米)
23、下图长方形ABCD中,AB=4厘米,BC=8厘米,M,N分别为两弧中点,求阴影部分的面积。
24、下图是由三个相同的圆围成,请你先将阴影部分割补成一个规则图形,若
R=4厘米,求阴影部分的面积。
25、求出下图的阴影部分面积。
(单位:厘米)
26、下图正方形ABCD的面积是30厘米,求阴影部分的面积。
午方法1:
方法2:
27、在下图中,O为圆心,AB垂直于CD,直角三角形ABC的面积是60平方厘米,扇形CAEB以CA为半径。
求阴影分部的面积。
28、如下图所示,两圆半径都是1厘米,且图中两个阴影部分部分的面积相等。
求长方形
O的面积。
ABO
1
29、求下图的面积。
(单位:厘米)
30、下图,四边形ABCD是正方形,三角形ABF的面积比正方形ABCD的面积大12厘米,线段BC的长为8厘米。
求线段CF的长是多少厘米?
31、求下面立体图形的体积。
(单位:cm)
32、如果,一个酒瓶里面深24厘米,底面内径是16厘米,瓶里酒深15厘米。
把酒瓶塞紧靠后,使其瓶口向下倒立,这时酒深19厘米,酒瓶容积是多少毫升?
33、一个瓶子,它的瓶身呈圆柱形(不计瓶颈),如图,已知瓶内装有1.6升的水,当瓶子正放时瓶内水面高为12厘米,当瓶子倒立时瓶内空余部分高3厘米,求瓶子的容积。
34、一个饮料瓶,它的瓶身呈圆柱形(不计瓶颈),如下图所示,已知它的容积为1200立方厘米,当瓶子正放时瓶内水面高为18厘米,倒放时瓶内空余部分高6厘米,瓶内装有多少立方厘米的饮料?
35、小明测量一瓶子容积,测得瓶子的底面直径12厘米,然后给瓶子内盛入一些水,正放时水高20厘米,倒放时水高25厘米,瓶子深30厘米,如图。
你能根据这些信息求出瓶子的容积吗?
35、如果图,将10毫升的水装入一个圆锥形容器中,水深正好占容器深的21。
请问:再添入多少毫升水,可装满此容器?
36、下图中三角形ABC 的高是5厘米,三角形的面积是30平方厘米,求阴影部分的面积。
37、如右图是四个半径均为1厘米的圆,求阴影部分的面积。
38、下图中,圆的周长为12.56厘米,平行四边形ABCD的面积为21.6平方厘米,求阴影部分的面积。
39、已知直径AB=AD=20厘米,∠CAB的度数为45度,
求图中阴影部分的面积(π取3.14)
40、如图,一条直线上放着一个长4厘米,宽为3厘米的长方形I,它的对角线恰好是5厘
米,让这个长方形绕定点B顺时针旋转90度后到达长方形Ⅱ的位置;连续做三次,A点到达E点的位置,求A点走过的路程长。
(结果用π表示)(请画出旋转轨迹)。
