重庆大学_结构动力学大作业
结构动力学大作业2
结构动力学大作业班级：学号：姓名：目录1. Wilson-θ法原理简介 (2)2. Wilson-θ程序验算 (3)2.1△t的影响 (4)2.2 θ的影响 (5)3. 非线性问题求解 (5)4. 附录 (8)Wilson-θ法源程序 (8)1. Wilson -θ法原理简介图1-1Wilson-θ法示意图Wilson-θ法是基于对加速度a 的插值近似得到的，图1-1为Wilson-θ法的原理示意图。
推导由t 时刻的状态求t +△t 时刻的状态的递推公式：{}{}{}{}()t tt t t y y y y tτθτθ++∆=+-∆ (1-1)对τ积分可得速度与位移的表达式如下：{}{}{}{}{}2()2t t t t t t yy y y ytτθττθ++∆=++-∆ (1-2){}{}{}{}{}{}23()26t t t t t t t y y y y y ytτθτττθ++∆=+++-∆ (1-3)其中τ=θt ，由式(1-2)、(1-3)可以解出：{}{}{}{}{}266()2()t t t tt t t y y y y y t tθθθθ+∆+∆=---∆∆(1-4){}{}{}{}{}3()22t t t t t t t tyy y y y t θθθθ+∆+∆∆=---∆(1-5)将式(1-4)、(1-5)带入运动方程：[]{}[]{}[]{}{}m y C y k y P ++=(1-6)[]{}[]{}[]{}{}t t t t t t t tm y C y k y P θθθθ+∆+∆+∆+∆++= (1-7)注意到此时的式子为{{}t t y θ+∆}和上一个时刻{}t y 、{}t y、{}t y 以及t +θ△t 时刻的荷载{}t t P θ+∆相关，可以运用迭代的思想来求解，下图给出线弹性条件下Wilson -θ法的流程图：图1-2Wilson-θ法流程图2.Wilson-θ程序验算对线弹性条件下的Wilson-θ法进行MATLAB编程，源代码见附录。
高等结构动力学大作业
高等结构动力学大作业引言：高等结构动力学是土木工程中的重要学科，涉及到结构的振动和响应分析。
为了加深学生对该学科的理解和运用能力，设计一份详细具体的大作业是非常有益的。
本文将介绍一个高等结构动力学大作业的设计，包括作业目标、内容和评价方式。
一、作业目标1.理论掌握：通过大作业，学生需要巩固和应用所学的高等结构动力学理论，提高对结构振动和响应分析方法的理解和运用能力。
2.实践能力培养：作业要求学生进行实际案例的分析和计算，培养他们的实践能力和问题解决能力。
3.创新思考：作业鼓励学生从不同的角度进行创新性思考，提出改进或优化现有结构的方法或方案。
4.报告撰写能力：作业要求学生以报告形式呈现研究成果，培养他们的科学写作能力和沟通表达能力。
二、作业内容1.理论分析：作业可以要求学生选择一个特定的结构，如悬索桥、高层建筑等，进行结构振动和响应分析。
学生需要运用所学的高等结构动力学理论，计算结构的固有频率、模态形态等。
2.实验模拟：作业可以设计实验模拟任务，要求学生使用相关软件或设备进行结构的振动试验，获取结构的模态参数和响应曲线数据。
3.结构优化：作业可以要求学生对给定的结构进行优化设计，以降低结构的振动响应或改善结构的抗震性能。
学生需要提出具体的优化方案，并进行相应的计算和分析。
4.报告撰写：作业最终要求学生将研究成果整理成报告。
报告应包括问题陈述、理论分析或实验过程、计算方法和结果分析等内容，以及对结论和进一步研究的讨论。
三、评价方式1.报告评估：根据学生的报告内容、结构分析和计算准确性、结果分析等方面，评估学生对高等结构动力学的理解和应用能力。
可以采用定量评价指标和评分标准进行评估。
2.讨论与答辩：在评价阶段，可以组织学生进行讨论和答辩，让学生互相交流和分享研究成果，进一步加深对问题的理解和探讨。
3.同伴评价：可以引入同伴评价的方式，让学生互相评价和给出建议，促进学生之间的交流和学习。
4.教师评价：教师对学生的报告进行评价，包括对报告内容、分析思路和计算方法的评估，提供及时的反馈和指导。
特征值解法——精选推荐
《结构动力学》大作业结构大型特征值问题的求解0810020035 吴亮秦1振动系统的特征值问题1.1实特征值问题n 自由度无阻尼线性振动系统的运动微分方程可表示为：[]{}[]{}(M u K u F t += （1.1）其中，{}u 是位移向量，[]M 和[]K 分别是系统的质量矩阵和刚度矩阵，都是n 阶正定矩阵，()F t 是激励向量。
此系统的自由振动微分方程为[]{}[]{}0M u K u += （1.2） 设其主振型为： {}{}sin()u v t ωϕ=+ （1.3） 其中，{}v 为振幅向量，ω为圆频率，ϕ为初相位。
将(1.3)代入自由振动微分方程(1.2)， 得：[]{}[]{K v M v λ= （1.4） 其中2λω=，(1.4)具有非零解的条件是()[][]d e t 0M K λ-= (1.5)式(1.4)称为系统的特征方程，由此可以确定方程的n 个正实根1{}n i i λ=，称为系统的特征值，1{}n i i ω=称为系统的固有频率，{}i v （i=1,2,…..n ）为对应于特征值的特征向量或称为系统的振型或模态。
因为[]M 矩阵正定，则[]M 有Cholesky 分解：[][][]TM L L = (1.6)其中，[]L 是下三角矩阵。
引入向量{}x 满足：{}[]{}T x L v =，则：1{}([]){}T v L x -= (1.7)代入(1.4)，得：([][]){}I P x λ-= (1.8) 其中，()11[][][][]TP L K L --=，式(1.8)称为标准实特征值问题。
1.2复特征值问题多自由度阻尼自由振动系统的运动方程为如下二阶常系数微分方程组：[]{()}[]{()}[]{(M x t C x t K x t ++= (1.9) 其中 []M ，[]C ，[]K 分别是n 阶的质量、阻尼和刚度矩阵，{()}q t 是n 维可微向量函数。
重庆大学结构力学本科习题
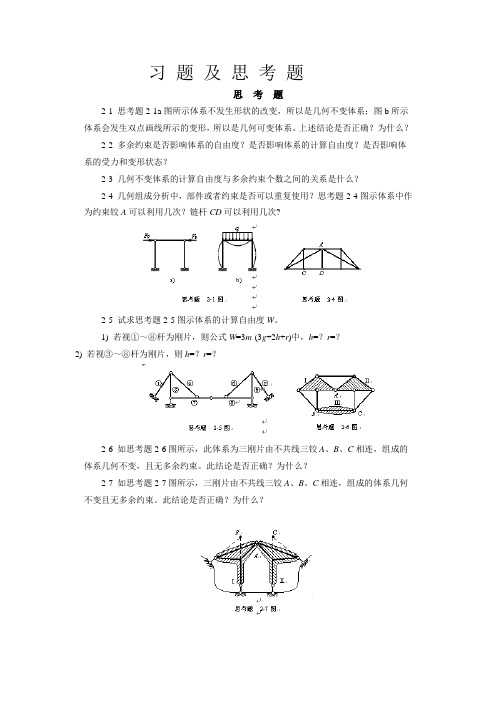
习题及思考题思考题2-1 思考题2-1a图所示体系不发生形状的改变，所以是几何不变体系；图b所示体系会发生双点画线所示的变形，所以是几何可变体系。
上述结论是否正确？为什么？2-2 多余约束是否影响体系的自由度？是否影响体系的计算自由度？是否影响体系的受力和变形状态？2-3 几何不变体系的计算自由度与多余约束个数之间的关系是什么？2-4 几何组成分析中，部件或者约束是否可以重复使用？思考题2-4图示体系中作为约束铰A可以利用几次？链杆CD可以利用几次?2-5 试求思考题2-5图示体系的计算自由度W。
1) 若视①～⑧杆为刚片，则公式W=3m-(3g+2h+r)中，h=？r=？2) 若视③～⑧杆为刚片，则h=？r=？2-6 如思考题2-6图所示，此体系为三刚片由不共线三铰A、B、C相连，组成的体系几何不变，且无多余约束。
此结论是否正确？为什么？2-7 如思考题2-7图所示，三刚片由不共线三铰A、B、C相连，组成的体系几何不变且无多余约束。
此结论是否正确？为什么？2-8 几何常变体系和几何瞬变体系的特点是什么？（试从约束数目、运动方式、受力及变形情况等方面讨论）。
2-9 静定结构的几何特征是什么？力学特性是什么？2-10 超静定结构的几何特征是什么？力学特性是什么？习题2-1是非判断(1)若平面体系的实际自由度为零，则该体系一定为几何不变体系。
( )(2)若平面体系的计算自由度W=0，则该体系一定为无多余约束的几何不变体系。
( )(3)若平面体系的计算自由度W＜0，则该体系为有多余约束的几何不变体系。
( )(4)由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5)习题2-1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。
( )(6)习题2-1(6)a图所示体系去掉二元体ABC后，成为习题2-1(6) b图，故原体系是几何可变体系。
( )(7)习题2-1(6)a图所示体系去掉二元体EDF后，成为习题2-1(6) c图，故原体系是几何可变体系。
高等结构动力学大作业
高等结构动力学大作业
摘要：
一、高等结构动力学的概念和意义
二、高等结构动力学的主要研究内容
三、高等结构动力学的应用领域
四、高等结构动力学的发展趋势
正文：
一、高等结构动力学的概念和意义
高等结构动力学是研究结构在动力载荷作用下的响应和稳定性的学科，它主要关注结构在振动、冲击、地震等外部激励下的反应。
高等结构动力学在现代工程技术中具有重要意义，因为它可以帮助我们设计和分析各种结构，以确保它们在地震、风、水等自然灾害或人为冲击下能保持稳定和安全。
二、高等结构动力学的主要研究内容
高等结构动力学主要研究以下几个方面的内容：
1.结构动力学的基本理论：包括结构的自由振动、强迫振动和随机振动等。
2.结构动力学的数值计算方法：包括常用的有限元法、有限体积法和有限差分法等。
3.结构动力学的建模和识别：包括结构的建模、参数识别和模型更新等。
4.结构动力学的分析和设计：包括结构的动力响应分析、稳定性分析和抗震设计等。
三、高等结构动力学的应用领域
高等结构动力学在许多工程领域都有广泛的应用，包括：
1.建筑结构：包括高层建筑、桥梁、隧道和机场等。
2.机械结构：包括汽车、飞机、火车和船舶等。
3.航空航天结构：包括火箭、卫星和空间站等。
4.核电站结构：包括核反应堆、冷却塔和燃料棒等。
四、高等结构动力学的发展趋势
随着计算机技术的发展，高等结构动力学的数值计算方法越来越精确，可以更准确地模拟结构的动力响应。
同时，随着大数据和人工智能技术的发展，结构动力学的建模和识别也将更加智能化和自动化。
最新结构动力学大作业
结构动力学大作业------------------------------------------作者xxxx------------------------------------------日期xxxx结构动力学大作业班级土木卓越１２0１班学号U20１２10323姓名陈祥磊指导老师叶昆20１４。
１2.30 结构动力学大作业-—SDO Ｆ体系在任意荷载作用下的动力响应 一、结构参数计算结构为右图所示的 １、kg m 3101000⨯=m N k /1020006⨯= ２、m m m m N =⋅⋅⋅⋅⋅⋅==21 k k k k N λ==⋅⋅⋅⋅⋅⋅==213、结构参数中5=N ;0.1=λ。
二、确定各阶频率和振型多自由度体系自由振动时的运动方程为012121111=+⋅⋅⋅+++n n y k y k y k y m 022221212=+⋅⋅⋅+++n n y k y k y k ym .。
．.。
.12jN-1N02211=+⋅⋅⋅+++n nn n n n y k y k y k y m 写成矩阵形式即为[]{}[]{}{}0=+y K yM 假设此方程的解答为{}{}()αω+=t Y y sin ,带入到运动方程中得到振动方程[][](){}{}02=-Y M K ω此方程要有非零解必须满足频率方程[][]02=-M K ω,可解得各阶主频率i ω再根据 [][](){}(){}02=-i i Y M K ω可求出结构的主振型。
在主振型中,通常将最后一个位移值设定为1,只要在程序中加入下列语句：MDOF ．YMa ｔrix(：，ｉ)=ＭDO Ｆ.YMat ｒix(：,i ）/ＭDOF 。
YMatr ｉx(MD ＯF 。
ND,i)运行程序之后得到如下结果： 1、各阶频率i ω和周期i TW1 12.7２9０2６1 T1 ０。
49３６10８43W ２ 37.1558483２T ２ 0。
结构动力学大作业1.
结构动力学课程论文结构动力学课程论文一、题目1、试设计一个3层框架，根据实际结构参数，求出该结构的一致质量矩阵、一致刚度矩阵；2、至少采用两种方法求3层框架的频率和振型；3、采用时程分析法，输入地震波，求出所设计的3层框架各层的非线性位移时程反应，要求画出所设计的框架图、输入的地震波的波形图、所求得的各楼层位移时程反应图。
二、问题解答1、问题1解答1.1、框架设计框架立面图如下图一所示，梁截面均为400⨯700mm2，柱子的截面均为600⨯600mm2，跨度为7.2m，层高为3.6m，混凝土采用C30。
图一框架立面图设梁、柱均不产生轴向变形，且只考虑在框架的平面内变形，那么有3个平结构动力学课程论文移自由度和12个转角自由度，一共有15个自由度，自由度以及梁柱单元编号如下图二所示：V1V2V3图二单元编号及自由度方向先计算各个单元的一致质量矩阵和一致刚度矩阵，然后把相关的单元叠加组合计算得到整个结构的一致质量矩阵和一致刚度矩阵。
1.2、结构的一致质量矩阵梁：=0.4⨯0.7⨯2500=700kg/m, L=7.2m;梁、柱都为均布质量,故：⎧f⎪f⎪⎨⎪f⎪⎩fI1I2I3I4⎫⎪⎪L⎬=420⎪⎪⎭5622L⎡156⎢5415613L⎢⎢22L13L4L⎢⎣-13L-22L-3L-13L⎤-22L⎥⎥-3L⎥⎥4L⎦221⎫⎧v⎪v⎪⎪ 2⎪⎨⎬3⎪⎪v⎪ 4⎪⎩v⎭结构动力学课程论文结构动力学课程论文柱：=0.6⨯0.6⨯2500=900kg/m,L=3.6m 单元刚度矩阵如下：结构动力学课程论文结构动力学课程论文(m)(n)(p)ˆijˆijˆij由mij=m+m+m+....可计算一致质量矩阵中的各元素：(1)(2)(3)(10)(11)(12)(13)ˆ11ˆ11ˆ11ˆ11ˆ11ˆ11ˆ11m11=m+m+m+m+m+m+m=3⨯5040+ 4⨯1203.43=19933.72(10)(11)(12)(13)ˆ12ˆ12ˆ12ˆ12m12=m+m+m+m=4⨯416.57=1666.28结构动力学课程论文m13=0(10)m14=m15=m16=m17=m14=610.97(10)m18=m19=m1,10=m1,11=m18=-361.03 m1,12=m1,13=m1,14=m1,15=0(4)(5)(6)(10)(11)(12)(13)(14)(15)(16)(17)ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22ˆ22m22=m+m+m+m+m+m+m+m+m+m+m=3⨯5040+8⨯1203.43=24747.44(14)(15)(16)(17)ˆ23ˆ23ˆ23ˆ23m23=m+m+m+m=4⨯416.57=1666.28(10)m24=m25=m26=m27=m24=361.03(14)(10)ˆ28ˆ28m28=m+m=610.97-610.97=0 同理 m29=m2,10=m2,11=0(14)m2,12=m2,13=m2,14=m2,15=m2.03 ,12=-361(7)(8)(9)(14)(15)(16)(17)(18)(19)(20)(21)ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33ˆ33m33=m+m+m+m+m+m+m+m+m+m+m=3⨯5040+8⨯1203.43=24747.44(14)m34=m35=m36=m37=0 m38=m39=m3,10=m3,11=m38=361.03 (14)ˆ3ˆ(18)m3,12=m3,13=m3,14=m3,15=m.97-610.97=0 ,12+m3,12=610(1)(10)(1)ˆ44ˆ44ˆ45m44=m+m=2488.32+399.91=2888.23 m45=m=-1866.24m46=m47=0(10)ˆ48m48=m=-299.93m49=m4,10=m4,11=m4,12=m4,13=m4,14=m4,15=0(2)(1)(2)(11)ˆ56ˆ55ˆ55ˆ55=-1866.24m55=m+m+m=2488.32+2488.32+399.91=5376.55m56=mm57=m58=0(11)ˆ59m59=m=-299.93 m5,10=m5,11=m5,12=m5,13=m5,14=m5,15=0(2)(3)(12)ˆ66ˆ66ˆ66m66=m+m+m=2488.32+2488.32+399.91=5376.55(3)ˆ67m67=m=-1866.24 m68=m69=0(12)ˆ6m6,10=m.93 m6,11=m6,12=m6,13=m6,14=m6,15=0 ,10=-299(3)(13)ˆ77ˆ77m77=m+m=2488.32+399.91=2888.23m78=m79=m7,10=0(13)ˆ7m7,11=m.93 m7,12=m7,13=m7,14=m7,15=0 ,11=-299结构动力学课程论文(4)(10)(14)ˆ88ˆ88ˆ88m88=m+m+m=2488.32+399.91+399.91=3288.14(4)ˆ89m89=m=-1866.24 m8,10=m8,11=0(14)ˆ8m8,12=m.93 m8,13=m8,14=m8,15=0 ,12=-299(4)(5)(11)(15)ˆ99ˆ99ˆ99ˆ99m99=m+m+m+m=2488.32+2488.32+399.91+399.91=5776.46(5)ˆ9m9,10=m.24 ,10=-1866(15)ˆ9.93 m9,14=m9,15=0 m9,11=m9,12=0 m9,13=m,13=-299(5)(6)(12)(16)ˆ10ˆ10ˆ10ˆ10m10,10=m.32+2488.32+399.91+399.91=5776.46 ,10+m,10 +m,10+m,10=2488(6)(16)ˆ10ˆ m10,11=m=-1866.24m=m.93 m10,15=0m=m=010,1210,13,1110,1410,14=-299(6)(13)(17)ˆ11ˆ11ˆ11m11,11=m.32+399.91+399.91=3288.14,11+m,11+m,11=2488m11,12=m11,13=m11,14=0(17)ˆ11m11,15=m.93,15=-299(7)(14)(18)ˆ12ˆ12ˆ12m12,12=m.32+399.91+399.91=3288.14 ,12+m,12+m,12=2488 (7)ˆ12m12,13=m.24 m12,14=m12,15=0 ,13=-1866(7)(8)(15)(19)ˆ13ˆ13ˆ13ˆ13m13,13=m.32+2488.32+399.91+399.91=5776.46 ,13+m,13 +m,13+m,13=2488(8)ˆ13m13,14=m.24 m13,15=0 ,14=-1866(8)(9)(16)(20)ˆ14ˆˆˆm14,14=m+m+m+m.32+2488.32+399.91+399.91=5776.46 ,1414,1 414,1414,14=2488(9)ˆ14m14,15=m.24 ,15=-1866(9)(17)(21)ˆ15ˆ15ˆ15m15,15=m.32+399.91+399.91=3288.14 ,15+m,15+m,15=2488则得：一致质量矩阵（该矩阵为对称矩阵，故下三角省略）单位（kg）结构动力学课程论文0⎡19933.721666.28⎢24747.441666.28⎢⎢24747.44⎢⎢⎢⎢⎢⎢⎢M=⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣610.97361.0302888.23610.97361.030-1866.245376.55610.97361.0300-1866.245376.55610.97361.03000-1866.242888.23-361.030361.03-299.930003288.14-361.030361.030-299.9300-1866.245776.46-361.030361.0300-299.9300-1866.245776.46-361.030361.03000-299.9300-1866.243288.140-361.0300000-299.930003288.14⎤-361.03-361.03-361.03⎥⎥⎥000⎥000⎥⎥000⎥000⎥⎥000⎥000⎥⎥-299.9300⎥⎥0-299.930⎥00-299.93⎥⎥-1866.2400⎥5776.46-1866.240⎥5776.46-1866.24⎥⎥3288.14⎦⎥0001.3、结构的一致刚度矩阵各梁、柱均为等截面，故单元刚度矩阵为：-63L3L⎤⎧v1⎫⎧fs1⎫⎡6⎪f⎪⎪v⎪⎢6-3L-3L⎥⎪s2⎪2EI⎢-6⎪2⎪⎥=⎨⎬⎨⎬ 223⎢⎥f3L-3L2LLL⎪s3⎪⎪v3⎪⎢22⎥⎪⎪f3L-3LL2L⎣⎦⎪⎩v4⎪⎭⎩s4⎭框架梁：C30混凝土E=3⨯107KN/m2，0.40⨯0.73EI=3⨯10⨯=3.43⨯105kN·m2，L=7.2m 127结构动力学课程论文7框架柱：0.60⨯0.603EI=3⨯10⨯=3.24⨯105KN·m2 L=3.6m12结构动力学课程论文结构动力学课程论文结构动力学课程论文ˆ(m)+kˆ(n)+kˆ(p)+....可计算一致刚度矩阵中的各元素：由kij=kijijijˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)=4⨯0.833⨯105=3.332⨯105 k11=k11111111ˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)=4⨯(-0.833k12=k)⨯105=-3.332⨯105 k13=0 12121212 (10)k14=k15=k16=k17=k18=k19=k1,10=k1,11=k14=1.50⨯105k1,12=k1,13=k1,14=k1,15=0ˆ(10)+kˆ(11)+kˆ(12)+kˆ(13)+kˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)=8⨯0.833⨯105=6.664⨯105 k22=k2222222222222222ˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)=4⨯(-0.833k23=k)⨯105=-3.332⨯1052323232310k24=k25=k26=k27=k24=-0.861⨯105ˆ(10)+kˆ(14)=0.861⨯105-0.861⨯105=0 同理 k28=k2828k29=k2,10=k2,11=0结构动力学课程论文ˆ(14)=1.50⨯105 k2,12=k2,13=k2,14=k2,15=k2,12ˆ(14)+kˆ(15)+kˆ(16)+kˆ(17)+kˆ(18)+kˆ(19)+kˆ(20)+kˆ(21)=8⨯0.833⨯105=6.664⨯105 k33=k3333333333333333k34=k35=k36=k37=0(14)k38=k39=k3,10=k3,11=k38=-1.50⨯105ˆ(14)+kˆ(18)=1.50⨯105-1.50⨯105=0 k3,12=k3,13=k3,14=k3,15=k3,123,12ˆ(1)=0.953⨯105 ˆ(1)+kˆ(10)=1.906⨯105+3.60⨯105=5.506⨯105 k=kk44=k44444545 k46=k47=0ˆ(10)=1.80⨯105k48=k48k49=k4,10=k4,11=k4,12=k4,13=k4,14=k4,15=0ˆ(1)+kˆ(2)+kˆ(11)=1.906⨯105+1.906⨯105+3.60⨯105=7.412⨯105k55=k555555ˆ(2)=0.953⨯105 k56=k56k57=k58=0 ˆ(11)=1.80⨯105 k59=k59k5,10=k5,11=k5,12=k5,13=k5,14=k5,15=0ˆ(2)+kˆ(3)+kˆ(12)=1.906⨯105+1.906⨯105+3.60⨯105=7.412⨯105k66=k666666ˆ(3)=0.953⨯105 k67=k67ˆ(12)=1.80⨯105 k=k=k=k=k=0 k68=k69=0 k6,10=k6,116,126,136,146,156,10ˆ(3)+kˆ(13)=1.906⨯105+3.60⨯105=5.506⨯105k77=k7777k78=k79=k7,10=0ˆ(13)=1.80⨯105 k=k=k=k=0 k7,11=k7,127,137,147,157,11ˆ(4)+kˆ(10)+kˆ(14)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k88=k888888ˆ(4)=0.953⨯105 k89=k89ˆ(14)=1.80⨯105 k=k=k=0 k8,10=k8,11=0 k8,12=k8,138,148,158,12ˆ(4)+kˆ(5)+kˆ(11)+kˆ(15)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k99=k999999 99=11.012⨯105 14结构动力学课程论文ˆ(5)=0.953⨯105 k9,10=k9,10k9,14=k9,15=0k9,11=k9,12=0ˆ(15)=1.80⨯105 k9,13=k9,13ˆ(5)+kˆ(6)+kˆ(12)+kˆ(16)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k10,10=k10,1010,1010,1010,10=11.012⨯1055ˆ(6)=0.953⨯105 kˆ(16)k10,11=k10,12=k10,13=0 k10,14=k10,14=1.80⨯10 k10,15=0 10,11ˆ(6)+kˆ(13)+kˆ(17)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k11,11=k11,1111,1111,11ˆ(17)=1.80⨯105 k11,12=k11,13=k11,14=0 k11,15=k11,15 ˆ(4)+kˆ(7)+kˆ(18)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k12,12=k12,1212,1212,12ˆ(7)=0.953⨯105 kk12,13=k12,14=k12,15=0 12,13ˆ(7)+kˆ(8)+kˆ(15)+kˆ(19)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k13,13=k13,1 313,1313,1313,13=11.012⨯105ˆ(8)=0.953⨯105 kk13,14=k13,15=0 13,14ˆ(8)+kˆ(9)+kˆ(16)+kˆ(20)=1.906⨯105+1.906⨯105+3.60⨯105+3.60⨯105k14,14=k14,1 414,1414,1414,14=11.012⨯105ˆ(9)=0.3125⨯105k14,15=k14,15ˆ(9)+kˆ(17)+kˆ(21)=1.906⨯105+3.60⨯105+3.60⨯105=9.106⨯105k15,15=k15,1515,1515,15得到一致刚度矩阵（该矩阵为对称矩阵，故下三角省略）单位（kN/m）⎡3.332⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢K=105⨯⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣-3.3326.6640-3.3326.6641.50-1.5005.5061.50-1.5000.9537.4121.50-1.50000.9537.4121.50-1.500000.9535.5061.500-1.501.800009.1061.500-1.5001.80000.95311.0121.500-1.50001.80000.95311.0121.500-1.500001.80000.9539.10601.50000001.800009.10601.500000001.80000.95311.01201.5000000001.80000.95311.01201.50000000001.80000.9539.106⎤⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦结构动力学课程论文 2 问题2 解答2.1采用振型分解反应谱法，求解框架的频率和振型ˆ}={0}的特征值得到频率ω和振型φ：由[K]-ω2[M]{v在Matlab中导入质量矩阵[M]和刚度矩阵[K],输[v,ω2]=eig(K,M);ω=sqrt(ω2)可得框架的频率为： []ωT={ω1ω2ω3........ω14ω15}={32.861, 109.022, 199.133, 234.897, 299.589, 307.809 , 378.000, 388.414, 454.501, 480.646, 583.896 , 637.664, 747.045, 828.365, 1056.507 }框架的振型为[φ]=[{φ1}{φ2}{φ3}......{φ14}{φ15}]=φ1 φ2 φ3 φ4 φ5 φ6 φ7 φ8φ9 φ10 φ11 φ12 φ13 φ14 φ15结构动力学课程论文2.2 用Stodola法计算三层框架的频率和振型此结构的柔度矩阵是f=K-1=D=fm=⎡52612⎢34661⎢⎢13564⎢⎢-2919⎢-2009⎢⎢-2009⎢-2919⎢10-5⨯⎢-4627⎢-3739⎢⎢-3739⎢⎢-4627⎢-4436⎢⎢-3429⎢-3429⎢⎢⎣-4436453153846316844-648-547-547-648-3237-2622-2622-3237-5313-4034-4034-5313179831712511915-95-55.4-55.4-95-395-408-408-395-2546-1883-1883-2546 1933.61502.4600.3585.14-403.97.9103-69.43-330.8-46.98-141.3-151.2-164.3-169.8-202-2022088.51495.3606.51-631828.14-463.5-16.66-39.22-52.13-197.9-226.6-226.6-114.2-168.9-189.520471488.4605.89-7.983-467.4891.72-635.4-193.6-45.69-344.3-30.81-189.2-169.2-112.1-227.41933.61502.4600.3-69.437.9103-403.9585.14-151.2-141.3-46.98-330.8-202-149.4-169.8-164.3-959-507-53.6-141139.935.2281.15567.3-144114.5114.5109.7-71.595.5537.1-466.3-466.3-74.97214.41-174.8143.1345.392-214.1713.23-171.7134.55129.58-99.996.75140.084-885-466-7545.39143.1-175214.4134.6-172713.2-21440.0896.75-99.9129.6-959.1-507.2-53.6281.15235.225139.93-141.1109.67114.46-143.6567.357.99237.09595.548-71.52-959.1-507.2-53.6281.15235.225139.93-141.1109.67114.46-143.6567.357.99237.09595.548-71.52-768.9-687.5-306.5-28.0246.216-14.4511.743129.09-99.9796.6839.588-186.8664.53-159.7122.14-768.9-687.5-306.511.743-14.4546.216-28.0239.58896.68-99.97129.09122.14-159.7664.53-186.8-898.5⎤-828.5⎥⎥-387.3⎥⎥-1.176⎥7.242⎥⎥-15.89⎥45.168⎥⎥58.04⎥37.49⎥⎥95.943⎥⎥-71.48⎥113.72⎥⎥107.89⎥-127.1⎥⎥525⎥⎦结构动力学课程论文V1(1)=DV1(0)迭代过程列表如下根据D V1(0)⎡52612⎢34661⎢⎢13564⎢⎢-2919⎢-2009⎢⎢-2009⎢-2919⎢10-5⨯⎢-4627⎢-3739⎢⎢-3739⎢⎢-4627⎢-4436⎢⎢-3429⎢-3429⎢⎢-4436⎣453153846316844-648-547-547-648-3237-2622-2622-3237-5313-4034-4034-5313179831712511915-95-55.4-55.4-95-395-408-408-395-2546-1883-1883-2546 1933.61502.4600.3585.14-403.97.9103-69.43-330.8-46.98-141.3-151.2-164.3-169.8-202-2022088.51495.3606.51-631828.14-463.5-16.66-39.22-52.13-197.9-226.6-226.6-114.2-168.9-189.520471488.4605.89-7.983-467.4891.72-635.4-193.6-45.69-344.3-30.81-189.2-169.2-112.1-227.41933.61502.4600.3-69.437.9103-403.9585.14-151.2-141.3-46.98-330.8-202-149.4-169.8-164.3-959-507-53.6-141139.935.2281.15567.3-144114.5114.5109.7-71.595.5537.1-466.3-466.3-74.97214.4-174.8143.145.39-214.1713.2-171.7134.5129.5-99.996.7540.08-885-466-7545.39143.1-175214.4134.6-172713.2-21440.0896.75-99.9129.6-959.1-507.2-53.6281.1535.22139.93-141.1109.67114.46-143.6567.357.9937.0195.54-71.52-959.1-507.2-53.6281.1535.22139.93-141.1109.67114.46-143.6567.357.9937.0995.54-71.52-768.9-768.9-687.5-306.5-28.0246.21-14.4511.74129.1-99.9796.6839.58-186.8664.5-159.7122.14-687.5-306.511.743-14.4546.216-28.0239.58896.68-99.97129.09122.14-159.7664.53-186.8-898.5⎤-828.5-387.3⎥-1.1767.242-15.89⎥45.1658.04⎥37.4995.94⎥-71.48113.7107.8⎥-127.1525⎦⎥⎡1⎤⎢1⎥⎢⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢1⎥⎢1⎥⎢⎥⎢⎣1⎥⎦V1(1) V1(1) V1(2) V1(2) V1(3) V1(3) V1(4) V1(4 ) V1(5)⎡116889⎤⎢91257.8⎥⎢⎥⎢43091⎥⎢⎥-3558.1⎢⎥⎢-2480.4⎥⎢⎥⎢-2412.9⎥⎢-3571.2⎥⎢⎥-8221.3⎢⎥⎢-6697.9⎥⎢⎥⎢-6710.8⎥⎢⎥-8217.2⎢⎥⎢-12347⎥⎢⎥-9334.2⎢⎥⎢-9331.7⎥⎢⎥⎢⎣-12348⎥⎦10.7810.369-0.03-0.02-0.02-0.03-0.07-0.06-0.06-0.07-0.11-0.08-0.08-0.11949641928321926271926086917330082-3452-2444-2446-3451-7208-5858-5857-7208-9276-7082-7082-9276712580.7504311920.3285-3477-0.037-2465-0.026-2465-0.026-3477-0.037-7335-0.077-5965-0.063-5965-0.063-7335-0.077-9574-0.101-7305-0.077-7305-0.077-9574-0.101693690.7473301840.3252-3454-0.037-2446-0.026-2448-0.026-3454-0.037-7221-0.078-5868-0.063-5868-0.063-7221-0.078-0.1-9304-7103-0.077-7103-0.077-0.1-9304691890.747300910.325-3452-0.04-2444-0.03-2446-0.03-3451-0.04-7209-0.08-5859-0.06-5858-0.06-7209-0.08-9278-0.1-7084-0.08-7084-0.08-9278-0.1则得到第一振型形式为φ1=（-0.1585 -0.1184 -0.0515 0.005910.00418 0.00419 0.00591 0.01234 0.01003 0.01002 0.01234 0.01588 0.01212 0.01212 0.01588）再用公式ω12=(V1)TmV1(0)(V)mV(1)T1(1)1(1)，将数据代入得ω1=32.75。
结构动力学大作业分析
结构动力学大作业姓名：学号：习题1用缩法减进行瞬态构造动力学剖析以确立对有限上涨时间得恒定力的动力学响应。
是一根钢梁支撑着集中质量并蒙受一个动向荷载。
实质构造钢梁长L，支撑着一个集中质量M。
这根梁蒙受着一个上涨时间为t，最大值为F1的动向荷载F(t)。
梁的质量能够忽视，需确立产生最大位移响应时间t max及响应y max 。
同时要确立梁中的最大曲折应力bend。
：资料特征：E x 2E5 MPa ，质量M＝，质量阻尼ALPHAD=8;几何尺寸：L＝450mm mm4h=18mm;荷载为：F1＝20N t ＝提示：减少法需定义主自由度。
荷载需三个荷载步〔0至加质量，再至，最后至1s〕ANSYS命令以下：FINISH/CLE$/CONFIG,NRES,2000/prep7L=450$H=18ET,1,BEAM3ET,2,MASS21,,,4R,1,1,800.6,18R,2,30!MASS21的实常数次序N,1,0,0,0N,2,450/2,0,0N,3,450,0,0E,1,2$E,2,3!创办单元TYPE,2$REAL,2E,2M,2,UYFINISH/SOLU!进入求解层ANTYPE,TRANSTRNOPT,REDUC!定义时间积分步长ALPHAD,8 !质量阻尼为8D,1,UY$D,3,UX,,,,,UY!节点1Y方向,拘束节点3X、Y方向拘束F,2,FY,0LSWRITE,1 !生成荷载步文件1FDELE,ALL,ALLF,2,FY,20LSWRITE,2 !生成荷载步文件 2TIME,1LSWRITE,3 !生成荷载步文件 3LSSOLVE,1,3,1!求解荷载文件1,2,3FINISH/SOLU!扩展办理SOLVEFINISH/POST26NUMVAR,0FILE,fdy,rdsp!注意，成立的工程名称为fdy,否那么高出最大变量数200，结果无效NSOL,2,2,U,Y,NSOL PLVAR,2 !时间位移曲线PRVAR,2 !得出在该时间点上跨中位移最大/POST1 !查察某个时辰的计算结果SET,FIRSTPLDISP,1 !系统在秒时总变形图ETABLE,Imoment,SMISC,6 !单元I点弯矩ETABLE,Jmoment,SMISC,12 !单元J点弯矩ETABLE,Ishear,SMISC,2 !单元I点剪力ETABLE,Jshear,SMISC,8 !单元J点剪力PLLS,IMOMENT,JMOMENT,1,0 !画出弯矩图PLLS,ISHEAR,JSHEAR,,1,0 !画出剪力争结果以下;跟着时间位移的大小：可知系统在秒时总变形最大。
高等结构动力学大作业
在高等结构动力学领域，大作业可以选择一个特定的主题或问题进行深入研究和分析。
以下是一些可能的大作业主题和相关内容，供参考：
1. 结构振动分析
-可以选择某种结构（如梁、柱、桥梁等）进行振动特性分析，包括自由振动和强迫振动的计算和模拟。
-可以探讨不同振动模式对结构的影响，以及振动频率、振型等参数的计算方法。
2. 结构地震响应分析
-研究结构在地震作用下的响应特性，包括地震波传播、结构的地震响应计算和分析。
-可以探讨结构的地震易损性评估方法，以及如何通过设计和加固措施提高结构的地震抗性。
3. 结构动力优化设计
-结合结构动力学理论和优化方法，研究如何在结构设计过程中考虑动力学要求，实现结构的轻量化和性能优化。
-可以探讨多目标优化方法在结构动力学设计中的应用，如考虑刚度、强度和振动等多个指标的优化设计。
4. 结构非线性动力学
-研究结构在非线性荷载下的动力学行为，包括非线性振动、共振现象、失稳分析等。
-可以探讨结构在非线性动力作用下的特殊现象和行为，如超谐波振动、周期加速等。
5. 结构阻尼与能量耗散
-探讨结构的阻尼机制和能量耗散特性，包括材料阻尼、结构阻尼器设计等内容。
-可以研究不同类型的阻尼器在减震和能量耗散中的应用效果，以提高结构的动力学性能。
以上是一些可能的大作业主题，你可以根据自己的兴趣和专业背景选择一个合适的主题，并展开深入的研究和分析，从而完成一份高质量的高等结构动力学大作业。
《结构动力学》结构动力学大作业 研究生课程考核试卷
《结构动力学》结构动力学大作业研究生课程考核试卷研究生课程考核试卷（适用于课程论文、提交报告）科目：结构动力学大作业教师：姓名：学号：专业：岩土工程类别：专硕上课时间： 2015年 9 月至2015 年11 月考生成绩：卷面成绩平时成绩课程综合成绩阅卷评语：阅卷教师 (签名)2重庆大学研究生院制土木工程学院2015级硕士研究生考试试题1 题目及要求1、按规范要求设计一个3跨3层钢筋混凝土平面框架结构（部分要求如附件名单所示；未作规定部分自定）。
根据所设计的结构参数，求该结构的一致质量矩阵、一致刚度矩阵；2、至少采用两种方法求该框架结构的频率和振型；3、输入地震波（地震波要求如附件名单所示），采用时程分析法，利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
342 框架设计2.1 初选截面尺寸取所设计框架为3层3跨，跨度均为4.5m ，层高均为3.9m 。
由于基础顶面离室内地面为1m ，故框架平面图中底层层高取 4.9m 。
梁、柱混凝土均采用C30，214.3/c f N mm =，423.010/E N mm =⨯，容重为325/kN m 。
估计梁、柱截面尺寸如下： （1）梁：梁高b h 一般取跨度的11218，取梁高b h =500mm ；5取梁宽300b b mm =；所以梁的截面尺寸为：300500mm mm ⨯ （2）柱：框架柱的截面尺寸根据柱的轴压比限值，按下列公式计算： ①柱组合的轴压力设计值...E N F g n β=其中：β：考虑地震作用组合后柱轴压力增大系数； F ：按简支状态计算柱的负荷面积；E g ：折算在单位建筑面积上的重力荷载代表值，可近似取为21214/KN m ；n ：验算截面以上的楼层层数。
②c N cNA u f ≥其中：N u ：框架柱轴压比限值；8度（0.2g ），查抗震规范轴压比限值0.75N u =；cf ：混凝土轴心抗压强度设计值，混凝土采用30C ，214.3/cfN mm =。
结构动力学大作业
结构动力学作业姓名：学号：目录1.力插值法 (1)1.1分段常数插值法 (1)1.2分段线性插值法 (4)2.加速度插值法 (7)2.1常加速度法 (7)2.2线加速度法 (9)附录 (12)分段常数插值法源程序 (12)分段线性插值法源程序 (12)常加速度法源程序 (13)线加速度法源程序 (13)1.力插值法力插值法对结构的外荷载进行插值，分为分段常数插值法和分段线性插值法，这两种方法均适用于线性结构的动力反应计算。
1.1分段常数插值法图1-1为一个单自由度无阻尼系统，结构的刚度为k ，质量为m ，位移为y (t )，施加的外力为P (t )。
图1-2为矩形脉冲荷载的示意图，图中t d 表示作用的时间，P 0表示脉冲荷载的大小。
图1-1 单自由度无阻尼系统示意图图1-2 矩形脉冲荷载示意图对于一个满足静止初始条件的无阻尼单自由度体系来说，当施加一个t d 时间的矩形脉冲荷载，此时结构在t d 时间内的位移反应可以用杜哈梅积分得到：0()sin ()2 (1cos )(1cos ) (0)tst st d P y t t d m ty t y t t Tωττωπω=-=-=-≤≤⎰(1-1)如果结构本身有初始的位移和速度，那么叠加上结构自由振动的部分，结构的位移反应为：02()cos sin (1cos) (0)st d y ty t y t t y t t Tπωωω=++-≤≤& (1-2)图1-3 分段常数插值法微段示意图对于施加于结构任意大小的力，将其划分为Δt 的微段，每一段的荷载都为一个常数(每段相当于一个矩形的脉冲荷载)，如图1-3所示，则将每一段的位移和速度写成增量的形式为：1cos t sin t (1cos t)iii i y P y y kωωωω+=∆+∆+-∆& (1-3)i+1/sin t cos t sin t iii y P y y kωωωωω=-∆+∆+∆&& (1-4)程序流程图如下i+1cos t sin t (1cos t)iii y P y y kωωωω=∆+∆+-∆i+1/sin t cos t sin ti i i y Py y kωωωωω=-∆+∆+∆图1-4 分段常数插值法流程图根据流程图可以编写相应的算法，利用MATLAB 进行编程，程序源代码见附录。
(整理)重庆大学级硕士研究生《结构动力学》课程作业
1 题目及要求1、按规定设计一个2跨3层钢筋混凝土平面框架结构（部分要求如附件名单所示；未作规定部分自定）。
根据所设计的结构参数，求该结构的一致质量矩阵、一致刚度矩阵；2、至少采用两种方法求该框架结构的频率和振型；3、输入地震波（地震波要求如附件名单所示），采用时程分析法，利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
2 框架设计2.1 初选截面尺寸取所设计框架为3层2跨，跨度均为4.7m ，层高均为4.1m 。
由于基础顶面离室内地面为1m ，故框架平面图中底层层高取5.1m 。
梁、柱混凝土均采用C30，214.3/c f N mm =，423.010/E N mm =⨯，容重为325/kN m 。
估计梁、柱截面尺寸如下： （1）梁：梁高b h 一般取跨度的11218，取梁高b h =500mm ；取梁宽300b b mm =；所以梁的截面尺寸为：300500mm mm ⨯ （2）柱：框架柱的截面尺寸根据柱的轴压比限值，按下列公式计算： ①柱组合的轴压力设计值...E N F g n β=其中：β：考虑地震作用组合后柱轴压力增大系数； F ：按简支状态计算柱的负荷面积；E g ：折算在单位建筑面积上的重力荷载代表值，可近似取为21214/KN m ；n ：验算截面以上的楼层层数。
②c N cNA u f ≥其中：N u ：框架柱轴压比限值；按二级抗震等级，查抗震规范地0.75N u =；c f ：混凝土轴心抗压强度设计值，混凝土采用30C ，214.3/c f N mm =。
经计算取柱截面尺寸为：300300mm mm ⨯ 该榀框架立面图如图2.1所示。
图2.2 框架立面图2.2 框架几何刚度特征（1）梁：截面惯性矩：3394300500 3.125101212b bh I mm ⨯===⨯； 刚度：491323.010 3.125109.37510b EI N mm =⨯⨯⨯=⨯⋅ 293750KN m =⋅ 梁的单位长度质量（按照计算重力荷载代表值的方法计算）： 一二层（考虑楼板恒载及楼面活载作用）：分布质量：b (0.30.52500 4.70.12500 4.7200)2490/m kg m =⨯⨯+⨯⨯+⨯= 顶层（仅考虑楼板恒载不考虑屋面活载作用）：分布质量：b (0.30.52500 4.70.122500)1785/m kg m =⨯⨯+⨯⨯=； （2）柱：截面惯性矩：3384300300 6.75101212c bh I mm ⨯===⨯； 刚度：481323.010 6.7510 2.02510c E I N mm =⨯⨯⨯=⨯⋅ 220250KN m =⋅ 分布质量：c 0.30.32500/225/m bh kg m kg m γ==⨯⨯=根据以上计算结果，将其列入表中，如下表2.1所示：表2.1 梁柱力学参数截面尺寸（2mm ）力学参数300500⨯300300⨯截面惯性矩I （4mm ） 93.12510⨯ 86.7510⨯ 刚度EI （2kN m ⋅）49.37510⨯ 42.02510⨯单位长度质量m （/kg m ） 一、二层2490 225顶层17852.3 动力自由度框架单元编号及动力自由度编号见图2.2所示：123456789101112141513图2.2 框架单元编号及自由度编号框架结构可以理想化为在节点处相互连接的单元（梁和柱）的集合。
结构动力学大作业
结构动力学作业姓名：学号：目录1.力插值法 (1)1.1分段常数插值法 (1)1.2分段线性插值法 (4)2.加速度插值法 (7)2.1常加速度法 (7)2.2线加速度法 (9)附录 (12)分段常数插值法源程序 (12)分段线性插值法源程序 (12)常加速度法源程序 (13)线加速度法源程序 (13)1.力插值法力插值法对结构的外荷载进行插值，分为分段常数插值法和分段线性插值法，这两种方法均适用于线性结构的动力反应计算。
1.1分段常数插值法图1-1为一个单自由度无阻尼系统，结构的刚度为k ，质量为m ，位移为y (t )，施加的外力为P (t )。
图1-2为矩形脉冲荷载的示意图，图中t d 表示作用的时间，P 0表示脉冲荷载的大小。
图1-1 单自由度无阻尼系统示意图图1-2 矩形脉冲荷载示意图对于一个满足静止初始条件的无阻尼单自由度体系来说，当施加一个t d 时间的矩形脉冲荷载，此时结构在t d 时间内的位移反应可以用杜哈梅积分得到：0()sin ()2 (1cos )(1cos ) (0)tst st d P y t t d m ty t y t t Tωττωπω=-=-=-≤≤⎰(1-1)如果结构本身有初始的位移和速度，那么叠加上结构自由振动的部分，结构的位移反应为：002()cos sin (1cos) (0)st d yty t y t t y t t Tπωωω=++-≤≤ (1-2)图1-3分段常数插值法微段示意图对于施加于结构任意大小的力，将其划分为Δt 的微段，每一段的荷载都为一个常数(每段相当于一个矩形的脉冲荷载)，如图1-3所示，则将每一段的位移和速度写成增量的形式为：1cos t sin t (1cos t)i ii i yP y y kωωωω+=∆+∆+-∆ (1-3)i+1/sin t cos t sin t i ii yP yy kωωωωω=-∆+∆+∆ (1-4)程序流程图如下图1-4分段常数插值法流程图根据流程图可以编写相应的算法，利用MATLAB 进行编程，程序源代码见附录。
高等结构动力学大作业
高等结构动力学大作业【原创版】目录1.高等结构动力学的概念和意义2.高等结构动力学的研究方法和应用3.高等结构动力学的大作业要求和内容4.高等结构动力学大作业的完成方法和技巧5.高等结构动力学大作业的实际应用案例正文一、高等结构动力学的概念和意义高等结构动力学，作为力学的一个分支，主要研究结构在动力载荷作用下的响应和稳定性。
其研究的核心目标是为了提高结构的安全性、可靠性和经济性，从而在工程设计中发挥重要作用。
高等结构动力学具有很强的理论性和实践性，对于工程技术人员来说，掌握高等结构动力学的基本理论和方法具有重要意义。
二、高等结构动力学的研究方法和应用高等结构动力学主要采用数学建模、数值分析和实验研究等方法进行研究。
数学建模是将实际问题抽象为数学模型，以便于进行理论分析；数值分析是通过计算机模拟和计算，求解数学模型，得到结构在动力载荷作用下的响应；实验研究是通过实验设备和仪器，对结构进行实际测试，以验证理论分析和数值计算的结果。
高等结构动力学的应用领域非常广泛，包括建筑结构、机械结构、航空航天结构、桥梁结构等。
在实际工程中，通过应用高等结构动力学的理论和方法，可以有效地指导工程设计和施工，提高工程质量和安全性。
三、高等结构动力学的大作业要求和内容高等结构动力学的大作业通常要求学生具备一定的理论基础和实践能力，能够独立完成结构动力学的分析和计算。
大作业的内容主要包括以下几个方面：1.对给定的结构进行数学建模和动力学分析；2.采用数值分析方法，求解结构的动力响应；3.对结构进行稳定性分析和疲劳寿命预测；4.根据计算结果，对结构进行优化设计，以提高其性能。
四、高等结构动力学大作业的完成方法和技巧1.熟悉课程教材，掌握高等结构动力学的基本理论和方法；2.根据题目要求，选择合适的数学建模方法和数值分析方法；3.认真分析题目，确定计算模型的边界条件和初始条件；4.采用适当的计算机软件或编程语言进行数值计算；5.分析计算结果，编写完整的计算报告。
结构动力学大作业分析
结构动力学大作业姓名：学号：习题1用缩法减进行瞬态结构动力学分析以确定对有限上升时间得恒定力的动力学响应。
实际结构是一根钢梁支撑着集中质量并承受一个动态荷载。
钢梁长L ，支撑着一个集中质量M 。
这根梁承受着一个上升时间为t τ，最大值为F1的动态荷载F(t)。
梁的质量可以忽略，需确定产生最大位移响应时间max t 及响应max y 。
同时要确定梁中的最大弯曲应力bend σ。
已知：材料特性：25x E E MPa =，质量M ＝0.03t ，质量阻尼ALPHAD=8; 几何尺寸：L ＝450mm I=800.64mm h=18mm; 荷载为：F1＝20N t τ＝0.075s提示：缩减法需定义主自由度。
荷载需三个荷载步（0至加质量，再至0.075s ， 最后至1s ）ANSYS 命令如下： FINISH/CLE$/CONFIG,NRES,2000 /prep7L=450$H=18 ET,1,BEAM3 ET,2,MASS21,,,4 R,1,1,800.6,18R,2,30 !MASS21的实常数顺序MASSX, MASSY , MASSZ, IXX, IYY , IZZ MP,EX,1,2E5$MP,NUXY ,1,0.3 N,1,0,0,0 N,2,450/2,0,0 N,3,450,0,0E,1,2$E,2,3 !创建单元 TYPE,2$REAL,2 E,2 M,2,UY FINISH/SOLU !进入求解层 ANTYPE,TRANSTRNOPT,REDUCOUTRES,ALL,ALL$DELTIM,0.004 !定义时间积分步长ALPHAD,8 !质量阻尼为8D,1,UY$D,3,UX,,,,,UY !节点1Y方向,约束节点3X、Y方向约束F,2,FY,0LSWRITE,1 !生成荷载步文件1TIME,0.075FDELE,ALL,ALLF,2,FY,20LSWRITE,2 !生成荷载步文件2TIME,1LSWRITE,3 !生成荷载步文件3LSSOLVE,1,3,1 !求解荷载文件1,2,3FINISH/SOLUEXPASS,ON$EXPSOL,,,0.10000 !扩展处理SOLVEFINISH/POST26NUMV AR,0FILE,fdy,rdsp !注意，建立的项目名称为fdy,否则超出最大变量数200，结果无效NSOL,2,2,U,Y,NSOLPLV AR,2 !时间位移曲线PRV AR,2 !得出在0.10000该时间点上跨中位移最大/POST1 !查看某个时刻的计算结果SET,FIRSTPLDISP,1 !系统在0.10000秒时总变形图ETABLE,Imoment,SMISC,6 !单元I点弯矩ETABLE,Jmoment,SMISC,12 !单元J点弯矩ETABLE,Ishear,SMISC,2 !单元I点剪力ETABLE,Jshear,SMISC,8 !单元J点剪力PLLS,IMOMENT,JMOMENT,1,0 !画出弯矩图PLLS,ISHEAR,JSHEAR,,1,0 !画出剪力图结果如下;随着时间位移的大小：可知系统在0.10000秒时总变形最大。
10结构的动力计算习题解答,重庆大学,文国治版教材课后答案
第10章 结构的动力计算习题解答习题10.1 是非判断题(1) 引起单自由度体系自由振动的初速度值越大，则体系的自振频率越大。
（ ） (2) 如果单自由度体系的阻尼增大，将会使体系的自振周期变短。
（ ） (3) 在土木工程结构中，阻尼对自振周期的影响很小。
（ ）(4) 由于各个质点之间存在几何约束，质点体系的动力自由度数总是小于其质点个数。
（ ）(5) 多自由度的自振频率与引起自由振动的初始条件无关。
（ ） (6) n 个自由度体系有n 个自振周期，其中第一周期是最长的。
（ ）(7) 如果考虑阻尼，多自由度体系在简谐荷载作用下的质点振幅就不能用列幅值方程的方法求解。
（ ）【解】(1) 错误。
体系的自振频率与初速度无关，由结构本身的特性所决定。
(2) 错误。
由阻尼结构的自振频率r ω=可知，阻尼增大使自振频率减小，自振周期变长。
(3) 正确。
(4) 错误。
由动力自由度的概念知，动力自由度数与计算假定有关，而与集中质量数目和超静定次数无关。
(5) 正确。
(6) 正确。
(7) 正确。
习题10.2 填空题(1) 单自由度体系运动方程为2P 2()/y y y F t m ξωω++=，其中未考虑重力，这是因为__________。
(2) 单自由度体系自由振动的振幅取决于__________。
(3) 若要改变单自由度体系的自振周期， 应从改变体系的__________或__________着手。
(4) 若由式()211βθω=-求得的动力系数为负值，则表示__________。
(5) 习题10.2(5)图所示体系发生共振时，干扰力与__________平衡。
Wsin θ t12-2(5)习题 图习题10.2(5)图(6) 求习题10.2(6)图所示质点系的自振频率时(EI ＝常数)，其质量矩阵[M ]=__________。
m2m12-2(6)习题 图12-2(7)习题 图习题10.2(6)图 习题10.2(7)图(7) 习题10.2(7)图所示体系不考虑阻尼，EI ＝常数。
结构动力学大作业
《高等结构动力学》课程大作业姓名：学号：电话：二〇二〇年十二月目录三层建筑物动力学建模与分析......................................................................................................... 一．研究对象..................................................................................................................................... 二．研究方案.....................................................................................................................................2.1、研究目的............................................................................................................................2.2、研究方案............................................................................................................................ 三．结构动力学建模.........................................................................................................................3.1.模型简化...............................................................................................................................3.2、结构动力学建模................................................................................................................建模方法一：层模型.........................................................................................................建模方法二：杆系模型..................................................................................................... 四．动力学特性分析.........................................................................................................................4.1.固有频率与固有模态...........................................................................................................4.2.阻尼矩阵...............................................................................................................................五.动力学响应分析...........................................................................................................................5.1.结构在EL Centro地震波下的反应 .....................................................................................5.1.1.基于Runge-Kutta方法的动力学响应（方法1）...................................................5.1.2.基于中心差分法方法的动力学响应（方法2）.....................................................5.2.结构在风载荷下的反应.......................................................................................................三层建筑物动力学建模与分析一．研究对象在农村很多自建房都为三层结构，大多为自主设计，在地震中许多自建房由于地基不稳、结构和材料等原因损坏，现将三层混泥土结构房屋作为研究对象，进行动力学建模，分析建筑物在地震、风载荷激励下的响应。
(精品)重庆大学结构动力学大作业
研究生课程考核试卷
（适用于课程论文、提交报告）
科目：结构动力学大作业教师：刘纲
姓名：刘亚南学号：20131613144 专业：建筑与土木工程类别：专业
上课时间：2013 年11 月至2014 年1 月
考生成绩：
卷面成绩平时成绩课程综合成绩阅卷评语：
阅卷教师(签名)
重庆大学研究生院制
土木工程学院2013级硕士研究生考试试题
科目名称：结构动力学考试日期：2014年1月总分：20分
1、按规定设计一个2跨3层钢筋混凝土平面框架结构（部分要求如附件名单所示；未作规定部分自定）。
根据所设计的结构参数，求该结构的一致质量矩阵、一致刚度矩阵；
2、至少采用两种方法求该框架结构的频率和振型；
3、输入地震波（地震波要求如附件名单所示），采用时程分析法，利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
要求给出：
（1）框架结构图，并给出一致质量矩阵和一致刚度矩阵；
（2）出两种方法名称及对应的频率和振型；
（3）输入地震波的波形图，计算所得各楼层位移反应时程图。
结构动力学-刘亚南（20131613144）
目录
题目一
1、框架设计 (2)
2、结构的一致质量矩阵 (3)
3、结构的一致刚度矩阵 (6)
题目二
1、建立框架结构的运动微分方程 (10)
2、用Rayleigh法求近似基频 (10)
3、用Stodola法求频率 (12)
题目三
1、框架资料 (15)
2、分析方法 (15)
3、具体操作步骤 (16)
4、地震波的波形图 (21)
5、时程反应图 (21)
第1页/共26页。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
研究生课程考核试卷（适用于课程论文、提交报告）科目：结构动力学大作业教师：刘纲姓名：学号：专业：土木工程类别：学术上课时间：2016 年9 月至2016 年12 月考生成绩：阅卷评语：阅卷教师(签名)重庆大学研究生院制土木工程学院2016级硕士研究生考试试题科目名称：结构动力学考试日期：2016年12月总分：20分1、按规定设计一个2跨3层钢筋混凝土平面框架结构（部分要求如附件名单所示；未作规定部分自定）。
根据所设计的结构参数，求该结构的一致质量矩阵、一致刚度矩阵；2、至少采用两种方法求该框架结构的频率和振型；3、输入地震波（地震波要求如附件名单所示），采用时程分析法，利用有限元软件或自编程序求出该框架结构各层的线性位移时程反应。
要求给出：（1）框架结构图，并给出一致质量矩阵和一致刚度矩阵；（2）写出两种方法名称及对应的频率和振型；（3）输入地震波的波形图，计算所得各楼层位移反应时程图。
第 1 页共1页1框架概况1.1框架截面尺寸框架立面图如图 1.1所示，各跨跨度为13900L mm =，各层建筑层高均为33700L mm =，对应的梁截面分别为2200400mm ⨯，柱截面均为2300300mm ⨯。
设楼层进深为24200L mm =,板厚为100mm ，顶层板厚取最小值120mm 。
图1.1框架立面图1.2动力自由度框架结构可以理想化为在节点处相互连接的单元（梁和柱）的集合。
设梁、柱的轴向变形均忽略不计，只考虑横向平面位移，则该框架有3平动自由度和9角自由度，共12自由度。
自由度编号及梁柱单元编号如图1.2所示。
图1.2自由度编号和梁柱单元编号图1.3力学参数计算梁柱混凝土都采用C30，其弹性模量为423.010/E N mm=⨯2200400mm⨯梁截面惯性矩：334 12004001212bhI mm⨯==2300300mm⨯柱截面惯性矩：334 23003001212bhI mm⨯==2200400mm⨯梁刚度：3442 12004003.010 3.21012EI kN m⨯=⨯⨯=⨯⋅2300300mm⨯柱刚度：3442 23003003.010 2.0251012EI kN m⨯=⨯⨯=⨯⋅2200400mm⨯梁的单位长度质量（按照计算重力荷载代表值的方法计算）：一二层（考虑楼板恒载及楼面活载作用）：1(0.20.42500 4.20.12500 4.2200)2090/m kg m =⨯⨯+⨯⨯+⨯= 顶层（仅考虑楼板恒载不考虑屋面活载作用）：2(0.20.42500 4.20.122500)1460/m kg m =⨯⨯+⨯⨯=2300300mm ⨯柱的单位长度质量30.30.32500/225/m bh kg m kg m γ==⨯⨯=根据以上计算结果，将其列入表中，如下表1.3所示：截面惯性矩I （4mm ）91.06710⨯86.7510⨯刚度EI （2kN m ⋅）43.210⨯42.02510⨯单位长度质量m （/kg m ）一、二层 2090 225顶层 14602一致质量矩阵、一致刚度矩阵2.1一致质量矩阵在节点位移作用下框架梁和柱上所引起的变形形状采用Hermite 多项式。
因此均布质量梁特殊情形中的一致质量矩阵为：2222156542213541561322221343420132234e L L L L mL M L LL L L L L L -⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥---⎣⎦2.1.1计算梁单元（单位：kg ）梁单元水平位移自由度产生的质量影响系数ii m转角自由度产生的质量影响系数ij m○1 11211460 3.95694m m L -==⨯=232144551146044 3.9824.82420420m L m m L --==⨯=⨯⨯= 2321455411460(3)3 3.9618.61420420m L m m L --==⨯-=-⨯⨯=-②11211460 3.95694m m L -==⨯=232155661146044 3.9824.82420420m L m m L --==⨯=⨯⨯=2321566511460(3)3 3.9618.61420420m L m m L --==⨯-=-⨯⨯=-③22112090 3.98151m m L -==⨯=231177881209044 3.91180.73420420m L m m L --==⨯=⨯⨯=2311788712090(3)3 3.9885.55420420m L m m L --==⨯-=-⨯⨯=-④22112090 3.98151m m L -==⨯=231199881209044 3.91180.73420420m L m m L --==⨯=⨯⨯=2311988912090(3)3 3.9885.55420420m L m m L --==⨯-=-⨯⨯=-⑤33112090 3.98151m m L -==⨯=2311101011111209044 3.91180.73420420m L m m L --==⨯=⨯⨯=23111011111012090(3)3 3.9885.55420420m L m m L --==⨯-=-⨯⨯=-⑥33112090 3.98151m m L -==⨯=2311111112121209044 3.91180.73420420m L m m L --==⨯=⨯⨯=23111112121112090(3)3 3.9885.55420420m L m m L --==⨯-=-⨯⨯=-2.1.2计算柱单元（单位：kg）层号柱单元质量影响系数三层⑦331122225 3.7156156309.21420420m Lm m--⨯==⨯=⨯=331221225 3.75454107.04420420m Lm m--⨯==⨯=⨯=3314413225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=3317713225 3.7(13)(13 3.7)95.34420420m Lm m L--⨯==⨯-=⨯-⨯=-3324423225 3.7(13)13 3.795.34420420m Lm m L--⨯==⨯=⨯⨯=3327723225 3.7(22)(22 3.7)161.35420420m Lm m L--⨯==⨯-=⨯-⨯=-223344773225 3.744 3.7108.54420420m Lm m L--⨯==⨯=⨯⨯=223347743225 3.7(3)(3 3.7)81.41420420m Lm m L--⨯==⨯-=⨯-⨯=-⑧331122225 3.7156156309.21420420m Lm m--⨯==⨯=⨯=331221225 3.75454107.04420420m Lm m--⨯==⨯=⨯=3315513225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=3318813225 3.7(13)(13 3.7)95.34420420m Lm m L--⨯==⨯-=⨯-⨯=-3325523225 3.7(13)(13 3.7)95.34420420m Lm m L--⨯==⨯=⨯⨯=3328823225 3.7(22)(22 3.7)161.35420420m Lm m L--⨯==⨯-=⨯-⨯=-223355883225 3.744 3.7108.54420420m Lm m L--⨯==⨯=⨯⨯=223358853225 3.7(3)(3 3.7)81.41420420m Lm m L--⨯==⨯-=⨯-⨯=-⑨331122225 3.7156156309.21420420m Lm m--⨯==⨯=⨯=331221225 3.75454107.04420420m Lm m--⨯==⨯=⨯=3316613225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=29923420420-- 3326623225 3.7(13)(13 3.7)95.34420420m L m m L --⨯==⨯=⨯⨯=3329923225 3.7(22)(22 3.7)161.35420420m L m m L --⨯==⨯-=⨯-⨯=- 223366993225 3.744 3.7108.54420420m L m m L --⨯==⨯=⨯⨯= 223369963225 3.7(3)(3 3.7)81.41420420m L m m L --⨯==⨯-=⨯-⨯=-层号柱单元质量影响系数二 层 ⑩332233225 3.7156156309.21420420m L m m --⨯==⨯=⨯= 333223225 3.75454107.04420420m L m m --⨯==⨯=⨯= 3327723225 3.72222 3.7161.35420420m L m m L --⨯==⨯=⨯⨯=332101023225 3.7(13)(13 3.7)95.34420420m L m m L --⨯==⨯-=⨯-⨯=- 3324423225 3.7(13)(13 3.7)95.34420420m L m m L --⨯==⨯=⨯⨯=333101033225 3.7(22)(22 3.7)161.35420420m L m m L --⨯==⨯-=⨯-⨯=- 22337710103225 3.744 3.7108.54420420m L m m L --⨯==⨯=⨯⨯= 22337101073225 3.7(3)(3 3.7)81.41420420m L m m L --⨯==⨯-=⨯-⨯=- ○11 332233225 3.7156156309.21420420m L m m --⨯==⨯=⨯=333223225 3.75454107.04420420m L m m --⨯==⨯=⨯= 3328823225 3.72222 3.7161.35420420m L m m L --⨯==⨯=⨯⨯=332111123225 3.7(13)(13 3.7)95.34420420m L m m L --⨯==⨯-=⨯-⨯=-3338833225 3.7(13)(13 3.7)95.34420420m L m m L --⨯==⨯=⨯⨯=333111133225 3.7(22)(22 3.7)161.35420420m L m m L --⨯==⨯-=⨯-⨯=- 22338811113225 3.744 3.7108.54420420m L m m L --⨯==⨯=⨯⨯=8111183420420 --○12332233225 3.7156156309.21420420m Lm m--⨯==⨯=⨯=332332225 3.75454107.04420420m Lm m--⨯==⨯=⨯=3329923225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=332121223225 3.7(13)(13 3.7)95.34420420m Lm m L--⨯==⨯-=⨯-⨯=-3339933225 3.7(13)(13 3.7)95.34420420m Lm m L--⨯==⨯=⨯⨯=333121233225 3.7(22)(22 3.7)161.35420420m Lm m L--⨯==⨯-=⨯-⨯=-22339912123225 3.744 3.7108.54420420m Lm m L--⨯==⨯=⨯⨯=22339121293225 3.7(3)(3 3.7)81.41420420m Lm m L--⨯==⨯-=⨯-⨯=-层号柱单元质量影响系数一层○133333225 3.7156156309.21420420m Lm-⨯=⨯=⨯=333101033225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=223310103225 3.744 3.7108.54420420m Lm L-⨯=⨯=⨯⨯=○143333225 3.7156156309.21420420m Lm-⨯=⨯=⨯=333111133225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=223311113225 3.744 3.7108.54420420m Lm L-⨯=⨯=⨯⨯=○153333225 3.7156156309.21420420m Lm-⨯=⨯=⨯=333121233225 3.72222 3.7161.35420420m Lm m L--⨯==⨯=⨯⨯=223312123225 3.744 3.7108.54420420m Lm L-⨯=⨯=⨯⨯=2.1.3计算整体坐标系的ij m()()()ˆˆˆ...m n p ij ij ij ij m m m m =+++根据可知第一行：111213141516171819110111112256943309.2112315.63kg 3107.4321.12kg 0161.35kg95.340m m m kgm m m m m kg m m m m kg ------------=⨯+⨯==⨯=======-====；第二行：2223242526272829210211212281516309.2118157.26kg3107.04321.12=95.34kg =161.3595.340m m kgm m m m m m m m m -----------=⨯+⨯==⨯======-== 第三行：33343536373839310311312281516309.2118157.26kg 095.34kg 0m m m m kg m m m m m m ----------=⨯+⨯==========第四行：444546474849410411412=824.82108.54933.36kg 618.61kg 081.41kg 0m m m kg m m m m m m kg ---------+==-==-=====；第五行：55824.822108.541758.18m kg -=⨯+=56575859510511512618.61kg 081.41kg 0m m kgm m m m m kg -------=-==-====；第六行：66676869610611612824.82108.54933.36kg 0081.410m m m kgm kgm m m kg-------=+====-===第七行：7778710797117121180.73108.5421397.81885.5581.41kg 0m kg m kg m m m m kg ------=+⨯==-=-===；第八行：88898108118121180.732108.5422578.54885.55081.410m kg m kg m kg m kg m kg-----=⨯+⨯==-==-=第九行：999109119121180.731108.5421397.81081.41m kg m m kg m kg ----=+⨯====-；第十行：1010101110121180.73108.5421397.81885.550m kg m kg m kg ---=+⨯==-=第十一行：111111121180.732108.5422578.54885.55m kg m kg --=⨯+⨯==-第十二行：12121180.73108.5421397.81m kg -=+⨯=M 一致质量矩阵是对称矩阵,故只写出上三角（单位：kg ）12315.63321.120161.35161.35161.3595.3495.3418157.26321.1295.3495.3495.34161.35161.35161.3595.340018157.2600095.3495.3495.34000933.36618.61081.41000001758.18618.61081.410000933.360081.410M --------=001397.81885.5581.410002578.54885.55081.4101397.810081.411397.81885.5502578.54885.551397.81⎧⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎬--⎪⎪⎪⎪--⎪⎪-⎪⎪⎪⎪-⎪⎪-⎪⎪⎪⎪⎩⎭2.2一致刚度矩阵在节点位移作用下框架梁和柱上所引起的变形形状采用Hermite 多项式。