《结构力学习题集及标准答案》(下)-2a
大学《工程力学》课后习题解答-精品
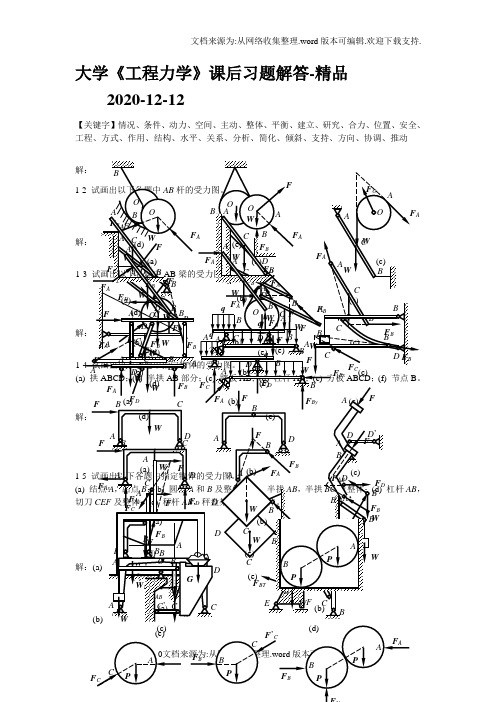
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
高层建筑结构与抗震综合练习题及参考答案(2)

高层建筑结构与抗震综合练习题一、单项选择题(每小题3分,共计30分,将选择结果填入括弧内)1.()既具有极大的抗侧移刚度,又能因剪力墙的集中而获得较大的空间,使建筑平面获得良好的灵活性,适用于30层以上的超高层房屋。
A.框架结构B.剪力墙结构C.砌体结构D.筒体结构2.我国《建筑结构抗震规范》以()作为抗震设计的依据,其数值应依据烈度、场地类别、设计地震分组以及结构自振周期和阻尼比确定。
A.地震系数B.动力系数C.地震影响系数D.冲击影响系数3.框架结构在节点水平集中力作用下,()。
A.柱的弯矩图呈直线形,梁的弯矩图呈曲线形B.梁的弯矩图呈直线形,柱的弯矩图呈曲线形C.梁和柱的弯矩图都呈直线形D.梁和柱的弯矩图都呈曲线形4.地震作用或风荷载对框架结构的水平作用,一般都可简化为作用于()上的水平力。
A.框架梁B.框架柱C.框架板D.框架节点5.关于框架-剪力墙结构刚度特征值λ,下列叙述错误的是()。
A.λ是框架抗推刚度与剪力墙抗弯刚度的比值B.λ值很大,结构的变形特性及受力将以框架为主C.λ值很小,结构的变形特性及受力将以剪力墙为主D.λ是剪力墙抗弯刚度与框架抗推刚度的比值6.所谓框架的抗推刚度,是使框架产生()。
A.单位扭转角所需的剪力值B.单位扭转角所需的弯矩值C.单位剪切角所需的剪力值D.单位位移所需的推力值7.()在水平荷载作用下,利用材料力学公式计算内力和侧移,再考虑局部弯曲应力的影响,进行修正。
A.整体剪力墙B.小开口整体剪力墙C.双肢剪力墙D.多肢剪力墙8.下列关于高层建筑结构平面布置的一般规定中,不正确的是()。
A.平面宜简单、规则、对称,减少偏心B.平面长度不宜过长,突出部分长度宜减小C.宜选用风压较小的形状,并应考虑邻近高层建筑对其风压分布的影响D.应尽量设置变形缝来划分结构单元9.目前,国内设计规范,仍沿用()方法计算结构内力,按弹塑性极限状态进行截面设计。
A.弹性B.塑性C.弹塑性D.刚性10.下列关于荷载对结构影响的叙述中,错误的是()。
工程力学课后答案_单祖辉主编
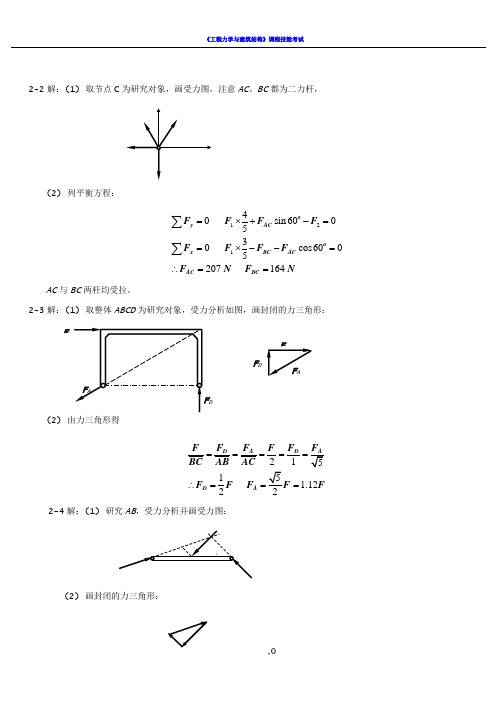
2-2解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 oy ACo x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2) 由力三角形得211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4解:(1) 研究AB ,受力分析并画受力图:(2) 画封闭的力三角形:xFDDF F AF DF deF相似关系:B A F F FCDE cde CD CE ED∆≈∆∴== 几何尺寸:11 22CE BD CD ED =====求出约束反力:12010 22010.4 245arctan 18.4B A o oCE F F kNCDED F F kN CDCECD α=⨯=⨯==⨯=⨯==-=2-6解:(1) 取DE 为研究对象,DE 为二力杆;F D = F E(2) 取ABC 为研究对象,受力分析并画受力图;画封闭的力三角形:'15166.7 23A D E F F F F N ===⨯= 2-7解:(1)取铰链B 为研究对象,AB 、BC 均为二力杆,画受力图和封闭力三角形;FFF BCF AB1BC F =(2) 取铰链C 为研究对象,BC 、CD 均为二力杆,画受力图和封闭力三角形;22cos302o CB F F F ==由前二式可得:121222120.61 1.634BC CB F F F F F F or F F ==∴===2-9 解:(1) 取整体为研究对象,受力分析,AB 、AB 、AD 均为二力杆,画受力图,得到一个空间汇交力系; (2) 列平衡方程:0 cos 45 cos 4500 cos 6000 sin 60sin 45sin 450o o x AC AB o yAD o o o zAD AC AB F F F F F F FF F F =⨯-⨯==-==--=∑∑∑解得:2 1.2 0.735 4AD AC AB AD F F kN F F F kN ===== AB 、AC 杆受拉,AD 杆受压。
(完整版)结构力学_习题集(含答案)

《结构力学》课程习题集一、单项选择题1. 弯矩图必定发生突变的截面是()。
A. 有集中力作用的截面;B.剪力为零的截面;C.荷载为零的截面;D.有集中力偶作用的截面。
2. 图示梁中 C 截面的弯矩是()。
12kN . m 4kN 3kN / mC4m 4m 2mA.12kN.m( 下拉 );B.3kN.m( 上拉 );C.8kN.m( 下拉 );D.11kN.m( 下拉 )。
3. 静定结构有变温时,()。
A. 无变形,无位移,无内力;B.有变形,有位移,有内力;C.有变形,有位移,无内力;D.无变形,有位移,无内力。
4. 图示桁架 a 杆的内力是()。
A.2P ;B. -2P;; D. - 3P。
P P Pda3 d5. 图示桁架,各杆EA 为常数,除支座链杆外,零杆数为()。
A. 四根;B. 二根;C.一根;D. 零根。
P PaP Pl = 6a6. 图示梁 A 点的竖向位移为(向下为正)()。
A. Pl 3 /( 24 EI ) ;B. Pl 3 /(16 EI ) ;C. 5Pl3/( 96EI );D. 5Pl3/(48 EI )。
P2 EI EIl/ 2 A l/ 27. 静定结构的内力计算与()。
A.EI 没关;B.EI 相对值相关;C.EI 绝对值相关;D.E 没关, I 相关。
8. 图示桁架,零杆的数量为:()。
A.5 ;;; D.20 。
9. 图示结构的零杆数量为()。
A.5 ;B.6 ;; D.8 。
10. 图示两结构及其受力状态,它们的内力切合()。
A. 弯矩同样,剪力不一样;B.弯矩同样,轴力不一样;C.弯矩不一样,剪力同样;D.弯矩不一样,轴力不一样。
P P P P2P 2PEI EI EI EIh 2EI EIl ll l11. 刚结点在结构发生变形时的主要特点是()。
A. 各杆能够绕结点结心自由转动;B.不变形;C.各杆之间的夹角可随意改变;D.各杆之间的夹角保持不变。
《结构力学习题集及标准答案》(下)-2a

第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
结构力学习题资料

结构力学复习题一、单选题1、①下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1正确答案(B)②下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(C)③下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(A)④下图结构的自由度为。
(A)0 (B)-1 (C)-2 (D)1 正确答案(D)2、①分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(A)②分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(D)③分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(D)④分析下图所示体系的几何组成为。
(A)几何不变,无多于约束(B)几何可变(C)几何瞬变(D)几何不变,有多于约束正确答案(B)3、①指出下列结构的零杆个数为。
(A)2 (B)3 (C)4 (D)5正确答案(C)②指出下列结构的零杆个数为。
(A)9 (B)10 (C)11 (D)12 正确答案(C)③指出下列桁架的类型。
(A)简单桁架(B)联合桁架(C)组合桁架(D)复杂桁架正确答案(B)④指出下列桁架的类型。
(A)简单桁架(B)联合桁架(C)组合桁架(D)复杂桁架正确答案(A)⑤指出下列结构的单铰个数为。
(A)13 (B)14 (C)15 (D)16正确答案(D)4、①指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(B)②指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(C)③指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(A)④指出下列结构的超静定次数为。
(A)2 (B)3 (C)4 (D)5 正确答案(B)⑤指出下列结构的超静定次数为。
工程力学课后答案_单祖辉主编

2-2解:(1) 取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆,(2) 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3解:(1) 取整体ABCD 为研究对象,受力分析如图,画封闭的力三角形:(2)211 1.122D A D D A F F FF F BC AB AC FF F F F =====∴===2-4解:(1) 研究AB ,受力分析并画受力图:(2) 画封闭的力三角形:相似关系:B A F F FCDE cde CD CE ED∆≈∆∴==Q F FDF F AF DFF BF A dce几何尺寸:11222CE BD CD ED=====求出约束反力:1201022010.445arctan18.4BAo oCEF F kNCDEDF F kNCDCECDα=⨯=⨯==⨯===-=2-6解:(1) 取DE为研究对象,DE为二力杆;F D = F E(2) 取ABC为研究对象,受力分析并画受力图;画封闭的力三角形:'15166.723A D EF F F F N===⨯=2-7解:(1)取铰链B为研究对象,AB、BC均为二力杆,画受力图和封闭力三角形;1BCF=(2) 取铰链C为研究对象,BC、CD均为二力杆,画受力图和封闭力三角形;22cos30oCBF F==FFFF BCF ABF1CF CD F2F CBF CD由前二式可得:12122210.61 1.634BC CB F F F F F or F F ==∴===2-9 解:(1) 取整体为研究对象,受力分析,AB 、AB 、AD 均为二力杆,画受力图,得到一个空间汇交力系;(2) 列平衡方程:0 cos 45 cos 4500 cos 6000 sin 60sin 45sin 450o o x AC AB o yAD o o o zAD AC AB F F F F F F FF F F =⨯-⨯==-==--=∑∑∑解得:2 1.2 0.735 AD AC AB AD F F kN F F kN ===== AB 、AC 杆受拉,AD 杆受压。
结构力学复习材料(含规范标准答案)

《结构力学》课程习题集西南科技大学成人、网络教育学院版权所有习题【说明】:本课程《结构力学》(编号为06014)共有单选题,判断题,计算题1,计算题2,计算题3,计算题4,几何构造分析等多种试题类型,其中,本习题集中有[计算题4]等试题类型未进入。
一、单选题1.弯矩图肯定发生突变的截面是()。
A.有集中力作用的截面;B.剪力为零的截面;C.荷载为零的截面;D.有集中力偶作用的截面。
2.图示梁中C截面的弯矩是()。
4m2m4mA.12kN.m(下拉);B.3kN.m(上拉);C.8kN.m(下拉);D.11kN.m(下拉)。
3.静定结构有变温时,()。
A.无变形,无位移,无内力;B.有变形,有位移,有内力;C.有变形,有位移,无内力;D.无变形,有位移,无内力。
4.图示桁架a杆的内力是()。
A.2P;B.-2P;C.3P;D.-3P。
5.图示桁架,各杆EA为常数,除支座链杆外,零杆数为()。
A.四根;B.二根;C.一根;D.零根。
Pal= aP PP66.图示梁A点的竖向位移为(向下为正)()。
A.)24/(3EIPl; B.)16/(3EIPl; C.)96/(53EIPl; D.)48/(53EIPl。
PEI EIAl/l/2227.静定结构的内力计算与()。
A.EI无关;B.EI相对值有关;C.EI绝对值有关;D.E无关,I有关。
8.图示桁架,零杆的数目为:()。
A.5;B.10;C.15;D.20。
9.图示结构的零杆数目为()。
A.5;B.6;C.7;D.8。
10.图示两结构及其受力状态,它们的内力符合()。
A.弯矩相同,剪力不同;B.弯矩相同,轴力不同;C.弯矩不同,剪力相同;D.弯矩不同,轴力不同。
PPll11. 刚结点在结构发生变形时的主要特征是( )。
A.各杆可以绕结点结心自由转动;B.不变形;C.各杆之间的夹角可任意改变;D.各杆之间的夹角保持不变。
12. 若荷载作用在静定多跨梁的基本部分上,附属部分上无荷载作用,则( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 结构的动力计算一、判断题:1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。
2、仅在恢复力作用下的振动称为自由振动。
3、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。
4、结构在动力荷载作用下,其动内力与动位移仅与动力荷载的变化规律有关。
5、图示刚架不计分布质量和直杆轴向变形,图a 刚架的振动自由度为2,图b 刚架的振动自由度也为2。
6、图示组合结构,不计杆件的质量,其动力自由度为5个。
7、忽略直杆的轴向变形,图示结构的动力自由度为4个。
8、由于阻尼的存在,任何振动都不会长期继续下去。
9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率,ω与ωD 的关系为ωω=D 。
二、计算题:10、图示梁自重不计,求自振频率ω。
l l /411、图示梁自重不计,杆件无弯曲变形,弹性支座刚度为k ,求自振频率ω。
l /2l /212、求图示体系的自振频率ω。
l l0.5l 0.513、求图示体系的自振频率ω。
EI = 常数。
ll 0.514、求图示结构的自振频率ω。
l l15、求图示体系的自振频率ω。
EI =常数,杆长均为l 。
16、求图示体系的自振频率ω。
杆长均为l 。
17、求图示结构的自振频率和振型。
l /2l /2l /18、图示梁自重不计,W EI ==⨯⋅2002104kN kN m 2,,求自振圆频率ω。
B2m2m19、图示排架重量W 集中于横梁上,横梁EA =∞,求自振周期ω。
EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。
求自振周期T 。
EIEIWEI 221、求图示体系的自振频率ω。
各杆EI = 常数。
a aa22、图示两种支承情况的梁,不计梁的自重。
求图a 与图b 的自振频率之比。
l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ,各杆EA 相同,杆重不计。
求水平自振周期T 。
3m 3m24、忽略质点m 的水平位移,求图示桁架竖向振动时的自振频率ω。
各杆EA = 常数。
m 4m4m25、图示体系E P W I =⨯====-2102052048004kN /cm s kN, kN, cm 214,,θ。
求质点处最大动位移和最大动弯矩。
W4mm2t26、图示体系EI k =⨯⋅==2102035kN m s 2-1,,θ×1055N /m, P =×N 103。
kN W 10=。
求质点处最大动位移和最大动弯矩。
m2m2sin P27、求图示体系在初位移等于l/1000,初速度等于零时的解答。
θωω=020.( 为自振频率),不计阻尼。
l28、图示体系受动力荷载作用,不考虑阻尼,杆重不计,求发生共振时干扰力的频率θ。
/3P tsin( )29、已知:m P ==38t, kN ,干扰力转速为150r/min ,不计杆件的质量,EI =⨯⋅6103kN m 2。
求质点的最大动力位移。
2m2m30、图示体系中,电机重kN 10=W 置于刚性横梁上,电机转速n r =500/min ,水平方向干扰力为) sin(kN 2)(t t P θ⋅=,已知柱顶侧移刚度kN/m 1002.14⨯=k ,自振频率ω=-100s 1。
求稳态振动的振幅及最大动力弯矩图。
m31、图示体系中,kN 10=W ,质点所在点竖向柔度917.1=δ,马达动荷载P t t ()sin()=4kN θ,马达转速nr =600/min 。
求质点振幅与最大位移。
32、图示体系中,W =8kN ,自振频率ω=-100s 1,电机荷载P (t ) = 5kN ·sin(θt ),电机转速n = 550r/min 。
求梁的最大与最小弯矩图。
2m2mP t ()33、求图示体系支座弯矩M A 的最大值。
荷载P t P t (),.==004sin θθω 。
/2/234、求图示体系的运动方程。
llm0.50.535、求图示体系稳态阶段动力弯矩幅值图。
θωω=05.( 为自振频率),EI = 常数,不计阻尼。
lll36、图示体系分布质量不计,EI = 常数。
求自振频率。
aa37、图示简支梁EI = 常数,梁重不计,m m m m 122==,,已求出柔度系数()δ123718=a EI /。
求自振频率及主振型。
aaa38、求图示梁的自振频率及主振型,并画主振型图。
杆件分布质量不计。
a aa39、图示刚架杆自重不计,各杆EI = 常数。
求自振频率。
2m2m40、求图示体系的自振频率和主振型。
EI = 常数。
l ll /3/3/341、求图示体系的自振频率及主振型。
EI = 常数。
l /2l /2l /2l /242、求图示体系的自振频率及相应主振型。
EI = 常数。
/2l l/2l /2l /2l43、求图示结构的自振频率和主振型。
不计自重。
l/2l/244、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
ma aa45、求图示体系的第一自振频率。
l/2l/2l/2l/246、求图示体系的自振频率。
已知:m m m12==。
EI = 常数。
m1.51m1.5m1m1m47、求图示体系的自振频率和主振型,并作出主振型图。
已知:m m m12==,EI = 常数。
2m 24m4m48、求图示对称体系的自振频率。
EI = 常数。
l l l l/2/2/2/249、图示对称刚架质量集中于刚性横粱上,已知:m1=m,m2=2m 。
各横梁的层间侧移刚度均为k。
求自振频率及主振型。
m 1m 22150、求图示体系的自振频率并画出主振型图。
m51、求图示体系的自振频率和主振型。
EI = 常数。
l l52、用最简单方法求图示结构的自振频率和主振型。
l l53、求图示体系的频率方程。
l54、求图示体系的自振频率和主振型。
EI =常数。
2a aa55、求图示体系的自振频率和主振型。
不计自重,EI = 常数。
a /2a /2a /2a /256、求图示体系的自振频率。
设 EI = 常数。
l57、图示体系,设质量分别集中于各层横梁上,数值均为m 。
求第一与第二自振频率之比ωω12:。
258、求图示体系的自振频率和主振型。
lm m 2EI =∞ EI =∞ EI 1EI 12EI 12EI 159、求图示体系的自振频率和主振型。
m m m m 122==,。
60、求图示桁架的自振频率。
杆件自重不计。
m 3m3m61、求图示桁架的自振频率。
不计杆件自重,EA = 常数。
m mm3362、作出图示体系的动力弯矩图,已知:θ=0825673.EIml 。
0.5l0.5l263、作图示体系的动力弯矩图。
柱高均为h ,柱刚度EI =常数。
l lθ=13257.EImh30.50.5P64、绘出图示体系的最大动力弯矩图。
已知:动荷载幅值P =10kN ,θ=-209441.s ,质量m =500kg ,a =2m ,EI =⨯⋅481062.N m 。
()P t sin θ65、已知图示体系的第一振型如下,求体系的第一频率。
EI = 常数。
振型101618054011 ..⎧⎨⎪⎩⎪⎫⎬⎪⎭⎪ /2第九章 结构的动力计算(参考答案)1、(X)2、(X)3、(X)4、(X)5、(O)6、(O)7、(O) 8、(X) 9、(X)10、ω=19253EIg Wl / 11、()ω=4kg /W12、)/(16,48/332311ml EI EI l ==ωδ13、)5/(48,48/5323ml EI EI l ==ωδ14、33477.11124ml EIml EI ==ω15、)5/(3,3/5323ml EI EI l ==ωδ16、323119,/9mlEIl EI k ==ω 17、()06424 , 5.123213231=--=A l m A l m EI mlEI ωωω, 0)248(3 , 28.423213232=-+=A EI l m A l m mlEI ωωω 振 型 1振 型 218、1s 2.54-=ω19、()T Wh EIg =263π/20、()T WhEIg =2483π/21、)/(889.23ma EI =ω22、2:1:=b a ωω23、)/(56.16EAg W T =24、m EA m 5.10//1==δω25、cmYstp Y M ml EI 3029.1,,127.3)/1/(1,s 25.24)2/8/(Max Mstp Dmax 22-1====-===μμωθμω26、ωδ==+=-1143143416//(//).m m EI k s 1 μθω=-=11152222/(/).m,006.0stp max ==y Y D μ ,m, kN 61.7Dmax ==stp M M μ27、),sin(04167.1)sin(20833.0)cos(001.0,1000/ ,),cos()cos()sin(,04067.1 ,/st st st 22st t Y t Y t l Y l B Y A t m Pt B t A Y m P Y DD D θωωωθμθμωωωμω+-===++===28、)/(273ml EI =θ29、-1s 92.38=ω ,-1s 71.15=θ ,19.1=μ ,m 10/09.23max =y 30、,378.1 ,s 36.52-1==βθ,mm 27.0 m,9610.1st 4st ===-y A y βMM F M D 756.2==β31、,s 83.62 ,s 50.71-1-1==θω;β=4389. ;A F ==βδ337.mm ;m m 28.5)(max =+=δβF w y32、θβ==575961496.,.s -1,M F M M D ==β748. ,{}M M M M TD 52.0 48.15st max =+=33、333 , 3l EIk ml EI ==ω,运动方程: mPy yk ky y m P 165, 21=+∆⋅=+ω 特征解y *:y P m t P mt *sin .sin =-=51600595222ωθωθθ11()l P M t l P t l P l P Pll ym M A A 0max 000*56.0, sin 56.0 sin )20595.0(2==+=+=θθ 34、 16)sin(533t P y l EI ym θ=+35、))(sit (3,3/4,4/3st t EIPlY EI Pl Y θμ-===36、{}EIma /1211.02123.3/1T32==ωλ)/(874.2,)/(558.03231ma EI ma EI ==ωω37、{}EI ma /07350.0125984.0/1T32==ωλ)/(|6886.3,)/(8909.03231ma EI ma EI ==ωω954.0/1/2111=Y Y ,()097.2/1/2212-=Y Y38、EIa EI a 6/,3/231232211===δδδ,)/(414.1,)/(0954.13231ma EI ma EI ==ωω{}λω==1561223////ma EI T,Y Y Y Y 112112221111//,//()==-M1M21第二主振型第一主振型图图111139、EIEIEI2834122211-===δδδ,,,⎭⎬⎫⎩⎨⎧==779.0554.812EImωλmEImEI1328.1,3419.021==ωω40、对称:,162/53EIl=δ,)/(69.52/131mlEI=ω反对称:,/00198.03EIl=δ,)/(46.222/132mlEI=ω41、EIlEIlEIl96/5,24/,48/532112322311====δδδδ3231/054.9,/736.2mlEImlEI==ωω{}[]Φ1105653=.,()T分{}[]Φ2117663=-.()T分42、对称:,)/(191.2,24/52/132311mlEIEIl==ωδ反对称:δδδ1132112348===l EI l EI/,/,δ22348=l EI/,,)/(69.7,)/(5.02/1322/131mlEImlEI==ωω{}[]Y 1=1 0.03 -0.03T,{}[]Y 2=0 1 1T,,{}[]Y 3=1 -31.86 31.86T43、ωω13231282==.,.,EI ml EIml 1.01,4.101,16,382,482212211132112322311-======Y Y Y Y EI l EI l EI l δδδδ 44、321321/2.397.0;/0975.007.1ma EI EI ma ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=ωωλλ61.3/;28.0/)2(2)2(1)1(2)1(1+=-=A A A A45、3/48ml EI =ω46、),/(7708.1,/)(4393.0),/(3189.0),/(1818.5),/(6875.1),/(1),/(5.4212121122211m EI m EI EI m EI m EI EI EI ====-====ωωλλδδδδ47、)/(6664.2),/(6645.12)3/(32),/(4),3/(142122211211EI m EI m EI EI EI ===-===λλδδδδ5.0:1:,2:1:)/(6124.0,)/(281.022********=ΦΦ-=ΦΦ==m EI m EI ωω 48、31/47.10ml EI =ω,,/86.1332ml EI =ω49、k k k k k k k 112212212====-,,ωωω21222808021920468215102=⎧⎨⎩⎫⎬⎭==k m k m km..,.,.Y Y Y Y 112112221178110281==-.,. 50、k i l k k i l k i l 112211222226630===-=/,/,/,ω11/20146=.(/)EI m ,2/12)/(381.0ml EI =ω,{}[]{}[]TT4.24- 1,0.236 121=Φ=Φ51、k EI l k EI l k EI l 1131232231812998==-=/,/,/,ωω132316925245==.,.EI m l EIm l 52、利用对称性: 反对称:δω11313366245===l EIEI m l EIm l ,. , 对称:δω1132339696737===l EIEI m l EIm l ,.53、列幅值方程:δωδωδωδω1121222122222222m x m y x m x m y y +=+=⎫⎬⎭,21210211122221112m m m m ωδδωωδδω--=, δδδδ113122132233243====l EI l EI l EI,,22xδ112254、对称:δω223230183333032==.,.a EI EIma反对称:δω11313407071==a EI EI ma ,. 55、对称:11δ11324=a EI /(),ω1324=EI ma /()反对称:11δ1137768=a EI /(),ω137687=EI ma /()56、ωω132********==./,./EI ml EI ml57、设k EI l =243/ 频率方程:()()()22,024,0322242222±==+-=---mkk km m km k m k ωωωωω828.5:11:1716.0:21==ωω58、ωω14241248==EIml EIml ,,ΦΦΦΦ11211222051==-., 59、k EI l k EI l k EIl1131232233351==-=,, []M m EI ml EIml =⎡⎣⎢⎤⎦⎥==100216735071323,.,. ωω,[]Φ=-⎡⎣⎢⎤⎦⎥1114020132.. 60、W EAg W EAg /506.0,/379.021==ωω61、ωω12034048==././EA m EA m , 62、EIPl A A EI l EIl EI l 3213223123111397.00531.0348524⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧===,,,δδδ 0.Pl0047612.Pl63、EIPh A A h EI k h EI k h EI k 3213123223110500.00538.0242448⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧-===,,,0.0252Ph0.3220Ph0.347Ph64、反对称结构:δ=8EI,ω=-346411.s ,μ=15762. 两竖杆下端动弯矩为31524.kN m ⋅,左侧受拉。
