第三章扩展式博弈与完全信息动态博弈讲义
第3讲 完全信息动态博弈

最优化的一阶条件意味着: s(q1) (a q1 c) =1 2 2
第3讲 完全信息动态博弈
假定q1 a c。这实际上是库诺特模型中企业2的反应函数,不同的 是,这里,s(q1)是当企业1选择q1时企业2的实际选择,而在库诺 2 特模型中,R2 q1)是企业2对于假设的q1的最优反应。 ( 因为企业1预测到企业2将根据s(q1)选择q 2,企业1在第一阶段的问 2 题是: max 1 = q1,s(q1)=q1 a q1 s(q1) c) ( 2 2
第3讲 完全信息动态博弈
• 这个例子也说明,在博弈中,拥有信息优势可能 使参与人处于劣势,而这在单人决策中是不可能 的。企业2在斯坦克尔伯格博弈中的利润之所以低 于库诺特博弈中的利润,是因为它在决策之前就 知道了企业1的产量。即使企业1先行动,但如果 企业2在决策之前不能观测到企业1的产量,我们 就回到了库诺特均衡,因为此时,企业1的先动优 势就不存在了。
第3讲 完全信息动态博弈
* 1 回忆一下,在上一讲得到的库诺特模型的纳什均衡是q1 =q* = (a c), 2 3 3 比较这两个结果,发现斯坦克尔伯格均衡的总产量 (a c)大于库诺特 4 2 的总产量 (a c)。但是,企业1的斯坦克尔伯格均衡产量大于库诺特 3
均衡产量,而企业2的斯坦克尔伯格均衡产量小于库诺特均衡产量。 因为企业1本来可以选择库诺特均衡产量但它没有选择,说明企业1在斯坦 克尔伯格博弈中的利润大于库诺特博弈中的利润,而总产量上升意味着 总利润下降了从而企业2的利润一定下降了。这就是所谓的“先动优势”。
第3讲 完全信息动态博弈
• 宏观经济政策的动态一致性 宏观经济学上与子博弈精炼纳什均衡相对应的概 念是政府政策的动态一致性(dynamic consistency 或time consistency)。政府政策 的动态一致性指的是,一个政策不仅在制定阶段 应该是最优的(从政府的角度),而且在指定之 后的执行阶段也应该是最优的,假设没有任何新 的信息出现。如果一个政策只是在制定阶段是最 优的,而在执行阶段并不是最优的,这个政策就 是动态不一致的。说它是动态不一致的,是因为
第三章 完全信息动态博弈 ppt课件

条路径。但每条路径可由不同的策略组合决定。
例如, (开发,(不开发,开发))决定了
A -> 开发 -> B -> 不开发 -> (1,0)
该路径还可由(开发,(不开发,不开发))决定。
事实上,该问题共有4条路径,8种策略组合。
ppt课件
12
§2 子博弈精炼纳什均衡
对于动态博弈,Nash均衡可能并不是一个合理的预测。 如房地产博弈:
又如,上例中,如果进入者先行动,而在位者在 行动前能准确知道前者的行动,那么在位者的信息 集为 {进入}或{不进入}。 反之,若在位者先行动, 则在位者的信息集为{进入,不进入}。
ppt课件
7
三、 动态博弈的相关概念
(3) • 完美信息(Perfect information):一个局中人在行动
时,对之前博弈进程有准确了解,即每一个信息集只包含 一个值,则称该局中人具有完美信息。 • 如果动态博弈的所有局中人都有完美信息,则称为完美信 息的动态博弈。 • 如果动态博弈中,存在部分局中人具有不完美信息,称为 不完美信息的动态博弈。
思考:若进入者真的进入,在位者的最优行动是“默许”。 所以“斗争”是一种不可置信的威胁(即使在位企业摆出 一副“你进入我就斗争”的架势,进入企业不应被吓到)。 而静态博弈承认这种不可置信的威胁,使(不进入,斗争) 成为一个Nash均衡。
动态博弈解决方案:剔除不可置信的威胁策略
ppt课件
3
扩展阅读:不可置信的威胁策略 引出信息经济学重要的概念—— 承诺行动(Commitment)。
ppt课件
18
三、 逆向归纳法求解子博弈精炼Nash均衡
• 从动态博弈的最后一个阶段局中人的行为开始分析
第三讲完全且完美信息动态博弈a讲义

本章讨论动态博弈,所有博弈方都对博弈过程和 得益完全了解的完全且完美信息动态博弈。这类博 弈也是现实中常见的基本博弈类型。由于动态博弈 中博弈方的选择、行为有先后次序,因此在表示方 法、利益关系、分析方法和均衡概念等方面,都与 静态博弈有很大区别。本章对动态博弈分析的概念 和方法,特别是子博弈完美均衡和逆推归纳法作系 统介绍,并介绍各种经典的动态博弈模型。
企业、政府与商业环境
博弈论与企业竞争
两个纳什均衡
纳什均衡之一是如果A进入市场,B就威胁选择商战,所以A不进入市场 另一个纳什均衡是A选择进入,B随之选择容纳
容纳 (900,1100)
进入
A
B
商战 (-200,600)
不进入
(0, 3000)
企业、政府与商业环境
博弈论与企业竞争
一个子博弈纳什精炼均衡
可信性:动态博弈中先行为的博弈方是否应该相信后 行为博弈方会采取某种策略或行为。
后行为博弈方将来采取对先行为博弈方有利的行为为 “许诺”,采取对先行方不利的行为为“威胁”。
8
2020/7/31
多阶段博弈
序列博弈
参与者选择策略有时间先后的顺 序,通常采用博弈的扩展形式来 进行分析
例子:进入博弈
形成额外的剩余生产能力可以阻止进入,潜在进入者知道他一旦进入,价格战就必然发生, 因而构成可置信的威胁
形成剩余生产能力的行动在序列博弈中常带有先发制人的意图,因此这种行动被称为事先承 诺博弈
企业、政府与商业环境
博弈论与企业竞争
3.1.1开金矿
条件:甲去开采一价值4万元的金矿,缺1万元,乙恰 好有1万元可以投资。甲向乙借1万元可以可开金矿, 并“许诺”成功后与对半分成。
第三讲 完全信息动态博弈
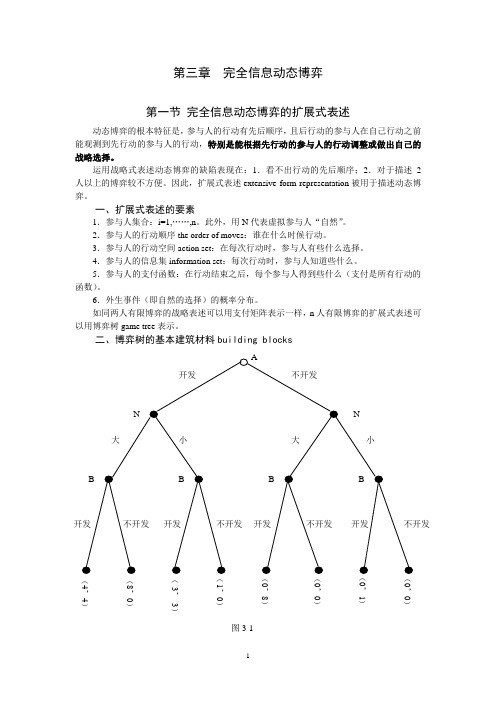
第三章完全信息动态博弈第一节完全信息动态博弈的扩展式表述动态博弈的根本特征是,参与人的行动有先后顺序,且后行动的参与人在自己行动之前能观测到先行动的参与人的行动,特别是能根据先行动的参与人的行动调整或做出自己的战略选择。
运用战略式表述动态博弈的缺陷表现在:1.看不出行动的先后顺序;2.对于描述2人以上的博弈较不方便。
因此,扩展式表述extensive form representation被用于描述动态博弈。
一、扩展式表述的要素1.参与人集合:i=1,……,n。
此外,用N代表虚拟参与人“自然”。
2.参与人的行动顺序the order of moves:谁在什么时候行动。
3.参与人的行动空间action set:在每次行动时,参与人有些什么选择。
4.参与人的信息集information set:每次行动时,参与人知道些什么。
5.参与人的支付函数:在行动结束之后,每个参与人得到些什么(支付是所有行动的函数)。
6.外生事件(即自然的选择)的概率分布。
如同两人有限博弈的战略表述可以用支付矩阵表示一样,n人有限博弈的扩展式表述可以用博弈树game tree表示。
二、博弈树的基本建筑材料building blocks(4,4)(8,)(-3,-3)1,),8),),1),)图3-1(一)结nodes1.结的分类(1)决策结decision nodes:参与人采取行动的时点。
包括:起点结——initial nodes非起点结——(2)终点结terminal nodes:博弈行动路径的终点。
2.结的顺序关系precedence relation用X表示所有结的集合,x∈X表示某个特定的结。
x≺x"表示“x在x"之前”≺3.前列集the set of predecessors和后续集the set of successors定义P(x)为在x之前的所有结的集合,简称为x的前列集;定义T(x)为x之后的所有结的集合,简称为x的后续集。
第三章扩展型博弈论

如果甲先行动,但在博弈开始前商铺主乙有一次行动A的机会, 请利用子博弈完美纳什均衡概念分析下述两种情况下的博弈结果
(1)A:商铺主乙逢人便说自己一定要进货,无论对方如何行 动他都不会改变这个决定;
(2)A:商铺主乙与某个嘲笑他说大话的第三者丙打赌:如果 自己到时不进货,向丙支付1500元;如果自己到时候进货,丙 向他支付100元。并且,乙将这个赌局通知甲。
甲
甲
进 乙
不进 乙
进 乙
不进 乙
进
不进 进
不 进
进
不进 进
不 进
(-1000,-1000) (0,1000) (0,0)(-1000,-900)
(0,1100)(0,-1500)
(1000,0)
(1000,-1500)
作业: 阅读“蜈蚣博弈”
拍卖人拿出一张10元钞票,请大家给这张
钞票开价,无底价,竞拍者可无限制的轮 流叫价,每次叫价的增幅以5毛为单位,出 价最高者可以得到这张10元钞票,但出价
即每阶段都选“不坦白”,A总得益贴现为
2 ( 2 ) ( 2 ) 2 .. . 2
当
1(6) 2 1 1
1 时,A选“不坦白”是最优的,即
当
1 5
时,A在没有人先选“坦白”时选“不坦白”是最优的,并且A 在之后每阶段都选“不坦白”是最优的选择。
乙
甲
坦白 不坦白
坦白 -6,-6 -1,-8
最高和次高者都要向拍卖人支付出价数目 的费用。
——苏比克拍卖模型
第四节
重复博弈
重复博弈
单次博弈重复进行构成的博弈过程,但博 弈方的行为和博弈结果不一定是单次博弈 的简单重复,其中,单次博弈可称为阶段 博弈
博弈论全套上课课件ch3 完全信息动态博弈

16
智猪博弈的扩展式表述?
小猪 按 大猪 按
5,1
等待
4,4 0,0
等待 9,-1
南京农业大学经济管理学院 王艳
17
3、完美记忆博弈game of perfect recall
所有参与人都不会忘记曾经知道过的任何 信息,清楚他们前面所选择的行动。
南京农业大学经济管理学院 王艳
第三章 完全信息动态博弈
主要内容
一、博弈扩展式表述 二、逆向归纳法与子博弈精炼纳什均衡 三、应用举例
南京农业大学经济管理学院 王艳
2
引例- 房地产开发项目
假设有A、B两家开发商
市场需求:可能大,也可能小 投入:1亿
假定市场上有两栋楼出售:
需求大时,每栋售价1.4亿, 需求小时,售价7千万;
支付
6
南京农业大学经济管理学院 王艳
一 、博弈扩展式表述
结: 包括决策结和终点结两类;决策结是参与人行 动的时点,终点结是博弈行动路径的终点. 结满足传递性和非对称性 枝: 枝是从一个决策结到它的直接后续结的连线, 每一个枝代表参与人的一个行动选择. 信息集: 每个信息集是决策结集合的一个子集,该 子集包括所有满足下列条件的决策结:
R L
R
图3.7
南京农业大学经济管理学院 王艳
15
囚徒困境博弈的扩展式表述
A
坦白 抵赖
B
坦白
抵赖
B
抵赖 坦白
B
坦白
A
抵赖 坦白
A
抵赖 坦白 抵赖
(-8,-8)
(0,-10)
(-10,0) (-1,-1)
(-8,-8) (0,-10) (-10,0)
(完整版)完全信息动态博弈.ppt

(四)参与人在博弈树中的顺序
1、排序的基本原则
一个参与人在决策之前知道的事情必须出现在该 参与人的决策结之前。
2、自然人的排序
– 如果参与人不能观测到虚拟人——自然的行动, 自然的决策结置于该参与人的前后都一样;
– 自然的信息集总是假定为单结。
N
大 1/2 A
小 1/2 A
开
不
发开
发
B
B
开发
不开发 开发 不开发
– 博弈的战略式表述只包括三个要 素
– 扩展式表述包括以下六个方面的 要素
扩展式表述包括以下六个方面的要素:
– 参与人集合:i=1、2、…,n;并且用大写N代表 虚拟的参与人——“自然”;
– 参与人的行动顺序(The order of moves):谁在什么 时候行动;
– 参与人的行动空间(Action set):在每次行动时, 参与人有些什么选择;
A
坦白 抵赖
B
B
坦白
抵赖
抵赖
坦白
(-8, -8) (0,-10) (-10, 0) (-1,-1)
B
坦白 A
抵赖 A
坦白
抵赖
抵赖
坦白
(-8, -8) (0,-10) (-10, 0) (-1,-1)
(五)完美回忆
完美回忆(Perfect recall)是指没有参与人会 忘记自己以前知道的事情,所有参与人都 知道自己以前的选择。
第三章 完全信息动态博弈
Dynamic Games of Complete Information
@ 2009 Zheng Daowen, All Rights Reserved
动态博弈:参与人的行动有先后顺序,且后 行动者在自己行动之前能观测到先行动者 的行动。
博弈论 完全信息动态博弈(1)

完美信息博弈:N → A →B情形
自然先确定市场需求状态:高需求或低 需求;开发商A在观察到市场需求状态后 决定是否开发;开发商B在观察到市场需 求状态和A的决策后再决定是否开发。 开发 开发 高需求 ○ N 低需求 不开发 A 开发 不开发 B (2,2)
不开发 (4,0) 开发 不开发 (0,4) (0,0)
不开发 开发 不开发 开发 不开发
1-p
不开发
完全信息静态博弈的博弈树
开发 开发 高需求 ○ N 低需求 不开发 A 开发 不开发 B (2,2) 不开发 (4,0) 开发 (0,4) 不开发 (0,0) 开发 (-1,-1) 不开发 (1,0) 开发 (0,1) 不开发 (0,0)
不完全信息静态博弈的博弈树
枝的图示
枝是一个从决策结到它 的直接后续结的连线, 代表参与人的一个行动 选择。 枝:不但完整地描述了 每一个决策结参与人的 行动空间,而且给出了 从一个决策结到下一个 决策结的路径。
1 U z1 L z2 P z3 D 2 R 3 Q z4
(3) 信息集
博弈树上所有决策结分割成不同的信息集(记为 h∈H),它是X的一个子集,满足: (1)每一个决策结都是同一参与人的决策结; (2)该参与人知道博弈进入该集合的某个决策结, 但不知道究竟处于哪一个决策结。 记h(x)是X中包含x的信息集,如果x″∈h(x),则满足: (1)x∉P(x″),且x″ ∉P(x); (2)i(x)=i(x″); (3)A(x)=A(x″)。 在此基础上,即可用A(h)表示给定信息集h下的行动 集合。
要素详解
参与人:博弈中的决策主体,有时包括“自然” 作为“虚拟参与人”。 行动:是参与人在博弈的某个时点的决策变量。 行动组合:参与人的行动的有序集。 行动顺序:静态博弈和动态博弈 信息:是参与人有关博弈的知识,如有关“自然” 的选择、其他参与人的特征和行动的知识等。 完全信息(complete information) 完美信息(perfect information) 对称信息(symmetric information) 确定信息(certain information)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信息集中哪一个决策结上)。
例如
• 在“新产品开发博弈”中,假设企业1先行动, 企业2后行动,但企业2行动时不知道企业1的 行动。
企业2行动时,只知道 博弈要么到达点x2,要 么达到点x3 ,但具体在 哪一点上,企业2不清 楚。也就是说,企业2 只知道自己位于决策结 集合{x2, x3 }上,但不知 道位于{x2, x3 }中哪一个 决策结上。
完全信息动态的“新产品开发博弈”的扩 展式博弈包括以下要素:
(1) 参与人是企业1和2;
(2) 企业1先行动,企业2后行动;
(3) 企业1行动时有两种选择——“开发”和 “不开发”,企业1行动时不知道企业2 的行动;企业2行动时有两种选择—— “开发”和“不开发”,但企业2行动时 已经知道企业1的行动;
下图表示参与人3选择时,知道参与人1的选择, 但不知道参与人2的选择的博弈情形。
1
L
x1
R
2
2
L x2 R
L x3 R
3
3
L x4 R L x5 R L x6 R L x7 R
的选择”这一问题,实际上就等价于
“企业2行动时是否知道自己是在博弈树
中的点x2上还是在点x3上”。
• 为了将“企业2行动时是否知道自己是
在博弈树中的点x2上还是在点x3上”这 一点说清楚,需要引入“信息集”(infor
mation set)的概念。
• 在博弈树中,参与人i的一个信息集(用Ii表示) 是参与人i决策结的一个集合,它满足以下两
• 设X为一决策结集合,用Ii(X)表示参与人 的由决策结集X构成的一个信息集。
• 例如,I2({x2, x3})表示企业2的由决策结集 {x2, x3}构成的信息集,I2({x2})和I2({x3}) 分别表示企业2的由决策结集{x2}和{x3}构 成的信息集。
• 可以在博弈树中将同一信息集中的决策结 用虚线连接起来。
第三章 扩展式博弈与完全信 息动态博弈
主要内容: 一、扩展式博弈 二、扩展式博弈的战略及其Nash均衡 三、两种博弈描述形式的比较
一、扩展式博弈
• 所谓扩展式博弈(extensive form game)是 博弈问题的一种规范性描述。与战略式 博弈侧重博弈结果的描述相比,扩展式 博弈更注重对参与人在博弈过程中所遇 到决策问题的序列结构的详细分析。
动; (3) 每个参与人行动时面临的决策问题,包括参
与人行动时可供他选择的行动方案以及他所 了解的信息; (4) 参与人的支付函数,即博弈结束时每个参与 人得到的博弈结果。
例子: “新产品开发博弈”
• 试用扩展式博弈对两个企业都知道市场 需求,且企业1先决策,企业2观测到企 业1的选择后再进行选择的博弈情形即完 全信息动态的“新产品开发博弈”进行 建模。
• 十分直观的扩展式博弈的描述方 式——博弈树。
• 所谓博弈树就是由结和有向枝构成的 “有向树”。
企有最业“上1开端的发的选”一择和个点(用空心圆 “表不示开),发表”示,博弈的开始 。 分表别示用博标弈有达到 “该开点发时”企和业的 “所不得开,发其”中的, 有支向付枝向表量示中。的 第一个数字表 示企业1的所得, 第二个数字表 示企业2的所 得。
研究博弈问题的具体进程必须弄清楚的两个问题
(1) 每个参与人在什么时候行动(决策); (2) 每个参与人行动时,他所面临决策问题
的结构。这包括参与人行动时可供他选 择的行动方案,以及参与人行动时所了 解的信息。
扩展式博弈的定义:
扩展式博弈包括以下要素: (1) 参与人集合 {1, 2,..., n} ; (2) 参与人的行动顺序,即每个参与人在何时行
(4) 两个企业的支付如下:
对手不开发,获利润800万元
需求大
企业 开发(a):投入2千万元资金需求小对 对对手 手手不 开开开 发发发 ,,, 赔获获 4利0利0润万润3元0200万0万元元
不开发(b):不投入资金,利润为0
• 例子中,用文字描述的方法给出了博弈 问题的扩展式描述。
• 但可以想象,如果我们遇到的是更为复 杂的博弈问题,文字描述可以?
择,即知道企业1选择了“开发”还是
“不开发”,因此,企业2知道博弈是从
x1到了x2还是从x1到了x3。这就意味着当 轮到企业2决策时,他知道自己是在点x2 上还是在点x3上;
• 对于第二种情形,企业2不知道企业1的
选择,即不知道博弈是从x1到了x2还是从 x1到了x3。因此,当轮到企业2决策时, 他不知道自己是在点x2上还是在点x3上。 所以,“企业2行动时是否观测到企业1
问题:
• 如何在博弈树中,将“企业2行动时 是否观测到企业1的选择”这一信息 表示出来?
• 在完全信息动态的“新产品开发博弈” 中,企业2决策时,企业1已经做出选 择。此时,企业2面临的决策情形就 有以下两种:
(1) 企业2知道企业1的选择;
(2) 企业2不知道企业1的选择。
• 对于第一种情形,企业2知道企业1的选
将“企业1”标示在点x
1上,表示博弈开始于 企业1的选择。
决策结
称为博弈树的结(node)
回过来再考察上图中的博弈树,可以得到 这样的信息:
(1) 博弈中的参与人是企业1和企业2; (2) 博弈中企业1先选择,企业2后选择; (3) 企业1选择时有行动“开发”和“不开
发”,企业2选择的行动有“开发”和 “不开发”;
个条件:
(1) Ii中的每个决策结都是参与人i的决策结;
(2) 当博弈到达信息集Ii(即博弈到达Ii中某个决策 结)时,参与人i知道自己是在信息集Ii中的决 策结上,但不知道自己究竟在Ii中哪个决策结 上。
• 因此,参与人i的信息集Ii可以用来描述: 当轮到参与人i行动时,他所了解到的信
息,即他知道什么(知道自己位于哪一个
(4) 博弈中企业的支付。
• 也就是说,除了“企业2行动时是否观测 到企业1的选择”这一点,暂时无法从上 图中知道以外,完全信息动态的“新产 品开发博弈”的扩展式描述所需要的信 息(或要素),都可以从上图中得到。
• 如果还能够直接从博弈树中知道“企业2 行动时是否观测到企业1的选择”,那么 给出博弈树,就意味着给出了完全信息 动态的“新产品开发博弈”的扩展式描 述。
