向量法求空间角(高二数学,立体几何)

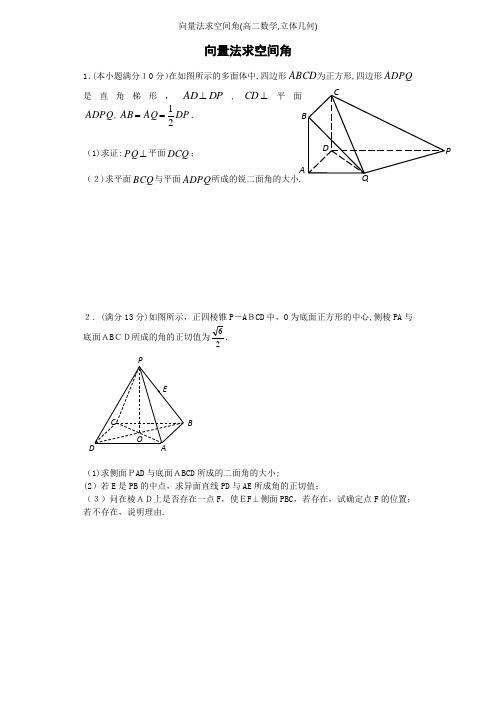
A B CD PQ 向量法求空间角1．（本小题满分10分）在如图所示的多面体中，四边形ABCD 为正方形，四边形ADPQ 是直角梯形，DP AD ⊥，⊥CD 平面ADPQ ，DP AQ AB 21==．（1）求证：⊥PQ 平面DCQ ； （2）求平面BCQ 与平面ADPQ 所成的锐二面角的大小．2．（满分13分）如图所示，正四棱锥P －ABCD 中，O 为底面正方形的中心，侧棱PA 与底面ABCD 所成的角的正切值为26．（1）求侧面PAD 与底面ABCD 所成的二面角的大小；（2）若E 是PB 的中点，求异面直线PD 与AE 所成角的正切值；（3）问在棱AD 上是否存在一点F ，使EF ⊥侧面PBC ，若存在，试确定点F 的位置；若不存在，说明理由．B3．（本小题只理科做，满分14分）如图,已知AB⊥平面ACD,DE//AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.（1）求证:AF//平面BCE;（2）求证:平面BCE⊥平面CDE;（3）求平面BCE与平面ACD所成锐二面角的大小.P-中,PD⊥底面ABCD,且底面4．（本小题满分12分）如图，在四棱锥ABCDABCD为正方形,GPD=分别为CBPC,,的中点．=PDF,2EAD,,AP平面EFG;（1）求证://（2）求平面GEF和平面DEF的夹角.HPGFE DCB 5．如图，在直三棱柱111ABC A B C -中，平面1A BC ⊥ 侧面11A ABB 且12AA AB ==.（Ⅰ）求证：AB BC ⊥；（Ⅱ）若直线AC 与平面1A BC 所成的角为6π,求锐二面角1A A C B --的大小.6．如图，四边形ABCD 是正方形，EA ⊥平面ABCD ，EA PD ，2AD PD EA ==，F ，G ， H 分别为PB ，EB ，PC 的中点．（1）求证：FG 平面PED ；（2）求平面FGH 与平面PBC 所成锐二面角的大小.参考答案1．（1）详见解析；（2）4π 【解析】试题分析：（1）根据题中所给图形的特征，不难想到建立空间直角坐标，由已知，DA ，DP ，DC 两两垂直，可以D 为原点，DA 、DP 、DC 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系．表示出图中各点的坐标：设a AB =，则)0,0,0(D ，),0,0(a C ，)0,,(a a Q ，)0,2,0(a P ，则可表示出),0,0(a DC =，)0,,(a a DQ =，)0,,(a a -=，根据数量积为零与垂直的充要条件进行证明，由0=⋅，0=⋅，故⊥，⊥，即可证明；（2）首先求出两个平面的法向量，其中由于⊥DC 平面ADPQ ，所以可取平面ADPQ 的一个法向量为)1,0,0(1=n ；设平面BCQ 的一个法向量为),,(2z y x n = ，则02=⋅QB n ，02=⋅QC n，故⎩⎨⎧=+--=+-,0,0az ay ax az ay 即⎩⎨⎧=+--=+-,0,0z y x z y 取1==z y ，则0=x ，故)1,1,0(2=n ，转化为两个法向量的夹角，设1n 与2n 的夹角为θ，则2221||||cos 2121==⋅=n n n n θ．即可求出平面BCQ 与平面ADPQ 所成的锐二面角的大小.试题解析：（1）由已知，DA ，DP ，DC 两两垂直，可以D 为原点，DA 、DP 、DC 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系．设a AB =，则)0,0,0(D ，),0,0(a C ，)0,,(a a Q ，)0,2,0(a P ， 故),0,0(a =，)0,,(a a =，)0,,(a a -=， 因为0=⋅，0=⋅，故⊥，⊥，即PQ DC ⊥，PQ DQ ⊥， 又DCDQ D = 所以，⊥PQ 平面DCQ ．（2）因为⊥平面ADPQ ，所以可取平面ADPQ 的一个法向量为)1,0,0(1=n，点B 的坐标为),0,(a a ，则),,0(a a -=，),,(a a a --=，设平面BCQ 的一个法向量为),,(2z y x n = ，则02=⋅QB n ，02=⋅n ，故⎩⎨⎧=+--=+-,0,0az ay ax az ay 即⎩⎨⎧=+--=+-,0,0z y x z y 取1==z y ，则0=x ，故)1,1,0(2=n ．设1n 与2n 的夹角为θ，则2221||||cos 2121==⋅=n n n n θ． 所以，平面BCQ 与平面ADPQ 所成的锐二面角的大小为4π 考点：1.空间向量的应用；2.二面角的计算；3.直线与平面的位置关系2．（1）60︒; （2）5102; （3）F 是AD 的4等分点，靠近A 点的位置. 【解析】试题分析：（1）取AD 中点M ，连接MO ，PM ，由正四棱锥的性质知∠PMO 为所求二面角P －AD－O 的平面角，∠PAO 为侧棱PA 与底面ABCD 所成的角∴tan ∠PAO ＝26，设AB ＝a ，则AO ＝22a ，PO ＝23a ，MO=12a , tan ∠PMO ＝3,∠PMO ＝60°; （2）依题意连结AE ，OE ，则OE ∥PD ，故∠OEA 为异面直线PD 与AE 所成的角，由正四棱锥的性质易证OA ⊥平面POB,故AOE ∆为直角三角形，OE ＝21PD ＝2122DO PO +＝45a ∴tan ∠AEO ＝EO AO ＝5102；（3）延长MO 交BC 于N ，取PN 中点G ，连BG ，EG ，MG ，易得BC ⊥平面PMN ，故平面PMN ⊥平面PBC ，而△PMN 为正三角形，易证MG ⊥平面PBC ，取MA 的中点F,连EF,则四边形MFEG 为平行四边形，从而MG//FE,EF ⊥平面PBC,F 是AD 的4等分点，靠近A 点的位置.试题解析：（1）取AD 中点M ，连接MO ，PM ，依条件可知AD ⊥MO ，AD ⊥PO ，则∠PMO 为所求二面角P －AD －O 的平面角 （2分） M DB A CO EP∵PO ⊥面ABCD ，∴∠PAO 为侧棱PA 与底面ABCD 所成的角．∴tan ∠PAO ＝26设AB ＝a ，AO ＝22a ，∴PO ＝AO·tan∠POA ＝23a ，tan ∠PMO ＝MO PO ＝3．∴∠PMO ＝60°． （4分）（2）连接AE ，OE ， ∵OE ∥PD ，∴∠OEA 为异面直线PD 与AE 所成的角． （6分）∵AO ⊥BD ，AO ⊥PO ，∴AO ⊥平面PBD ．又OE ⊂平面PBD ，∴AO ⊥OE ．∵OE ＝21PD ＝2122DO PO +＝45a ， ∴tan ∠AEO ＝EOAO ＝5102． （8分） （3）延长MO 交BC 于N ，取PN 中点G ，连BG ，EG ，MG ． M D BACOEPM D B ACO E PN GF∵BC ⊥MN ，BC ⊥PN ，∴BC ⊥平面PMN∴平面PMN ⊥平面PBC ． （10分）又PM ＝PN ，∠PMN ＝60°，∴△PMN 为正三角形．∴MG ⊥PN ．又平面PMN∩平面PBC ＝PN ，∴MG ⊥平面PBC ． （12分）∴F 是AD 的4等分点，靠近A 点的位置 （13分）考点：立体几何的综合问题3．（1）见解析；（2）见解析；（3）45︒.【解析】试题分析：（1）取CE 中点P ，连接FP 、BP ，根据中位线定理可知FP||DE ，且且FP=.21DE ，而AB||DE ，且AB=.21DE 则ABPF 为平行四边形，则AF||BP ，AF ⊄平面BCE ，BP ⊂平面BCE ，满足线面平行的判定定理，从而证得结论；（2）根据AB ⊥平面ACD ，DE||AB ，则DE ⊥平面ACD ，又AF ⊂平面ACD ，根据线面垂直的性质可知DE AF AF CD CD DE D ⊥⊥=．又，，满足线面垂直的判定定理，证得AF ⊥平面CDE ，又BP||AF ，则BP ⊥平面CDE ，BP ⊂平面BCE ，根据面面垂直的判定定理可证得结论；（3）由（2），以F 为坐标原点，FA ，FD ，FP 所在的直线分别为x ，y ，z 轴建立空间直角坐标系F ﹣xyz ．设AC=2，根据线面垂直求出平面BCE 的法向量n ，而m=（0，0，1）为平面ACD 的法向量，设平面BCE 与平面ACD 所成锐二面角为α，根据||cos ||||m n m n α⋅=⋅可求出所求．试题解析：（1）解:取CE 中点P,连结FP 、BP,∵F 为CD 的中点,∴FP||DE,且FP=.21DE 又AB||DE,且AB=.21DE ∴AB||FP,且AB=FP,∴ABPF 为平行四边形,∴AF||BP 又∵AF ⊄平面BCE,BP ⊂平面BCE,∴AF||平面BCE （2）∵△ACD 为正三角形,∴AF CD ⊥.∵AB ⊥平面ACD,DE||AB,∴DE ⊥平面ACD,又AF ⊂平面ACD,∴DE ⊥AF.又AF ⊥CD,CD∩DE=D,∴AF ⊥平面CDE 又BP||AF,∴BP ⊥平面CDE.又∵BP ⊂平面BCE,∴平面BCE ⊥平面CDE （3）法一、由（2）,以F 为坐标原点,FA,FD,FP 所在的直线分别为x,y,z 轴（如图）,建立空间直角坐标系F —xyz.设AC=2,则C （0,—1,0）,).2,1,0(,),1,0,3(E B -设(,,)n x y z =为平面BCE 的法向量，300,0,220x y z n CB n CE y z ⎧++=⎪∴⋅=⋅=∴⎨+=⎪⎩，令n=1,则(0,1,1)n =-显然,)1,0,0(=m 为平面ACD 的法向量.设面BCE 与面ACD 所成锐二面角为,α则||2cos ||||2m n m n α⋅===⋅∴ 45=α.即平面BCE 与平面ACD 所成锐二面角为45︒法二、延长EB 、DA,设EB 、DA 交于一点O,连结CO.则面EBC面DAC CO =.由AB 是EDO ∆的中位线,则AD DO 2=.在OCD ∆中22OD AD AC ==, 060=∠ODC .CD OC ⊥,又DE OC ⊥.OC ∴⊥ 面,ECD 而CE ⊂面ECD,为所求二面角的平面角ECD CE OC ∠∴⊥∴,在Rt EDC ∆中，ED CD =，045=∠∴ECD 即平面BCE 与平面ACD 所成锐二面角为45︒.考点：与二面角有关的立体几何综合题；直线与平面平行的判定；平面与平面垂直的判定．4．证明见解析【解析】试题分析：：（1）利用已知的线面垂直关系建立空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算.其中灵活建系是解题的关键.（2）证明线面平行，需证线线平行，只需要证明直线的方向向量与平面的法向量垂直；（3）把向量夹角的余弦值转化为两平面法向量夹角的余弦值;（4）空间向量将空间位置关系转化为向量运算，应用的核心是要充分认识形体特征，建立恰当的坐标系，实施几何问题代数化.同时注意两点：一是正确写出点、向量的坐标，准确运算；二是空间位置关系中判定定理与性质定理条件要完备. 试题解析：（1）如图，以D 为原点,以,,DA DC DP 为方向向量建立空间直角坐标系,xyz D -则)0,0,2(),1,0,0(),1,1,0(),0,2,1(),0,2,0(),2,0,0(A F E G C P .)11,1(),0,1,0(),2,0,2(-=-=-=∴EG EF AP .设平面EFG 的法向量为(,,)n x y z =0,0,n EF n EG ⎧⋅=⎪∴⎨⋅=⎪⎩即⎩⎨⎧=-+=-.0,0z y x y ⎩⎨⎧==∴.0,y z x 令1=x 则(1,0,1)n =.1(2)00120,.n AP n AP ⋅=⨯-+⨯+⨯=∴⊥又⊄AP 平面//,AP EFG ∴平面.EFG（2） 底面ABCD 是正方形,,DC AD ⊥∴又⊥PD 平面ABCD.AD PD ⊥∴又D CD PD = ,AD ∴⊥平面PCD∴向量是平面PCD 的一个法向量,)0,0,2(=又由（1）知平面EFG 的法向量(1,0,1)n =.cos ,2||||22DA n DA n DA n ⋅∴<>===⋅ ∴二面角D EF G --的平面角为045.考点：（1）证明直线与平面平行；（2）利用空间向量解决二面角问题.5．（Ⅰ）详见解析;（Ⅱ）3π. 【解析】试题分析：（Ⅰ）取1A B 的中点D ，连接AD ，由已知条件推导出AD ⊥平面1A BC ，从而AD BC ⊥，由线面垂直得1AA BC ⊥．由此能证明AB BC ⊥．（Ⅱ）方法一：连接CD ，由已知条件得ACD ∠即为直线AC 与平面1A BC 所成的角，AED ∠即为二面角1A A C B --的一个平面角，由此能求出二面角1A A C B --的大小．解法二（向量法）：由（1）知AB BC ⊥且1BB ABC ⊥底面，所以以点B 为原点，以1BC BA BB 、、所在直线分别为,,x y z 轴建立空间直角坐标系B xyz -，设BC a =，则(0,2,0)A ，(0,0,0)B ，(,0,0)C a ，1(0,2,2)A ，(,0,0)BC a =，1(0,2,2)BA =，(,2,0)AC a =-， 1(0,0,2)AA =，求出平面1A BC 的一个法向量1(,,)n x y z =，设直线AC 与平面1A BC 所成的角为θ，则6πθ=得12121sin6242AC n AC n a π-===+，解得2a =，即(2,2,0)AC =-，求出平面1A AC 的一个法向量为2(1,1,0)n =，设锐二面角1A A C B --的大小为α，则1212121cos cos ,2n n n n n n α=<>==，且(0,)2πα∈， 即可求出锐二面角1A A C B --的大小.试题解析：解（1）证明：如图，取1A B 的中点D ，连接AD ，因1AA AB =，则1AD A B ⊥ 由平面1A BC ⊥侧面11A ABB ，且平面1A BC侧面11A ABB 1A B =，得1AD A BC ⊥平面，又BC ⊂平面1A BC ， 所以AD BC ⊥.因为三棱柱111ABC A B C —是直三棱柱，则1AA ABC ⊥底面，所以1AA BC ⊥. 又1=AA AD A ，从而BC ⊥侧面11A ABB ，又AB ⊂侧面11A ABB ，故AB BC ⊥.-------6分解法一：连接CD ，由（1）可知1AD A BC ⊥平面，则CD 是AC 在1A BC 平面内的射影 ∴ACD ∠即为直线AC 与1A BC 平面所成的角，则=6ACD π∠ 在等腰直角1A AB ∆中，12AA AB ==，且点D 是1A B 中点，∴1122AD A B ==，且=2ADC π∠，=6ACD π∠ ∴22AC =过点A 作1AE A C ⊥于点E ，连DE ，由（1）知1AD A BC ⊥平面，则1AD A C ⊥，且AE AD A =∴AED ∠即为二面角1A A C B --的一个平面角且直角1A AC ∆中：113A A ACAEAC⋅===，又AD，=2ADEπ∠∴sin=ADAEDAE∠==且二面角1A A C B--为锐二面角∴=3AEDπ∠，即二面角1A A C B--的大小为3π----12分解法二（向量法）：由（1）知AB BC⊥且1BB ABC⊥底面，所以以点B为原点，以1BC BA BB、、所在直线分别为,,x y z轴建立空间直角坐标系B xyz-，如图所示，且设BC a=，则(0,2,0)A，(0,0,0)B，(,0,0)C a，1(0,2,2)A，(,0,0)BC a=，1(0,2,2)BA =，(,2,0)AC a=-，1(0,0,2)AA =设平面1A BC的一个法向量1(,,)n x y z=，由1BC n⊥，11BA n⊥得：0220xay z=⎧⎨+=⎩令1y=，得0,1x z==-，则1(0,1,1)n=-设直线AC与1A BC平面所成的角为θ，则6πθ=得111sin624AC nAC nπ⋅===，解得2a=，即(2,2,0)AC=-又设平面1A AC的一个法向量为2n，同理可得2(1,1,0)n=，设锐二面角1A A C B--的大小为α，则1212121cos cos,2n nn nn nα⋅=<>==，且(0,)2πα∈，得3πα=∴锐二面角1A A C B--的大小为3π.考点：1.用空间向量求平面间的夹角；2.空间中直线与直线之间的位置关系．6．（1）证明见解析；（2）045【解析】试题分析：（1）利用已知的线面垂直关系建立空间直角坐标系，准确写出相关点的坐标，从而将几何证明转化为向量运算.其中灵活建系是解题的关键.（2）证明证线线垂直，只需要证明直线的方向向量垂直；（3）把向量夹角的余弦值转化为两平面法向量夹角的余弦值;（4）空间向量将空间位置关系转化为向量运算，应用的核心是要充分认识形体特征，建立恰当的坐标系，实施几何问题代数化.同时注意两点：一是正确写出点、向量的坐标，准确运算；二是空间位置关系中判定定理与性质定理条件要完备. 试题解析：（1）证明：F ,G 分别为PB ，BE 的中点，FG∴PE .又FG ⊄平面PED ，PE ⊂平面PED ，FG∴平面PED .（2）解:EA ⊥平面ABCD ，EA PD ，PD ∴⊥平面.ABCD,AD CD ⊂平面,ABCD PD AD ∴⊥，PD CD ⊥.四边形ABCD 是正方形，AD CD ∴⊥.以D 为原点,分别以直线,,DA DC DP 为x 轴, y 轴,z 轴 建立如图所示的空间直角坐标系，设 1.EA = 2AD PD EA ==,D ∴()0,0,0，P ()0,0,2，A ()2,0,0，C ()0,2,0，B ()2,2,0，(2,0,1)E , (2,2,2)PB =-,(0,2,2)PC =-.F ，G ，H 分别为PB ，EB ，PC 的中点，F ∴()1,1,1，G 1(2,1,)2，H (0,1,1),1(1,0,)2GF =-,1(2,0,).2GH =-（解法一）设1111(,,)x y z =n 为平面FGH 的一个法向量，则110GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩，令11y =，得1(0,1,0)=n . 设2222(,,)x y z =n 为平面PBC 的一个法向量,则2200PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n ,即222222220220x y z y z +-=⎧⎨-=⎩，令21z =，得2(0,1,1)=n .所以12cos ,n n =1212⋅⋅n n n n=2. 所以平面FGH 与平面PBC 所成锐二面角的大小为π4（或45︒） （解法二）(0,1,1)(2,0,0)0DH BC ⋅=⋅-=，(0,1,1)(0,2,2)0DH PC ⋅=⋅-=,DH ∴是平面PBC 一个法向量.(0,2,0)(1,0,0)0DC FH ⋅=⋅-=，1(0,2,0)(1,0,)02DC FG ⋅=⋅-=,DC ∴是平面平面FGH 一个法向量.cos ,,22DH DC DH DC DH DC⋅===⋅ ∴平面FGH 与平面PBC 所成锐二面角的大小为π4（或45︒）. （解法三）延长AE 到,Q 使得,AE EQ =连,.PQ BQQP HGFE D CBA2PD EA AQ ==，EA PD ，∴四边形ADPQ 是平行四边形，.PQAD 四边形ABCD 是正方形，,.BCAD PQBC ∴F ，H 分别为PB ，PC 的中点，,.FH BC FH PQ ∴FH ⊄平面PED ，PQ ⊂平面PED ， FH ∴平面PED .,,FHFG F FH FG =⊂平面,ADPQ ∴平面FGH平面.ADPQ故平面FGH 与平面PBC 所成锐二面角与二面角D PQ C --相等.,PQ CD PQ PD ⊥⊥,,,PD CD D PD DC =⊂平面,PDC PQ ∴⊥平面.PDCPC ⊂平面,,PDC PQ PC ∴⊥DPC ∠是二面角D PQ C --的平面角.,,45.AD PD AD PD DPC =⊥∴∠=︒∴平面FGH 与平面PBC 所成锐二面角的大小为π4（或45︒）. 考点：1、直线与平面平行的判定；2、平面与平面所成的角.。