(完整word版)高中数学必修一试卷

合集下载

高中数学(必修1) 各章节测试题全套含答案

目录：数学1（必修）数学1（必修）第一章：（上）集合[训练A 、B 、C] 数学1（必修）第一章：（中）函数及其表[训练A 、B 、C] 数学1（必修）第一章：（下）函数的基本性质[训练A 、B 、C] 数学1（必修）第二章：基本初等函数（I ）[基础训练A 组] [1A C 2．下列四个集合中，是空集的是（）A ．}33|{=+x xB ．},,|),{(22R y x x y y x ∈-=C ．}0|{2≤x xD ．},01|{2R x x x x ∈=+- 3．下列表示图形中的阴影部分的是（）A ．()()A CB CB ．()()A B AC C ．()()A B B CD ．()A B C 4．下面有四个命题：A B C（1）集合N 中最小的数是1；（2）若a -不属于N ，则a 属于N ；（3）若,,N b N a ∈∈则b a +的最小值为2；（4）x x 212=+的解可表示为{}1,1；其中正确命题的个数为（）A ．0个B ．1个C ．2个D ．3个5．若集合{},,M a b c =中的元素是△ABC 的三边长，则△ABC 一定不是（）A C 6A 1（（（ 2.B ，则C 3B =_____________4,且A B ⊇5B =_________1．已知集合⎭⎬⎫⎩⎨⎧∈-∈=N x N x A 68|，试用列举法表示集合A 。

2．已知{25}A x x =-≤≤，{121}B x m x m =+≤≤-，B A ⊆,求m 的取值范围。

3．已知集合{}{}22,1,3,3,21,1A a a B a a a =+-=--+，若{}3A B =-，求实数a 的值。

4．设全集U R =，{}2|10M m mx x =--=方程有实数根，{}()2|0,.U N n x x n C M N =-+=方程有实数根求（数学1必修）第一章（上）集合[综合训练B 组]一、选择题1．下列命题正确的有（）（1）很小的实数可以构成集合；（222（3（423N M =BN N =C N M =D N =∅4⎩⎨⎧=-=+122y x y x 的解集是（）56A ．若A B A B A =⊆ 则, B ．若B A B B A ⊆=，则 C ．)(B A A )(B AD ．()()()B C A C B A C U U U =二、填空题1．用适当的符号填空（1）{}()(){}1|,____2,1,2|______3+=≤x y y x x x （2）{}32|_______52+≤+x x ，（3）{}31|,_______|0x x x R x x x x ⎧⎫=∈-=⎨⎬⎩⎭2．设{}{}34|,|,<>=≤≤==x x x A C b x a x A R U U 或 34B B =，则5}0=至多有一个元素，则的取值范围。

(word版)高一数学必修一期末试卷及答案,文档

高一数学必修1试题一、选择题。

〔共10小题，每题4分〕1、设集合A={x Q|x>-1} ，那么〔〕A 、AB 、2 AC 、2AD 、2A2、设A={a ，b}，集合B={a+1，5}，假设A∩B={2}，那么A∪B=〔〕A 、{1，2}B 、{1，5}C 、{2，5}D、{1，2，5}3、函数f(x)x1〕的定义域为〔x 2A 、[1，2)∪(2，+∞〕B 、(1，+∞〕C 、[1，2)D 、[1，+∞)4、设集合M={x|-2 ≤x≤2}，N={y|0≤y≤2}，给出以下四个图形，其中能表示以集合 M 为定义域， N 为值域的函数关系的是〔〕5、三个数70。

3，0。

37，，㏑，的大小顺序是〔〕 0。

3 ， 7，，㏑ 0.3, 0。

3 ，，㏑0.3, 7 A 、7 B 、7C 、7,,70。

3，，㏑ 0.3,D 、㏑0.3,70。

3，7， 6、假设函数f(x)=x 3+x 2-2x-2 的一个正数零点附近的函数值用二分法逐次计算，参考数据如下表：f(1)=-2那么方程x 3+x 2-2x-2=0的一个近似根〔精确到〕为〔〕A 、B 、 C、D、7、函数y2x,x 0〕2x ,x的图像为〔高一数学试卷第1页〔共6页〕8、设f(x)log a x〔a>0，a≠1〕，对于任意的正实数x，y，都有〔〕A、f(xy)=f(x)f(y)B、f(xy)=f(x)+f(y)C、f(x+y)=f(x)f(y)D、f(x+y)=f(x)+f(y)9、函数y=ax2+bx+3在〔-∞，-1]上是增函数，在[-1，+∞)上是减函数，那么〔〕A、b>0且a<0B、b=2a<0C、b=2a>0D、a，b的符号不定10、某企业近几年的年产值如图，那么年增长率最高的是〔万元〕〔〕〔年增长率=年增长值/年产值〕1000800A、97年B、98年600C、99年D、00年400200二、填空题〔共4题，每题4分〕9697989900(年〕11、f(x)的图像如以下列图，那么f(x)的值域为；12、计算机本钱不断降低，假设每隔3年计算机价格降低1/3，现在价格为8100元的计算机，那么9年后价格可降为；13、假设f(x)为偶函数，当x>0时，f(x)=x,那么当x<0时，f(x)=；14、老师给出一个函数，请三位同学各说出了这个函数的一条性质：①此函数为偶函数；②定义域为{xR|x0}；③在(0,)上为增函数.老师评价说其中有一个同学的结论错误，另两位同学的结论正确。

(word完整版)高一数学必修1综合测试题3套[含解析],文档

范文模范参照高一数学综合检测题〔1〕一、选择题：5 分，共60 分，请将所选答案填在括号内〕〔每题1．会集 M{4,7,8},且 M中至多有一个偶数, 那么这样的会集共有()(A)3个(B) 4个(C) 5个(D) 6个2． S={x|x=2n,n∈ Z}, T={x|x=4k± 1,k ∈ Z}, 那么〔〕(A)S T(B) T S(C)S≠T(D)S=T3．会集 P= y | y x22,x R， Q=y| y x 2,x R ，那么PI Q 等〔〕(A) 〔 0， 2〕，〔 1， 1〕(B){〔 0，2〕，〔 1， 1〕 } (C){1， 2}(D)y | y24．不等式ax2ax40 的解集为，那么a 的取值范围是〔〕R(A)16 a 0(B)a16(C)16 a0(D) a 05. f ( x) =x5( x6)，那么 f(3)的值为〔〕f (x4)( x6)(A)2(B)5(C)4( D)36. 函数y x24x3, x[0,3]的值域为〔〕(A)[0,3](B)[-1,0](C)[-1,3](D)[0,2]7．函数 y=(2k+1)x+b 在 (- ∞,+ ∞ ) 上是减函数，那么〔〕(A)k> 1(B)k<1(C)k>1(D).k<1 22228. 假设函数f(x)=x2+2(a-1)x+2在区间 ( ,4]内递减，那么实数 a 的取值范围为〔〕(A)a≤ -3(B)a≥ -3(C)a≤ 5(D)a≥39．函数y(2 a23a 2) a x是指数函数，那么 a 的取值范围是(A) a 0, a1(B) a 1(C)a a 1或 a1212〔〕( D)10．函数 f(x)4 a x 1的图象恒过定点p，那么点 p 的坐标是〔〕〔A〕〔 1 ，5 〕〔B〕〔 1, 4 〕〔C〕〔 0 ，4〕〔 D〕〔 4 ，0〕11.函数 y log 1 (3 x2)的定义域是〔〕2〔A〕 [1,+](B) (32 ,)(C) [32 ,1](D)(32 ,1]12.设a,b,c都是正数，且3a4b6c，那么下列正确的是〔〕(A)111(B)221(C)122(D)212 c a b C a b C a b c a b二、填空题：〔每题 4 分，共 16 分，答案填在横线上〕13．〔 x,y 〕在照射f下的象是(x-y,x+y)，那么(3,5)在f下的象是，原象是。

(word完整版)高中数学必修一试题和答案解析

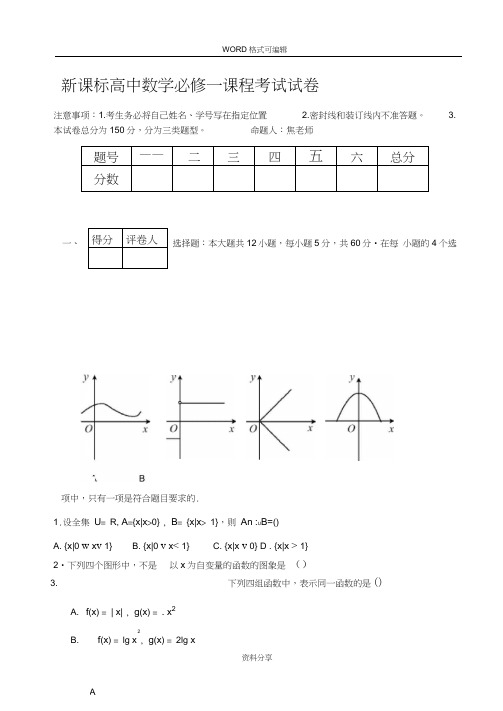
新课标高中数学必修一课程考试试卷一、选择题：本大题共12小题，每小题5分，共60分•在每小题的4个选项中，只有一项是符合题目要求的.1.设全集 U = R, A ={x |x >0} , B = {x |x > 1}，则 An :U B=() A. {x |0 w x v 1}B. {x |0 v x < 1}C. {x |x v 0} D . {x |x > 1}2•下列四个图形中，不是以x 为自变量的函数的图象是（）3.下列四组函数中，表示同一函数的是 ()A. f (x ) = | x | , g (x ) = . x 22B. f (x ) = lg x , g (x ) = 2lg x得分评卷人题号——一二三四五六总分分数注意事项：1.考生务必将自己姓名、学号写在指定位置 2.密封线和装订线内不准答题。

3.本试卷总分为150分，分为三类题型。

命题人：焦老师A. —定经过点（0 , 0）专业技术B. —定经过点(1 , 1)C. f(x) = , g(x) = x+1x-1D. f(x) = x+1 • .. x-1 , g(x) = x2-14. 幕函数y = x"（a是常数）的图象（）.In 2、 ln 3 In 512.若a2 ,3,C5 ,则()c.—定经过点（一1, 1）D. 一定经过点（1 , - 1）5.已知函数 f (x ) = lOg2X ，x >0 ，则 f ( —10)的值是(). f( x +3) , x w 0A. — 2 B .— 1C. 0D. 16.函数f （x ）具"3）2满足f[ f（x ）] x，则常数c 等于（A. 3 B .3 C . 3或 3 D . 5或3已知函数ly f （x°定义域是2，3]则|y f （2x°的定义域是（2 210 .方X9的解集是（A.5,4B .5,4C5,4 D . 5, 411.设函数51 f ( )lg x x1，则f （10）的值为A. 1 B .1 C .10D1107 .a的范围是（2 .(8分)求函数y2x 2A . a b cB . c b aC . cabD . ba c 二、填空题:本大题共4小题，每小题5分，共20分•将答案填在题中横线上.2 21.已知函数f (x ) (m 1)x (m 2)x (m 7m 12)为偶函数，则m的值是 ________三、解答题：本大题共6小题，共60分•解答应写出文字说明、证明过程或演算步骤.1. (10 分)已知函数 f (x ) = lg(3 + x ) + lg(3 — x ).(1) 求函数f (x )的定义域；(2) 判断函数f (x )的奇偶性，并说明理由.2.求满足1X 2 —8> 4— 2x的x 的取值集合是f(x)3 .若函数 3x 2 4(x 0)(x 0)0(x 0)，则 f(f(0))= __________4 .若函数f(2x 1)2x 2x ，贝y f (3) = _________3. (10 分)设a 为实数，函数f(x) x2 |x a| 1, x R (1)讨论f (x)的奇偶性；(2)求f (x)的最小值。

(完整word版)高一数学必修一试卷及答案

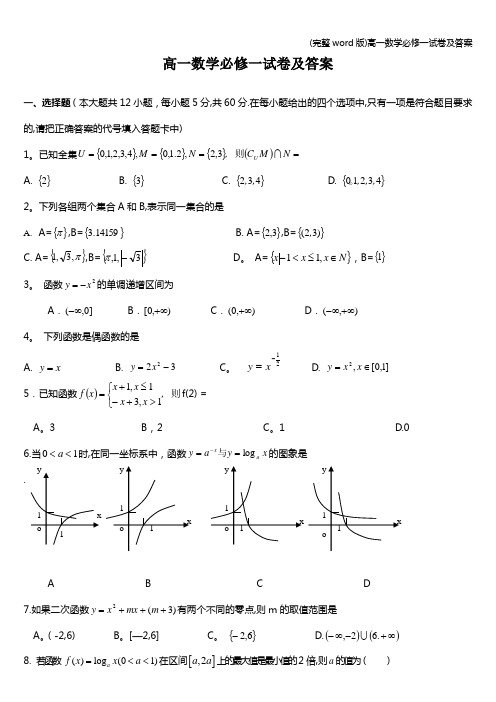
高一数学必修一试卷及答案一、选择题（本大题共12小题，每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填入答题卡中)1。

已知全集{}{}{}()====N M C ，N M U U 则3,2,2.1,0,4,3,2,1,0 A. {}2 B. {}3 C. {}432，， D. {}43210，，，。

2。

下列各组两个集合A 和B,表示同一集合的是A. A={}π,B={}14159.3 B. A={}3,2,B={})32(， C. A={}π,3,1,B={}3,1,-π D 。

A={}N x x x ∈≤<-,11，B={}1 3。

函数2x y -=的单调递增区间为A ．]0,(-∞B ．),0[+∞C ．),0(+∞D ．),(+∞-∞ 4。

下列函数是偶函数的是A. x y =B. 322-=x y C 。

21-=xy D. ]1,0[,2∈=x x y5．已知函数()则，x x x x x f ⎩⎨⎧>+-≤+=1,31,1f(2) =A 。

3B ，2C 。

1 D.0 6.当10<<a 时,在同一坐标系中，函数x y a y a x log ==-与的图象是 .A B C D 7.如果二次函数)3(2+++=m mx x y 有两个不同的零点,则m 的取值范围是A 。

（-2,6)B 。

[—2,6]C 。

{}6,2- D.()()∞+-∞-.62, 8. 若函数 ()log (01)a f x x a =<<在区间[],2a a 上的最大值是最小值的2倍,则a 的值为（）ABC 、14D 、129.三个数3.0222,3.0log ,3.0===c b a 之间的大小关系是A b c a <<. B. c b a << C. c a b << D.a c b << 10。

(word完整版)高一数学必修1综合试卷(带答案)(2)

1. 2. 3. 4. 高—数学试卷时量：100分钟总分：120分、选择题(本大题共12小题，每小题项是符合题目要求的) 下列各项中，不可以组成集合的是( A .所有的正数 B .等于下列四个集合中，空集的是( A . {x | x 3 3} B . 2C . {x | x 0}D . 下列表示图形中的阴影部分的是( A . (AUC)I (B UC) C . (AU B)I (BUC) 若集合M4分，共48分。

在每小题给出的四个选项中，只有一 2的数 ) {(x,y) | {x|x 2 x ) B . (AU B)I D . (AU B) I 接近于0的数 D .不等于0的偶数 2x ,x, y R}0,x R} (AUC) C a,b,c 中的元素是△ ABC 的三边长，则△ ABC 一定不是( D .等腰三角形) A .锐角三角形 B .直角三角形 C .钝角三角形 5. 函数y f(x)的图象与直线x 1的公共点数目是( A . 1 B .6. 已知集合A 使B 中元素 0 C . 0 或 1 D . 1 或 2 1,2,3, k , B 4,7,a 4,a 2 3a ，且y 3x 1和A 中的元素x 对应，则a, k 的值分别为( N ,x Ay B 行车，最后两人同时到达 B 地，又知甲骑自行车比乙骑自行车的速度快，并且二人骑车速度均比跑步速度快.若某人离开 A 地的距离S 与所用时间t 的函数关系可用图象表示，则下列给出的四个函数图象中，甲、乙各人的图象只可能是 ()④①乙是图②乙是图②甲是图①，乙是图④ 甲是图③，乙是图④A.甲是图①, C.甲是图③, 二、填空题 13.若全集UB. D.每小题4分，共24分。

将正确答案填在题中横线上 )，则集合A 的子集共有 ________________ 个.x|2 x 10，则 AU B ________________ .6小题，且 C u A 2 x|3 x2y x(本大题共 0,123 14 •若集合A 15.已知A 16.函数f x17. 已知 f (X ) 18. 已知函数flog 2 x ， )ax 22x 1 ,By y 2x 1，则 A B=x 那么 / 3(a-的定义域是3f(f (4))—1在(.(要求写区间)A . 2,3B . 3,4C . 3,5D . 2,5x 2(x 1)三、解答题 (本大题共4小题，共48分。

(完整版)高一数学必修一试卷及答案

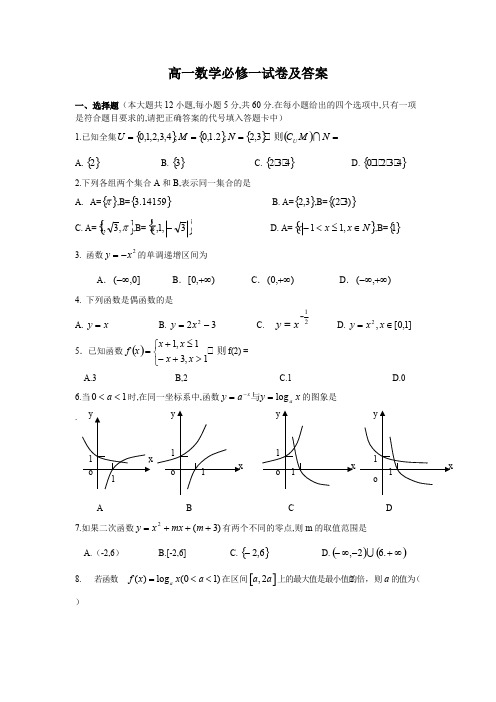
高一数学必修一试卷及答案一、选择题（本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填入答题卡中）1.已知全集{}{}{}()====N M C 。

N M U U 则3,2,2.1,0,4,3,2,1,0A. B. C. D. {}2{}3{}432。

{}43210。

2.下列各组两个集合A 和B,表示同一集合的是A.A=,B=B. A=,B={}π{}14159.3{}3,2{})32(。

C. A=,B=D. A=,B={}π,3,1{}3,1,-π{}N x x x ∈≤<-,11{}13. 函数的单调递增区间为2x y -=A ． B ． C ．D ．]0,(-∞),0[+∞),0(+∞),(+∞-∞4. 下列函数是偶函数的是A. B.C.D. x y =322-=x y 21-=xy ]1,0[,2∈=x x y 5．已知函数f(2) =()则。

x x x x x f ⎩⎨⎧>+-≤+=1,31,1A.3B,2C.1D.06.当时,在同一坐标系中,函数的图象是10<<a x y a y a xlog ==-与 A BCD7.如果二次函数有两个不同的零点,则m 的取值范围是)3(2+++=m mx x y A.（-2,6）B.[-2,6]C. D.{}6,2-()()∞+-∞-.62, 8. 若函数在区间上的最大值是最小值的2倍，则的值为（()log (01)a f x x a =<<[],2a a a ）A B C 、D 、14129.三个数之间的大小关系是3.0222,3.0log ,3.0===c b a A . B. C. D.b c a <<c b a <<c a b <<a c b <<10. 已知奇函数在时的图象如图所示，则不等式的解集为()f x 0x ≥()0xf x <Ａ．Ｂ．(1,2)(2,1)--Ｃ．Ｄ．(2,1)(1,2)-- (1,1)-11.设,用二分法求方程内近似解的过程中得()833-+=x x f x()2,10833∈=-+x x x在则方程的根落在区间()()(),025.1,05.1,01<><f f f A.（1,1.25）B.（1.25,1.5）C.（1.5,2）D.不能确定12.计算机成本不断降低,若每隔三年计算机价格降低,则现在价格为8100元的计算机9年31后价格可降为A.2400元B.900元C.300元D.3600元二、填空题（每小题4分,共16分.）13.若幂函数y =的图象经过点（9,）, 则f(25)的值是_________-()x f 1314. 函数的定义域是()()1log 143++--=x x xx f 15. 给出下列结论（1）2)2(44±=-（2）331log 12log 22-=21 (3) 函数y=2x-1， x [1，4]的反函数的定义域为[1，7 ]∈（4）函数y=的值域为(0,+)x12∞其中正确的命题序号为16. 定义运算则函数的最大值为．()() ,.a ab a b b a b ≤⎧⎪*=⎨>⎪⎩()12x f x =*三、解答题（本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤）17. （12分）已知集合，，全集，求：{|240}A x x =-<{|05}B x x =<<U R =（Ⅰ）；（Ⅱ）.A B ()U C A B 18. 计算:（每小题6分,共12分）（1） 36231232⨯⨯19．（12分）已知函数，(Ⅰ) 证明在上是增函数；1()f x x x=+()f x [1,)+∞(Ⅱ) 求在上的最大值及最小值．()f x [1,4]20. 已知A 、B 两地相距150千米,某人开车以60千米／小时的速度从A 地到B 地,在B 地停留一小时后,再以50千米／小时的速度返回A 地.把汽车与A 地的距离y （千米）表示为时间t （小时）的函数（从A 地出发时开始）,并画出函数图象. （14分）.18lg 7lg 37lg 214lg )2(-+-21.（本小题满分12分）二次函数f （x ）满足且f （0）=1.(1) 求f （x ）的解析式;(2) 在区间上,y=f(x)的图象恒在y =2x +m 的图象上方,试确定实数m 的范围.22.已知函数对一切实数都有成立，且()f x ,x y R ∈()()f x y f y +-=(21)x x y ++. （Ⅰ）求的值；（Ⅱ）求的解析式；(1)0f =(0)f ()f x （Ⅲ）已知，设：当时，不等式恒成立；a R ∈P 102x <<()32f x x a +<+Q ：当时，是单调函数。

高中数学必修1全册章节测试题集含答案

人教A版高中数学必修1全册章节测试题目录必修一第1章第1节集合试题必修一第1章第2节函数及其表示试题必修一第1章第3节函数的基本性质试题必修一第2章基本初等函数综合试题必修一第2章第1节指数函数试题必修一第2章第2节对数函数试题必修一第2章第3节幂函数试题必修一第3章第1节方程的根与函数的零点试题必修一第3章第2节函数的应用试题必修一综合试题1必修一综合试题2集合试题一、选择题（每小题5分，计5×12=60分）1．下列集合中，结果是空集的为（ D ）（A）（B）（C）（D）2．设集合，，则（A ）（A）（B）（C）（D）3．下列表示①②③④中,正确的个数为(A )（A）1 （B）2 （C）3 （D）44．满足的集合的个数为（ A ）（A）6 （B） 7 （C） 8 （D）95．若集合、、，满足，，则与之间的关系（ C ）（A）（B）（C）（D）6．下列集合中，表示方程组的解集的是（ C）（A）（B）（C）（D）7．设，，若，则实数的取值范围是（ A ）（A）（B）（C）（D）8．已知全集合，，，那么是（ D ）（A）（B）（C）（D）9．已知集合，则等于（ D ）（A）（B）（C）（D）10．已知集合，，那么（ C ）（A）（B）（C）（D）11．如图所示，，，是的三个子集，则阴影部分所表示的集合是（ C ）（A）（B）（C）（D）12．设全集，若，，，则下列结论正确的是（ B ）（A）且（B）且（C）且（D）且二、填空题（每小题4分，计4×4=16分）13．已知集合，，则集合_.14．用描述法表示平面内不在第一与第三象限的点的集合为_.15．设全集，，，则的值为2或8.16．若集合只有一个元素，则实数的值为三、解答题（共计74分）17．（本小题满分12分）若，求实数的值。

解：或或当时，，，，适合条件；当时，，，，适合条件从而，或18．（本小题满分12分）设全集合，，，求，，，解：，19．（本小题满分12分）设全集，集合与集合，且，求，解：，且，，，，20（本小题满分12分）已知集合，，且，求实数的取值范围。

数学必修1测试题及答案

数学必修1测试题及答案一、选择题（每题3分，共30分）1. 下列哪个选项是实数集的子集？A. 整数集B. 有理数集C. 无理数集D. 复数集答案：B2. 函数f(x) = 2x + 3的值域是？A. (-∞, +∞)B. [3, +∞)C. (-∞, 3]D. [0, +∞)答案：A3. 已知集合A = {1, 2, 3}，集合B = {2, 3, 4}，则A∩B等于？A. {1}B. {2, 3}C. {4}D. {1, 2, 3}答案：B4. 计算(2x - 3)(x + 1)的结果，其中x = 2。

A. 5B. 7C. 9D. 11答案：B5. 已知a = 3，b = 4，c = 5，下列哪个等式是正确的？A. a² + b² = c²B. a² + b² > c²C. a² + b² < c²D. a² + b² = 2bc答案：C6. 函数y = sin(x)在区间[0, π]上是：A. 增函数B. 减函数C. 先增后减D. 先减后增答案：D7. 计算极限lim(x→0) (sinx/x)的值。

A. 0B. 1C. πD. ∞答案：B8. 已知等差数列{an}的首项a1 = 1，公差d = 2，则第5项a5的值是？A. 9B. 11C. 13D. 15答案：A9. 计算定积分∫(0 to 1) x² dx的值。

A. 1/3B. 1/2C. 1D. 2答案：B10. 已知函数f(x) = x³ - 3x + 2，求其导数f'(x)。

A. 3x² - 3B. x² - 3C. 3x - 3D. x³ - 3答案：A二、填空题（每题4分，共20分）1. 计算(3x + 2)(2x - 1) = ________。

答案：6x² - x - 22. 已知函数f(x) = x² - 4x + 4，求其对称轴方程。

(完整)高一数学必修1第一章测试题及答案,推荐文档

高一第一章测试题一．选择题(本大题共 12 小题，第小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项符是合题目要求的．)1. 设集合 AQ x，则（）A. ∅ ∉AB.∉ AC. ∈ AD ．{ 2}⊆ A2、已知集合 A 到 B 的映射 f:x→y=2x+1，那么集合 A 中元素 2 在 B 中对应的元素是：A 、2B 、5C 、6D 、83. 设集合A = {x |1 < x < 2},B = {x | x < a }. 若 A ⊆ B , 则 a 的范围是()A ． a ≥ 24. 函数 y B. a ≤ 1 的定义域是（）C. a ≥ 1D. a ≤ 21 1 11A . ( , +∞)B . [ , +∞)C . (-∞, )D . (-∞, ]2 22 25．全集 U ＝｛0,1,3,5,6,8｝,集合 A ＝{ 1，5, 8 }, B ={2},则集合（C U A ) B = （）A ．{0,2,3,6}B ．{ 0,3,6}C ． {2,1,5,8}D ． ∅ 6．已知集合 A = {x -1 ≤ x < 3}, B = {x 2 < x ≤ 5}, 则A B = （）A. ( 2, 3 )B. [-1,5]C. (-1,5)D. (-1,5]7. 下列函数是奇函数的是（）A ． y = x8. 化简：B ． y = 2x 2 - 3(-4)2＋＝（）1C ． y = x2D ． y = x 2 , x ∈[0,1]A ． 4B ． 2－ 4C ． 2－ 4 或 4D ． 4 － 29. 设集合 M2 x 2，Ny，给出下列四个图形，其中能表示以集合M 为定义域， N 为值域的函数关系的是（） 10、已知 f （x ）=g （ x ）+2，且 g(x)为奇函数，若 f （2）=3，则 f （-2）= 。

2 2 2x -1x ⎩}A 0B ．-3C ．1D ．3⎧ 2 ⎪ 11、已知 f （x ）=⎨ ⎪⎩x > 0x = 0 ，则 f [ f (-3)]等于x < 0 A 、0 B 、π C 、π2D 、912．已知函数 f是 R 上的增函数， A,1， B ,1是其图像上的两点，那么f二．填空题（本大题共 4 小题，每小题 5 分，共 20 分．把答案填在题中横线上．）⎧ x + 5(x > 1) 13.已知 f (x ) = ⎨2x 2 +1(x ≤ 1) ，则 f [ f (1)] =.14.已知 f (x -1) = x 2 ，则 f (x ) =.15. 定义在 R 上的奇函数 f (x ) ,当 x > 0 时, f (x ) = 2 ；则奇函数 f (x ) 的值域是．16. 关于下列命题:①若函数 y = 2 x 的定义域是｛ x | x ≤ 0}，则它的值域是{y | y ≤ 1}；② 若函数 y =1 的定义域是{x | x > 2}，则它的值域是{y | y ≤1； x2③若函数 y = x 2 的值域是{y | 0 ≤ y ≤ 4}，则它的定义域一定是{x | -2 ≤ x ≤ 2}；④若函数 y = 2 x 的定义域是{y | y ≤ 4}，则它的值域是{x | 0 < x ≤ 8}. 其中不正确的命题的序号是( 注:把你认为不正确的命题的序号都填上).0 (x ) < 1的解集是（）A ． (-3, 0)B ． (0, 3)C ． (-∞, -1]⋃[3, +∞)D ． (-∞, 0]⋃ [1, +∞)（第 II 卷）三、解答题：本大题共 5 小题，共 70 分．题解答应写出文字说明，证明过程或演算步骤．17.设 A ={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0}，其中x∈R，如果A∩B=B，求实数 a 的取值范围。

高中数学必修一试卷

高中数学必修一试卷一、选择题（每题5分，共60分）1. 设集合A = {xx^2-3x + 2 = 0}，B={xx^2-ax + a - 1 = 0}，若A∪ B = A，则实数a的值为（）A. 2B. 3C. 2或3D. 1或2或32. 函数y=√(x^2)-1的定义域为（）A. (-∞,-1]∪[1,+∞)B. [-1,1]C. (-∞,-1)∪(1,+∞)D. (-1,1)3. 已知函数f(x)=log_a(x + 1)（a>0且a≠1）在区间[1,7]上的最大值比最小值大(1)/(2)，则a的值为（）A. (1)/(2)或(7)/(2)B. (2)/(3)或(3)/(2)C. (1)/(2)或(3)/(2)D. (2)/(3)或(7)/(2)4. 若函数y = f(x)是函数y = a^x(a>0且a≠1)的反函数，且f(2)=1，则f(x)=（）A. log_2xB. (1)/(2^x)C. log_(1)/(2)xD. 2^x - 25. 函数y = x^2+2x - 3在区间[-3,0]上的值域为（）A. [-4, - 3]B. [-4,0]C. [-3,0]D. [0,1]6. 下列函数中，在(0,+∞)上为增函数的是（）A. y=<=ft((1)/(2))^xB. y = x^-2C. y=log_(1)/(2)xD. y=ln x7. 设a = log_32，b=log_52，c=log_23，则（）A. a>c>bB. b>c>aC. c>b>aD. c>a>b8. 已知函数f(x)是定义在R上的奇函数，当x>0时，f(x)=x^2-2x，则f(x)在R上的表达式为（）A. f(x)=x(x - 2)B. f(x)=<=ft{begin{array}{ll}x(x - 2),x>0 0,x = 0 -x(x + 2),x<0end{array}right.C. f(x)=<=ft{begin{array}{ll}x(x - 2),x≥slant0 -x(x + 2),x<0end{array}right.D. f(x)=x(x2)9. 若函数f(x)=a^x-x - a(a>0且a≠1)有两个零点，则实数a的取值范围是（）A. (0,1)B. (1,+∞)C. (0,+∞)D. (0,1)∪(1,+∞)10. 已知y = f(x)是偶函数，当x>0时，f(x)=x+(4)/(x)，且当x∈[-3,-1]时，n≤slant f(x)≤slant m恒成立，则m - n的最小值是（）A. (1)/(3)B. (2)/(3)C. 1D. (4)/(3)11. 函数y = f(x)的图象与函数y = log_3x(x>0)的图象关于直线y = x对称，则f(x)=（）A. 3^x(x∈ R)B. 3^x(x>0)C. <=ft((1)/(3))^x(x∈ R)D. <=ft((1)/(3))^x(x>0)12. 设函数f(x)=<=ft{begin{array}{ll}2^x,x≤slant0 log_2x,x>0end{array}right.，若f(a)=(1)/(2)，则a=（）A. -1或√(2)B. -1或(1)/(2)C. -1D. (1)/(2)二、填空题（每题5分，共20分）13. 计算：log_2√(2)+log_927=_ 。

(完整word版)高一数学必修1试题附答案详解

高一数学必修1试题1。

已知全集I ＝{0，1,2｝，且满足C I （A ∪B )＝{2}的A 、B 共有组数2。

如果集合A ＝｛x |x ＝2k π+π，k ∈Z}，B ＝{x |x ＝4k π+π，k ∈Z ｝，则集合A,B 的关系3.设A ＝｛x ∈Z ｜｜x |≤2},B ＝｛y ｜y ＝x 2＋1，x ∈A ｝,则B 的元素个数是4.若集合P ＝{x ｜3〈x ≤22},非空集合Q ＝{x |2a +1≤x 〈3a －5}，则能使Q ⊆ (P ∩Q ）成立的所有实数a 的取值范围为5。

已知集合A ＝B ＝R ,x ∈A ，y ∈B ，f ：x →y ＝ax ＋b ，若4和10的原象分别对应是6和9, 则19在f 作用下的象为6。

函数f （x ）＝错误! (x ∈R 且x ≠2)的值域为集合N ,则集合{2，－2，－1,－3}中不属于N 的元素是7.已知f (x )是一次函数，且2f (2)－3f （1)＝5，2f (0)－f (－1)＝1，则f (x )的解析式为8。

下列各组函数中，表示同一函数的是 A.f (x )＝1，g （x ）＝x 0B.f （x ）＝x ＋2，g (x ）＝错误!C.f (x )＝｜x |，g (x )＝错误! D 。

f （x )＝x ，g （x ）＝（错误!)29。

f （x )＝⎩⎪⎨⎪⎧x 2 x ＞0π x ＝00 x ＜0，则f {f ［f （－3)］｝等于10。

已知2lg （x －2y ）＝lg x ＋lg y ，则错误!的11。

设x ∈R ,若a 〈lg （|x －3｜＋|x ＋7|)恒成立，则a 取值范围是12.若定义在区间(－1，0）内的函数f(x)＝log2a(x＋1）满足f(x)>0，则a的取值范围是高一数学必修1试题一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知全集I＝｛0，1,2｝，且满足C I （A∪B）＝｛2｝的A、B共有组数A。

(完整word版)人教版数学必修一期末考试试题(含答案),推荐文档

期中考试考前检测试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟．第Ⅰ卷(选择题)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．如果A ＝{x |x ＞－1}，那么A ．0⊆AB ．{0}∈AC ．∅∈AD ．{0}⊆A 2．函数f (x )＝3x 21－x＋lg(3x ＋1)的定义域是A.⎝⎛⎭⎫－13，＋∞ B.⎝⎛⎭⎫－13，1 C.⎝⎛⎭⎫－13，13 D ．⎝⎛⎭⎫－∞，－13 3．下列各组函数中，表示同一函数的是 A ．y ＝x 2和y ＝(x )2B ．y ＝lg(x 2－1)和y ＝lg(x ＋1)＋lg(x －1)C ．y ＝log a x 2和y ＝2log a xD ．y ＝x 和y ＝log a a x4．a ＝log 0.7 0.8，b ＝log 1.1 0.9，c ＝1.10.9的大小关系是 A ．c >a >b B ．a >b >c C ．b >c >aD ．c >b >a5．若函数f (x )＝⎩⎪⎨⎪⎧⎝⎛⎭⎫14x ，x ∈[－1，0)，4x ，x ∈[0，1]，则f (log 43)＝A. 13 B . 14 C ． 3 D ．4 6．已知函数f (x )＝7＋a x－1的图象恒过点P ，则P 点的坐标是A ．(1,8)B ．(1,7)C ．(0,8)D ．(8,0)7．若x＝1是函数f(x)＝ax＋b(a≠0)的一个零点，则函数h(x)＝ax2＋bx的零点是A．0或－1 B．0或－2 C．0或1 D．0或2 8．利用计算器，列出自变量和函数值的对应值如下表：A．(0.6,1.0) B．(1.4,1.8) C．(1.8,2.2) D．(2.6,3.0)9．设α∈{－1,1，12，3}，则使函数y＝xα的定义域为R且为奇函数的所有α的值为A．1,3 B．－1,1C．－1,3 D．－1,1,310．函数y＝f(x)是R上的偶函数，且在(－∞，0]上是增函数，若f(a)≤f(2)，则实数a的取值范围是A．(－∞，2] B．[－2，＋∞)C．[－2,2]D．(－∞，－2]∪[2，＋∞) 11．已知a>0，b>0且ab＝1，则函数f(x)＝a x与g(x)＝－log b x的图象可能是12．函数y＝4x＋12x的图象()A．关于原点对称B．关于y＝x对称C ．关于x 轴对称D ．关于y 轴对称第Ⅱ卷(非选择题)二、填空题(本大题共4小题，每小题5分，共20分．)13．已知集合M ＝{(x ，y )|y ＝－x ＋1}，N ＝{(x ，y )|y ＝x －1}，那么M ∩N 为__________． 14．设f (x )＝2x 2＋3，g (x ＋1)＝f (x )，则g (3)＝________. 15．若指数函数f (x )与幂函数g (x )的图象相交于一点(2,4)，则f (x )＝___________， g (x )＝__________.16．设P ，Q 是两个非空集合，定义集合间的一种运算“⊙”：P ⊙Q ＝{x |x ∈P ∪Q ，且x ∉P ∩Q }，如果P ＝{y |y ＝4－x 2}，Q ＝{y |y ＝4x ，x >0}，则P ⊙Q ＝________.三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分) 已知全集为实数集R ，集合A ＝{x |y ＝x －1＋3－x }， B ＝{x |log 2x ＞1}． (1)求A ∩B ，(∁R B )∪A ；(2)已知集合C ＝{x |1＜x ＜a }，若C ⊆A ，求实数a 的取值范围． 18．(本小题满分12分)计算： (1)lg 25＋23lg 8＋lg 5lg 20＋(lg 2)2；(2)⎝⎛⎭⎫278-23－⎝⎛⎭⎫4990.5＋(0.008)-23×225. 19．(本小题满分12分)已知函数f (x )是定义在R 上的奇函数，当x >0时，f (x )＝log 2x . (1)求f (x )的解析式；(2)解关于x的不等式f(x)≤1 2.20．(本小题满分12分)某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元．该厂为鼓励销售商订购，决定当一次订购量超过100件时，每多订购1件，订购的全部服装的出场单价就降低0.02元，根据市场调查，销售商一次订购量不会超过600件．(1)设销售商一次订购x件，服装的实际出厂单价为p元，写出函数p＝f(x)的表达式．(2)当销售商一次订购多少件服装时，该厂获得的利润最大？最大利润是多少？21.(本小题满分12分)设函数f(x)的定义域为(－3,3)，满足f(－x)＝－f(x)，且对任意x，y，都有f(x)－f(y)＝f(x－y)，当x<0时，f(x)>0，f(1)＝－2.(1)求f(2)的值；(2)判断f(x)的单调性，并证明；(3)若函数g(x)＝f(x－1)＋f(3－2x)，求不等式g(x)≤0的解集．22．(本小题满分12分)已知函数f(x)＝a－22x＋1(a∈R).(1) 判断函数f(x)的单调性并给出证明；(2) 若存在实数a使函数f(x)是奇函数，求a；(3)对于(2)中的a，若f(x)≥m2x，当x∈[2,3]时恒成立，求m的最大值．期中考试考前检测试题(答案)一、选择题1．解析：由集合与集合之间的关系可以判断只有D 正确．2．解析：要使函数有意义，须使⎩⎪⎨⎪⎧1－x ＞0，3x ＋1＞0，解得－13＜x ＜1.故选B.3．解析：要表示同一函数必须定义域、对应法则一致，A 、B 、C 中的定义域不同，选D. 4．解析：a ＝log 0.70.8∈(0,1)，b ＝log 1.10.9∈(－∞，0)，c ＝1.10.9∈(1，＋∞)，故c >a >b . 选A 5．解析： ∵log 43∈(0,1)，∴f (log 43)＝44log 3＝3，故选C.6．解析：过定点则与a 的取值没有关系，所以令x ＝1，此时f (1)＝8.所以P 点的坐标是(1,8)．选A.7．解析：因为1是函数f (x )＝ax ＋b (a ≠0)的零点，所以a ＋b ＝0，即a ＝－b ≠0.所以h (x )＝－bx (x －1)．令h (x )＝0，解得x ＝0或x ＝1.故选C.8．解析：构造f (x )＝2x －x 2，则f (1.8)＝0.242，f (2.2)＝－0.245，故在(1.8,2.2)内存在一点使f (x )＝2x －x 2＝0，所以方程2x ＝x 2的一个根就位于区间(1.8,2.2)上．选C9．解析：当α＝－1时，y ＝x －1＝1x ，定义域不是R ；当α＝1,3时，满足题意；当α＝12时，定义域为[0，＋∞)．选A10．解析：∵y ＝f (x )是偶函数，且在(－∞，0]上是增函数， ∴y ＝f (x )在[0，＋∞)上是减函数，由f (a )≤f (2)，得f (|a |)≤f (2)．∴|a |≥2，得a ≤－2或a ≥2. 选D11．解析：当a >1时，0<b <1，又g (x )＝－log b x 的图象与y ＝log b x 的图象关于x 轴对称，故B 符合题意．12．解析： ∵f (x )＝4x ＋12x ＝2x ＋2－x ，∴f (－x )＝2－x ＋2x ＝f (x )．∴f (x )为偶函数．故选D二、填空题(本大题共4小题，每小题5分，共20分．)13．解析：本题主要考查集合中点集的交集运算．由⎩⎪⎨⎪⎧ y ＝－x ＋1，y ＝x －1，得⎩⎪⎨⎪⎧x ＝1，y ＝0，∴M ∩N ＝{(1,0)}．答案：{(1,0)}14．解析：∵g (x ＋1)＝f (x )＝2x 2＋3∴g (3)＝f (2)＝2×22＋3＝11.答案：11 15．解析：设f (x )＝a x ，g (x )＝x α，代入(2,4)，∴f (x )＝2x ，g (x )＝x 2.答案：2x x 2 16．解析：P ＝[0,2]，Q ＝(1，＋∞)，∴P ⊙Q ＝[0,1]∪(2，＋∞)．答案：[0,1]∪(2，＋∞)三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤) 17．解：(1)由已知得A ＝{x |1≤x ≤3}， B ＝{x |log 2x ＞1}＝{x |x ＞2}，所以A ∩B ＝{x |2＜x ≤3}，(∁R B )∪A ＝{x |x ≤2}∪{x |1≤x ≤3}＝{x |x ≤3}． (2)①当a ≤1时，C ＝∅，此时C ⊆A ； ②当a ＞1时，若C ⊆A ，则1＜a ≤3. 综合①②，可得a 的取值范围是(－∞，3]． 18．解：(1)原式＝2lg 5＋2lg 2＋lg 5(1＋lg 2)＋(lg 2)2＝2(lg 2＋lg 5)＋lg 5＋lg 2×lg 5＋(lg 2)2＝2＋lg 5＋lg 2(lg 5＋lg 2) ＝2＋lg 5＋lg 2＝3.(2)原式＝⎝⎛⎭⎫82723－⎝⎛⎭⎫49912＋⎝⎛⎭⎫1 000823×225＝49－73＋25×225＝－179＋2＝19. 19．解：(1)∵f (x )是奇函数，∴f (0)＝0. 当x <0时，－x >0， ∴f (－x )＝log 2(－x )．又f (x )是奇函数，∴f (x )＝－f (－x )＝－log 2(－x )．综上，f (x )＝⎩⎪⎨⎪⎧log 2x ，x >0，0，x ＝0，－log 2(－x )，x <0.(2)由(1)得f (x )≤12等价于⎩⎪⎨⎪⎧ x >0，log 2 x ≤12或⎩⎪⎨⎪⎧ x ＝0，0≤12或⎩⎪⎨⎪⎧x <0，－log 2(－x )≤12，解得0<x ≤2或x ＝0或x ≤－22，即所求x 的集合为⎩⎨⎧x ⎪⎪⎭⎬⎫0≤x ≤2或x ≤－22. 20．解：(1)当0<x ≤100且x ∈N *时，p ＝60；当100<x ≤600且x ∈N *时，p ＝60－(x －100)×0.02＝62－0.02x .∴p ＝⎩⎪⎨⎪⎧60，0<x ≤100且x ∈N *，62－0.02x ，100<x ≤600且x ∈N *.(2)设该厂获得的利润为y 元，则当0<x ≤100时且x ∈N *，y ＝60x －40x ＝20x ；当100<x ≤600时且x ∈N *，y ＝(62－0.02x )x －40x ＝22x －0.02x 2.∴y ＝⎩⎪⎨⎪⎧20x ，0<x ≤100且x ∈N *，22x －0.02x 2，100<x ≤600且x ∈N *.当0<x ≤100时且x ∈N *，y ＝20x 是单调增函数， ∴当x ＝100时，y 最大，y max ＝20×100＝2 000；当100<x ≤600时且x ∈N *，y ＝22x －0.02x 2＝－0.02(x －550)2＋6 050， ∴当x ＝550时，y 最大，y max ＝ 6 050. 显然6 050>2 000，∴当销售商一次订购550件时，该厂获得的利润最大，最大利润为6 050元． 21．解：(1)在f (x )－f (y )＝f (x －y )中，令x ＝2，y ＝1，代入得：f (2)－f (1)＝f (1)，所以f (2)＝2f (1)＝－4. (2)f (x )在(－3,3)上单调递减．证明如下：设－3<x 1<x 2<3，则x 1－x 2<0，所以f (x 1)－f (x 2)＝f (x 1－x 2)>0，即f (x 1)>f (x 2)，所以f (x )在(－3,3)上单调递减．(3)由g (x )≤0得f (x －1)＋f (3－2x )≤0，所以f (x －1)≤－f (3－2x )．又f (x )满足f (－x )＝－f (x )，所以f (x －1)≤f (2x －3)，又f (x )在(－3,3)上单调递减，所以⎩⎪⎨⎪⎧－3<x －1<3，－3<2x －3<3，x －1≥2x －3，解得0<x ≤2，故不等式g (x )≤0的解集是(0,2]．22．解：(1)不论a 为何实数，f (x )在定义域上单调递增．证明：设x 1，x 2∈R ，且x 1<x 2，则f (x 1)－f (x 2)＝⎝ ⎛⎭⎪⎫a －22x 1＋1－⎝ ⎛⎭⎪⎫a －22x 2＋1＝2(2x 1－2x 2)(2x 1＋1)(2x 2＋1). 由x 1<x 2可知0<2x 1<2x 2，所以2x 1－2x 2<0,2x 1＋1>0,2x 2＋1>0，所以f (x 1)－f (x 2)<0，f (x 1)<f (x 2)．所以由定义可知，不论a 为何数，f (x )在定义域上单调递增．(2)由f (0)＝a －1＝0得a ＝1，经验证，当a ＝1时，f (x )是奇函数． (3)由条件可得： m ≤2x ⎝ ⎛⎭⎪⎫1－22x ＋1＝(2x ＋1)＋22x ＋1－3恒成立．m ≤(2x ＋1)＋22x ＋1－3的最小值，x ∈[2,3]．设t ＝2x ＋1，则t ∈[5,9]，函数g (t )＝t ＋2t －3在[5,9]上单调递增，所以g (t )的最小值是g (5)＝125，所以m ≤125，即m 的最大值是125.。