北京理工大学 材料力学课本答案 第一次课(1[1].5+0.5学时)实际
材料力学课后习题答案5章

∑ Fy = 0,FS左 + F + qdx − FS右 = 0
保留有限量,略去微量 qdx 后,得
FS右 − FS左 = F 为了更一般地反映 F 作用处剪力的突变情况(把向下的 F 也包括在内),可将上式改写为
FS右 − FS左 = F
(a)
1
仍据题图 a,由
∑MC
= 0,M 右
−
F
(
dx 2
5-7 .........................................................................................................................................................3
5-11 .....................................................................................................................................................10
5-13 .....................................................................................................................................................11
− Me
−
qdx(
dx 2
)
−
FS左
0
保留有限量,略去一阶和二阶微量后,得
M右 −M左 = Me
为了更一般地反映 M e 作用处弯矩的突变情况(把逆钟向的 M e 也包括在内),可将上式改写
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
《材料力学》课后习题答案详细

《材料力学》课后习题答案详细在学习《材料力学》这门课程时,课后习题是巩固知识、检验理解程度的重要环节。
一份详细准确的课后习题答案不仅能够帮助我们确认自己的解题思路是否正确,还能进一步加深对知识点的理解和掌握。
材料力学是一门研究材料在各种外力作用下产生的应变、应力、强度、刚度和稳定性的学科。
它对于工程领域的学生来说至关重要,无论是机械工程、土木工程还是航空航天工程等,都离不开材料力学的知识支撑。
对于课后习题的解答,我们首先要明确每个问题所涉及的核心概念和原理。
比如,在研究杆件的拉伸和压缩问题时,需要清楚胡克定律的应用条件和计算公式。
胡克定律指出,在弹性限度内,杆件的伸长或缩短量与所受的拉力或压力成正比。
以一道常见的拉伸习题为例:一根直径为 20mm 的圆杆,受到100kN 的拉力,材料的弹性模量为 200GPa,求杆的伸长量。
解题思路如下:首先,根据圆杆的直径计算出横截面积 A =π×(d/2)^2 ,其中 d 为直径。
然后,根据胡克定律ΔL = FL/EA ,其中F 为拉力,L 为杆长,E 为弹性模量,A 为横截面积,代入已知数据进行计算。
在计算过程中,要注意单位的统一。
拉力的单位通常为牛顿(N),长度的单位要与弹性模量的单位相匹配,面积的单位要为平方米(m²)。
再来看一个关于梁的弯曲问题。
梁在受到横向载荷作用时,会产生弯曲变形。
在解答这类习题时,需要运用到弯矩方程、挠曲线方程等知识。
例如:一简支梁,跨度为 L,承受均布载荷 q,求梁的最大弯矩和最大挠度。
解题时,首先要根据梁的支座情况列出弯矩方程。
然后,通过积分求出挠曲线方程,再根据边界条件确定积分常数。
最后,求出最大弯矩和最大挠度的位置及数值。
在求解过程中,要理解弯矩和挠度的物理意义,以及它们与载荷、梁的几何形状和材料性质之间的关系。
对于扭转问题,要掌握扭矩的计算、切应力的分布规律以及扭转角的计算方法。
比如,一根轴受到扭矩 T 的作用,已知轴的直径和材料的剪切模量,求轴表面的最大切应力和扭转角。
材料力学课后答案

材料⼒学课后答案第⼆章⼏何组成分析[⼏何可变体系与⼏何不变体系]⼏何可变体系——在任意荷载的作⽤下,即使不考虑材料的应变,它的形状和位置也是可以改变的。
⼏何不变体系——如果不考虑材料的应变,它的形状和位置是不能改变的。
[⾃由度与刚⽚]物体在运动时决定其位置的⼏何参变数称为⾃由度。
⼏何形状不变的平⾯体称为刚⽚。
⼀个刚⽚在平⾯内运动有三个⾃由度;⼀个点在平⾯内运动有两个⾃由度;⼀个点在空间内运动有三个⾃由度;⼀个刚体在空间内运动有六个⾃由度。
[约束]减少⾃由度的装置称为约束。
[约束的影响](1)⽀座约束可动铰⽀座相当于⼀个约束,减少⼀个⾃由度;固定铰⽀座相当于两个约束,减少两个⾃由度;固定端⽀座相当于三个约束,减少三个⾃由度;定向⽀座相当于两个约束,减少两个⾃由度。
(2)链杆两刚⽚加⼀链杆约束,减少⼀个⾃由度。
(3)铰结点单铰:两刚⽚加⼀单铰结点约束,减少两个⾃由度。
复铰:n个刚⽚在同⼀点⽤铰连接,相当于n-1个单铰的约束。
(4)刚结点单刚结点:两刚⽚加⼀刚结点约束,减少三个⾃由度。
复刚结点:n个刚⽚在同⼀点⽤刚结点连接,相当于n-1个单刚结点的约束。
[结构体系⾃由度的计算公式](1)⼀般公式=各部件⾃由度总和-全部约束数为结构体系⾃由度。
(2)平⾯杆件体系⾃由度的计算公式式中为刚⽚个数,为单刚结点个数;为单铰结点个数;为链杆个数;为⽀座约束个数,如果为⾃由体,即⽆⽀座约束,则=3 。
(3)平⾯桁架⾃由度的计算公式式中为结点个数;为链杆个数;为⽀座约束个数,如果为⾃由体,即⽆⽀座约束,则=3 。
[⾃由度与⼏何不变性的关系]体系为⼏何不变的必要条件是⾃由度等于或⼩于零,此条件并⾮充分条件。
如果>0,则体系为⼏何可变体系;如果<0或=0 ,则不能确定。
[实铰与虚铰]两根不共线链杆的约束作⽤与⼀个单铰的约束作⽤是等效的。
两链杆交于⼀点所构成的铰为实铰。
两链杆的延长线交于⼀点,约束作⽤等效于该点⼀个单铰的约束作⽤,这种铰称为虚铰或瞬铰。
材料力学1-1-绪论-第1章-1

安全, 安全, 承载力强 实例: 实例
一对矛盾
经济, 体积小, 经济, 体积小, 重量轻
如何能够承受重物而不沿根 部折断或弯曲变形太大? 部折断或弯曲变形太大
8
“泰坦尼克号”1912年4月14日撞上冰山而沉没,造成 泰坦尼克号” 日撞上冰山而沉没, 泰坦尼克号 年 月 日撞上冰山而沉没 1500多人丧生在大西洋中。传统理论认为,“泰坦尼克 多人丧生在大西洋中。 多人丧生在大西洋中 传统理论认为, 是在船头进水、船尾升高到45度斜角后 度斜角后, 号”是在船头进水、船尾升高到 度斜角后,造成船体 断裂发生沉没的。 断裂发生沉没的。 9
集中载荷——集中力,集中力偶 集中载荷 集中力, 集中力 0.5 约束条件 约束条件——各种支座、铰链、固支端等 各种支座、铰链、 各种支座
15
§1 杆件在一般外力作用下的内力分析
变形体产生变形的原因: 变形体产生变形的原因: 外力( 外力 载荷、 载荷、温度湿度 ) 引起内力 引起内力 产生变形 变化、 变化、尺寸误差 载荷——包括主动力和约束力 载荷 包括主动力和约束力 内力——在外力的作用下构件一部分对另一部分的 内力 在外力的作用下构件一部分对另一部分的 作用力。 作用力。 变形体的分析思路: 变形体的分析思路: 找出全部外力 (包括支座约束力 包括支座约束力) 包括支座约束力 截面法 (对静定杆件 对静定杆件) 对静定杆件
10
§0 绪论
0.1 材料力学概述 三大基本任务——构件的强度、刚度、稳定性 构件的强度、刚度、 三大基本任务 构件的强度 研究对象——构件及简单的结构(均为变形体) 构件及简单的结构(均为变形体) 研究对象 构件及简单的结构 0.2 材料力学对变形固体的基本假设 1.连续性 连续性 变形前及变形后,应不开裂、 变形前及变形后,应不开裂、不相入 变形前的一个点——变形后仍为一个点 变形后仍为一个点 变形前的一个点 变形前的一条线——变形后仍为一条线 变形后仍为一条线 变形前的一条线
材料力学课后习题答案

材料力学课后习题答案1. 弹性力学。
1.1 问题描述,一根钢丝的弹性模量为200GPa,其截面积为0.01m²。
现在对这根钢丝施加一个拉力,使其产生弹性变形。
如果拉力为2000N,求钢丝的弹性变形量。
解答:根据胡克定律,弹性变形量与拉力成正比,与材料的弹性模量和截面积成反比。
弹性变形量可以用以下公式计算:$$。
\delta = \frac{F}{AE}。
$$。
其中,$\delta$表示弹性变形量,F表示拉力,A表示截面积,E表示弹性模量。
代入已知数据,可得:$$。
\delta = \frac{2000N}{0.01m² \times 200GPa} = 0.001m。
$$。
所以,钢丝的弹性变形量为0.001m。
1.2 问题描述,一根长为1m,截面积为$10mm^2$的钢棒,两端受到拉力为1000N的作用。
求钢棒的伸长量。
解答:根据胡克定律,钢棒的伸长量可以用以下公式计算:$$。
\delta = \frac{F \cdot L}{AE}。
$$。
其中,$\delta$表示伸长量,F表示拉力,L表示长度,A表示截面积,E表示弹性模量。
代入已知数据,可得:$$。
\delta = \frac{1000N \times 1m}{10mm² \times 200GPa} = 0.005m。
$$。
所以,钢棒的伸长量为0.005m。
2. 塑性力学。
2.1 问题描述,一块金属材料的屈服强度为300MPa,现在对其施加一个拉力,使其产生塑性变形。
如果拉力为500MPa,求金属材料的塑性变形量。
解答:塑性变形量与拉力成正比,与材料的屈服强度无关。
塑性变形量可以用以下公式计算:$$。
\delta = \frac{F}{A}。
$$。
其中,$\delta$表示塑性变形量,F表示拉力,A表示截面积。
代入已知数据,可得:$$。
\delta = \frac{500MPa}{300MPa} = 1.67。
(完整版)材料力学课后习题答案
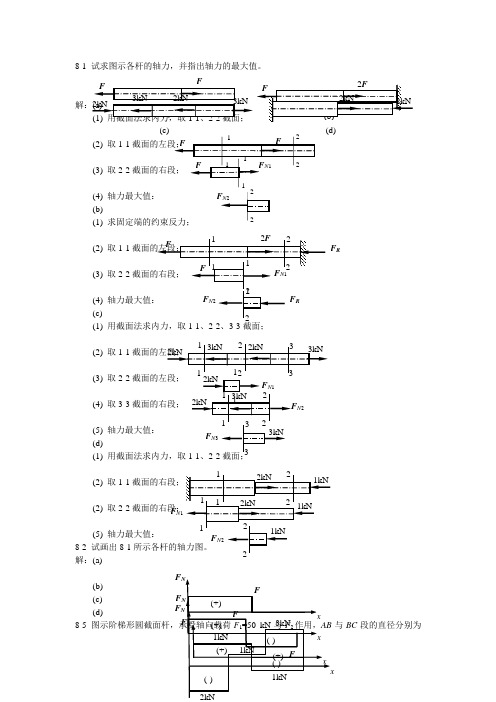
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
材料力学课后答案

材料力学课后答案1. 弹性力学基础题。
题目,一根长为L的均匀横截面圆柱形杆,端部固定,另一端受力F,求受力端的应变。
解答,根据弹性力学的基本公式,应变ε=σ/E,其中σ为应力,E为弹性模量。
由于杆的横截面积为A,受力F导致的应力σ=F/A。
因此,受力端的应变ε=F/(AE)。
2. 弹性力学应用题。
题目,一根钢丝的长度为L,直径为d,受力F时产生的应力为σ,求其应变。
解答,首先计算钢丝的横截面积A=πd^2/4,然后根据应变ε=σ/E,其中E为钢的弹性模量,求得应变ε=σ/(E)。
3. 材料的破坏。
题目,一块材料在受力时产生的应力达到了其屈服强度,求此时的应变。
解答,当材料的应力达到屈服强度时,材料开始发生塑性变形,此时的应变无法简单地通过弹性力学公式来计算。
需要通过材料的本构关系来确定应变。
4. 弯曲应力与应变。
题目,一根横截面为矩形的梁,在受力时产生的最大应力为σ,求其最大应变。
解答,根据梁的弯曲应力公式σ=My/I,其中M为弯矩,y为梁的截面离中性轴的距离,I为梁的惯性矩。
最大应变发生在最大应力处,由应变ε=σ/E,可以求得最大应变。
5. 拉伸与压缩。
题目,一根长为L的杆在受拉力F时产生的应变为ε,求其长度变化量。
解答,根据胡克定律,拉伸或压缩材料的长度变化量ΔL=εL。
6. 应变能。
题目,一根长为L的弹簧,在受力F时产生的应变为ε,求其弹性势能。
解答,弹簧的弹性势能U=1/2kε^2,其中k为弹簧的弹性系数。
根据ε=F/(kL),代入可得弹性势能U=1/2F^2/(kL)。
7. 疲劳破坏。
题目,一根金属材料在受到循环载荷时,经过了n次循环后发生疲劳破坏,求其疲劳寿命。
解答,根据疲劳寿命公式N=K(σ_max)^(-1/α),其中N为疲劳寿命,K为材料常数,σ_max为循环载荷的最大应力,α为材料的疲劳指数。
代入循环载荷的应力值,可以求得疲劳寿命。
8. 蠕变。
题目,一根材料在高温下受到持续载荷时发生了蠕变,求其蠕变应变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+
Iy
− 2
Iz
cos2α
−
I yzsin2α
Iz1
=
Iy
+ 2
Iz
−
Iy
− 2
Iz
cos2α
+
I yzsin2α
I y1z1
=
Iy
− 2
Iz
sin2α
+
I yzcos2α
图形对过同一点的任意一 对垂直轴的惯性矩之和为 常数。即在轴转动时,其 惯性矩和保持不变。
∫ ( ) ∫ I y1 + I z1 = I y + I z =
n
Ai zCi
i =1 n
⎪ ⎪⎪ ⎬ ⎪ ⎪ ⎪
Ai
i =1
⎪ ⎪⎭
第II.2节
§II.2 惯性矩 极惯性矩 惯性积
惯性矩和极惯性矩
z
∫ I y =
z2dA > 0
A
-图形对 y 轴的惯性矩
y
dA
∫ Iz =
y2dA > 0
A
A
ρz
-图形对 z轴的惯性矩
O
y
∫ IP =
ρ2dA > 0
A
-图形对 O 点的极惯性矩
iy =
Iy A
-图形对 y 轴的惯性半径
iz =
I z -图形对 z 轴的惯性半径 A
§II.2 惯性矩 极惯性矩 惯性积
惯性矩和极惯性矩性质
∫ ∫ ∫ I y =
z 2dA
A
Iz =
y2dA
A
IP =
ρ 2dA
A
¾ 截面图形对不同坐标轴的惯性矩是 不同的,但惯性矩恒为正。量纲:L4
¾ 组合截面对某一轴的惯性矩等于各部 分对该轴的惯性矩之代数和。
∑ S z ∑ S y
= =
A1 yC1 A1 zC1
+ +
A2 A2
yC2 zC2
+ +
⋅⋅⋅+ ⋅⋅⋅+
An yCn An zCn
= =
i
n
i =1 n
=1
Ai yCi Ai zCi
⎫ ⎪⎪ ⎬ ⎪ ⎪⎭
n
⎫
∑ yC ∑∑∑ zC
= Sz A
= Sy A
= =
Ai yCi ⎪
i =1
⎪
n
Ai
i =1
z
y
dA
∫ Sz =
ydA
A
z
O
y
z —图形对于 z 轴的静矩
yC
A
C
zC
O
yC
=
Sz A
, zC
=
Sy A
y
— 截面图形形心坐标
返回
II.1 静矩和形心
静矩与形心坐标的关系
∫ S y =
zdA
A
S y = AzC
∫ Sz =
ydA
A
S z = AyC
¾ 已知静矩可以确定图形的形心坐标
¾ 已知图形的形心坐标可以确定静矩
返回
引言
实际构件的承载能力与变形形式有关,不同变形形式下的承载 能力,不仅与截面的大小有关,而且与截面的几何形状有关。
不同的分布内力系,组成不同的内力分量时,将涉及不同的几
何量。这些几何量不仅与截面的大小有关,而且与截面的几何形
状有关。
z τ dA
σ dA
∫ 拉伸:σx = const.
σ
A
xdA
=
FNx
σx
=
FNx A
扭转:
τ
=
Gγ
=
G
dϕ
dx
ρ
∫A(τ dA) ρ = T
∫ τ = T ρ IP
IP =
ρ 2dA
A
y
弯曲: σ x = Cy
∫ σ x
=
My Iz
Iz =
y 2dA
A
∫A(σxdA) y = M
返回
第II.1节
II.1 静矩和形心
定义
∫ S y =
zdA
A
—图形对于 y 轴的静矩
yCC00 ,zCC00 轴是图形的形心主惯性 轴图形对于yCC00 ,zCC00 轴的惯性矩称 为形心主惯性矩
对于任意一点(图形内或图形外)都 有主轴, 通过形心的主轴称为形心主惯性轴,图 形对形心主轴的惯性矩称为形心主惯性 矩。 工程计算中有意义的是形心主轴与形心 主矩。
zC0 zC
α0
C
y C0
附录II
附录II 平面图形的几何性质
为什么要研究截面图形的几何性质 静矩和形心及其相互关系 惯性矩 极惯性矩 惯性积 平行移轴公式 转轴公式、主惯性轴与主惯性矩 确定组合图形的形心主轴和形心主矩的
方法
结论与讨论
第13.3节
引言
研究杆件的应力与变形,研究失效问题 以及强度、刚度、稳定问题,都要涉及到 与截面图形的几何形状和尺寸有关的量。 这些量统称为几何量,包括:形心、静矩、 惯性矩、惯性半径、极惯性矩、惯性积、主 轴等。
+ 2
Iz
±
⎛ ⎜ ⎝
Iy
− 2
Iz
⎞2 ⎟ ⎠
+
I
2 yz
I y1
=
Iy
+ 2
Iz
+
Iy
− 2
Iz
cos2α
−
I yzsin2α
Iz1
=
Iy
+ 2
Iz
−
Iy
− 2
Iz
cos2α
+
I yzsin2α
II.4.2 主惯性轴和主惯性矩
形心主惯性轴和形心主惯性矩
∫ I = yC0zC0 A yC0zC0dA = 0
⎫ ⎪⎪ ⎬
I y1z1 = I yz + abA⎪⎪⎭
§II.3 平行移轴公式
平行移轴公式
z
zC
I y = I yc + a2 A Iz = Izc + b2 A I yz = I yczc + abA b
A
¾ 因为面积及包含a2、b2的项恒为正,故
C
yC
自形心轴移至与之平行的任意轴,惯性矩
a
总是增加的。
已知: Iy、Iz、Iyz
求: Iy1、Iz1、Iy1z1
∫ I y1 = A z12d A
∫ I z1 =
A
y
2 1
d
A
∫ I y1 z1 = A y1 z1d A
y1=y+b , z1=z+a
z1
z
y1
y
dA
z
O
z1
a O´
b
A
y
y1
§II.3 平行移轴公式
平行移轴公式
已知: Iy、Iz、Iyz
z0 z
y
α0
y0
O
dA
z
z0
α0
y0 y
y00,z00 轴是图形的主惯性轴,简称主轴 图形对于主轴的惯性矩I y0 , I z0 称为主惯性矩
II.4.2 主惯性轴和主惯性矩
主惯性轴和主惯性矩 任意平面图形上的任意点 O(图形内或图形外)都 有主轴,即过该点存在坐 标系y0 Oz0,满足
∫ I = y0 z0 A y 0 z 0 d A = 0
dA
z
¾ Iyz的数值可正、可负、可为零。
O
y
量纲:L4
¾ 当 y ,z 轴中有一个是图形的对称轴时,
图形对这一对坐标的惯性积 Iyz 恒为零
例题II.1
z
dA
dr
r C
d
已知:圆截面直径d 求:Iy, Iz
dA = 2πrdr
∫ I y
= Iz
=
IP 2
=1 2
d
2 r 2dA
0
y
∫ = 1
d 2
r2
(2πr )dr
=
πd 4
20
64
IP
=
πd 4 32
例题II.2
z
dA
dz
已知:矩形截面b× h
dA z
h
求:Iy, Iz
C y dy
y
Iy
=
bh3 12
Iz
=
hb3 12
b
第II.3节
§II.3 平行移轴公式
平行移轴公式
移轴定理是指图形对于互相平行轴的惯性矩、惯性积 之间的关系。即通过已知图形对于一对坐标的惯性矩、惯 性积,求图形对另一对坐标的惯性矩与惯性积。
∫ yC
=
Sz A
=
ydA
A
A
z
∫ zC
=
Sy A
=
zdA
A
A
y
dA
C(yC zC) z
O
y
¾ 截面图形对不同的坐标轴静矩是不同的。 z
静矩的数值可正、可负、可为零。 A
zC
量纲为长度的三次方。 ¾ 截面图形对形心轴的静矩等于零。
C O
yC
y
S yC = 0, SzC = 0
II.1 静矩和形心
组合图形的形心坐标
z z0
y
α0
y0
dA
z
z0
α0
y0
O
y
主轴的方位由α0确定,α0满足下式
I y0z0
=
Iy
− Iz 2
sin2α0
+
I yzcos2α0=0
