数据结构课后习题答案第九章
数据结构第九章排序习题与答案

习题九排序一、单项选择题1.下列内部排序算法中:A.快速排序 B.直接插入排序C. 二路归并排序D.简单选择排序E. 起泡排序F.堆排序(1)其比较次数与序列初态无关的算法是()(2)不稳定的排序算法是()(3)在初始序列已基本有序(除去n 个元素中的某 k 个元素后即呈有序, k<<n)的情况下,排序效率最高的算法是()(4)排序的平均时间复杂度为O(n?logn)的算法是()为 O(n?n) 的算法是()2.比较次数与排序的初始状态无关的排序方法是( )。
A.直接插入排序B.起泡排序C.快速排序D.简单选择排序3.对一组数据( 84, 47, 25, 15, 21)排序,数据的排列次序在排序的过程中的变化为(1) 84 47 25 15 21(2) 15 47 25 84 21(3) 15 21 25 84 47(4) 15 21 25 47 84则采用的排序是 ()。
A. 选择B.冒泡C.快速D.插入4.下列排序算法中 ( )排序在一趟结束后不一定能选出一个元素放在其最终位置上。
A. 选择B.冒泡C.归并D.堆5.一组记录的关键码为(46,79,56, 38,40, 84),则利用快速排序的方法,以第一个记录为基准得到的一次划分结果为()。
A. (38,40,46,56,79,84) B. (40,38,46,79,56,84)C. (40,38,46,56,79,84) D. (40,38,46,84,56,79)6.下列排序算法中,在待排序数据已有序时,花费时间反而最多的是()排序。
A.冒泡 B. 希尔C. 快速D. 堆7.就平均性能而言,目前最好的内排序方法是() 排序法。
A. 冒泡B.希尔插入C.交换D.快速8.下列排序算法中,占用辅助空间最多的是:()A. 归并排序B.快速排序C.希尔排序D.堆排序9.若用冒泡排序方法对序列 {10,14,26,29,41,52}从大到小排序,需进行()次比较。
数据结构 第9章答案

第9章 查找参考答案一、填空题(每空1分,共10分)1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 8 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ;平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n nn ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m -1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!!4.【计研题2000】折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)二、单项选择题(每小题1分,共27分)( B )1.在表长为n的链表中进行线性查找,它的平均查找长度为A. ASL=n; B. ASL=(n+1)/2;C. ASL=n +1; D. ASL≈log2(n+1)-1( A )2.【计研题2001】折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
数据结构(C语言版)9-12章练习 答案 清华大学出版社

数据结构(C语言版)9-12章练习答案清华大学出版社9-12章数据结构作业答案第九章查找选择题1、对n个元素的表做顺序查找时,若查找每个元素的概率相同,则平均查找长度为( A )A.(n+1)/2 B. n/2 C. n D. [(1+n)*n ]/2 2. 下面关于二分查找的叙述正确的是 ( D )A. 表必须有序,表可以顺序方式存储,也可以链表方式存储B. 表必须有序且表中数据必须是整型,实型或字符型 C. 表必须有序,而且只能从小到大排列 D. 表必须有序,且表只能以顺序方式存储3. 二叉查找树的查找效率与二叉树的( (1)C)有关, 在 ((2)C )时其查找效率最低 (1): A. 高度 B. 结点的多少 C. 树型 D. 结点的位置(2): A. 结点太多 B. 完全二叉树 C. 呈单枝树 D. 结点太复杂。
4. 若采用链地址法构造散列表,散列函数为H(key)=key MOD 17,则需 ((1)A)个链表。
这些链的链首指针构成一个指针数组,数组的下标范围为 ((2)C) (1) A.17 B. 13 C. 16 D. 任意(2) A.0至17 B. 1至17 C. 0至16 D. 1至16判断题1.Hash表的平均查找长度与处理冲突的方法无关。
(错) 2. 若散列表的负载因子α<1,则可避免碰撞的产生。
(错)3. 就平均查找长度而言,分块查找最小,折半查找次之,顺序查找最大。
(错)填空题1. 在顺序表(8,11,15,19,25,26,30,33,42,48,50)中,用二分(折半)法查找关键码值20,需做的关键码比较次数为 4 .算法应用题1. 设有一组关键字{9,01,23,14,55,20,84,27},采用哈希函数:H(key)=key mod7 ,表长为10,用开放地址法的二次探测再散列方法Hi=(H(key)+di) mod 10解决冲突。
要求:对该关键字序列构造哈希表,并计算查找成功的平均查找长度。
数据结构第9章作业 查找答案

第9章 查找答案一、填空题1. 在数据的存放无规律而言的线性表中进行检索的最佳方法是 顺序查找(线性查找) 。
2. 线性有序表(a 1,a 2,a 3,…,a 256)是从小到大排列的,对一个给定的值k ,用二分法检索表中与k 相等的元素,在查找不成功的情况下,最多需要检索 9 次。
设有100个结点,用二分法查找时,最大比较次数是 7 。
3. 假设在有序线性表a[20]上进行折半查找,则比较一次查找成功的结点数为1;比较两次查找成功的结点数为 2 ;比较四次查找成功的结点数为 8 ;平均查找长度为 3.7 。
解:显然,平均查找长度=O (log 2n )<5次(25)。
但具体是多少次,则不应当按照公式)1(log 12++=n nn ASL 来计算(即(21×log 221)/20=4.6次并不正确!)。
因为这是在假设n =2m-1的情况下推导出来的公式。
应当用穷举法罗列:全部元素的查找次数为=(1+2×2+4×3+8×4+5×5)=74; ASL =74/20=3.7 !!!4.折半查找有序表(4,6,12,20,28,38,50,70,88,100),若查找表中元素20,它将依次与表中元素 28,6,12,20 比较大小。
5. 在各种查找方法中,平均查找长度与结点个数n 无关的查找方法是 散列查找 。
6. 散列法存储的基本思想是由 关键字的值 决定数据的存储地址。
7. 有一个表长为m 的散列表,初始状态为空,现将n (n<m )个不同的关键码插入到散列表中,解决冲突的方法是用线性探测法。
如果这n 个关键码的散列地址都相同,则探测的总次数是 n(n-1)/2=( 1+2+…+n-1) 。
(而任一元素查找次数 ≤n-1)二、单项选择题( B )1.在表长为n的链表中进行线性查找,它的平均查找长度为A. ASL=n; B. ASL=(n+1)/2;C. ASL=n +1; D. ASL≈log2(n+1)-1( A )2. 折半查找有序表(4,6,10,12,20,30,50,70,88,100)。
数据结构第三版第九章课后习题参考答案
}
}
设计如下主函数:
void main()
{ BSTNode *bt;
KeyType k=3;
int a[]={5,2,1,6,7,4,8,3,9},n=9;
bt=CreatBST(a,n);
//创建《教程》中图 9.4(a)所示的二叉排序树
printf("BST:");DispBST(bt);printf("\n");
#define M 26 int H(char *s)
//求字符串 s 的哈希函数值
{
return(*s%M);
}
构造哈希表 void Hash(char *s[]) //
{ int i,j;
char HT[M][10]; for (i=0;i<M;i++)
//哈希表置初值
HT[i][0]='\0'; for (i=0;i<N;i++) { j=H(s[i]);
//求每个关键字的位置 求 // s[i]的哈希函数值
while (1)
不冲突时 直接放到该处 { if (HT[j][0]=='\0') //
,
{ strcpy(HT[j],s[i]);
break;
}
else
//冲突时,采用线性线性探测法求下一个地址
j=(j+1)%M;
}
} for (i=0;i<M;i++)
printf("%2d",path[j]);
printf("\n");
}
else { path[i+1]=bt->key;
(完整word版)数据结构第九章查找

第九章查找:习题习题一、选择题1.散列表查找中k个关键字具有同一散列值,若用线性探测法将这k个关键字对应的记录存入散列表中,至少要进行( )次探测。
A. k B。
k+l C. k(k+l)/2 D. l+k (k+l)/22.下述命题( )是不成立的。
A。
m阶B-树中的每一个结点的子树个数都小于或等于mB。
m阶B-树中的每一个结点的子树个数都大于或等于『m/2-1C。
m阶B-树中的每一个结点的子树高度都相等D。
m阶B—树具有k个子树的非叶子结点含有(k-l)个关键字3.如果要求一个基本线性表既能较快地查找,又能适应动态变化的要求,可以采用( )查找方法.A。
分块 B. 顺序 C. 二分 D.散列4.设有100个元素,用折半查找法进行查找时,最大比较次数是( ),最小比较次数是( ).A。
7,1 B.6,l C.5,1 D. 8,15.散列表长m=15,散列表函数H(key)=key%13。
表中已有4个结点:addr(18)=5;addr(32)=6; addr(59)=7;addr(73)=8;其余地址为空,如果用二次探测再散列处理冲突,关键字为109的结点的地址是( )。
A. 8 B。
3 C. 5 D。
46.用分块查找时,若线性表中共有729个元素,查找每个元素的概率相同,假设采用顺序查找来确定结点所在的块时,每块应分( )个结点最佳。
A。
15 B. 27 C。
25 D。
307.散列函数有一个共同性质,即函数值应当以( )取其值域的每个值。
A.同等概率B。
最大概率C。
最小概率D。
平均概率8.设散列地址空间为O.。
m—1,k为关键字,假定散列函数为h(k)=k%p,为了减少冲突,一般应取p为( )。
A.小于m的最大奇数B. 小于m的最大素数C.小于m的最大偶数D.小于m的最大合数9.当向一棵m阶的B-树做插入操作时,若使一个结点中的关键字个数等于( ),则必须分裂成两个结点。
A。
m B。
m-l C.m+l D。
《数据结构》习题集:第9章查找(第1次更新2019-5)

第9章查找一、选择题1.顺序查找一个共有n个元素的线性表,其时间复杂度为(),折半查找一个具有n个元素的有序表,其时间复杂度为()。
【*,★】A.O(n)B. O(log2n)C. O(n2)D. O(nlog2n)2.在对长度为n的顺序存储的有序表进行折半查找,对应的折半查找判定树的高度为()。
【*,★】A.nB.C.D.3.采用顺序查找方式查找长度为n的线性表时,平均查找长度为()。
【*】A.nB. n/2C. (n+1)/2D. (n-1)/24.采用折半查找方法检索长度为n的有序表,检索每个元素的平均比较次数()对应判定树的高度(设高度大于等于2)。
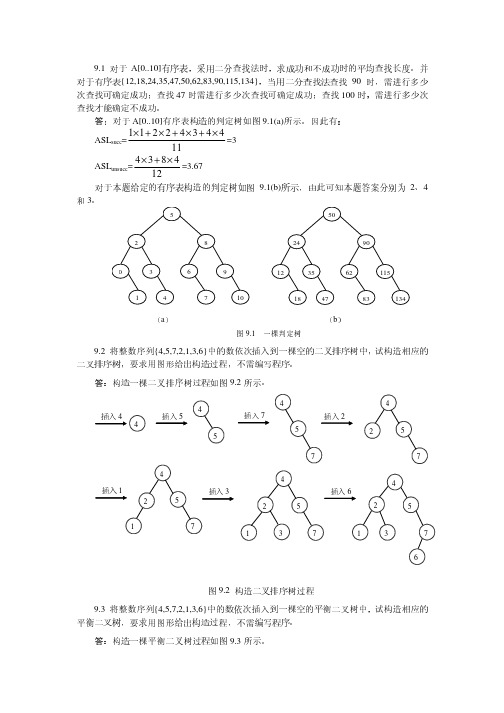
【**】A.小于B. 大于C. 等于D. 大于等于5.已知有序表(13,18,24,35,47,50,62,83,90,115,134),当折半查找值为90的元素时,查找成功的比较次数为()。
【*】A. 1B. 2C. 3D. 46.对线性表进行折半查找时,要求线性表必须()。
【*】A.以顺序方式存储B. 以链接方式存储C.以顺序方式存储,且结点按关键字有序排序D. 以链接方式存储,且结点按关键字有序排序7.顺序查找法适合于存储结构为()的查找表。
【*】A.散列存储B. 顺序或链接存储C. 压缩存储D. 索引存储8.采用分块查找时,若线性表中共有625个元素,查找每个元素的概率相同,假设采用顺序查找来确定结点所在的块时,每块应分()个结点最佳。
【**】A.10B. 25C. 6D. 6259.从键盘依次输入关键字的值:t、u、r、b、o、p、a、s、c、l,建立二叉排序树,则其先序遍历序列为(),中序遍历序列为()。
【**,★】A.abcloprstuB. alcpobsrutC. trbaoclpsuD. trubsaocpl10.折半查找和二叉排序树的时间性能()。
【*】A.相同B. 不相同11.一棵深度为k的平衡二叉树,其每个非终端结点的平衡因子均为0,则该树共有()个结点。
第九章 严蔚敏数据结构课后答案-查找

else if(key<r[mid].key) high=mid; else low=mid; } //本算法不存在查找失败的情况,不需要 return 0; }//Locate_Bin
while(p->data>key) p=p->pre; L.sp=p;
} else if(p->data<key) { while(p->data<key) p=p->next;
L.sp=p; } return p; }//Search_DSList 分析:本题的平均查找长度与上一题相同,也是 n/3.
}//while //借助中序遍历找到元素 x 及其前驱和后继结点 if(!ptr) return ERROR; //未找到待删结点 Delete_BSTree(ptr); //删除 x 结点 if(pre&&pre->rtag) pre->rchild=suc; //修改线索 return OK; }//BSTree_Delete_key
printf("a=%d\n",last); if(last<=x&&T->data>x) //找到了大于 x 的最小元素 printf("b=%d\n",T->data); last=T->data; if(T->rchild) MaxLT_MinGT(T->rchild,x); }//MaxLT_MinGT
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
return(binsearch(s,low,mid-1,k)
else return(mid);
}
else return(0);
} // 算法结束
9.5 int level(bstnode *bst, keytype K)
// 在二叉排序树bst中,求关键字K所在结点的层次
q->next=p->next;
while (q!=L && q->freq<p-freq) q=q->prior; // 找p结点位置
q->next->prior=p; // 将p结点插入链表
p->next=q->next;
p->prior=q;
q->next=p;
} // 算法结束
void locate(snode L[],int n;keytype X)
else { freq=L[i].freq;
while ( L[i-1].freq<freq) { L[i].freq=L[l-1].freq; i--; }
L[i+1].freq=freq;
}
} // 算法结束
9.3
注:判定树中的编号为元素在有序表中的序号
9.4 int binsearch(rectype s[],int low,int high, keytype k)
if(p= =null){printf(“没有关键字k”);return(null);}
else{pre->next=p->next;free(p);return(k);}
}
}//hashdelete
9.12(1)
0 1 2 3 4 5 6 7 8 9 10 11 12
14
01
68
27
55
19
20
84
{bstnode *p; // p为工作指针
int num=0; // 记层数
p=bst;
while (p && p->key!=K) // 二叉排序树不空 且关键字不等
if (p->key<K) { num++; p=p->rchild; } // 沿右子树
else { num++; p=p->lchild; } // 沿左子树
if (i>0 && r[i].key==k) return(i);
else 过程的判定树是单支树。
查找成功的平均查找长度为
ASL=∑PICI =1/n*∑i = 1/2*(n+1)
查找不成功的平均查找长度为 ASL=1/(n+1)(∑i+(n+1))=(n+2)/2.
// 为1,调用本函数后,若仍为1,是二叉排序树,否则,不是二叉排序树。
{if (bst!=null)
{bstree(bst->lchild,pre);
if (pre==null) pre=bst;
else if (pre->key>bst->key)
{printf (“非二叉排序树\n”);flag=0; return 0;}
// 有序的顺序表s,其元素的低端和高端下标分别为low和 high.
// 本算法递归地折半查找关键字为k的数据元素,若存在,则返回其在有序
// 顺序表中的位置,否则,返回0。
{ if (low<=high)
{mid=(low+high)/2;
if (s[mid].key<k )
return binsearch(s,mid+1,high,k);
(2)
0
1
2
3
4
5
6
7
8
9
10
11
12
查找成功时平均查找长度=(1*6+4*2+1*3+1*4)/12=21/12
查找不成功时的平均查找长度=(1*7+2*2+3*3+1*5)/13=25/13
9.13各种查找方法均有优点和缺点,不能笼统地说某种方法的好坏。
顺序查找的时间为o(n),在n较小时使用较好,它对数据元素的排列没有要求;二分查找时间为o(log2n),效率高但它要求数据元素有序排列;散查找时间为o(1),它只能按关键字随机查找(使用散列函数),不能顺序查找,也不能折半查找。
else pre=p;
bstree(bst->rchild,pre);
}
}
9.8(1)
ASL=(1*1+2*2+3*3+3*4+2*5+1*6)/12=42/12
(2)
L
R
(一)
R
L
(二)
R
R
(三)
(四)
ASL=(1*1+2*2+4*3+4*4+1*5)/12=38/12
9.9
L
LR
L
RL
(LL型)(LR型)(RL型)
R
R
(RR型)
9.10
(1)插入关键字B后,B-树的结点无变化
(2)插入关键字L后,结点E和G产生分裂
(3)插入关键字P后,结点H产生分裂
(4)插入关键字Q后,结点不变
(5)插入关键字R后,三个层次结点产生分裂,使B-树增高
9.11hegtype hashdelete(hashtable ht,hegtype k)
H(11)=11%13=11
H(10)=10%13=10冲突,3次成功
H(79)=79%13=1冲突,9次成功
成功时的平均查找长度=(1*6+1*2+3*3+1*4+1*9)/12=30/12
查找不成功时的平均查找长度=(1+13+12+11+10+9+8+7+6+5+4+3+2+1)/13=92/13
else return(ancestor(p->rchild)); // 沿右子树
} // 算法结束
9.7 int bstree(bstnode *bst, bstnode *pre)
// bst是二叉树根结点的指针,pre总指向当前访问结点的前驱,调用本函数
// 时为null。本算法判断bst是否是二叉排序树。设一全程变量flag,初始值
else if (p->key==b) { printf(“B 是A的祖先。\n”); return(p); }
else if (p-key>a && p->key<b) return(p);/ p是A和B的最近公共祖先
else if (p->key>b) return(ancestor(p->lchild)); // 沿左子树
if (p->key==K) return (++num); // 查找成功
else return(0); // 查找失败
} // 算法结束
其递归算法如下:
int level(bstnode *bst, keytype K,int num)
// 在二叉排序树中,求关键字K所在结点的层次的递归算法,调用时num=0
{if (bst==null) return 0;
else if (bst->key==K) return ++num;
else if (bst->key<K) return(bst->rchild,K,num++);
else return(bst->lchild,K,num++);
} // 算法结束
//ht是拉链法解决冲突的散列表,本算法删除关键字
//为k的指定结点,若删除成功,返回K;否则
//返回null
{设I=H(heg);//I为关键字k用指定哈希函数计算的哈希地址
if(ht[i]=null) {printf(“没有关键字k”);return(null);}
else{p=ht[i];pre=p;while(p&&p->data!=k){pre=p;p=p->next;}
79
23
11
10
121431139113
H(19)=19%13=6
H(14)=14%13=1
H(23)=23%13=10
H(01)=01%13=1冲突,2次成功
H(68)=68%13=3
H(20)=20%13=7
H(84)=84%13=6冲突,3次成功
H(27)=27%13=1冲突,4次成功
H(55)=55%13=3冲突,3次成功
9.6 bstnode *ancestor(bstnode *bst)
// bst是非空二叉排序树根结点的指针。
// A和B是bst树上的两个不同结点,本算法求A和B的最近公共祖先。
// 设A和B的关键字分别为a和b,不失一般性,设a<b。
{bstnode *p=bst;
if (p->key==a) { printf(“A 是B的祖先。\n”); return(p); }
keytype key; // 关键字
ElemType other;
}snode;
void locate(seqlist L,keytype X)
// 在链表中查找给定值为X的结点,并保持访问频繁的结点在前
