计量经济学ARCH模型
时间序列模型--ARMA模型与ARCH模型(2008.11)

时间序列模型时间序列分析是现代计量经济学的重要内容,是研究经济变量的动态特征和周期特征及其相关关系的重要工具,被广泛应用经济分析和预测中。
时间序列按其平稳性与否又分为平稳时间序列和非平稳时间序列。
1.ARMA与ARCH模型2.协整与误差修正模型3.向量自回归模型1第五讲ARMA与ARCH模型本讲中将讨论时间序列的平稳性(stationary)概念及自回归模型(Autoregressive models)、移动平均模型(Moving average models)、自回归移动平均模型(Autoregressive moving average models)、自回归条件异方差模型(Autoregressivec conditional Heteroscedasticity models)的识别、估计、检验、应用。
23一、时间序列的平稳性(一)平稳时间序列所谓时间序列的平稳性,是指时间序列的统计规律不会随着时间的推移而发生变化。
严格地讲,如果一个随机时间序列,对于任何时间,都满足下列条件:t y t Ⅰ)均值;()t E y μ=∞ Ⅱ)方差,是与时间无关的常数;22()()t t Var y E y μσ=-=t Ⅲ)自协方差,是只与时期间隔有关,{}(,)t t k t t k k Cov y y E y y μμγ--=--=()()k 与时间无关的常数。
t4则称该随机时间序列是平稳的。
生成该序列的随机过程是平稳过程。
例5.1.一个最简单的随机时间序列是一具有零均值同方差的独立分布序列:= ~该序列常被称为是一个白噪声(white noise )。
t y t εt ε2(0,)iid σ 由于具有相同的均值与方差,且协方差为零,满足平稳性条件,是平稳的。
t y 例5.2.另一个简单的随机时间列序被称为随机游走(random walk ):~,是一个白噪声。
1t t t y y ε-=+t ε2(0,)iid σ 容易判断该序列有相同的均值:,但是方差,即1()()t t E y E y -=2()t Var y t σ=的方差与时间t 有关而非常数,它是一非平稳序列。
ARCH模型 计量经济学 EVIEWS建模课件

例如Engle-Ito-Lin(1990)在对日元兑美元汇率
的研究中得到如下结果,
st2= 0.0006 + 0.1169et-12- 0.0627 et-22 - 0.0047 et-32 0.0181 et-42 + 0.9581st-12
虽然参数的和是0.9895,小于1。但δi, i = 2, 3, 4 是负的。Nelson-Cao(1992)认为参数非负的约束
可以放宽要求。对于GARCH(1, q) 模型,
t2
=
δ0
+
δ1
εt
–1
2
+
…
+
δq
εt
–q
2
+
1
t
2 -1
t2非负的充分与必要条件是:δ0 0;1 0;
k
ki i1 1
0, k
0,1,q
1
i0
二、ARCH模型的建立
㈠检验均值模型的残差ARCH效果
⒈ 残差的分布及其假设 选择Y=XB或A(L)Y=W(L)ε对均值模型的估计会 得到残差的估计值,如果模型的残差具有异方差 性,那么使用非线性的估计才是有效的。 在模型的误差项服从ARCH过程的情况下,如 果模型仍然服从其他的基本假设,则OLS估计仍然 有效,即使误差项非正态也会渐近有效。
1
2ht
exp
(Yt
Yt )2
2ht
⑵对于误差服从t分布的GARCH(1,1)过程,在 k→∞时,接近正态分布,其对数似然函数为:
容量为T。
εt ARCH (q)可以表示为:εt=σtvt。要注意:
E(εt) = 0;vt iidN(0, 1);2t = E(ε2t) = ht;
arch模型
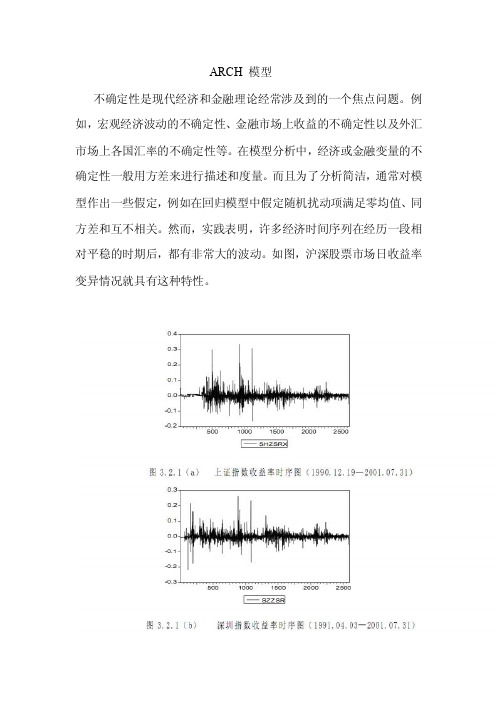
ARCH 模型不确定性是现代经济和金融理论经常涉及到的一个焦点问题。
例如,宏观经济波动的不确定性、金融市场上收益的不确定性以及外汇市场上各国汇率的不确定性等。
在模型分析中,经济或金融变量的不确定性一般用方差来进行描述和度量。
而且为了分析简洁,通常对模型作出一些假定,例如在回归模型中假定随机扰动项满足零均值、同方差和互不相关。
然而,实践表明,许多经济时间序列在经历一段相对平稳的时期后,都有非常大的波动。
如图,沪深股票市场日收益率变异情况就具有这种特性。
在这种情况下,同方差假定是不恰当的。
在这种情况下,人们关心的是如何预测序列的条件方差。
例如,作为资产持有者,他既关心收益率的预测值,同时也关心持有期内方差的大小。
如果一位投资者计划在第 t 时期买入某项资产,在第 t+1 时期售出,则无条件方差(即方差的长期预测值)对他来讲就不重要了。
对于这一类问题,可以使用自回归条件异方差模型 (autoregressive conditiona heteroskedastic model ,简称 ARCH 模型)来进行分析。
最早的 ARCH 模型是由 Robert Engle 于 1982 年建立的,因此它的发展历史不长。
但是,这种模型及其各种推广形式已被广泛应用于经济和金融数据序列的分析,ARCH 模型族已成为研究经济变量变异聚类特性的有效工具。
第一节 ARCH 模型的概念与性质 1、ARCH 过程ARCH 模型的一般性定义如下。
假设时间序列{}t y 服从如下回归模型:'t t ty x u ξ=+(8.1.1)其中 t x 是外生变量向量,它可以包含被解释变量的滞后项,ξ是回归参数向量。
如果扰动项序列{}t u 满足:11|~(0,)(,,)t t t t t t q u N h h h u u ---Ω= (8.1.2)其中:11122{,',,'}t t t t t y x y x -----Ω= 为t 时期以前的信息集。
金融计量经济第三讲ARCH模型的理论与应用

讨论课内容
• 1、利用证券市场指数数据分析股票市场的 衰减系数; • 2、非对称ARCH模型—TARCH和EGARCH模型的应用
练习,可采用自回归模型和单指数模型; • 3、准备讨论课内容,分小组,每组最多3人,讨论较前沿 的金融计量应用论文,最好是外文文献,若有思想较好的 个人作品也可。课堂讨论时间每组30分钟左右,听课的同 学可提问。请在二周后上报小组成员名单及分工。 • 1和2需要将分析结果做成文挡,电邮给老师(下周前)。 • Zhujin@
• (*)和(**)有何区别? • 此方法可以用于期货价格、自由汇率等时间序列 的计算,不同问题结果分析时有所侧重。
不同阶段的时间序列的结果(当堂演算): • 从1991年3月到95年12月:衰减系数>1,不符 合GARCH模型的要求; • 从95年12月到98年12月,衰减系数=0.92; • 98年12月到今,衰减系数=0.97
H0 : 1 2 q 0; H1 : i 0,1 i q
ht 0 1 t 1 q t q t (3.6)
例3.1:开放式基金与股价指数因果 关系分析
• 选指数型基金一家,上证180指数为解释变 量,讨论之间是否有ARCH特征。
时间序列分析上机练习参考
• 有用的时间序列数据:各市场中的股价指数、行 业指数、个股价格、成交量;开放式基金或封闭 式基金净值与价格,开放式基金规模;期货价格、 持仓量、交易量;外汇交易价格;CPI;GDP; 其它金融时间序列; • 练习目的:掌握并熟练ADF检验、单整与协整检 验、EMC、Granger因果检验、ARCH系列应用 • 建模参考:A、B市场关联性、基金与股价指数的 关联性、购买力平价模型、股价与CPI或GDP的 关系,基金规模与股价或净值的关系等; • 选择一些建模主题,寻找数据,进行各项检验及 回归分析。Βιβλιοθήκη 第三节 其它ARCH类模型
时间序列计量经济学模型概述

时间序列计量经济学模型概述时间序列计量经济学模型是在经济学研究中广泛使用的一种方法,用于分析经济变量随时间的变化。
该模型基于时间序列数据,即经济变量在一段时间内的观测值。
时间序列计量经济学模型的核心是建立经济变量之间的关系,以解释和预测经济现象的变化。
其中最常用的模型是自回归移动平均模型(ARMA)、自回归条件异方差模型(ARCH)和季节性时间序列模型。
自回归移动平均模型(ARMA)是一个包含自回归项和移动平均项的线性模型。
该模型以过去的观测值和随机项为输入,预测当前观测值。
ARMA模型基于假设,即经济变量的行为受到历史观测值的影响。
自回归条件异方差模型(ARCH)是一种考虑了随时间变化方差的模型。
该模型通过引入一个条件异方差项,模拟经济变量中的波动性。
ARCH模型的应用范围广泛,特别是在金融市场波动性分析中。
季节性时间序列模型用于分析具有明显季节性特征的经济变量,如销售额、就业人数等。
这些模型通常基于季节、趋势和随机成分的组合,以预测未来观测值。
在建立时间序列计量经济学模型时,常常需要进行模型识别、参数估计和模型诊断等步骤。
识别模型的目标是确定适当的模型结构,参数估计则是利用历史数据估计模型的参数值。
模型诊断用于检验模型的拟合程度和误差分布是否符合模型假设。
时间序列计量经济学模型在经济研究中有广泛的应用,例如预测未来经济指标、分析经济周期和波动性、评估政策效果等。
它提供了一种量化的方法,使经济学家可以更好地理解和解释经济变量的演变。
时间序列计量经济学模型是经济学研究中一种重要的统计工具,广泛应用于宏观经济、金融市场和企业经营等领域。
它可以帮助我们理解和解释经济变量随时间的变化规律,进行预测和政策分析。
本文将进一步探讨时间序列计量经济学模型的相关概念和应用。
在构建时间序列计量经济学模型之前,首先需要了解时间序列数据的特点。
时间序列数据是按照时间顺序排列的一系列观测值,通常具有趋势性、季节性、周期性和随机性等特征。
计量经济学(3)

则称
t 服从EGARCH过程。
模型中条件方差采用了自然对数形式,意味着 ht 非负且杠 杆效应是指数型的。若 0 ,说明信息作用非对称。 当 0 时,杠杆效应显著。
17
2. (G)ARCH-M模型
如果随机过程{ y t}有表现形式
t = 1,2,.......,T。
yt = x t' + g ( ht ) + t 其中, t = ht v t { v t }独立同分布,且 v t ~N(0,1),
6
(2) 模型形式
ARCH模型也可以表述为
t =
ht v t
ht
= a 0 + a1 t21 + ...... + a q t2q
其中,{ v t} 独立同分布,且 v t ~ N(0,1), t = 1,2,.......,T。
7
3. ARCH效应检验 拉格朗日乘子检验(LM检验) 辅助回归模型
22
5. PARCH模型
t
=
ht v t
q
ht 0 j ( t j j t j ) i ht i
p
其中,
j 1
> 0,
1.
i 1
是标准差 ht
的幂参数,
用来评价冲击对条件方差的影响幅度; 0 ,存在非 对称效应. 模型中, = 2 , = 0 ,则PARCH模型为GARCH模型.
上述过程称为广义的ARCH过程,简称为GARCH过程, 记作 t ~ GARCH(p ,q)。 与ARMA模型类似,当ARCH( q )中, q 很大时, 可以进行结构变化。 12
计量经济学经典eviewsARCH和GARCH估计

计量经济学经典eviews ARCH 和GARCH 估计本章讨论的工具是建立变量的条件方差或变量波动性模型。
自回归条件异方差((Autoregressive Conditional Heteroscedasticity Model ,ARCH )模型是特别用来建立条件方差模型并对其进行预测的。
ARCH 模型由Engle (1982)提出,并由Bollerslev(1986)发展成为GARCH(Generalized ARCH)——广义自回归条件异方差。
这些模型被广泛的应用于经济学的各个领域。
尤其在金融时间序列分析中。
§16.1 ARCH 的说明ARCH 的主要思想是时刻t 的ε的方差(= σ 2)依赖于时刻(t ─ 1)的平方误差的大小,即依赖于21-t ε。
t t k k t t X X Y εβββ++++= 110 (1)并假设在时刻(t-1)所有信息的条件下,干扰项的分布是:t ε~())(,02110-+t N εαα (2) 即t ε遵循以0为均值,)(2110-+t εαα为方差的正态分布。
由于(2)中的t ε的方差依赖于前期的平方干扰,我们称它为ARCH(1)过程。
然而,容易加以推广,一个ARCH (p )过程可以写为:222221102)var(p t p t t t t ---++++==εαεαεαασε (3)如果误差方差中没有自相关,就会有H 0:021====p ααα 。
这时02)var(ασε==t ,从而得到误差方差的同方差性情形。
恩格尔曾表明,容易通过以下的回归去检验上述虚拟假设:222221102ˆˆˆˆˆp t p t t t ---++++=εαεαεααε(4) 其中,t εˆ表示从原始回归模型(1)估计得到的OLS 残差。
一、GARCH (1,1)模型在标准化的GARCH(1,1)模型中:t t t x y εγ+= (16.1)21212--++=t t t βσαεωσ (16.2)(16.1)中给出的均值方程是一个带有误差项的外生变量函数。
计量经济学讲义第十讲(共十讲)

第十讲 ARCH 模型及其扩展一、数学准备:迭代期望定律我们在第二讲中的笔记部分涉及到迭代期望定律。
作为复习,此处把该定律再展示一次。
如果信息集Θ⊆Ω,则有][()()E E X E X ΩΘ=Θ,此即迭代期望定律。
为了理解上述等式,考虑一个极端情况:Ω包含了全部的信息,则基于信息集Ω对x 的预测将没有任何预测误差,即有:()E X X Ω=,因此必有][()()E E X E X ΩΘ=Θ。
另外,无条件期望所对应的信息集是空集,因此按照迭代期望定律必有:[()]()E E XE X Ω=。
二、ARCH 模型考虑如下一个模型:01t t t y x φφε=++ (1)其中t tv ε=t v 是白噪声,方差为21vδ=;t v 和(1)t i i ε-≥相互独立;0110,,...,0,1ppi i a a a a =>≥<∑。
对上述模型,可以验证: (1))0(t E ε=练习:证明上式。
(2))0,0(t t i i E εε-=≠,即误差项序列无关。
证明:首先,,...,,...,1212,,...,,,...,)))0(((t t t t i t i t i t p t i t t t p t i t t E E E εεεεεεεεεεεεεε-----------=== 其次,按照迭代期望定律有:,...,12,,...,)])[((t t t i t i t p t i t t E E E εεεεεεεε------=因此有:)0,0(t t i i E εε-=≠(3)201)1(tpii a a E ε==-∑证明:22220011[()]())(tppt i t i i t i i i v a a a a E EE εεε--==+=+=∑∑令2)(t t x E ε=,则有差分方程:01t t i pi i x a a x -==+∑由于11,...,0,1ppi i a a a =≥<∑,故上述差分方程满足平稳性的充分条件:11pii a =<∑(参见第八讲附 录),因此,当t 趋于无穷大时t x 收敛于均衡值x*,其中01pi i xa a x**==+∑,即11pii a a x*==-∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从深证综指收益率的自相关图可知:深证综指收益率与 滞后1 阶、4 阶相关性相对较强,因此,应建立深证综指 日收益率的自回归模型对深证综指收益率进行修正。 Quick-series statistics-correlogram
平稳性检验结果
单位根检验
均值方程估计
由上述自相关(偏自相关)检验可知, 应建立一个AR(4)模型。 即:Rt =a1Rt-1 +a2Rt-4 +ut 命令: LS R R(-1) R(-4)
(1)ARCH 模型 均值方程 xt = 0 + 1 xt -1 + 2 xt -2 + … + p xt - p + ut t2 = E(ut2) = 0 + 1 ut -1 2 + 2 ut -22 + … + q ut - q2 (2)GARCH 模型 方差方程 xt = 0 + 1 xt -1 + 2 xt -2 + … + p xt - p + ut t2 = 0 + 1 ut –1 2 + 1 t -12 (3)TGARCH 模型 t2 = 0 + 1 ut –1 2 + ut –1 2 dt –1 + 1 t -12
方差方程估计——GARCH模型
GARCH(1,1)模型是指含有一个ARCH项,一个GARCH项。 即: 2 2 2 σ t =α0+αu t-1 +βσ t-1
σ t =0.0001+0.0846u
(1.9870)(2.3376)
2
2 t-1
+0.7788σ
2 t-1
(8.6083)
(经检验GARCH滞后阶数选择1阶拟合效果是最好的,同时,回归结果也显示,均值方程系
数显著性下降,故GARCH模型拟合效果不太理想)
方差方程估计——GARCH模型
一般的,GARCH(p,q), p是GARCH 项的最大滞后阶数,q是ARCH项的最大滞后 阶数。 GARCH模型更一般的形式是:
t
2
= t -i
i 1
q
2
t j
j 1
p
2
当所有 项都等于0时, GARCH(p, q)模型变成了纯ARCH(q)模型。
参数估计
由参数估计结果可得以下结果: Rt =0.068Rt-1 +0.121Rt-4 +ut (0.043) (0.043)
标准差
ARCH 模型的选择
残差图显示模型存在自回归条件异方差
ARCH-LM效应检验
由于股票市场的股票价格及收益率的预 测误差常常是成群出现而呈现出异方差, 因此,有必要对深证综指收益率自回归模 型的残差是否存在条件异方差(ARCH)进行 检验。 ARCH-LM 检验是检验模型的残差系 列中是否存在ARCH 效应的拉格朗日乘数 检验,该检验的原假设:残差系列中直到p 阶都不存在ARCH 效应。
方差方程估计——ARCH模型
Quick-estimate equation-ARCH σ2t =α0+αu2t-1
σ t =0.000646+0.1124u
2 2 t-1
(14.3753) (2.0105) (经检验ARCH滞后阶数选择1阶拟合效果是最好的)
方差方程估计——GARCH模型
滞后项中1、4、9阶显著,阶数较多可以尝试建立 GARCH模型,这里尝试建立GARCH(1,1)模型。
高峰厚尾分布曲线
正态分布曲线
日元兑美元汇率差分序列(收益)D(JPY)
高峰厚尾分布特征示意图
案例:深圳综指的建模研究
选取深圳综指2007.1.4-2009.3.30间每个 交易日收盘价P(共544个有效样本数据) 作为样本序列。
用深圳综合指数收益率Rt=ln( pt/pt-1)建 立时间序列模型(共543个有效样本数据) 。
回 归 分 析
时间序列回归 联立方程模型(结构、简化型、递归模型) PANEL(面板数据)模型、空间计量模型 DS(离散选择)模型、有序响应、计数模型 LDV(受限因变量)模型(删失、截断模型)
截面数据回归
蒙特卡罗模拟技术
ARCH模型简介
ARCH模型是获得2003年诺贝尔经济学 奖的计量经济学成果之一。被认为是最集 中反映了方差变化特点而被广泛应用于金 融数据时间序列分析的模型。 目前所有的波动率模型中,ARCH类模型 无论从理论研究的深度还是从实证运用的 广泛性来说都是独一无二的。
ARCH检验结论
显然,无论是ARCH-LM检验还是残差相关图 检验,都显示P值很大,即残差的自相关关系不 再显著,最终剩余的残差是真正的白噪声。 残差ARCH 效应检验结果表明深证综指收益 率的自相关修正后的TARCH 模型的残差系列不 存在ARCH 效应,即含有一阶非对称效应TARCH 模型较好的消除了深证综指收益率残差的条件异 方差。因此,深证综指日收益率的TARCH模型能 较好的反映收益率的波动变化。
单位根检验
时间序列的加法、乘法模型,X12 季节调整 ARIMA(时间序列)模型
线性时间序列 单 序
SARIMA(季节时间序列)模型 GAR(广义自回归)模型 BL(双线性)模型
当 代 计 量 经 济 模 型 体 系
时 间 序 列 分 析
列 非线性时间序列 TAR、STAR(门限自回归、平滑转移)模型 ARCH、GARCH (自回归条件异方差)模型 向 量 序 列 波动模型 SV(随机波动)模型 ACD、SCD(自回归、随机条件久期)模型 研究 VAR、VEC(向量自回归、误差修正)模型 单方程(线性、非线性) 、分位数回归模型
Quick-series statistics-unit root test
平稳性检验结论
在1%、5%、10%的显著性水平之下, 都拒绝有一个单位根的假设,说明深证综 指收益率平稳。 这个结果与国外学者对发达成熟市场波 动性的研究一致:金融资产的价格一般是 非平稳的,而收益率序列通常是平稳的。
自相关检验
总结
ARCH模型通常对主体模型的随机扰动项进 行建模分析。以便充分的提取残差中的信息,使 得最终的模型残差ηt成为白噪声序列。该残差最 终消除了深证综指收益率波动的集群效应(即方 差具有记忆性),这便是模型的精髓 。 整体思路: 1、自相关——均值方程 2、ARCH效应检验——方差方程(初步提取残 差中的相关信息) 3、建模——最终残差(白噪声)
序列的特征是“波动集群”、分布是“高峰厚尾”
ARCH,GARCH模型可以预测被解释变量的方差。对于金融时间 序列预测的是风险。 建立ARCH,GARCH模型可以提高均值方程参数估计的有效性。
6 4 2 0 -2 -4 -6 -8 200 400 600 800 1000 1200 1400 D(JPY) (1995-2000)
0, 其中 d t 1, ut 0 ut 0
TARCH 模型对于利好和利坏消息反应是不一样的。
ARCH模型基本思想
在以前信息集下,某一时刻一个噪声的 发生是服从正态分布。该正态分布的均值 为零,方差是一个随时间变化的量(即为条 件异方差)。并且这个随时间变化的方差是 过去有限项噪声值平方的线性组合(即为自 回归)。这样就构成了自回归条件异方差模 型。
ARCH-LM效应检验结果
1阶
View-residual test-ARCH test F 统计量及T×R2 统计量的P 值都小于0.05,因此, 在5%的显著性水平下,深证综指收益率自回归模型的残 差存在ARCH 效应。 滞后阶数选择1阶(2阶及以后阶数P值无1阶显著)
2阶
3阶
4阶
5阶
相比较而言,4阶又比2、3、5及5阶以后的残差更具显著 性
Rt描述性统计(尖峰厚尾)
深证综指日收益率峰度为3.755,高于正态分布的峰度值3,说 明深证综指具有一定的尖峰厚尾的特征,J-B检验也证实了深证综指 日收益率的分布显著异于正态分布。 View-Descriptive Statistics-Histo列是非平稳的,即 使使用最小二乘法拟合模型的效果很好, 建立的模型也可能由于序列的非平稳性而 导致伪回归。因此,有必要在对时间序列 分析前,先对序列的平稳性进行检验。
