全国版2017版高考数学一轮复习第七章立体几何7.4直线平面平行的判定及其性质课件理
高考数学一轮复习 第7章 立体几何 第4讲 直线、平面平行的判定与性质课件

图形
条件 结论
a∩α=∅ a∥α
a⊂α,b⊄α,_a_∥__b____ __a_∥__α___
b∥α
a∩α=∅
a∥α,a⊂β,_α_∩__β_=__b___ __a_∥__b___
12/11/2021
• 知识点二 面面平行的判定与性质
判定
性质
定义
定理
图形
条件 α∩β=∅
结论
α∥β
a⊂β,b⊂β, a∩b α∥β,α∩γ=a, =P, a∥α,b∥α β∩γ=b
∴EF∥平面 PCD.
12/11/2021
②∵四边形 ABCD 是矩形,
∴AD⊥AB,AD∥BC.
又 AD⊂平面 PAD,BC⊄平面 PAD,
∴BC∥平面 PAD.
∵平面 PAB⊥平面 ABCD,平面 PAB∩平面 ABCD=AB,AD⊂平面 ABCD,
∴AD⊥平面 PAB,∴AD⊥BP,平面 PAD⊥平面 PAB.
12/11/2021
证法三:取 CD 的中点 H,连 BH,HE, ∵E 为 PC 中点,∴EH∥PD, 又 EH⊄平面 PAD,PD⊂平面 PAD, ∴EH∥平面 PAD, 又由题意知 AB 綊 DH,∴BH∥AD, 又 AD⊂平面 PAD,BH⊄平面 PAD, ∴BH∥平面 PAD,又 BH∩EH=H,
12/11/2021
空间中证明两条直线平行的常用方法 (1)利用线面平行的性质定理,即 a∥α,a⊂β,α∩β=b⇒a∥b. (2)利用平行公理推论:平行于同一直线的两条直线互相平行. (3)利用垂直于同一平面的两条直线互相平行.
12/11/2021
〔变式训练 2〕 (1)(角度 2)如图所示,四边形 ABCD 是平行四边形,点 P 是 平面 ABCD 外一点,M 是 PC 的中点,在 DM 上取一点 G,过 G 和 PA 作平面 PAHG 交平面 BMD 于 GH. 求证:PA∥GH. (2)(角度 1)(2019·贵州黔东南州二模)在四棱锥 P-ABCD 中, 四边形 ABCD 是矩形,平面 PAB⊥平面 ABCD,点 E,F 分别为 BC,AP 的中点. ①求证:EF∥平面 PCD; ②若 AD=AP=PB= 22AB=1.求三棱锥 P-DEF 的体积.
高考数学一轮复习 第七章 立体几何 第4讲 直线、平面平行的判定及性质课件 文 高三全册数学课件

2021/12/8
第十八页,共五十页。
因为侧面 PAD 为等边三角形且垂直于底面 ABCD,平面 PAD∩ 平面 ABCD=AD,所以 PM⊥AD,PM⊥底面 ABCD,因为 CM⊂底 面 ABCD,所以 PM⊥CM.
(1)B,C,H,G 四点共面; (2)平面 EFA1∥平面 BCHG.
2021/12/8
第三十二页,共五十页。
[证明] (1)因为 G,H 分别是 A1B1,A1C1 的中点,所以 GH 是△ A1B1C1 的中位线,所以 GH∥B1C1.又因为 B1C1∥BC,所以 GH∥BC, 所以 B,C,H,G 四点共面.
∴FA 綊12CD.∴FA 綊 GE.
∴四边形 AFGE 为平行四边形,∴FG∥AE. 又 FG⊄平面 AEC,AE⊂平面 AEC,∴FG∥平面 AEC.
2021/12/8
第二十七页,共五十页。
题型二 平面与平面平行的判定与性质(重点保分题,共同探讨) 例 1 如图,四棱柱 ABCD-A1B1C1D1 的底面 ABCD 是正方形,O 是底面中心,A1O⊥底面 ABCD,AB=AA1= 2.
所以 GK=3.
故四边形 GEFH 的面积 S=GH+2 EF·GK=4+2 8×3=18.
2021/12/8
第二十三页,共五十页。
方法感悟 1.证明直线与平面平行的关键是设法在平面内找到一条与已知 直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面 平行的性质,或者构造平行四边形等证明两直线平行.注意说明已知 的直线不在平面内. 2.判断或证明线面平行的常用方法: (1)利用线面平行的定义(无公共点); (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α); (3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β); (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
高考数学一轮复习第7章立体几何第4节直线、平面平行的判定及其性质教师用书
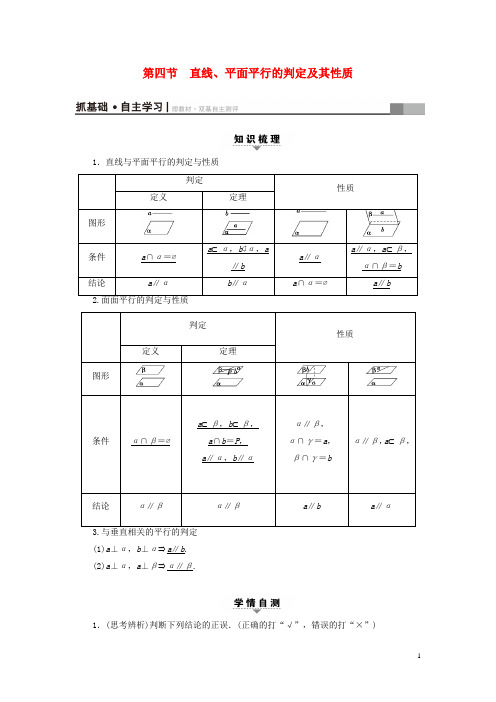
第四节 直线、平面平行的判定及其性质1.直线与平面平行的判定与性质(1)a ⊥α,b ⊥α⇒a ∥b . (2)a ⊥α,a ⊥β⇒α∥β.1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)若一条直线和平面内一条直线平行,那么这条直线和这个平面平行.( )(2)若直线a∥平面α,P∈α,则过点P且平行于直线a的直线有无数条.( )(3)若一个平面内有无数条直线与另一个平面平行,则这两个平面平行.( )(4)若两个平面平行,则一个平面内的直线与另一个平面平行.( )[答案](1)×(2)×(3)×(4)√2.(教材改编)下列命题中,正确的是( )A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何平面B.若直线a和平面α满足a∥α,那么a与α内的任何直线平行C.若直线a,b和平面α满足a∥α,b∥α,那么a∥bD.若直线a,b和平面α满足a∥b,a∥α,b⊄α,则b∥αD[根据线面平行的判定与性质定理知,选D.]3.设α,β是两个不同的平面,m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则α∥β的一个充分不必要条件是( )A.m∥β且l1∥αB.m∥β且n∥l2C.m∥β且n∥βD.m∥l1且n∥l2D[m∥l1且n∥l2⇒α∥β,但α∥βD/⇒m∥l1且n∥l2,∴“m∥l1且n∥l2”是“α∥β”的一个充分不必要条件.]4.在正方体ABCDA1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系是________.平行[如图所示,连接BD交AC于F,连接EF,则EF是△BDD1的中位线,∴EF∥BD1,又EF⊂平面ACE,BD1⊄平面ACE,∴BD1∥平面ACE.]5.(2017·杭州二中质检)设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊂α,n∥α,则m∥n;②若α∥β,β∥γ,m⊥α,则m⊥γ;③若α∩β=n,m∥n,m∥α,则m∥β;④若α⊥γ,β⊥γ,则α∥β.其中是真命题的是________(填上序号).②[①,m∥n或m,n异面,故①错误;易知②正确;③,m∥β或m⊂β,故③错误;④,α∥β或α与β相交,故④错误.]) A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行...,则在α内不存在...与β平行的直线D.若m,n不平行...垂直于同一平面...,则m与n不可能D[A项,α,β可能相交,故错误;B项,直线m,n的位置关系不确定,可能相交、平行或异面,故错误;C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;D项,假设m,n垂直于同一平面,则必有m∥n,所以原命题正确,故D项正确.] [规律方法] 1.判断与平行关系相关命题的真假,必须熟悉线、面平行关系的各个定义、定理,无论是单项选择还是含选择项的填空题,都可以从中先选出最熟悉最容易判断的选项先确定或排除,再逐步判断其余选项.2.(1)结合题意构造或绘制图形,结合图形作出判断.(2)特别注意定理所要求的条件是否完备,图形是否有特殊情形,通过举反例否定结论或用反证法推断命题是否正确.[变式训练1] (2017·宁波中学模拟)若m,n表示不同的直线,α,β表示不同的平面,则下列结论中正确的是( )A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α⊥β,m∥α,n∥β,则m∥nD.若α∥β,m∥α,n∥m,n⊄β,则n∥βD[在A中,若m∥α,m∥n,则n∥α或n⊂α,故A错误.在B中,若m⊂α,n⊂β,m∥β,n∥α,则α与β相交或平行,故B错误.在C中,若α⊥β,m∥α,n∥β,则m与n相交、平行或异面,故C错误.在D中,若α∥β,m∥α,n∥m,n⊄β,则由线面平行的判定定理得n∥β,故D正确.](2017·南通模拟)如图741所示,斜三棱柱ABCA1B1C1中,点D,D1分别为AC ,A 1C 1上的点.图741(1)当A 1D 1D 1C 1等于何值时,BC 1∥平面AB 1D 1? (2)若平面BC 1D ∥平面AB 1D 1,求AD DC的值. 【导学号:51062232】 [解] (1)如图所示,取D 1为线段A 1C 1的中点,此时A 1D 1D 1C 1=1.2分连接A 1B ,交AB 1于点O ,连接OD 1.由棱柱的性质知,四边形A 1ABB 1为平行四边形, ∴点O 为A 1B 的中点.在△A 1BC 1中,点O ,D 1分别为A 1B ,A 1C 1的中点, ∴OD 1∥BC 1.4分又∵OD 1⊂平面AB 1D 1,BC 1⊄平面AB 1D 1, ∴BC 1∥平面AB 1D 1. ∴当A 1D 1D 1C 1=1时,BC 1∥平面AB 1D 1.6分 (2)由平面BC 1D ∥平面AB 1D 1,且平面A 1BC 1∩平面BC 1D =BC 1,平面A 1BC 1∩平面AB 1D 1=D 1O 得BC 1∥D 1O ,8分∴A 1D 1D 1C 1=A 1OOB, 又由题(1)可知A 1D 1D 1C 1=DC AD ,A 1OOB=1, ∴DC AD =1,即AD DC=1.15分[规律方法] 1.判断或证明线面平行的常用方法有:(1)利用反证法(线面平行的定义);(2)利用线面平行的判定定理(a ⊄α,b ⊂α,a ∥b ⇒a ∥α); (3)利用面面平行的性质定理(α∥β,a ⊂α⇒a ∥β); (4)利用面面平行的性质(α∥β,a ⊄β,a ∥α⇒a ∥β).2.利用判定定理判定线面平行,关键是找平面内与已知直线平行的直线.常利用三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线.[变式训练2] 如图742,四棱锥P ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.图742(1)证明:PB ∥平面AEC ;(2)设AP =1,AD =3,三棱锥P ABD 的体积V =34,求A 到平面PBC 的距离. [解] (1)证明:设BD 与AC 的交点为O ,连接EO .因为四边形ABCD 为矩形, 所以O 为BD 的中点, 又E 为PD 的中点, 所以EO ∥PB .4分因为EO ⊂平面AEC ,PB ⊄平面AEC , 所以PB ∥平面AEC .6分 (2)由V =16PA ·AB ·AD =36AB ,又V =34,可得AB =32. 作AH ⊥PB 交PB 于点H .10分由题设知BC ⊥平面PAB ,所以BC ⊥AH , 故AH ⊥平面PBC .在Rt △PAB 中,由勾股定理可得PB =132,所以AH =PA ·AB PB =31313.所以A 到平面PBC 的距离为31313.15分如图743所示,在三棱柱ABC A 1B 1C 1中,E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点,求证:图743(1)B ,C ,H ,G 四点共面; (2)平面EFA 1∥平面BCHG .[证明] (1)∵G ,H 分别是A 1B 1,A 1C 1的中点, ∴GH 是△A 1B 1C 1的中位线,GH ∥B 1C 1.4分 又∵B 1C 1∥BC , ∴GH ∥BC ,∴B ,C ,H ,G 四点共面.6分(2)在△ABC 中,E ,F 分别为AB ,AC 的中点, ∴EF ∥BC .∵EF ⊄平面BCHG ,BC ⊂平面BCHG , ∴EF ∥平面BCHG .8分 ∵A 1G 綊EB ,∴四边形A 1EBG 是平行四边形,则A 1E ∥GB . ∵A 1E ⊄平面BCHG ,GB ⊂平面BCHG , ∴A 1E ∥平面BCHG .12分 ∵A 1E ∩EF =E ,∴平面EFA 1∥平面BCHG .15分[迁移探究] 在本例条件下,若点D 为BC 1的中点,求证:HD ∥平面A 1B 1BA . [证明] 如图所示,连接HD ,A 1B ,∵D为BC1的中点,H为A1C1的中点,∴HD∥A1B.8分又HD⊄平面A1B1BA,A1B⊂平面A1B1BA,∴HD∥平面A1B1BA.15分[规律方法] 1.判定面面平行的主要方法:(1)面面平行的判定定理.(2)线面垂直的性质(垂直于同一直线的两平面平行).2.面面平行的性质定理的作用:(1)判定线面平行;(2)判断线线平行,线线、线面、面面平行的相互转化是解决与平行有关的问题的指导思想.解题时要看清题目的具体条件,选择正确的转化方向.易错警示:利用面面平行的判定定理证明两平面平行时,需要说明是一个平面内的两条相交直线与另一个平面平行.[变式训练3] 如图744所示,在正方体ABCDA1B1C1D1中,S是B1D1的中点,E,F,G 分别是BC,DC,SC的中点,求证:图744(1)直线EG∥平面BDD1B1;(2)平面EFG∥平面BDD1B1.【证明】(1)如图所示,连接SB,∵E,G分别是BC,SC的中点,∴EG∥SB.3分又∵SB⊂平面BDD1B1,EG⊄平面BDD1B1,∴直线EG∥平面BDD1B1.7分(2)连接SD,∵F,G分别是DC,SC的中点,∴FG∥SD.10分又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1,∴FG∥平面BDD1B1,且EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G,∴平面EFG∥平面BDD1B1.15分[思想与方法]1.线线、线面、面面平行的相互转化其中线面平行是核心,线线平行是基础,要注意它们之间的灵活转化.2.直线与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)面与面平行的性质.3.平面与平面平行的主要判定方法(1)定义法;(2)判定定理;(3)推论;(4)a⊥α,a⊥β⇒α∥β.[易错与防范]1.在推证线面平行时,一定要强调直线不在平面内,否则会出现错误.2.(1)在面面平行的判定中易忽视“面内两条相交直线”这一条件.(2)如要一个平面内有无数条直线与另一个平面平行,易误认为这两个平面平行,实质上也可以相交.3.在应用性质定理时,要遵从由“高维”到“低维”,但也要注意,转化的方向总是由题目的具体条件而定,决不可过于“模式化”,另外要注意符号语言的规范应用.课时分层训练(三十九)直线、平面平行的判定及其性质A组基础达标(建议用时:30分钟)一、选择题1.设m,n是不同的直线,α,β是不同的平面,且m,n⊂α,则“α∥β”是“m ∥β且n∥β”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A[若m,n⊂α,α∥β,则m∥β且n∥β;反之若m,n⊂α,m∥β,且n∥β,则α与β相交或平行,即“α∥β”是“m∥β且n∥β”的充分不必要条件.]2.正方体ABCDA1B1C1D1中,E,F,G分别是A1B1,CD,B1C1的中点,则正确的命题是( )图745A.AE⊥CGB.AE与CG是异面直线C.四边形AEC1F是正方形D.AE∥平面BC1FD[由正方体的几何特征知,AE与平面BCC1B1不垂直,则AE⊥CG不成立;由于EG∥A1C1∥AC,故A,E,G,C四点共面,所以AE与CG是异面直线错误;在四边形AEC1F中,AE=EC1=C1F=AF,但AF与AE不垂直,故四边形AEC1F是正方形错误;由于AE∥C1F,由线面平行的判定定理,可得AE∥平面BC1F.]3.(2017·湖州模拟)如图746所示的三棱柱ABCA1B1C1中,过A1B1的平面与平面ABC 交于DE,则DE与AB的位置关系是( )图746A.异面B.平行C.相交D.以上均有可能B[在三棱柱ABCA1B1C1中,AB∥A1B1.∵AB⊂平面ABC,A1B1⊄平面ABC,∴A1B1∥平面ABC.∵过A1B1的平面与平面ABC交于DE,∴DE∥A1B1,∴DE∥AB.]4.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )【导学号:51062233】A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥αB[若m∥α,n∥α,则m,n平行、相交或异面,A错;若m⊥α,n⊂α,则m⊥n,因为直线与平面垂直时,它垂直于平面内任一直线,B正确;若m⊥α,m⊥n,则n∥α或n⊂α,C错;若m∥α,m⊥n,则n与α可能相交,可能平行,也可能n⊂α,D错.] 5.给出下列关于互不相同的直线l,m,n和平面α,β,γ的三个命题:①若l 与m 为异面直线,l ⊂α,m ⊂β,则α∥β; ②若α∥β,l ⊂α,m ⊂β,则l ∥m ;③若α∩β=l ,β∩γ=m ,γ∩α=n ,l ∥γ,则m ∥n . 其中真命题的个数为( ) A .3 B .2 C .1D .0C [①中,当α与β不平行时,也可能存在符合题意的l ,m ;②中,l 与m 也可能异面;③中,⎩⎪⎨⎪⎧l ∥γ,l ⊂α,α∩γ=n⇒l ∥n ,同理,l ∥m ,则m ∥n ,正确.]二、填空题6.设α,β,γ为三个不同的平面,a ,b 为直线,给出下列条件:①a ⊂α,b ⊂β,a ∥β,b ∥α;②α∥γ,β∥γ;③α⊥γ,β⊥γ;④a ⊥α,b ⊥β,a ∥b .其中能推出α∥β的条件是________(填上所有正确的序号). ②④ [在条件①或条件③中,α∥β或α与β相交. 由α∥γ,β∥γ⇒α∥β,条件②满足.在④中,a ⊥α,a ∥b ⇒b ⊥α,从而α∥β,④满足.]7.如图747所示,正方体ABCD A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.图7472 [在正方体ABCD A 1B 1C 1D 1中,AB =2, ∴AC =2 2.又E 为AD 中点,EF ∥平面AB 1C ,EF ⊂平面ADC , 平面ADC ∩平面AB 1C =AC , ∴EF ∥AC ,∴F 为DC 中点, ∴EF =12AC = 2.]8.(2017·衡水模拟)如图748,在四面体ABCD 中,M ,N 分别是△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________.图748平面ABC ,平面ABD [连接AM 并延长交CD 于E ,则E 为CD 的中点.由于N 为△BCD 的重心, 所以B ,N ,E 三点共线,且EM MA =EN NB =12,所以MN ∥AB . 于是MN ∥平面ABD 且MN ∥平面ABC .] 三、解答题9.一个正方体的平面展开图及该正方体的直观图的示意图如图749所示. (1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (2)判断平面BEG 与平面ACH 的位置关系,并证明你的结论.【导学号:51062234】图749[解] (1)点F ,G ,H 的位置如图所示.6分(2)平面BEG ∥平面ACH ,证明如下: 因为ABCD EFGH 为正方体, 所以BC ∥FG ,BC =FG .9分又FG ∥EH ,FG =EH ,所以BC ∥EH ,BC =EH , 于是四边形BCHE 为平行四边形,所以BE ∥CH .12分 又CH ⊂平面ACH ,BE ⊄平面ACH , 所以BE ∥平面ACH .同理BG∥平面ACH.又BE∩BG=B,所以平面BEG∥平面ACH.15分10.(2017·绍兴质检)如图7410,在直三棱柱ABCA1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.图7410求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.[证明](1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.2分又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.6分(2)因为棱柱ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.8分因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.12分因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.15分B组能力提升(建议用时:15分钟)1.在四面体ABCD中,截面PQMN是正方形,则在下列结论中,错误的是( )A.AC⊥BDB.AC∥截面PQMNC.AC=BDD.异面直线PM与BD所成的角为45°C[因为截面PQMN是正方形,所以MN∥PQ,则MN∥平面ABC,由线面平行的性质知MN∥AC,则AC∥截面PQMN,同理可得MQ∥BD,又MN⊥QM,则AC⊥BD,故A、B正确.又因为BD∥MQ,所以异面直线PM与BD所成的角等于PM与QM所成的角,即为45°,故D正确.]2.如图7412所示,棱柱ABCA1B1C1的侧面BCC1B1是菱形,设D是A1C1上的点且A1B ∥平面B1CD,则A1D∶DC1的值为________. 【导学号:51062235】图74121 [设BC1∩B1C=O,连接OD.∵A1B∥平面B1CD且平面A1BC1∩平面B1CD=OD,∴A1B∥OD.∵四边形BCC1B1是菱形,∴O为BC1的中点,∴D为A1C1的中点,则A1D∶DC1=1.]3.如图7413所示,在三棱锥PABC中,平面PAC⊥平面ABC,PA⊥AC,AB⊥BC,设D,E分别为PA,AC的中点.(1)求证:DE∥平面PBC.(2)在线段AB上是否存在点F,使得过三点D,E,F的平面内的任一条直线都与平面PBC 平行?若存在,指出点F的位置并证明;若不存在,请说明理由.[解](1)证明:∵点E是AC中点,点D是PA的中点,∴DE∥PC.2分又∵DE⊄平面PBC,PC⊂平面PBC,∴DE∥平面PBC.6分(2)当点F是线段AB中点时,过点D,E,F的平面内的任一条直线都与平面PBC平行.8分证明如下:取AB的中点F,连接EF,DF.由(1)可知DE∥平面PBC.∵点E是AC中点,点F是AB的中点,∴EF∥BC.12分又∵EF⊄平面PBC,BC⊂平面PBC,∴EF∥平面PBC.又∵DE∩EF=E,∴平面DEF∥平面PBC,∴平面DEF内的任一条直线都与平面PBC平行.故当点F是线段AB中点时,过点D,E,F所在平面内的任一条直线都与平面PBC平行.15分。
【名师A计划】2017高考数学一轮复习 第七章 立体几何 第四节 直线、平面平行的判定及其性质课件 理

【参考答案】由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC, 所以四边形A1B1CD为平行四边形, 从而B1C∥A1D, 又A1D⊂平面A1DE,B1C⊄平面A1DE, 于是B1C∥平面A1DE.
又B1C⊂平面B1CD1,平面A1DE∩平面B1CD1=EF,
所以EF∥B1C.
线面平行的性质定理与判定定理的关系 直线与平面平行的判定定理和性质定理经常交替使用,要弄清定理的条件和结论,防止错用,它们有如下关 系:利用判定定理实施线线平行向线面平行的转化,利用性质定理实施线面平行向线线平行的转化.
3.已知m,n为异面直线,m∥平面α,n∥平面β,α∩β=l,则l ( A.与m,n都相交
)
B.与m,n中至少一条相交
C.与m,n都不相交 D.与m,n中一条相交 3.C 【解析】∵m∥平面α,n∥平面β,∴m与平面α没有公共点,n与平面β没有公共点,又∵α∩β=l,∴l⊂α,l⊂β, ∴l与m,n都不相交. 4.若M,N分别是△ABC边AB,AC的中点,MN与过直线BC的平面β的位置关系是 4.MN∥β或MN⊂β .
【变式训练】
已知四棱锥P-ABCD中,底面ABCD为平行四边形.点M,N,Q分别在PA,BD,PD上,且 PM∶MA=BN∶ND=PQ∶QD.求证:平面MNQ∥平面PBC. 【解析】∵PM∶MA=BN∶ND=PQ∶QD, ∴MQ∥AD,NQ∥BP,而BP⊂平面PBC,NQ⊄平面PBC,∴NQ∥平 面PBC. 又∵ABCD为平行四边形,BC∥AD, ∴MQ∥BC,而BC⊂平面PBC,MQ⊄平面PBC, ∴平面MNQ∥平面PBC.
面面平行的判定定理的应用 平面与平面平行的判定定理是证明面面平行的重要工具,由判定定理可知,要证明平面与平面平行,只要证明 一个平面上有两条相交直线都平行于另一个平面.由比例线段得到线线平行,依据线面平行的判定定理得到 线面平行,证得两条相交直线平行于一个平面后,转化为面面平行.一般证“面面平面”问题最终转化为证线与 线的平行.
高考数学一轮复习第7章立体几何第4讲直线平面平行的判定及性质课件

∴四边形 A1EBG 是平行四边形,∴A1E∥GB. ∵A1E⊄平面 BCHG,GB⊂平面 BCHG, ∴A1E∥平面 BCHG. ∵A1E∩EF=E,∴平面 EFA1∥平面 BCHG.
核心规律 1.平行问题的转化关系
2.判断直线与平面平行的关键是找平面内与已知直线平 行的直线.常考虑三角形的中位线、平行四边形的对边或过 已知直线作一平面找其交线.
∴VABCDFE=31×4×
3×2=8 3
3 .
(2)证明:由(1)知 AO∥FG,AO=FG, ∴四边形 AOFG 为平行四边形, ∴AG∥OF. 又∵DE∥BC,DE∩AG=G,DE⊂平面 ADE,AG⊂平 面 ADE,FO∩BC=O,FO⊂平面 BCF,BC⊂平面 BCF, ∴平面 ADE∥平面 BCF.
解析 由 m⊥n,m⊥α,可得 n∥α 或 n 在 α 内,当 n ∥β 时,α 与 β 可能相交,也可能平行,故①错.易知②③ 都正确.
触类旁通 解决有关线面平行、面面平行的基本问题要注意
(1)判定定理与性质定理中易忽视的条件,如线面平行 的判定定理中,条件“线在面外”易忽视.
(2)结合题意构造或绘制图形,结合图形作出判断. (3)举反例否定结论或用反证法推断命题是否正确.
跟踪训练 如图所示,在正方体 ABCD-A1B1C1D1 中,点 N 在 BD 上,点 M 在 B1C 上,且 CM=DN,求证:MN∥平面 AA1B1B.
证明 证法一:如下图,作 ME∥BC,交 BB1 于 E,作 NF∥AD,交 AB 于 F,连接 EF,则 EF⊂平面 AA1B1B.
触类旁通 判断或证明线面平行的常用方法
(1)利用线面平行的定义(无公共点); (2)利用线面平行的判定定理(a⊄α,b⊂α,a∥b⇒a∥α); (3)利用面面平行的性质定理(α∥β,a⊂α⇒a∥β); (4)利用面面平行的性质(α∥β,a⊄α,a⊄β,a∥α⇒a∥β).
2017届高三数学一轮复习课件:7-4 直线、平面平行的判定及其性质

[规律方法] 判定面面平行的四种方法 (1)利用定义:即证两个平面没有公共点(不常用)。 (2)利用面面平行的判定定理(主要方法)。 (3)利用垂直于同一条直线的两平面平行(客观题可用)。 (4)利用平面平行的传递性,即两个平面同时平行于第三个平面,则这两个 平面平行(客观题可用)。
第十九页,编辑于星期六:点 五十八分。
∴BC⊥PA,又PA∩AC=A,∴BC⊥平面PAC, ∴BC⊥PC。 在Rt△PAB中,M为PB的中点,则AM=12PB, 在Rt△PBC中,M为PB的中点,则CM=12PB, ∴AM=CM。
第二十页,编辑于星期六:点 五十八分。
(2)若N是PC的中点,求证:DN∥平面AMC。
第十一页,编辑于星期六:点 五十八分。
3.若一直线上有相异三个点A,B,C到平面α的距离相等,那么直线l与平
面α的位置关系是( )
A.l∥α
B.l⊥α
C.l与α相交且不垂直 D.l∥α或l⊂α
解析:由于l上有三个相异点到平面α的距离相等,则l与α可以平行,l⊂α 时也成立。
答案:D
第十二页,编辑于星期六:点 五十八分。
第十六页,编辑于星期六:点 五十八分。
(2)设AA1=AC=CB=2,AB=2 2,求三棱锥C-A1DE的体积。 解析:(2)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD。由已知AC=
CB,D为AB的中点,所以CD⊥AB。又AA1∩AB=A,于是CD⊥平面ABB1A1。 由AA1=AC=CB=2,AB=2 2得 ∠ACB=90°,CD= 2,A1D= 6,DE= 3,A1E=3, 故A1D2+DE2=A1E2, 即DE⊥A1D。 所以VC-A1DE=13×12× 6× 3× 2=1。
非常考案通用版2017版高考数学一轮复习第七章立体几何第4节直线平面平行的判定及其性质课件
研 考 点
第四节 直线、平面平行的判定及其性质
分 层 限 时 跟 踪 练
理 教 材
备高考| 3 个任务 1.理解线面平行的判定与性质定理. 2.理解面面平行的判定与性质定理. 3.学会使用线面平行、面面平行的判定与性质定理解决空间中的平行问题.
理教材| 回扣自测 要点梳理 一、直线与平面平行的判定定理和性质定理 文字语言 判 平面外一条直线与 此平面 定 的一条直线平行,则该直线 定 与此平面平行(线线平行⇒ 理 线面平行)
(2)连接 FH,OH, ∵F,H 分别是 PC,CD 的中点, ∴FH∥PD,∴FH∥平面 PAD. 又∵O 是 BE 的中点,H 是 CD 的中点, ∴OH∥AD,∴OH∥平面 PAD. 又 FH∩OH=H, ∴平面 OHF∥平面 PAD. 又∵GH⊂平面 OHF, ∴GH∥平面 PAD.
[规律总结] 证明直线与平面平行的常用方法: (1)用线面平行的判定定理来证明, 关键是在平面内找(或作)一条直线与已知 直线平行,常常构造三角形的中位线或平行四边形的一组对边来完成. (2)用两平面平行的一个性质证明,即先通过证面面平行,由一个平面内的 任何一条直线都与另一平面平行得证.
[变式训练] 一个多面体的直观图和三视图如图 745 所示,其中 M 是 AB 的中点,G 是 DF 上的一点.当 FG=GD 时,在棱 AD 上确定一点 P,使得 GP∥平面 FMC, 并给出证明.
图 745
【解】 由三视图可得直观图为直三棱柱,且底面 ADF 中 AD⊥DF,DF= AD=DC,点 P 在 A 点处. 如图,取 DC 中点 S,连接 AS、GS、GA. ∵G 是 DF 的中点, ∴GS∥FC,AS∥CM. ∵GS∩AS=S,FC∩CM=C, ∴平面 GSA∥平面 FMC, ∵GA⊂平面 GSA, ∴GA∥平面 FMC,即 GP∥平面 FMC.
高考数学总复习第七章立体几何7.4直线、平面平行的判定及其性质课件
证明线面平行的常用方法与思路 (1)证明直线与平面平行的关键是设法在平面内找到一条与 已知直线平行的直线,解题的思路是利用几何体的特征,合理利 用中位线定理、线面平行的性质,或者构造平行四边形、寻找比 例式证明两直线平行. (2)应用线面平行性质定理的关键是确定交线的位置,有时需 要经过已知直线作辅助平面来确定交线.
【条件探究 2】 在本典例中,若将条件“E,F,G,H 分别是 AB, AC,A1B1,A1C1 的中点”变为“D1,D 分别为 B1C1,BC 的中点”,求 证:平面 A1BD1∥平面 AC1D.
证明:如图所示,连接 A1C 交 AC1 于点 M,
∵四边形 A1ACC1 是平行四边形, ∴M 是 A1C 的中点,连接 MD, ∵D 为 BC 的中点,∴A1B∥DM. ∵A1B⊂平面 A1BD1,DM⊄平面 A1BD1, ∴DM∥平面 A1BD1,
获得的结论证明一些空 平行、线面平行及面面平行的判
间图形的平行关系的简 定及应用,题型为解答题中的一
单命题.
问.
课堂探究 考点突破
真题模拟演练
课堂探究 考点突破
考点一 与线、面平行相关命题的判定
(1)(2015·安徽卷)已知 m,n 是两条不同直线,α,β 是两个不
同平面,则下列命题正确的是( D )
(2019·安徽合肥一中模拟)如图,四棱锥 P ABCD 中,E 为 AD 的 中点,PE⊥平面 ABCD,底面 ABCD 为梯形,AB∥CD,AB=2DC=2 3, AC∩BD=F,且△PAD 与△ABD 均为正三角形,G 为△PAD 重心.
(1)求证:GF∥平面 PDC; (2)求三棱锥 G PCD 的体积.
第七章
立体几何
第4节 直线、平面平行的判定及其性质
高考数学一轮总复习第七章立体几何7.4直线平面平行的判定及其性质课件理
【解】 (1)证明:取 PA 的中点 F,连接 EF,BF,因为 E 是 PD 的中点,所以 EF∥AD,EF=12AD.由∠BAD=∠ABC=90°,得 BC∥AD,又 BC=21AD,所以 EF 綊 BC,四边形 BCEF 是平行四边形,所以 CE∥BF,又 BF⊂平面 PAB,CE⊄平面 PAB, 故 CE∥平面 PAB.
第十九页,共41页。
因为 BM 与底面 ABCD 所成的角为 45°,而 n=(0,0,1)是底面 ABCD 的法向量, 所以|cos〈B→M·n〉|=sin45°,即 x-1|2z+| y2+z2= 22,
即(x-1)2+y2-z2=0.① 又 M 在棱 PC 上,设P→M=λP→C,则 x=λ,y=1,z= 3- 3λ.②
第三十一页,共41页。
[自 主 演 练] 如图,在三棱柱 ABC-A1B1C1 中,E,F,G,H 分别是 AB,AC,A1B1,A1C1 的 中点,求证: (1)B,C,H,G 四点共面; (2)平面 EFA1∥平面 BCHG.
第三十二页,共41页。
证明:(1)∵GH 是△A1B1C1 的中位线, ∴GH∥B1C1. 又∵B1C1∥BC, ∴GH∥BC, ∴B,C,H,G 四点共面. (2)∵E,F 分别为 AB,AC 的中点, ∴EF∥BC. ∵EF⊄平面 BCHG,BC⊂平面 BCHG, ∴EF∥平面 BCHG.
第二十八页,共41页。
【证明】 (1)如图,连接 AE,设 DF 与 GN 的交点为 O, 则 AE 必过 DF 与 GN 的交点 O, 连接 MO,则 MO 为△ABE 的中位线, 所以 BE∥MO,又 BE⊄平面 DMF,MO⊂平面 DMF, 所以 BE∥平面 DMF.
第二十九页,共41页。
高考数学一轮复习第七章立体几何第三节直线、平面平行的判定与性质讲义(含解析)
第三节 直线、平面平行的判定与性质突破点一 直线与平面平行的判定与性质[基本知识]直线与平面平行的判定定理和性质定理[基本能力]一、判断题(对的打“√”,错的打“×”)(1)若一条直线和平面内一条直线平行,那么这条直线和这个平面平行.( )(2)若直线a ∥平面α,P ∈α,则过点P 且平行于直线a 的直线有无数条.( )(3)空间四边形ABCD 中,E ,F 分别是AB ,AD 的中点,则EF ∥平面BCD .( ) 答案:(1)× (2)× (3)√二、填空题1.若两条直线都与一个平面平行,则这两条直线的位置关系是________________. 答案:平行、相交或异面2.若直线a ∩直线b =A ,a ∥平面α,则b 与α的位置关系是____________________. 解析:因为a ∥α,∴a 与平面α没有公共点,若b ⊂α,则A ∈α,又A ∈a ,此种情况不可能.∴b ∥α或b 与α相交.答案:b ∥α或b 与α相交3.如图,在正方体ABCD A 1B 1C 1D 1中,E 为DD 1的中点,则BD 1与平面AEC 的位置关系为________.答案:平行[全析考法]考法一线面平行的判定[例1] 如图,空间几何体ABCDFE中,四边形ADFE是梯形,且EF∥AD,P,Q分别为棱BE,DF的中点.求证:P Q∥平面ABCD.[证明] 法一:如图,取AE的中点G,连接PG,Q G.在△ABE中,PB=PE,AG=GE,所以PG∥BA,又PG⊄平面ABCD,BA⊂平面ABCD,所以PG∥平面ABCD.在梯形ADFE中,D Q=Q F,AG=GE,所以G Q∥AD,又G Q⊄平面ABCD,AD⊂平面ABCD,所以G Q∥平面ABCD.因为PG∩G Q=G,PG⊂平面P Q G,G Q⊂平面P Q G,所以平面P Q G∥平面ABCD.又P Q⊂平面P Q G,所以P Q∥平面ABCD.法二:如图,连接E Q并延长,与AD的延长线交于点H,连接BH.因为EF∥DH,所以∠EF Q=∠HD Q,又F Q=Q D,∠E Q F=∠D Q H,所以△EF Q≌△HD Q,所以E Q=Q H.在△BEH中,BP=PE,E Q=Q H,所以P Q∥BH.又P Q⊄平面ABCD,BH⊂平面ABCD,所以P Q∥平面ABCD.考法二线面平行性质定理的应用[例2] 如图所示,四边形ABCD是平行四边形,点P是平面ABCD 外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线面平行性质 主要考查利用线面平行性质定理得出 定理的应用 线线平行,进而求解其他问题
【考题例析】 命题方向1:证明直线与平面平行 【典例1】(2015·山东高考改编题)如图, 在三棱台DEF-ABC中,AB=2DE,点G,H分别
为AC,BC的中点.求证:BD∥平面FGH.
【解题导引】构造线线平行或面面平行证明线面平行. 【规范解答】如图,连接DG,CD,设CD∩FG=O,连接OH.
因为∠NAC=∠DAC=60°,AC⊥CD,所以点C为ND的中点,
又因为点E为PD的中点,所以EC∥PN,因为EC⊄平面 PAB,PN⊂平面PAB,所以CE∥平面PAB.
【一题多解】解答本题,还有以下方法: 取AD中点为M,连接ME,MC,因为点E为PD的 中点,所以EM∥PA,EM⊄平面PAB,PA⊂平面 PAB,所以EM∥平面PAB,由已知得AC=2AB=2,AD=2AC=4, 则CM=AM=2,所以∠BAC=∠ACM=60°,所以MC∥AB,又因 为CM⊄平面PAB,所以CM∥平面PAB,而CM∩EM=M,所以平 面EMC∥平面PAB,又因为CE⊂平面EMC, 所以CE∥平面PAB.
“α ∥β ”的必要而不充分条件.
4.(2016·兰州模拟)设l为直线,α ,β 是两个不同的平 面.下列命题中正确的是 ( )
A.若l∥α ,l∥β ,则α ∥β
B.若l⊥α ,l⊥β ,则α ∥β C.若l⊥α ,l∥β ,则α ∥β D.若α ⊥β ,l∥α ,则l⊥β
【解析】选B.选项A,若l∥α ,l∥β ,则α 和β 可能平行 也可能相交,故错误;选项B,若l⊥α ,l⊥β ,则α ∥β ,
故正确;选项C,若l⊥α ,l∥β ,则α ⊥β ,故错误;选项D,
若α ⊥β ,l∥α ,则l与β 的位置关系有三种可能:l与β 相交,l∥β ,l⊂β,故错误.
5.(2016·合肥模拟)已知平面α ,β 和直线m,给出条件: ①m∥α ;②m⊥α ;③m⊂α ;④α ⊥β ;⑤α ∥β .能推
a⊥β ,则α ∥β . (2)平行于同一平面的两个平面平行,即若α ∥β , β ∥γ , 则α ∥γ .
2.在推证线面平行时,一定要强调直线不在平面内,否 则会出现错误.
【小题快练】 链接教材 练一练 ( )
1.(必修2P61练习改编)下列命题中正确的是
A.若a,b是两条直线,且a∥b,那么a平行于经过b的任何 平面 B.若直线a和平面α 满足a∥α ,那么a与α 内的任何直 线平行
导出m∥β 的是
A.①④
(
)
C.②⑤ D.③⑤
B.①⑤
【解析】选D.由两平面平行的性质可知,两平面平行, 在一个平面内的直线必平行于另一个平面,故选D.
考向一
直线与平面平行的判定与性质 【考情快递】
命题方向
命题视角
证明直线与平 主要考查利用线面平行的判定定理或 面平行 利用面面平行的性质证明线面平行
2.(2016·昆明模拟)在三棱锥S-ABC中, △ABC是边长为6的正三角形,SA=SB=SC=
15,平面DEFH分别与AB,BC,SC,SA交于点
D,E,F,H,且点D,E,F,H分别是AB,BC,SC,SA的中点,如果 直线SB∥平面DEFH,求四边形DEFH的面积.
【解析】因为点D,E,F,H分别是AB,BC,SC,SA的中点, 所以DE∥AC,FH∥AC,DH∥SB,EF∥SB, 则四边形DEFH是平行四边形,且 DE= AC=3,
又因为FH∩OH=H, 所以平面OHF∥平面PAD. 又因为GH⊂平面OHF,所以GH∥平面PAD.
考向二
面面平行的判定与性质
【典例3】(2016·长春模拟)如图,在三棱柱ABC-A1B1C1 中,点D是BC上一点,且A1B∥平面AC1D,点D1是B1C1的中 点,求证:平面A1BD1∥平面AC1D.
【题组通关】 1.(2014·全国卷Ⅱ改编)如图所示,在四棱锥P-ABCD
中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,点E为PD的
中点,AB=1, 求证:CE∥平面PAB.
【证明】由已知条件有AC=2AB=2,AD=2AC=4,CD=2 . 3 如图所示,延长DC,AB,设其交于点N,连接PN,
在三棱台DEF-ABC中,
AB=2DE,点G为AC的中点,可得DF∥GC,DF=GC, 所以四边形DFCG为平行四边形, 所以点O为CD的中点.
又因为点H为BC的中点, 所以OH∥BD.又因为OH⊂平面FGH,BD⊄平面FGH,
所以BD∥平面FGH.
【一题多解】解答本题,还有以下解法: 因为DEF-ABC是三棱台,且AB=2DE,所以BC=2EF,因为点H
2
所以四边形ABCE是平行四边形,
所以点O为AC的中点,
又因为点F是PC的中点,所以FO∥AP,
又FO⊂平面BEF,AP⊄平面BEF,
所以AP∥平面BEF.
(2)连接FH,OH,
因为点F,H分别是PC,CD的中点,
所以FH∥PD,FH⊄平面PAD,PD⊂平面PAD,所以FH∥平面
PAD,
又因为点O是AC的中点,点H是CD的中点, 所以OH∥AD,同理OH∥平面PAD,
第四节
直线、平面平行的判定及其性质
【知识梳理】 1.直线与平面平行的判定定理和性质定理 文字语言 平面外一条直线 与_________ 此平面内 的一 条直线平行,则该 直线与此平面平 行(线线平行⇒线 面平行) 图形语言 符号语言
判 定 定 理
因为_____ l∥a, __________, a⊂αl∥ , l⊄ 所以 αα
所以GH∥BC,同理可证EF∥BC,因此GH∥EF.
(2)连接AC,BD交于点O,设BD交EF于点K,连接OP,GK, 因为PA=PC,
点O是AC的中点,所以PO⊥AC,
同理可得PO⊥BD, 又因为BD∩AC=O,且AC,BD都在底面内, 所以PO⊥底面ABCD,
又因为平面GEFH⊥平面ABCD,且PO⊄平面GEFH, 所以PO∥平面GEFH, 因为平面PBD∩平面GEFH=GK, 所以PO∥GK,且GK⊥底面ABCD,从而GK⊥EF, 所以GK是梯形GEFH的高,由AB=8,EB=2得
为BC的中点,
所以BH∥EF,BH=EF, 所以四边形BHFE为平行四边形,所以BE∥HF. BE⊂平面ABED,FH⊄平面ABED,
所以FH∥平面ABED, 在△ABC中,点G为AC的中点,点H为BC的中点,
所以GH∥AB,同理GH∥平面ABED.
又因为GH∩HF=H,所以平面FGH∥平面ABED. 因为BD⊂平面ABED,所以BD∥平面FGH.
性 质 定 理
文字语言 一条直线与一个平 面平行,则过这条 直线的任一平面 与此平面的_____ 交线 与该直线平行 (简 记为“线面平行⇒ 线线平行)
图形语言
符号语言 因为______ l∥ α , _____, l⊂β _________, α∩ =b 所以 lβ ∥b
2.平面与平面平行的判定定理和性质定理 文字语言 判 定 定 理 一个平面内的两条 _________与另一个 相交直线 平面平行,则这两 个平面平行(简记 为“线面平行⇒面 面平行”) 图形语言 符号语言 因为_______ a∥β , _______ b∥β , ________ a∩b=P, _______ a⊂α , ______, 所以 α ∥β b⊂α
【解题导引】(1)由线面平行得出BC平行于直线EF,GH.
(2)连接AC,BD交于点O,设BD交EF于点K,连接OP,GK,则 点K为OB的中点,由面面垂直得出GK⊥EF,再由梯形面积 公式S= ·GK计算求解.
GH EF 2
【规范解答】(1)因为BC∥平面GEFH,BC⊂平面PBC,且 平面PBC∩平面GEFH=GH,
EB∶AB=KB∶DB=1∶4,
从而KB= DB= OB,即点K是OB的中点.
1 4
1 2
再由PO∥GK得GK= 1 PO,即点G是PB的中点, 2 且GH= 1 BC=4,由已知可得OB=4 , 2 PO= 2
2 2 PB OB 68 32 的面积 6, S= 所以GK=3,故四边形 GEFH
答案:平行
感悟考题
试一试
3.(2015·北京高考)设α ,β 是两个不同的平ቤተ መጻሕፍቲ ባይዱ,m是直
线且m⊂α ,“m∥β ”是“α ∥β ”的
A.充分而不必要条件 C.充分必要条件
(
)
B.必要而不充分条件 D.既不充分也不必要条件
【解析】选B.当m∥β 时,可能α ∥β ,也可能α 与β 相 交.当α ∥β 时,由m⊂α可知,m∥β .因此,“m∥β ”是
命题方向2:线面平行性质定理的应用 【典例2】(2014·安徽高考)如图,四棱
锥P-ABCD的底面是边长为8的正方形,四
条侧棱长均为2 .点G,E,F,H分别是
17 棱PB,AB,CD,PC上共面的四点 ,平面GEFH⊥平面ABCD,
BC∥平面GEFH.
(1)证明:GH∥EF. (2)若EB=2,求四边形GEFH的面积.
所以BD1∥C1D.
BD1⊄平面AC1D,C1D⊂平面AC1D,
所以BD1∥平面AC1D,
又因为A1B∩BD1=B,
所以平面A1BD1∥平面AC1D.
【规律方法】 1.判定面面平行的方法 (1)利用定义:常用反证法. (2)利用面面平行的判定定理. (3)利用垂直于同一条直线的两平面平行. (4)利用两个平面同时平行于第三个平面,则这两个平 面平行.
【解题导引】先证点D是BC的中点,再证BD1∥DC1.
【规范解答】如图,连接A1C交AC1于点E,连接ED.
因为四边形A1ACC1是平行四边形,
所以点E是A1C的中点,
因为A1B∥平面AC1D,平面A1BC∩平面AC1D=ED, 所以A1B∥ED,
