实验4复摆振动的研究
北京大学复摆实验报告

1.28140 1.27314 1.26429 1.25752 1.25029 1.24472 1.23855 1.23435 1.23137 1.23021 1.22986 1.23189 1.23572 1.24205 1.25219 1.26689 1.28497 1.30712 1.33931 1.37785 1.43054 1.49646 1.58282 1.70131 1.866637 2.05579 2.43580
2. 将复摆安装到支架上,利用铅直线调整铁架下部支脚螺钉,使复摆在垂直平面内 摆动,且尽可能使平衡位置在光电门中央;
3. 利用复摆上位置不同的小孔作为刀口悬挂点,记下此点到零刻度线(即质心)的 距离hi,用光电计时器记录此时复摆运动20个周期的时间20Ti,列表记录数据;
4. 数据处理
1) 作T 2h ∼ h2图,用线性拟合法求重力加速度g 2) 用公式求g 3) 作T ∼ h图,求出复摆对于任意悬挂点的等值摆长,从而求出g
g11 = 4π2/k1 = 4π2/4.063 = 9.718m · s−2
(25)
右半部分如Figure 6所示:
斜率k2 = 4.028s2/m, 截距b1 = 0.1420s2m, 相关系数R22 = 0.999996 计算得:
g12 = 4π2/k1 = 4π2/4.028 = 9.802m · s−2
RG = h0
也是图中两条曲线的极小值之间的距离,且h1 + h2 = EF = 2RG. 取一周期为T值 (H点 ) 处 引 一 直 线MN平 行 于 横 轴 , 交 两 条 对 称 曲 线 于A,B,C,D四 点 , 把 这 四 点 分 成A,C和B,D两组,在摆杆上每一组中两点都位于质心G(Figure 3所示)的两旁,并与
★复摆的振动周期(小论文示范)

复摆的振动周期1、引言复摆是大学物理中三个简谐振动模型之一,是刚体绕光滑水平轴作小角度摆动。
研究复摆的振动周期可以运用转动定律,也可以运用机械能守恒定律。
本文先介绍与研究复摆振动周期有关的概念和规律,然后用两种方法推导复摆的周期公式,最后讨论复摆周期公式在测量刚体转动惯量中的应用。
2、原理刚体定轴转动定律的表达式为M J α= (1)其中M 为对转轴的力矩,J 为刚体对转轴的转动惯量,α为刚体转动的角加速度。
转动惯量的定义式为2=i i J m r ∑,其中r i 为质点m i 到转轴的距离。
转动角速度为ω的转动刚体的转动动能为 212k E J ω= (2)在重力场中,刚体质心坐标为(C x ,C y )的重力势能为P C E mgy = (3)以摆角θ为变量的简谐振动的表达式为0Θcos()f θωt φ=+ (4)式中Θ和0φ分别为摆幅和初相位,f ω振动圆频率,与振动周期间的关系为 2f πT ω= (5)3、模型如图所示,质量为m 的复摆对转轴O 的转动惯量为J ,质心C 到转轴O 的距离为b 。
当OC 与铅垂线的夹角为θ时,复摆受到的对转轴O 的力矩为sin M mgb θ=-。
根据刚体定轴转动定律M J α=,得sin mgb mgb αθθJ J =-≈-。
将0=Θcos()f θωt φ+代入可得,f mgb ωJ =。
于是求得,复摆振动周期为22f πJ T πωmgb ==。
复摆振动时只有重力作功,因此振动系统的机械能守恒,即21cos 2J ωmgb θC -=。
等式两边对时间t 求导,得sin 0J ωαmgb ωθJ ωαmgb ωθ+≈+=。
将0=Θcos()f θωt φ+代入b可得,f ω=。
同样,求得复摆振动周期为22f πT ω==。
4、讨论对于单摆,b =l ,J =ml 2,周期为2T =。
利用复摆的周期公式可得2T J mgb π=2(),即测量了刚体的质量、质心位置和振动周期,即可计算出刚体的转动惯量。
复摆振动的研究实验报告

复摆振动的研究
实验目的:1、考查复摆振动时振动周期与质心到支点距离的关系; 2、测出重力加速度、回转半径和转动惯量。
实验仪器:
实验原理:一个围绕定轴转动的刚体就是复摆,刚体绕固定轴O 在竖直平面内作左右摆动,C 是该物体的质心,与轴O 的距离为 h ,θ 为其摆动角度。
如图 1 所示
当摆的振幅甚小时,其震动周期 T 为
(1)
设 I G 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知
(2)
而 I G 又可以写成为 I G =mk 2, k 就是复摆对 G 轴的回转半径,由此可将式(1)改为
(3)
实验内容:1、重心G 的位置S G = (h=│S -S G │)
的重心端作为正端,选择复摆上以下刻度位置作为支点位
4、用物理天平测量复摆的质量m. m=
数据处理与分析:(h=│S-S
│)
G
S xx=∑x i2-(∑x i)2/n=
S yy =∑y i 2-(∑y i )2/n = S xy =∑x i y i -∑x i ∑y i /n=
=
∙==-===∑∑yy xx xy i i xx
xy S S S r
n x b n y a
S S b ˆˆˆ
r b n r S b ⋅⎪⎪⎭
⎫ ⎝
⎛--=2
12= b g ⋅=24π =
b s g g U b
=)(=
b
s g g g U g
g U b =)
(=)(=
实验结果与评价:
实验感想:。
实验报告_复摆实验
1.764
1.764
1.764
4
1.774
1.774
1.774
6
1.537
1.533
1.535
6
1.527
1.527
1.527
8
1.379
1.389
1.384
8
1.406
1.406
1.406
10
1.301
1.306
1.304
10
1.317
1.317
1.317
12
1.265
1.269
1.267
12
1.262
姓名
学号
院系
时间
地点
【实验题目】复摆实验
【实验记录】
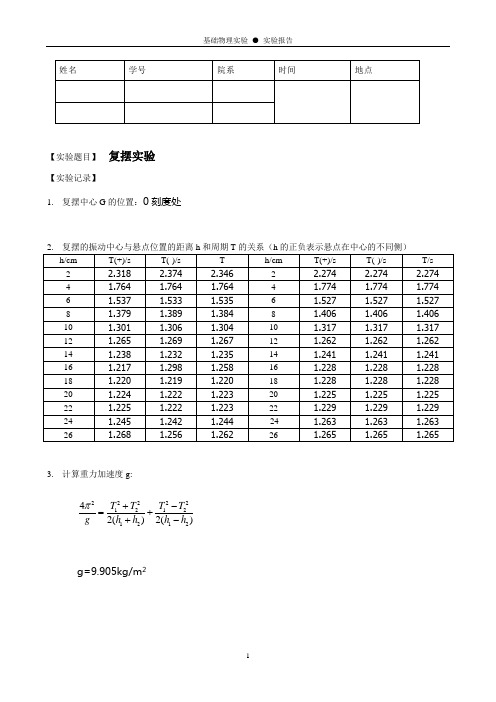
1.复摆中心G的位置:0刻度处
2.复摆的振动中心与悬点位置的距离h和周期T的关系(h的正负表示悬点在中心的不T(-)/s
T
h/cm
T(+)/s
T(-)/s
T/s
2
2.318
2.374
2.346
2
2.274
2.274
2.274
1.262
1.262
14
1.238
1.232
1.235
14
1.241
1.241
1.241
16
1.217
1.298
1.258
16
1.228
1.228
1.228
18
1.220
1.219
1.220
18
1.228
1.228
1.228
20
1.224
1.222
1.223
复摆振动

1.计算出重力加速度g,并把测量结果与本地区的公认值比较,求实验的相对误差。
实验报告成绩单
学院:___________专业:___________学号:__________姓名:___________
预习(30分)
操作(30分)
数据处理(30分)
其他(10分)
总成绩
指导教师
1.观看仪器介绍并掌握其使用方法及注意事项;
2.仔细阅读课本,初步了解实验并且能够独立回答问题;
3.左侧问题预习前完成,右侧空白处实验后完善与总结。
1.请推导复摆振动周期。(需画出刚体的受力分析图)。
2.实验中取 ,推导用复摆测重力加速度的公式。
3.写出利Leabharlann 复摆测重力加速度的实验步骤。4.在该实验中,如果两砝码置于复摆的摆杆上刻线非对称处的位置固定,对该实验的有怎样的影响?
复摆的振动周期
次数
1
2
3
4
5
平均
——
——
3.原始实验数据不能用铅笔记录,实验数据不能任意涂改,发现错误应重新完成实验。
实验组成员:(1)学号:____________姓名:____________
(2)学号:____________姓名:____________
(3)学号:____________姓名:____________
指导教师签字:____________
实验名称:复摆的振动研究
学生学号:_______________学生姓名:_______________学院专业班级:_______________
上课时间:_______________指导教师:_______________实验报告成绩:_______________
复摆运动状态的研究

复摆运动状态的研究
曲光伟 王艳辉 邹德滨 张天洋 (大连理工大学物理与光电工程学院,辽宁大连
(收稿日期:2008—07-02)
1 16023)
摘要 关键词
从复摆的运动方程出发,利用计算机对其各种运动情况进行模拟,研究复摆从周期运 动转化到混沌运动的过程,深化复摆实验内容,拓宽复摆实验的研究空间. 复摆;倍周期;混沌;相空间
相似文献(2条)
1.期刊论文 李万祥.何玮.唐恭佩.Li Wanxiang.He Wei.Tang Gongpei 一类复摆系统的非线性动力学研究 -华中科
技大学学报(自然科学版)2007,35(5)
通过对一类复摆系统的建模,利用数值分析法,较为全面地论证了复摆系统通向混沌的倍周期道路、拟周期道路等复杂的混沌演化行为.用相图、庞加 莱映射图和分岔图等方式揭示出了系统混沌运动的形式和参数.对该系统分岔与混沌行为的研究,为工程实际中相关机械系统和振动系统的混沌预测和控 制具有指导意义,同时对这些系统的优化设计提供了理论依据.
的非线性运动及混沌现象,这不仅可以使实验内 容现代化,还可以有效地培养学生的科研能力.
参考 文 献
[1]赵凯华.从单摆到混沌[J].现代物理知识。1993。5(5):25 ~28
[2]符五九,饶黄云.单摆系统通向混沌的道路[J].大学物理, 2008,27(1):5~10
[3]李文胜.复摆运动中的混沌现象及其计算机模拟[J].物理 与工程,2001.11(1):26~31
(1)
对式(1)进行无量纲化得
ddJrO。+2卢磊dO+sin臼一厂c。s∞F
(2)
其中,卢一万ki,称为无量纲阻尼系数;∞。=  ̄/瓦再7了是复摆的固有频率;厂一F/1w:是无量纲
复摆的实验报告.doc

复摆的实验报告.doc摘要:本实验通过利用复摆的摆动周期和摆长与摆角度之间的关系,通过多次实验来研究复摆的动力学规律和特性。
实验结果表明,复摆的摆动周期受到重力加速度和摆长的影响,摆长越长,摆臂相对较长,振幅相对小,周期越长。
同时,复摆的摆角度对振幅和周期都产生了影响,当摆角度较小时,振幅较小,周期较长。
关键词:复摆,摆动周期,摆角度,摆长Abstract:In this experiment, the dynamic laws and characteristics of the compound pendulum are studied by utilizing the relationship between the swinging period and the swinging length and swing angle of the compound pendulum. The experimental results show that the swinging period of the compound pendulum is affected by the gravity acceleration and the swinging length. The longer the swinging length, the longer the swinging arm, the smaller the amplitude, andthe longer the period. At the same time, the swinging angle of the compound pendulum affects the amplitude and period. When the swinging angle is small,the amplitude is small and the period is long.Keywords: compound pendulum, swinging period, swinging angle, swinging length实验方案:所用仪器:复摆、计时器、卡尺、直尺、秤。
大学物理实验复摆实验讲义

⼤学物理实验复摆实验讲义复摆【实验⽬的】(1)研究复摆的物理特性; (2)⽤复摆测定重⼒加速度;(3)⽤作图法和最⼩⼆乘法研究问题及处理数据。
【仪器⽤具】复摆,光电计时器,电⼦天平,⽶尺等。
【实验原理】1.复摆的振动周期公式在重⼒作⽤下,绕固定⽔平转轴在竖直平⾯内摆动的刚体称为复摆(即物理摆).设⼀复摆 (见图1-1)的质量为m ,其重⼼G 到转轴O 的距离为h ,g 为重⼒加速度,在它运动的某⼀时刻t,参照平⾯(由通过O 点的轴和重⼼G 所决定)与铅垂线的夹⾓为0,相对于O 轴的恢复⼒矩为M=-mgh sin θ(1.1)图 1-1复摆⽰意图根据转动定理, 复摆(刚体)绕固定轴O 转动,有M=I β (1.2)其中M 为复摆所受外⼒矩,I 为其对O 轴的转动惯量,β为复摆绕O 轴转动的⾓加速度, 且22dtd θβ=则有M=I22dt d θ(1.3)结合式(1.1)和式(1.3),有I 22dtd θ+mgh sin θ=0 (1.4) 当摆⾓很⼩的时候, sin θ≈θ, ,式(1.4)化为22dt d θ+θImgh =0 (1.5) 解得θ=A cos(ωt+θ0) (1.6)式中A ,θ由初条件决定;ω是复摆振动的⾓频率,ω=I mgh /,则复摆的摆动周期T=2πmghI(1.7)2.复摆的转动惯量,回转半径和等值单摆长由平⾏轴定理,I=I G +mh 2,式中I G 为复摆对通过重⼼G 并与摆轴平⾏的轴的转动惯量, (1.7)式可写为 T=2πmghmh I G 2+ (1.8)可见, 复摆的振动周期随悬点O 与质量中⼼G 之间的距离h ⽽改变。
还可将I =I G +mh 2改写22G 2I mR mh mR =+= (1.9)式中R G =m I G 为复摆对G 轴的回转半径, 同样也有R=mI, R 称为复摆对悬点O 轴的回转半径。
复摆周期公式也可表⽰为T=2πgh h R G+2 (1.10)事实上, 总可以找到⼀个单摆,它的摆动周期等于给定的复摆的周期,令L =h hR G+2 (1.11)则 T= 2πgL(1.12) 式中L 称为复摆的等值单摆长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四复摆振动的研究
复摆又称为物理摆,是一刚体绕固定的水平轴在重力的作用下作微小摆动的动力运动体系——简谐振动。
通过复摆物理模型的分析,可以用来测量重力加速度、测量物体的转动惯量以及验证平行轴定理等等。
【实验目的】
1.分析复摆的振动,研究振动周期与质心到支点距离的关系。
2.掌握用复摆来测量重力加速度和回转半径的方法。
3.了解用复摆物理模型来测量物体的转动惯量和验证平行轴定理的方法。
【实验仪器】
JD-2型复摆实验仪,光电门装置,J-25型周期测定仪,天平,米尺等
【实验原理】
刚体绕固定轴O在竖直平面内作左右摆动,C是该物体的质心,与轴O的距离为h
,θ为其摆动角度,如图4-1所示。
若规定右转角为正,此时刚体所受力矩与角位移方向相反,即有
h
mg
=sin
-
Mθ
若θ很小时(θ在05以内)近似有
θ
=(4-1)
mgh
M-
又据转动定律,该复摆又有
θ I
M=(4-2)其中I为该物体转动惯量。
由(4-1)和(4-2)可得
20θωθ=- (4-3)
其中2
0mgh
I
ω=。
此方程说明该复摆在小角度下作简谐振动,该复摆周期为 mgh
I
T π=2 (4-4)
设c I 为转轴过质心且与O 轴平行时的转动惯量,那么根据平行轴定律可知 2mh I I c += (4-5)
代入(4-4)式得:
mgh
mh I T c 2
2+π
= (4-6) 由此可见,周期T 是质心到回转轴距离h 的函数,且当0h →或h →∞时,T →∞。
因此,对下面的情况分别进行讨论:
(1)h 在零和无穷大之间必存在一个使复摆对该轴周期为最小的值,此时所对应h 值叫做复摆的回转半径,用R 表示。
由(4-6)式和极小值条件
0dT
dh
=得: min
c
T T
I R h m
===
(4-7) 代入公式(4-7)又得最小周期为
min 22R
T g
= (4-8) (2)在h R =两边必存在无限对回转轴,使得复摆绕每对回转轴的摆动周期相等。
而把这样的一对回转轴称为共轭轴,假设某一对共轭轴分别到重心的距离为1h 、2h (12h h ≠),测其对应摆动周期为1T 、2T 。
将此数据分别代入(4-6)式并利用12T T =得:
12c I mh h = (4-9) 12
2h h T g
+= (4-10) 把公式(4-10)与单摆的周期公式2l
T g
=复摆绕距的重心为1h (或其共轭轴2h )的回转轴的摆动周期与所有质量集中于离该轴为12h h +点的单摆周期
相等,故称h 1+h 2为该轴的等值摆长。
可见,实验测出复摆的摆动周期T 及该轴的等值摆长h 1+h 2,由公式(4-10)就可求出当地的重力加速度g 的值。
本实验所用复摆为一均匀钢板,它上面从中心向两端对称地开一些小孔。
测量时分别将复摆通过小圆孔悬挂在固定刀刃上,如图4-2所示,便可测出复摆绕不同回转摆动的周期以及回转轴到质心的距离,得到一组T 、h 数据,作T h 图,如图4-3所示,从而直观地反映出复摆摆动周期与回转轴到质心距离的关系。
由于钢板是均匀的,复摆上的小圆孔也是对称的,所以在摆的质心两侧测T 随h 的变化也是相同的,则实验曲线必为两条。
在曲线上最低的两点E 、F ,这两点
的横坐标1
2
h R EF ==
为回转半径,纵坐标就振动周期最小值。
如图4-3,取一周期为T 值(H 点)处引一直线MN 平行于横轴,交曲线于A 、B 、C 、D 四点,把这四点分成A 、C 和D 、F 两组,在摆杆上每一组中两点都位于质心C 的两旁,并与质心处在同一直线上,不难看出:1AH HD h ==,2BH HC h ==,12AC BD h h ==+为复摆在相应周期下的等值摆长,点A 和C 的、B 和D 具有共轭性,通过它们的回转轴为共轭轴。
【实验步骤与要求】
一、研究复摆周期与转轴位置的关系
1.确定均匀钢板的质心位置(方便起见,让质心的位置正好在“0”刻度上) 方法:将钢板水平放在支架的刀刃上(图4-4),其“0”刻度正好对应刀刃,利用杠杆原理调节钢板两端的微调螺母使其平衡,要求误差在1mm 以内。
图4-2 刚体悬挂在固定刀刃平面图 图4-3 周期与回转轴到质心距离曲线图
2.将座架放置于实验桌边沿,使上面的三角刀口水平朝外
方法:把复摆摆杆悬挂在三角刀口上,调节座架底下水平螺丝使刀口与孔内径上沿相密合,要求摆杆摆动时没有扭动情况。
3.测量不同回转轴对应的周期
将复摆摆杆的每一小孔依次悬挂在三角刀口上以小摆幅摆动,用周期测定仪测定对每一个孔的振动周期,要求质心到回转轴距离每改变2cm 测振动周期,并记录表4-1。
注意:使用周期测定仪时,面板上的周期选择拨到10T 档;在复摆处于平衡位置时,周期测定仪的光电门应对准复摆下端的挡光针,拨动复摆并把周期仪置零,即自动开始测周期至10个周期停止计时,所显示的数字就是10个周期的时间间隔,计时精度为0.01ms 。
表4-1 与h 的关系
()h cm
10()T ms
()T s
2x h =(2m )
2y T h =2()s m ⋅
2 4 6 8 10 12 14 16 18 20 22 24 26 28
4.绘出复摆周期与转轴位置之间的关系图T h ,要求横轴上标上转轴与摆杆质心的距离左边或右边均为正值,纵轴为摆动周期。
图4-4 调节钢板平衡示意图
二、测出摆杆的回转半径,重力加速度和通过质心轴的转动惯量
1.根据你所绘出的T h 图,很容易量出最低两点的距离以及所对应的周期值。
2.由上述测量数据,再根据(4-8)式得到重力加速度:
2min
8R g T π=
3.根据回转半径的定义即(4-7)式,易得通过质心轴的转动惯量c I 。
三、用最小二乘法求出摆杆的回转半径,重力加速度和通过质心轴的转动惯量
1.由(4-6)与(4-7)式,得到
22
2R h T gh
+=将上式改写成为
222
22
44T h R h g g
ππ=+
令22,y T h x h ==,则上式又变成为
22
244y R x g g
ππ=+
从测量可得出n 组(,)x y 值并填入表4-1中,
2.用最小二乘法求出拟合直线y A Bx =+的224()A R g π=和2
4()B g
π=,再由A 、B 求出g 和R 值,再求出c I 。
3.计算结果与上述测量结果进行比较,并计算g 的不确定度。
【预习思考题】
1. 单摆和复摆最本质的区别是什么?
2. 什么是回转轴、回转半径、等值摆长?
3. 为什么复摆的摆动周期存在一个极小值?出现极小值的条件是什么? 4. 在复摆的某一位置加一配重时,其振动周期将如何变化?
2. 3.
(2)在实验中用较大的角度(θ≈20o
)摆动复摆,记录在10个周期内,每个周期与角度的关系,会得到什么样的结果?
【作业】
1. 改变悬挂点时,等值摆长将会改变吗?摆动周期会改变吗? 2. 公式(4-5)成立的条件是什么?在实验操作时,怎样才能保证满足这些条件呢? 3. 如果所用复摆不是均匀的钢板,重心不在板的几何中心,对实验的结果有无影
响?两实验曲线还是否对称?为什么?
4. 试推导θ角不是很小时的摆动方程。
在实验中用较大的角度(θ≈20o
)摆动复
摆,记录在10个周期内,每个周期与角度的关系,会得到什么样的结果? 5. 试设计一个实验方案来验证平行轴定理。
【附录】
一、JD-2型复摆实验仪
1.T 形座架
2.调节螺丝
3.平衡块
4.立柱
5.立柱的接拆部
6.立柱上座
7.U 形刀承
8.刀口
9.摆杆10.微调螺母11.桌子12.挡光针13.光电门14.光电门支架15.周期测定仪16.桌上刀口17.固定上座的螺丝18.摆杆接拆部 二、J-25周期测定仪
J-25周期测定仪在物理实验中用来测量周期,性能可靠稳定,计时精度高的实验仪器。
该仪器用单片机来显示周期数和时间,有记忆功能,可以任意提取1次、10次、20次、30次周期的时间。
使用方法如下:
1)先将光电开关连接线插入“信号输入”口。
调整好光电开关。
2)接通电源,显示“——HELLO ——”后,周期数显示“01”,时间显示“0.00000”,图4-5 JD-2型复摆实验仪
“1”上方的指示灯亮。
3)按“周期数/时间”按钮,选择周期数“1、10、20、30”。
相应的指示灯亮,然后按“开始测量”按钮。
显示“——YES——”。
开始进入测量状态。
有信号通过时,周期数两数码管显示所测的周期数,时间显示“——BUSY——”测量完后,自动停止。
4)提取周期“1、10、20、30”的时间,按“周期数/时间”按钮即可。
