有限元大作业
有限元的大作业报告示例

1.题目概况
矩形板尺寸如下图1,板厚为5mm。
材料弹性模量为
松比μ= 0.27 。
施加约束和载荷并讨论:
图
1 计算简图
1.1基本数据
E = 2⨯105N/mm2,泊
序号载荷约束备注42 向下集中载荷F=800N, 作用于cd 边3/4 处(近d) c d 点简支
1.2分析任务/分析工况
讨论板上开孔、切槽等对于应力分布的影响。
(载荷约束组合不变)。
提示:各种圆孔,椭圆孔随大小、形状、数量,分布位置变化引起的应力分布变化;各种形状,大小的切槽及不同位置引起应力分布的变化等,选择二至三种情况讨论,并思考其与机械零部件的构型的相对应关系。
2.模型建立
2.1单元选择及其分析
由于平板长宽分别为300x100,故可取网格单元大小为1。
如图:
2.2模型建立及网格划分
模型按单元为1 划分后的网格大小如图所示:
2.3载荷处理
向下集中载荷F=800N, 作用于cd 边3/4 处(近d) c d 点简支
3.计算分析
3.1位移分布及其分析
(1)位移分布如图:。
有限元大作业
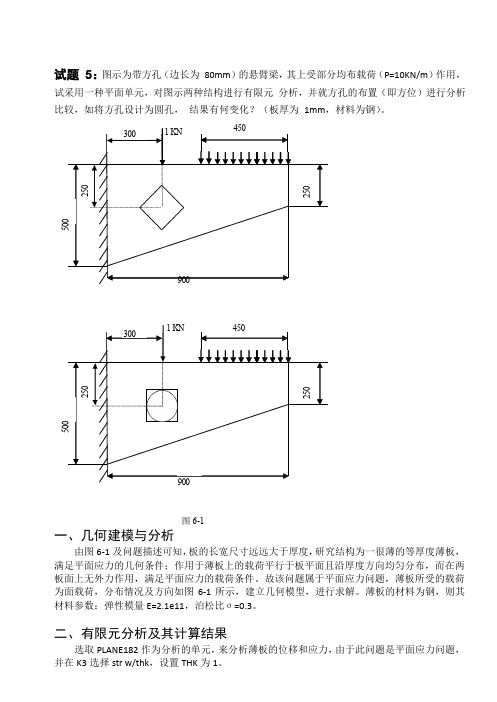
250250试题 5:图示为带方孔(边长为 80mm )的悬臂梁,其上受部分均布载荷(P=10KN/m )作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置(即方位)进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为 1mm ,材料为钢)。
3001KN9003001KN图6-1一、几何建模与分析由图6-1及问题描述可知,板的长宽尺寸远远大于厚度,研究结构为一很薄的等厚度薄板,满足平面应力的几何条件;作用于薄板上的载荷平行于板平面且沿厚度方向均匀分布,而在两板面上无外力作用,满足平面应力的载荷条件。
故该问题属于平面应力问题,薄板所受的载荷为面载荷,分布情况及方向如图6-1所示,建立几何模型,进行求解。
薄板的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3。
二、有限元分析及其计算结果选取PLANE182作为分析的单元,来分析薄板的位移和应力,由于此问题是平面应力问题,并在K3选择str w/thk ,设置THK 为1。
1)方孔竖直制,划分方式采用自由方式,划分后网格的模型如图6-2所示。
计算得到的位移和应力分布如图6-3所示。
图6-2 方孔竖直的网格划分图6-3 位移及应力分布云图2)方孔正直制,划分方式采用自由方式,划分后网格的模型如图6-4所示。
计算得到的位移和应力分布如图6-5所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图3)圆孔按图6-1所示模型进行建模。
并用PLANE182单元进行划分网格,网格大小采用全局网格控制,划分方式采用自由方式,划分后网格的模型如图6-6所示。
计算得到的位移和应力分布如图6-7所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图根据以上的模型分析的位移和应力图,可以得出方孔竖直、方孔正直、圆孔的最大最小位移应力的分布如表6-1所示。
三、比较与分析1)方孔竖直与方孔正直的比较,发现方孔正直的位移变形较小,应力相差不大2)圆孔与方孔比较,发现圆孔的位移变性最小,应力也最小,故可以得出圆孔的布置结构对整体布置的效果最好。
有限元分析大作业 展示

二 不同单元对计算结果的影响
实例:一简支梁,各项数据如表所示:
q / kN l / m b / m h / m E / GPa
0.25
Hale Waihona Puke 100161
3
200
分析其变形和 受力情况。 (分析均取梁 结构的一半进 行计算)
对本例分别采用3节点三角形、4节点矩形、8节点六 面体、20节点六面体进行计算分析,且用平面单元分析时, 还考虑网格的划分不同对结果的影响,分别对梁高划分15 和30等份进行计算, 比较结果。 用平面plane 42 单元建立模型,建模图如下:
谱分析整体结果列表
之后读取结果,在File>Read Input from 里面选择 “.MCOM” 文件,查看各个结果。
谱分析6个节点的反作用力表
读取第一组结果的变形和应力图,如下图 所示:
第一组结果的变形图
第一组结果的应力图
3. 时程分析 实例:上题的三层框架结构,施加了两个x方向大小随时 间变化的力(如下图所示),进行时程分析,最后选择节 点,绘制时程图。
梁高划分30等份三角形3节点建模图
梁高划分15等份三角形3节点建模图
梁高划分30等份4节点矩形建模 图
梁高划分15等份4节点矩形建模图
用六面体8节点单元solid 45和六面体20节点单元solid 95进行分析,建模图如下:
六面体8节点建模图
六面体20节点建模图
各个分析数据均是结构的x方向的应力图,最后进过 汇总,所得的结果如下:
计算分以下几歩完成: 1. 设置为模态分析,进行模态分析求解; 2. 设置为谱分析,输入单点响应谱的频率和 谱值之后(阻尼为0),获得谱解; 3. 再设置为模态分析,扩展模态,扩展5阶模 态,进行扩展模态求解; 4. 最后设置成谱分析,进行模态叠加,选择 SRSS方法,输出类型为Displacement , 最后求解,得出结果,整体结果如下图:
有限元分析大作业

超静定梁的有限元分析本文分别通过材料力学解法和有限元解法,求出了超静定梁的支反力、最大位移及最大位移出现位置,并对两者进行了比较和误差分析。
一、超静定梁的材料力学解法梁的约束反力数目超过了有效平衡方程数,单纯使用静力平衡不能确定全部未知力的梁称为超静定梁。
超静定梁比静定梁有许多优点,如可用较少材料获得较大的刚度和强度,个别约束破坏后仍可工作等。
因而超静定梁在工程中得到较多的应用。
超静定梁的解法有很多种,本文采用力法的一种——变形比较法求解未知量。
图1图2选取C 点的支座为多余约束,Rc 为多余支座反力,则相应的基本静定梁为一外伸梁,如图2所示,其上受集中载荷P 、均布载荷q 和多余支座反力Rc 的作用。
相应的变形条件为:c cP cq cRc f f f f =++=其中316cP B Pl f l EI θ=⨯= 4724cq ql f EI =-323c cRc R l f EI =则316Pl EI 4724ql EI -+323c R l EI=0 将已知数据带入可求得 6.25c R =- 负号表示c R 的方向与假设的方向相反。
再列出平衡方程:0X =∑AX R =0A M =∑ 232022B C ql Pl R l R l ---=0C M =∑ 232022AY B ql PllR R l +--=带入已知条件求得:AX R = 393.75AY R = 812.5B R =用叠加法求最大位移:最大的向下位移在A 与B 两点中间:334410.7910481632C R l Pl ql f EI EI EI -=-++=-⨯最大的向上位移在B 与C 两点中间:3344213490.22525103248512C R l Pl ql f EI EI -=--=⨯二、超静定梁的有限元解法在ANSYS 平台上,求解超静定梁。
建模、单元划分、加载后结果如图3所示。
图3求解后可以通过图形和列表两种方式查看结果。
有限元大作业

1.推导有限元计算格式,理解有限元原理:建立图示受拉直杆在自重(设单位长度重度为q ,截面积为A )和外力P 作用下的拉伸问题的微分方程,并分别利用不同的原理(变分求极值(最小势能或虚功原理)、加权残值法)推导有限元计算格式(取两个单元)。
手工求出端点的位移(自己给定参数值)。
设杆长为L ,截面面积为A(x),弹性模数为E,单位长重量q ,受拉杆x 处的位移为u(x)。
取微元dx 的力平衡,建立受拉杆位移所满足的微分方程()du x dx ε=,()du x E E dxσε== dx 上下截面内力与微元自重相等得()*()()*()A x dx x dx A x x dx qdx σσ++-+=-(()())dA x x q dxσ∴=- (())d duEA x q dx dx=- 0x L << ()0u x = 0x =()duEA x p dx= x L = 得解析解:2()2q x P u Lx x EA EA=-+将其分为两个单元,节点为1,2,3,得22382qL PL u EA EA=+232qL PL u EA EA=+有限元法:1)位移函数01u α= 2111u u l α-=得1211(1)x x u u u l l =-+ 令11(1)x N l =-21x N l = 11122122u u N u N u N N u⎧⎫⎪⎪⎡⎤=+=⎨⎬⎣⎦⎪⎪⎩⎭{}1u N d ⎡⎤=⎣⎦ 2)应变、应力表达{}{}111211du dN d d dx dx l l ε⎡⎤⎡⎤===-⎢⎥⎣⎦⎣⎦{}1B d ε⎡⎤=⎣⎦ {}1E E B d σε⎡⎤==⎣⎦ {}1S d σ⎡⎤=⎣⎦3)势能表示{}{}(){}{}(){}{}{}{}{}1111''112211''121112210111111111111111121221222T V ll T T T T T U W D dV F u F u qdx u u d B E d Adx F u F u ql EA EA ql l l d d d F d EA EA ql l l εε⎡⎤=-=-+-⎣⎦+⎡⎤=-+-⎣⎦⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦∏⎰⎰⎰4)单元平衡方程 a)最小势能原理110u ∂=∂∏120u ∂=∂∏111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭b)虚位移原理{}(){}(){}TeTdd F qdx d δδδεσΩ+=Ω⎰⎰{}{}1B d σεδ⎡⎤=⎣⎦ {}1E E B d σεδ⎡⎤==⎣⎦{}(){}{}(){}111111TTT l d F d B E B d Adxδδ⎡⎤=⎣⎦⎰ 由虚位移任意性得,{}{}1111T lF B E B Adxd ⎡⎤=⎣⎦⎰ 积分得111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭ 记为{}{}111k d F ⎡⎤=⎣⎦ 同理222212323112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭{}{}222k d F ⎡⎤=⎣⎦ {}{}ei i eF R =∑ 12220F F += 23F P =11111112211223222022202EAEAql F l l u ql ql EA EA EA EA u l l l l u ql EAEA P l l ⎡⎤⎧⎫-⎢⎥+⎪⎪⎢⎥⎧⎫⎪⎪⎢⎥⎪⎪⎪⎪⎢-+-⎥=+⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎪⎪+⎢⎥⎪⎪--⎢⎥⎩⎭⎣⎦可得:22382qL PLu EA EA=+232qL PL u EA EA=+与解析解结果一致。
有限元分析大作业报告

有限元分析大作业报告一、引言有限元分析是工程领域中常用的数值模拟方法,通过将连续的物理问题离散为有限个子区域,然后利用数学方法求解,最终得到数值解。
有限元分析的快速发展和广泛应用,为工程领域提供了一种强大的工具。
本报告将介绍在大作业中所进行的有限元分析工作及结果。
二、有限元模型建立本次大作业的研究对象是工程结构的应力分析。
首先,通过对结构进行几何建模,确定了结构的尺寸和形状。
然后,将结构离散为有限个单元,每个单元又可以看作一个小的子区域。
接下来,为了求解结构的应力分布,需要为每个单元确定适当的单元类型和单元属性。
最后,根据结构的边界条件,建立整个有限元模型。
三、材料属性和加载条件在建立有限元模型的过程中,需要为材料和加载条件确定适当的参数。
本次大作业中,通过实验获得了结构材料的弹性模量、泊松比等参数,并将其输入到有限元模型中。
对于加载条件,我们选取了其中一种常见的加载方式,并将其施加到有限元模型中。
四、数值计算和结果分析为了求解结构的应力分布,需要进行数值计算。
在本次大作业中,我们选用了一种常见的有限元求解器进行计算。
通过输入模型的几何形状、材料属性和加载条件,求解器可以根据有限元方法进行计算,并得到结构的应力分布。
最后,我们通过对计算结果进行分析,得出了结论。
五、结果讨论和改进方法根据计算结果,我们可以对结构的应力分布进行分析和讨论。
根据分析结果,我们可以得出结论是否满足设计要求以及结构的强度情况。
同时,根据分析结果,我们还可以提出改进方法,针对结构的特点和问题进行相应的优化设计。
六、结论通过对工程结构进行有限元分析,我们得到了结构的应力分布,并根据分析结果进行了讨论和改进方法的提出。
有限元分析为工程领域提供了一种有效的数值模拟方法,可以帮助工程师进行结构设计和分析工作,提高设计效率和设计质量。
【1】XXX,XXXX。
【2】XXX,XXXX。
以上是本次大作业的有限元分析报告,总结了在建立有限元模型、确定材料属性和加载条件、数值计算和结果分析等方面的工作,并对计算结果进行讨论和改进方法的提出。
有限元分析大作业

有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。
(完整word版)有限元分析大作业报告要点

有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
风电主轴承有限元分析XXX摘要:基于有限元法在接触问题中的应用,对风电主轴承进行非线性分析。
以轴承外圈的内表面和内圈的外表面为目标面,以滚子为接触面创建接触对分析滚子的接触应力情况。
最大应力值出现在滚子边缘出,对最大承载滚子环向接触应力分析表明,有限元分析结果与理论计算结果相近,验证了利用有限元法分析风电主轴承应力状态的可行性。
关键词:风电主轴承;接触应力;有限元分析0 引言随着传统能源的日益枯竭以及环境污染问题愈发严重,风能作为一种清洁的的可再生能源近些年受到越来越多的关注。
风力发电技术已广泛运用于世界各地。
一些发达国家风力发电产业已得到了迅猛发展,技术日趋成熟,并开始走向产业化规模化发展阶段[1-3]。
风电主轴承是风力发电机重要的组成部分。
其结构形式图下图1所示。
据统计,如今安装的所有风力发电机中,采用主轴轴承支撑原理的占总数的75-80%[4],这种支撑是轴承内圈安装在旋转的主轴上,外圈固定在单独的轴承座上,相对于圆锥滚子轴承或圆柱滚子轴承来说,主轴轴承位置处轴产生变形,需要轴承具有一定的调心作用,所以都采用了调心滚子轴承。
近年来由于计算机技术的飞速发展,轴承的受力分析计算已经普遍采用有限元分析的方法,能够准确合理地解决轴承复杂的非线性接触问题,为轴承的分析和计算提供了一种新的方法,成为未来的一个发展方向。
在机械设备的设计过程中,对受力较大且复杂的零件进行受力分析,校核其整体和局部强度并进行合理的布局设计,是为了防止因应力过大而导致在实际工作中损坏或寿命降低[5]。
本文主要运用ANSYS Workbench有限元软件对风电主轴承进行静力学计算,分析轴承内部结构参数对轴承载荷分布和最大接触应力的影响规律。
图1 风电主轴承结构及安装图1 有限元分析过程1.1 风电轴承有限元分析基本步骤不同的物理性质和数学模型的问题,有限元法求解的基本步骤是相同的,只不过具体公式推导和运算求解不尽相同。
有限元分析求解问题的基本计算步骤[6]:1.问题及求解域定义;2.求解域离散化;3.确定状态变量及控制方法;4.单元推导;5.总装求解;6.联立方程组求解和结果解释。
简单的说,有限元分析步骤可分成前处理、处理和后处理三个阶段。
具体到该主轴承分析中,其分析过程为:用SolidWorks建模软件建立主轴承三维模型,然后将建好的模型导入到ANSYS Workbench中进行前处理,根据需要选择材料模型,生成有限元模型,划分网格,随后对划分好的模型施加载荷和约束,进而进行求解,得到所定义工况下风电主轴承关键部件的应力、变形及接触应力分析结果。
1.2 实体建模利用三维建模软件Solidworks按所给主轴承工程图尺寸完成轴承各零件的模型建立,并根据装配要求对各零件进行装配,最后完成整个风电主轴承的模型建立,其三维图如下图2所示。
图2 风电主轴承结构图由于几何模型是按照制造、加工、装配的实际部件、零件装配顺序搭建起来的,没有考虑建立有限元模型的环境和细节要求,不适用于直接转化成有限元模型,必须在转化过程中在原有几何模型基础上进行模型简化,使其成为适合有限元分析所需的模型。
几何模型简化成有限元分析所需模型的原则:1)保持分析内容的总体结构不改变;2)删除对分析结果影响不大的细节,尽量减少节点数量;3)合理修改保证计算结果的准确性;4)在简化过程中需要保留危险部位的局部细节结构。
模型简化的方法:1)对不必要的圆角尽量略去;2)倒圆角处以倒斜角取代;3)结构中的工艺结构需要略去;4)不重要区的小孔及小尺寸细节结构尽量略去;5)简化非敏感区域小尺寸的细节结构[7]。
简化后的三维模型如下图3所示。
图3 简化后主轴承整体结构同时考虑到如果对轴承整体进行分析,将会有上百个接触对需要定义、求解;计算量远远超过一般计算机的求解能力,且这样算滚子的接触应力与实际情况相差较大[8],所以综合考虑,建立有限元模型时只对单个滚子对进行考虑,模型如下图4所示。
图4 单对滚子简化模型1.3 添加模型材料属性首先根据已知的轴承各部件材料查找确定其力学参数。
在ANSYS Workbench进行有限元分析时,所需要输入的材料参数主要有两个:材料的杨氏模量和泊松比。
查找可知,轴承钢G20Cr2Ni4的杨氏模量为206GPa,泊松比为0.3。
确定各零件这两个参数后,在ANSYS Workbench中Engineering Data材料参数设置界面中将这些新材料添加到材料库中,进行相关参数设置后,将其应用与该模型属性中。
这样,就将材料属性赋予了之前所建立的模型之中。
1.4 网格划分网格划分的好坏关系着整个求解过程的精确性和效率。
网格划分粗糙,计算时间快,但是精确程度低,甚至造成求解结果完全与实际不符;而网格划分过细,虽然理论上精确程度高,但计算时间长,需要的计算机存储空间大,效率低;同时在划分网格时若网格类型选择不合理同样会影响有限元计算结构,甚至造成求解不收敛。
因此在本文在划分网格时,综合考虑精度和效率两方面因素,选用四面体单元和六面体单元对风电主轴承进行网格划分。
且将轴承内外圈离滚子较远处网格划分的较少,并且采用了自动划分方法,效率高,但是足够体现变形协调和传力的准确;而在内外圈靠近滚子处、滚子等分析的重点零件网格划分的足够细密,网格分布足够均匀;所建的单元有限元网格模型如下图5所示。
整体节点数为487557个,单元数为136923个。
图5 整体网格划分1.4.1 滚子网格划分由于对滚子与滚道的接触分析是本次有限元分析的重点,因此滚子滚道接触部分的网格划分相对较细。
这里采用将滚子与滚道接触部分切开,其他部分网格相对较粗(六面体单元,单元大小2mm),而接触部分网格相对较细(六面体单元,单元尺寸1mm),如下图6所示。
图6 滚子网格划分1.4.2 外圈网格划分外圈由于尺寸较大,因此也采用分区域划分方法,靠近滚子出网格划分较细(六面体单元),而远离滚子处网格相对较粗(自动划分),划分结果如下图7所示。
图7 外圈网格划分1.4.3 内圈网格划分与外圈相似,内圈网格划分时也将其与滚子接触区域网格划分细些(六面体单元,单元尺寸1mm),远离滚子处网格较粗(自动划分),如下图8所示。
图8 内圈网格划分1.5 边界条件设定1.5.1 位移边界条件由于轴承在实际安装时,轴承外圈通过螺孔与风机机架固定在一起,因此有限元分析时,将轴承外圈孔进行全约束。
如下图9所示。
图9 位移边界条件1.5.2 载荷边界条件根据实际情况,该主轴承同时收到轴向力、径向力和倾覆力矩的作用。
载荷作用在轴承内圈上。
因此在有限元分析时,将轴承轴向力、径向力及力矩施加在轴承内圈表面节点上,如下图10所示。
图10 载荷边界条件1.5.3 接触边界条件由于要分析滚子与滚道的接触情况,因此需要定义其接触条件。
根据实际情况,滚子与滚道的接触为摩擦接触,并查阅相关资料可知,摩擦系数为0.15。
除滚子与滚道接触外,其余接触为计算方便定义为绑定基础,如下图11所示。
图11 定义接触情况2 算例结果分析按前述方法分析了某型号风电主轴承的滚动体载荷分布和接触应力,根据实际工况,在单个滚子对上施加轴向力20kN,径向力10kN,并施加倾覆力矩25000NM。
对轴承的应力分布、变形、等效应力以及滚子与滚道的接触应力的分析计算,计算结果如下图所示。
图12 滚子对总变形由分析结果可知,滚子对的最大变形处出现在轴承内圈靠近载荷接触区域,但变形量不是很大,符合实际情况。
图13 滚子弹性变形通过分析结果看出,滚子变形最大处出现在与轴承内圈接触区域,且靠近滚子边缘处。
这时由于这个区域既要承受轴向载荷,又要承受径向载荷和倾覆力矩,因此变形较大。
但由图可知,其变形量仍在一个较小的范围内,滚子没有发生破坏。
图14 滚子等效应力由分析结果看出,滚子的等效应力区域与弹性变形区域是对应的,且分布情况类似。
滚子最大应力为241.38MPa。
图示为滚子与滚道的接触应力,又有限元分析结果可知,滚子的最大接触应力为14.183MPa。
3 结论通过利用有限元对风电主轴承滚子接触应力的分析,以及与理论计算的对比可知:1)内外圈发生弯扭变形,滚动体载荷分布与采用刚性条件假设时滚动体载荷分布差异较大,因此对于风电轴承必须考虑支撑结构柔度对滚动体载荷分布影响;2)滚子的最大接触应力出现在距外载最近的滚子上与内圈接触的一侧,应力极值发生在距滚子大径端约1/3处;滚子在接触面中心的接触应力最大,远离接触中心后接触应力值逐渐减小,应力分布呈抛物线状,符合赫兹弹性接触理论。
这为为判断轴承的失效形式提供了一定的理论依据。
本文的意义在于:用有限元分析法变连续结构为离散结构,取代了传统的理论分析,并将分析结果与传统理论分析结果进行对比,弥补了理论分析的不足;图示出滚动轴承在径向载荷和轴向载荷作用下的变形和应力情况,显示出某时刻各滚动体的变化,有效地判断轴承的失效形式。
参考文献[1]赵永强,李俊峰等,许洪华.风力发电技术发展状况与趋势分析[J].中国科技产业,2006,(2):69-71.[2]何家群.风电产业和风电轴承[J].电气制造,2009,(9):58-61.[3]郭金东,赵栋利,李亚西等.风力发电浅谈[J].电力设备,2004,5(6):82-84.[4]翟保超.大型风电机组主轴轴承故障分析及疲劳寿命数值模拟[D].河北:燕山大学,2011:13.[5]刘耀中.Tinlken滚子轴承计算.轴承,2004(1).[6]韩晓建,邓家褆.机械产品设计的过程建模[J].北京航空航天大学学报,2000(05).[7]张昭.有限元方法与应用[M].大连:大连理工大学出版社,2011:43-64.[8] Ludwik Kania. Modelling of rollers in calculation of slewing bearing with the use of finiteelements[J]. Mechanism and Machine Theory, 2006(41): 1359-1376.。
