岩土所考博2017弹性力学
岩土所考博复习资料土力学(个人总结)第八章

第八章土的抗剪强度及地基稳定第一节概述土的抗剪强度(附)(2009 年概念)土体抵抗剪应力的极限值,或土体抵抗剪切破坏的受剪能力(强度)。
第二节土的抗剪强度抗剪强度的库伦定律库伦公式(库伦定律):砂土:粘性土:由库伦公式看以看出,无粘性土的抗剪强度与剪切面上的法向应力成正比,其本质是由于土粒间的滑动摩擦以及凹凸面间的镶嵌作用所产生的摩阻力,其大小决定于表面的粗糙度、土的密实度以及颗粒级配等因素。
粘性土的抗剪强度由两部分组成,一部分是摩阻力,另一部分是土粒之间的粘聚力,它是由于粘土颗粒之间的胶结作用和静电引力效应等因素引起的。
二抗剪强度的构成摩擦力:颗粒间的表面摩擦和颗粒间的咬合力。
粘聚力。
第三节土的极限平衡条件(2008 年计算与论述)1微元体上任意截面上法向应力和剪应力的确定方法:公式法和应力圆法。
2极限平衡状态时,土体剪切破坏面上的法向应力与剪应力之间的关系:无粘性土粘性土:一无粘性土图示:极限平衡条件:剪切破裂面的位置:二粘性土1图示:2极限平衡条件:3剪切破裂面的位置:第四节抗剪强度指标的测定一总应力法与有效应力法1总应力法和有效应力法的抗剪强度表达式:总应力法:有效应力法:2总应力法1)按排水条件不同:三轴剪力仪做试验,分为不排水剪、排水剪、固结不排水剪;直接剪仪做试验,对应为快剪、慢剪、固结快剪。
2)不排水剪(快剪):试验时,无论在法向应力下或在剪切过程中都不让土中水排出,试验中土的含水量不变。
3)排水剪(慢剪):试验时,无论在法向应力作用下或在整个剪切过程中都让土样排水,土样在应力变化过程中始终处于孔隙水应力为0 的完全固结状态。
4)固结不排水剪(固结快剪):试验时,先让土样在法向应力下完全固结,在剪切的全过程中则不让土样含水量变化。
5)慢剪的值最大,快剪的值最小,固结快剪居中,三种方法得到的C 值也不同。
6)各种剪切试验方法适用范围(2009年计算与论述):见书206表。
3有效应力法总应力法和有效应力法确定土的抗剪强度的优缺点?(2008 年计算与论述)总应力法和有效应力法各有其优缺点。
武汉岩土所考博真题-2014数值分析

湘 使用复化
一 法积 的 个 新 的估 计 。( 计 分g 求得 该积岔 ∫ 请使用 Romber 算 过程 中保 留 )湘 /← 4 位小 数 )
)设函数 /⑺ 在区间m,2]上 三 、(本 连续导数,并 且已知其部 具有 5阶 题 15分 分函数值和导数值如下表:
艿 `
0
1
2
/(冯 ) /【 冯)
2-2=0的 一 、(本 )取初值为 2,利 用 Newton迭 代法求方程 /⑺ =豸 题 10分 ,若计算结果用小数表示 ,请保留 6位 正的近似根 。计算要求 :迭代 4次 小数 。 二 、(本 )用 ‰ 表示在将区间 D,剑 阴等分后对 ㈨ 题 10分 梯形法得到的近似积分值 。己知:
rl=2.5o54。 马 =2.8090, r。 =2.8841, 「 :=2.9030
题
':丶
问
如下形 式 :
= 、 钭 y 刀 O y 刀 + 2 + α1 y+ 刀1 + α ⒒+ 2
是计算步长。 常数,勿 其中α 0,%,'是 其具有尽可能高的截断误差阶 请确定常数α 1,''使 0,α
I 丶 J '
科 目名称 :数 值 分析
ο
第 2 页
共 2 页
o
)考虑线J跬 代数方程 七 、(本 题 10分 (D 写 代法; 出求解此方程组 Gauss-seidel迭 上 曰 ,使 (2) 定确的取值范围 面的迭代法收敛 。
r 丨
矽T 刃
l < I l ι
儿 (`’
/ 〓 ) 一 一 ο
`
题 本
分
值 初 程ˇ 方 分 微 常 解 求
2017年中国科学院武汉岩土力学研究所博士研究生招生专业
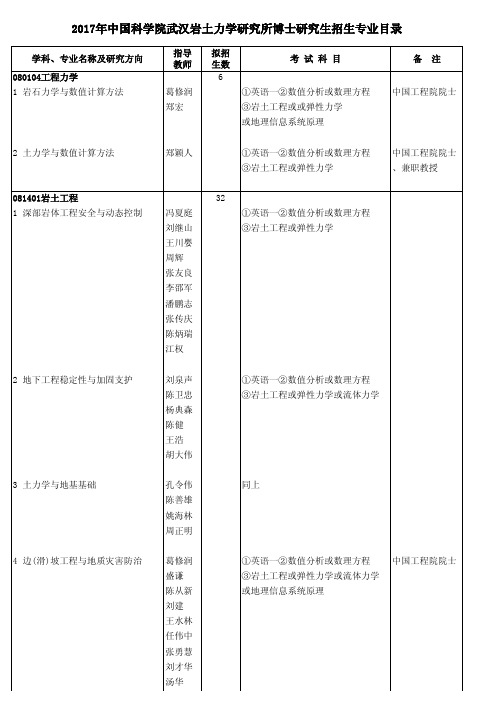
5 能源地下储存与废弃物地质处置 杨春和 李银平
6 岩体工程动力安全性与控制 7 海洋土力学性质与工程安全 8 二氧化碳地质封存与利用 9 固体废弃物安全处置
李海波 李建春 邓守春 刘亚群
韦昌富 朱长歧 孟庆山 叶剑红
李小春 李琦
薛强
①英语一②数值分析或数理方程 ③岩土工程或弹性力学或流体力学 同上
①英语一②数值分析或数理方程 ③岩土工程或弹性力学或流体力学
3 土力学与地基基础
孔令伟 陈善雄 姚海防治
葛修润 盛谦 陈从新 刘建 王水林 任伟中 张勇慧 刘才华 汤华
①英语一②数值分析或数理方程 ③岩土工程或弹性力学或流体力学 或地理信息系统原理
中国工程院院士
2017年中国科学院武汉岩土力学研究所 博士研究生招生专业目录
学科、专业名称及研究方向 080104工程力学 1 岩石力学与数值计算方法
指导 教师
葛修润 郑宏
拟招 生数
6
考试科目
①英语一②数值分析或数理方程
③岩土工程或或弹性力学
或地理信息系统原理
备注 中国工程院院士
2 土力学与数值计算方法
郑颖人
①英语一②数值分析或数理方程 ③岩土工程或弹性力学
中国工程院院士 、兼职教授
081401岩土工程 1 深部岩体工程安全与动态控制
冯夏庭 刘继山 王川婴 周辉 张友良 李邵军 潘鹏志 张传庆 陈炳瑞 江权
32 ①英语一②数值分析或数理方程 ③岩土工程或弹性力学
2 地下工程稳定性与加固支护
刘泉声 陈卫忠 杨典森 陈健 王浩 胡大伟
同上
同上 同上
岩土弹性力学分析报告

岩土弹性力学分析报告
本岩土弹性力学分析报告旨在对一个岩土体的力学行为进行分析,以评估其在荷载作用下的变形和稳定性能。
以下是对该岩土体进行的弹性力学分析的内容:
1. 介绍
1.1 目的
1.2 范围与方法
2. 岩土体特性描述
2.1 岩土体组成与结构
2.2 岩土体物理性质
2.3 岩土体力学性质
3. 弹性力学理论
3.1 弹性力学基本原理
3.2 应变-应力关系
3.3 弹性模量与泊松比
4. 应力分析
4.1 荷载条件与边界条件
4.2 岩土体内应力分布
4.3 最大主应力与最小主应力
5. 变形分析
5.1 应变分布
5.2 横向应变与纵向应变
5.3 压缩模量与剪切模量
6. 稳定性分析
6.1 岩土体的稳定性问题
6.2 应力变形特征
6.3 失稳机理与临界状态
7. 结论
7.1 对岩土体的弹性力学特性进行总结
7.2 对岩土体的稳定性进行评估
8. 建议与改进
8.1 基于分析结果提出的建议
8.2 对分析方法的改进意见
9. 参考文献
以上内容将涵盖对岩土体的弹性力学分析所需的主要方面,以便评估岩土体的力学性能,提供对其变形和稳定性的深入理解。
力学所博士面试题目(3篇)

第1篇一、面试背景力学所博士面试是选拔具有优秀学术素养、创新能力和实践能力的博士研究生的过程。
本次面试将重点考察应聘者的基础知识、专业素养、科研能力和综合素质。
以下为力学所博士面试题目。
二、面试题目1. 基础知识(1)请简要介绍牛顿三大定律。
(2)简述动量守恒定律和角动量守恒定律。
(3)什么是连续介质力学?请举例说明其在工程领域的应用。
(4)什么是弹性力学?请简述其基本假设和求解方法。
(5)什么是流体力学?请列举流体力学的主要分支。
2. 专业素养(1)请结合实例,说明力学在工程领域的应用。
(2)什么是有限元方法?请简述其原理和特点。
(3)什么是数值模拟?请列举数值模拟在力学研究中的应用。
(4)什么是计算力学?请简述其研究内容和目标。
(5)什么是实验力学?请列举实验力学在力学研究中的应用。
3. 科研能力(1)请谈谈你对力学研究领域的最新进展有何了解。
(2)请结合实例,说明你在力学研究中的创新点。
(3)请简述你已完成或正在进行的科研项目。
(4)请谈谈你在科研过程中遇到的问题及解决方法。
(5)请谈谈你对力学研究领域的未来发展趋势有何看法。
4. 综合素质(1)请谈谈你的学术背景和研究兴趣。
(2)请谈谈你在学术交流、团队协作方面的经验。
(3)请谈谈你的英语水平,以及你在英语学习方面的计划。
(4)请谈谈你对力学所的了解,以及你为什么选择加入力学所。
(5)请谈谈你的职业规划,以及你在博士期间的目标。
三、面试流程1. 报到:应聘者需携带身份证、学历证书、学位证书等材料,按照规定时间到达面试地点。
2. 面试:面试分为自我介绍、基础知识、专业素养、科研能力和综合素质等环节。
3. 问答环节:面试官根据应聘者的回答进行提问,考察应聘者的综合素质。
4. 评分:面试官根据应聘者的表现进行评分,最终确定录取名单。
四、面试要求1. 应聘者需按时参加面试,迟到者视为自动放弃面试资格。
2. 应聘者需保持礼貌,尊重面试官和在场人员。
注册岩土工程师-基础知识分类模拟题弹性力学.doc

基础知识分类模拟题弹性力学一、单项选择题1、关于弹性力学的正确认识是()。
A.弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析B.弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C.任何弹性变形材判都是弹性力学的研究对象D.计算力学在工程结构设计中的作用日益重要2、弹性力学对杆件分析是()。
A.无法分析B.得出精确的结果C.得出近似的结果D.需采用一些关于变形的近似假定3、关于应力状态分析,正确的是()oA.应力状态特征方程的根是确定的,因此任意截面的应力分量相同B.应力不变量表示主应力不变C.主应力的大小是可以确定的,但方向不是确定的D.应力分量随着截面方位改变而变化,但是应力状态是不变的4、根据圣维南原理,作用在物体一小部分边界上的力系可以用下列的力系代替,则仅在近处应力分布有改变,而在远处所受的影响可以不计()。
A.静力上等效B.几何上等效C.平衡D.任意5、弹性力学的基木未知量没有()。
A.应变分量B.位移分量C.应力D.而力6、下列关于弹性力学基木方程描述正确的是()oA.平衡微分方程是确定弹性体平衡的唯一条件B.几何方程适用小变形条件C.物理方程与材料性质无关D・变形协调方程是确定弹性体位移单值连续的唯一条件7、所谓''应力状态〃是指()。
A.—点不同截面的应力随着截面方位变化而改变B.斜截面应力矢量与横截面应力矢量不同C・3个主应力作用平面相互垂直D.不同截面的应力不同,因此应力矢量是不可确定的8、应力不变量说明()oA・应力随着截面方位改变,但是应力状态不变B.—点的应力分量不变C・主应力的方向不变D.应力状态特征方程的根是不确定的9、下列关于几何方程的叙述,没有错误的是()oA.几何方程是一点位移与应变分量Z间的唯一关系B.几何方程建立了位移与变形的关系,因此通过几何方程可以确定一点的应变分量C・几何方程建立了位移与变形的关系,因此通过几何方程可以确定一点的位移D.由于几何方程是由位移导数组成的,因此位移的导数描述了物体的变形位移10、下列关于应变状态的描述,错误的是()oA.坐标系的选取不同,应变分量不同,因此一点的应变是不可确定的B.不同坐标系下,应变分量的值不同,但是描述的一点变形的应变状态是确定的C・应变分量在不同坐标系中是变化的,但是其内在关系是确定的D. —点主应变的数值和方位是不变的11>弹性力学平面问题的求解中,平面应力问题与平面应变问题的三类基本方程具有下列关系(A.平衡方程、几何方程、物理方程完全相同B.平衡方程、物理方程相同,几何方程不同C・平衡方程、几何方程相同,物理方程不同D.几何方程、物理方程相同,平衡方程不同12、关于弹性力学平面问题的极坐标解,下列说法正确的是()<>A.坐标系的选取,改变了问题的基本方程和边界条件描述B.坐标系的选取,从根本上改变了弹性力学问题的性质C.对于极坐标解,平面应力和平面应变问题没有任何差别D.对于极坐标解,切应力互等定理不再成立13、所谓''完全弹性体〃是指()。
弹性力学在岩石工程中的应用
-8-
西北工业大学动力与能源学院
弹性力学在岩土工程中的应用
由此可求得摩擦体的剪应力 与剪应变 及相应位移。当不考虑摩擦力时求得 的 就是 1 。
6
计算举例
下面通过一个算例,用非摩擦体的传统弹性力学,计算土体内的位移,同时再
用本文方法,即摩擦体的弹性力学计算土体内的位移,以比较两种计算方法所得结 果的差别。 模型为长 20m 、深 15m 地基,两侧水平及底部被约束的平面应变问题。单元剖 分如图6所示,模型参数为 E 9 MPa , v 0.3 ,中间单元加均布荷载 q0 70kPa 。 当 q0 70kPa ,仅个别高斯点达到极限条件,所以可认为此时土体仍处于弹性 状态。计算得到 y 方向位移变化见表1。表中情况1为不考虑摩擦因素时的位移,情 况2~5为不同摩擦角时的位移。节点位置如图6所示。 表2为单元5,6,15,16,55,56,69四个高斯点的剪应力 xy 及折减因子 F (
-2-
西北工业大学动力与能源学院
弹性力学在岩土工程中的应用
将把岩土材料视作线弹性材料只是一种假设, 正是这种假设掩盖了岩土材料非线性 弹性特征,而且使弹性地基的弹性变形高于实测的弹性变形,从而使其偏离实际。
图1
土的应力—应变曲线
岩土材料是双强度材料,既具有黏聚力强度,又具有摩擦强度,在岩土工程的 弹性力学计算中,必须要考虑摩擦力,而摩擦力的发挥受材料变形的约束。由试验 可知,变形愈大摩擦因数也愈大,直到达到极限摩擦因数。这就决定岩土材料的应 力—应变关系为非线性,因而其相应的岩土材料弹性力学也将是非线性弹性力学。 岩土材料属于颗粒摩擦体,存在着内摩擦力,内摩擦力对应力的影响也是很大 的,因而其力学单元与传统弹性力学单元不同,如图 2 的传统固体的力学单元, 图 3 的摩擦材料的力学单元所示,图中 为正应力, 为剪应力, s 为摩擦应力。摩 擦体的单元中存在摩擦应力 s ,在非极限状态下,仍假设摩擦应力与法向应力成正 比,即:
《弹性力学》历年考博真题10-17
x、 y、 xy yx 三个应力分量。
(2)平面应变问题 : 很长的柱形体,在柱面上受有平行于横截面并且不沿长度变化的面力,而且体力 也平行于横截面且不沿长度变化。这一类问题可以简化为平面应变问题。例如挡土墙和重力坝的受力分析。
该种问题
xz zx 0; yz zy 0而一般 z并不等于零。
平面问题的几何方程: 揭示的是形变分量与位移分量间的相互关系。应注意当物体的位移分量完全确 定时,形变量即完全确定。反之,当形变分量完全确定时,位移分量却不能完全确定。
平面问题中的物理方程:揭示的是形变分量与应力分量间的相互关系。应注意平面应力问题和平面应 变问题物理方程的转换关系。
2.按照边界条件的不同,弹塑性力学问题分为那几类边界问题?试作简要说明。
2.什么是圣维南原理?其在弹塑性力学的问题求解中有什么实际意义?
圣维南原理可表述为: 如果把物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢量相同,对于同一点的主 矩也相同),那麽近处的应力分布将有显著的改变,但远处所受的影响可以不计. 弹塑性力学的问题求解中可利用圣维南原理将面力分布不明确的情况转化为静力等效但分布表达明确 的情况而将问题解决。还可解决边界条件不完全满足的问题的求解。
3.什么是平面应力问题?其受力特点如何,试举例予以说明。
答:平面应力问题 是指很薄的等厚度板,只在板边上受有平行于板面并且不沿厚度变化的面力,这 一类问题可以简化为平面应力问题。例如深梁在横向力作用下的受力分析问题。在该种问题中只存在
x、 y、 xy yx 三个应力分量。
4
2014 年北京工业大学攻读博士研究生入学考试试题 《弹塑性力学》
1
答:按照边界条件的不同,弹塑性力学问题分为位移边界问题、应力边界问题和 混合边界问题。
2017年岩土工程师考试专业知识真题及标准答案
)。(分数:2.00)
A.起重量
B.起重动力设备
√
C.起重高度
D.起重半径
解析:
20.在进行网络计划的工期-费用优化时,如果被压缩对象的直接费用率等于工程 间接费用率时(
)。
(分数:2.00)
A.应压缩关键工作的持续时间
B.应压缩非关键工作的持续时间
C.停止压缩关键工作的持续时间
√
D.停止压缩非关键工作的持续时间
)。(分数:2.00)
A.压应力
B.拉应力
√
C.剪应力
D.零
解析:
31.下列物体结构抗震设计的概念,正确的是(
)。(分数:2.00)
A.6 度设防,多层砌体结构既不需做承载力抗震验算,也不需考虑抗震构造 措施
B.6 度设防,多层砌体结构不需做承载力抗震验算,但要满足抗震构造措施
√
C.8 度设防,多层砌体结构需进行薄弱处抗震弹性变形验算
)。(分数:2.00)
A.双方的质量期限条款无效,故建筑公司无需赔偿受害者
B.事故发生时已超过合同质量期限条款,故建筑公司无需赔偿受害者
C.双方的质量期限条款无效,建筑公司应当向受害者承担赔偿责任
√
D.虽事故发生时已超过合同质量期限条款,但人命关天,故建筑公司必须赔 偿死者而非伤者
解析:
17.在沉桩前进行现场定位放线时,需设置的水准点应不少于(
)。(分数:2.00)
A.气孔状构造
B.层理构造
C.褶皱构造
D.断裂构造
√
解析:
47.下列现象中,不是滑坡造成的是(
)。(分数:2.00)
A.双沟同源地貌
B.直线状分布的泉水
√
C.马刀树
考博弹塑性力学,第一章
第三节
弹性力学中的基本假定
基本假定
为什么要提出基本假定? 任何学科的研究,都要略去影响很 小的次要因素,抓住主要因素 → 建立计 算模型 → 归纳为学科的基本假定。
第三节
弹性力学中的基本假定
材料性质假定
弹性力学中的五个基本假定
关于材料性质的假定及其在建立弹性力 学理论中的作用: (1)连续性 ─ 假定物体是连续的
体力─(定义)作用于物体体积内的力。
(表示)以单位体积内所受的力来量 度,f x , f y , f z (量纲) ML T . (符号)坐标正向为正。
−2 −2
第二节
弹性力学中的几个基本概念
面力─(定义)作用于物体表面上的力。
(表示)以单位面积所受的力来量 度,f x , f y , f z
ML−1T −2 . (量纲)
→ E、μ等与位置 ( x, y, z ) 无关
(4)各向同性 ─ 假定物体各向同性
→ E、μ等与方向无关
根据(3)和(4)→ E、μ等为常数 符合(1)—(4)假定的称为理想弹性体。
第三节
弹性力学中的基本假定
变形状态假定
变形状态假定: (5)小变形假定─假定位移和形变很小。 (a) 位移远小于物体尺寸 例:梁的挠度v 远小于梁高h
y
τyx
σy
第二节
弹性力学中的几个基本概念
应力与面力,在正面上,两者正方向一致, 在负面上,两者正方向相反。
O (z )
τxy
σx
fx fy
τxy
x
σx
fx fy
y
第二节
弹性力学中的几个基本概念
弹力与材力相比,正应力符号,相同 切应力符号,不同
