直线的倾斜角与斜率清实.ppt
合集下载
直线的倾斜角、斜率及直线的方程ppt

通过斜率可以判断直线的倾斜方向,进而确定直线的位置和 走势。
点斜式方程的局限性
点斜式方程只适用于已知一点和 斜率的直线,对于其他情况需要
使用其他形式的直线方程。
当直线与x轴垂直时,斜率不存 在,点斜式方程不适用。
在实际应用中,需要根据具体情 况选择合适的直线方程形式。
05 直线的两点式方程与斜率 的关系
点斜式方程
01
点斜式方程是直线方程的一种形 式,它表示通过一个固定点(x1, y1)和斜率m的直线。
02
点斜式方程可以用来求解直线的 方程,特别是当已知直线上的一 点和斜率时。
两点式方程
两点式方程是直线方程的另一种形式, 它表示通过两点(x1, y1)和(x2, y2)的 直线。
两点式方程也可以用来验证两点是否 在同一直线上。
整理得到$y - y_1 = m(x - x_1)$,其中$m$为直线斜率。
因此,点斜式方程为$y - y_1 = m(x - x_1)$,它是通过直线上两点坐标推导出来的。
斜率在点斜式方程中的应用
斜率$m$表示直线在坐标系上的倾斜程度,当$m > 0$时, 直线从左下到右上倾斜;当$m < 0$时,直线从左上到右下 倾斜;当$m = 0$时,直线与x轴平行。
两点式方程仅适用于已知两点坐标的情 况,对于其他情况可能不适用。
当两点坐标相同时,即直线过一个点时, 另外,当直线与坐标轴平行或重合时,
两点式方程将失去意义。
斜率不存在,此时两点式方程也无法表
示直线。
06 直线的方程在实际问题中 的应用
利用直线方程解决几何问题
确定两点间的直线方程
已知两点坐标,利用直线方程求解直线方程。
推导过程中,利用了直线上两点间斜率相等的性质,即斜率是固定的值。
点斜式方程的局限性
点斜式方程只适用于已知一点和 斜率的直线,对于其他情况需要
使用其他形式的直线方程。
当直线与x轴垂直时,斜率不存 在,点斜式方程不适用。
在实际应用中,需要根据具体情 况选择合适的直线方程形式。
05 直线的两点式方程与斜率 的关系
点斜式方程
01
点斜式方程是直线方程的一种形 式,它表示通过一个固定点(x1, y1)和斜率m的直线。
02
点斜式方程可以用来求解直线的 方程,特别是当已知直线上的一 点和斜率时。
两点式方程
两点式方程是直线方程的另一种形式, 它表示通过两点(x1, y1)和(x2, y2)的 直线。
两点式方程也可以用来验证两点是否 在同一直线上。
整理得到$y - y_1 = m(x - x_1)$,其中$m$为直线斜率。
因此,点斜式方程为$y - y_1 = m(x - x_1)$,它是通过直线上两点坐标推导出来的。
斜率在点斜式方程中的应用
斜率$m$表示直线在坐标系上的倾斜程度,当$m > 0$时, 直线从左下到右上倾斜;当$m < 0$时,直线从左上到右下 倾斜;当$m = 0$时,直线与x轴平行。
两点式方程仅适用于已知两点坐标的情 况,对于其他情况可能不适用。
当两点坐标相同时,即直线过一个点时, 另外,当直线与坐标轴平行或重合时,
两点式方程将失去意义。
斜率不存在,此时两点式方程也无法表
示直线。
06 直线的方程在实际问题中 的应用
利用直线方程解决几何问题
确定两点间的直线方程
已知两点坐标,利用直线方程求解直线方程。
推导过程中,利用了直线上两点间斜率相等的性质,即斜率是固定的值。
3-1-1 倾斜角与斜率(共36张PPT)

3.1 直线的倾斜角与斜率
3.1.1 倾斜角与斜率
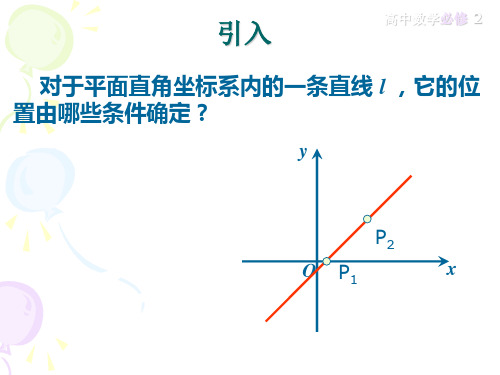
阅读教材P82~86回答 1.x轴正方向与直线l 向上的 方向所成的角α叫做直线 l的倾斜角,当l与x轴平行或重合时倾斜角为 0°,当l与x 轴垂直时,倾斜角为 90° ,直线l倾斜角的范围是
[0°,180°) .
下面图(1)中直线l的倾斜角为 140° , 图 (2) 中 直 线 a 的倾斜角为 0°.
总结评述:(1)利用此题结论可解决三点共线问题. (2)斜率是反映直线相对于x轴正方向的倾斜程度的, 在同一直线上任何不同的两点所确定的斜率相等.
[例7] 已知A(-2,1)、B(2,3)、C(1,-1),直线l经过 点C与线段AB相交,求直线l斜率的取值范围.
[错解] ∵kAC=1--2(--11)=-23,kBC=3-2-(-11)=4, ∴直线l斜率k的取值范围是-23,4.
[点评] 直线l越靠近y轴,其斜率的绝对值越大.
直线l1与l2的斜率分别为k1、k2如图,则k1与k2的大小关 系为________.
[答案] k1>k2
[例5] 如图所示,直线l1的倾斜角α1=30°,直线l1与 l2垂直,求l1、l2的斜率.
[解析]
直线l1的斜率k1=tanα1=tan30°=
[例3] 求经过下列两点的直线的斜率,并判断其倾斜 角是锐角还是钝角.
(1)(1,1),(2,4);(2)(-3,5),(0,2); (3)(4,4),(4,5);(4)(10,2),(-10,2).
[解析] (1)k=42- -11=3>0,∴倾斜角是锐角; (2)k=0-2-(-53)=-1<0,∴倾斜角是钝角; (3)斜率不存在,倾斜角是90°; (4)k=-21- 0-210=0,倾斜角为0°.
3.1.1 倾斜角与斜率
阅读教材P82~86回答 1.x轴正方向与直线l 向上的 方向所成的角α叫做直线 l的倾斜角,当l与x轴平行或重合时倾斜角为 0°,当l与x 轴垂直时,倾斜角为 90° ,直线l倾斜角的范围是
[0°,180°) .
下面图(1)中直线l的倾斜角为 140° , 图 (2) 中 直 线 a 的倾斜角为 0°.
总结评述:(1)利用此题结论可解决三点共线问题. (2)斜率是反映直线相对于x轴正方向的倾斜程度的, 在同一直线上任何不同的两点所确定的斜率相等.
[例7] 已知A(-2,1)、B(2,3)、C(1,-1),直线l经过 点C与线段AB相交,求直线l斜率的取值范围.
[错解] ∵kAC=1--2(--11)=-23,kBC=3-2-(-11)=4, ∴直线l斜率k的取值范围是-23,4.
[点评] 直线l越靠近y轴,其斜率的绝对值越大.
直线l1与l2的斜率分别为k1、k2如图,则k1与k2的大小关 系为________.
[答案] k1>k2
[例5] 如图所示,直线l1的倾斜角α1=30°,直线l1与 l2垂直,求l1、l2的斜率.
[解析]
直线l1的斜率k1=tanα1=tan30°=
[例3] 求经过下列两点的直线的斜率,并判断其倾斜 角是锐角还是钝角.
(1)(1,1),(2,4);(2)(-3,5),(0,2); (3)(4,4),(4,5);(4)(10,2),(-10,2).
[解析] (1)k=42- -11=3>0,∴倾斜角是锐角; (2)k=0-2-(-53)=-1<0,∴倾斜角是钝角; (3)斜率不存在,倾斜角是90°; (4)k=-21- 0-210=0,倾斜角为0°.
直线的倾斜角与斜率.ppt
观察
0
a
180 .
直线的倾斜角
高中数学必修 2
直线的倾斜程度与倾斜角有什么关系? 观察
①平面直角坐标系中每一条直线都 有确定的倾斜角
y
l
l
l
②倾斜程不同的直线有不同的倾斜角
③倾斜程度相同的直线其倾斜角相同 O
x
确定直线的要素 高中数学必修 2
观察 发现: 已知直线上的一个点不能确定一条直线的位置 已知直线的倾斜角α,不能确定一条直线的位置
直线上的一个点和这条直线的倾斜角可以唯一确定一 条直线.
确定平面直角坐标系中一条直线位置的几何 要素是:
直线上的一个定点以及它的倾斜角, 二者缺 一不可.
应用举例
高中数学必修 2
例1:请标示出以下直线的倾斜角
y
y
y
O
xO
xO
x
高中数学必修 2
倾斜程度的代数表示
日常生活中,还有没有表示倾斜程度的量?
解:由30o a 45o
y
tan 30o 3 , tan 45o 1 3
结合tana的图像可知
O
x
3 k 1 3
应用举例
高中数学必修 2
例3:设直线 l 的斜率为 k, 倾斜角为a , 若1 k 1,求 a的取值范围。
解: 由-1<k<1
y
tan 45o 1, tan135o 1
结合tana的图像可知
斜率(slope). 通常用小写字母k表示,即
k tan a
探索斜率
高中数学必修 2
是否所有直线都有斜率呢?
当倾斜角
y
a=90o时斜
率不存在
O
x
直线的倾斜角与斜率PPT课件

(1) 与两点的顺序无关; (2) 公式表明,直线的斜率可以通过直线上任意两
点的坐标来表示,而不需要求出直线的倾斜角 (3) 当x1=x2时,公式不适用,此时α=900
Y
.p
00 900 Y K>0
. 900 1800
p
K<0
O
X
O
X
(1)
(2)
Y
. K不存在 Y
p 90o
.p
K=0
1 2
钝角
O
x
kCA
1 2 03
1
锐角
C
(2)k [1,+) (-,- 1]
2
例题分析
例2、在平面直角坐标系中,画出经过原点且斜率
分别为1,-1,2和-3的直线 l1, l2 , l3及l4 。
y
l3
l1
A3 (1,2) A1 (1,1)
O
x
A2 (1,-1)
Al44 (l12,-3)
例2 从 M(2, 2 )射出一条光线,经过 x轴反射
直线
圆
圆
直线
3.1.1 直线的倾斜角与斜率
y
A
1.由一点能否确定一条直线吗?
2.观察并回答问题:
1
B
CO
1x
在图中,直线 AB,AC 都经过哪一点?
它们相对于 x 轴的倾斜程度相同吗?
直线的倾斜角定义 一般地,平面直角坐标系内,直线向上
的方向与 x 轴正方向所成的最小正角 叫做
这条直线的倾斜角.
已知直线的倾斜角,求对应的斜率 k :
(=0;
(2)=30;
(3)=135;
(4)=120.
如果给定直线的倾斜角,我们当然可以根据斜率
直线的斜率与倾斜角ppt

斜率的计算公式
对于直线上的两点$(x_1, y_1)$和 $(x_2, y_2)$,斜率$m$可由下式计算: $m = frac{y_2 - y_1}{x_2 - x_1}$。
当$x_2$与$x_1$相等时,斜率不存在 ,表示直线垂直于x轴。
斜率与倾斜角的关系
斜率与倾斜角$alpha$之间存在一一 对应关系,即斜率等于倾斜角正切值, 即$m = tanalpha$。
倾斜角定义
直线倾斜角是指直线与x 轴正方向之间的夹角,通 常用α表示,取值范围为 [0,π)。
计算方法
斜率m=tan(α),其中α为 直线的倾斜角。
直线的斜率与倾斜角的关系及应用
关系
直线的斜率与倾斜角α是线性关系,即 m=tan(α)。当α在[0,π/2)范围内时,斜 率为正,表示直线从左下到右上上升; 当α在(π/2,π)范围内时,斜率为负,表 示直线从左上到右下下降。
直线的斜率与倾斜角
目录
• 直线的斜率 • 直线的倾斜角 • 直线的斜率与倾斜角的应用 • 特殊情况的讨论 • 总结与回顾
01 直线的斜率
斜率的定义
01
斜率是直线在平面上的倾斜程度 ,表示为直线上的任意两点间纵 坐标差与横坐标差之商。
02
斜率是直线的重要属性,用于描 述直线的方向和倾斜程度,是解 析几何中重要的概念之一。
中研究直线的基础。
计算距离和角度
利用直线的斜率和倾斜角,可以计 算直线上的点到直线的垂直距离, 以及两条直线之间的夹角。
解决几何问题
在解决几何问题时,如求两条直线 的交点、判断直线与圆的位置关系 等,需要使用直线的斜率和倾斜角。
在物理学中的应用
描述运动轨迹
在物理学中,直线的斜率和倾斜 角可以用来描述物体的运动轨迹, 如自由落体运动、抛物线运动等。
直线的倾斜角与斜率、直线方程_图文

直线的倾斜角θ越大,斜率k就越大,这种说法正确吗?
(1)过点M(-2,m),N(m,4)的直线的斜率为1,则m= ________.
(2)直线x+y=1的倾斜角为________.
2.
填一填:(1)1 (2)135° 2.填一填:(1)3x+4y-14=0 (2)x+y-3=0 (3)x-y -7=0或4x+3y=0
直线l2的方程为( )
A. x+3y-5=0
B. x+3y-15=0
C. x-3y+5=0
D. x-3y+15=0
B
[] 已知直线l经过A(2,1),B(1,m2)(m∈R)两点,那 么直线l的倾斜角的取值范围是________.
2 [2013·](1)过点(-1,3)且平行于直线x-2y+3=0
的直线方程为( )
A. x-2y+7=0
B. 2x+y-1=0
C. x-2y-5=0
D. 2x+y-5=0
1. (1)直线的倾斜角 ①定义:x轴________与直线________的方向所成的角叫 做这条直线的倾斜角.当直线与x轴平行或重合时,规定它的 倾斜角为________. ②倾斜角的范围为__________.
(2)直线的斜率 ①定义:一条直线的倾斜角α的________叫做这条直线的 斜率,斜率常用小写字母k表示,即k=________,倾斜角是 90°的直线没有斜率. ②过两点的直线的斜率公式 经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式 为k=________.
备考· No.1 角度关键词:易错分析 解题过程中容易犯有两处错误:一是未考查点P与圆的位 置关系;二是运用直线方程的点斜式时,忽视了点斜式方程中 隐含的条件:此方程只能表示斜率存在的直线.
《直线倾斜角和斜率》课件
斜率决定了直线与x轴之间的夹角,即倾斜角。
斜率与直线图像的平移
01 斜率不变,平移直线图像
当直线沿x轴或y轴平移时,其斜率保持不变。
02 平移影响直线与坐标轴的交点
平移会导致直线与x轴或y轴的交点发生变化。
03 平移影响直线与坐标轴的距离
平移距离决定了直线与坐标轴之间的距离。
斜率与直线图像的旋转
斜率的计算公式
总结词
斜率的计算公式是$frac{y_2 - y_1}{x_2 - x_1}$,其中 $(x_1, y_1)$和$(x_2, y_2)$是直线上任意两点的坐标。
详细描述
根据定义,斜率是直线在坐标系中倾斜程度的数值表示 。通过两点坐标可以计算出直线的斜率。当两点横坐标 相等时,斜率不存在。
在电磁学中,斜率可以用来描述电流与电 压之间的关系。
在重力场中,斜率可以用来描述物体下落 的加速度。
在光学中,斜率可以用来描述光的折射率 。
斜率在经济学中的应用
斜率在经济学中常被用于描述供求关 系,即需求曲线和供给曲线的斜率。
斜率在经济学中还可以用于描述边际 效用、边际成本等概念。
需求曲线的斜率表示价格与需求量之 间的关系,供给曲线的斜率表示价格 与供给量之间的关系。
1 2
斜率随旋转角度而变化
当直线围绕原点旋转时,其斜率会发生变化。
旋转影响直线与坐标轴的夹角
旋转角度决定了直线与x轴之间的夹角。
3
旋转影响直线图像的对称性
在某些旋转角度下,直线图像可能会呈现对称性 。
直线的斜率在实际生活中的05 Nhomakorabea应用
斜率在物理中的应用
斜率在物理中常被用于描述物体的运动状 态,如速度、加速度等。
关系图通常以角度为横轴,以 斜率为纵轴,使用不同的线型 或标记表示不同倾斜角下的斜 率值。
斜率与直线图像的平移
01 斜率不变,平移直线图像
当直线沿x轴或y轴平移时,其斜率保持不变。
02 平移影响直线与坐标轴的交点
平移会导致直线与x轴或y轴的交点发生变化。
03 平移影响直线与坐标轴的距离
平移距离决定了直线与坐标轴之间的距离。
斜率与直线图像的旋转
斜率的计算公式
总结词
斜率的计算公式是$frac{y_2 - y_1}{x_2 - x_1}$,其中 $(x_1, y_1)$和$(x_2, y_2)$是直线上任意两点的坐标。
详细描述
根据定义,斜率是直线在坐标系中倾斜程度的数值表示 。通过两点坐标可以计算出直线的斜率。当两点横坐标 相等时,斜率不存在。
在电磁学中,斜率可以用来描述电流与电 压之间的关系。
在重力场中,斜率可以用来描述物体下落 的加速度。
在光学中,斜率可以用来描述光的折射率 。
斜率在经济学中的应用
斜率在经济学中常被用于描述供求关 系,即需求曲线和供给曲线的斜率。
斜率在经济学中还可以用于描述边际 效用、边际成本等概念。
需求曲线的斜率表示价格与需求量之 间的关系,供给曲线的斜率表示价格 与供给量之间的关系。
1 2
斜率随旋转角度而变化
当直线围绕原点旋转时,其斜率会发生变化。
旋转影响直线与坐标轴的夹角
旋转角度决定了直线与x轴之间的夹角。
3
旋转影响直线图像的对称性
在某些旋转角度下,直线图像可能会呈现对称性 。
直线的斜率在实际生活中的05 Nhomakorabea应用
斜率在物理中的应用
斜率在物理中常被用于描述物体的运动状 态,如速度、加速度等。
关系图通常以角度为横轴,以 斜率为纵轴,使用不同的线型 或标记表示不同倾斜角下的斜 率值。
2.1直线的倾斜角和斜率.PPT课件
x
y
. k不存 p 直在线垂直于
x轴
O
(4)
x
26
练习 1.下列哪些说法是正确的(E、F )
A 、任一条直线都有倾斜角,也都有斜率 B、直线的倾斜角越大,斜率也越大 C 、平行于x轴的直线的倾斜角是0或π D 、两直线的倾斜角相等,它们的斜率也相等 E 、两直线的斜率相等,它们的倾斜角也相等 F 、直线斜率的范围是R G、过原点的直线,斜率越大,越靠近y轴。
l2
l1
,
y
l1
解:l1 的斜率为
k1 tan1
3 3
1 2 x l2 的倾斜角为 2 900 300 1200
o
l2 的斜率为 k2 tan2 3
l2
练习 已知直线的倾斜角满足 cos a , (| a | 5),
求该直线的斜率.
5
解:
(1)当a 0时, cos 0, 900, k不存在;
2、直线的倾斜角范围的探索
规定:当直线和x轴平行或重合时, 它的倾斜角为0°
y
l
p
o x
y
ly
p
o x
o p x
y
p
l
o
x
l
由此我们得[到0直o线,1倾8斜0角oα的) 范围为:
想一想
你认为下列说法对吗?
1、所有的直线都有唯一确定的倾斜
角与它对应。
对
2、每一个倾斜角都对应于唯一的一条直线。
错
3、直线倾斜角的意义
17
3、探究:由两点确定k的直ta线n的 斜率
锐角
能不能构造
y
y2
y1
P2 (x2, y2 )
Q(x2, y1)
y
. k不存 p 直在线垂直于
x轴
O
(4)
x
26
练习 1.下列哪些说法是正确的(E、F )
A 、任一条直线都有倾斜角,也都有斜率 B、直线的倾斜角越大,斜率也越大 C 、平行于x轴的直线的倾斜角是0或π D 、两直线的倾斜角相等,它们的斜率也相等 E 、两直线的斜率相等,它们的倾斜角也相等 F 、直线斜率的范围是R G、过原点的直线,斜率越大,越靠近y轴。
l2
l1
,
y
l1
解:l1 的斜率为
k1 tan1
3 3
1 2 x l2 的倾斜角为 2 900 300 1200
o
l2 的斜率为 k2 tan2 3
l2
练习 已知直线的倾斜角满足 cos a , (| a | 5),
求该直线的斜率.
5
解:
(1)当a 0时, cos 0, 900, k不存在;
2、直线的倾斜角范围的探索
规定:当直线和x轴平行或重合时, 它的倾斜角为0°
y
l
p
o x
y
ly
p
o x
o p x
y
p
l
o
x
l
由此我们得[到0直o线,1倾8斜0角oα的) 范围为:
想一想
你认为下列说法对吗?
1、所有的直线都有唯一确定的倾斜
角与它对应。
对
2、每一个倾斜角都对应于唯一的一条直线。
错
3、直线倾斜角的意义
17
3、探究:由两点确定k的直ta线n的 斜率
锐角
能不能构造
y
y2
y1
P2 (x2, y2 )
Q(x2, y1)
直线的倾斜角和斜率(课件)(共19张PPT)
如果 是锐角,如图6-13(2)所示,此时 =180°-∠P1P2M ,
|P1M|= y1-y2, |P2M|=x1-x2, 因此直线P1P2的斜率为
在数学中,我们常用倾斜角和斜率来衡量直线相对 于 x 轴的倾斜程度.
一般地,在平面直角坐标系中,直线向上的方向与 x 轴正方向所成的最小正角 称为这条直线的倾斜角.特 别地,当直线与 y 轴垂直时,规定这条直线的倾斜角为 0°.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
探索研究 我们知道,在平面直角坐标系中,给定两个不同的
点 P1( x1 ,y1)和 P2(x2 ,y2 ),通过这两点的直线 P1P2 是 确定的.这样一来,这条直线的倾斜角是确定的,如果倾 斜角不是90°的话,它的斜率也是确定的.
试着研究 P1,P2的坐标与直线 P1P2的斜率以及倾斜 角之间的关系.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
不难看出,当 x1=x2时,直线 P1P2 垂直于 x 轴, 此时它的倾斜角为90°,斜率不存在,如图6-12(1)所 示.
情感目标 通过本节课学习,使学生养成乐于学习、勇于探索的良好品质
核心素养
通过思考、讨论等活动,提升学生数学的直观想象、数据分析、数学建模的 核心素养
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
|P1M|= y1-y2, |P2M|=x1-x2, 因此直线P1P2的斜率为
在数学中,我们常用倾斜角和斜率来衡量直线相对 于 x 轴的倾斜程度.
一般地,在平面直角坐标系中,直线向上的方向与 x 轴正方向所成的最小正角 称为这条直线的倾斜角.特 别地,当直线与 y 轴垂直时,规定这条直线的倾斜角为 0°.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
探索研究 我们知道,在平面直角坐标系中,给定两个不同的
点 P1( x1 ,y1)和 P2(x2 ,y2 ),通过这两点的直线 P1P2 是 确定的.这样一来,这条直线的倾斜角是确定的,如果倾 斜角不是90°的话,它的斜率也是确定的.
试着研究 P1,P2的坐标与直线 P1P2的斜率以及倾斜 角之间的关系.
调动思维,探究新知 在在活初初动中中2,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
不难看出,当 x1=x2时,直线 P1P2 垂直于 x 轴, 此时它的倾斜角为90°,斜率不存在,如图6-12(1)所 示.
情感目标 通过本节课学习,使学生养成乐于学习、勇于探索的良好品质
核心素养
通过思考、讨论等活动,提升学生数学的直观想象、数据分析、数学建模的 核心素养
创设情境,生成问题 在在活初初动中中1,,我我们们用用过过““自自然然数数集集””““有有理理数数集集””等等表表述述,,这这里里的的““集集””就就是是集集合合的的简简称称,,那那么么什什么么是是集集合合呢呢??
直线的倾斜角与斜率PPT教学课件
kAD
BD AD
tan
C升
高
量
A 前进量
B
1、定义:
a 我们把一条直线的倾斜角 的正切值叫做这
条直线的斜率。
k tan a 用小写字母 k 表示,即:
思考: 是否每条直线都有斜率?
1. 如果倾斜角是锐角? k tan a
2. 如果倾斜角是直角? k不存在
3. 如果倾斜角是钝角? k tan
k tan
y2
P2 (x2, y2 )
能不能构造
y1
Q(x2, y1)
P1(x1, y1)
一P个2直P1Q角三 且x1 角 形x2去, y求1 ?y2
o x1
x2 x
在RtP2P1Q中
0 k
tan
tan P2P1Q
QP2 P1Q
y2 x2
y乙炔的实验室制法:
1.发生装置:“固+液 气”的制取装置;
2.收集方法:排水法; 3.注意事项:
(1)可用饱和食盐水代替水,以得到平稳气流. (2)不能使用启普发生器, (3)产物气体中因含有AsH3,PH3而有特殊气味.
二、有冷凝装置的实验
制备实验 性质实验
(1)制溴苯;
(1)石油分镏;
(2)制乙酸乙酯; (3)制硝基苯;
(2)石油产品的催化裂化;
(3)煤的干镏;
(4)制酚醛树脂;
返回
返回
返回
石油分馏
石油分馏产品的催化裂化
煤的干馏
三、需要水浴加热的实验
A、制备硝基苯,需要温度计 B、制备酚醛树脂 C、银镜反应(热水浴) D、乙酸乙酯的水解(700C-800C)
E、蔗糖的水解(热水浴) F、纤维素的水解(15min,热水浴)
