考点跟踪训练47方程与函数相结合型综合问题
2014中考数学 专题 方程与函数相结合型综合问题题型专讲专练(12、13真题为例) (无答案)
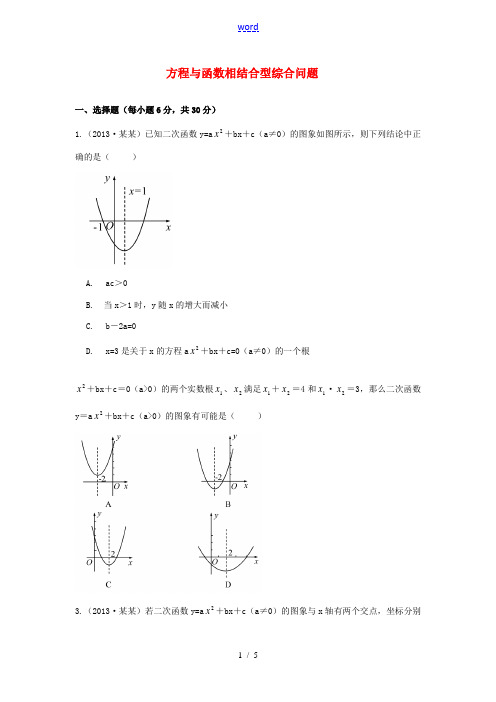
方程与函数相结合型综合问题一、选择题(每小题6分,共30分) 1.(2013·某某)已知二次函数y=a 2x +bx +c (a ≠0)的图象如图所示,则下列结论中正确的是( ) A.ac >0B.当x >1时,y 随x 的增大而减小C.b -2a=0D.x=3是关于x 的方程a 2x +bx +c=0(a ≠0)的一个根2x +bx +c =0(a>0)的两个实数根1x 、2x 满足1x +2x =4和1x ·2x =3,那么二次函数y =a 2x +bx +c (a>0)的图象有可能是( )3.(2013·某某)若二次函数y=a 2x +bx +c (a ≠0)的图象与x 轴有两个交点,坐标分别为(1x ,0),(2x ,0),且1x <2x ,图象上有一点M (0x ,0y )在x 轴下方,则下列判断正确的是( )A.a >0 B.2b -4ac ≥0 C.1x <0x <2x D.a (0x -1x )(0x -2x )<04.(2013·某某)目前,我国大约有1.3亿高血压病患者,占15岁以上总人口数的10%-15%,预防高血压不容忽视.“千帕kpa ”和“毫米汞柱mmHg ”都是表示血压的单位,前者是法定的国际计量单位,而后者则是过去一直广泛使用的惯用单位.请你根据下表所提供的信息,判断下列各组换算正确的是( )千帕kpa 10 12 16 … 毫米汞柱mmHg 75 90 120 …A.13kpa=100mmHgB.21kpa=150mmHgC.8kpa=60mmHgD.22kpa=160mmHg5.(2012·某某)二次函数y =a 2x +bx +1(a ≠0)的图象的顶点在第一象限,且过点(-1,0).设t =a +b +1,则t 值的变化X 围是( )A.0<t <1 B.0<t <2 C.1<t <2 D.-1<t <1二、填空题(每小题6分,共30分)6.(2013·某某)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y (单位:升)与时间x (单位:分)之间的部分关系.那么,从关闭进水管起分钟该容器内的水恰好放完.7.(2013·某某)若抛物线y=2x +bx +c 与x 轴只有一个交点,且过点A (m ,n ),B (m +6,n ),则n=.8.(2013·某某)函数y=x 1与y=x -2图象交点的横坐标分别为a ,b ,则a 1+b1的值为.9.(2013·某某)设甲、乙两车在同一直线公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车向原地返回.设x 秒后两车间的距离为y 米,y 关于x 的函数关系如图所示,则甲车的速度是米/秒.10.(2013·某某)若关于t 的不等式组⎩⎨⎧≤+≥-4120t a t 恰有三个整数解,则关于x 的一次函数y=41x-a 的图象与反比例函数y=xa 23+的图象的公共点的个数为.三、解答题(共40分)11.(12分)(2012·某某)已知一元二次方程2x +px +q=0(2p -4q ≥0)的两根为1x 、2x .(1)求证:1x +2x =-p ,1x ·2x =q ; (2)已知抛物线y=2x +px +q 与x 轴交于A ,B 两点,且过点(-1,-1),设线段AB 的长为d ,当p 为何值时,2d 取得最小值,并求出最小值.12.(12分)(2013·某某)某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.(1)不妨设该种品牌玩具的销售单价为x 元(x >40),请你分别用x 的代数式来表示销售量y 件和销售该品牌玩具获得利润w 元,并把结果填写在表格中:销售单价(元)x 销售量y (件) 销售玩具获得利润w (元)(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x 应定为多少元;(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?13.(16分)(2013·荆州)如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.(1)直接写出y与x之间的函数关系式;(2)分别求出第10天和第15天的销售金额;(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?。
高中数学课时跟踪检测:函数与方程

高中数学课时跟踪检测:函数与方程一抓基础,多练小题做到眼疾手快 1.已知函数f (x )=23x+1+a 的零点为1,则实数a 的值为______. 解析:由已知得f (1)=0,即231+1+a =0,解得a =-12. 答案:-122.已知关于x 的方程x 2+mx -6=0的一个根比2大,另一个根比2小,则实数m 的取值范围是______.解析:设函数f (x )=x 2+mx -6,则根据条件有f (2)<0,即4+2m -6<0,解得m <1. 答案:(-∞,1)3.已知函数f (x )=⎩⎨⎧-2,x >0,-x 2+bx +c ,x ≤0,若f (0)=-2,f (-1)=1,则函数g (x )=f (x )+x 的零点个数为______.解析:依题意得⎩⎨⎧c =-2,-1-b +c =1,由此解得b =-4,c =-2.由g (x )=0得f (x )+x =0, 该方程等价于⎩⎨⎧x >0,-2+x =0, ①或⎩⎨⎧x ≤0,-x 2-4x -2+x =0.②解①得x =2,解②得x =-1或x =-2. 因此,函数g (x )=f (x )+x 的零点个数为3. 答案:34.(连云港调研)已知函数f (x )=2-x 2-x +b 有一个零点,则实数b 的取值范围为________.解析:由已知,函数f (x )=2-x 2-x +b 有一个零点,即函数y =x -b 和y =2-x 2的图象有1个交点,如图,其中与半圆相切的直线方程为y =x +2,过点(0,2)的直线方程为y =x +2,所以满足条件的b 的取值范围是b =-2或-2<b ≤ 2.答案:{-2}∪(-2,2]5.(苏州质检)已知函数f (x )=⎝ ⎛⎭⎪⎫12x -cos x ,则f (x )在[0,2π]上的零点个数为________.解析:作出g (x )=⎝ ⎛⎭⎪⎫12x与h (x )=cos x 的图象如图所示,可以看到其在[0,2π]上的交点个数为3,所以函数f (x )在[0,2π]上的零点个数为3.答案:36.(泰州中学上学期期中)已知函数y =f (x )的周期为2,当x ∈[-1,1]时,f (x )=x 2,那么函数y =f (x )的图象与函数y =|lg x |的图象的交点共有________个.解析:在同一直角坐标系中分别作出y =f (x )和y =|lg x |的图象,如图,结合图象知,共有10个交点.答案:10二保高考,全练题型做到高考达标1.设x 0为函数f (x )=2x +x -2的零点,且x 0∈(m ,n ),其中m ,n 为相邻的整数,则m +n =________.解析:函数f (x )=2x +x -2为R 上的单调增函数,又f (0)=1+0-2=-1<0,f (1)=2+1-2=1>0,所以f (0)·f (1)<0,故函数f (x )=2x +x -2的零点在区间(0,1)内,故m =0,n =1,m +n =1.答案:12.(镇江中学检测)已知函数f (x )=2x +2x -6的零点为x 0,不等式x -4>x 0的最小的整数解为k ,则k =________.解析:函数f (x )=2x +2x -6为R 上的单调增函数,又f (1)=-2<0,f (2)=2>0,所以函数f (x )=2x +2x -6的零点x 0满足1<x 0<2,故满足x 0<n 的最小的整数n =2,即k -4=2,所以满足不等式x -4>x 0的最小的整数解k =6.答案:63.已知方程2x +3x =k 的解在[1,2)内,则k 的取值范围为________. 解析:令函数f (x )=2x +3x -k , 则f (x )在R 上是增函数.当方程2x +3x =k 的解在(1,2)内时,f (1)·f (2)<0, 即(5-k )(10-k )<0,解得5<k <10. 当f (1)=0时,k =5.综上,k 的取值范围为[5,10). 答案:[5,10)4.(太原模拟)若函数f (x )=(m -2)x 2+mx +(2m +1)的两个零点分别在区间(-1,0)和区间(1,2)内,则实数m 的取值范围是________.解析:依题意并结合函数f (x )的图象可知,⎩⎨⎧m ≠2,f -1·f0<0,f 1·f 2<0,即⎩⎨⎧m ≠2,[m -2-m +2m +1]2m +1<0,[m -2+m +2m +1][4m -2+2m +2m +1]<0,解得14<m <12.答案:⎝ ⎛⎭⎪⎫14,125.(无锡期末)设函数f (x )=⎩⎨⎧1,x ≥1,x ·log 2x +1,x <1,若方程f (x )-mx =0恰好有3个零点,则实数m 的取值范围为________.解析:当x ≥1时,方程f (x )-mx =0变为1-mx =0,解得x =1m;当-1<x <1时,方程f (x )-mx =0变为x [log 2(x +1)-m ]=0,解得x =0或x =2m -1. 因为f (x )-mx =0恰好有3个零点,所以1m≥1,且-1<2m -1<1,解得0<m <1,故实数m 的取值范围为(0,1).答案:(0,1)6.(镇江调研)已知k 为常数,函数f (x )=⎩⎨⎧x +2x -1,x ≤0,|ln x |,x >0,若关于x 的方程f (x )=kx +2有且只有4个不同的解,则实数k 的取值范围为________.解析:作出函数y =f (x )的大致图象如图所示,若关于x 的方程f (x )=kx +2有且只有4个不同解,当直线y =kx +2与y =ln x 的图象相切时,设切点为(m ,n ),可得n =ln m ,y =ln x 的导数为y ′=1x (x >1),可得k =1m,则n =km +2,解得m =e 3,k =e -3,则实数k 的取值范围为(0,e -3).答案:(0,e -3)7.(苏州调研)已知函数f (x )=⎩⎨⎧ln x ,x >0,2x +1,x ≤0,若直线y =ax 与y =f (x )交于三个不同的点A (m ,f (m )),B (n ,f (n )),C (t ,f (t ))(其中m <n <t ),则n +1m+2的取值范围是________.解析:由已知条件可得⎩⎨⎧2m +1=am ,ln n =an ,所以⎩⎪⎨⎪⎧2+1m =a ,ln n n =a ,所以n +1m +2=n +ln nn,令g (n )=n +ln nn,当f (x )=ln x ,x >0与y =ax 相切时,由f ′(x )=1x ,得1x=a ,又ln x =ax ,解得x =e,所以要满足题意,则1<n <e.由g ′(n )=1+1-ln nn 2>0,所以g (n )=n +ln nn在(1,e)上单调递增,所以g (n )=n +1m +2∈⎝⎛⎭⎪⎫1,e +1e .答案:⎝⎛⎭⎪⎫1,e +1e 8.(南京、盐城一模)设f (x )是定义在R 上的奇函数,且f (x )=2x +m2x ,设g (x )=⎩⎨⎧f x ,x >1,f-x ,x ≤1,若函数y =g (x )-t 有且只有一个零点,则实数t 的取值范围是________.解析:因为f (x )为奇函数,所以f (-x )=-f (x ),即2-x +m ·2x =-(2x +m ·2-x ),解得m =-1,故g (x )=⎩⎨⎧2x -2-x , x >1,2-x -2x,x ≤1,作出函数g (x )的图象(如图所示).当x >1时,g (x )单调递增,此时g (x )>32;当x ≤1时,g (x )单调递减,此时g (x )≥-32,所以当t ∈⎣⎢⎡⎦⎥⎤-32,32时,y =g (x )-t 有且只有一个零点.答案:⎣⎢⎡⎦⎥⎤-32,329.已知二次函数f (x )=x 2+(2a -1)x +1-2a ,(1)判断命题:“对于任意的a ∈R,方程f (x )=1必有实数根”的真假,并写出判断 过程;(2)若y =f (x )在区间(-1,0)及⎝⎛⎭⎪⎫0,12内各有一个零点,求实数a 的取值范围.解:(1)“对于任意的a ∈R,方程f (x )=1必有实数根”是真命题.依题意,f (x )=1有实根,即x 2+(2a -1)x -2a =0有实根,因为Δ=(2a -1)2+8a =(2a +1)2≥0对于任意的a ∈R 恒成立,即x 2+(2a -1)x -2a =0必有实根,从而f (x )=1必有实根.(2)依题意,要使y =f (x )在区间(-1,0)及⎝ ⎛⎭⎪⎫0,12内各有一个零点, 只需⎩⎪⎨⎪⎧f -1>0,f 0<0,f ⎝ ⎛⎭⎪⎫12>0,即⎩⎪⎨⎪⎧3-4a >0,1-2a <0,34-a >0,解得12<a <34.故实数a 的取值范围为⎝ ⎛⎭⎪⎫12,34.10.(通州中学检测)已知二次函数f (x )=ax 2+bx +1,g (x )=a 2x 2+bx +1.若函数f (x )有两个不同零点x 1,x 2,函数g (x )有两个不同零点x 3,x 4.(1)若x 3<x 1<x 4,试比较x 2,x 3,x 4的大小关系;(2)若x 1=x 3<x 2,m ,n ,p ∈(-∞,x 1),f ′mg n =f ′n g p =f ′pg m,求证:m =n =p .解:(1)因为函数g (x )的图象开口向上,且零点为x 3,x 4, 故g (x )<0⇔x ∈(x 3,x 4). 因为x 1,x 2是f (x )的两个不同零点, 故f (x 1)=f (x 2)=0.因为x 3<x 1<x 4,故g (x 1)<0=f (x 1),于是(a 2-a )x 21<0. 注意到x 1≠0,故a 2-a <0. 所以g (x 2)-f (x 2)=(a 2-a )x 22<0, 故g (x 2)<f (x 2)=0,从而x 2∈(x 3,x 4), 于是x 3<x 2<x 4.(2)证明:记x 1=x 3=t ,故f (t )=at 2+bt +1=0,g (t )=a 2t 2+bt +1=0,于是(a -a 2)t 2=0.因为a ≠0,且t ≠0,故a =1. 所以f (x )=g (x )且图象开口向上.所以对∀x ∈(-∞,x 1),f ′(x )递增且f ′(x )<0,g (x )递减且g (x )>0. 若m >n ,则f ′(n )<f ′(m )<0,1g n>1g p>0,从而g (p )>g (n )>0,故n >p .同上,当n >p 时,可推得p >m .所以p >m >n >p ,矛盾.所以m >n 不成立. 同理,n >m 亦不成立. 所以m =n .同理,n =p . 所以m =n =p .三上台阶,自主选做志在冲刺名校1.(镇江期中)函数f (x )=⎩⎨⎧|ln x |+3,x >0,-x 2-2x -2,x ≤0,若关于x 的方程f 2(x )+bf (x )+4b+1=0有4个不同的实数根,则实数b 的取值范围是________.解析:令t =f (x ),则原方程等价于t 2+bt +1+4b =0.作出函数f (x )的图象如图所示.由图象可知,当t >3,-2≤t <-1时,函数y =t 和y =f (x )各有两个交点, 要使方程f 2(x )+bf (x )+4b +1=0有4个不同的实数根, 则方程t 2+bt +1+4b =0有两个根t 1,t 2,且t 1>3,-2≤t 2<-1.令g (t )=t 2+bt +1+4b ,则由根的分布可得⎩⎨⎧g-2=5+2b ≥0,g-1=2+3b <0,g3=10+7b <0,解得-52≤b <-107. 答案:⎣⎢⎡⎭⎪⎫-52,-1072.(南京调研)设函数f k (x )=2x +(k -1)·2-x (x ∈R,k ∈Z). (1)若f k (x )是偶函数,求不等式f k (x )>174的解集; (2)设不等式f 0(x )+mf 1(x )≤4的解集为A ,若A ∩[1,2]≠∅,求实数m 的取值范围; (3)设函数g (x )=λf 0(x )-f 2(2x )-2,若g (x )在x ∈[1,+∞)上有零点,求实数λ的取值范围.解:(1)因为f k (x )是偶函数,所以f k (-x )=f k (x )恒成立, 即2-x +(k -1)·2x =2x +(k -1)·2-x , 所以k =2. 由2x +2-x >174,得4·22x -17·2x +4>0, 解得2x <14或2x >4,即x <-2或x >2,所以不等式f k (x )>174的解集为{x |x <-2或x >2}. (2)不等式f 0(x )+mf 1(x )≤4,即为2x -2-x +m ·2x ≤4, 所以m ≤2-x -2x +42x ,即m ≤⎝ ⎛⎭⎪⎫12x 2+4·12x -1.令t =12x ,x ∈[1,2],则t ∈⎣⎢⎡⎦⎥⎤14,12,设h (t )=t 2+4t -1,t ∈⎣⎢⎡⎦⎥⎤14,12,则h (t )max =h ⎝ ⎛⎭⎪⎫12=54.由A ∩[1,2]≠∅,即不等式f 0(x )+mf 1(x )≤4在[1,2]上有解, 则需m ≤h (t )max ,即m ≤54.所以实数m 的取值范围为⎝ ⎛⎦⎥⎤-∞,54.(3)函数g (x )=λ(2x-2-x)-(22x+2-2x)-2在x ∈[1,+∞)上有零点,即λ(2x -2-x )-(22x +2-2x )-2=0在x ∈[1,+∞)上有解, 因为x ∈[1,+∞),所以2x -2-x >0,所以问题等价于λ=22x +2-2x +22x -2-x 在x ∈[1,+∞)上有解.令p =2x ,则p ≥2,令u =p -1p,则u 在p ∈[2,+∞)上单调递增, 因此u ≥32,λ=u 2+4u.设r (u )=u 2+4u =u +4u ,则r ′(u )=1-4u 2,当32≤u ≤2时,r ′(u )≤0,即函数r (u )在⎣⎢⎡⎦⎥⎤32,2上单调递减,当u ≥2时,r ′(u )≥0,即函数r (u )在[2,+∞)上单调递增,所以函数r (u )在u =2时取得最小值,且最小值r (2)=4, 所以r (u )∈[4,+∞),从而满足条件的实数λ的取值范围是[4,+∞).。
中考数学(要点 自测 题型 易错)复习课件:第49课 方程、函数与几何相结合型综合问题

助学微博
一个考向
代数几何综合题从内容上来说,是把代数中的数与式、 方程与不等式、函数、几何中的三角形、四边形、圆等图形 的性质,以及解直角三角形的方法、图形的变换、相似等内 容有机地结合在一起,同时也融入了开放性、探究性等问题, 如探究条件、探究结论、探究存在性等.经常考查的题目类 型主要有坐标系中的几何问题(简称坐标几何问题),以及图 形运动过程中求函数解析式问题等.
【例 2】 (2012·连云港) 如图,抛物线 y=-x2+bx+c 与 x 轴交于 A、B 两点,与 y 轴交于点 C,点 O 为坐标原点, 点 D 为抛物线的顶点,点 E 在抛物线上,点 F 在 x 轴上, 四边形 OCEF 为矩形,且 OF=2,EF=3. (1)求抛物线所对应的函数解析式; (2)求△ABD 的面积; (3)将△AOC 绕点 C 逆时针旋转 90°, 点 A 对应点为点 G,问点 G 是否在 该抛物线上?请说明理由.
解答下列问题:如图②,抛物线顶点坐标为点 C(1,4),交 x 轴于点 A(3,0),交 y 轴于点 B. (1)求抛物线和直线 AB 的解析式; (2)点 P 是抛物线(在第一象限内)上的一个动点,连接 PA、
PB,当 P 点运动到顶点 C 时,求△CAB 的铅垂高 CD 及 S△CAB; 9
(3)是否存在一点 P,使 S△PAB=8S△CAB?若存在,求出 P 点的坐 标;若不存在,请说明理由.
2≤x<3
2).
故选 B.
【例 1】 阅读材料:如图①,过△ABC 的三个顶点分别作出与 水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽(a)”,中间的这条直线在△ABC 内部线段的长 度叫△ABC 的“铅垂高(h)”.我们可得出一种计算三角形 1 面积的新方法:S△ABC=2ah,即三角形面积等于水平宽与铅 垂高乘积的一半.
2024年新高考版数学专题1_3.5 函数与方程及函数的综合应用(分层集训)

B.3
答案 B
C.4
D.5
)
3.(2022南京师范大学附中期中,7)用二分法研究函数f(x)=x3+2x-1的零点
时,第一次计算,得f(0)<0,f(0.5)>0,第二次应计算f(x1),则x1等于 (
A.1
B.-1
答案 C
C.0.25
D.0.75
)
4.(多选)(2022湖南师大附中三模,11)已知函数f(x)的定义域为R,且f(x)=f(x
1.(2023届长春六中月考,7)若函数f(x)=ln x+x2+a-1在区间(1,e)内有零点,则
实数a的取值范围是 (
A.(-e2,0)
C.(1,e)
答案 A
B.(-e2,1)
D.(1,e2)
)
2.(2017课标Ⅲ,文12,理11,5分)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,
A型
0.4
3
B型
0.3
4
C型
0.5
3
D型
0.4
4
则保温效果最好的双层玻璃的型号是 (
A.A型
答案 D
B.B型
C.C型
D.D型
)
3.(2020课标Ⅲ理,4,5分)Logistic模型是常用数学模型之一,可应用于流行
病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数
I(t)(t的单位:天)的Logistic模型:I(t)=
1 e
K
0.23( t 53)
,其中K为最大确诊病例数.
当I(t*)=0.95K时,标志着已初步遏制疫情,则t*约为(ln 19≈3) (
中考数学总复习 考点跟踪训练57 方程、函数与几何相结合型综合问题(无答案)(2021学年)

浙江省中考数学总复习考点跟踪训练57 方程、函数与几何相结合型综合问题(无答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(浙江省中考数学总复习考点跟踪训练57 方程、函数与几何相结合型综合问题(无答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为浙江省中考数学总复习考点跟踪训练57 方程、函数与几何相结合型综合问题(无答案)的全部内容。
考点跟踪训练57 方程、函数与几何相结合型综合问题A组基础过关练一、选择题1.(2013苏州)如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函数y=错误!(x>0)的图象经过顶点B,则k的值为( )A. 12 B.20C。
24 D. 322. (2012福州)如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数y=\f(k,x)(x>0)的图像与△ABC有公共点,则k的取值范围是()A。
2≤k≤9B。
2≤k≤8C. 2≤k≤5D. 5≤k≤83.(2014铜仁)如图所示,在矩形ABCD中,F是DC上一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=26,则MF的长是( )A。
错误!B。
错误!C.1 D。
错误!4。
(2014丽水)如图,AB=4,射线BM和AB互相垂直,点D是AB上的一个动点,点E在射线BM上,BE=\f(1,2)DB,作EF⊥DE并截取EF=DE,连接AF并延长交射线BM于点C.设BE=x,BC=y,则y关于x的函数解析式是( )A。
y=-\f(12x,x-4) B. y=-\f(2x,x-1)C.y=-错误! D. y=-错误!二、填空题5. (2014黔东南)在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为________.6. (2014孝感)如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=错误!经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为________.7。
中考数学 专题 方程、函数与几何相结合型综合问题题型专讲专练课件(12、13真题为例)

3.
【例 3】(2013·宁波)如图,在平面直角坐标系中, O为坐标原点,点A的坐标为(0,4),点B的坐标 为(4,0),点C的坐标为(-4,0),点P在射线 AB上运动,连接CP与y轴交于点D,连接BD.过P,D, B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q 于点F,连接EF,BF.
(1)求直线AB的函数解析式;
解 (1)当 k=-2 时,A(1,-2), ∵点 A 在反比例函数图象上, m ∴设反比例函数的解析式为:y= , x m 将 A(1,-2)代入得,-2= ,解得 m=-2, 1 2 ∴反比例函数的解析式为:y=- . x
(2)要使反比例函数和二次函数都是 y 随着 x 的增大而增大, 则 k<0, 1 2 5 2 ∵二次函数 y=k(x +x-1)=k(x+ ) - k, 2 4 1 对称轴为直线 x=- , 2 2 要使二次函数 y=k(x +x-1)满足上述条件, 在 k<0 的情况下,x 必须在对称轴的左边, 1 即 x<- 时,才能使得 y 随着 x 的增大而增大. 2 1 ∴综上所述,k<0 且 x<- . 2
对应训练
(1)求抛物线的解析式; (2)若点P为线段OB上的一个动点(不与点O,B重 合),直线PC与抛物线交于D,E两点(点D在y轴右 侧),连接OD,BD. ①当△OPC为等腰三角形时,求点P的坐标; ②求△BOD面积的最大值,并写出此时点D的坐标.
(1)若OA=10,求反比例函数解析式;
(2)若点F为BC的中点,且△AOF的面积S=12,求 OA的长和点C的坐标;
(3)在(2)中的条件下,过点F作EF∥OB,交OA于 点E(如图②),点P为直线EF上的一个动点,连接PA, PO.是否存在这样的点P,使以P,O,A为顶点的三角 形是直角三角形?若存在,请直接写出所有点P的坐标; 若不存在,请说明理由.
中考数学一轮复习考点跟踪训练47方程与函数相结合型综合问题试题

考点跟踪训练47 方程与函数相结合型综合问题一、选择题(每一小题6分,一共30分)1.在平面直角坐标系中,抛物线y=x2-1与x轴的交点的个数是( ) A.3 B.2C.1 D.02.(2021·)如下图的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)2a错误..的有( )A.2个 B.3个C.4个 D.1个3.(2021·)一元二次方程ax2+bx+c=0(a>0)的两个实数根x1、x2满足x1+x2=4和 x1·x2=3,那么二次函数y=ax2+bx+c (a>0)的图象有可能是( )4.(2021·)如图为反比例函数y =1x在第一象限的图象,点A 为此图象上的一动点,过( )A .4B .3C .2D .15.(2021·)二次函数y =ax 2+bx +1(a≠0)的图象的顶点在第一象限,且过点(-1,0).设 t =a +b +1,那么t 值的变化范围是( )A .0<t <1B .0<t <2C .1<t <2D .-1<t <1二、填空题(每一小题6分,一共30分)6.(2021·)如图,直线y =kx +b 经过A(3,1)和B(6,0)两点,那么不等式组0<kx +b <13x 的解集为________.7.关于x 的分式方程 a +2x +1=1的解是非正数,那么a 的取值范围是________.8.(2021·)新定义:[a ,b]为一次函数y =ax +b(a≠0,a 、b 为实数)的“关联数〞.假设“关联数〞[1,m -2]的一次函数是正比例函数,那么关于x 的方程1x -1+1m=1的解为 ______________.9.(2021·黔东南)设函数y =x -3与y =2x 的图象的两个交点的横坐标为a 、b ,那么1a +1b= ________.10.(2021·)如图,第一象限内的图象是反比例函数y =1x图象的一个分支,第二象 限内的图象是反比例函数y =-2x图象的一个分支,在x 轴的上方有一条平行于x 轴的 直线l 与它们分别交于点A 、B ,过点A 、B 作x 轴的垂线,垂足分别为C 、D.假设四边 形ABCD 的周长为8且AB <AC ,那么点A 的坐标为________.三、解答题(每一小题20分,一共40分)11.假如一个二次函数的图象经过点A(6,10),与x 轴交于B 、C 两点,点B 、C 的横坐标 为x 1、x 2,且x 1+x 2=6,x 1·x 2=5.求这个二次函数的解析式.12.(2021·)关于x 的一元二次方程(x -m)2+6x =4m -3有实数根.(1)求m 的取值范围;(2)设方程的两实根分别为x1与x2,求代数式x1·x2-x21-x22的最大值.四、附加题(一共20分)13.(2021·)(1)一元二次方程x2+px+q=0(p2-4q≥0)的两根为x1、x2.求证:x1+x2=-p,x1·x2=q;(2)抛物线y=x2+px+q与x轴交于A、B两点,且过点(-1,-1),设线段AB的长为d,当p为何值时,d2获得最小值,并求出最小值.励志赠言经典语录精选句;挥动**,放飞梦想。
中考数学 专题 方程、函数与几何相结合型综合问题题型专讲专练课件(12、13真题为例)

中,得
15 y1= 4 .
∴P 点坐标为23,145.
【点评】
理解“铅垂高(h)”,且能利用“铅垂高”来计算三 角形面积.根据题意,求二次函数解析式时,应用顶点 式 y=a(x+m)2+h,可以简捷地求得函数解析式;是否
9 存在点 P,可由等量关系 S△PAB=8S△CAB,列出方程,若方 程有实数根,则点 P 存在;反之,点 P 不存在.
近几年中考试题中的综合题大多以代数几何综合题的形 式出现,其解题关键是借助几何直观解题,运用方程、函数 的思想解题,灵活运用数形结合,由形导数,以数促形,综 合运用代数和几何知识解题.值得注意的是近年中考几何综 合计算的呈现形式多样,如折叠类型、探究型、开放型、运 动型、情境型等,背景鲜活,具有实用性和创造性,在考查 考生计算能力的同时,考查考生的阅读理解能力、动手操作 能力、抽象思维能力、建模能力,力求引导考生将数学知识 运用到实际生活中去.
方程、函数与 几何相结合型综合问题
以几何量为一元二次方程的根或系数构成方程与几何相 结合型综合题,解决这类问题的关键,是把一元二次方程的 知识与几何图形的性质以及计算与证明有机结合起来.
函数与几何相结合型综合题,各地中考常常作为压轴题 进行考查,这类题目难度大,考查知识多,解这类习题的关 键就是善于利用几何图形的有关性质和函数的有关知识,并 注意挖掘题目中的一些隐含条件,以达到解题目的.
解 (1)设抛物线的解析式为:y1=a(x-1)2+4,
把 解 A((31,)设0)抛代物入线解的析解式析,式得为a:=- y1=1,a(x-1)2+4, ∴ 把yA1(=3- ,(0x)- 代入1)解2+析4=式-,x得2+a2=x+-31,, ∴ ∴By1点 =-的坐(x标-为1)(2+0,4=3)-.x2+2x+3, 设 ∴直B 点线的A坐B 的标解为析(0式,为3):.y2=kx+b, 把 设直A(线3,AB0)的,解B(析0,式3为)代:入y2=y2k=x+kx+ b,b 中, 解 把得A(3k= ,0-),1,B(b0=,33,)代入 y2=kx+b 中,解得 k=-1,b=3, ∴ ∴yy22= =- -xx+ +33.. ((22))∵ ∵CC 点 点坐 坐标 标为 为((11, ,44)), ,∴当 x=1 时,y1=4,y2=2, ∴ ∴当CD=x=4-1 时2=,2, y1=4,y2=2, ∴ ∴SCD△C=AB=4-121×2=3×2,2=3(平方单位). ∴S△CAB=2×3×2=3(平方单位).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点跟踪训练47 方程与函数相结合型综合问题一、选择题1.在平面直角坐标系中,抛物线y =x 2-1与x 轴的交点的个数是( ) A .3 B .2 C .1 D .0答案 B解析 令y =0,得x 2-1=0,x =1或-1,抛物线交x 轴于点(1,0),(-1,0).2.(2011·兰州)如图所示的二次函数y =ax 2+bx +c 的图象中,刘星同学观察得出了下面四条信息:(1)b 2-4ac >0;(2)c >1;(3)2a -b <0;(4)a +b +c <0.你认为其中错误..的有( )A .2个B .3个C .4个D .1个 答案 D解析 由抛物线与x 轴交于两点,可知关于x 的二次方程ax 2+bx +c =0有两个不相等的实数根,则b 2-4ac >0;又抛物线的对标轴直线x =-b 2a >-1,而a <0,所以b >2a,2a -b <0;当x =1时,函数值y =a +b +c <0,信息(1),(3),(4)正确;抛物线与y 轴交于点(0,c ),在点(0,1)下方,c <1,信息(2)错误.3.(2011·潍坊)已知一元二次方程ax 2+bx +c =0(a >0)的两个实数根x 1、x 2满足x 1+x 2=4和x 1·x 2=3,那么二次函数y =ax 2+bx +c (a >0)的图象有可能是( )答案 C解析 由x 1+x 2=4和x 1x 2=3,可解得两根为1、3,抛物线与x 轴交点为(1,0),(3,0),选C.4.(2011·呼和浩特)已知一元二次方程x 2+bx -3=0的一根为-3,在二次函数y =x 2+bx -3的图象上有三点⎝⎛⎭⎫-45,y 1、⎝⎛⎭⎫-54,y 2、⎝⎛⎭⎫16,y 3,y 1、y 2、y 3的大小关系是( ) A . y 1<y 2<y 3 B .y 2<y 1<y 3 C . y 3<y 1<y 2 D .y 1<y 3<y 2答案 A解析 当方程的一根为x =-3时,(-3)2-3b -3=0,b =2,所以y =x 2+2x -3=(x +1)2-4,∴对称轴x =-1,∴x =-54与x =-34时y 值相同,∵在x =-1右侧,y 随x 增大而增大,∴y 1<y 2<y 3,选A.5.已知函数y =ax 2+bx +c 的图象如图所示,那么关于x 的方程ax 2+bx +c +2=0的根的情况是( )A .无实数根B .有两个相等实数根C .有两个异号实数根D .有两个同号不等实数根 答案 D解析 画直线y =-2,与抛物线y =ax 2+bx +c 交于两点,且在第四象限,故方程ax 2+bx +c =-2,有两个不等的正数根.二、填空题 6.(2008·义乌)李老师给出了一个函数,甲、乙、丙三位学生分别指出这个函数的一个特征.甲:它的图象经过第一象限;乙:它的图象也经过第二象限;丙:在第一象限内函数值y 随x 增大而增大.在你学过的函数中,写出一个满足上述特征的函数解析式____________________.答案 形如y =kx +b (k >0,b >0)或y =ax 2+bx +c (a >0,b >0)7.要在街道旁修建一个奶站,向居民区A 、B 提供牛奶,奶站应建在什么地方,才能使从A 、B 到它的距离之和最短?小聪根据实际情况,以街道旁为x 轴,建立了如图所示的平面直角坐标系,测得A 点的坐标为(0,3),B 点的坐标为(6,5),则从A 、B 两点到奶站距离之和的最小值是__________.答案 10解析 如图,画点A 关于x 轴的对称点A 1,其坐标为(0,-3),根据两点之间线段最短,可知AC 、BC 距离之和的最小值为线段A 1B ,画BD ⊥y 轴于D ,在Rt △A 1BD 中,A 1D =3+5=8,BD =6,所以A 1B =62+82=10.8.(2010·绥化)已知关于x 的分式方程 a +2x +1=1的解是非正数,则a 的取值范围是____________.答案 a ≤-1且a ≠-2解析 去分母,a +2=x +1,∵x ≠-1,a ≠-2,x =a +1≤0,∴a ≤-1且a ≠-2.9.(2008·西宁)如图所示的是函数y =kx +b 与y =mx +n 的图象,则方程组⎩⎪⎨⎪⎧y =kx +b ,y =mx +n 的解关于原点对称的点的坐标是___________.答案 (-3,-4)解析 两直线y =kx +b 与y =mx +n 交于点(3,4),所以关于原点对标的点的坐标为(-3,-4).10.如图,点D 的纵坐标等于______________;点A 的横坐标是方程______________的解;大于点B 的横坐标是不等式______________的解集;点C 的坐标是方程组______________的解;小于点C 的横坐标是不等式______________的解集.答案 b ;k 1x +b 1=0;kx +b <0;⎩⎪⎨⎪⎧y =k 1x +b 1,y =kx +b;kx +b >k 1x +b 1三、解答题11.如果一个二次函数的图象经过点A (6,10),与x 轴交于B 、C 两点,点B 、C 的横坐标为x 1、x 2,且x 1+x 2=6,x 1·x 2=5.求这个二次函数的解析式.解 ∵这个二次函数的图象与x 轴交于B (x 1,0)、C (x 2,0)两点,∴这个二次函数的解析式是y =a (x -x 1)(x -x 2),即y =a [x 2-(x 1+x 2)x +x 1x 2]. ∵x 1+x 2=6,x 1·x 2=5, ∴y =a (x 2-6x +5).∵这个二次函数的图象经过点A (6,10), ∴a ×(62-6×6+5)=10, 解之,得a =2,∴所求二次函数的解析式为:y =2x 2-12x +10.12.如图,在平面直角坐标系中,将一块腰长为5的等腰直角三角尺ABC 放在第二象限,且斜靠在两坐标轴上,直角顶点C 的坐标为(-1,0),点B 在抛物线y =ax 2+ax -2上.(1)点A 的坐标为________,点B 的坐标为________; (2)抛物线的关系式为________________;(3)设(2)中抛物线的顶点为D ,求△DBC 的面积; (4)将三角尺ABC 绕顶点A 逆时针方向旋转90°,到达△AB ′C ′的位置.请判断点B ′、C ′是否在(2)中的抛物线上,并说明理由.解 (1)A (0,2),B (-3,1). (2)y =12x 2+12x -2.(3)如图①,可求得抛物线的顶点D ⎝⎛⎭⎫-12,-178.设直线BD 的关系式为y =kx +b ,将点B 、D 的坐标代入,求得k =-54,b =-114,∴BD 的关系式为y =-54x -114.设直线BD 和x 轴交点为E ,则点E ⎝⎛⎭⎫-115,0,CE =65. ∴△DBC 的面积为12×65×⎝⎛⎭⎫1+178=158.(4)如图②,过点B ′作B ′M ⊥y 轴于点M ,过点B 作BN ⊥y 轴于点N ,过点C ′作C ′P ⊥y 轴于点P .在Rt △AB ′M 与Rt △BAN 中,∵AB =AB ′,∠AB ′M =∠BAN =90°-∠B ′AM , ∴Rt △AB ′M ≌Rt △BAN .∴B ′M =AN =1,AM =BN =3,∴B ′(1,-1).同理:△AC ′P ≌△CAO ,C ′P =OA =2,AP =OC =1, ∴C ′(2,1).将点B ′、C ′的坐标代入y =12x 2+12x -2,可知点B ′、C ′在抛物线上(事实上,点P与点N 重合).13.已知抛物线y =(9-m 2)x 2-2(m -3)x +3m 的顶点D 在双曲线y =-5x上,直线y =kx+c 过点D 和点C (a ,b ),且y 随x 的增大而减小,a 、b 满足方程组⎩⎪⎨⎪⎧a 2-b 2-3=0,2a 2-5ab +2b 2=0.求直线y =kx +c 的解析式.解 ∵y =(9-m 2)x 2-2(m -3)x +3m ,∴抛物线的顶点D 的坐标为⎝⎛⎭⎫-1m +3,3m 2+10m -3m +3.∵点D 在双曲线y =-5x 上,∴⎝⎛⎭⎫-1m +3·⎝⎛⎭⎫3m 2+10m -3m +3=-5, 整理得:m 2+10m +24=0, 解之,得m 1=-4,m 2=-6,∴D 点的坐标为D 1(1,-5)或D 2⎝⎛⎭⎫13,-15.解方程组⎩⎪⎨⎪⎧a 2-b 2-3=0,2a 2-5ab +2b 2=0,得⎩⎪⎨⎪⎧ a 1=-2,b 1=-1,,⎩⎪⎨⎪⎧a 2=2,b 2=1,∴C 点的坐标为C 1(-2,-1)或C 2(2,1).∵直线y =kx +c 经过D 、C 两点,且y 随x 的增大而减小, ∴点C 2(2,1)不合题意,舍去.∴直线x 1y =kx +c 经过点D 1(1,-5)和点C 1(-2,-1)或点D 2⎝⎛⎭⎫13,-15和C 1(-2,-1).∴⎩⎪⎨⎪⎧k +c =-5,-2k +c =-1,或⎩⎪⎨⎪⎧13k +c =-15,-2k +c =-1,解之,得⎩⎨⎧k =-43,c =-113,或⎩⎪⎨⎪⎧k =-6,c =-13. ∴这条直线的解析式为y =-43x -113或y =-6x -13.。
