正方体的展开图 (2) - 360文档中心

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
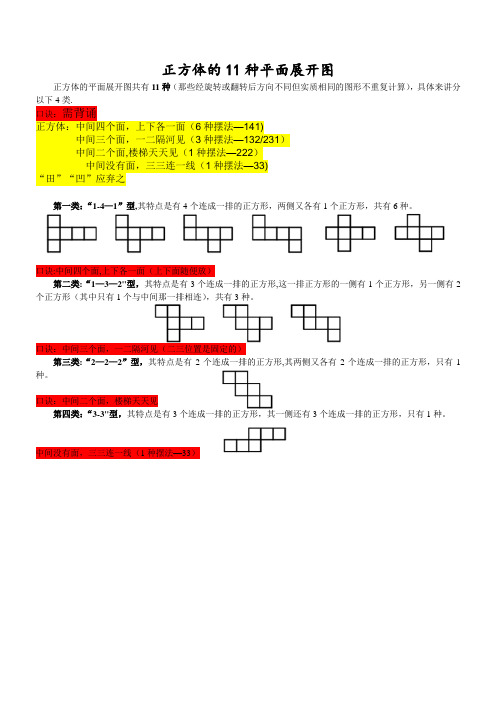
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类.
口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法—141)
中间三个面，一二隔河见（3种摆法—132/231）
中间二个面,楼梯天天见（1种摆法—222）
中间没有面，三三连一线（1种摆法—33)
“田”“凹”应弃之
第一类：“1-4—1”型,其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀:中间四个面,上下各一面（上下面随便放）
第二类:“1—3—2"型，其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类:“2—2—2”型，其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3-3"型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法—33）。

人教版同步教参数学五年级下册——长方体和正方体：2.长方体和正方体的表面积

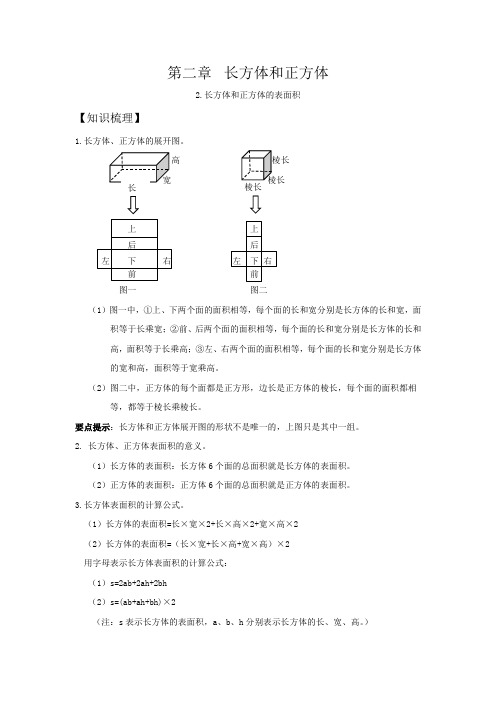
第二章长方体和正方体2.长方体和正方体的表面积【知识梳理】1.长方体、正方体的展开图。

高图一图二（1）图一中，①上、下两个面的面积相等，每个面的长和宽分别是长方体的长和宽，面积等于长乘宽；②前、后两个面的面积相等，每个面的长和宽分别是长方体的长和高，面积等于长乘高；③左、右两个面的面积相等，每个面的长和宽分别是长方体的宽和高，面积等于宽乘高。

（2）图二中，正方体的每个面都是正方形，边长是正方体的棱长，每个面的面积都相等，都等于棱长乘棱长。

要点提示：长方体和正方体展开图的形状不是唯一的，上图只是其中一组。

2. 长方体、正方体表面积的意义。

（1）长方体的表面积：长方体6个面的总面积就是长方体的表面积。

（2）正方体的表面积：正方体6个面的总面积就是正方体的表面积。

3.长方体表面积的计算公式。

（1）长方体的表面积=长×宽×2+长×高×2+宽×高×2（2）长方体的表面积=（长×宽+长×高+宽×高）×2用字母表示长方体表面积的计算公式：（1）s=2ab+2ah+2bh（2）s=(ab+ah+bh)×2（注：s 表示长方体的表面积，a 、b 、h 分别表示长方体的长、宽、高。

）4.长方体表面积的计算公式。

正方体的表面积=棱长×棱长×6用字母表示正方体表面积的计算：s=6a2。

（注：s表示正方体的表面积，a表示正方体的棱长。

）5.拓展提高。

如果正方体的棱长扩大到原来的n倍，它的表面积就扩大到原来的n2倍。

如正方体的棱长扩大到原来的3倍，它的表面积就扩大到原来的9倍。

6.温馨提示：在实际生活中，并不是所有的长方体形状的物体都有6个面，如长方体形状的鱼缸、游泳池等只有5个面，长方体形状的烟囱、通风管等只有4个面。

【诊断自测】1.填空。

（1）一个长方体的长是15cm，宽是4cm，高是6cm，这个长方体的表面积是（）cm2。

正方体的展开图

3．“222”型，两行只能有1个正方形相连。
4.“33”型，两行只能有1个正方形相连。
长方体、正方体的展开图
上
后
左下右前
你能找出展开图中相对的面吗？
上前左后右下
你能找出展开图中相对的面吗？
上
右
前下
左
后
你能找出展开图中相对的面吗？
3 1 5 4 6
2
你能找出展开图中相对的面吗？上前下左后
右
你能找出展开图中相对的面吗？
上
后右
左
前
下
你能找出展开图中相对的面吗？
2 1 5 3 4
6
你能找出展开图中相对的面吗？
前
右
后
上
左
下
你能找出展开图中相对的面吗？
上右
后
左
前
下
141型
不能出现“田” 字型
132型
33型
222型Βιβλιοθήκη 1．“141型”，中间一行4个作侧面，上下两个各作为上下底面，• 共有6种基本图形。
2．“231型”，中间3个作侧面，上（或下）边2• 个那行，相连的正方形作底面，不相连的再下折作另一个侧面，共3种基本图形。

正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

口诀：需背诵
正方体：中间四个面，上下各一面（6种摆法-141）
中间三个面，一二隔河见（3种摆法-132/231）
中间二个面，楼梯天天见（1种摆法-222)
中间没有面，三三连一线（1种摆法-33）
“田”“凹”应弃之
第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

口诀：中间四个面，上下各一面（上下面随便放）
第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

口诀：中间三个面，一二隔河见（二三位置是固定的）
第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

口诀：中间二个面，楼梯天天见
第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

中间没有面，三三连一线（1种摆法-33）。

数学五下4.6《长方体、正方体的展开图》(2)

1300×（700÷10）
1.计算各题的运算有没有错误？把错的圈出来。
（1）480＋120×4－800÷2 = 600×4－400
= 2000 （2）750＋250÷250＋750
= 1000÷1000
=1
2.递等式计算： 246－163＋237
204×75÷15
（361＋439） × 125
在大约六、七百年前，中国人发明了算盘，它结合了十进制计数法和一整套计算口诀并一直沿用至今，被许多人看作是最早的数字计算机。
1.复习加、减、乘、除四则运算及两、三
步计算式题。
2.在探究过程中巩固四则运算的运算顺序，
会对题目进行辨析，并选择合适的方法进行解答。
3.结合教材内容了解有关奥运知识，激发
456÷19×83
33×（225÷15）
1996年，中国派
出了（ 495）人的
代表团参加亚特兰大奥运会，共获得 16枚金牌。
944÷（105－89）
在2000年举行的悉尼奥运会上，中国体育代表团获得了在雅典奥运会上， 28枚金牌，奖牌总中国体育代表团取
数一达举到跃入了（了奖59牌）榜枚，得获了得优金异牌的（成32绩），
挑战赛：
（1）380×426＝ 161800 （2）12×20= 240 （3）625÷25＋87＝ 112 （4）26×5×2＝ 260
选用合适的方法计算下列各题：
（1）93＋70＋30＝ 193 （2）3363÷57＝ 59 （3）2800－1798＝1002 （4）126×7÷18＝ 49 （5）25×7×4＝ 700 （6）6848－579＋386＝ 6655
我国射击名将王义夫在 2004年雅典奥运会男子10 米气手枪比赛中夺冠，

正方体的11种展开图2(1)

坚
持就是
胜
利
圆柱圆锥
三棱锥
四棱锥
五棱锥
开始时我们已经在正方体的相对的面上标上相同的数字，现在观察一下这些数字在展开图中有什么规律？
“一四一” 型
“二三一” 型
“三三” 型
“二二二” 型
考考你下图是正方体的表面展开图。
1、如果“你”在前面，那么谁在后面？
了！太棒你们
2、“坚”在下，“就”在后，“胜”、 “利”在哪里？
“一四一” 型
“二三一”型
“三三”型
“二二二”型
判断下列图形能不能折成正方体？
(1)
(2)
(3)
(4)
Байду номын сангаас5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
在展开的过程中注意你剪开了几条棱？
将正方体展开成平面图形需要剪开 7条棱（无论用哪种方案展开）
正方体展开图
将正方体剪开展成一个平面图形。
一四一型：中间四个一连串、两边各一随便放二三一型：二三紧连挪一个、三一相连一随便二二二型：两两相连各挪一(楼梯型）三三型:三个两排一对齐异层“日”字连、整体没有“田” 找相对面：要找两个向对面、切记相隔一个面
在同一行（或同一列）中隔开一个正方形的两个正方形必为对面；不在同一行（或同一列）但中间隔着一行（或一列）的两个正方形也是对面

(完整word版)正方体的11种展开图

正方体的11种展开图
判断技巧
我们知道,同一个立方体图形,按不同的方式展开得到的平面展开图形一般是不一样的。

常见的正方体平
面展开图究竟有几种不同的形状呢？
同学们一定熟悉这样一种操作：把一个正方形纸片平均分成9个小正方形,剪去角上四个小正方形，可以拼成一个无盖的正方体纸盒,其中五个面按习惯不妨记为下、左、右、前、后,如图一。

好啦！现在只要把刚才剪去的一个小正方形作为“上"面,就可拼成一个正方体。

作为正方体平面展开图，这个“上”应该和图1（1)中哪个面拼接在一起呢?观察图1(2)，知“上”和前、后、左、右任一个面拼接都行（这四种拼接看作同一种情形),不妨和“后”拼接在一起,如图2.
根据上和下、左和右、前和后相间隔这一规律，现在我们把图2中的“左”或“右”平移，可得图3～图7五种情形.
平移图2中的“前”,可得图8；再平移图8中的“左”,可得图9、图10；把图10中的“上"向左平移,得图11；若移动图8（或图9、图10)中的“左"，又可得图12。

同学们,当你和我一样,把图2～图12这11个图剪下来，动手折一折,得到11个漂亮的小正方体时,你一定为我们的收获感到欢欣鼓舞吧!
对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀:一四一呈6种,一三二有3种，二二二与三三各1种,展开图共有11种。

“动手实践，自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法，而实践活动是培养我们进行主动探索与合作交流的重要途径。

只要通过自己主动观察、实验、猜想、验证等数学活动，就能使我们“建立空间观念，发展几何直觉”，提高思维能力.。

正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

(完整版)正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

正方体11种平面展开图

正方体的11种平面展开图正方体的平面展开图共有11种（那些经旋转或翻转后方向不同但实质相同的图形不重复计算），具体来讲分以下4类。

第一类：“1—4—1”型，其特点是有4个连成一排的正方形，两侧又各有1个正方形，共有6种。

第二类：“1—3—2”型，其特点是有3个连成一排的正方形，这一排正方形的一侧有1个正方形，另一侧有2个正方形（其中只有1个与中间那一排相连），共有3种。

第三类：“2—2—2”型，其特点是有2个连成一排的正方形，其两侧又各有2个连成一排的正方形，只有1种。

第四类：“3—3”型，其特点是有3个连成一排的正方形，其一侧还有3个连成一排的正方形，只有1种。

注：①将长方体、正方体展开：无论怎么剪，都要剪7条棱。

②“隔”的原理：相对的面如果在同一行或同一排，中间一定只隔一个面；相对的面如果不在同一行或同一排，中间可以隔着一些面。

③长方体、正方体中各面的关系：相对、相邻。

每个面都有1个相对的面，4个相邻的面。

注：立体图中相对的面在展开图中符合“隔”的原理，而相邻的面在展开图中不符合“隔”的原理。

④长方体、正方体中最多可以同时看到三个面，且这三个面都是相邻的面。

⑤要区分好是从“立体图”到“展开图”，还是从“展开图”到“立体图”：互逆正方体、长方体展开图⑥长方体（不包含正方体）最多有1组相对的面是正方形；当有2组相对的面是正方形时，长方体就变成了正方体（特殊的长方体）。

长方体（不包含正方体）的6个面中，最多有4个面的面积相等；12条棱中，最多有8条棱长度相等。

（即2个相对的面是正方形，其余四个面变为完全相同的长方形。

）⑦正方体的棱长扩大a倍：棱长和扩大a倍，表面积扩大a2倍，体积扩大a3倍。

（给出其中一个，要能将其余的都求出来）⑧常见的平方、立方（需熟记在心）12=1 22=4 32=9 42=16 52= 25 62=36 72=49 82=64 92=81 ……13=1 23=8 33=27 43=64 53= 125 63=216 ……。

正方体的11种展开图

正方体的11种展开图
正方体有11种平面展开图，不可谓不多，那么，我们该如何理解掌握这11种正方体的平面展
开图呢？正方体的平面展开图有11种之多，不容易记牢记全．为了更好的记忆掌握，我们可以把这11种展开图分成4类，只要把握各类的特征，就容易记忆了．
第一类：中间四连方，两侧各一个，共6种。

第二类：中间三连方，两侧各一、二个，共3种。

第三类：中间二连方，两侧各两个，只有1种。

第四类：两排各3个，也只有1种。

对正方体表面展开图的11种情况，为加深记忆，可编成如下口诀：
一四一呈6种，一三二有3种，二二二与三三各1种，展开图共有11种．
1．“141型”，中间一行4个作侧面，上下两个各作为上下底面，•共有6种基本图形。

2．“132型”，中间3个作侧面，共3种基本图形。

3．“222型”，两行只能有1个正方形相连。

4．“33型”，两行只能有1个正方形相连。

（当132型、 222型时要注意不能出现田字形）。

正方体的 11 种展开图打印附带讲解

正方体的11种展开图打印附带讲解本文章主要带孩子认识11种正方体展开图，家人可以把它打印下来，陪孩子一起制作。

（PS：1、如果A4的纸太软不好固定，可以用纸箱、纸质购物袋等画出对应的图形进行裁剪；2、亦或者可以用包书的纸裁剪出展开图的样子，做成精美的包装纸贴在正方体外面，做一个精美的小礼盒哦）（为了方便打印，文章末尾，把所有资料汇总了一遍，可直接跳转到末尾打印11钟展开图）在正式学习之前，可以将家中的魔方拿出来，看看正方体有几面？每一面都是什么形状？以此区分一下正方体和正方形。

分别有前面、后面、上面、下面、左面、右面这六面。

接着介绍“正方体的展开图”，带着孩子观察展开图的特点，并知道其名称。

（一）首先认识一下1-4-1型，为了更形象的记忆，我把它概括为“1头4身体1脚”（头是由1个正方形组成的，身体是由4个正方形组成的，脚是由1个正方形组成的，）家人可以先把图形制作出来，然后带孩子去观察特点。

打印图纸：1-4-1打印专用：1-4-1共有6种，身体均是4个正方体，头和脚各一个，头和脚的位置可左右移动改变（二）接下来认识2-3-1型，2-3-1共有3种，头2个正方体，身体3个，脚1个。

脚的位置可左右移动改变，以此展开图为例，虽然身体部分较原来少了一个，但是恰好可以由头部多的一个补上。

操作演示时，先把身体折起来，发现身体少了一个，接着把上面脑袋部分拼好，拼好之后脑袋部分多的一个刚好可以补充身体。

2-3-1打印专用：2-3-1共有3种，头2个正方体，身体3个，脚1个。

脚的位置可左右移动改变（三）接下来认识2-2-2型，与3-3型，可以把资料打印下来，通过操作去提升动手以及想象能力。

2-2-2与3-3打印专用。

正方体11种展开图

类型六：十字型
总结词
由两个相同的等腰直角三角形和两个相同的矩形组成的展开图，呈十字形状。
详细描述
这种类型的展开图在正方体的两个相对的面上保留了一个矩形，而其他面则由两个等腰直角三角形组成，整体呈十字形状。
类型七：二字型
总结词
由两个相同的矩形和两个相同的等腰直角三角形组成的展开图，呈二字形状。
详细描述
正方体11种展开图
• 正方体的基本特性 • 正方体的11种展开图 • 正方体展开图的制作方法 • 正方体展开图的应用场景 • 正方体展开图的挑战与未来发展
01
正方体的基本特性
定义与特性
01
正方体是一种三维几何体，由六个正方形面组成，每个面都是等大的正方形。
02
正方体的体对角线、棱和面都是对称的，具有高度的空间对称性。
05
正方体展开图的挑战与未来发展
当前面临的挑战
寻找新的展开方式
目前已知的正方体展开图种类有限，需要探索新的展开方式以丰
富其多样性。
证明无解的存在
对于某些特定条件下的正方体展开问题，需要证明无解的存在，这需要深入的数学理论支持。
实际应用中的限制
正方体展开图在实际应用中可能受到材料、工艺等因素的限制，需要解决这些实际问题。
正方体的几何属性
正方体的体积是边长的三次方，记作 V=a^3，其中a是正方体的边长。
正方体的表面积是6倍的边长的平方，记作A=6a^2。
正方体的展开与折叠
正方体的展开是将正方体的表面沿某些边展开成平面的过程，通常用于制作纸盒等包装材料。
正方体的折叠则是将展开的平面重新折回成立体的过程，常用于制作纸艺模型和玩具。
详细描述

人教版七年级数学上册《正方体的十一种展开图》课件

能力提升
分类标准：观察中间分为四连方、三连方、两连方，我们可以按照这个分类去记忆．四连方
以上六种展开图可归结为四连方线，另外两个小方块在四个方块的上下两侧，共六种情况．可归纳为口诀：“四方成线两相卫，六种图形巧连方、两连方，我们可以按照这个分类去记忆．三连方
指点迷津
• 不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另一眼睛看到纸的背面。2022年4月12日星期二上午8时52分9秒08:52:0922.4.12
• 书籍是屹立在时间的汪洋大海中的灯塔。2022年4月上午8时52分22.4.1208:52April 12, 2022 • 正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022年4月12日星期二8时52分9秒08:52:0912 April 2022 • 书籍是屹立在时间的汪洋大海中的灯塔。
如果展开图中，出现以下几种情况，是错误的
如果图中出现图（1）中的“7”形结构的图形不可能是正方体的展开图，因为1、3对面，3、5对面，3有两个对面，不可能．口诀为：“对面相隔不相连”．
如果图形中出现图（2）中的“田”形结构图形，不可能是正方体的展开图，因为同一顶点处不可能出现四个面．
如果图形中出现（3）中的“凹”形结构图形不可能是正方体展开图，因为如果把该图形折叠起来，必将有两个面重合．
正方体的十一种展开图
课标引路
知识梳理
长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体．几何体也简称体．
包围着体的是面．面和面相交的地方形成线．线和线相交的地方是点．
思考：（1）面和体有哪些区别于联系？（2）“点动成线、线动成面、面动成体” 体现了一个什么数学思想？（3）面分为平面和曲面，线分为直线和曲线，那么直线与直线相交是什么？平面与平面相交是什么？（4）构成图形的基本元素是什么？（点）（5）几何图形都是由什么构成的？（点、线、面、体）