多元样条函数及其应用(王仁宏等著)思维导图
《应用多元分析》(第四版,王学民编著)SPSS22的应用
10
图 5.1
图 5.2
图 5.3
11
图 5.4
图 5.5
12
图 5.6
13
图 5.7
注:Dis_1 表示经判别归属的组,Dis1_1 和 Dis2_1 分别表示归属第 1 组和第 2 组的后 验概率。 二、对书中例 5.4.2 中的数据作 Fisher 判别 打开 examp5.4.2.sav 数据表 分析 分类 > 判别… 在“判别分析”对话框中, 将花萼长[x1]、 花萼宽[x2]、花瓣长[x3]和花瓣宽[x4]选入 “自变量” 列表框中;将组别[g]
图1
第三章
多元正态分布
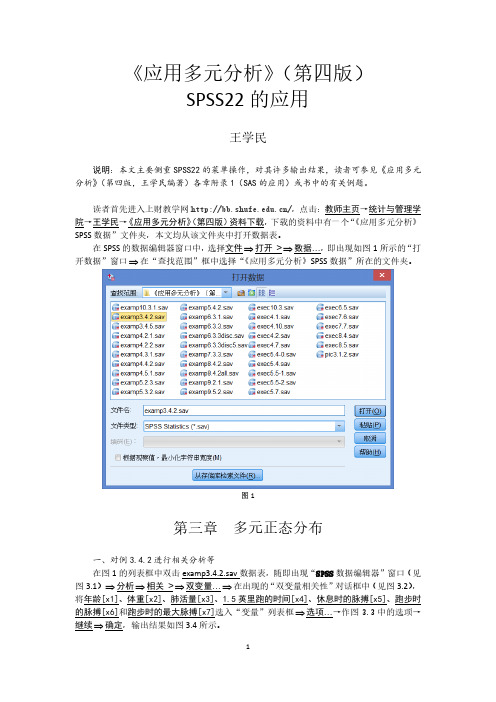
一、对例 3.4.2 进行相关分析等 在图 1 的列表框中双击 examp3.4.2.sav 数据表,随即出现“SPSS 数据编辑器”窗口(见 图 3.1) 分析 相关 > 双变量… 在出现的 “双变量相关性”对话框中(见图 3.2) , 将年龄[x1]、体重[x2]、肺活量[x3]、1.5 英里跑的时间[x4]、休息时的脉搏[x5]、跑步时 的脉搏[x6]和跑步时的最大脉搏[x7]选入“变量”列表框 选项…→作图 3.3 中的选项→ 继续 确定,输出结果如图 3.4 所示。
24
图 6.8
图 6.9
25
图 6.10
26
图 6.10(续)
27
第七章
主成分分析
一、对书中例 6.3.3 作主成分分析 打开 examp6.3.3.sav 数据表 分析 降维 > 因子分析… 在“因子分析”对话框 中,将食品[x1]、衣着[x2]、家庭设备用品及服务[x3]、医疗保健[x4]、交通和通讯[x5]、 娱乐教育文化服务[x6]、 居住[x7]和杂项商品和服务[x8]选入 “变量” 列表框中 (见图 7.1) 描述…→在弹出的“因子分析:描述统计”对话框中(见图 7.2),作图中的选择→继 续;抽取…→在弹出的“因子分析:抽取”对话框中(见图 7.3),作图中的选择→继续 确定,生成图 7.4。
第十章 多元函数微分法及其应用

若点集 E 的余集Ec为开集, 则称 E 为闭集。
0
2
x 8
若点P 的任一邻域内, 既含有属于 E 的点又含有 不属于 E 的点,则称 P 为 E 的边界点。 边界点的全体称为 E 的边界。
例 : E1 ( x , y ) x 2 y 2 4
E
· P
0
y
满足 x2 + y2 = 4 的点 ( x, y ) 都为边界点。 2 2 曲线 x y 4 为 E1 的边界。
函数对 x 的偏增量
f ( x 0 D x , y0 ) f ( x 0 , y0 ) ,
f ( x 0 D x , y0 ) f ( x 0 , y 0 ) 如果 存在,则称 Dx 此极限为函数 z f ( x , y ) 在点 ( x0 , y0 ) 处对 x 的 偏导数 ,记为
( x, y)
x0
(
0
x0
.
x0
)
x
y
y0
0
( x x 0 ) ( y y0 )
2 2
p0 x0
ˆ U ( P0 , ) ( x, y ) 0 ( x x0 )2 ( y y0 )2
x
7
2.区域 E (内点、边界点、聚点、边界、 . .P 连通集、开集、闭集、有界点集) P 设 E 是平面上的一个点集, 对点 P,若存在 U ( P , ) E , 则称 P 为 E 的内点。 若 E 中的点都为内点, 则称 E 为开集。 y 2 2 例:E1 ( x , y ) x y 4
80
全微分的定义:
dz ADx BDy .
多元数据图表示法

第二类分类方法可用后面介绍的主成分分析、因 子分析等去解决。这一章只对第一类方法介绍四种 图表示法,更多的方法可在有关专著中找到。
多元数据图表示法
作图步骤为: (1)作平面坐标系,横坐标取 p 个点表示 p 个变量。 (2)对给定的一次观测值,在 p 个点上的纵 坐标(即高度)和它对应的变量取值成正比。 (3)连接 p 个高度的顶点得一折线,则一次观
例 考察北京、上海、陕西、甘肃四个省市人均生 活消费支出情况,选取以下五项指标,具体数据如下 表:
肉禽及制品 住房 医疗保健 交通和通讯 文娱用品及服务
北京 上海 陕西 甘肃
563.51 678.92 237.38 253.41
227.78 365.07 174.48 156.13
147.76 112.82 119.78 102.96
测值的轮廓为一条多角折线形。n 次观测值可 画出n 条折线,构成轮廓图。
多元数据图表示法
800 700 600 500 400 300 200 100
0
品 制 禽及 肉
北京 上海 陕西 甘肃
房
健
讯
化
住
保
通
文
医疗
交通
教育
轮廓图
乐 娱
由轮廓图可以看出:北京、上海的居民生活 消费较高且相似;陕西、甘肃生活消费较低且相 似。
利用SPSS制作矩阵散点图的步骤如下: (1)在SPSS中按图11.6的形式组织数据,即把支 出指标当成变量,而把不同地区当成观测。
图11.6 作散点图时的数据组织形式
(2)选择菜单项Graphs→Scatter,打开 Scatter plot对话框,如图11.7。该对话框用于 选择散点图的形式。选定Matrix,即矩阵散 点图 ,单击Define按钮,打开Scatter plot Matrix对话框,如图11.8。
样条函数及三次样条插值PPT课件

(x)
lim
x xk
Sk 1( x)
lim
x
x
k
Sk (x)
lim
x
x
k
Sk1( x)
k 1,2,,n 1
------(4)
lim
x
x
k
Sk( x)
lim
x
x
k
Sk1( x)
共4n 2个条件
5
Sk (x)是[xk , xk 1 ]上的三次样条插值多项式,应有4个待定的系数 即要确定S(x)必须确定4n个待定的系数 少两个条件 并且我们不能只对插值函数在中间节点的状态进行限制 也要对插值多项式在两端点的状态加以要求 也就是所谓的边界条件:
例. 使用不同的插值方法于函数
y
1
1 x2
x [5,5]
最后,介绍一个有用的结论
定理 . 设f (x) C 2[a,b], S(x)是以xk (k 0,1,, n)
为节点, 满足任意边界条件的三次样条插值函数,
设hi
xi 1
xi
,
h
max
0in1
hi
,
min
0in1
hi
,
则当 h
c 时
S(x)和S(x)在[a,b]上一致收敛到f (x)和f (x)
------(6)
13
由(11)式,可知
S0( x0
)
6( x0
x1 h03
2 x0
) ( y1
y0 )
6 x0
2 x0 h02
4 x1
m0
6 x0
4 x0 h02
2 x1
m1
6 h02
(
应用多元分析课件 (2)

§4.3 单个总体均值分量间 结构关系的检验
v 设x1,x2,⋯ ,xn是取自多元正态总体Np(μ,Σ)的一个样本,Σ>0, n>p,欲检验
H0:Cμ=φ,H1:Cμ≠φ
其中C为一已知的k×p矩阵,k<p,rank(C)=k,φ为已知的k维 向量。
v 根据多元正态分布的性质知
Cx~Nk(Cμ,CΣC′)
当原假设H0:Cμ=φ为真时,
k
nk
n 1
T
2
F
k,n
k
对于给定的显著性水平α,拒绝规则为:
其中T2
k
n 1
nk
若T 2 T2,则拒绝H0
F k ,n k 。
v 特别地,若欲检验
则T2可简化为
H0:Cμ=0,H1:Cμ≠0
T 2 nxCCSC1 Cx
多元正态总体的统计推断
v §4.1 一元情形的回顾 v §4.2 单个总体均值的推断 v §4.3 单个总体均值分量间结构关系的检验 v §4.4 两个总体均值的比较推断 v §4.5 两个总体均值分量间结构关系的检验 v §4.6 多个总体均值的比较检验(多元方差分析) v §4.7 总体相关系数的推断
区间。由该联合置信区间可得到置信度至少为0.90 的矩形置信区域(见图4.2.1中的实线矩形),但其 矩形面积要大于椭圆面积。
图4.2.1 置信椭圆和联合置信区间
利用置信区域进行假设检验
v 在例4.2.2中,如果在 α=0.10下对假设
H0:μ=μ0,H1:μ≠μ0 进行检验,其中μ=(μ1,μ2)′,μ0=(μ01,μ02)′ ,则我们容易利用图 4.2.1中的椭圆得出检验的结果。若被检验值μ0位于图4.2.1中 的椭圆外,则拒绝;反之,则接受。
第3章 多元函数微分学的应用

第3章多元函数微分学的应用第3章多元函数微分学应用§11 空间曲线的切线和法平面过点M 与切线垂直的平面称为曲线在该点的法平面.空间的一条光滑曲线在点M 处的切线,定义为此点处曲线割线的极限位置.ΓTMπ第3章多元函数微分学应用1. 曲线方程为参数方程ΓTX 0Xt =t 0:X 0=(x (t 0), y (t 0), z (t 0))t =t 0+∆t :X =(x (t 0 +∆t ), y (t 0 +∆t ), z (t 0 +∆t ))⎪⎭⎫⎝⎛∆-∆+∆-∆+∆-∆+t t z t t z t t y t t y t t x t t x )()(,)()(,)()(000000为X 0X 的一个方向向量,令∆t →0 (X →X 0),得())(),(),(000t z t y t x '''s =称为曲线Γ在点X 0的一个切向量.这里不全为0,且s 指向曲线Γ的参数t 增加的方向.)(,)(,)(000t z t y t x '''★ :x =x (t ), y =y (t ), z =z (t )第3章多元函数微分学应用◆曲线Γ在点X 0的切线方程为)()()()()()(000000t z t z z t y t y y t x t x x '-='-='-或:X -X 0= λ⋅s (-∞<λ<+∞)◆曲线Γ在点X 0的法平面方程为))()(())()(())()((000000=-'+-'+-'t z z t z t y y t y t x x t x 或:s ⋅(X -X 0)= 0例1 求曲线x =t , y =t 2, z =t 3 在点(1,1,1)处的切线和法平面.第3章多元函数微分学的应用2. 曲线方程为一般方程★ :y =y (x ), z =z (x )视为参数方程x =x ,y =y (x ), z =z (x )当y =y (x ), z =z (x )可导,则得到 在点X 0(x 0, y (x 0), z(x 0))的切向量())(),(,100x z x y ''=s 于是切线的方程为)()(100000x z z z x y y y x x '-='-=-法平面方程)(0x x -)()(00y y x y -'+0))((00=-'+z z x z第3章多元函数微分学的应用当F , G ∈C 1,且,则在U (X 0)内确定函数y =y (x ), z =z (x ),且★ :F (x , y , z ) =0, G (x , y , z ) =00),(),(0≠∂∂=Xz y G F J 0),(),(1)(0X x z G F J x y ∂∂='0),(),(1)(0Xy x G F J x z ∂∂='于是得到 在点X 0(x 0, y (x 0), z(x 0))的切向量⎪⎪⎭⎫ ⎝⎛∂∂∂∂=00),(),(1,),(),(1,1X X y x G F J x z G F J s 或⎪⎪⎭⎫⎝⎛∂∂∂∂∂∂=000),(),(,),(),(,),(),(X X X y x G F x z G F z y G F s第3章多元函数微分学的应用例2.求曲线0,6222=++=++z y x z y x 在点M ( 1,–2, 1) 处的切线和法平面.第3章多元函数微分学的应用§22 曲面的切平面和法线1. 曲面的切平面和法线设X 0=(x 0, y 0, z 0)为∑上一点,F (x,y,z )=0 在X 0可微,且JF (X 0) ≠0 .设t =t 0对应点为X 0 且不全为0,)(,)(,)(000t z t y t x '''则Γ在X 0 有切向量))(),(),((000t z t y t x '''=s •X 0s★曲面∑:F (x , y , z ) = 0若在∑上过点X 0任意做一条完全在曲面上的曲线Γ:x =x (t ),y =y (t ),z =z (t ),第3章多元函数微分学应用又Γ在∑上,故F (x (t ),y (t ),z (t )) ≡0.上式微分得0d d 0==t t tF 即0)()()()()()(000000=''+''+''t z X F t y X F t x X F z y x 也即0))(),(),(())(),(),((000000='''⋅'''t z t y t x X F X F X F z y x 或JF (X 0) ⋅s = 0•X 0sJF (X 0)由Γ的任意性,知任一过X 0的曲线之切线均与JF (X 0) 垂直,因此这些切线确定一个平面.该平面称为曲面∑在X 0的切平面. JF (X 0) 是其法向量.第3章多元函数微分学应用JF (X 0)亦称曲面∑在X 0的一个法向量,X 0称为切点.•X 0sJF (X 0)记n =JF (X 0) =))(),(),((000X F X F X F z y x '''则切平面方程为n ⋅(X -X 0)=0或0))(())(())((000000=-'+-'+-'z z X F y y X F x x X F z y x 过点X 0与切平面垂直的直线称为曲面∑在X 0的法线:)()()(000000X F z z X F y y X F x x z y x '-='-='-或X -X 0=λ⋅n (-∞< λ<+∞)第3章多元函数微分学的应用★曲面 :z =f (x , y )取F (x ,y ,z )≡z -f (x ,y )=0,则有1,,=''-=''-='z y y x x F f F f F 故有)1),,(),,((0000y x f y x f y x '-'-=n 显然n 的方向朝“上”,即它与z 轴正向间的夹角为锐角.例1.求椭球面上点(x 0,y 0,z 0)处的切平面和法线.1222222=++c z b y a x 例2.求曲面z =x 2+y 2-1在点(2,1,4) 的切平面和法线.第3章多元函数微分学应用2. 二元函数全微分的几何意义切平面方程其中z 0=f (x 0, y 0),记,则00,y y y x x x -=∆-=∆yy x f x y x f z z y x ∆'+∆'=-),(),(00000当z =f (x , y )在点(x 0, y 0)可微时,曲面∑在点(x 0, y 0, z 0) 有)(),()(),(0000000y y y x f x x y x f z z y x -'+-'=-上式右边为d z ,左边对应于PQ ,则∆z ≈d z 表明|∆x | 和|∆y | 很小时,PR 可用PQ 近似代替.P O z xy X 0+∆X X 0Q z=f (x,y )∆x ∆y R点X 0称为极大值点(极小值点); 极大值和极小值统称为极值.第3章多元函数微分学应用§33 多元函数的极值定义1 设函数z =f (X ) 在U (X 0)⊂R n 内有定义,若∀X ∈Û(X 0) 有 f (X ) ≤f (X 0) ( f (X ) ≥f (X 0))则称函数在点X 0 取得极大值(极小值).1. 多元函数的极值函数在点(0,0) 有极小值;2243y x z +=221y x z --=函数在点(0,0) 有极大值;第3章多元函数微分学应用zx y定理1(必要条件) 设u=f (X)在点X取得极值,且Jf(X0)存在,则必有Jf(X0)=0.使得Jf(X)=0成立的点X0称为f (X) 的驻点.可偏导的函数其极值点一定是驻点. 但驻点不一定是极值点.函数z=xy在点(0,0),是驻点但不是极值点.第3章多元函数微分学应用二元函数取得极值的一个充分条件:定理2设z =f (X )= f (x ,y )∈C 2(U (X 0)),且Jf (X 0)=0,其中X 0=(x 0, y 0).记, , ,则f (X ))(0X f A xx ''=)(0X f B xy ''=)(0X f C yy ''=△= AC -B 2> 0 A < 0,取极大值f (X 0) ;A > 0,取极小值f (X 0) ;△= AC -B 2< 0,在点X 0 不取极值.例1 求f (x ,y )=x 3-y 3+3x 2+3y 2-9x 的极值.第3章多元函数微分学应用◇f (X )在其偏导数不存在的点处也可能取极值.例如函数在点(0,0)取极小值.22y x z +=◇定理中的△=AC -B 2= 0,则不能判定f (X )在点X 0 是否取极值.例如函数和在点(0,0)均有△=AC -B 2= 0,但显然前者不取极值,而后者取得最小值.33y x z +=222)(y x z +=第3章多元函数微分学应用2. 最大值和最小值极值是局部(邻域内)的概念,最值是全局范围(区域) 上的概念.ΩΩ若f (X)在有界闭域上连续,则f (X)在上必有最值.此时最值或者在Ω内部达到,或者在∂Ω上达到. 若最值在Ω内达到,而f (X)在Ω内只有有限个极值点,则最值必是某个极值;若在∂Ω上达到,则最值也必是f (X)在∂Ω上的最值.第3章多元函数微分学应用例2 求f (x ,y )=sin x +sin y -sin(x +y ) 在由x 轴、y 轴及直线x +y =2π所围成的区域D 上的最大值和最小值.例3求的最大值和最小值.122+++=y x y x z xyO 2第3章多元函数微分学应用Rz xyO 例4 若用钢板制造一个容积为2m 3的有盖长方体水箱, 问当长、宽、高各为多少时,能使所用钢板材料最省?例5 在半径为R 的半球内求一个体积为最大的内接长方体.第3章多元函数微分学应用3. 条件极值定义2 设区域Ω⊂R n ,L ={X | X ∈Ω;ϕ1(X )=0, ϕ2(X )=0, ⋯,ϕm (X )=0, m <n },若X 0∈L ,且∀X ∈L ∩Û(X 0) ,有f (X ) ≤f (X 0) ( f (X ) ≥f (X 0))则称f (X 0)为函数f (X )在约束条件ϕ1(X )=0, ϕ2(X )=0, ⋯, ϕm (X )=0下的条件极大值(条件极小值).● LX 0统称条件极值. 类似定义条件最值.这里给出的约束条件是等式约束.第3章多元函数微分学应用求解条件极值问题:将其转化为无约束极值问题.1) 代入法.求函数z =f (x,y) 在条件ϕ(x,y)=0 下的极值:从约束条件解出y=ψ(x) 代入z =f (x,ψ(x)) 求无约束极值.例6 若用钢板制造一个容积为2m3的有盖长方体水箱, 问当长、宽、高各为多少时,能使所用钢板材料最省?设水箱长x、宽y、高z,则此问题便是求表面积S=2( xy+ yz+ xz)在约束条件xyz=2下的极小值.第3章多元函数微分学应用2) Lagrange 乘数法.讨论函数z =f (x ,y ) 在条件ϕ(x ,y )=0下的极值.构造Lagrange 函数F (x ,y ,λ)= f (x ,y ) + λϕ(x ,y )其中λ为待定参数,称为Lagrange 乘数.问题便化为求F (x ,y ,λ) 的无约束极值.一般地,求u =f (X ) 在约束条件ϕ1(X )=0, ϕ2(X )=0, ⋯, ϕm (X )=0 (m <n )下的极值,则构造Lagrange 函数∑=+=mi i i m X X f X F 121)()(),,,;(ϕλλλλ第3章多元函数微分学应用例6 若用钢板制造一个容积为2m 3的有盖长方体水箱, 问当长、宽、高各为多少时,能使所用钢板材料最省?例7 在旋转抛物面z =x 2+y 2和平面x +y +z =1的交线上,求到坐标原点的最长和最短距离.z y x O (x,y,z )条件极值问题更一般地发展成为数学规划问题。
函数概念多元表征学习与教学探知
函数概念多元表征学习与教学探知摘要:函数是中学数学的核心内容。
函数贯穿了整个髙中数学的始终,而函数多元表征对数学概念理解、数学问题解决具有积极的影响。
本文通过对函数概念多元表征学习认知原理进行分析,提出函数概念多元表征教学策略改善课堂教学效果,提高学生的学习能力关键词:函数概念;多元表征;教学策略函数概念多元表征学习对学生的函数概念理解能力、数学问题解决能力具有积极的影响。
通过函数概念多元表征学习与教学,不仅改善学生的数学学习效果,提高他们的数学理解,也丰富了老师的教学策略;实践上,为改善函数概念教学、促进学生函数概念理解提供教学与指导参考。
如何学习函数概念的多元表征,实现函数概念多元表征的转换与转译,以提高学生函数学习能力,是我们探讨的内容。
1.函数概念多元表征学习认知原理数学多元表征学习不但要学习数学对象的多元表征,更要促使数学对象多元表征的转换与转译。
学习函数概念过程中,不但要学习函数概念的多元表征,并且要实现函数概念多元表征的转换与转译。
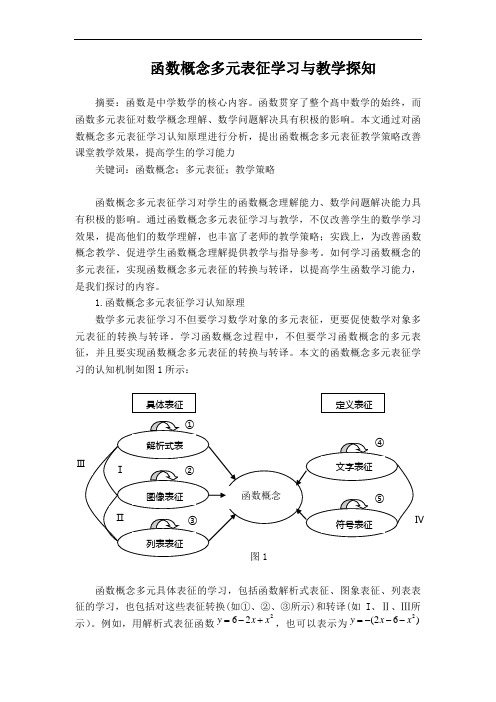
本文的函数概念多元表征学习的认知机制如图1所示:函数概念多元具体表征的学习,包括函数解析式表征、图象表征、列表表征的学习,也包括对这些表征转换(如①、②、③所示)和转译(如I、Ⅱ、Ⅲ所示)。
例如,用解析式表征函数262y x x=-+,也可以表示为2(26)y x x=---和2(1)5y x =-+,形式改变了,但函数的本质没有改变,不同表达形式具有不同的意义,2(1)5y x =-+就可以表示出函数的最低点在哪里。
我们可以通过转换函数解析式表征、图象表征、列表表征来加深对函数的理解。
函数概念定义表征的学习,包括函数定义的文字表征和函数符号表征的学习,也包括对这些表征的转换(如④、⑤所示)和转译(如IV 所示)。
例如函数的文字表征是函数就是两个非空数集的对应关系;函数即是在一个对应关系下,由一个非空数集到另一个非空数集的对应模型,相应的函数的符号表征是,(),,A B y f x x A y B →=∈∈。
6-1多元数量函数积分的概念与性质

Vi f ( i , i )i (i 1, 2,, n) 。
z
o x D
而且与定积分中的问题相比较,思想方法完全 是一致的,只是闭区间换成了闭区域(也可是 闭曲面),一元函数换成了二元函数(也可是 三元函数)。保留其数学结构的特征,抽象出 其共性,可得数量函数积分的概念。
二、 数量函数积分的概念
定义1.1设是一个有界的可以度量 的几何形体,函数 f 在
上有定义.将任意分割成 n个小部分 (k k 1,2,, n),
M2 的度量 f (M )d M1 的度量
5、中值定理 设f (M ) C,则存在 M * ,使
f (M )d f (M *) 的度量
f (M )d,即
n
f
(M )d
lim
d 0
k 1
f
(M k )k
n
二重积分:
D
f x, yd
lim d 0
k 1
f (k ,k ) k
n
三重积分:
f
(x,
y, z)dv
lim
d 0
k 1
f
(k ,k , k )vk
lim d 0 i1
f (i ,i ) i.
实例 2.平面薄片的质量
设有一平面薄片在xoy 平面上占有区域 D,其面密度 为 D 上的连续函数( x, y) ,求该平面薄片的质量 m。
y
均匀薄片的质量 面密度 薄片面积
