SPSS在数学建模中应用
SPSS在数学建模中的应用

04 SPSS在数学建模中的实 践案例
案例一:利用SPSS进行市场细分
总结词
利用SPSS的统计分析功能,对市场进 行细分,为企业的市场策略提供依据。
详细描述
通过收集市场数据,利用SPSS的聚类 分析、因子分析等统计方法,将市场 划分为不同的细分市场,了解各细分 市场的特点,为企业制定针对性的市 场策略提供依据。
02 SPSS在数学建模中的优 势
强大的统计分析能力
描述性统计
SPSS提供了丰富的描述性统计功 能,如均值、中位数、方差等, 帮助用户快速了解数据的基本特 征。
推论性统计
SPSS支持多种推论性统计方法, 如回归分析、方差分析、卡方检 验等,能够揭示数据之间的内在 关系。
高级统计
SPSS还提供了许多高级统计方法, 如主成分分析、因子分析、聚类 分析等,能够满足复杂的数据分 析需求。
方便的数据处理功能
01
数据导入导出
数据清洗
02
03
数据转换
SPSS支持多种数据格式的导入和 导出,方便用户进行数据交换和 整合。
SPSS提供了数据筛选、缺失值处 理、异常值检测等功能,帮助用 户清洗和整理数据。
SPSS支持对数据进行分组、排序、 变量转换等操作,能够满足用户 对数据处理的各种需求。
03 SPSS在数学建模中的具 体应用
线性回归分析
总结词
线性回归分析是利用SPSS软件对因变量和自变量之间的关系进行建模的一种方法,通过最小二乘法拟合出最佳直 线,并计算出各因素对因变量的影响程度。
详细描述
在SPSS中,可以使用“回归”菜单下的“线性”命令来进行线性回归分析。用户需要指定因变量和自变量,并选 择适当的选项,如置信区间、模型拟合度等。SPSS将输出回归系数、标准误差、置信区间等统计量,帮助用户了 解自变量对因变量的影响程度。
SPSS在数学建模中的应用实例_周静
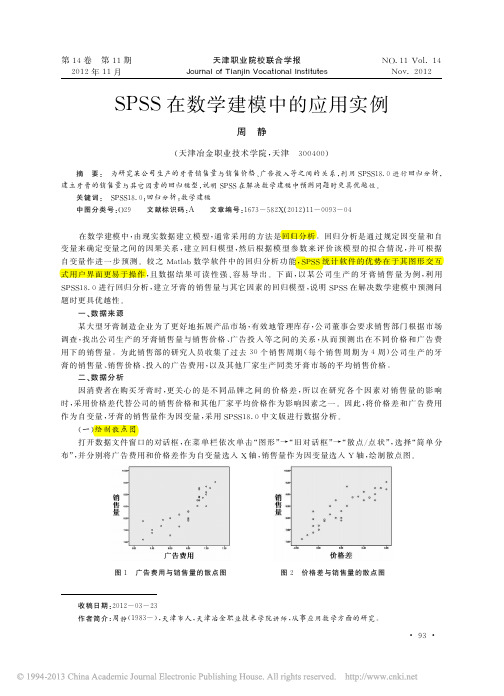
b2
b3
-1.728 -3.674 2.802
由表2可以看出,三个模型的拟合度基本相同 ,其 中 拟 合 度 最 好 的 是 立 方 曲 线 模 型 ,其 次 是 二 次 项 曲 线模型,但立方曲线模型的参数比另外两种模型的 参 数 多 ,更 为 复 杂。若 从 F 值 来 看,线 性 模 型 拟 合 的 最 为显著。但以上的结果还不足以作出判断 ,还需要对各模型系数作显著性检验 。重复上述 操 作,并 且 在 曲 线估计对话框勾选“显示 ANOVE 表格”。
多元回归分析之前 ,需引入新的变量 。从“转换”菜单中,打开计算变量对话框 ,输入 新 的 目 标 变 量 名, 即广告费用的平方 ,然后在数字表达式中编辑函 数 ,生 成 新 的 变 量。 接 下 来 在“分 析”菜 单 中,打 开 线 性 回
· 94 ·
归对话框,将广告费用、价格差和广告费用的平方同时选为自变量 ,将销售量选为因变量 ;单击“统 计 量”按
互作用;若变量包含分类变量和连续变量 ,可将分类变 量 转 换 为 虚 拟 变 量 后 ,当 成 连 续 变 量 再 进 行 回 归 分
以数学建模竞赛为例基于SPSS建立ARIMA模型

以数学建模竞赛为例基于SPSS建立ARIMA模型一、引言数学建模竞赛是在各种学科领域中,通过数学方法解决实际问题的一种竞赛形式。
参加数学建模竞赛需要队员具备一定的数学建模能力,包括数学建模的理论知识、数学工具的使用和数学模型的构建能力。
在数学建模竞赛中,队员需要根据给定的问题和数据,使用数学方法建立合适的数学模型,并进行模型的求解和分析。
数学建模竞赛中的数学建模和数据分析方法对于队员来说是至关重要的。
在本文中,我们将以数学建模竞赛的一个实际问题为例,演示如何利用SPSS软件建立ARIMA模型对相关数据进行预测和分析。
我们将首先介绍ARIMA模型的基本原理和建模流程,然后利用SPSS软件对给定的数据进行ARIMA模型的建立和检验,最后对模型的效果进行评价并给出相关建议。
二、ARIMA模型的基本原理ARIMA模型是时间序列分析中常用的一种模型,用于对时间序列数据进行预测和分析。
ARIMA模型包括自回归(AR)、差分(I)和移动平均(MA)三部分,分别表示时间序列数据中的自相关、季节性趋势和误差项。
ARIMA模型的建立包括模型的识别、参数的估计和模型的检验三个步骤。
1. 模型的识别:首先需要对时间序列数据进行平稳性和自相关性检验,确定ARIMA模型的参数p、d、q。
p表示自回归的阶数,d表示差分的阶数,q表示移动平均的阶数。
2. 参数的估计:利用最大似然估计等方法,对ARIMA模型中的参数进行估计,得到模型的估计系数。
3. 模型的检验:对估计的ARIMA模型进行残差分析和预测检验,对模型的拟合效果进行评价,并进行模型的调整和优化。
三、SPSS建立ARIMA模型的步骤在SPSS软件中,利用时间序列建模功能可以方便地进行ARIMA模型的建立和分析。
下面我们以一个实际的数据为例,演示在SPSS中建立ARIMA模型的具体步骤。
1. 数据导入:首先在SPSS中导入要分析的时间序列数据,可以是Excel表格或者文本文件格式。
数学建模SPSS案例分析

02
CATALOGUE
数据准备与预处理
数据来源与获取
确定数据来源
01
根据研究目的和问题,确定合适的数据来,如问卷调查、实验数据、公开数据库等。
数据获取
02
通过相应的方法和工具,如网络爬虫、数据接口、数据库查询
等,获取所需数据。
数据初步检查
03
对获取的数据进行初步检查,包括数据完整性、一致性、异常
SPSS建模过程演示
数据准备
根据研究目的和问题,收集和整理相关数据,并进行预处理和清洗, 确保数据质量和一致性。
变量定义与测量
明确研究中的自变量、因变量和控制变量,并进行相应的测量和编码 。
模型构建
根据研究假设和理论框架,选择合适的统计方法和模型进行构建,例 如回归分析、方差分析等。
模型检验与修正
通过案例分析,展示 数学建模在解决实际 问题中的优势和作用 。
案例分析概述
案例选择
选取具有代表性的案例,涉及不同领域和数 据类型,以便全面展示数学建模在SPSS中 的应用。
分析方法
采用数学建模方法,如回归分析、聚类分析、因子 分析等,对案例数据进行深入挖掘和分析。
结果展示
通过图表、表格等形式展示分析结果,直观 呈现数学建模在SPSS中的应用效果。
输标02入题
同时,可以深入研究数学建模和SPSS统计分析在大数 据处理和分析中的应用,以应对日益增长的数据量和 复杂性。
01
03
最终,我们希望通过不断的研究和实践,推动数学建 模和SPSS统计分析的进一步发展,为社会进步和科技
发展做出更大的贡献。
04
此外,还可以关注数学建模和SPSS统计分析在人工智 能、机器学习等新兴技术中的应用,探索其在智能化 决策和自动化处理中的潜力。
SPSS软件与应用-数学建模用

绘制直方图
• 统计指标只能给出数据的大致情况,没有 直方图那样直观,我们就来画个直方图瞧 瞧!选择Graphs==>Histogram
进行统计分析
• 用SPSS来做成组设计两样本均数比较的t检 验,选择Analyze==>Compare Means==>Independent-Samples T test
Means过程
• • • • • • • 界面说明 【Dependent List框】 用于选入需要分析的变量。 【Independent List框】 用于选入分组变量。 【Options钮】 弹出Options对话框,选择需要计算的描述 统计量和统计分析:
• Statistics框 可选的描述统计量。它们是: • 1.sum,number of cases 总和,记录数 • 2.mean, geometric mean, harmonic mean 均数,几何均 数,修正均数 • 3.standard deviation,variance,standard error of the mean 标准差,均数的标准误, 方差 • 4.median, grouped median 中位数,频数表资料中位数 (比如30岁组有5人,40岁组有6人,则在计算grouped median时均按组中值35和45进行计算)。 • 5.minimum,maximum,range 最小值,最大值,全距 • 6.kurtosis, standard error of kurtosis 峰度系数,峰度系数 的标准误 • 7.skewness, standard error of skewness 偏度系数,偏度 系数的标准误 • 8.percentage of total sum, percentage of total N 总和的 百分比,样本例数的百分比
2-统计分析与SPSS应用-数学建模

(1)定性变量。 (2)定序变量。 (3)定距变量。
列格式、对齐、测度方式
返回
2.1.2 变量定义信息的复制
如果有多个变量的类型相同,可以先定义 一个变量,然后把该变量的定义信息复制给新 变量。
2.2 数据的输入与保存 2.2.1 录入数据的一般方法
定义了所有变量后,单击“Data View” 标签,即可在出现的数据视图(编辑)窗中输 入数据。 数据录入时可以逐行录入,也可以逐列。
8.变量的显示宽度(Columns)
输入变量的显示宽度,默认为8。
9.变量显示的对齐方式(Align)
选择变量值显示时的对齐方式:Left(左 对齐)、Right(右对齐)、Center(居中对 齐)。默认是右对齐。
10.变量的测量尺度(Measure)
变量按测量精度可以分为定性变量、定序 变量、定距变量几种。
3.变量长度(Width)
设置变量的长度,当变量为日期型时无效。
4.变量小数点位数(Decimal)
设置变量的小数点位数,当变量为日期型 时无效。
5.变量标签(Label)
变量标签是对变量名的进一步描述,变量 只能由不超过8个字符组成,而8个字符经常不 足以表示变量的含义。而变量标签可长达120 个字符,变量标签可显示大小写,需要时可用 变量标签对变量名的含义加以解释。
实现数据文件的横向连接,必须有一个相 同的公共变量,这个变量是两个数据文件横向 对应连接的依据。 在合并的两个数据文件中,数据含义不同 的变量,变量名不应取相同的名称。
图2-42 数据文件横向合并窗口
2.6 读入其他格式文件数据
在前面的数据保存中,已经讲到SPSS数据 文件可以保存成其他格式的文件,如文本文件、 dbf文件等。反过来,SPSS是否可以直接读取 其他格式数据文件呢?答案是肯定的。SPSS可 以读取文本文件、数据库文件等内容。
以数学建模竞赛为例基于SPSS建立ARIMA模型

以数学建模竞赛为例基于SPSS建立ARIMA模型一、引言二、题目描述假设某市某项产品的月销售数据如下(单位:件):月份销售量1 2002 2203 2104 2405 2506 2607 2708 2809 29010 30011 32012 330请建立ARIMA模型预测未来3个月的销售量。
三、建立ARIMA模型1. 数据处理在SPSS软件中导入上述数据,然后对数据进行时间序列图的绘制和基本统计分析。
通过时间序列图可以观察到数据是否存在趋势和季节性,基本统计分析可以得到数据的均值、标准差等关键统计量。
2. 差分运算由于ARIMA模型对原始数据的平稳性要求比较高,因此在建立模型之前需要进行差分运算以确保数据的平稳性。
在SPSS软件中,可以使用“Transform”菜单中的“Difference”功能对数据进行一阶差分或二阶差分操作。
在这个例子中,我们选择进行一阶差分操作。
3. 自相关和偏自相关图在差分运算之后,需要使用自相关和偏自相关图来确定ARIMA模型的p和q值。
在SPSS软件中,可以使用“Analyze”菜单中的“Forecasting”功能来生成自相关和偏自相关图,并根据图形来判断p和q的取值。
4. 建立ARIMA模型在确定了差分次数、p和q的取值之后,可以使用“Analyze”菜单中的“Forecasting”功能来建立ARIMA模型。
在输入模型参数的时候,需要根据之前的分析结果来设定差分次数、自回归阶数和移动平均阶数。
四、结果分析通过以上步骤,我们成功地建立了ARIMA模型并进行了未来3个月销售量的预测。
预测结果显示未来3个月销售量分别为340、350和360件。
我们还对模型的拟合效果进行了检验,结果表明模型的残差序列符合白噪声特性,预测结果较为可靠。
五、总结本文以一次数学建模竞赛题目为例,介绍了如何使用SPSS软件建立ARIMA模型进行时间序列分析和预测。
通过差分运算、自相关和偏自相关分析、模型建立和诊断以及预测分析等步骤,我们成功地对未来3个月销售量进行了预测。
以数学建模竞赛为例基于SPSS建立ARIMA模型

以数学建模竞赛为例基于SPSS建立ARIMA模型ARIMA模型是一种时间序列的分析方法,可以用来对未来一段时间内的序列数据进行预测和分析,常常被应用于经济、金融、气象、流行病等领域。
在数学建模竞赛中,ARIMA模型也是常见的分析方法之一。
本文将以数学建模竞赛为例,介绍如何基于SPSS软件建立ARIMA模型。
一、数据收集与概览在建立ARIMA模型之前,需要先收集数据,并对数据进行概览。
假设我们研究的是某电商平台的销售数据,数据的格式为时间序列。
下面是部分数据:|日期 |销售额 ||--------|--------||2019-01-01|1000 ||2019-01-02|1200 ||2019-01-03|1300 ||2019-01-04|1150 ||2019-01-05|1400 ||2019-01-06|1250 ||2019-01-07|1350 ||2019-01-08|1500 ||2019-01-09|1650 ||2019-01-10|1800 ||2019-01-11|2000 ||2019-01-12|2200 ||2019-01-13|2300 ||2019-01-14|2400 ||2019-01-15|2500 |通过对数据的概览,我们可以看到销售额有逐渐增加的趋势,并且在一周内出现周期性的波动。
二、建立ARIMA模型1. 模型选择在建立ARIMA模型之前,需要先选择合适的模型。
ARIMA模型的选择最好基于时间序列的图形表示,以及ACF和PACF的分析。
可以通过以下步骤进行模型选择:① 绘制时序图,观察数据的整体趋势、周期变化和异常点等信息。
在SPSS中绘制时序图的方法是:点击菜单Data→Time Series→Line Chart,然后在弹出的对话框中选择“Month-Year”并勾选数据和选项,即可绘制出时序图。
② 绘制ACF和PACF的图形,观察自相关性和偏自相关性。
