2017年高考新课标Ⅲ卷文科数学试题解析
2017年数学真题及解析_2017年全国统一高考数学试卷(文科)(新课标ⅲ)
2017年全国统一高考数学试卷(文科)(新课标Ⅲ)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
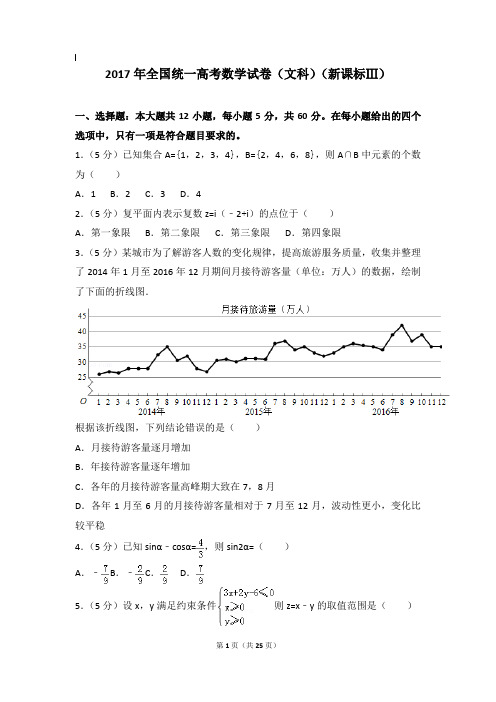
1.(5分)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为()A.1 B.2 C.3 D.42.(5分)复平面内表示复数z=i(﹣2+i)的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是()A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.(5分)已知sinα﹣cosα=,则sin2α=()A.﹣ B.﹣ C.D.5.(5分)设x,y满足约束条件则z=x﹣y的取值范围是()A.[﹣3,0]B.[﹣3,2]C.[0,2]D.[0,3]6.(5分)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.B.1 C.D.7.(5分)函数y=1+x+的部分图象大致为()A. B.C.D.8.(5分)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为()A.5 B.4 C.3 D.29.(5分)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为()A.πB. C.D.10.(5分)在正方体ABCD﹣A1B1C1D1中,E为棱CD的中点,则()A.A1E⊥DC1B.A1E⊥BD C.A1E⊥BC1D.A1E⊥AC11.(5分)已知椭圆C:=1(a>b>0)的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切,则C的离心率为()A.B.C.D.12.(5分)已知函数f(x)=x2﹣2x+a(e x﹣1+e﹣x+1)有唯一零点,则a=()A.﹣ B.C.D.1二、填空题13.(5分)已知向量=(﹣2,3),=(3,m),且,则m=.14.(5分)双曲线(a>0)的一条渐近线方程为y=x,则a=.15.(5分)△ABC的内角A,B,C的对边分别为a,b,c,已知C=60°,b=,c=3,则A=.16.(5分)设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是.三、解答题17.(12分)设数列{a n}满足a1+3a2+…+(2n﹣1)a n=2n.(1)求{a n}的通项公式;(2)求数列{}的前n项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:以最高气温位于各区间的频率估计最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.19.(12分)如图四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD,若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx﹣2与x轴交于A、B两点,点C的坐标为(0,1),当m变化时,解答下列问题:(1)能否出现AC⊥BC的情况?说明理由;(2)证明过A、B、C三点的圆在y轴上截得的弦长为定值.21.(12分)已知函数f(x)=lnx+ax2+(2a+1)x.(1)讨论f(x)的单调性;(2)当a<0时,证明f(x)≤﹣﹣2.[选修4-4:坐标系与参数方程]22.(10分)在直角坐标系xOy中,直线l1的参数方程为,(t为参数),直线l2的参数方程为,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(1)写出C的普通方程;(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣=0,M为l3与C的交点,求M的极径.[选修4-5:不等式选讲]23.已知函数f(x)=|x+1|﹣|x﹣2|.(1)求不等式f(x)≥1的解集;(2)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.2017年全国统一高考数学试卷(文科)(新课标Ⅲ)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分。
2017年高考新课标Ⅲ卷文数试题解析(正式版)(解析版)

皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
1.已知集合 A={1,2,3,4},B={2,4,6,8},则 A B 中元素的个数为
根据该折线图,下列结论错误的是
1
精品文档,名师推荐! 来源网络,造福学生
———————欢迎下载,祝您学习进步,成绩提升———————
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在 7,8 月
D.各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月,波动性更小,变化比较平稳
【答案】A
【解析】由折线图,可知每年 7 月到 8 月折线图呈下降趋势,月接待游客量减少,A 错误.
本题选择 A 选项.
4.已知 sin cos 4 ,则 sin 2 = 3
A. 7 9
B. 2 9
2
C.
9
7
D.
9
【答案】A
【解析】 sin 2 2sin cos sin cos 2 1 7 .
【答案】75°
【解析】由正弦定理
b sin B
c sin C
,得 sin B
bsin C
6 3 2
2 ,结合 b c 可得 B 45 ,
精品文档,名师推荐! 来源网络,造福学生
———————欢迎下载,祝您学习进步,成绩提升———————
绝密★启用前
2017 年普通高等学校招生全国统一考试
文科数学
注意事项:
17年高考真题——文科数学(全国Ⅲ卷)+Word版后附解析

绝密★启用前2017年普通高等学校招生全国统一考试文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B中元素的个数为A.1 B.2 C.3 D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos 3αα-=,则sin 2α= A .79-B .29-C .29D .795.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是 A .–3,0]B .–3,2]C .0,2]D .0,3]6.函数f (x )= sin(x +3π)+cos(x −6π)的最大值为 A .65B .1C .D .7.函数y =1+x +2sin xx的部分图像大致为 A . B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π410.在正方体1111ABCD A BC D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A B C D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12- B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
2017年全国3高考文科数学试题及答案-全国卷3

2017年普通高等学校招生全国统一考试(全国卷3)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A B 中元素的个数为( )A .1B .2C .3D .42.复平面内表示复数(2)z i i =-+的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图. 根据该折线图,下列结论错误的是( ) A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 4.已知4sin cos 3αα-=,则sin 2α=( ) A .79-B .29-C .29D .795.设,x y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z x y =-的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]6.函数1()sin()cos()536f x x x ππ=++-的最大值为( ) A .65 B .1 C .35D .157.函数2sin 1xy x x =++的部分图像大致为( ) A . B .C .D .8.执行右面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .2 9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .πB .34π C .2πD .4π10.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( )A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆2222:1(0)x y C a b a b+=>>的左、右顶点分别为12,A A ,且以线段12A A 为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为( )A BC .3D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =( )A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分。
2017年高考全国文数(新课标Ⅲ)答案

2017年全国普通高等学校统一招生考试·丙卷(新课标Ⅲ)文科数学1.B 【解析】由集合交集的定义{2,4}AB =,选B .2.C 【解析】∵i(2i)12i z =-+=--,∴复数z 在复平面内对应的点(1,2)Z --,位于第三象限,选C .3.A 【解析】由折线图,7月份后月接待游客量减少,A 错误;选A . 4.A 【解析】由4sin cos 3αα-=,两边平方得161sin 29α-=,所以7sin 29α=-,选A . 5.B 【解析】不等式组的可行域如图,目标函数的几何意义可得函数在点()0,3A 处取得最小值033z =-=- . 在点()2,0B 处取得最大值202z =-=,选B .x6.A 【解析】∵cos()cos[()]sin()6233x x x ππππ-=-+=+, 则 16()sin()sin()sin()53353f x x x x πππ=+++=+,函数的最大值为65.7.D 【解析】当1x =时,(1)2sin12f =+>,排除A 、C ;当x →+∞时,1y x →+,排除B .选D .8.D 【解析】若2N =,第一次循环,12≤成立,100S =,10M =-,22i =≤成立,第二次循环,此时90S =,1M =,32i =≤不成立,所以输出9091S =<成立,所以输入的正整数N 的最小值是2,故选D .9.B 【解析】圆柱的轴截面如图,1AC =,12AB =,所以圆柱底面半径2r BC ==,那么圆柱的体积是223(124V r h πππ==⨯⨯=,故选B . CBA10.C 【解析】如图,连结1A D ,易知1AD ⊥平面1A DE ,所以11AD A E ⊥,又11BC AD ∥,所以1BC ⊥平面1A DE ,故11AE BC ⊥,选C .C 11A 1A11.A 【解析】以线段12A A 为直径的圆是222x y a+=,直线20bx ay ab -+=与圆相切,所以圆心到直线的距离d a ==,整理为223a b =,即()22222323a a c a c =-⇒=,即2223c a = ,c e a ==,故选A .12.C 【解析】令()0f x =,则方程112()2x x a e e x x --++=-+有唯一解,设2()2h x x x =-+,11()x x g x ee --+=+,则()h x 与()g x 有唯一交点,又11111()2x x x x g x ee e e --+--=+=+≥,当且仅当1x =时取得最小值2.而2()(1)11h x x =--+≤,此时1x =时取得最大值1,()()ag x h x =有唯一的交点,则12a =.选C . 13.2【解析】由题意0⋅=a b ,所以2330m -⨯+⨯=,即2m =. 14.5【解析】由双曲线的标准方程可得渐近线方程为:3y x a=±,结合题意可得:5a =.15.75°【解析】由正弦定理sin sin b cB C=,即sin 2sin 3b C Bc ===, 结合b c < 可得45B = ,则18075A B C =--=.16.1(,)4-+∞【解析】当12x >时,不等式为12221x x-+>恒成立;当102x <≤,不等式12112xx +-+>恒成立; 当0x ≤时,不等式为11112x x ++-+>,解得14x >-,即104x -<≤;综上,x 的取值范围为1(,)4-+∞.17.【解析】(1)因为123(21)2n a a n a n ++⋅⋅⋅+-=,故当2n ≥时,1213(23)2(1)n a a n a n -++⋅⋅⋅+-=-.两式相减得(21)2n n a -=. 所以221n a n =-(2)n ≥. 又由题设可得12a =. 从而{}n a 的通项公式为221n a n =-. (2)记{}21na n +的前n 项和为n S , 由(1)知21121(21)(21)2121n a n n n n n ==-++--+.则11111121335212121n nS n n n =-+-+⋅⋅⋅+-=-++. 18.【解析】(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为216360.690++=, 所以这种酸奶一天的需求量不超过300瓶的概率估计值为0.6.(2)当这种酸奶一天的进货量为450瓶时, 若最高气温不低于25,则Y =6⨯450-4⨯450=900;若最高气温位于区间 [20,25),则Y =6⨯300+2(450-300)-4错误!未找到引用源。
2017年高考真题全国新课标三卷文科数学(解析版)

2017年高考真题全国新课标三卷文科数学(解析版)已知集合A={1,2,3,4},B={2,4,6,8},则A∩B中元素的个数为几个?答案:2解析:A∩B={2,4},共2个元素。
选择B选项。
复平面内表示复数z=i(–2+i)的点位于哪个象限?答案:第二象限解析:z=-i(2-i)=-2i+i^2=-2i-1.所以z在第二象限。
选择B选项。
根据该折线图,下列结论错误的是?A。
月接待游客逐月增加B。
年接待游客量逐年增加C。
各年的月接待游客量高峰期大致在7,8月D。
各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳答案:A解析:由折线图,7月份后月接待游客量减少,所以A错误。
选择A选项。
已知sinα-cosα=4/9,则sin2α=?答案:-2/17解析:sin2α=2sinαcosα=2(sinα-cosα)cosα=2(4/9)cosα=-8/81.所以sin2α=-2/17.选择A选项。
设x,y满足约束条件{3x+2y-6≤0,x≥0,y≥0},则z=x-y 的取值范围是?A。
[-3,0]B。
[-3,2]C。
[0,2]D。
[0,3]答案:B解析:绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点A(0,3)处取得最小值z=-3,在点B(2,0)处取得最大值z=2.所以z的取值范围是[-3,2]。
选择B选项。
函数f(x)=sin(x+π/6)+cos(x-π/3)的最大值为多少?A。
5/6B。
1C。
1/5D。
5答案:A解析:由诱导公式可得:cos(x-π/3)=sin(π/2-(x-π/3))=sin(x-π/6),所以f(x)=sin(x+π/6)+sin(x-π/6)=2cos(π/6)sinx=√3sinx。
∵|sinx|≤1,∴f(x)的最大值为√3,即5/6.选择A选项。
函数y=1+x+sinx?(此处有格式错误,请删除)答案:无法判断解析:此题缺少函数的定义域和范围,无法判断。
2017年高考文科数学(3卷)答案详解(word版+详细解析)
2017年普通高等学校招生全国统一考试文科数学III 卷 答案详解一、选择题:本大题共12小题,每小题5分,共60分. 1.已知集合A={1,2,3,4},B={2,4,6,8},则A B I 中元素的个数为 A .1B .2C .3D .4【解析】}4,2{=B A I ,∴A B I 中元素的个数为2. 【答案】B2.复平面内表示复数z =i (–2+i )的点位于 A .第一象限B .第二象限C .第三象限D .第四象限【解析】i i i i i z 212)2(2--=+-=+-=,∴复数z 的点位于第三象限. 【答案】C3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳【解析】由折线图可知:2014年8月到9月、10月到11月等月接待游客量都是减少的,所以A 错误. 【答案】A4.已知4sin cos 3αα-=,则sin 2α=A .79-B .29-C .29D .79【解析】∵4sin cos 3αα-=,∴216(sin cos )12sin cos 1sin 29ααααα-=-=-=,∴7sin 29α=-. 【答案】A5.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]【解析】可行域如图所示,目标函数z x y =-化为y x z =-,当直线y x z =-过点A 时,其在y 轴上的截距最大,即z 取最小值,所以z min =-3;当直线y x z =-过点B 时,其在y 轴上的截距最小,即z 取最大值,所以z max =2 . [A 、B 的坐标联立方程求出:A(0,3)、B(2,0) ] ∴z =x -y 的取值范围是[–3,2].图A7【答案】B6.函数1()sin()cos()536f x x x ππ=++-的最大值为A .65B .1C .35D .15【解析】∵πππππcos()cos()cos[()]sin()66233x x x x -=-+=-+=+,∵16()sin()cos()sin()53653f x x x x πππ=++-=+,∵函数()f x 的最大值为65.【答案】A 7.函数2sin 1xxx y ++=的部分图像大致为A .B .C .D .【解析】∵当x 趋于无穷大时,y 也趋于无穷大,因此排除B 、C ;∵21sin 2)1(>+=f ,因此排除A.【答案】D8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .2【解析】正整数N 在框图中起到控制循环体执行次数的作用,因此可以逐步循环,直至到“输出S 的值小于91”即可.第1次循环:输入S =0,M =100,t =1, 第2次循环:输入S =100,M =-10,t =2,第3次循环:输入S =90,M =1,t =3,符合“输出S 的值小于91”,t =3≤N 不成立,则N =2即可.【答案】D9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4C .π2D .π4【解析】由题可知,圆柱的轴截面如图所示,AC=2,BC=1,故AB=3,圆柱底面圆的半径为23,所以圆柱的体积为43π1)23(π2=⨯⨯.【答案】B10.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥【解析】取C 1C 的中点F ,连接A 1F 、EF ,∵E 为棱CD 的中点,∵EF ∵DC 1. 设正方体的边长为2,于是有22EF =,219A E =,219A F =,∵∵A 1EF 不是直角三角形,∵1A E EF ⊥不成立,即11A E DC ⊥不成立. 故A 错误.同理,取BC 的中点Q ,连接A 1Q 、EQ (图中未画出),可以证明1A E BD ⊥不成立. 故B 错误. 同理,取AD 的中点M ,连接A 1M 、EM (图中未画出),可以证明1A E AC ⊥不成立. 故D 错误. 连接A 1D 、B 1C ,∵11BC B C ⊥,11BC A B ⊥,∵111BC A DCB ⊥平面,又∵111A E A DCB ⊂平面,∵11BC A E ⊥. 故C 错误.图A1011.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .13【解析】以线段A 1A 2为直径的圆的圆心在原点(0,0),半径为a ,因为与直线20bx ay ab -+=相切,所以原点到直线20bx ay ab -+=的距离为a ,即222ab a a b =+,化简得223a b =,∴椭圆C 的离心率为222222222233c a b b e a a b -====,63e =.【答案】A12.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1【解析】11()22()x x f x x a e e --+'=-+-,当1x =时,00(1)22()0f a e e '=-+-=;若0a >,根据函数图像及其性质可知,当1x >时,220x ->,11()0x x a ee --+->,故()0f x '>恒成立;当1x <时,同理()0f x '<恒成立. 故函数()f x 在(,1)-∞单调递减,在(1,)+∞单调递增. ∵函数()f x 有唯一零点,∵该唯一零点一定是1,即(1)120f a =-+=,∵12a =. 同理,若00a a <=或,根据函数图像及其性质,可以证明函数()f x 的零点不唯一.图A12二、填空题:本题共4小题,每小题5分,共20分. 13.已知向量(2,3),(3,)a b m =-=,且a ∵b ,则m = .【解析】∵a b ⊥rr ,∵2330m -⨯+=,解得2m =.【答案】214.双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = . 【解析】双曲线的渐近线方程为b y x a =±,根据已知,则有535==b a . 【答案】515.∵ABC 的内角A ,B ,C 的对边分别为a ,b ,c . 已知C =60°,b =6,c =3,则A =_________.【解析】由正弦定理得,sin 6sin 602sin 32b C Bc ⨯===o ,∵ο1200<<B ,∴ο45=B . ∴οοοο754560180=--=A .【答案】75°16.设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________.【解析】当12x >时,121()()2212x xf x f x -+-=+>恒成立;当102x ≤≤时,111()()2(1)21222x x f x f x x x +-=+-+=++>恒成立; 当0x <时,113()()1(1)21222f x f x x x x +-=++-+=+>,解得14x >-,故104x -<<.综上所述,x 的取值范围是1(,)4-+∞.【答案】1(,)4-+∞三、解答题:共70分. 解答应写出文字说明、证明过程或演算步骤. 第17~21题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-=K .(1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和. 【解析】(1)因为123(21)2n a a n a n +++-=K ,故当n ≥2时,1213(23)2(1)n a a n a n -+++-=-K两式相减得(21)2n n a -=, 所以 221n a n =-(n ≥2),又因题设可得 a 1=2. 从而{a n } 的通项公式为 221n a n =-. (2)记 {21na n +}的前n 项和为S n , 由(1)知211=21(21)(21)2121n a n n n n n =-++--+, 则 111112=1335212121n nS n n n -+-++-=-++L . 18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:∵)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温 [10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率. (1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.【解析】(1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为216360.690++=,所以这种酸奶一天的需求量不超过300瓶的概率估计值为0.6. (2)当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则Y =6×450-4×450=900;若最高气温位于区间 [20,25),则Y =6×300+2(450-300)-4×450=300; 若最高气温低于20,则Y =6×200+2(450-200)-4×450=-100. 所以,Y 的所有可能值为900、300、-100.Y 大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为3625740.890+++=,因此Y 大于零的概率的估计值为0.8.19.(12分)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.【解析】(1)取A C 的中点O 连结DO ,BO .因为AD =CD ,所以AC ∵DO .又由于∵ABC 是正三角形,所以AC ∵BO . 从而AC ∵平面DOB ,故AC ∵BD .图A19(2)连结EO .由(1)及题设知∵ADC =90°,所以DO =AO . 在Rt∵AOB 中,BO 2+AO 2=AB 2.又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2,故∵DOB =90°.由题设知∵AEC 为直角三角形,所以12EO AC =. 又∵ABC 是正三角形,且AB =BD ,所以12EO BD =.故E 为BD 的中点,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1:1. 20.(12分)在直角坐标系xOy 中,曲线y =x 2+mx –2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题:(1)能否出现AC ∵BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值. 【解析】(1)不能出现AC ∵BC 的情况,理由如下:设A (x 1,0), B (x 2,0),则x 1,x 2满足x 2+mx −2=0所以x 1x 2=−2. 又C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为121112x x --⋅=-,所以不能出现AC ∵BC 的情况.(2)BC 的中点坐标为21(,)22x ,可得BC 的中垂线方程为221()22x y x x -=-. 由(1)可得x 1+x 2=−m ,所以AB 的中垂线方程为2mx =-.联立221()222x y x x m x ⎧-=-⎪⎪⎨⎪=-⎪⎩,又x 22+mx 2−2=0,可得212m x y ⎧=-⎪⎪⎨⎪=-⎪⎩, 所以过A 、B 、C 三点的圆的圆心坐标为1(,)22m -,半径292m r +=, 故圆在y 轴上截得的弦长为222()32mr -=,即过A 、B 、C 三点的圆在y 轴上的截得的弦长为定值.21.(12分)已知函数f (x )=ln x +ax 2+(2a +1)x . (1)讨论f (x )的单调性;(2)当a <0时,证明3()24f x a≤--. 【解析】(1)f (x )的定义域为(0, +∞),1(1)(21)()221x ax f x ax a x x++'≤+++=. 若a ≥0,则当x ∵(0, +∞)时,()0f x '>,故f(x)在(0, +∞)单调递增. 若a <0,则当1(0,)2x a ∈-时,()0f x '>;当1(,)2x a ∈-+∞时,()0f x '<.故f(x)在1(0,)2a-单调递增,在1(,)2a-+∞单调递减. (2)由(1)知,当a <0时,f(x)在12x a =-取得最大值,最大值为111()In()1224f a a a-=---. 所以3()24f x a≤--等价于113In()12244a a a ---≤--,即11In()1022a a -++≤, 设()In 1g x x x =-+,则1()1g x x'=-,当x ∵(0,1)时,g ’(x )>0;当x ∵(1,+∞)时,g ’(x )<0.所以g (x )在(0,1)单调递增,在(1,+∞)单调递减.故当x =1时,g (x )取得最大值,最大值为g (1)=0.所以当x >0时,g (x )≤0,.从而当a <0时,ln (−12a)+12a +1≤0,即f (x )≤−34a −2. (二)选考题:共10分. 请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线l 1的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线l 2的参数方程为2,,x m m m y k =-+⎧⎪⎨=⎪⎩(为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)−2=0,M 为l 3与C 的交点,求M 的极径. 学*科@网【解析】(1)消去参数t 得l 1的普通方程l 1: y =k (x −2); 消去参数m 得l 2的普通方程 l 2:y =1k (x +2).设P (x ,y ),由题设得{y =k(x −2)y =1k(x +2)消去k 得 x 2 −y 2 =4(y ≠0).所以C 的普通方程为 x 2 −y 2 =4(y ≠0).(2)C 的极坐标方程为 ρ2(cos 2θ−sin 2θ)=4(0<θ<2π,θ≠π) 联立{ρ2(cos 2θ−sin 2θ)=4ρ(cos θ+sin θ)−√2=0 得 cos θ−sin θ=2(cos θ+sin θ)故tan θ=−13 ,从而cos 2θ=910, sin 2θ=110.代入ρ2(cos 2θ−sin 2θ)=4 得ρ2=5,所以交点M 的极径为√5 .23.[选修4—5:不等式选讲](10分)已知函数()f x =│x +1│–│x –2│. (1)求不等式()f x ≥1的解集;(2)若不等式()f x ≥x 2–x +m 的解集非空,求m 的取值范围.【解析】(1)f (x )={−3, x <−1,2x −1, −1≤x ≤2,3, x >2.当x <-1时,f(x)≥1无解;当−1≤x ≤2时,由f(x)≥1得,2x -1≥1,解得1≤x ≤2; 当 x >2时,由f(x)≥1解得x >2. 所以f(x)≥1的解集为{x |x ≥1}.(2)由f (x )≥x 2−x +m 得m ≤|x +1|-|x -2|-x 2+x .而 |x +1|-|x -2|-x 2+x ≤|x |+1+|x |−2−x 2+|x| =−(|x |−32)2+54≤54,且当x =32时,|x +1|-|x -2|-x 2+x =54.故m 的取值范围为(-∞,54].2017年普通高等学校招生全国统一考试(新课标∵)文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑. 如需改动,用橡皮擦干净后,再选涂其他答案标号. 回答非选择题时,将答案写在答题卡上. 写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={1,2,3,4},B={2,4,6,8},则A⋂B中元素的个数为A.1B.2C.3D.42.复平面内表示复数z=i(–2+i)的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳4.已知4sin cos3αα-=,则sin2α=A.79-B.29-C.29D.795.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .157.函数y =1+x +2sin xx的部分图像大致为A .B .C .D .8.执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .29.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A .πB .3π4C .π2D .π410.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥11.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .1312.已知函数211()2()x x f x x x a ee --+=-++有唯一零点,则a =A .12-B .13C .12D .1二、填空题:本题共4小题,每小题5分,共20分. 13.已知向量(2,3),(3,)a b m =-=,且a ∵b ,则m = .14.双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = . 15.∵ABC 的内角A ,B ,C 的对边分别为a ,b ,c . 已知C =60°,b =6,c =3,则A =_________. 16.设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________.三、解答题:共70分. 解答应写出文字说明、证明过程或演算步骤. 第17~21题为必考题,每个试题考生都必须作答. 第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-=K . (1)求{}n a 的通项公式; (2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:∵)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温[10,15)[15,20)[20,25)[25,30)[30,35)[35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.学#科@网19.(12分)如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E为棱BD上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.20.(12分)在直角坐标系xOy中,曲线y=x2+mx–2与x轴交于A,B两点,点C的坐标为(0,1).当m变化时,解答下列问题:(1)能否出现AC∵BC的情况?说明理由;(2)证明过A,B,C三点的圆在y轴上截得的弦长为定值.21.(12分)f x=ln x+ax2+(2a+1)x.已知函数()(1)讨论()f x 的单调性; (2)当a ﹤0时,证明3()24f x a≤--. (二)选考题:共10分. 请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4―4:坐标系与参数方程](10分)在直角坐标系xOy 中,直线l 1的参数方程为2+,,x t y kt =⎧⎨=⎩(t 为参数),直线l 2的参数方程为2,,x m m m y k =-+⎧⎪⎨=⎪⎩(为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)−2=0,M 为l 3与C 的交点,求M 的极径. 学*科@网 23.[选修4—5:不等式选讲](10分)已知函数()f x =│x +1│–│x –2│. (1)求不等式()f x ≥1的解集;(2)若不等式()f x ≥x 2–x +m 的解集非空,求m 的取值范围.。
2017年高考全国Ⅲ卷文数试题(解析版)
试卷点评
命题特点 该口古7 新课标 导导导 高考数学试卷,试卷内容 体 新课程理念,贴 中学数学教学,坚持
对基础知识 基本技能 及数学思想方法的考查 在保持稳定的基础 ,进行适度的改革和 创新 该口古7 稳 的 古 的数学试卷 稳中求进 试卷考查
试卷结构 稳, 时题目 和 无偏怪题,难度控制理想 体知识点 变化 回 教材,注重基础 该口古7
1.已知集合 A={1,2,3,4},B={2,4,6,8},则 A I B 中元素的个数 A.1 答案 B B .2 C .3 D.4
解析 由题意可得 考点 集合 算
A I B = {2, 4} , A I B 中元素的个数
该,所 选 B.
师点睛 集合的基本 算的关注点 (古)看元素 成.集合是由元素 成的,从研究集合中元素的构成入手是解决集合 算问题 的前提. (该) 些集合是可 化简的,先化简再研究 关系并进行 算,可使问题简单明了,易于解 决. (详)注意数形结合思想的 用,常用的数形结合形式 数轴 坐标系和 有enn 图. 2.复 面内表示复数 z = i( −2 + i) 的点 于 A.第一象限 答案 叶 解析 由题意 考点 复数 算 师点睛 首先对于复数的四则 算,要 实掌握 算技 和常规思路,如 次要熟悉复数相关基本概念, 对 点 B.第 象限 C.第 象限 D.第四象限
z = −1 − 2i ,在第 象限. 所 选 叶.
(a + bi )(c + di ) = (ac − bd ) + (ad + bc ) i , (a , b, c.d ∈ R) .
如复数 a + bi (a , b ∈ R ) 的实部
a
虚部
b
2017年全国III卷高考文科数学真题及答案
2017 年全国 III 卷高考文科数学真题及答案注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动, 用橡皮擦干净后, 再选涂其他答案标号。
回答非选择题时, 将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
5 分,共 60 分。
在每小题给出的四个选项中,只 有一项是符合题目要求的。
2016 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在 7,8 月D .各年 1 月至 6 月的月接待游客量相对于 7月至 12 月,波动性更小,变化比较平稳4.已知 sin cos4,则 sin 2 =37227A .B .C .D .99 9 9、选择题:本大题共 12 小题,每小题 1. 已知集合 A={1,2,3,4} , B={2,4,6,8} ,则 B 中元素的个数为 2. 3.A .1B .2C .D .4复平面内表示复数 z=i( –2+i) 的点位于 A .第一象限B .第二象限C . 第三象限D .第四象限 某城市为了解游客人数的变化规律,提高旅游服务质量, 收集并整理了 2014 年 1 月至3x 2y 5.设 x ,y 满足约束条件 x 0yB 1 D5A BCD .C .3D .2 B .4 A .5 B .1C .[0,2]D .[0,3]60C .35A .65 8.执行下面的程序框图,为使输出 S 的值小于 91,则输入的正整数N 的最小值为9.已知圆柱的高为 1,它的两个底面的圆周在直径为 2 的同一个球的球面上,则该圆柱的[ – 3,2]16.函数 f (x )= sin( x + )+cos( x - ) 的最大值为 5 3 67.函数 y =1+x + sin 2 x 的部分图像大致为 x 20 ,则 z =x -y 的取值范围是A .[ –3,0]A . A 1E ⊥DC 1B . A 1E ⊥BDC . A 1E ⊥BC 1D . A 1E ⊥ AC2 y 2 1,( a >b >0)的左、右顶点分别为 b1(a >0)的一条渐近线方程为 y 3x , 95A ,B ,C 的对边分别为 a ,b ,c 。
数学-2017年高考真题——全国Ⅲ卷(文)(精校解析版)
2017年普通高等学校招生全国统一考试(全国Ⅲ卷)文科数学一、选择题(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2017·全国Ⅲ文,1)已知集合A ={1,2,3,4},B ={2,4,6,8},则A ∩B 中元素的个数为( ) A .1 B .2 C .3 D .42.(2017·全国Ⅲ文,2)复平面内表示复数z =i(-2+i)的点位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限3.(2017·全国Ⅲ文,3)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( ) A .月接待游客量逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 4.(2017·全国Ⅲ文,4)已知sin α-cos α=43,则sin 2α等于( )A .-79B .-29C .29D .795.(2017·全国Ⅲ文,5)设x ,y 满足约束条件⎩⎪⎨⎪⎧3x +2y -6≤0,x ≥0,y ≥0,则z =x -y 的取值范围是( )A .[-3,0]B .[-3,2]C .[0,2]D .[0,3]6.(2017·全国Ⅲ文,6)函数f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6的最大值为( ) A .65 B .1 C .35 D .157.(2017·全国Ⅲ文,7)函数y =1+x +sin xx2的部分图象大致为( )8.(2017·全国Ⅲ文,8)执行下面的程序框图,为使输出S 的值小于91,则输入的正整数N 的最小值为( )A .5B .4C .3D .29.(2017·全国Ⅲ文,9)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( ) A .π B .3π4 C .π2 D .π410.(2017·全国Ⅲ文,10)在正方体ABCDA 1B 1C 1D 1中,E 为棱CD 的中点,则( ) A .A 1E ⊥DC 1 B .A 1E ⊥BD C .A 1E ⊥BC 1D .A 1E ⊥AC11.(2017·全国Ⅲ文,11)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线bx -ay +2ab =0相切,则椭圆C 的离心率为( ) A .63 B .33 C .23 D .1312.(2017·全国Ⅲ文,12)已知函数f (x )=x 2-2x +a (e x -1+e -x +1)有唯一零点,则a 等于( )A .-12B .13C .12D .1二、填空题(本题共4小题,每小题5分,共20分)13.(2017·全国Ⅲ文,13)已知向量a =(-2,3),b =(3,m ),且a ⊥b ,则m =________. 14.(2017·全国Ⅲ文,14)双曲线x 2a 2-y 29=1(a >0)的一条渐近线方程为y =35x ,则a =________.15.(2017·全国Ⅲ文,15)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知C =60°,b =6,c =3,则A =________.16.(2017·全国Ⅲ文,16)设函数f (x )=⎩⎪⎨⎪⎧x +1,x ≤0,2x ,x >0,则满足f (x )+f ⎝⎛⎭⎫x -12>1的x 的取值范围是________.三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22~23题为选考题,考生根据要求作答) (一)必考题:共60分17.(2017·全国Ⅲ文,17)设数列{a n }满足a 1+3a 2+…+(2n -1)a n =2n . (1)求{a n }的通项公式;(2)求数列⎩⎨⎧⎭⎬⎫a n 2n +1的前n 项和.18.(2017·全国Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.19.(2017·全国Ⅲ文,19)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.20.(2017·全国Ⅲ文,20)在直角坐标系xOy 中,曲线y =x 2+mx -2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题: (1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.21.(2017·全国Ⅲ文,21)已知函数f (x )=ln x +ax 2+(2a +1)x . (1)讨论f (x )的单调性;(2)当a <0时,证明f (x )≤-34a -2.选考题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.22.(2017·全国Ⅲ文,22)[选修4-4:坐标系与参数方程]在直角坐标系xOy 中,直线l 1的参数方程为⎩⎪⎨⎪⎧x =2+t ,y =kt (t 为参数),直线l 2的参数方程为⎩⎪⎨⎪⎧x =-2+m ,y =m k(m 为参数).设l 1与l 2的交点为P ,当k 变化时,P 的轨迹为曲线C . (1)写出C 的普通方程;(2)以坐标原点为极点,x 轴正半轴为极轴建立极坐标系,设l 3:ρ(cos θ+sin θ)-2=0,M 为l 3与C 的交点,求M 的极径.23.(2017·全国Ⅲ文,23)[选修4-5:不等式选讲] 已知函数f (x )=|x +1|-|x -2|. (1)求不等式f (x )≥1的解集;(2)若不等式f (x )≥x 2-x +m 的解集非空,求m 的取值范围.参考答案一、选择题(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】B【解析】∵A ={1,2,3,4},B ={2,4,6,8}, ∴A ∩B ={2,4}.∴A ∩B 中元素的个数为2. 故选B. 2.【答案】C【解析】∵z =i(-2+i)=-1-2i ,∴复数z =-1-2i 所对应的复平面内的点为Z (-1,-2),位于第三象限. 故选C. 3.【答案】A【解析】对于选项A ,由图易知月接待游客量每年7,8月份明显高于12月份,故A 错; 对于选项B ,观察折线图的变化趋势可知年接待游客量逐年增加,故B 正确; 对于选项C ,D ,由图可知显然正确. 故选A. 4.【答案】A【解析】∵sin α-cos α=43,∴(sin α-cos α)2=1-2sin αcos α=1-sin 2α=169,∴sin 2α=-79.故选A. 5.【答案】B【解析】画出不等式组表示的平面区域,如图中阴影部分所示.由题意可知,当直线y =x -z 过点A (2,0)时,z 取得最大值,即z max =2-0=2;当直线y =x -z 过点B (0,3)时,z 取得最小值,即z min =0-3=-3.所以z =x -y 的取值范围是[-3,2]. 故选B. 6.【答案】A【解析】方法一 ∵f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6 =15⎝⎛⎭⎫12sin x +32cos x +32cos x +12sin x =110sin x +310cos x +32cos x +12sin x =35sin x +335cos x =65sin ⎝⎛⎭⎫x +π3, ∴当x =π6+2k π(k ∈Z )时,f (x )取得最大值65.故选A.方法二 ∵⎝⎛⎭⎫x +π3+⎝⎛⎭⎫π6-x =π2, ∴f (x )=15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫x -π6 =15sin ⎝⎛⎭⎫x +π3+cos ⎝⎛⎭⎫π6-x =15sin ⎝⎛⎭⎫x +π3+sin ⎝⎛⎭⎫x +π3 =65sin ⎝⎛⎭⎫x +π3≤65. ∴f (x )max =65.故选A. 7.【答案】D【解析】当x →+∞时,sin x x 2→0,1+x →+∞,y =1+x +sin xx 2→+∞,故排除选项B.当0<x <π2时,y =1+x +sin xx 2>0,故排除选项A ,C.故选D. 8.【答案】D【解析】假设N =2,程序执行过程如下: t =1,M =100,S =0,1≤2,S =0+100=100,M =-10010=-10,t =2,2≤2,S =100-10=90,M =--1010=1,t =3,3>2,输出S =90<91.符合题意.∴N =2成立.显然2是N 的最小值.故选D. 9.【答案】B【解析】设圆柱的底面半径为r ,球的半径为R ,且R =1,由圆柱两个底面的圆周在同一个球的球面上可知,r ,R 及圆柱的高的一半构成直角三角形. ∴r =1-⎝⎛⎭⎫122=32.∴圆柱的体积为V =πr 2h =34π×1=3π4.故选B. 10.【答案】C【解析】方法一 如图,∵A 1E 在平面ABCD 上的投影为AE ,而AE 不与AC ,BD 垂直,∴B ,D 错;∵A 1E 在平面BCC 1B 1上的投影为B 1C ,且B 1C ⊥BC 1, ∴A 1E ⊥BC 1,故C 正确;(证明:由条件易知,BC 1⊥B 1C ,BC 1⊥CE ,又CE ∩B 1C =C ,∴BC 1⊥平面CEA 1B 1. 又A 1E ⊂平面CEA 1B 1, ∴A 1E ⊥BC 1)∵A 1E 在平面DCC 1D 1上的投影为D 1E ,而D 1E 不与DC 1垂直,故A 错. 故选C.方法二 (空间向量法)建立如图所示的空间直角坐标系,设正方体的棱长为1,则A (1,0,0),B (1,1,0),C (0,1,0),D (0,0,0),A 1(1,0,1),C 1(0,1,1),E ⎝⎛⎭⎫0,12,0,∴A 1E →=⎝⎛⎭⎫-1,12,-1,DC 1→=(0,1,1),BD →=(-1,-1,0),BC 1→=(-1,0,1),AC →=(-1,1,0),∴A 1E →·DC 1→≠0,A 1E →·BD →≠0,A 1E →·BC 1→=0,A 1E →·AC →≠0,∴A 1E ⊥BC 1. 故选C. 11.【答案】A【解析】由题意知以A 1A 2为直径的圆的圆心坐标为(0,0),半径为a . 又直线bx -ay +2ab =0与圆相切, ∴圆心到直线的距离d =2aba 2+b2=a ,解得a =3b ,∴b a =13, ∴e =c a =a 2-b 2a =1-⎝⎛⎭⎫b a 2=1-⎝⎛⎭⎫132=63.故选A. 12.【答案】C【解析】方法一 f (x )=x 2-2x +a (e x -1+e-x +1)=(x -1)2+a [e x -1+e-(x -1)]-1,令t =x -1,则g (t )=f (t +1)=t 2+a (e t +e -t )-1. ∵g (-t )=(-t )2+a (e -t +e t )-1=g (t ),∴函数g (t )为偶函数.∵f (x )有唯一零点,∴g (t )也有唯一零点. 又g (t )为偶函数,由偶函数的性质知g (0)=0, ∴2a -1=0,解得a =12.故选C.方法二 f (x )=0⇔a (e x -1+e-x +1)=-x 2+2x .e x -1+e-x +1≥2e x -1·e-x +1=2,当且仅当x =1时取“=”.-x 2+2x =-(x -1)2+1≤1,当且仅当x =1时取“=”. 若a >0,则a (e x -1+e-x +1)≥2a ,要使f (x )有唯一零点,则必有2a =1,即a =12.若a ≤0,则f (x )的零点不唯一. 故选C.二、填空题(本题共4小题,每小题5分,共20分) 13.【答案】2【解析】∵a =(-2,3),b =(3,m ),且a ⊥b , ∴a·b =0,即-2×3+3m =0,解得m =2. 14.【答案】5【解析】∵双曲线的标准方程为x 2a 2-y 29=1(a >0),∴双曲线的渐近线方程为y =±3ax .又双曲线的一条渐近线方程为y =35x ,∴a =5.15.【答案】75°【解析】如图,由正弦定理,得3sin 60°=6sin B ,∴sin B =22.又c >b ,∴B =45°, ∴A =180°-60°-45°=75°. 16.【答案】⎝⎛⎭⎫-14,+∞ 【解析】由题意知,可对不等式分x ≤0,0<x ≤12,x >12三段讨论.当x ≤0时,原不等式为x +1+x +12>1,解得x >-14,∴-14<x ≤0.当0<x ≤12时,原不等式为2x +x +12>1,显然成立.当x >12时,原不等式为2x +2x -12>1,显然成立.综上可知,x 的取值范围是⎝⎛⎭⎫-14,+∞. 三、解答题(共70分,解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22~23题为选考题,考生根据要求作答) 17.解 (1)因为a 1+3a 2+…+(2n -1)a n =2n , 故当n ≥2时,a 1+3a 2+…+(2n -3)a n -1=2(n -1), 两式相减,得(2n -1)a n =2, 所以a n =22n -1(n ≥2).又由题设可得a 1=2,满足上式, 所以{a n }的通项公式为a n =22n -1. (2)记⎩⎨⎧⎭⎬⎫a n 2n +1的前n 项和为S n .由(1)知a n 2n +1=2(2n +1)(2n -1)=12n -1-12n +1,则S n =11-13+13-15+…+12n -1-12n +1=2n2n +1.18.解 (1)这种酸奶一天的需求量不超过300瓶,当且仅当最高气温低于25,由表格数据知,最高气温低于25的频率为2+16+3690=0.6,所以这种酸奶一天的需求量不超过300瓶的概率的估计值为0.6.(2)当这种酸奶一天的进货量为450瓶时,若最高气温不低于25,则Y =6×450-4×450=900;若最高气温位于区间[20,25),则Y =6×300+2(450-300)-4×450=300;若最高气温低于20,则Y =6×200+2(450-200)-4×450=-100,所以,Y 的所有可能值为900,300,-100.Y 大于零当且仅当最高气温不低于20,由表格数据知,最高气温不低于20的频率为36+25+7+490=0.8. 因此Y 大于零的概率的估计值为0.8.19.(1)证明 如图,取AC 的中点O ,连接DO ,BO .因为AD =CD ,所以AC ⊥DO .又由于△ABC 是正三角形,所以AC ⊥BO .又DO ∩OB =O ,所以AC ⊥平面DOB ,故AC ⊥BD .(2)解 连接EO .由(1)及题设知∠ADC =90°,所以DO =AO .在Rt △AOB 中,BO 2+AO 2=AB 2.又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2,故∠DOB =90°.由题设知△AEC 为直角三角形,所以EO =12AC . 又△ABC 是正三角形,且AB =BD ,所以EO =12BD . 故E 为BD 的中点,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1∶1. 20.(1)解 不能出现AC ⊥BC 的情况.理由如下:设A (x 1,0),B (x 2,0),则x 1,x 2满足x 2+mx -2=0,所以x 1x 2=-2.又点C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为-1x 1·-1x 2=-12, 所以不能出现AC ⊥BC 的情况.(2)证明 BC 的中点坐标为⎝⎛⎭⎫x 22,12,可得BC 的中垂线方程为y -12=x 2⎝⎛⎭⎫x -x 22. 由(1)可得x 1+x 2=-m ,所以AB 的中垂线方程为x =-m 2. 联立⎩⎨⎧ x =-m 2,y -12=x 2⎝⎛⎭⎫x -x 22,又x 22+mx 2-2=0,可得⎩⎨⎧ x =-m 2,y =-12.所以过A ,B ,C 三点的圆的圆心坐标为⎝⎛⎭⎫-m 2,-12,半径r =m 2+92. 故圆在y 轴上截得的弦长为2 r 2-⎝⎛⎭⎫m 22=3,即过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.21.(1)解 f (x )的定义域为(0,+∞),f ′(x )=1x +2ax +2a +1=(x +1)(2ax +1)x. 若a ≥0,则当x ∈(0,+∞)时,f ′(x )>0,故f (x )在(0,+∞)上单调递增.若a <0,则当x ∈⎝⎛⎭⎫0,-12a 时,f ′(x )>0; 当x ∈⎝⎛⎭⎫-12a ,+∞时,f ′(x )<0. 故f (x )在⎝⎛⎭⎫0,-12a 上单调递增,在⎝⎛⎭⎫-12a ,+∞上单调递减. (2)证明 由(1)知,当a <0时,f (x )在x =-12a处取得最大值,最大值为f ⎝⎛⎭⎫-12a =ln ⎝⎛⎭⎫-12a -1-14a, 所以f (x )≤-34a -2等价于ln ⎝⎛⎭⎫-12a -1-14a ≤-34a-2,即ln ⎝⎛⎭⎫-12a +12a +1≤0.设g (x )=ln x -x +1,则g ′(x )=1x -1.当x ∈(0,1)时,g ′(x )>0;当x ∈(1,+∞)时,g ′(x )<0.所以g (x )在(0,1)上单调递增,在(1,+∞)上单调递减. 故当x =1时,g (x )取得最大值,最大值为g (1)=0.所以当x >0时,g (x )≤0.从而当a <0时,ln ⎝⎛⎭⎫-12a +12a +1≤0,即f (x )≤-34a -2.22.解 (1)消去参数t ,得l 1的普通方程l 1:y =k (x -2); 消去参数m ,得l 2的普通方程l 2:y =1k (x +2).设P (x ,y ),由题设得⎩⎪⎨⎪⎧ y =k (x -2),y =1k (x +2).消去k 得x 2-y 2=4(y ≠0).所以C 的普通方程为x 2-y 2=4(y ≠0).(2)C 的极坐标方程为ρ2(cos 2θ-sin 2θ)=4(0<θ<2π,θ≠π).联立⎩⎪⎨⎪⎧ρ2(cos 2θ-sin 2θ)=4,ρ(cos θ+sin θ)-2=0,得 cos θ-sin θ=2(cos θ+sin θ).故tan θ=-13,从而cos 2θ=910,sin 2θ=110.代入ρ2(cos 2θ-sin 2θ)=4,得ρ2=5,所以交点M 的极径为 5.23.解 (1)f (x )=⎩⎪⎨⎪⎧ -3,x <-1,2x -1,-1≤x ≤2,3,x >2.当x <-1时,f (x )≥1无解;当-1≤x ≤2时,由f (x )≥1,得2x -1≥1,解得1≤x ≤2; 当x >2时,由f (x )≥1,解得x >2.所以f (x )≥1的解集为{x |x ≥1}.(2)由f (x )≥x 2-x +m ,得 m ≤|x +1|-|x -2|-x 2+x . 而|x +1|-|x -2|-x 2+x ≤|x |+1+|x |-2-x 2+|x | =-⎝⎛⎭⎫|x |-322+54≤54,当x =32时,|x +1|-|x -2|-x 2+x =54.故m 的取值范围为⎝⎛⎦⎤-∞,54.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绝密★启用前2017年普通高等学校招生全国统一考试文科数学注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={1,2,3,4},B={2,4,6,8},则A ⋂B 中元素的个数为 A .1B .2C .3D .4【答案】B【解析】由题意可得:{}2,4A B = .本题选择B 选项. 2.复平面内表示复数z=i(–2+i)的点位于 A .第一象限B .第二象限C .第三象限D .第四象限【答案】B【解析】由题意:12z i =-- .本题选择B 选项.3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B .年接待游客量逐年增加C .各年的月接待游客量高峰期大致在7,8月D .各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 【答案】A【解析】由折线图,7月份后月接待游客量减少,A 错误;本题选择A 选项. 4.已知4sin cos 3αα-=,则sin 2α=A .79-B .29-C .29D .79【答案】A【解析】()2sin cos 17sin 22sin cos 19ααααα--===-- .本题选择A 选项.5.设x ,y 满足约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩,则z =x -y 的取值范围是 A .[–3,0]B .[–3,2]C .[0,2]D .[0,3]【答案】B【解析】绘制不等式组表示的可行域,结合目标函数的几何意义可得函数在点()0,3A 处取得最小值033z =-=- . 在点()2,0B 处取得最大值202z =-= .本题选择B 选项.6.函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为A .65B .1C .35D .15【答案】A【解析】由诱导公式可得:cos cos sin 6233x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦ , 则:()16sin sin sin 53353f x x x x πππ⎛⎫⎛⎫⎛⎫=+++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ , 函数的最大值为65.本题选择A 选项. 7.函数y =1+x +2sin xx 的部分图像大致为A .B .C .D .【答案】D【解析】当1x =时,()111sin12sin12f =++=+>,故排除A,C,当x →+∞时,1y x →+,故排除B,满足条件的只有D,故选D.8.执行下面的程序框图,学@科网为使输出S 的值小于91,则输入的正整数N 的最小值为A .5B .4C .3D .2【答案】D【解析】若2N =,第一次进入循环,12≤成立,100100,1010S M ==-=-,2i =2≤成立,第二次进入循环,此时101001090,110S M -=-==-=,3i =2≤不成立,所以输出9091S =<成立,所以输入的正整数N 的最小值是2,故选D.9.已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 A .πB .3π4 C .π2D .π4【答案】C【解析】如右图,画出圆柱的轴截面11,2AC AB ==,所以32r BC ==,那么圆柱的体积是2233124V r h πππ⎛⎫==⨯⨯= ⎪ ⎪⎝⎭,故选B.10.在正方体1111ABCD A BC D -中,E 为棱CD 的中点,则A .11A E DC ⊥B .1A E BD ⊥C .11A E BC ⊥D .1AE AC ⊥【答案】C11.已知椭圆C :22221x y a b+=,(a >b >0)的左、右顶点分别为A 1,A 2,且以线段A 1A 2为直径的圆与直线20bx ay ab -+=相切,则C 的离心率为A .63B .33C .23D .13【答案】A【解析】以线段12A A 为直径的圆是222x y a +=,直线20bx ay ab -+=与圆相切,所以圆心到直线的距离222abd a a b==+,整理为223a b =,即()22222323a a c a c =-⇒=,即2223c a = ,63c e a ==,故选A. 12.已知函数211()2()x x f x x x a e e --+=-++有唯一零点,则a =A .12-B .13C .12D .1【答案】C二、填空题:本题共4小题,每小题5分,共20分。
13.已知向量(2,3),(3,)a b m =-=,且a ⊥b ,则m = . 【答案】2【解析】由题意可得:2330,2m m -⨯+=∴= .14.双曲线22219x y a -=(a >0)的一条渐近线方程为35y x =,则a = . 【答案】5【解析】由双曲线的标准方程可得渐近线方程为:3y x a=±,结合题意可得:5a = . 15.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c 。
已知C =60°,b =6,c =3,则A =_________。
【答案】75°【解析】由题意:sin sin b cB C= ,即36sin 22sin 32b C Bc ⨯===,结合b c < 可得45B = ,则18075A B C =--=16.设函数10()20x x x f x x +≤⎧=⎨>⎩,,,,则满足1()()12f x f x +->的x 的取值范围是__________。
【答案】1(,)4-+∞【解析】由题意得: 当12x >时12221x x -+> 恒成立,即12x >;当102x <≤时12112xx +-+> 恒成立,即102x <≤;当0x ≤时1111124x x x ++-+>⇒>-,即104x -<≤;综上x 的取值范围是1(,)4-+∞ 第Ⅱ卷三、解答题:共70分。
解答应写出文字说明、证明过程或演算步骤。
第17~21题为必考题,每个试题考生都必须作答。
第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)设数列{}n a 满足123(21)2n a a n a n +++-= . (1) 求{}n a 的通项公式;(2)求数列21n a n ⎧⎫⎨⎬+⎩⎭的前n 项和.18.(12分)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:最高气温 [10,15) [15,20) [20,25) [25,30) [30,35) [35,40)天数216362574以最高气温位于各区间的频率代替最高气温位于该区间的概率。
(1)求六月份这种酸奶一天的需求量不超过300瓶的概率;(2)设六月份一天销售这种酸奶的利润为Y (单位:元),当六月份这种酸奶一天的进货量为450瓶时,写出Y 的所有可能值,并估计Y 大于零的概率.解:(1)需求量不超过300瓶,即最高气温不高于C 25,从表中可知有54天, ∴所求概率为539054==P . (2)Y 的可能值列表如下:最高气温[10,15) [15,20) [20,25) [25,30) [30,35) [35,40)Y 100- 100-300 900 900 900低于C20:100445022506200-=⨯-⨯+⨯=y ;)25,20[:300445021506300=⨯-⨯+⨯=y ;不低于C25:900)46(450=-⨯=y∴Y 大于0的概率为519016902=+=P . 19.(12分)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD . (1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比. 解:(1)证明:取AC 中点O ,连OB OD , ∵CD AD =,O 为AC 中点, ∴OD AC ⊥,又∵ABC ∆是等边三角形, ∴OB AC ⊥,又∵O OD OB = ,∴⊥AC 平面OBD ,⊂BD 平面OBD , ∴BD AC ⊥.20.(12分)在直角坐标系xOy 中,曲线y =x 2+mx –2与x 轴交于A ,B 两点,点C 的坐标为(0,1).当m 变化时,解答下列问题: (1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.解:(1)设()()12,0,,0A x B x ,则12,x x 是方程220x mx +-=的根,所以1212,2x x m x x +=-=-,则()()1212,1,112110AC BC x x x x ⋅=-⋅-=+=-+=-≠,所以不会能否出现AC ⊥BC 的情况。
(2)解法1:过A ,B ,C 三点的圆的圆心必在线段AB 垂直平分线上,设圆心()00,E x y ,则12022x x mx +==-,由EA EC =得()22221212100+122x x x x x y y +⎛⎫⎛⎫-+=+- ⎪ ⎪⎝⎭⎝⎭,化简得1201122x x y +==-,所以圆E 的方程为22221112222m m x y ⎛⎫⎛⎫⎛⎫⎛⎫+++=-+-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 令0x =得121,2y y ==-,所以过A ,B ,C 三点的圆在y 轴上截得的弦长为()123--=,所以所以过A ,B ,C 三点的圆在y 轴上截得的弦长为定值解法2:设过A ,B ,C 三点的圆与y 轴的另一个交点为D ,由122x x =-可知原点O 在圆内,由相交弦定理可得122OD OC OA OB x x ===, 又1OC =,所以2OD =,所以过A ,B ,C 三点的圆在y 轴上截得的弦长为3OC OD +=,为定值. 21.(12分)已知函数()f x =ln x +ax 2+(2a +1)x .(1)讨论()f x 的单调性;(2)当a ﹤0时,证明3()24f x a≤--. 解:(1))0()1)(12(1)12(2)('2>++=+++=x xx ax x x a ax x f当0≥a 时,0)('≥x f ,则)(x f 在),0(+∞单调递增当0<a 时,则)(x f 在)21,0(a -单调递增,在),21(+∞-a单调递减. (2)由(1)知,当0<a 时,)21()(max af x f -= 121)21ln()243()21(++-=+---aa a a f ,令t t y -+=1ln (021>-=a t ) 则011'=-=ty ,解得1=t∴y 在)1,0(单调递增,在),1(+∞单调递减∴0)1(max ==y y ,∴0≤y ,即)243()(max +-≤a x f ,∴243)(--≤ax f . (二)选考题:共10分。
