关于CDS的流水作业排序问题
流水线作业排序问题

流水线作业排序问题/productioncontrol/200908091604.html流水作业排序问题的基本特征是每个工件的加工路线都一致。
在流水生产线上制造不同的零件,遇到的就是流水作业排序问题。
我们说加工路线一致,是指工件的流向一致,并不要求每个工件必须经过加工路线上每台机器加工。
如果某些工件不经某些机器加工,则设相应的加工时间为零。
一般说来,对于流水作业排序问题,工件在不同机器上的加工顺序不尽一致。
但本节要讨论的是一种特殊情况,即所有工件在各台机器上的加工顺序都相同的情况。
这就是排列排序问题。
流水作业排列排序问题常被称作“同顺序”排序问题。
对于一般情形,排列排序问题的最优解不一定是相应的流水作业排序问题的最优解,但一般是比较好的解;对于仅有2台和3台机器的特殊情况,可以证明,排列排序问题下的最优解一定是相应流水作业排序问题的最优解。
这里只讨论排列排序问题。
但对于2台机器的排序问题,实际上不限于排列排序问题。
一、最长流程时间Fmax的计算这里所讨论的是n/m/P /Fmax,问题,其中n为工件数,m为机器数,P表示流水线作业排列排序问题,Fmax为目标函数。
目标函数是使最长流程时间最短,最长流程时间又称作加工周期,它是从第一个工件在第一台机器开始加工时算起,到最后一个工件在最后一台机器上完成加工时为止所经过的时间。
由于假设所有工件的到达时间都为零(ri=0,i= 1,2,…,n),所以Fmax等于排在末位加工的工件在车间的停留时间,也等于一批工件的最长完工时间Cmax。
设n个工件的加工顺序为S=(S1,S2,S3,…,Sn),其中Si为第i位加工的工件的代号。
以表示工件Si在机器M k上的完工时间, 表示工件Si在Mk上的加工时间,k= 1,2,…,m;i=1,2,…,n,则可按以下公式计算:在熟悉以上计算公式之后,可直接在加工时间矩阵上从左向右计算完工时间。
下面以一例说明。
例9.4 有一个6/4/p/F max问题,其加工时间如表9—6所示。
生产作业排序

)
华中科技大学管理学院
一、基本概念
4、排序问题的假设条件
• 一个工件不能同时在几台不同的机器上加工。 • 工件在加工过程中采取平行移动方式。 • 不允许中断。 • 每道工序只在一台机器上完成。 • 每台机器同时只能加工一个工件。 • 工件数、机器数和加工时间已知,加工时间与加工
顺序无关。
)
华中科技大学管理学院
一个实例: D=
2,1,3 2,2,1 2,3,2
241
T= 345
i {Ot} Tk
T’k
T*
M*
Oj
1 1,1,1 0
2
0
M1 1,1,1
2,1,3 0
3
0
M3
2 1,2,3 2
6
2,1,3 0
3
0
M3 2,1,3
3 1,2,3
3
7
3
M3 1,2,3
2,2,1 3
7
3
M1
4 1,3,2 7 2,2,1 3
四、一般n/m/P/ Fmax问题的 启发式算法
2、关键工件法:
• 计算Pi= Pij ,找出Pi最长的工件,将之作为 关键工件C。
• 对其余工件,若Pi1≤Pim ,则按Pi1由小到大排 成序列SA。若Pi1> Pim ,则按Pim由大到小排成 序列SB。
• 顺序(SA,C,SB)即为近优解。
)
四、一般n/m/P/ Fmax问题的 启发式算法
1、Palmer法
m
• 计算工件斜度指标i : i [k (m 1) / 2]pik
m : 机器数
k 1
pik :工件i在机器k上的加工时间。 i=1,2, ,n
生产与运作管理的计算题

-、流水作业排序1. 最长流程时间的计算例:有一个6/4/F/Fmax 问题,其加工时间如下表所示,当按顺序 加工 S=(6, 1, 5, 2, 4, 3) 时,求Fmax工件代号i 14 6 35 2 P 订 4 5 3 4 8 5 P 「23 9 1 3 7 5 PQ7 6 8 2 5 g563924解:列出加工时间矩阵根 据 公式Gsi 二max{Gk-i )si , C KSM }+ P sik,计算各行加丄时间,最后得出结果 Fmax=CmsnFmax=572•两台机器排序冋题的最优算法(Johnson 算法)例:求下表所示的6/2/F/Fmax 的最优解将工件2排在第1位 2将工件 将工件 将工件将工件将工件 3排在第 5排在第 6排在第 4排在第 最优加6位2位 3位5位4位2 56 1 4 S=(2, 5, 6, 1,4,33由上表可计算出,Fmax =283.—般n/m/F/Fmax问题的最优算法(一)Palmar算法(入i二刀[k-(m+l)/2]P ik k二1, 2,…,m按入i不增的顺序排列」】件)例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用Palmar求解.解:入i二刀[k-(3+l)/2]P ik , k=l,2 , 3入i二-Pil+ Pi3于是,入1=-PU+ P13 =-1+4=3入2二-P21+ P23 =2+5二3入3二-P31+ P33 =-6+8=2入4二-P41+ P43 =-3+2二T按入i不增的顺序排列工件,得到加工顺序(1, 2, 3, 4)和(2, 1, 3, 4 ),经计算,二者都是最优顺序,Fmax=28(二)关键工件法例:有一个4/3/F/Fmax问题,其加工时间如下表所示,用关键工件法求解.3■ ■Pa Pit 24解:由上表可知,力口 u工时间最长的是3号工件,Pil<=Pi3的工件为1和2,按Pil不减的顺序排成Sa=(l,2),Pil>Pi3 的工件为4号工件,Sb= (4),这样得到加工顺序为(1,2, 3,4 )。
作业排序问题

2)采用预订系统
对特定期间的服务需求做出较准确的估计
3)采用差异定价措施
5 调整服务能力的策略
1)进行有效的人员班次排序 2)利用临时工或兼职人员 3)招聘和培养多技能的员工
为何“集中使用”可以提高服务质量?
独立的系统
在此等待
“集中使用”系统
在此等待
减少等待时间的办法
减少平均服务时间 减少服务时间的可变性 增加服务人员 减少平均到达人数 通过顾客预约等办法来减少到达的可变性 集中使用服务资源 更好地计划和调度
i M1 M2
1 8 3
2 4 2
3 7 6
4 1 9
5 3 2
6 10 5
CWU-HRM
人力系
多工件多设备的排序问题启发算法
关键工件法
1983年提出 1.
2.
3.
计算每个工件的总加工时间Pi,找出加工时间最长 的工件C为关键工件 余下的工件,如果 Pi1 Pim 则按照Pi1 不减的顺 序排成序列S1,如果 Pi1 >Pim 则按照Pim 不增的顺 序排成序列S2, 序列( S1 ,C, S2,)为所求排序
2) 最高优先权法则(Highest Priority Principle) 为减少等待顾客离队可能,应让顾客知道预期等待 火警、救护车 时间的信息,并使顾客得到定期更新的信息。
4 调整顾客到达率的措施
1)利用预约系统
控制顾客到达时间 实现最高程度的服务能力利用率 减少顾客等待的时间 提高服务水平
CWU-HRM
例
人力系
I Pi1 Pi2 Pi3 Pi
1 1 8 4 13
2 2 4 5 11
3 6 2 8 16
作业排序
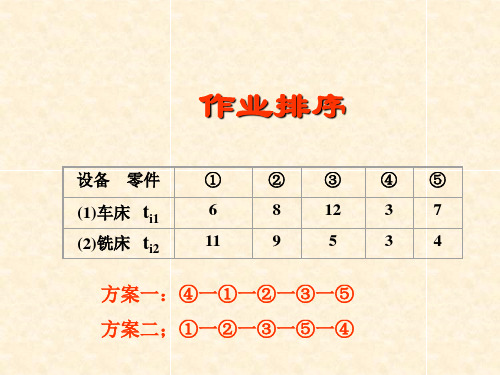
②③④ 8 6 12 156 10 5 7
②③④
minti1≥ maxti2
G
18 9 11 18
可得右下表:
H
7 11 10 13
按约翰逊法: 可得最优解为:②一④一③ 一①
设备零件 ① A 车床 15 B 铣床 3 C 磨床 4
②③④ 8 6 12 156 10 5 7
计算加工周期:
最优排序为:
Fi2 计算的根据:一个零件在设备(2)上加工必须等到该零件在设 备(1)上加工完并且设备(2)加工完前一个零件之后才能开始
故:从表中可以看出,最大流程时间( 零件的总加工周期)为40
3 三台设备流水型排序问题及解法
1)问题:n种零件在三台 设备零件 ①
设备上加工,其工艺顺
序均相同。
A 车床 15
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
加工顺序
12
3
4
5
6
零件号
③⑥①④②
⑤
作业时间 2
3
4
5
8
9
流程时间 2
5
9
14 22
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
答:最大流程时间:31 最大等待时间:22 平均流程时间=(2+5+9+14+22+31)/6=13.83 平均等待时间=(0+2+5+9+1+14+22)/6=8.67 最大交货延期:8 总交货延期:( 0+0+0+8+0+0)=8
生产与运作管理试卷及答案五

《生产与运作管理》试卷五一、填空题(本大题共7小题,每空2分,共计28分)1.用Johnson算法求下列6/2/F/F max问题的最优排序为,对应的F max。
i J1J2J3J4J5J6P i15 1 8 5 3 4Pi27 2 2 4 7 62.某装配线每天实际工作时间为480分钟,日产量为40台产品。
该装配线共有9道装配作业,各作业之间的关系及标准时间如下所示:那么它的节拍、最小工作地数、平衡的评价指标分别为、和。
作业 A B C D E F G H I紧前作业— A B B A C F DE GH时间(分)7 4 3 8 5 9 8 11 33.某产品流水生产,计划日产量为150件,两班生产,每班规定有12分钟停歇时间,计划废品率为5%,那么该产品生产的节拍的计算公式应为。
4.已知每件A产品需2件C部件,第6周C部件的库存量为110件,如A产品在第7周的计划订单投入量为190件,则C部件的净需求量为。
5.某超市的某种食用油平均日需求量为1000瓶,并且食用油的需求情况服从标准差为20瓶/天的正态分布,如果提前期是固定常数5天,如果该超市确定的客户服务水平不低于95%,请结合所提供的客户服务水平与安全系数对应关系的常用数据(见下表),计算出该食用油的订货点是;安全库存是。
服务水平0.9998 0.99 0.98 0.95 0.90 0.80 0.70安全系数 3.5 2.33 2.05 1.65 1.29 0.84 0.556.某装配车间零件需求率为490个/月,零件由厂内生产,生产率为900个/月,生产准备费为100元/每批,存储费为0.5元/个/月。
则经济生产批量、每月平均成本、最佳循环时间和最大库存水平分别为、和、。
7.n/3/P/C max表示。
二、简答题(本大题共4小题,每小题5分,共计20分)1.简述MRP的运算逻辑,并说明如何与OPT相结合。
2.按照对象专业化原则建立生产单位的优缺点是什么?3.简述OPT的三个财务指标和三个作业指标是什么?OPT的九原则是什么?4.简述网络计划方法的优点。
流水作业排列排序问题

C3(2)
P23
Fmax= Cm(sn)
GWM-PPT V2010.1
汇报人:杨猛
2、最长流程时间Fmax的计算
例题:6/4/p/ Fmax,其加工时间如表1所示
J1(精灵 精灵) 精灵 M1(冲压) M2(焊装) M3(涂装) M4(总装) M4( ) 4 4 5 4 J2(炫丽 炫丽) 炫丽 2 5 8 2 J3(酷熊 酷熊) 酷熊 3 6 7 4 J4(凌傲 凌傲) 凌傲 1 7 5 3 4 4 5 3
序列A为(2,5,6,1),序列B为(4,3),构 成最优顺序为(2,5,6,1,4,3)
J2 M1 M2
GWM-PPT V2010.1
J5 3 7
J6 4 4
J1 5 7
汇报人:杨猛
J4 5 4
J3 8 2
1 2
3、n/m/p/ Fmax问题的启发式算法
J1 M1 M2 M3 M4 3 7 4 5 J2 12 4 8 7 J3 9 6 7 11 J4 4 8 1 5 J5 5 5 3 9 J6 6 10 12 2
汇报人:杨猛
J4 113 727 535 338
J3 316 633 742 446
22 57 512 113
三、约翰逊算法及其启发式算法
GWM-PPT V2010.1
汇报人:杨猛
1、n/2/P/Fmax 约翰逊算法
◆Johnson算法:一短、二看、三排序
J3 J1 M1 M2 2 8 7 3 J2 5 4 J1 J3 8 2 3 7
表1
J5(腾翼) J6(哈弗) 腾翼) (哈弗) 腾翼 2 5 5 1
CDS启发式算法及Matlab程序
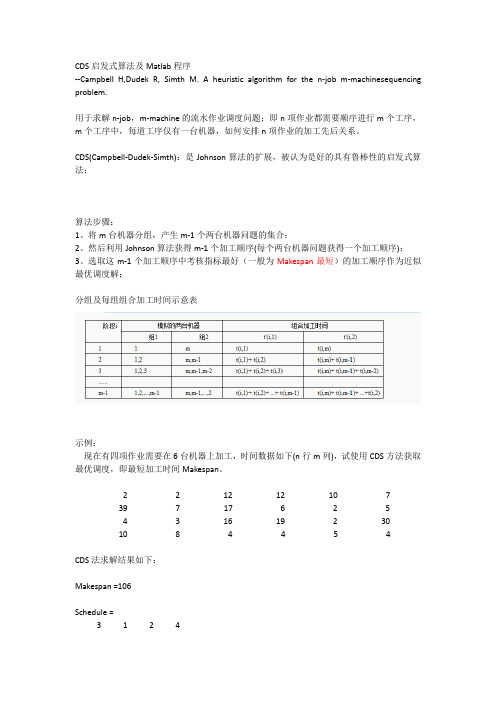
CDS启发式算法及Matlab程序--Campbell H,Dudek R, Simth M. A heuristic algorithm for the n-job m-machinesequencing problem.用于求解n-job,m-machine的流水作业调度问题;即n项作业都需要顺序进行m个工序,m个工序中,每道工序仅有一台机器,如何安排n项作业的加工先后关系。
CDS(Campbell-Dudek-Simth):是Johnson算法的扩展,被认为是好的具有鲁棒性的启发式算法;算法步骤:1、将m台机器分组,产生m-1个两台机器问题的集合;2、然后利用Johnson算法获得m-1个加工顺序(每个两台机器问题获得一个加工顺序);3、选取这m-1个加工顺序中考核指标最好(一般为Makespan最短)的加工顺序作为近似最优调度解;分组及每组组合加工时间示意表示例:现在有四项作业需要在6台机器上加工,时间数据如下(n行m列),试使用CDS方法获取最优调度,即最短加工时间Makespan。
2 2 12 12 10 739 7 17 6 2 54 3 16 19 2 3010 8 4 4 5 4CDS法求解结果如下:Makespan =106Schedule =3 1 2 43 1 2 43 1 2 43 1 2 4可以看出,分组后的5(m-1)组两机器问题中,通过Johnson法获取的最优调度中,有4组获得了最优调度: 3 1 2 4也验证了CDS法具有较高的Matlab程序--CDS.mfunction [Makespan,Schedule]=CDS(PT)[n,m]=size(PT);if n<=1error('The job qty must large than 2')endPT=double(PT);%Create new 2-stage-machine timeNewPT(1:n,1:2,1:m-1)=0.0;for i=1:m-1for j=1:iNewPT(:,1,i)=NewPT(:,1,i)+PT(:,j);NewPT(:,2,i)=NewPT(:,2,i)+PT(:,m-j+1);endend%Calculate the m-1 group 2-machine problem using Johnson Rulefor i=1:m-1[MidMakespan(i),MidSchedule(i,:)]=Johnson(NewPT(:,:,i)');end%Calculate the Makespan of the m-1 MidSchedulefor i=1:m-1StartTime(1:m,1:n)=0;StartTime(1,MidSchedule(i,1))=0;for j=2:nStartTime(1,MidSchedule(i,j))=StartTime(1,MidSchedule(i,j-1))+PT(MidSchedule(i,j-1),1);endfor k=2:mStartTime(k,MidSchedule(i,1))=StartTime(k-1,MidSchedule(i,1))+PT(MidSchedule(i,1),k-1);for j=2:nStartTime(k,MidSchedule(i,j))=max(StartTime(k,MidSchedule(i,j-1))+PT(MidSchedule(i,j-1),k),...StartTime(k-1,MidSchedule(i,j))+PT(MidSchedule(i,j),k-1));endendMMidMakespan(i)=StartTime(m,MidSchedule(i,n))+PT(MidSchedule(i,n),m); end% Sort the Makespan and obtain the optimal Schedule[Best,BestIndex]=sort(MMidMakespan);OptNum=1;Makespan=MMidMakespan(BestIndex(1));Schedule=MidSchedule(BestIndex(1),:);%Statistic the total optimal shedulesfor i=2:m-1if MMidMakespan(BestIndex(i))==MMidMakespan(BestIndex(1))OptNum=OptNum+1;Schedule(OptNum,:)=MidSchedule(BestIndex(i),:);endend。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用(palmer )法,关键工件法和CDS 法求4/4/P/Fmax 问题的最优解。
一,用palmer 法
i λ=m
ik k=1
k m+1/2p -∑
【()】=4
ik k=1
k +1/2p -∑【(4)】=-1.5i1p -0.5 i2p +0.5i3p +1.5i4p
1λ=7 2λ=-11 3λ= -4.5 4λ=5.5 1λ> 4λ>3λ>2λ
按i λ不增顺序排最优加工顺序为(1,4,3,2)则有如下
如p302计算得Fmax=34 二,用关键工件法
观察Pi 知 时间最长的是2号工件 (24>19>17>16) 即 C=2
对余下的工件1,3,4分析知,若Pi1<=Pi4则按Pi1不减的顺序排列Sa=1,4: 若Pi1>Pi4则按Pi4不增的顺序排列则有 Sb=3
则顺序(Sa ,C ,Sb )=(1,4,2,3)即为本例最优顺序 则有如下:
则如P302计算可得Fmax=33 三,用CDS 法
易知m=4,L=1,2……m-1知L=1,2,3则有
求ik
k=1
L
P ∑和4
ik
k=5L
P -∑
,L=1,2,3 则有
分别将L=1,2,3代入ik
k=1
L
P ∑得:
再分别将L=1,2,3代入4
ik
k=5L P -∑
得:
L=1时,所有第一列(i a )不大于第二列(
i
b )即
i a <=
i
b 的工件按
i
a 不减的顺序排列得 A= 1,4 将所有
i
a >i
b 的工件按i b 值不增的顺序排得
B=3,2 故L=1时最优排序为 AB=(1,4,3,2) 解得Fmax=34
L=2时,亦有上知:L=2时最优排序为 (1,4,2,3) 解得 Fmax=33 L=3时,亦有上知:L=3时最优排序为 (1,4,2,3) 解得 Fmax=33
综合上述情况知最佳排序为(1,4,2,3) 且 Fmax=33。
