数学人教版八年级上册全等三角形的判定复习课精品PPT课件
合集下载
人教版 八年级数学上册第十二章:全等三角形复习课件(共15张PPT)

O
\ PD = PE
用途:证线段相等
E
角平分线性质的逆定理 到一个角的两边 的距离相等的点, 在这个角的平分线上。
∵ PD OA PE OB
PD = PE
\ OP 是 AOB 的平分线
用途:判定一条射线是角平分线
A C
P B
一、已知:如图∠B=∠DEF,BC=EF,补充条件 求证:ΔABC≌ ΔDEF (1)若要以“SAS”为依据,还缺条件 _A_B=_D_E _; (2) 若要以“ASA”为依据,还缺条件∠_A_CB_= _∠D;FE
E
O
B
C
6. 已知:BD⊥AM于点D,CE⊥AN于点E, BD、CE交于点F,CF=BF, 求证:点F在∠A的平分线上。
CM D
F
A
N EB
7、如图所示,DC=EC,AB∥CD,∠D=90°, AE⊥BC于E,求证:∠ACB=∠BAC.
8. 如图,四边形ABCD中,AC平分∠BAC, CE⊥AB于E,AD+AB=2AE, 求证:∠B与∠ADC互补。
2.如图(2),点D在AB上,点E在AC上, B
D
CD与BE相交于点O,且AD=AE,AB=AC.若 O
A
∠B=20°,CD=5cm,则 ∠C= 20°,BE= 5.说cm说理由.
E C 图(2)
3.如图(3),AC与BD相交于o,若
A
D
OB=OD,∠A=∠C,若AB=3cm3c,m 则
CD=
友情. 说提说示理:由公. 共边,公共角,B
(3) 若要以“AAS”为依据,还缺条件∠_A_=_∠__D ;
AD
B E CF
(4)若∠B=∠DEF=90°BC=EF,要以“HL” 为依据, 还缺条件_A_C=_D_F _
三角形全等的判定+课件 2024—2025学年人教版数学八年级上册

12.2三角形全等的判定
自主学习
小莲家的衣柜上镶有两块全等三角形玻璃 装饰物,其中一块被打碎了,妈妈让小明到 玻璃店配一块回来,请你说说小莲该怎么 办?
三角形全等的 判定方法
合作探究 怎样判定三角形全等呢?
①三边对应相等; ②三个角对应相等; ③两角一边; ④两边一角······
归纳总结 全等三角形的判定方法(1)
三边分别相等的两个三角形全等 简写成“边边边”或“SSS”
三角形三条边的长度确定 了,这个三角形的形状、 大小也就确定了。这就是 三角形的稳定性。
小莲家的衣柜玻璃 能解决了吗?
如图所示,用数学语言表示为:
A
在△ABC和△A'B'C'中,
AB=A'B' BC=B'C' AC=A'C'
B
C
A'
∴ △ABC≌△A'B'C'(SSS) B'
C 证明: 连接AB
在△ACB 和 △ADB中
AC = AD
A
B
BC = BD
AB = AB (公共边)
∴△ACB≌△ADB (SSS) ∴∠C=∠D (全等三角形的对应角相等) D
用一用 1.工人师傅常用角尺平分一个任意角. 做法如下:如图, AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺, 使角尺两边相同的刻度分别与M,N重合. 过角尺顶点C的射线 OC便是 AOB的平分线.为什么?
AB=CD (已知)
A
B
AD=BC (已知)
BD=DB (公共边)
∴ ABD ≌ CDB (SSS)
∴ ∠A= ∠C ( 全等三角形的对应角相等 )
自主学习
小莲家的衣柜上镶有两块全等三角形玻璃 装饰物,其中一块被打碎了,妈妈让小明到 玻璃店配一块回来,请你说说小莲该怎么 办?
三角形全等的 判定方法
合作探究 怎样判定三角形全等呢?
①三边对应相等; ②三个角对应相等; ③两角一边; ④两边一角······
归纳总结 全等三角形的判定方法(1)
三边分别相等的两个三角形全等 简写成“边边边”或“SSS”
三角形三条边的长度确定 了,这个三角形的形状、 大小也就确定了。这就是 三角形的稳定性。
小莲家的衣柜玻璃 能解决了吗?
如图所示,用数学语言表示为:
A
在△ABC和△A'B'C'中,
AB=A'B' BC=B'C' AC=A'C'
B
C
A'
∴ △ABC≌△A'B'C'(SSS) B'
C 证明: 连接AB
在△ACB 和 △ADB中
AC = AD
A
B
BC = BD
AB = AB (公共边)
∴△ACB≌△ADB (SSS) ∴∠C=∠D (全等三角形的对应角相等) D
用一用 1.工人师傅常用角尺平分一个任意角. 做法如下:如图, AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺, 使角尺两边相同的刻度分别与M,N重合. 过角尺顶点C的射线 OC便是 AOB的平分线.为什么?
AB=CD (已知)
A
B
AD=BC (已知)
BD=DB (公共边)
∴ ABD ≌ CDB (SSS)
∴ ∠A= ∠C ( 全等三角形的对应角相等 )
人教版八年级上册数学《三角形全等的判定》全等三角形研讨说课复习课件

A
A . 1个
B. 2个
C. 3个
D. 4个
D
O
B
C
课堂检测
能力提升题
1. 已知:如图,AB=AE,AC=AD,BD=CE,
求证:△ABC ≌△AED.
证明:∵BD=CE,
=×
∴BD-CD=CE-CD .
∴BC=ED .
在△ABC和△ADE中,
AC=AD(已知),
AB=AE(已知),
BC=ED(已证),
30◦
4cm
30◦
4cm
结论:一条边一个角对应相等的两个三角形不一定全等.
探究新知
③如果三角形的两个内角分别是30°,45°时
30◦
45◦
30◦
45◦
结论:两个角对应相等的两个三角形不一定全等.
根据三角形的内角和为180°,则第三角一定确定,
所以当三个内角对应相等时,两个三角形不一定全等.
探究新知
AB=AC,
AD=AE,
BD=CE,
∴ △ ABD≌ △ ACE(SSS),
∴∠BAD=∠CAE.
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE.
巩固练习
已知:如图,AB=AD,BC=DC,
求证:△ABC≌△ADC,AC是∠BAD的角平分线.
证明:在△ABC和△ADC中
AB=AD, (已 知 )
A′
探究新知
用尺规作一个角等于已知角
已知:∠AOB.求作:∠A′O′B′=∠AOB.
作法:
(1)以点O 为圆心,任意长为半径画弧,分别交OA,
OB 于点C,D;
(2)画一条射线O′A′,以点O′为圆心,OC 长为半
人教版八年级数学上册教学:12-2 全等三角形的判定(SAS) (共11张)PPT课件

三角形全等的判定定理(SAS)
当两个三角形满足六个条件中的三个时,有四种 情况:
(1) 三个角 不能! (2) 三条边 SSS (3) 两边一角 ?
(4) 两角一边
继续探讨三角形全等的条件: 两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
A
B
C
图一
图2-39
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (3)△ABC和△A’B’C’ 的位置关系如图2-40.
图2-40
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ .
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (1)△ABC和△A’B’C’ 的位置关系如图2-38.
A’
B’
C’
图2-38
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (2)△ABC和△A’B’C’ 的位置关系如图2-39.
Байду номын сангаас证明:在△ACO和△BDO中, AO=BO, ∠AOC=∠BOD(对顶角相等), CO=DO, ∴△ACO≌△BDO(SAS).
图2-42
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
11
结束语
当你尽了自己的最大努力时,失 败也是伟大的,所以不要放弃,
当两个三角形满足六个条件中的三个时,有四种 情况:
(1) 三个角 不能! (2) 三条边 SSS (3) 两边一角 ?
(4) 两角一边
继续探讨三角形全等的条件: 两边一角
思考:已知一个三角形的两条边和一个角,那么这两条边
与这一个角的位置上有几种可能性呢?
A
A
B
C
图一
图2-39
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (3)△ABC和△A’B’C’ 的位置关系如图2-40.
图2-40
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ .
(4)△ABC和△A’B’C’ 的位置关系如图2-41.
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (1)△ABC和△A’B’C’ 的位置关系如图2-38.
A’
B’
C’
图2-38
探究
在△ABC和△A’B’C’ 中,∠ABC=∠ A’B’C’ ,AB=A’B’, BC=B’C’ . (2)△ABC和△A’B’C’ 的位置关系如图2-39.
Байду номын сангаас证明:在△ACO和△BDO中, AO=BO, ∠AOC=∠BOD(对顶角相等), CO=DO, ∴△ACO≌△BDO(SAS).
图2-42
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
11
结束语
当你尽了自己的最大努力时,失 败也是伟大的,所以不要放弃,
人教版初中八年级上册数学-期末复习 第12章全等三角形 课件(共48张PPT)
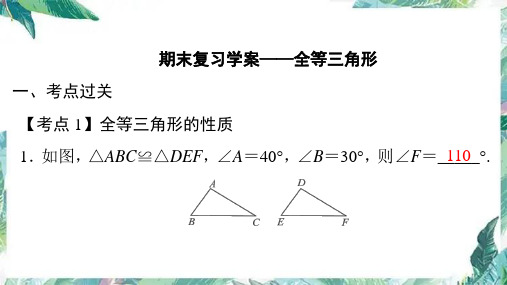
的依据是_H__L_.
第3题
4.如图,AO=BO,下列条件不能判定△AOD≌△BOC 的是( B )
A.OC=OD C. ∠A=∠B
第4题 B.AD=BC D.∠C=∠D
【考点 3】角平分线的性质和判定 5.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,AB=6,CD
=2,则点 D 到 AB 的距离是_2_,△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A=∠D, 从而 AB∥DE.
10.如图,在△ABC 和△DEF 中,下面有四个条件,请你在其中 选 3 个作为题设,余下的 1 个作为结论,写一个真命题,并加 以证明. ① AB=DE;②AC=DF;③∠ABC=∠DEF;④BE =CF.
题设:①③④;结论:② 证明提示:BC=BE+EC=CF+EC=EF. 用 SAS 证明△ABC≌△DEF,从而 AC=DF.
证明:(1)如图,连接 AF, ∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE, ∵∠ACB=∠AEF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF, ∴CF=EF.∴BF+EF=BF+CF=BC, ∴BF+EF=DE;
(2)如图,DE=BF-EF,理由是: 连接 AF,∵Rt△ABC≌Rt△ADE, ∴AC=AE,BC=DE, ∵∠E=∠ACF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF,∴CF=EF, ∴DE=BC=BF-FC=BF-EF,即 DE=BF-EF.
24.已知 Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°. (1)将这两个三角形按图①方式摆放,使点 E 落在 AB 上,DE 的延长线交 BC 于点 F.求证:BE+EF=DE; (2)改变△ADE 的位置,使 DE 交 BC 的延长线于点 F(如图②), 写出此时 BF、EF 与 DE 之间的等量关系,并说明理由.
第3题
4.如图,AO=BO,下列条件不能判定△AOD≌△BOC 的是( B )
A.OC=OD C. ∠A=∠B
第4题 B.AD=BC D.∠C=∠D
【考点 3】角平分线的性质和判定 5.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,AB=6,CD
=2,则点 D 到 AB 的距离是_2_,△ABD 的面积是_6_.
用 HL 证 Rt△ABC≌Rt△DEC. 得 ∠A=∠D, 从而 AB∥DE.
10.如图,在△ABC 和△DEF 中,下面有四个条件,请你在其中 选 3 个作为题设,余下的 1 个作为结论,写一个真命题,并加 以证明. ① AB=DE;②AC=DF;③∠ABC=∠DEF;④BE =CF.
题设:①③④;结论:② 证明提示:BC=BE+EC=CF+EC=EF. 用 SAS 证明△ABC≌△DEF,从而 AC=DF.
证明:(1)如图,连接 AF, ∵Rt△ABC≌Rt△ADE,∴AC=AE,BC=DE, ∵∠ACB=∠AEF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF, ∴CF=EF.∴BF+EF=BF+CF=BC, ∴BF+EF=DE;
(2)如图,DE=BF-EF,理由是: 连接 AF,∵Rt△ABC≌Rt△ADE, ∴AC=AE,BC=DE, ∵∠E=∠ACF=90°,AF=AF, ∴Rt△ACF≌Rt△AEF,∴CF=EF, ∴DE=BC=BF-FC=BF-EF,即 DE=BF-EF.
24.已知 Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°. (1)将这两个三角形按图①方式摆放,使点 E 落在 AB 上,DE 的延长线交 BC 于点 F.求证:BE+EF=DE; (2)改变△ADE 的位置,使 DE 交 BC 的延长线于点 F(如图②), 写出此时 BF、EF 与 DE 之间的等量关系,并说明理由.
人教版八上数学《1三角形全等的判定》课件

三角形全等的判定(1)
复习
1. 三角形全等的性质是什么?
Zx xk
2. 如果两个三角形满足三条边对应相等,三个角对 应相等,那么,这两个三角形全等吗?
3. 如果两个三角形满足上述六个条件中的一部分, 是否也能保证两个三角形全等呢?
探究1
先任意画出一个△ABC,再画 一个△A/B/C/,使△ABC与△A/B/C/ 满足上述六个条件中的一个或两个.
你画出的△A/B/C/与△ABC一定BC,再画 一个△A/B/C/,使A/B/=AB, B/C/ =BC, A/C/ =AC. 把画好的Zx △xk A/B/C/剪下,放 到△ABC上,它们全等吗?
画法
已知:任意 △ ABC,画一个△ A’B’C’,使A’B’ =AB,A’C’=AC,B’C’=BC
练习
已知:点A、E、F、C在同一条直线上, AD=CB,DF=BE,AE=CF.证明△ADF≌△CBE 还应有什么条件?怎样才能得到这个条件?
A E
D
F
B
C
练习
如图,已知点B、E、C、F在同一条直线上,
AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
A
D
证明:∵BE=CF(已知)
∴ BE+EC=CF+EC
A 画法:1. 画线段B’C’=BC.
2. 分别以B’、C’为圆心,
B
A’ C
BA、CA为半径画弧,两弧
相交于点A’.
3. 连接A’B’、A’C’.
B问’ :通过实验可以发C’现什形△么. A事’实B?’C’就是所要画的三角
规律
探究2反映的规律是: 三条边对应相等的两个三角形全等(简写成“边
边边”或“SSS”)
复习
1. 三角形全等的性质是什么?
Zx xk
2. 如果两个三角形满足三条边对应相等,三个角对 应相等,那么,这两个三角形全等吗?
3. 如果两个三角形满足上述六个条件中的一部分, 是否也能保证两个三角形全等呢?
探究1
先任意画出一个△ABC,再画 一个△A/B/C/,使△ABC与△A/B/C/ 满足上述六个条件中的一个或两个.
你画出的△A/B/C/与△ABC一定BC,再画 一个△A/B/C/,使A/B/=AB, B/C/ =BC, A/C/ =AC. 把画好的Zx △xk A/B/C/剪下,放 到△ABC上,它们全等吗?
画法
已知:任意 △ ABC,画一个△ A’B’C’,使A’B’ =AB,A’C’=AC,B’C’=BC
练习
已知:点A、E、F、C在同一条直线上, AD=CB,DF=BE,AE=CF.证明△ADF≌△CBE 还应有什么条件?怎样才能得到这个条件?
A E
D
F
B
C
练习
如图,已知点B、E、C、F在同一条直线上,
AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
A
D
证明:∵BE=CF(已知)
∴ BE+EC=CF+EC
A 画法:1. 画线段B’C’=BC.
2. 分别以B’、C’为圆心,
B
A’ C
BA、CA为半径画弧,两弧
相交于点A’.
3. 连接A’B’、A’C’.
B问’ :通过实验可以发C’现什形△么. A事’实B?’C’就是所要画的三角
规律
探究2反映的规律是: 三条边对应相等的两个三角形全等(简写成“边
边边”或“SSS”)
最新人教版初中数学八年级上册《12.2 三角形全等的判定(第2课时)》精品教学课件

∴ ∠A=∠D(全等三角形的对应角相等).
A D C
E
探究新知
素养考点 2 利用全等三角形测距离
例2 如图,有一池塘,要测池塘两端A、B的距离,可先在平
地上取一个可以直接到达A和B的点C,连接AC并延长到点D,
使CD=CA,连接BC并延长到点E,使CE=CB.连接DE,
那么量出DE的长就是A、B的距离,为什么?
课堂检测
能力提升题
已知:如图,AB=AC, BD=CD,E为AD上一点.
求证: BE=CE.
证明: 在△ABD和△ACD中,
A
AB=AC (已知),
BD=CD (已知),
AD=AD(公共边), ∴△ABD≌△ACD(SSS).
E
∴ ∠BAD=∠CAD,
B DC
在△ABE和△ACE中,
AB=AC (已知),
证明:在△ABC 和△DEC 中,
AC = DC(已知),
A
B
∠ACB =∠DCE (对顶角相等), CB=EC(已知),
·C
∴△ABC ≌△DEC(SAS).
E
D
∴AB =DE .(全等三角形的对应边相等)
巩固练习
如图,两车从南北方向的路段AB的A端出发,分别向东、
向西行进相同的距离,到达C,D两地.此时C,D到B的距
三边对应相等的两个三角形全等(可以简写为“边边边”或
“SSS”).
2.符号语言表达:
A
在△ABC和△ DEF中
AB=DE, BC=EF, CA=FD,
B
D
C
∴ △ABC ≌△ DEF.(SSS)
E
F
探究新知
【思考】除了SSS外,还有其他情况吗? 当两个三角形满足六个条件中的3个时,有四种情况:
人教版八年级数学上册第十二章全等三角形复习课(共25张PPT)

【思维模式】在证明线段相等或角相等的题目中,通常通过证明 这两条线段或角所在的三角形全等来得到线段相等或角相等,若这 两条线段或角在不可能全等的两个三角形中,还可寻求题目中的已 知条件或图形中的隐含条件通过等量代换来达到证明全等的目的.
例3: 第一节数学课后,老师布置了一道课后练习:如图,已知在Rt△ABC中 ,AB=BC,∠ABC=90°,BO⊥AC于点O.点P,D分别在AO和BC上,PB= PD,DE⊥AC于点E.
O,请写出图中一组相等的线段______________.
5. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
_____.
20
AC=BD或BC=AD OD=OC或OA=OB.
考点3 等腰、等边三角形与全等的综合(考查频率:★★★☆☆) 命题方向:(1)等腰直角三角形与全等三角形的综合问题; (2)等边三角形与全等的综合问题.
D.1cm
例1:如图,AD是等腰直角三角形ABC的底角的平分线,∠C= 90°,求证:AB=AC+CD.
【思维模式】(1)不管是过点D作AB的垂线也 好,还是延长AC也好,实际上都是利用了角平分 线的轴对称性构造的全等三角形,得出一些相等 的线段或相等的角解决问题;(2)人教课本书 后习题给出了角平分线的另一条性质,即图中 CD∶BD=AC∶AB,这一结论在解决很多面积有 关问题的时候,也能带来方便.
6. 如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE =90°,D为AB边上一点.求证:BD=AE.
考点4 角平分线的性质与判定(考查频率:★★★☆☆) 命题方向:(1)直接考查角平分线基本图形能得到的一些基本结论;(2)角平 分线与其它知识(如中位线、等腰、垂直平分线等)的综合(后面再列举).
例3: 第一节数学课后,老师布置了一道课后练习:如图,已知在Rt△ABC中 ,AB=BC,∠ABC=90°,BO⊥AC于点O.点P,D分别在AO和BC上,PB= PD,DE⊥AC于点E.
O,请写出图中一组相等的线段______________.
5. 如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
_____.
20
AC=BD或BC=AD OD=OC或OA=OB.
考点3 等腰、等边三角形与全等的综合(考查频率:★★★☆☆) 命题方向:(1)等腰直角三角形与全等三角形的综合问题; (2)等边三角形与全等的综合问题.
D.1cm
例1:如图,AD是等腰直角三角形ABC的底角的平分线,∠C= 90°,求证:AB=AC+CD.
【思维模式】(1)不管是过点D作AB的垂线也 好,还是延长AC也好,实际上都是利用了角平分 线的轴对称性构造的全等三角形,得出一些相等 的线段或相等的角解决问题;(2)人教课本书 后习题给出了角平分线的另一条性质,即图中 CD∶BD=AC∶AB,这一结论在解决很多面积有 关问题的时候,也能带来方便.
6. 如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE =90°,D为AB边上一点.求证:BD=AE.
考点4 角平分线的性质与判定(考查频率:★★★☆☆) 命题方向:(1)直接考查角平分线基本图形能得到的一些基本结论;(2)角平 分线与其它知识(如中位线、等腰、垂直平分线等)的综合(后面再列举).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢谢大家
荣幸这一路,与你同行
It'S An Honor To Walk With You All The Way
演讲人:XXXXXX 时 间:XX年XX月XX日
A→∠CAB=∠DAB
例1 :如图,点B在AE上 ,∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的一 个条件是 ∠∠∠CACCBDB=A=E∠A==∠CD∠.DDBBAE
C
A
B E
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AD=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件
三角形全等 复习课
知识结构图
性质
全等三角形对应边相等 全等三角形对应角相等
全等三角形 全等形
判定 一般三角形 应用
SSS
SAS
直
ASA
角
三
AAS
角
HL
形
解决问题
火眼金睛:
A
AA B
SSA不能 判定全等
BB
CC
DD
B
C A
D
口答
1、如图所示,已知AC=AD,BC=BD, 求证:∠CAB= ∠DAB.
D
∠CBE=∠DBE也可以
(?)
2、证明角、边相等
例(12•区考题第21题)已知如图,点B、F、C、E在同一
1.
直线上, AC、DF相交于G, AB⊥BE,垂足为B , DE⊥BE,垂足为E, 且AB=DE, BF=CE。
求证(1)△ABC≌△DEF (2)GF=GC
练习
1(2014浙江杭州)在△ABC中,AB=AC,点E,F 分别在AB,AC上,AE=AF,BF与CE相交于点P ,求证:PB=PC,并请直接写出图中其他相等的 线段.
2.如图,在△ABC中,∠ACB=90º, D是AC上 的一点,且AD=BC,DE⊥AC于D, ∠EAB=90º .求证:AB=AE.
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
A
A
E
C
B
翻折
C
B
D
D A
D
A
如:课本P39 第2题
B 课本P41 第1题
DE
CB
C
课本P43 第2题
A
B
CE
如:课本P44 第9题 课本P44 第11题 课本P56 第8题
D
AD
FB
E
C
F
平移
D
A
E
F
B
C
E
A
E
D
A
B
D
C
B
C
如:课本P44 第10题 课本P55 第3题
旋转
主要题型1、添加条件分析:现在我们已知
C
A
B
D
口答
2、如图所示,已知AB=AC,AD=AE, 求证:BE= Hale Waihona Puke D.ADE
B
C
口答
3、如图所示,已知AB∥DE,AC∥DF, BE=CF, 求证:AB= DE.
A
D
B
EC
F
点拨:能用ASA的题目也能用AAS证明。
口答
4、(2013•昆明)已知:如图,AD,BC相 交于点O,OA=OD,AB∥CD. 求证:AB=CD.
