西北工业大学航空学院结构力学课后题答案第三章-受剪板式薄壁结构内力和位移计算
结构力学 第三章 作业参考答案
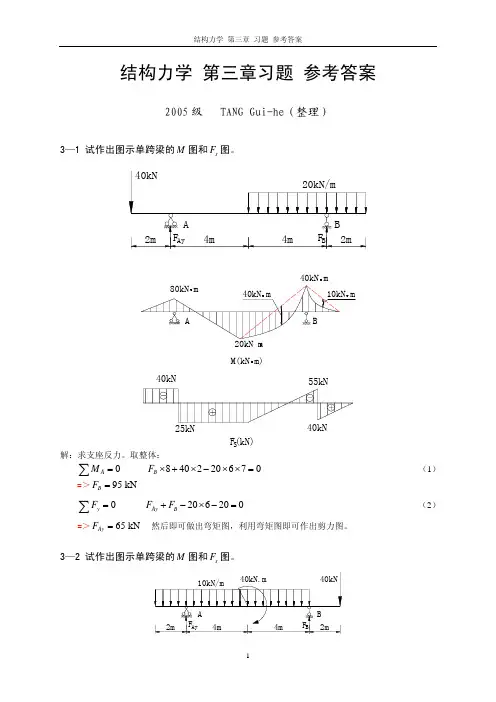
B
M图(kN m)
（1） （2）
解： （1）求支座反力
∑M = 0 ∑F = 0
A y
取左边或者右边为隔离体，可得：
∑M ∑F
x
C
=0
⇒ FBx =
M h
（3） （4）
=0
最后容易做出结构的弯矩图。
3—18 试作图示刚架的 M 图。
C 0.8kN/m 0.5kN/m D E
14.625 4.225 12.8375
3—19 试作图示刚架的 M 图。
20kN
24 16
C
24
16
B FAx A FBy FAy
FBx
1m
2m
2m
2m
M图(kN m)
（1） （2） （3）
解：对整体：
∑M ∑F
y
A
=0
FBy × 4 + FBx ×1 = 20 × 2 FAy + FBy = 20 FAx − FBx = 0 FBx × 2 − FBy × 2 = 0
40kN m
10kN m M图(kN m)
32.5kN
20kN
20kN F(kN) S
解：求支座反力。取整体：
47.5kN
∑M ∑F
A
=0
FB × 8 − 20 ×10 − 10 ×10 × 3 − 40 = 0 FAy + FB − 10 ×10 − 20 = 0
然后即可做出弯矩图，利用弯矩图即可作出剪力图。
然后即可做出整个刚架的弯矩图。结点受力校核如下图。
D
qL 4 qL 2 qL 2
qL 4
qL 4
E
qL 2 qL 2
(完整版)西北工业大学航空学院结构力学课后题答案第二章结构的几何组成分析
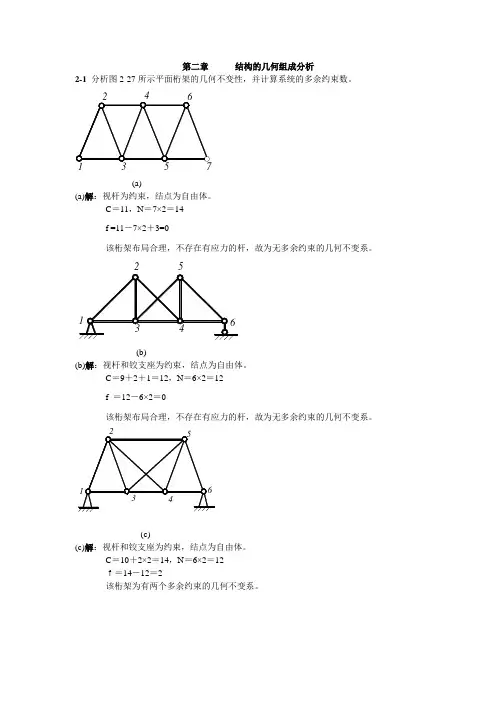
第二章结构的几何组成分析2-1分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。
(a)(a)解：视杆为约束，结点为自由体。
C＝11，N＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(b)(b)解：视杆和铰支座为约束，结点为自由体。
C＝9＋2＋1＝12，N＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(c)(c)解：视杆和铰支座为约束，结点为自由体。
C＝10＋2×2＝14，N＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。
1217(d)(d)解：视杆和铰支座为约束，结点为自由体。
C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。
(e)(e)解：视杆为约束，结点为自由体。
C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。
6 (f)(f)解：视杆和固定铰支座为约束，结点为自由体。
C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。
(g)(g)解：视杆和固定铰支座为约束，结点为自由体。
C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。
(h)(h)解：视杆和固定铰支座为约束，结点为自由体。
C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。
西北工业大学航空学院结构力学课后题答案第六章 薄壁工程梁理论
第六章 薄壁工程梁理论6-1 求如图所示剖面的弯曲正应力，设壁板不受正应力，缘条面积都是2200mm ，已知载荷.105,1056mm N M mm N M y x ⋅⨯=⋅=图中尺寸单位为mm.(a)（a ）解：确定形心坐标轴。
()()mm AAy mm AAx 50480120,804160160=+==+=则在形心坐标轴下，1点、2点、3点、4点的坐标分别为()()()()50,80,50,80,30,80,70,80----确定相应于形心坐标轴下的剖面惯性矩，惯性积和总面积。
43442442102.31056.21008.1Amm y x A J Amm x A J Amm y A J i i i xy i i y i i x ∑∑∑⨯-==⨯==⨯==求当量弯矩。
()()()()()-19.230M P a508025.842MPa 5080216MPa103080856MPa 34708045072.004132.0,1021154.0110973560196296.014321662=---=-⋅=⋅=-+-=⨯=⎪⎭⎫⎝⎛⨯+=⨯⋅=⎪⎭⎫⎝⎛⨯+==-=，，，，，，σσσσσy x y x J J M M k M J J M M k M J J J k x xy x y y y xy y x x yx xy(b)（b ）解：确定形心坐标轴。
()()mmAAy x 10042002000mm4AA100100=+==+-=在形心坐标轴下，1点、2点、3点、4点的坐标分别为()()()()100,100,100,0,100,0,100,100---。
确定相应于形心坐标轴下的剖面惯性矩，惯性积和总面积。
224x i 224244100()2100()2100()i y i i xy i i i J A y A mm J A x A mm J A x y A mm ==⨯==⨯==-⨯∑∑∑求当量弯矩。
(完整版)西北工业大学航空学院结构力学课后题答案第三章静定结构的内力与变形
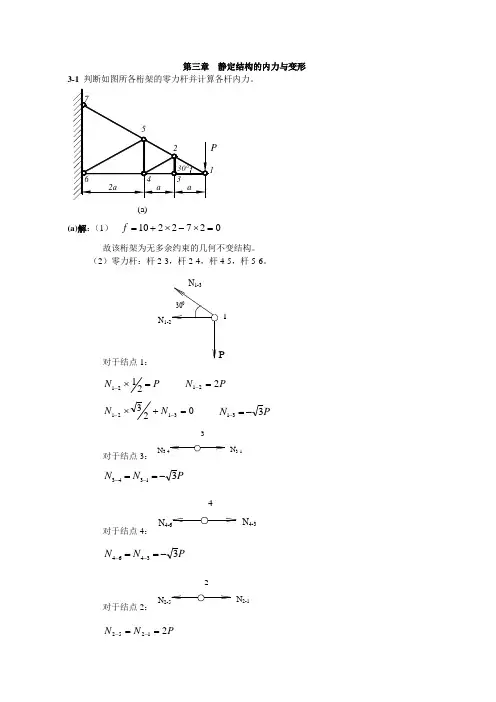
第三章 静定结构的内力与变形3-1 判断如图所各桁架的零力杆并计算各杆内力。
1P(a) (a)解：（1）0272210=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
（2）零力杆：杆2-3，杆2-4，杆4-5，杆5-6。
对于结点1：N 1-2PN 1-33001P N =⨯-2121 P N 221=-0233121=+⨯--N N P N 331-=-对于结点3：N 3-43N 3-1P N N 31343-==--对于结点4：N 4-64N 4-3P N N 33464-==--对于结点2：N 2-52N 2-1PN N 21252==--对于结点5：N 5-75N 5-2P N N 22575==--(b)(b)解：（1）082313=⨯-+=f故该桁架为无多余约束的几何不变结构。
（2）零力杆：杆1-2，杆2-3，杆2-4，杆5-4，杆6-4，杆6-7，杆6-8，杆1-5。
对于结点5：P5N 5-8P N -=-85对于结点8：N 7-88N 5-8Fθ05528785=+⨯--N N P N 55287=-对于结点7：N 7-47N 7-8P N 55247=-对于结点4：N 3-44N 7-4P N N 5524743==--对于结点3：N 1-33N 3-4P N N 5524331==--2(c)(c)解：（1）026228=⨯-⨯+=f故该桁架为无多余约束的几何不变结构。
（2）零力杆：杆1-2，杆2-3，杆2-4，杆4-3，杆4-6。
对于结点1：N 1-61N 1-3Pθ05561=+⨯-P N P N 561-=-05526131=⨯+--N N P N 231=-对于结点3：3N 3-1N 3-5P N N 21353==--(e)(d)解：（1）02112316=⨯-⨯+=f故该结构为无多余约束的几何不变结构。
（2）零力杆：杆4-5，杆5-6，杆4-6，杆7-6，杆2-3，杆2-8，杆2-9，杆1-2，杆9-11,杆8-9，杆9-11.对于结点4：4N 4-7N 3-4450PP N 2243=- P N 2274=-对于结点7：7N 4-7N 3-7N 8-7P N N 22227374=⨯-=-- P N -=-73P N 2278=-对于结点3：3N 3-4N 3-7N 8-7022734332=⨯+=---N N N P N 2283=-对于结点8：022228982=⨯⎪⎭⎫ ⎝⎛+=--N P N运用截面法：N 1-2N 9-10N 9-11PP23456789由对9点的力矩平衡：0222221=⨯⨯-⨯+⨯-P a P a a N 021=-N对于结点9：9N 2-9N 9-11N 9-10N 9-88911910922---=⨯+N N N P N 22109-=-8N 3-8(e)(e)解：（1）024125=⨯-++=f故该结构为无多余约束的几何不变结构。
西北工业大学航空学院结构力学课后题答案第三章-受剪板式薄壁结构内力和位移计算
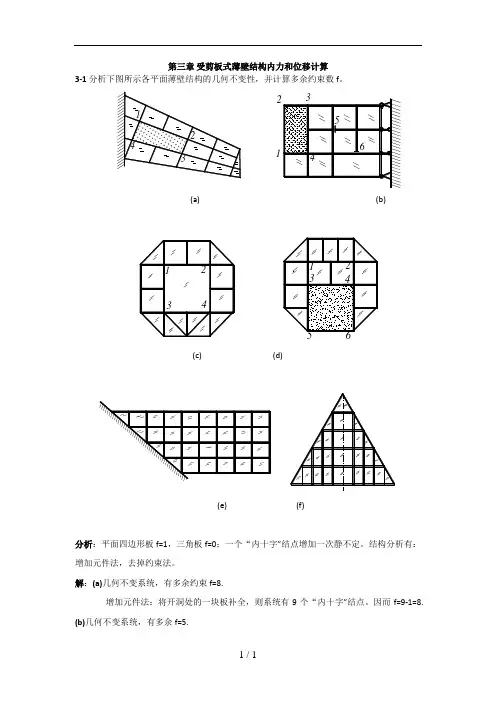
第三章 受剪板式薄壁结构内力和位移计算3-1分析下图所示各平面薄壁结构的几何不变性，并计算多余约束数f 。
1(a)(b)(c) (d)(e) (f)分析：平面四边形板f=1，三角板f=0；一个“内十字”结点增加一次静不定。
结构分析有：增加元件法，去掉约束法。
解：(a)几何不变系统，有多余约束f=8.增加元件法：将开洞处的一块板补全，则系统有9个“内十字”结点。
因而f=9-1=8.(b)几何不变系统，有多余f=5.增加元件法：将开洞处的一块板补全，切开端口杆的杆端处连上，则系统有4个“内十字”结点，外部多余约束数为3，对于端口切开的杆：丁字节点6处为零力杆端切开与否对静不定次数无影响，而处于“内十字”结点处的5处，则解除一次静不定。
因而f=4+3-1-1=5.(c)几何不变系统，有多余约束f=4.有4个“内十字”结点。
因而f=4.(d)几何不变系统，有多余约束f=3.增加元件法：将开洞处的一块板补全，则系统有4个“内十字”结点。
因而f=4-1=3.(e)几何不变系统，有多余约束f=21.有21个“内十字”结点。
因而f=21.(f)几何不变系统，有多余约束f=12.有12个“内十字”结点。
因而f=12.3-2分析下图所示空间薄壁结构的几何不变性，并计算多余约束数f。
(a)(b)(c) (d)(e)(f)(g) (h)6(i)(j)67(k)(l)78(m) (n)(o)分析：三缘条盒段若以四边形面与基础连接则有1次静不定（进行结构分析：视结点为自由体有3个自由度，板和杆各自起一个约束作用），若以三边与基础相连则为无多余约束的静定结构；对于一端固定的一段空心薄壁结构，端框有n个结点，其静不定次数为(n-3),故单边连接的四缘条盒段有1次静不定；对于四缘条盒段若以相邻两面和基础相连则由结构分析可知有3次静不定；对于三缘条盒段若以一边为三角形另一边为四边形和基础相连则由结构分析可知有2次静不定，若以双边四边形形式连接三缘条盒段则静不定次数为3。
结构力学第3章习题及参考答案
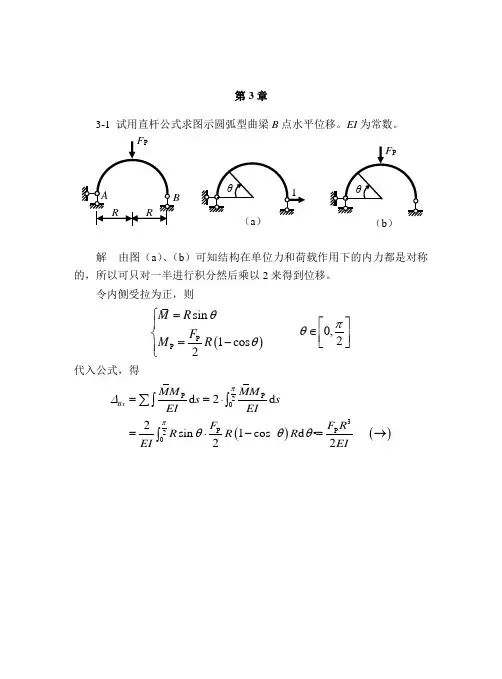
解（1）C点的竖向位移
（2）CD杆与CE杆夹角的改变量
3-5图示桁架AB杆的 ，其他杆的 。试求B点水平位移。
解本题中，AB杆的应力-应变关系不是线性的，计算时要用单位荷载法最基本的公式。
解
3-9试求图示刚架在温度作用下产生的D点的水平位移。梁为高度h=0.8m的矩形截面梁，线膨胀系数为 =10-5 oC-1。
解
3-10图示桁架各杆温度上升t，已知线膨胀系数 。试求由此引起的K点竖向位移。（画出需要的图）
解
*3-11图示梁截面尺寸为b×h=0.2m×0.6m，EI为常数，线膨胀系数为 ，弹簧刚度系数k=48EI/l3(l=2m)。梁上侧温度上升10℃，下侧上升30℃，并有图示支座移动和荷载作用。试求C点的竖向位移。
解利用虚功互等定理。
1状态：1kN的外力及其引起的15个结点的已知位移。
2状态：15个结点上10kN/15的集中荷载及其引起的15个结点的未知位移。
1状态的外力在2状态位移上做的功为
2状态的外力在1状态位移上做的功为
由
得
3-6 (b)
解
3-6 (c)
解
3-6 (d)
解
3-6 (e)
解
3-6 (f)
解（1)相对水平位移
（2)相对竖向位移
对称结构在对称荷载作用下的反对称位移等于零。
（3)相对转角
3-6 (g)
解
3-6 (h)
解
3-7试求图示结构在支座位移下的指定位移。
3-7 (a)
解
3-7 (b)
解
3-8图示结构各杆件均为截面高度相同的矩形截面，内侧温度上升t，外侧不变。试求C点的竖向位移。线膨胀系数为 。
结构力学第三章习题参考解答
FAy 6 FAx 2 0
1 ql 2A
1 ql 4
取整体：M A 0
Fy 0
取AC： MC 0
取整体： Fx 0
l
l
0.45ql
FBy
1 2l
ql 3l 2
3 ql 4
FAy
ql
3 4
ql
1 4
ql
FAx
2 ql 2 l4
1 ql 2
FBx
1 ql 2
l 2
1 ql B2 3 ql 4
取左段
FNK
ql cos
3l 4
1 q 3 l 2 2 4
9 ql 2 32
D
C
q
3 ql
4
A
1 ql
l
4
1 ql
4
1 ql 4
3 ql
4
FQ KN
1 ql 2
E
4
1 ql 2 4
9 ql2 32
1 ql
B
4
ql 2 8
M KNm
l
1 ql
4
1 ql
4
1 ql
4
FN KN
1 ql2 4
1 ql 4
3－12解：
q C
q
3 ql
4
A
l
1 ql
B
4
Fy 0
FAy
1 ql 4
1 ql 4
l
l
1 ql
4
取BC：
MC 0
FBx
1 4
ql
取整体：
Fx 0
FAx
ql
1 ql 4
3 ql 4
AD段的最大弯矩 M x 3 qlx 1 qx2 dM 3 ql qx 0
西北工业大学机械原理课后答案第3章
O OO OP 2P 3F 23(P 24Pl 3(P 34)(a)(b)Pl 3Pl 6A 1题3-6在图a 所示的四杆机构中,第三章平面机构的运动分析题3-3试求图示各机构在图示位置时全部瞬心的位置（用符号P j 直接标注在图上）解：题3-4在图示在齿轮-连杆机构中，试用瞬心法求齿轮1与齿轮3的传动比w1/w3.C 2P 12P 23St -解：1）计算此机构所有瞬心的数目K N （N1）2152） 为求传动比 < 3需求出如下三个瞬心 R 6、P 36、P 13如图3-2所示。
; 1 巳6只33） 传动比 仁3计算公式为： —3P 16P 13I AB =60mm , l cD =90mm , l AD =|Bc =120mm , w 2=10rad/s ，试用瞬心P134 C 4L CP 12AM B3P iP 34CBMF 24F 34P ?4(d)Pl 4法求:V B3I AB2IAB lBPI32.56rad sV ClCR 3 3 0.4m s量得 1 26.42 226.6P 3434B P 233 22A ,D- i Pl4P 12 1(a)P 131） 当0 =165。
时，点C 的速度Vc ;2） 当$ =165。
时，构件3的BC 线上速度最小的一点 E 的位置及速度的大小; 3） 当Vc=O 时，0角之值（有两个解）解：1）以选定比例尺，绘制机构运动简图。
（图3-3 ）2）求V c ，定出瞬心P 13的位置。
如图 3-3 （a ）3）定出构件3的BC 线上速度最小的点 E 的位置。
因为BC 线上速度最小的点必与 P 13点的距离最近，所以过 P 13点引BC 线延长线的垂线交于 E 点。
如图3-3 （a ）v E1ER 3 3 0.375ms4）当V C 0时，P 13与C 点重合，即AB 与BC 共线有两个位置。
作出 V C 0的两个位置。
题3-12在图示的各机构中，设已知各构件的尺寸、原动件 1以等角速度3 1顺时针方向转动。
飞机结构力学第三章
第三章结构变形计算一、单位载荷法3-1、求图3-4所示结构的下列各种变形时，广义单位力应如何施加？1、求1点水平位移。
答：在1点沿水平方向施加2、求2点和4点在垂直方向上的相对位移。
答：在2点和4点垂直方向上施加单位力偶。
3、求结构端部1-1、杆的角位移答：在1点和1、点沿水平方向施加单位力偶4、求杆1-1、和3-3、的相对角位移3-2、图3-5示出一空间盒式结构，求下列变形时，广义单位力应如何施加？1、求翼肋Ⅰ、Ⅱ之间的相对转角。
答：在Ⅰ、Ⅱ翼肋上施加一对相反的平面单位力矩。
2、求1-1、-1、、杆的伸长。
答：在1点和1、、点施加沿杆方向的相反的单位力。
3、求节点1和2、之间沿1-2、方向的相对位移答：在1点和2、点施加沿1-2、方向的相反的单位力。
4、求上部开口1-2-2、-1、的剪切变形。
5、求肋Ⅰ、Ⅲ之间的相对翘曲角。
二、结构变形计算3-3、（例题）已知图3-7中所示平面桁架结构，各杆截面积均为f，材料相同，弹性模量均为E，在节点7上受一向下的力P作用。
求：用单位载荷法，计算节点2的垂直位移。
解：结构是逐次连接节点法形成的简单桁架，是静定结构，且不可移动。
（1）求解<P>状态由节点6平衡得：由节点2平衡得：由节点7平衡得：由节点3平衡得：由节点5平衡得：将各杆轴力标在图中。
（2）根据题意加单位载荷，求解<1>状态。
在节点2加向下的垂直力1，单位力由2-5,1-5,4-5杆承受并传到基础上，其余各杆的力均为零。
将各杆内力标在图上，或列在表中。
将<P>状态下的结构变形形态作为虚位移，施加在<1>状态上，因<1>状态，可利用虚位移原理，得：编号杆长度L1 1-2 A 0 2p 02 1-5 p pa3 2-3 A 0 2p 04 2-5 A -1 0 05 3-5 a 0 p 06 3-6 A 0 0 07 3-7 a 0 p 08 4-5 A -1 -3p 3pa9 5-6 A 0 -p 010 6-7 A 0 -p 0答：2点垂直位移大小为，方向向下。
西北工业大学机械原理课后答案第3章_1
第三章 平面机构的运动分析题3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号P ij 直接标注在图上) 解：1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w1/w3.P 13P 23P 363D 652C 4B P 16A 1P 12解：1）计算此机构所有瞬心的数目152)1(=-=N N K2）为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3）传动比31ω计算公式为：1316133631P P P P =ωω题3-6在图a 所示的四杆机构中，l AB =60mm ，l CD =90mm ，l AD =l BC =120mm ，ω2=10rad/s ，试用瞬心法求：231） 当φ=165°时，点C 的速度Vc ；2） 当φ=165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小； 3） 当Vc=0时，φ角之值（有两个解） 解：1) 以选定比例尺,绘制机构运动简图。
(图3-3 ) 2）求V C ，定出瞬心P 13的位置。
如图3-3（a ）s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3）定出构件3的BC 线上速度最小的点E 的位置。
因为BC 线上速度最小的点必与P 13点的距离最近，所以过P 13点引BC 线延长线的垂线交于E 点。
如图3-3（a ）s m EP v l E 375.0313==ωμ4）当0=C v 时，P 13与C 点重合，即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-12 在图示的各机构中，设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解：a)速度方程：32233C C C B C B C v v v v v +=+=加速度方程：r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+b) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+题3-14 在图示的摇块机构中，已知l AB =30mm ，l AC =100mm ，l BD =50mm ，l DE =40mm 。
结构力学 第三章 作业参考答案
∑M = 0 ∑F = 0 ∑F = 0
A
FBy × l − q × l ×
l =0 2
（1） （2） （3）
y
FAy + FBy = 0 FAx + FBx − q × l = 0
FBx × l − FBy × l =0 2
x
取右边部分为隔离体：
∑M
C
=0
（4）
解以上方程可得：
ql ⎧ ⎪ FAx = 4 ⎪ 3ql ⎪ =＞ ⎨ FBx = 4 ⎪ ql ⎪ ⎪ FAy = FBy = 2 ⎩
3—10 试不计算反力绘出梁的 M 图。
16
12
4
A
B
8 2m 2m 4m 4m
12 4m
6m
2m
解：从悬臂端和 AB 开始作图。利用区段叠加法和铰结点的弯矩为零，即可做出全部的弯矩图。
3—12 试不计算反力绘出梁的 M 图。
5
华南农业大学 水利与土木工程学院（College of water conservancy and Civil Engineering, SCAU）
1m
D 80
30
40 E
20 40
40 C F
80 E
40
A
解： （1） 求支座反力
B
40
∑F = 0 ∑M = 0 ∑F = 0
y A x
FC − 10 × 4 − 20 = 0 FA − FB = 0
⇒ FC = 60 kN ⇒ FC = 10 kN
（1） （2） （3）
FB ×1 − 50 − 10 × 4 × 6 − 20 × 10 = 0 ⇒ FB = 10 kN
（1）
《结构力学习题》(含答案解析)
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。
二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。
l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。
ll21、求图示结构B点的竖向位移，EI = 常数。
西北工业大学结构力学及其参考答案
西北工业大学结构力学试卷及其答案一、单项选择题(每小题2分，共20分)1. 下图中的哪一个不是二元体（或二杆节点）（）A. B. C. D.2. 图1所示体系，铰K相当的约束个数为（）图1 图 2 图3A. 4B. 5C. 6D. 73. 不考虑轴向变形，图2所示结构用先处理法建立的结构刚度矩阵阶数是 ( )A. 3×3B. 4×4C. 5×5D. 6×64. 静定结构的支座反力或内力，可以通过解除相应的约束并使其产生虚位移，利用刚体虚功方程即可求解，虚功方程相当于（）A. 几何方程B. 物理方程C. 平衡方程D. 位移方程5. 图3所示结构，用力法求解时最少未知个数为（）A. 2B. 3C. 4D. 56. 图示结构中，不能直接用力矩分配法计算的结构是( )A. B. C. D.7. 根据影响线，使跨中截面K产生最大弯矩的均布活荷载最不利分布是( )A. B.C. D.8. 图示三单跨梁的自振频率分别为ωa，ωb，ωc，它们之间的关系是( )(a) (b) (c)A. cbaωωω>> B.bcaωωω>> C.bacωωω>> D.cabωωω>>9. 静定结构在支座移动时，会产生：（）A. 内力B. 应力C. 刚体位移D. 变形10. 力法方程是沿基本未知量方向的：（）A．力的平衡方程B．位移为零方程C．位移协调方程 D．力的平衡及位移为零方程。
二、填空题(每空2分，共20分)1. 具有基本部分和附属部分的结构，进行受力分析的次序是：先计算____部分，后计算____部分。
2. 图4所示桁架中杆a、b的轴力分别为F Na=____，F Nb=____。
图4 图5 图63. 图5所示静定梁在移动荷载作用下，截面C的弯矩影响线方程为MC=___________（0≤x≤2m）；MC=_____（2m≤x≤6m）。
西北工业大学飞行器结构力学电子教案7资料
q23 0
同理可得 q12 、q31 也都等于零 。 所以，对三角形板：
q12 q23 q31 0
三角形板在受剪板式计 算模型中是不受力的。
（2）长方形板的平衡
长方形板四个边上的四个未知剪流q12、q14、 q32、q34，板在其作用下处于平衡 由平面力系有三个平衡方程，可得：
采用了上述简化假设的受剪板式薄壁结构计算模型中，只 包含两类结构元件：承受轴力的杆和承受剪流的板，杆和板之 间只有剪流作用。
▄ 受剪板式薄壁结构计算模型的几个例子。
图(a)机身圆形框，可以简化为由若 干段直梁所组成的受力模型
图(b)机翼，可以简化为由若干个盒式结构 组成的受力模型
机翼盒式模型
机身笼式计算模型
即杆子两端的轴力仅相当于一个独 N ( x) N12 q12 x 杆轴力沿杆轴线线性变化，其斜率为 立变量 。 N ( x) 因此，受剪杆相当于起一个约束。 q12 x
（4） 杆轴力的内力图，有4中可能。
返回
飞行器结构力学基础
——电子教学教案
西北工业大学航空学院 航空结构工程系
第七章
受剪板式薄壁结构内力和位移 计算
第二讲 7.3 静定平面薄壁结构内力计算
一、平面薄壁结构的组成分析
受剪板式薄壁结构的计算模型是由结点、杆和板元件组成。如果这些元件 的中心点和中线都在同一平面内，则称为平面薄壁结构，它只能承受作用在 此平面内的外载荷。
▄ 飞机薄壁结构典型元件受力分析及其理想化
（1）蒙皮
在结构作为一个整体的受力和传力过程中，蒙皮的主要作用是支承和传递由于剪 切和扭转而引起的剪应力，同时它还部分支承和传递由于弯曲而引起的正应力。正应 力主要由较强的长桁和突缘等纵向元件承担，蒙皮在这方面的作用是第二位的。因此， 在对蒙皮进行理想化的时候，假设蒙皮只承受并传递剪应力；蒙皮实际上具有的承受 并传递正应力的能力将人为地附加到纵向元件（如长桁）上去。 由于蒙皮壁厚一般很薄，可近似认 为蒙皮上的剪应力大小沿厚度方向不变化， 且剪应力沿厚度中线的切线方向。因为剪 应力的值沿厚度方向不变，所以可以用剪 应力沿厚度方向的合力 q = τ ×t 来替代剪 应力，称 q 为剪流，用半箭头表示。
(2024版)西北工业大学航空学院结构力学课后题答案第四章-力法
可编辑修改精选全文完整版第四章 力法4-1 利用对称与反对称条件，简化图4-15所示各平面刚架结构，要求画出简化图及其位移边界条件。
P P(a)(a)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。
由静力平衡条件∑=0X可得23P N =再由两个静力平衡条件，剩余4个未知力，为二次静不定。
本题中通过对称性条件的使用，将6次静不定的问题转化为2次静不定。
1PP(b)(b)解：对称结构，在反对称载荷作用下，在对称轴上对称的内力为零。
受力分析如图所示有2根对称轴，结合平衡方程，剩下三个未知数，为3次静不定。
本题中通过对称性条件的使用，将6次静不定问题转化为3次静不定。
(c)(c)解：对称结构，在对称载荷作用下，在对称轴上反对称内力为零。
有一根对称轴，减少了两个静不定度本题中通过对称性条件的使用，将3次静不定问题转化为1次静不定。
4-2图4-16所示桁架各杆的EA均相同，求桁架各杆的内力。
(a)(a)解：1、分析结构静不定次数。
结构有4个结点8个自由度，6根杆6个约束，3个外部约束。
因此结构静不定次数为1，f=1。
2、取基本状态。
切开2-4杆，取<P>,<1>状态，各杆内力如图。
1234P-P √2P<P>1234P<1>11√22√22√22√22计算影响系数∑=∆EAl N N i p P 11()2422222+=⎪⎪⎭⎫ ⎝⎛⨯+⨯=EA Pa P P EA a ∑=EAl N i1211δ()22222142222+=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=EA a EA a 列正则方程：()()02242221=+++P X解之()P X 42321-=3、由11N X N N P +=，得()P X N 423220112-=⎪⎪⎭⎫ ⎝⎛-⋅+= ()P X P N 42212113+=⋅+=()P X N 423220114-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423220123-=⎪⎪⎭⎫ ⎝⎛-⋅+=()P X N 423210124-=⋅+=()P X P N 42122134+-=⎪⎪⎭⎫ ⎝⎛-⋅+-=4、校核。
结构力学第三章习题及答案精品资料
结构力学第三章习题及答案静定结构计算习题)解：首先分析几何组成：AB 为基本部分，EC 为附属部分画出层叠图，如图 (b)所示。
按先属附后基本的原则计算各支反力(c)图。
之後，逐段作出梁的弯矩图和剪力图。
3 — 1试做图示静定梁的M 、F Q 图。
36.67KNM 图（单位：KN/m）13.313.333—3试做图示静定刚架的内力（M 、F Q 、F N ）图，并校核所得结果解：（1）计算支反力F Ax =48kN （―） M A =60 KN ?m （右侧受拉） （2） 逐杆绘M 图 （3） 绘F Q 图 （4） 绘N 图）3—7试做图示静定刚架的内力（M 、F QF N ）图，并校核所得结果F Q 图（单F N 图（单20KN/m（5）校核：内力图作出后应进行校核。
（略）r P IT°'25qL0.25q|D解：(1)计算支反力FAx=20kN (J) F A y=38kN( T ) F B y=62kN( T )⑵逐杆绘M 图 ⑶绘F Q 图⑷(5)校核：内力图作出后应进行校核。
(略)做图示 静定刚 架的内38(MKN)F N 图(单位:KN )0.25qL£o ・ 25qL (£6220F Q 、 图，并校核所得结0.25qLF N图解：(1)计算支反力FAx=0.75qL (J) FAY=-0.25qL( ) FBY=0.25qL( T )(2) 逐杆绘於图(3) 绘F Q图(4) 绘N图(5) 校核：内力图作出后应进行校核。
(略) 3-11试做图示静定刚架的内力(力、Fo、F N)图，并校核所得结果解:(1) 计算支反力F BX=40KN (J) F AY=30KN ( T ) F B y=50kN( T )(2) 逐杆绘〃图(3) 绘F Q图(4) 绘N图(5) 校核：内力图作出后应进行校核。
(略)120解：1、由已知设抛物线方程为y=ax+bx+c 坐标系如图（a）所示，有图可以看出，x=0 y=0 ； x=10 y=4 ； x=20 y=0 可以求得M图（单位:KN/m）3-17试求图示抛物线三钱拱的支座反力,501 24y X25524y X25_5X D5m0.4F N81 =-5分析桁架的几何组成：此桁架为简单桁架，由基本三角形 345按二元体规则依 次装入新结点构成。
(完整版)西北工业大学航空学院结构力学课后题答案第二章结构的几何组成分析
第二章结构的几何组成分析2-1分析图2-27所示平面桁架的几何不变性，并计算系统的多余约束数。
(a)(a)解：视杆为约束，结点为自由体。
C＝11，N＝7×2＝14f =11－7×2＋3=0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(b)(b)解：视杆和铰支座为约束，结点为自由体。
C＝9＋2＋1＝12，N＝6×2＝12f ＝12－6×2＝0该桁架布局合理，不存在有应力的杆，故为无多余约束的几何不变系。
(c)(c)解：视杆和铰支座为约束，结点为自由体。
C＝10＋2×2＝14，N＝6×2＝12ｆ＝14－12＝2该桁架为有两个多余约束的几何不变系。
1217(d)(d)解：视杆和铰支座为约束，结点为自由体。
C ＝30＋3＝33，N ＝17×2＝34ｆ＝33－34＝-1故该桁架为几何可变系。
(e)(e)解：视杆为约束，结点为自由体。
C ＝13，N ＝8×2＝16ｆ＝13－16＋3＝0将1-2-3-4、5-6-7-8看作两刚片，杆3-6、杆2-7、杆4-5相互平行，由两刚片原则知，为瞬时可变系统。
6 (f)(f)解：视杆和固定铰支座为约束，结点为自由体。
C ＝22＋3×2＝28，N ＝14×2＝28ｆ＝28－28＝0将12-13-14、7-11-12、1-2-3-4-5-6-7-8-9-10看作三刚片，三刚片由铰7、铰12、铰14连结，三铰共线，故该桁架为瞬时可变系统。
(g)(g)解：视杆和固定铰支座为约束，结点为自由体。
C＝24＋4×2＝32，N＝16×2＝32ｆ＝32－32＝0由于杆15-14-3、杆12-11-4、杆9-5相交于一点，故该桁架为瞬时可变系。
(h)(h)解：视杆和固定铰支座为约束，结点为自由体。
C＝12＋2×2＝16，N＝8×2＝16ｆ＝16－16＝0该桁架布局合理，加减二元体之后，无有应力的杆，故该桁架为无多余约束的几何不变系。
结构力学第3章习题答案
3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a) 4P F a2P F a 2P F aＭ4PF Ｑ34P F 2P F(b) ４2020M Q10/326/3４10A B C a a a a a F P a D E F F P 2m 6m 2m 4m 2m A B C D 10kN 2kN/m (c) 21018018040M1560704040Q(d) 7.5514482.524MQ3m 2m2m AB C E F15kN 3m 3m 4m 20kN/m D 3m 2m 2m 2m2m 2m 2m ABC D E FG H 6kN ·m 4kN ·m 4kN 2m 3-3 试作图示刚架的内力图。
试作图示刚架的内力图。
(a) 242018616MQ1820(b) 3030301101010QM 2104kN ·m 3m 3m 2kN A CBD 6m 10kN 40kN ·m ABC D(c) 664275MQ(d) 444444/32MQN2kN/m 6kN 6m 4kN AB CD2kN 6m 2kN 4kN ·m ACB D E(e) 44814``(f) 2222200.815MQN4m ABC4m D4kN A B C2m 3m 4m 2kN/m 3-4试找出下列各弯矩图形的错误之处，并加以改正。
(a) F P(b) (c) F P(d) M(e) (f) F PF P3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件，确定E 、F 两铰的位置。
B C EFDA28ql M2221()222116121618c B C BC C qql M l x x qx xM M M M ql ql x ql x l=-+===\=\=\= 中FD()2ql x -lBC EFxDAql lx3-6 试作图示刚架的弯矩和剪力图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 受剪板式薄壁结构内力和位移计算3-1分析下图所示各平面薄壁结构的几何不变性，并计算多余约束数f 。
1(a)(b)(c) (d)(e) (f)分析：平面四边形板f=1，三角板f=0；一个“内十字”结点增加一次静不定。
结构分析有：增加元件法，去掉约束法。
解：(a)几何不变系统，有多余约束f=8.增加元件法：将开洞处的一块板补全，则系统有9个“内十字”结点。
因而f=9-1=8.(b)几何不变系统，有多余f=5.增加元件法：将开洞处的一块板补全，切开端口杆的杆端处连上，则系统有4个“内十字”结点，外部多余约束数为3，对于端口切开的杆：丁字节点6处为零力杆端切开与否对静不定次数无影响，而处于“内十字”结点处的5处，则解除一次静不定。
因而f=4+3-1-1=5.(c)几何不变系统，有多余约束f=4.有4个“内十字”结点。
因而f=4.(d)几何不变系统，有多余约束f=3.增加元件法：将开洞处的一块板补全，则系统有4个“内十字”结点。
因而f=4-1=3.(e)几何不变系统，有多余约束f=21.有21个“内十字”结点。
因而f=21.(f)几何不变系统，有多余约束f=12.有12个“内十字”结点。
因而f=12.3-2分析下图所示空间薄壁结构的几何不变性，并计算多余约束数f。
(a)(b)(c) (d)(e)(f)(g) (h)6(i)(j)67(k)(l)78(m) (n)(o)分析：三缘条盒段若以四边形面与基础连接则有1次静不定（进行结构分析：视结点为自由体有3个自由度，板和杆各自起一个约束作用），若以三边与基础相连则为无多余约束的静定结构；对于一端固定的一段空心薄壁结构，端框有n个结点，其静不定次数为(n-3),故单边连接的四缘条盒段有1次静不定；对于四缘条盒段若以相邻两面和基础相连则由结构分析可知有3次静不定；对于三缘条盒段若以一边为三角形另一边为四边形和基础相连则由结构分析可知有2次静不定，若以双边四边形形式连接三缘条盒段则静不定次数为3。
解：(a)几何不变系统，多余约束数f=4。
增加元件法：将开洞处的板1-2-3-4补全，为5个单边连接的四缘条盒段。
因而f=5-1=4。
(b)几何不变系统，多余约束数f=3.增加元件法：将开洞处的板1-2-5-6、2-3-4-5补全，依次为一个三缘条盒段以四边形面与基础连接有1次静不定和四个四缘条盒段单边连接有1次静不定。
因而f=1+4-2=3.(c) 几何不变系统，多余约束数f=4.一个单边连接四缘条盒段，一个双边连接四缘条盒段。
因而f=1+3=4.(d)几何不变系统，多余约束数f=3.一个单边连接三缘条盒段，一个双边连接四缘条盒段。
因而f=3.(e)几何不变系统，多余约束数f=8.一个单边连接三缘条盒段，两个双边连接四缘条盒段，一个双边连接三缘条盒段。
因而f=2×3+2=8.(f) 几何不变系统，多余约束数f=2.进行结构分析，短的四缘条盒段与基础为单边连接静不定次数为1，在此基础上增加了4个结点，5个板，8根杆。
因而f=1+5+8-4×3=2.(g) 几何不变系统，多余约束数f=2.以自由短四缘条盒段为基础，静定结构；以四边形形式单边连接三缘条盒段，静不定次数为1；单边连接四缘条盒段，静不定次数为1。
因而f=1+1=2.(h) 几何不变系统，多余约束数f=10.以四边形形式单边连接三缘条盒段，静不定次数为1；连个双边连接的四缘条盒段，静不定次数为2×3；双边四边形形式连接三缘条盒段，静不定次数为3。
因而f=1+2×3+3=10.(i) 几何不变系统，多余约束数f=2.两个以单边四边形方式连接的三缘条盒段。
f=2×1=2.(j)几何不变系统，多余约束数f=5.单层端框有六个结点的有一个隔框笼式结构静不定次数为1；单端固定的单层端框有六个结点的有一个隔框笼式结构静不定次数为（6-3+1）.因而f=1+（6-3+1）=5。
(k) 几何不变系统，多余约束数f=3.单端固定的单层端框有六个结点的空心笼式结构静不定次数为（6-3）。
因而f=3.(l) 几何不变系统，多余约束数f=14.为两个单端固定的单层端框有八个结点的有两个隔框笼式结构静不定次数2×（8-3+2）.因而f=14.(m)几何不变系统，多余约束数f=7.单端固定的单层端框有八个结点的空心笼式结构静不定次数（8-3）；增加元件法：将开洞处的板补全后为单端固定的单层端框有六个结点的空心笼式结构静不定次数（（6-3）-1）。
因而f=7.(n) 几何不变系统，多余约束数f=32.一个三缘条盒段以四边形面与基础连接结构静不定次数为1；七个单边连接的四缘条盒段结构静不定次数为7；七个四缘条盒段双边连接结构静不定次数为7×3；再加两根杆和一个四边形板，三个约束。
因而f=1+7+7×3+3=32.(o) 几何不变系统，多余约束数f=31.一个自由的单层端框有10个结点的空心笼式结构为静定结构；三个单端固定的单层端框有10个结点的空心笼式结构静不定次数为3×（10-3）；增加元件法：将开洞处的板补全后为依次连接两个单端固定的单层端框有9个结点的空心笼式结构静不定次数 2×（（9-3）-1）.因而f=31.3-3 平面薄壁结构的形状、尺寸及受载情况如下图所示。
求各元件内力并作内力图。
2(a) (b)(c) (d)1234567P aa aa1234578aaPP2P2P(e) (f)PPaaa2a2345678(g)(a)解：(a)静定结构。
零力杆端：023=-N ，014=-N ，043=-N ，012=-N 。
取2-3杆aP q =；取杆3-4a Pb qb N /34==-； 取1-2杆a Pb qb N /21==-；取1-4杆Pqa N ==-41校核总体平衡，满足。
内力图：(b)静定结构。
零力杆端：0,0,0234312===---N N N .取总体平衡分析得：P N P N =-=--1241, 取2-3杆cP q 223=；取2-1杆P N =-21,cP q =； 从而c P q q q 2//23214==；取1-4杆1414/2N q c P P -=-=-；验证结构剩余局部3-4杆的平衡，满足。
内力图：PPb/aPb/aq=P/aP(c)静定结构。
零力杆端：0,0,0,0,0,0653654343212======------N N N N N N 分析总体平衡得：P N P N ==--4521, 对称结构，受对称载荷，内力具有对称性。
取1-2杆q=P/c;取2-3杆c Pb qb N /23==-； 取1-6杆c Pb N /16=-验证结构剩余局部3-6杆的平衡，满足。
内力图：PP P0.5P(d)静定结构。
零力杆端：,0,0,0,0,0,0,0,0,0,09687986545968949924323===========-----------N N N N N N N N N N N分析总体平衡得P N P N ==--6721,. 对称结构，受对称载荷，内力具有对称性。
a P q /=；取4-9杆，取3-4杆，a Pb qb N /34==-；取2-3杆，P qa N ==-32；012=q ；取1-2杆，a Pb qb N /92-=-=-取2-9杆，取结点2，12-N 32-N ,P N N ==--3212.PPPb/cPPq=P/cq=P/cPb/c验证其余局部结构平衡，满足。
内力图：(e)静定结构。
零力杆端：0,0,0,063345445====----N N N N取4-5杆得0=q ,即4-3-6-5板上无剪流分布。
从而043=-N ，则320N -=取总体平衡60M =∑，得122N P -=-， 取结点2 得272P N -=，232P N -=- 取杆3-2，有02P q a=取杆6-3，有632P N -=-校核总体平衡，满足。
内力图：PPb/a(f)静定结构。
零力杆端:.0,00,0,0,0,0,02152233454568767========--------N N N N N N N N杆3-4 2P q a=杆2-3 232N q a P -=-=- 杆5-4 542N q a P -== 杆7-6 32Pq a=， 杆5-6 5632N q a P -== 杆8-7 8732N q a P -=-=- 节点5 有 522N P -= ，58N P -= 杆2-5 122q a q a P += ，得 1P q a= 杆1-2 211N q a P -=-=-杆1-8 8110N q a P -++= ，得812N P -=- 校核总体平衡，满足。
内力图：0.5PP(g)静定结构。
零力杆端：,0,0,0,0,0,0,05654348576877121========--------N N N N N N N N取2-3杆得P N =-32;取结点2得''2821,22N P N P --=-=; 取1-2杆得12q a =;取1-7杆得P N 2217=-; 取3-4杆得aPq 221=； 取3-8杆得P a a Pa aq a a q N 22218338==⨯==--; 取结点8得P N 278=-;取7-8杆得aP q 222=； 取2-8杆得82128N q a N --=-+=; 取结点8得P N N 22858-=-=--;PP2P杆3-434q-==则38qa-=，544qa-=内力图：3-4空间薄壁结构的形状、尺寸及受载情况如下图，求各元件的内力并作内力图。
1H(a) (b)2P2P(c) (d)HH(e) (f) 解：(a)静定结构，受自平衡力系。
零力杆端:2343321234144121873767267656487858856515--------------------N N N N N N N N N N N N N N N N N N N N 、、、、、、、、、、、、、、、、、、、由杆1-2，2-3，3-4，8-7，1-4，5-8，知六个面的剪流大小相等，记为q 取2-6杆，由P Lq=2得LP q 2=; 分别取其余各杆进行分析可得:P N P N P N P N =-==-=----73845162,,, 内力图:(b)静定结构。
零力杆端:843414437323326212412151,,,,,,,,,,,------------N N N N N N N N N N N N记面1-2-6-5内剪流为1q ，面2-3-7-6内剪流为2q ，面4-3-7-8内剪流为3q ，面1-4-8-5内剪流为4q取杆1-2 有1q q = ， 取杆4-3 有3q q = 取杆2-3 有22231H q q qH == ， 取杆1-4 有14142H q q q H == 取杆2-6 有21()H q qL P H += 得112()PH q L H H =+ 取杆1-5 有1512()0H qq L N H -++= 得1512PH N H -=- 取杆3-7 有273231()()H N q q L qq L P H -=-+=-+=- 取杆4-8 有11843422()()H PH N q q L q q L H H -=+=+= 内力图:PPPP(c)静定结构。