【20套精选试卷合集】重庆市杨家坪中学2019-2020学年高考数学模拟试卷含答案
2020年重庆市高考数学(理科)模拟试卷(6)

∴ ?RA= { x|x< 3} ,
∵ B= { x|1<x≤9} ,
∴( ?RA)∩ B= { x|1< x< 3} ,
故选: A.
1
2.( 5 分)设 z= 4﹣ 3i,则在复平面内 对应的点位于(
)
??
A .第一象限
B .第二象限
C.第三象限
D .第四象限
【解答】 解:由题意得 z= 4﹣ 3i ,
2020 年重庆市高考数学(理科)模拟试卷( 6)
一.选择题(共 12 小题,满分 60 分,每小题 5 分)
1.( 5 分)设集合 A= { x|y= √??- 3} , B= { x|1<x≤ 9} ,则( ?RA)∩ B=( )
A .( 1, 3)
B .(3, 9)
C. [3, 9]
1
2.( 5 分)设 z= 4﹣ 3i,则在复平面内
+
的值.
|????| |????|
23.设函数 f (x)= |x﹣ a|+|x﹣ 4|( a≠ 0).
( 1)当 a= 1 时,求不等式 f(x)< x 的解集;
第 4页(共 23页)
( 2)若 ??(??+) 1 ≥ 4??恒成立,求 a 的取值范围.
第 5页(共 23页)
2020 年重庆市高考数学(理科)模拟试卷( 6)
级、中学高级; ⑥ 无论是否把我计算在内,以上条件都成立.由此队员的叙述可以推测
出他的学段及职称分别是
、
.
16.( 5 分)设函数 f ( x)是偶函数,当
??(3- ??), 0 ≤ ??≤ 3
x≥0 时, f( x) =
{ -
3 ??+
【20套精选试卷合集】重庆市杨家坪中学2019-2020学年高考英语模拟试卷含答案

高考模拟英语试卷时量:120分钟总分:150分本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
第I卷(选择题共100分)注意事项:1.答第I卷前考生务必将自己的姓名、准考证号填写在答题卡上。
2.选出每小题答案前,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号框,不能答在本试卷上,否则无效。
第一部分听力(共两节,满分30分)做题时,先将答案划在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Where does the conversation probably take place?A. In a restaurant.B. In a furniture store.C. In the woman's company.2. What does the man want to do first?A. See the elephants.B. Have a cup of tea.C. Watch the dolphin show.3. What is the woman probably going to do?A. Make a list.B. Do some shopping.C. Make a chocolate pie.4. Why does the woman look upset?A. She experienced a theft.B. She was given a parking ticket.C. She couldn't find a parking space.5. How will the woman go to the city church?A. By bike.B. By bus.C. By car.第二节(共15小题:每小题1.5分,满分22.5分)听下面5段对话或独白。
2020年重庆市直属校高考数学模拟试卷(文科)(3月份)-普通用卷

2020年重庆市直属校高考数学模拟试卷(文科)(3月份)一、选择题(本大题共12小题,共60.0分)1.已知集合,,则A. 1,B. 0,1,C. 0,1,D.2.在复平面内,复数所对应的点位于A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.古代数学名著九章算术有“米谷粒分”题:粮仓开仓收粮,有人送来米2016石,验得米内夹谷,抽样取米一把,数得270粒内夹谷30粒,则这批米内夹谷约为A. 222石B. 224石C. 230石D. 232石4.若实数x,y满足,若,则z的最大值为A. 1B. 2C. 3D. 45.设O为坐标原点,F为抛物线的焦点,若点满足,则a为A. B. 2 C. D.6.设等比数列的前n项和为,若,则A. B. 16 C. 12 D.7.在中,,,则的最大值是A. B. C. D.8.函数的部分图象如图所示,则函数的解析式为A.B.C.D.9.棱长为a的正方体中,点E,F,G分别为棱AB,,的中点,则过E,F,G三点的平面截正方体所得截面面积为A. B. C. D.10.若,,,则A. B. C. D.11.已知双曲线C:右焦点为F,过原点O的直线与C交于P,Q两点,若,,则双曲线C的离心率为A. B. 2 C. D. 312.已知函数是定义在R上的奇函数,且在单调递增.设,当时,恒有,则m的取值范围是A. B. C. D.二、填空题(本大题共4小题,共20.0分)13.已知向量与的夹角为,且,则______.14.古人认为,天下万物皆由金、木、水、火、土五类元素组成,如图,分别是金、木、水、火、土彼此之间存在的相生相克的关系,若从5类元素中任选2类元素,则2类元素相克的概率为______.15.,分别是关于x的方程和的根,则______.16.已知某圆柱轴截面的周长为12,当该圆柱体积最大时其侧面积为______.三、解答题(本大题共7小题,共82.0分)17.已知数列满足,,,数列满足,,且数列是等差数列.Ⅰ求数列和的通项公式;Ⅱ令,求数列的前n项和.18.如图,四边形ABCD为平行四边形,点E在AB上,,且以DE为折痕把折起,使点A到达点F的位置,且.Ⅰ求证:平面平面BDC;Ⅱ若直线DF与平面BCDE所成角的正切值为,求点C到平面DEF的距离.19.某企业有甲、乙两套设备生产同一种产品,为了检测两套设备的生产质量情况,随机从两套设备生产的大量产品中各抽取了50件产品作为样本,检测一项质量指标值,若该项质量指标值落在内,则为合格品,否则为不合格品.现统计得到相关统计情况如下:乙套设备的样本的频数分布表质量指标值频数16191851根据上述所得统计数据,计算产品合格率,并对两套设备的优劣进行比较;填写下面列联表,并根据列联表判断是否有的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.甲套设备乙套设备合计合格品不合格品合计附:参考公式:,其中.20.已知椭圆C:的左、右焦点分别为,,过点的直线与C交于M,N两点.的周长为8,且的最小值为3.Ⅰ求椭圆C的标准方程;Ⅱ设椭圆C的右顶点为A,直线AM,AN分别交直线于P,Q两点,当的面积是面积的5倍时,求直线MN的方程.21.已知函数.当时,求证:;若有两个零点,求a的取值范围.22.在平面直角坐标系xOy中,以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为,直线l的参数方程为为参数,直线l与曲线C交于M,N两点.Ⅰ若点P的极坐标为,求的值;Ⅱ求曲线C的内接矩形周长的最大值.23.已知函数,.Ⅰ当时,求a的取值范围;Ⅱ若,,,不等式恒成立,求a 的取值范围.-------- 答案及解析 --------1.答案:C解析:解:集合,0,1,,0,1,.故选:C.求出集合A,B,由此能求出.本题考查交集的求法,考查交集定义等基础知识,考查运算求解能力,是基础题.2.答案:A解析:解:,复数z所对应的点的坐标为,位于第一象限.故选:A.利用复数代数形式的乘除运算化简,求出z的坐标得答案.本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.3.答案:B解析:解:粮仓开仓收粮,有人送来米2016石,验得米内夹谷,抽样取米一把,数得270粒内夹谷30粒,设这批米内夹谷约为x石,则,解得石.故选:B.设这批米内夹谷约为x石,利用等可能事件概率计算公式能求出结果.本题考查这批米内夹谷的数量的求法,考查等可能事件概率计算公式等基础知识,考查运算求解能力,是基础题.4.答案:B解析:解:作出不等式组对应的平面区域,由,得,平移直线,由图象可知当直线经过点时,直线的截距最大,此时z最大,代入目标函数得.故选:B.作出不等式组对应的平面区域,利用z的几何意义即可得到结论.本题主要考查线性规划的应用,利用数形结合是解决线性规划问题中的基本方法.5.答案:C解析:解:因为O为坐标原点,F为抛物线的焦点,点;;,;;.故选:C.先求出焦点坐标,进而求得向量的坐标,代入数量积求解即可.本题考查向量的数量积的应用,考查向量的表示以及计算,考查计算能力.6.答案:D解析:解:由,可知,则,,,,故选:D.由已知,结合等比数列的求和公式即可求出.本题主要考查了等比数列的求和公式的简单应用,属于基础试题.7.答案:C解析:解:由余弦定理可得,,当且仅当即时,取等号,此时cos A最小,又因为在单调递减,所以此时A取得最大值.故选:C.要求A的最大值,只要求cos A的最小值,结合余弦定理及基本不等式即可求解.本题主要考查了余弦定理及基本不等式在求解三角形最值中的应用,属于基础试题.8.答案:D解析:解:根据函数的部分图象,根据周期性可得,.可再根据函数的最值得.若,由五点法作图可得,,不满足条件,故A,由五点法作图可得,,,故选:D.由函数的图象的顶点坐标求出A,由周期求出,由五点法作图求出的值,可得函数的解析式.本题主要考查由函数的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出,由五点法作图求出的值,属于基础题.9.答案:B解析:解:取中点M,连结MG、ME,则,且,四边形EFGM是平行四边形,过E,F,G三点的平面截正方体所得截面为四边形EFGM,以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,则0,,,,a,,,,,,四边形EFGM是矩形,,过E,F,G三点的平面截正方体所得截面面积为:.故选:B.取中点M,连结MG、ME,推导出四边形EFGM是平行四边形,从而过E,F,G 三点的平面截正方体所得截面为四边形EFGM,以D为原点,DA为x轴,DC为y轴,为z轴,建立空间直角坐标系,利用向量法能求出过E,F,G三点的平面截正方体所得截面面积.本题考查截面面积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.10.答案:B解析:解:,,,,,.故选:B.将m,n平方,利用同角三角函数的关系可得,,结合x,y的范围及正弦函数在的单调性,即可得出结论.本题考查同角三角函数的基本关系以及三角函数的图象及性质,属于基础题.11.答案:C解析:解:双曲线C:右焦点为F,过原点O的直线与C交于P,Q两点,若,,可得,,取左焦点,连接,可得:,即,解得.故选:C.利用已知条件,求出P的坐标,结合,,转化求解双曲线的离心率即可.本题考查双曲线的简单性质的应用,是基本知识的考查,是中档题.12.答案:B解析:解:根据题意,函数为定义在R上的奇函数,则有,又由在在单调递增,则在单调递增,则在R上为增函数,则,当时,,即,不恒成立,当时,,此时,不成立,当时,,此时不能满足恒成立,故x的取值范围为;故选:B.根据题意,由奇函数的性质可得在R上为增函数且,据此对m进行分情况讨论,分析是否成立,综合即可得答案.本题考查抽象函数的性质以及应用,涉及函数的奇偶性与单调性的综合应用,属于基础题.13.答案:解析:解:因为向量与的夹角为,且,所以:;则;故答案为:.由题意可得向量的模长,再直接代入数量积可得.本题考查平面向量的数量积和夹角,属基础题.14.答案:解析:解:如图,分别是金、木、水、火、土彼此之间存在的相生相克的关系,从5类元素中任选2类元素,基本事件总数,其中2类元素相克包含的基本事件个数,则2类元素相克的概率为.故答案为:.从5类元素中任选2类元素,基本事件总数,其中2类元素相克包含的基本事件个数,由此能求出2类元素相克的概率.本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,是基础题.15.答案:5解析:解:分别作出函数,,的图象,相交于点P,Q.,.而与互为反函数,直线与直线互相垂直,点P与Q关于直线对称...故答案为:5.分别作出函数,,的图象相交于点P,利用,再借助于互为反函数的两个函数之间的关系以及直线与直线互相垂直,可得点P与Q关于直线对称.即可得出结论.本题考查了同底的指数函数与对数函数互为反函数的性质、相互垂直的直线之间的关系,属于难题.16.答案:解析:解:设圆柱的底面半径为r,高为h.,得.圆柱体积.当且仅当,即时取等号.此时,则圆柱的侧面积.故答案为:.设圆柱的底面半径为r,高为可得,可得圆柱体积,再利用基本不等式的性质求解r,得到h,再由圆柱的侧面积公式求解.本题考查了圆柱的轴截面性质、体积与侧面积的计算公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.17.答案:解:Ⅰ由,,,可知:数列是以2为首项,2为公比的等比数列,,.由题意,设等差数列的公差为d,,,,解得,,,.Ⅱ由Ⅰ知,.,.解析:本题第Ⅰ题先根据等比数列的定义计算出数列的通项公式,然后设等差数列的公差为d,通过计算出,的值即可得到公差d的值,即可得到等差数列的通项公式,进一步可计算出数列的通项公式;第Ⅱ题先根据第Ⅰ题的结果计算出数列的通项公式,进一步计算出数列的通项公式,根据通项公式的特点采用分组求和法和裂项相消法计算出前n项和.本题主要考查等差数列和等比数列的通项公式和求和公式的应用,以及运用分组求和法和裂项相消法求前n项和.考查了转化与化归思想,整体思想,方程思想,以及逻辑推理能力和数学运算能力.本题有一定的综合性,属中档题.18.答案:解:Ⅰ证明:,,,,平面BEF,平面BEF,,,,,,,,,,平面BCDE,平面BFC,平面平面BDC.Ⅱ解:以B为原点,BA为x轴,在平面ABCD中过B作AB的垂线为y轴,BP为z 轴,建立空间直角坐标系,如图,设,则a,,0,,0,,,直线DF与平面BCDE所成角的正切值为,直线DF与平面BCDE所成角的正弦值为,平面BCDE的法向量0,,直线DF与平面BCDE所成角的正切值为,,解得,2,,2,,2,,,0,,设平面EDF的法向量y,,则,取,得,点C到平面DEF的距离.解析:Ⅰ由,得,,从而平面BEF,进而,推导出,从而平面BCDE,由此能证明平面平面BDC.Ⅱ以B为原点,BA为x轴,在平面ABCD中过B作AB的垂线为y轴,BP为z轴,建立空间直角坐标系,利用向量法能求出点C到平面DEF的距离.本题考查面面垂直的证明,考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.19.答案:解:根据频率直方图知,甲套设备产品合格品为,计算甲套设备产品的合格率为;根据频率分布表知,乙套设备产品合格品为,计算乙套产品的合格率为;且,所以乙套设备产品的合格率大,设备更优秀;由此填写列联表如下;甲套设备乙套设备合计合格品434891不合格品729合计5050100将列联表中的数据代入公式计算得;且,所以没有的把握认为该企业生产的这种产品的质量指标值与甲、乙两套设备的选择有关.解析:根据频率直方图计算甲套设备产品合格品和产品合格率;根据频率分布表计算乙套设备产品合格品与产品合格率,比较即可;根据题意填写列联表,计算,对照临界值得出结论.本题考查了频率与独立性检验的应用问题,也考查了数据处理能力,是基础题.20.答案:解:根据椭圆的定义可得:,,则的周长,解得,又因为的最小值为3,所以,解得,所以椭圆的标准方程为,设,,,设直线MN的方程为,联立,整理得,则,,因为A,M,P三点共线,,,所以,即有,解得,同理,根据A,N,Q三点共线可得,,,则由的面积是面积的5倍,可得,即,代入,,得,化简得,解得,所以直线MN的方程为,即.解析:利用椭圆定义可得,,可将的周长表示为,解出,又最小值为,可解出b,即可表示椭圆方程;设,,,,设直线MN的方程为,联立,分别表示出的面积,面积,利用根于系数关系代入化简可得m的值,进而表示出直线方程.本题考查椭圆标准方程的求,考查椭圆中三角形面积表示,直线与椭圆的综合,属于中档偏难题.21.答案:证明:当时,定义域,令,则,当时,,函数单调递减,当时,,函数单调递增,故当时,取得最大值,所以即;解:由题意,由题意即有2个零点,令,则,当时,,函数单调递减,当时,,函数单调递增,故当时,取得最大值,又时,,时,,故,因为,故,而可得,结合的图象可得且故a的范围.解析:把代入,要证原不等式成立,转化为证明,构造函数,转化为求解该函数的范围问题,结合导数可求;问题转化为有2个零点,构造函数,结合导数可研究的性质,结合图象可求.本题主要考查了利用导数研究函数的单调性,证明不等式及由函数的零点求解参数的范围,构造函数并利用导数研究函数的性质是求解问题的关键.22.答案:解:Ⅰ曲线C的极坐标方程为,转换为直角坐标方程为.点P的极坐标为,转换为直角坐标为由于点在直线l上,所以直线l的参数方程为为参数,转化为为参数,所以代入曲线的方程为,整理得,所以.Ⅱ不妨设,,所以该矩形的周长为当时,矩形的周长的最大值为16.解析:Ⅰ直接利用转换关系的应用,把参数方程极坐标方程和直角坐标方程之间进行转换.Ⅱ利用一元二次方程根和系数关系式的应用和三角函数关系式的恒等变换和正弦型函数的性质的应用求出结果.本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,三角函数关系式的恒等变换,正弦型函数的性质的应用,一元二次方程根和系数关系式的应用,极径的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.23.答案:解:,可得,即,则或或,解得或或,则a的范围是;恒成立,等价为,其中当x,,,当且仅当取得等号,而,当且仅当时取得等号.所以,解得.解析:求得关于a的不等式,由绝对值的意义,去绝对值,解不等式,求并集即可;原不等式等价为,运用家的孩子不等式的性质和二次函数的最值求法,分别求得最值,解不等式可得所求范围.本题考查绝对值不等式的解法,注意运用分类讨论思想,考查不等式恒成立问题解法,注意运用转化思想和绝对值不等式的性质,以及二次函数的最值求法,考查运算能力和推理能力,属于中档题.。
2020年重庆市高考数学模拟试卷(文科)(5月份)(有答案解析)
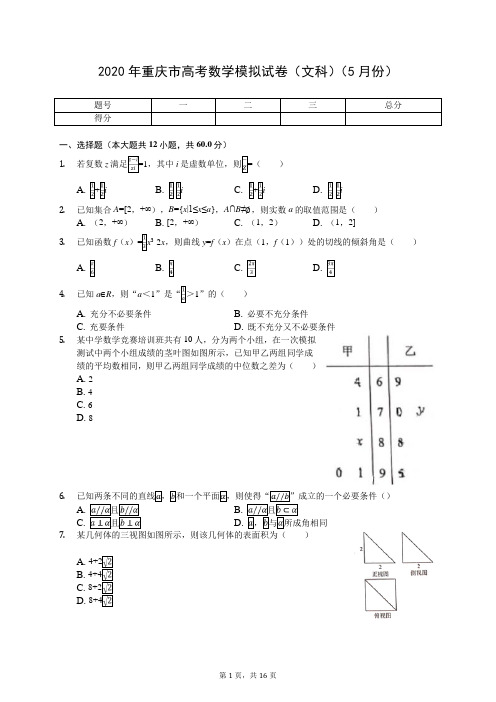
解析:【分析】 本题考查利用导数分析切线的方程,关键是掌握导数的几何意义,属于基础题. 设切线的斜率为 k,其倾斜角是 θ,求出函数 f(x)的导数,利用导数的几何意义可得 k=f′(1), 即 tanθ,结合 θ 的范围,分析可得答案. 【解答】
解:根据题意,函数 f(x)= x3-2x,设切线的斜率为 k,其倾斜角是 θ,
9.答案:B
解析:解:∵等腰梯形 ABCD 中, =2 ,E,F 分别为 AD,BC 的中点,G 为 EF 的中点,
∴
=
=
=
=
,
∵ =, =,
第 8 页,共 16 页
∴
=
,
故选 B. 利用向量的共线定理、平行四边形法则即可得出. 本题考查了平面向量加减混合运算,熟练掌握向量的共线定理、平行四边形法则是解题的关键,属 基础题.
函数 f(x)= x3-2x,则 f′(x)=x2-2,
则有 k=f′(1)=-1, 则 tanθ=-1,
又由 0≤θ<π,则 θ= ,
故选:D.
4.答案:B
解析:【分析】 本题考查充分条件、必要条件是一
第 6 页,共 16 页
种简单有效的方法,属于基础题. 根据 a<1,不一定能得到 (如 a=-1 时);但当 【解答】 解:由 a<1,不一定能得到 (如 a =-1 时);
解得 y=4+x, 甲组同学的中位数为:80+x,乙同学的中位数为 70+y ∴甲乙两组同学成绩的中位数之差为|(80+x)-(70+y)|=|10+x-y|=|10+x-4-x|=6. 故选:C. 甲乙两组同学成绩的平均数相同,得 y=4+x,甲组同学的中位数为:80+x,乙同学的中位数为 70+y, 由此能求出甲乙两组同学成绩的中位数之差. 本题考查平均数、方差、中位数的求法,考查茎叶图的性质等基础知识,考查运算求解能力,是基 础题.
2020年重庆市高考数学模拟试卷(文科)(4月份)(有答案解析)

2020年重庆市高考数学模拟试卷(文科)(4月份)题号一二三总分得分一、选择题(本大题共12小题,共60.0分)1.复数(i为虚数单位)的共轭复数为()A. 1+iB. 1-iC. 1+2iD. 1-2i2.已知全集U=R,集合M={x|-1<x<l},N={x|0<x<2},则图中阴影部分表示的集合是()A. {x|x≤0或x≥l}B. {x|x≤-1或x≥2}C. {x|0<x<l}D. {x|x-1<x<2}3.已知向量=(-1,2),=(λ,-4),若⊥,则|2|=()A. 6B. 10C. 8D. 124.已知函数f(x)=,则f(-1)=()A. log25B. log26C. 3D. 2+log235.已知等差数列{a n}的前n项和为S n,若S11=22,则a3+a5+a10=()A. 2B. 3C. 6D. 126.若用如图所示的程序框图寻找使1+++…+>成立的正整数i的最小值,则图中①处应填入()A. 输出i-1B. 输出iC. 输出i+1D. 输出i+27.中华文化博大精深,我国古代算书《周髀算经》中介绍了用统计概率得到圆周率π的近似值的方法.古代数学家用体现“外圆内方”文化的钱币(如图1)做统计,现将其抽象成如图2所示的图形,其中圆的半径为2cm,正方形的边长为lcm,在圆内随机取点,若统计得到此点取自阴影部分的概率是P,则圆周率π的近似值为()A. B. C. D.8.函数y=(e x+e-x)sin x的部分图象大致为()A. B. C. D.9.若“p∨q”成立的一个必要条件是“¬r”,则下列推理:①p∨q⇒¬r;②p⇒¬r;③¬r⇒q;④(¬p)∧((¬q)⇒r.其中正确的个数为()A. 1B. 2C. 3D. 410.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为()A. B. C. D.11.已知-<α<,2tanβ=tan2α,tan(β-α)=-8,则sinα=()A. -B. -C.D.12.已知函数f(x)=若F(x)=f(x)+m有两个零点x1,x2,则x1x2的取值范围是()A. (-∞,e)B. (-∞,0)C. [e,0]D. [-l,0]二、填空题(本大题共4小题,共20.0分)13.在△ABC中,角A,B,C所对的边分别为a,b,c,若cos A=,a=,b=,则sin B=______14.设变量x,y满足约束条件,则目标函数z=3y-x的最小值是______15.如图,圆柱OO1中,两半径OA,O1B等于1,且OA⊥O1B,异面直线AB与OO1所成角的正切值为则该圆柱OO1的体积为______16.已知双曲线C:=1(a>0,b>0)的左右焦点为F1,F2.过点F的直线1与双曲线C的左支交于A,B两点,△BF1F2的面积是△AF1F2面积的三倍,∠F1AF2=90°,则双曲线C的离心率为______三、解答题(本大题共7小题,共82.0分)17.已知正项数列{a n}的前n项和为S n,2S n=a n2+a n(1)求数列{a n}的通项公式(2)令b n=3-a n+,求数列{b n}的前n项和.18.某农科站技术员为了解某品种树苗的生长情况,在该批树苗中随机抽取一个容量为100的样本,测量树苗高度(单位:cm).经统计,高度均在区间[20,50]内,将其按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50]分成6组,制成如图所示的频率分布直方图,其中高度不低于40cm的树苗为优质树苗.(1)求频率分布直方图中a的值(2)已知所抽取的这100棵树苗来自于甲、乙两个地区,部分数据如下2×2列联表所示,将列联表补充完整,并根据列联表判断是否有99.9%的把握认为优质树苗与地区有关?甲地区乙地区合计优质树苗5非优质树苗25合计附:K2=,其中n=a+b+c+dP(K2≥k0)0.0250.0100.0050.001k0 5.024 6.6357.87910.82819.如图,在棱长为2的正方体ABCD-A1B1C1D1中,M为AD中点,N为BC中点,P为B1D1上一点,B1P=3D1P,Q为AA1中点(1)证明:D1Q⊥平面B1MN(2)求四面体PMNB1的体积20.如图,已知A(0,1),B(0,-1)为椭圆C:=1(a>b>0)轴的两个端点,且椭圆的离心率为(1)求椭圆C的方程;(2)若经过点B的直线l与椭圆C的另一个交点记为M,经过原点O且与AM垂直的直线记为11,且直线l与直线l1的交点记为N,证明:•是定值,并求出这个定值.21.已知函数f(x)=ln x-ax+a,a∈R.(1)若f(x)存在极大值f(x0),证明:f(x0)≥0;(2)若关于x的不等式f(x)+e x-1≥1在区间[1,+∞)上恒成立,求a的取值范围.22.在直角坐标系xOy中,直线l的参数方程为(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ(1)求直线l的普通方程及曲线C的直角坐标方程;(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|23.设函数f(x)=|2x-3|+|x+2|(1)求不等式f(x)≤5的解集;(2)若关于x的不等式f(x)≤a-|x|在区间[-1,2]上恒成立,求实数a的取值范围-------- 答案与解析 --------1.答案:D解析:解:∵=,∴复数(i为虚数单位)的共轭复数为1-2i.故选:D.直接利用复数代数形式的乘除运算化简得答案.本题考查复数代数形式的乘除运算,考查复数的基本概念,是基础题.2.答案:B解析:解:∵全集U=R,集合M={x|-1<x<l},N={x|0<x<2},∴M∪N={x|-1<x<2},∴图中阴影部分表示的集合是:C U(M∪N)={x|x≤-1或x≥2}.故选:B.求出M∪N={x|-1<x<2},图中阴影部分表示的集合是C U(M∪N),由此能求出结果.本题考查集合的求法,考查并集、补集、维恩图的性质等基础知识,考查运算求解能力,是基础题.3.答案:B解析:解:∵向量=(-1,2),=(λ,-4),⊥,∴,∴λ=-8,∴,∴|2|=|(6,8)|==10,故选:B.根据⊥,可得,求出λ即可进一步得到|2|.本题考查平面向量的数量积与垂直的关系和向量的模,属基础题.4.答案:A解析:解:根据题意,函数f(x)=,则f(-1)=f(2)=f(5)=log25;故选:A.根据题意,由函数的解析式分析可得f(-1)=f(2)=f(5),进而计算可得答案.本题考查分段函数的解析式,涉及函数值的计算,属于基础题.5.答案:C解析:解:∵等差数列{a n}的前n项和为S n,S11=22,∴=11a6=22,解得a6=2,∴a3+a5+a10=3a6=6.故选:C.由等差数列{a n}的前n项和为S n,S11=22,求出a6=2,再由a3+a5+a10=3a6,能求出结果.本题考查等差数列的前n项和的求法,考查等差数列的性质等基础知识,考查运算求解能力,是基础题.6.答案:B解析:解:由程序框图的功能是使1+++…+>成立的正整数i的最小值,则循环结束时①中应为i的值.故选:B.分析程序中各变量、各语句的作用,根据流程图所示的顺序,得出该程序框图中①应填的内容.本题考查了算法与程序框图的应用问题,是基础题.7.答案:A解析:【分析】计算圆形钱币的面积和正方形的面积,求出对应面积比得P,则π可求.本题考查了几何概型的概率计算问题,是基础题.【解答】解:圆形钱币的半径为2cm,面积为S圆=π•22=4π;正方形边长为1cm,面积为S正方形=12=1.在圆形内随机取一点,此点取自黑色部分的概率是P=,则.故选:A.8.答案:C解析:解:函数f(-x)=-(e x+e-x)sin x=-f(x),图象是奇函数,图象关于原点对称,排除B,D,当x>0且x→0,f(x)>0,排除A,故选:C.先函数的奇偶性和对称性,然后利用极限思想进行排除即可.本题主要考查函数图象的识别和判断,利用函数奇偶性和对称性的关系以及极限思想是解决本题的关键.9.答案:C解析:解:若“p∨q”成立的一个必要条件是“¬r”,即为p∨q⇒¬r,⇔¬(p∨q)⇒r,⇔(¬p)∧((¬q)⇒r,可得①④正确;由p真,可得p∨q真,即有②正确;由q⇒¬r,可得③错误.故选:C.由复合命题的真假和充分必要条件的定义,可得p∨q⇒¬r,结合等价命题和复合命题的真值表,即可判断正确个数.本题考查复合命题的真假和充分必要条件的定义,考查判断能力,属于基础题.10.答案:A解析:解:由三视图还原原几何体如图,该几何体为多面体ABCDEF,底面为矩形ABCD,AB=5,AD=3.侧面CDEF为等腰梯形,EF=1,侧面CDEF⊥底面ABCD,则该几何体的体积V=.故选:A.由三视图还原原几何体,该几何体为多面体ABCDEF,底面为矩形ABCD,AB=5,AD=3.侧面CDEF 为等腰梯形,EF=1,侧面CDEF⊥底面ABCD.再由棱锥与棱柱的体积公式求解.本题考查由三视图求面积,体积,关键是由三视图还原原几何体,是中档题.11.答案:B解析:解:∵2tanβ=tan2α,∴2tan(β-α+α)=,∴=,∴=,化简得tanα=-2,∴α∈(-,0),∴sinα=-.故选:B.2tanβ=tan2α,∴2tan(β-α+α)=,变形可得tanα=-2,可得sinα=-.本题考查了两角和与差的三角函数,属中档题.12.答案:D解析:解:作出f(x)的图象,F(x)=f(x)+m有两个零点,即f(x)=-m有两个不等实根x1,x2,即为-m=x1+1=ln x2,可得x1=-m-1,x2=e-m,m≥-1,则x1x2=(-m-1)e-m,可设g(m)=(-m-1)e-m,g′(m)=me-m,由m>0时,g′(m)>0,g(m)递增,-1≤m<0时,g′(m)<0,g(m)递减,即m=0处g(m)取得极小值,且为最小值-1,又x1x2≤0,即有x1x2的范围是[-1,0].故选:D.作出f(x)的图象,由题意可得f(x)=-m有两个不等实根x1,x2,即为-m=x1+1=ln x2,可得m的函数,求得导数和单调性,可得极小值和最小值,结合图象可得所求范围.本题考查分段函数的零点个数问题,考查构造函数法和导数的运用:求单调性和最值,考查化简运算能力和推理能力,属于中档题.13.答案:解析:解:∵cos A=,a=,b=,∴sin A==,∴由正弦定理,可得:=,可得:sin B=.故答案为:.由已知利用同角三角函数基本关系式可求sin A的值,根据正弦定理即可得解sin B.本题主要考查了同角三角函数基本关系式,正弦定理在解三角形中的应用,考查了转化思想,属于基础题.14.答案:-4解析:解:作出变量x,y满足约束条件表示的平面区域,得到如图的△ABC及其内部,其中A(-2,3),C(-2,-2),B(3,)设z=F(x,y)=3y-x,将直线l:z=3y-x进行平移,当l经过点C时,目标函数z达到最小值,∴z最小值=F(-2,-2)=-4故答案为:-4.作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=3y-x对应的直线进行平移,可得当x=-2且y=-2时,z=3y-x取得最小值.本题给出二元一次不等式组,求目标函数的最小值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.15.答案:4π解析:解:过B作BC⊥底面O,交底面圆O于点C,连结OC,∵圆柱OO1中,两半径OA,O1B等于1,且OA⊥O1B,异面直线AB与OO1所成角的正切值为,∴OA⊥OC,AC==,OO1BC,∴∠ABC是异面直线AB与OO1所成角,∴tan∠ABC===,∴OO1=BC=4,∴该圆柱OO1的体积:V=πr2•OO1=4π.故答案为:4π.过B作BC⊥底面O,交底面圆O于点C,连结OC,则OA⊥OC,AC=,OO1BC,由∠ABC是异面直线AB与OO1所成角,得到tan∠ABC===,从而OO1=BC=4,由此能求出该圆柱OO1的体积.本题考查圆柱的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.16.答案:解析:解:设|AF1|=m,|BF1|=n,由双曲线的定义可得|AF2|=2a+m,|BF2|=2a+n,由△BF1F2的面积是△AF1F2面积的三倍,可得(2a+m)(m+n)-m(2a+m)=3•(2a+m)m,化简可得n=3m,由直角三角形ABF1可得(m+n)2+(2a+m)2=(2a+n)2,代入n=3m,化简可得m=a,在直角三角形AF1F2中,可得m2+(2a+m)2=4c2,即为a2+9a2=4c2,即c=a,则e==,故答案为:.设|AF1|=m,|BF1|=n,运用双曲线的定义和直角三角形的勾股定理和面积公式,化简可得n=3m,m=a,再由勾股定理和离心率公式,可得所求值.本题考查双曲线的定义和方程、性质,主要是离心率的求法,考查方程思想和运算能力,属于中档题.17.答案:解:(1)∵2S n=a n2+a n,∴n≥2时,2a n=2S n-2S n-1=a n2+a n-(+a n-1),∴(a n+a n-1)(a n-a n-1-1)=0,∵a n>0,∴a n-a n-1=1,n=1时,2a1=+a1>0,解得a1=1.∴数列{a n}是等差数列,首项为1,公差为1.∴a n=1+(n-1)=n.(2)b n=3-a n+=+,∴数列{b n}的前n项和=+(1-+……+)=+1-=--.解析:(1)由2S n=a n2+a n,可得n≥2时,2a n=2S n-2S n-1,化为(a n+a n-1)(a n-a n-1-1)=0,根据a n>0,可得a n-a n-1=1,利用等差数列的通项公式即可得出.(2)b n=3-a n+=+,利用等比数列的求和公式及其裂项求和方法即可得出.本题考查了数列递推关系、等差数列与等比数列的通项公式求和公式、裂项求和方法,考查了推理能力与计算能力,属于中档题.18.答案:解:(1)根据概率的性质可得:(a+3a+0.04+0.07+0.04+a)×5=1,解得a=0.01,(2)2×2列联表如下:甲地区乙地区合计优质树苗 5 20 25非优质树苗 502575合计55 45100k2=≈16.49>10.828.所以有99.9%的把握认为优质树苗与地区有关.解析:(1)根据概率的性质可得:(a+3a+0.04+0.07+0.04+a)×5=1,解得a=0.01,(2)根据列联表计算观测值,根据临界值表可得结论.本题考查了独立性检验,属中档题.19.答案:证明:(1)在棱长为2的正方体ABCD-A1B1C1D1中,M为AD中点,N为BC中点,P为B1D1上一点,B1P=3D1P,Q为AA1中点,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,D1(0,0,2),Q(2,0,1),B1(2,2,2),M(1,0,0),N(1,2,0),=(2,0,-1),=(1,2,2),=(0,2,0),•=0,=0,∴D1Q⊥MB1,D1Q⊥MN,∵MB1∩MN=M,∴D1Q⊥平面B1MN.解:(2)∵D1Q⊥平面B1MN,∴平面B1MN的一个法向量为==(2,0,-1),∴P(),=(-,),∴点P到平面B1MN的距离d==cos<>===,sin<>==,∴===.∴四面体PMNB1的体积V===1.解析:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明D1Q⊥平面B1MN.(2)求出平面B1MN的一个法向量,从而求出点P到平面B1MN的距离,由此利用向量法能求出四面体PMNB1的体积.本题考查线面垂直的证明,考查四面体的体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.20.答案:(1)解:由题意,,解得a=2,b=1,c=.∴椭圆C的方程为;(2)证明:设M(x0,y0)(x0≠0),则.,BM所在直线方程为y=.,则直线l1的方程为y=.联立,解得N(,).∴•=(x0,y0)•(,)=.∴•是定值-.解析:(1)由已知可得关于a,b,c的方程组,求解a,b的值,则椭圆方程可求;(2)设M(x0,y0)(x0≠0),则.分别求出直线l与直线l1的方程,联立求得N的坐标,再由数量积的坐标运算证明•是定值.本题考查椭圆方程的求法,考查直线与椭圆位置关系的应用,考查计算能力,是中档题.21.答案:(1)证明:f′(x)=-a.(x∈(0,+∞)).a≤0时,f′(x)>0,函数f(x)在x∈(0,+∞)上单调递增,无极值.a>0时,f′(x)=,在(0,)上f′(x),在(,+∞)上f′(x), 函数f(x)在(0,)上单调递增,在(,+∞)上单调递减,当x0=时,可得函数f(x)取得极大值=-ln a-1+a.令g(a)==-ln a-1+a.(a∈(0,+∞)).g′(a)=-+1=,可得当a=1时,函数g(a)取得极小值g(1)=0.∴g(a)=≥0,a∈(0,+∞).即f(x)存在极大值f(x0),f(x0)≥0.(2)解:令h(x)=f(x)+e x-1-1=ln x-ax+a+e x-1-1,x∈[1,+∞),h(1)=0.h′(x)=-a+e x-1=u(x),u′(x)=-+e x-1,在x∈[1,+∞)单调递增,u′(1)=0.∴u′(x)≥0,∴h′(x)=-a+e x-1≥u(1)=2-a,a≤2时,h′(x)≥0,函数h(x)在x∈[1,+∞)上单调递增,h(1)=0.∴h(x)≥h(1)=0,满足题意.a>2时,存在x0>1,使得x∈[1,x0)时,h′(x)<0,函数h(x)在x∈[1,x0)上单调递减,∴h (x)<h(1)=0,不满足题意,舍去.综上可得:a≤2.∴a的取值范围是(-∞,2].解析:(1)f′(x)=-a.(x∈(0,+∞)).对a分类讨论,即可得出单调性极值.进而证明结论.(2)令h(x)=f(x)+e x-1-1=ln x-ax+a+e x-1-1,x∈[1,+∞),h(1)=0.h′(x)=-a+e x-1=u(x),对a分类讨论,利用导数研究函数的单调性极值与最值即可得出.本题考查了利用导数研究函数的单调性极值与最值,方程与不等式的解法、分类讨论方法、等价转化方法,考查了推理能力与计算能力,属于难题.22.答案:解(1)由消去参数t可得直线l的普通方程为:x+y-a=0,由ρsin2θ=2cosθ得ρ2sin2θ=2ρcosθ可得曲线C的直角坐标方程为:y2=2x.(2)将P(1,1)代入x+y-a=0可得a=2,所以直线l的参数方程为(t为参数)将其代入曲线C的普通方程得:t2+4-2=0,设A,B对应的参数为t1,t2,则t1+t2=-4,t1t2=-2<0,∴|PA|+|PB|=|t1|+|t2|=|t1-t2|===2.解析:(1)消去参数t可得直线l的普通方程,根据互化公式可得曲线C的普通方程.(2)根据直线参数方程中参数条的几何意义可得.本题考查了参数方程化普通方程,极坐标方程化普通方程,参数t的几何意义,属中档题.23.答案:解:(1)f(x)≤5即为|2x-3|+|x+2|≤5,当x≥时,2x-3+x+2≤5,解得≤x≤2;当-2<x<时,3-2x+x+2≤5,解得0≤x<;当x≤-2时,3-2x-x-2≤5,解得x∈∅.可得不等式的解集为[0,2];(2)关于x的不等式f(x)≤a-|x|在区间[-1,2]上恒成立,可得|2x-3|+|x+2|+|x|≤a,设g(x)=|2x-3|+|x+2|+|x|,即g(x)=x+2+|x|+|2x-3|,-1≤x≤2,当≤x≤2时,g(x)=x+2+x+2x-3=4x-1;当0<x<时,g(x)=x+2+x+3-2x=5;当-1≤x≤0时,g(x)=x+2-x+3-2x=5-2x.可得g(x)的最大值为g(-1)=g(2)=7,可得a≥7.即a的范围是[7,+∞).解析:(1)运用绝对值的意义,对x讨论,去绝对值,解不等式,求并集即可;(2)由题意可得|2x-3|+|x+2|+|x|≤a,设g(x)=|2x-3|+|x+2|+|x|,对x讨论,去绝对值,由一次函数的单调性可得g(x)的最大值,可得a的范围.本题考查绝对值不等式的解法和不等式恒成立问题解法,注意运用分类讨论思想方法和转化思想,考查化简运算能力,属于中档题.。
重庆市重点中学2019-2020学年高考数学押题试卷含解析含解析【加15套高考模拟卷】

重庆市重点中学2019-2020学年高考数学押题试卷含解析一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知三棱柱111ABC A B C -中,1A A ⊥平面ABC ,24AB AC ==,tan 2ACB ∠=,点D 在棱1AA 上运动,记1A D x =,且1BC D ∆的面积为()f x ,则()y f x =的图像大致为( )A .B .C .D .2.一个圆锥的母线长为2,圆锥的母线与底面的夹角为4π,则圆锥的内切球的表面积为( ) A .8πB .24(22)π-C .24(22)π+ D .232(22)π-3.《中国好歌曲》的五位评委给一位歌手给出的评分分别是:118x =,219x =,320x =,421x =,522x =,现将这五个数据依次输入如图程序框进行计算,则输出的S 值及其统计意义分别是( )A .2S =,即5个数据的方差为2B .2S =,即5个数据的标准差为2C .10S =,即5个数据的方差为10D .10S =,即5个数据的标准差为104.已知()lg(10)lg(10)f x x x =++-,则()f x 是( ) A .偶函数,且在(0,10)是增函数B .奇函数,且在(0,10)是增函数C .偶函数,且在(0,10)是减函数D .奇函数,且在(0,10)是减函数5.已知函数()cos()1f x A x ωϕ=++(0A >,0>ω,0ϕπ<<)的最大值为3,()y f x =的图象的相邻两条对称轴间的距离为2,与y 轴的交点的纵坐标为1,则1()3f =( )A .1 B .-1C .3D .06.在三棱锥—P ABC 中,PA ⊥平面ABC ,2,30APC S ABC ∆=∠=︒,则三棱锥—P ABC 的外接球体积的最小值为 ( )A .4πB .43πC .π64D .332π7.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且tan 21tan A cB b+=,则角A 的大小为( ) A .6πB .4πC .3πD .23π8.在边长为1的等边三角形ABC 中,点P 是边AB 上一点,且.2BP PA =,则CP CB ⋅=u u u r u u u r( )A .13B .12C .23 D .19.如图所示,函数3tan 26y x π⎛⎫=+ ⎪⎝⎭的部分图象与坐标轴分别交于点,,D E F ,则DEF ∆的面积等于( )A .4πB .2πC .πD .2π10.在ABC ∆中,内角,,A B C 的对边分别为,,a b c .若ABC ∆的面积为S ,且1a =,2241S b c =+-,则ABC ∆外接圆的面积为( )A .4πB .2πC .πD .2π11.已知函数()sin()f x x ωϕ=+(0>ω,||2ϕπ<),其图象相邻两条对称轴之间的距离为4π,将函数()y f x =的图象向左平移316π个单位后,得到的图象关于y 轴对称,那么函数()y f x =的图象( )A .关于点(,0)16π-对称B .关于点(,0)16π对称C .关于直线16x π=对称 D .关于直线4πx =-对称12.已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤,则24z x y =+的最小值是( )A .6-B .5C .10D .10-二、填空题:本题共4小题,每小题5分,共20分。
2019-2020学年重庆市九龙坡区杨家坪中学高一上学期第一次月考数学试题(解析版)

2019-2020学年重庆市九龙坡区杨家坪中学高一上学期第一次月考数学试题一、单选题1.已知全集{1,2,3,4,5,6,7,8}U =,集合{1,2,3,4}A =,{3,4,5,6}B =,则()U C A B =( )A .{1,2,3,4,5,6}B .{7,8}C .{3,4}D .{}1,2,5,6,7,8【答案】B【解析】{}1,2,3,4,5,6A B ⋃=,所以(){}7,8U C A B ⋃=,故选B 。
2.已知函数223(0)()1(0)x x f x x x ⎧⎪-≥=⎨+<⎪⎩则f [f (1)]=()A .1-B .2C .1D .5【答案】B【解析】根据分段函数的解析式,直接把x =1代入即可求解. 【详解】∵f (x )()()223010x x x x ⎧-≥⎪=⎨+⎪⎩<,∴f (1)=﹣1,则f [f (1)]=f (﹣1)=2, 故选:B . 【点睛】本题主要考查了分段函数的函数值的求解,属于基础试题. 3.函数()12x f x a -=+(0a >且1a ≠)的图象恒过定点( )A .()0,3B .()1,3C .()1,2-D .()1,3-【答案】B【解析】计算当1x =时,()13f =,得到答案. 【详解】()12x f x a -=+,当1x =时,()13f =,即函数图像恒过定点()1,3故选:B本题考查了函数过定点问题,属于基础题型. 4.在下列四组函数中,表示同一函数的是( ). A .()()0,1f x x g x ==B .()()f x g x ==C .(1)(3)(),()31x x f x g x x x -+==+-D .()()=,f x x g x =【答案】D【解析】分别对四个选项中的两个函数的定义域、值域等进行分析,由此得出正确选项. 【详解】对于A 选项,()f x 的定义域为{}|0x x ≠,而()g x 的定义域为R ,所以两个是不相同的函数.对于B 选项,()f x 的定义域为{}|1x x ≥,而()g x 的定义域为{|1x x ≤-,或}1x ≥,所以两个是不相同的函数.对于C 选项,()f x 的定义域为{}|1x x ≠,()g x 的定义域为R ,所以两个是不相同的函数.对于D 选项,两个函数的定义域都为R ,值域都为[)0,+∞,且解析式都可以化为()()f x g x x ==,即对应关系也相同,所以是两个相同的函数.故选D 【点睛】本小题主要考查两个函数相同的概念和运用,考查函数的定义域、值域和对应关系,属于基础题.5.已知集合{|P x y ==,集合{|Q y y =,则P 与Q 的关系是( )A .P Q =B .P Q ⊆C .P Q ⊇D .PQ =∅【答案】C【解析】求函数定义域求得集合P ,求函数值域求得集合Q ,由此得出两个集合的关系. 【详解】对于集合A ,由10x +≥解得1x ≥-.对于集合Q ,0y ≥.故集合P 包含集合Q ,所以本小题选C.本小题主要考查集合与集合的关系,考查函数定义域和值域的求法,考查集合的研究对象,属于基础题.6.设0.6 1.50.60.60.6 1.5a b c ===,,,则a b c ,,的大小关系是( ) A .a b c << B . a c b << C .b a c << D .b c a <<【答案】C【解析】由0.6xy =在区间(0,)+∞是单调减函数可知, 1.50.600.60.61<<<,又0.61.51>,故选C .【考点】1.指数函数的性质;2.函数值比较大小.7.已知1)f x =+,则()f x 的解析式是( ) A .2()1f x x =-B .2()1(1)f x x x =-≥ C .2()41(1)f x x x x =--≥ D .2()1f x x =+【答案】B【解析】利用配方法,把f 1)的解析式配方,求出f (x )的解析式与定义域. 【详解】∵f 1)=x∴f 1)=x 1﹣1)21=-1,∴f (x )=x 2﹣1;≥01≥1, ∴f (x )的定义域是{x |x ≥1};即f (x )的解析式为f (x )=x 2﹣1(x ≥1). 故选:B . 【点睛】本题考查了求函数定义域的问题及函数解析式的求法,解题时应根据函数的解析式特点选择适当的方法,是基础题.8.若()f x 是偶函数,且对任意12,x x ∈(0,)+∞且12x x ≠,都有()()21210-f x f x x x -<,则下列关系式中成立的是( )A .123()()()234f f f >->B .132()()()243f f f >->C .312()()()423f f f >->D .321()()()432f f f ->>【答案】A【解析】由于对任意的x 1,x 2∈(0,+∞),都有()()21210-f x f x x x -<,可得函数f (x )在(0,+∞)上单调递减,即可得出. 【详解】∵对任意的x 1,x 2∈(0,+∞),都有()()21210-f x f x x x -<, ∴函数f (x )在(0,+∞)上单调递减, 又∵123234<<, ∴123234f f f ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭>>, 又∵f (x )是偶函数,∴f (﹣23)=f (23). ∴123234f f f ⎛⎫⎛⎫⎛⎫-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭>>. 故选:A . 【点睛】本题考查了函数的奇偶性、单调性的应用,属于基础题.9.某公司市场营销人员的个人月收入与其每月的销售量成一次函数关系,其图象如图所示,由图中给出的信息可知,营销人员没有销售量时的收入是( )A .3100元B .3000元C .2900元D .2800元【答案】B【解析】设()f x kx b =+ ,根据图像得到()()180002213000f k b f k b ⎧=+=⎪⎨=+=⎪⎩解得答案.【详解】设()f x kx b =+ ,根据图像知:()()180002213000f k b f k b ⎧=+=⎪⎨=+=⎪⎩ 解得:3000=b故选:B 【点睛】本题考查了函数解析式的计算,意在考查学生的应用能力.10.已知函数()241f x x kx =+-在区间[]1,2上是单调函数,则实数k 的取值范围是( ) A .(][),168,-∞--+∞B .[]16,8--C .()[),84,-∞--+∞D .[]8,4--【答案】A【解析】根据二次函数对称轴与区间[]1,2的相对关系即可求出k 的取值范围. 【详解】因为()241f x x kx =+-的对称轴方程为8kx =-,且在区间[]1,2上是单调函数, 所以18k -≤或28k-≥ 解得8k ≥-或16k ≤-,故选A. 【点睛】本题主要考查了二次函数单调区间与对称轴的关系,属于中档题.11.已知函数,1()(32)2,1ax f x x a x x ⎧-≤-⎪=⎨⎪-+>-⎩,在(—∞,+∞)上为增函数,则实数a 的取值范围是( )A .30,2⎛⎤⎥⎝⎦B .30,2⎛⎫ ⎪⎝⎭C .31,2⎡⎫⎪⎢⎣⎭D .31,2⎡⎤⎢⎥⎣⎦【答案】C【解析】若函数()()13221ax f x x a x x ⎧-≤-⎪=⎨⎪-+>-⎩,,是R 上的增函数,则0320232a a a a ⎧⎪-⎨⎪≤-+⎩>>,解得答案. 【详解】∵函数()()13221ax f x x a x x ⎧-≤-⎪=⎨⎪-+>-⎩,,是R 上的增函数,,∴0320232a a a a ⎧⎪-⎨⎪≤-+⎩>>, 解得a ∈312⎡⎫⎪⎢⎣⎭,, 故选:C . 【点睛】本题考查的知识点是分段函数单调性的性质,首先保证每一段单增,再保证分段点处增,属于中档题.12.定义在R 上的函数()f x 若满足:①对任意1x ,2x 且12x x ≠,都有()()()21210x x f x f x --<⎡⎤⎣⎦;②对任意x ,都有()()2f a x f a x b ++-=,则称函数()f x 为“中心捺函数”,其中点(),a b 称为函数()f x 的中心.已知函数()1y f x =-是以()1,0为中心的“中心捺函数”,若满足不等式()()2222f m n f n m +≤---,当1,12m ⎡⎤∈⎢⎥⎣⎦时,m m n +的最小值为( )A .2B .18C .14D .12【答案】C【解析】根据题意得到函数()f x 为单调递减函数和奇函数,化简不等式()()2222f m n f n m +≤---得到()()20m n m n -+-≥,画出表示的区域,将mm n+变换为11n m+,根据斜率得到最小值. 【详解】对任意1x ,2x 且12x x ≠,都有()()()21210x x f x f x --<⎡⎤⎣⎦,则函数单调递减;()()1y g x f x ==-是以()1,0为中心的“中心捺函数,则(1)(1)0g x g x ++-=即化简得到()()0f x f x +-= ,()f x 为奇函数.()()()2222222222f m n f n m f n m m n n m+≤---=+∴+≥+()()20m n m n∴-+-≥,1,12m⎡⎤∈⎢⎥⎣⎦,表示的区域如图所示:11mnm nm=++,根据图像知:nm表示点(),m n到原点的斜率当13,22m n==时有nm最大值为3,故11mnm nm=++最小值为14故选:C【点睛】本题考查了函数的单调性,奇偶性,线性规划,意在考查学生的综合应用能力和对于函数性质的灵活运用.二、填空题13.已知集合{}20,32A m m=-+,且2A∈,则实数m的值为_______.【答案】3或0【解析】根据题意得到方程2322m m-+=解得答案.【详解】{}20,32A m m=-+,2A∈则23220m m m-+=∴=或3m=故答案为:3或0【点睛】本题考查了元素和集合的关系,属于简单题. 14.函数24313x x y --+⎛⎫= ⎪⎝⎭的单调递增区间是________.【答案】()2,-+∞【解析】设13uy ⎛⎫= ⎪⎝⎭,243x u x -+=-,分别计算函数单调性利用复合函数单调性得到答案. 【详解】24313x x y --+⎛⎫= ⎪⎝⎭,设13uy ⎛⎫= ⎪⎝⎭,243x u x -+=- 易知:13uy ⎛⎫= ⎪⎝⎭单调递减;()224327x x u x -+=-++=-,在()2,-+∞单调递减;故24313x x y --+⎛⎫= ⎪⎝⎭的单调递增区间是()2,-+∞故答案为:()2,-+∞ 【点睛】本题考查了复合函数的单调性,掌握复合函数单调性同增异减的法则是解题的关键. 15.若函数()f x 的定义域为[]1,4-,则函数()21f x -的定义域为________. 【答案】50,2⎡⎤⎢⎥⎣⎦【解析】根据抽象函数定义域得到不等式1214x -≤-≤,计算得到答案. 【详解】函数()f x 的定义域为[]1,4-,则函数()21f x -的定义域满足:1214x -≤-≤ 解得502x ≤≤故答案为:50,2⎡⎤⎢⎥⎣⎦【点睛】本题考查了抽象函数定义域,意在考查学生对于定义域的理解掌握.16.已知()y f x =和()2y f x =+是偶函数,且()13f =,设()()()F x f x f x =+-,则()3F =________.【答案】6【解析】根据()2y f x =+得到()()22f x f x +=-+,故()()313f f ==,根据偶函数性质计算得到答案. 【详解】()2y f x =+是偶函数,即()()22f x f x +=-+,故()()313f f == ()()()()333236f f f F +-===故答案为:6 【点睛】本题考查了函数值的计算,意在考查学生对于函数性质的灵活运用.三、解答题17.已知{}13A x x =<≤,集合{}21B x m x m =≤≤-. (1)当1m =-时,求AB ;(2)若A B ⊆,求实数m 的取值范围; (3)若AB =∅,求实数m 的取值范围.【答案】(1){}23A B x x ⋃=-≤≤;(2)2m ≤-;(3)0m ≥ 【解析】(1)写出集合,A B ,再计算AB 得到答案.(2)根据A B ⊆得到不等式1321m m -≥⎧⎨≤⎩,解得答案.(3)讨论B =∅和B ≠∅两种情况,分别计算得到答案. 【详解】(1)1m =-时:{}13A x x =<≤,{}22B x x =-≤≤,故{}23A B x x ⋃=-≤≤(2)A B ⊆,则满足1321m m -≥⎧⎨≤⎩ 解得2m ≤-(3)当B =∅时:1123m m m -<∴>; 当B ≠∅时:满足1211m m m -≥⎧⎨-≤⎩ 或1223m m m -≥⎧⎨>⎩解得103m ≤≤;综上所述:0m ≥ 【点睛】本题考查了集合的运算,根据集合关系求参数,忽略掉空集是容易发生的错误.18.已知函数()f x 是定义在R 上的奇函数,且当0x ≤时,()22f x x x =+.(1)求函数()()f x x R ∈的解析式;(2)现已画出函数()f x 在y 轴左侧的图象,如图所示,请补全函数()f x 的图象; (3)根据(2)中画出的函数图象,直接写出函数()f x 的单调减区间.【答案】(1)()222,02,0x x x f x x x x ⎧+≤=⎨-+>⎩;(2)详见解析;(3)()f x 在(),1-∞-和()1,+∞上单调递减【解析】(1)设0x >时,0x -<,根据函数的奇偶性得到函数表达式. (2)画出函数图像得到答案. (3)根据函数图像直接写出答案. 【详解】(1)当0x >时,0x -<,则()22f x x x -=-,函数为奇函数,()()22f x f x x x =--=-+ 故()222,02,0x x x f x x x x ⎧+≤=⎨-+>⎩(2)如图所示:(3)根据函数图像知:()f x 在(),1-∞-和()1,+∞上单调递减 【点睛】本题考查了利用函数奇偶性求解析式,图像和单调性,意在考查学生对于函数知识的综合运用.19.为了保护环境,某单位采用新工艺,把二氧化碳转化为一种可利用的化工产品。
【附20套高考模拟试题】2020届重庆市重点中学高考数学模拟试卷含答案

圆上一动点(异于左右顶点),且 QF1F2 的周长为 4 4 2 .
1 求椭圆 E 的方程; 2 过点 F1, F2 分别作斜率为 k1, k2 的直线 l1,l2 ,分别交椭圆 E 于 A, B 和 C, D 四点,且
AB CD 6 2 ,求 k1k2的值.
21.(12 分)已知 a ( 3 cos x,cos x) , b (sin x, cos x) ,函数 f (x) a b .求 f (x) 的最小正周期及
(1 )求角 B 的大小.
BD 3 21
( 2 )已知 c 2 ,边 AC 边上的高
7 ,求 ABC 的面积 S 的值.
18.(12
分)已知函数
f
x
lnx
ax2
x
3 2
( a 为常数,且 a R
)当 a
1 时,求函数
f
x 的单调
区间;若函数 f x 在区间 0,1 上有唯一的极值点 x0 ,求实数 a 和极值 f x0 的取值范围.
上存在点 P ,使 PF1F2 是有一个内角为
2 3
的等腰三角形,
则 M 的离心率是( )
3 1
2 1
A. 3 1 B. 2 1 C. 2 D. 2
3.程大位《算法统宗》里有诗云“九百九十六斤棉,赠分八子做盘缠.次第每人多十七,要将第八数来言.
务要分明依次弟,孝和休惹外人传.”意为: 996 斤棉花,分别赠送给 8 个子女做旅费,从第一个开始,以
对称轴方程;当 x ( , ] 时,求 f (x) 单调递增区间.
22.(10 分) ABC 的内角 A、B、C 所对的边分别为 a、b、c ,且满足 a2 c2 2 3 ac b2 . 3
AD 6 ,求 ABD 的面积.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(Ⅲ)设 x1是方程 f (x) x 0 的实数根,求证:对于 f (x) 定义域中任意的 x2、x3 ,当| x2 x1 | 1,且 | x3 x1 | 1 时,| f (x3) f (x2 ) | 2 .
x
D
21、(本小题满分 14 分)设 M 是由满足下列条件的函数 f (x) 构成的集合:“①方程 f (x) x 0有实数 根;②函数 f (x) 的导数 f (x) 满足 0 f (x) 1”.
(Ⅰ)判断函数 f (x) x sin x 是否是集合 M 中的元素,并说明理由; 24
(Ⅱ)集合 M 中的元素 f (x) 具有下面的性质:若 f (x) 的定义域为 D,则对于任意[m,n] D,都存在 x0 [m,n],使得等式 f (n) f (m) (n m) f (x0 ) 成立”,试用这一性质证明:方程 f (x) x 0 只
A. 1 2
B. 2 2
C. 2
D. 3 2
3、如果执行的程序框图(右图所示),那么输出的 S ( ).
A.2450 B.2500 C.2550 D.2652
4、若曲线 y 2x2 的一条切线 l 与直线 x 4y 8 0
垂直,则切线 l 的方程为( ). A、 4x y 2 0 B、 x 4y 9 0
(Ⅰ)求首项 a1 和公比 q 的值; (Ⅱ)若 Sn 210 1,求 n 的值.
17、(本小题满分 12 分)设函数 f (x) 2 cos2 x sin 2x a(a R) . (Ⅰ)求函数 f (x) 的最小正周期和单调递增区间; (Ⅱ)当 x [0, ] 时, f (x) 的最大值为 2,求 a 的值,并求出 y f (x)(x R) 的对称轴方程.
高考模拟数学试卷
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中.只有一项是符合题目 要求的.
1、设函数 y x 2 的定义域为集合 M,集合 N= y | y x2, x R ,则 M N ( ).
A.
B.N
C.0,
D.M
开始
2、已知椭圆的长轴长是短轴长的 2 倍,则椭圆的离心率等于( ).
为
.
15、(几何证明选讲选做题)如图,平行四边形 ABCD 中,
AE : EB 1: 2 ,若 AEF 的面积等于 1cm 2 ,
则 CDF 的面积等于
cm 2 .
D
F
A
E
C B
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16、(本小题满分 12 分)设正项等比数列 an 的前 n 项和为 Sn , 已知 a3 4 , a4a5a6 212 .
.
10、已知
2
,
,
sin
3 5
,则 tan
=
.
11、 i 是虚数单位,则1 C61i C62i 2
C63i 3
C64i 4
C65i 5
C
6 6
i
6
.
12、函数 f (x) 由下表定义:
x
2
5
3
1
4
f (x) 1
2
3
4
5
若 a0 5 , an1 f (an ) , n 0,1, 2, ,则 a2007
6
18、(本小题满分 14 分)一个口袋中装有大小相同的 2 个白球和 4 个黑球. (Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
n
(方差: D pi (i E )2 ) i 1
19、(本小题满分 14 分)如图,已知四棱锥 P ABCD 的 底面 ABCD是菱形; PA 平面 ABCD, PA AD AC , 点 F 为 PC 的中点. (Ⅰ)求证: PA // 平面 BFD ; (Ⅱ)求二面角 C BF D 的正切值.
C、 4x y 3 0 D、 x 4y 3 0
5、方程 x2 x n 0(n (0,1)) 有实根的概率为( ).
k=1
Hale Waihona Puke S 0k 50?是
S S 2k
否
输出S
k k 1
结束
A、 1 2
B、 1 3
C、 1 4
D、 3 4
6、已知, 是平面, m, n 是直线,则下列命题中不正确的是( ).
若 2 x 10 ,记 y f (x) ,则 y f (x) 的图象是( ).
y
12
y
x
12
y 5
5
1
O2 A
10 x
1
O2
B
10
x
y
y
10
10
8、将函数 y sin(2x ) 的图象先向左平移 ,然后将所得图象上所有点的横坐标变为原来的 2 倍(纵
3
6
坐标不变),则所得到的图象对应的函数解析式为( ).
A、若 m ∥ n, m ,则 n B、若 m ∥, n ,则 m ∥ n
C、若 m , m ,则 ∥ D、若 m , m ,则
7、一张正方形的纸片,剪去两个一样的小矩形得到一个“ E ”图案,
如图所示,设小矩形的长、宽分别为 x 、 y ,剪去部分的面积为 20 ,
.
13 、 ( 坐 标 系 与 参 数 方 程 选 做 题 ) 曲 线
C1
:
x
y
1 cos sin
(为参数)
上的点到曲线
C2
:
x y
2 1
2 1t 2
1 2
t
(t为参数)上的点的最短距离为
.
14、(不等式选讲选做题)已知实数 a、b、x、y 满足 a 2 b2 1, x 2 y 2 3 ,则 ax by 的最大值
B
P
F
A
D
C
20、(本小题满分 14 分)给定圆 P x2 y2 2x 及抛物
线 S y2 4x ,过圆心 P 作直线 l ,此直线与上述两曲线 的四个交点,自上而下顺次记为 A、B、C、D ,如果线 段 AB、BC、CD 的长按此顺序构成一个等差数列,求直 线 l 的方程.
y A
B
P
o C
A. y cos x
B. y sin 4x
C. y sin(x ) 6
第Ⅱ卷(非选择题,共 110 分)
D. y sin x
二、填空题:本大题共7小题,其中13~15题是选做题,考生只能选做两题,三题全答的,只计算前两题
得分.每小题5分,满分30分.
9、已知向量 c (2x 1, 4) , d (2 x,3) ,若 c// d ,则实数 x 的值等于
