立体几何求体积方法总结及习题演练(精)
立体几何求体积大题

立体几何中有关体积问题一、知识归纳一、知识归纳1、柱体体积公式:.V S h =2、椎体体积公式:1.3V S h =3、球体体积公式:343V R π=二、点到平面的距离问题二、点到平面的距离问题 求解方法:求解方法:1、几何法:等体积法求h2、向量法:、向量法: 点A 到面α的距离AB nd n•=u u u u r r r其中,n →是底面的法向量,点B 是面α内任意一点。
内任意一点。
题型分析:题型分析:1、如图,在三棱柱111ABC A B C -中,AC BC ⊥,1AB BB ⊥12AC BC BB ===,D 为AB 中点,且1CD DA ⊥(1)求证:1BB ABC ⊥平面 (2)求证:1BC ∥平面1CA D (3)(3)求三棱椎求三棱椎11-A B DC 的体积的体积2、如图,在四棱锥E ABCD -中,ADE ∆是等边三角形,侧面ADE ABCD ⊥地面,AB ∥DC ,且,且2435BD DC AD AB ====,,.(1)若F 是EC 上任意一点,求证:面BDF ADE ⊥面(2)(2)求三棱锥求三棱锥C BDE -的体积。
的体积。
3、如图,在棱长为2的正方体中,,E F 分别为1DD DB 、的中点。
的中点。
(1)求证:EF ∥平面11ABC D (2) (2)求证求证1EF B C ⊥ (2)求三棱锥1B EFC -的体积。
1A 1B 1C A DCB1A 1B 1C AECBDF1D A ECBDF4、如图,已知四棱锥P ABCD -的底面为等腰梯形,AB ∥CD ,AC BD ⊥,垂足为H ,PH 是四棱锥的高。
(Ⅰ)证明:平面PAC ⊥ 平面PBD ; (Ⅱ)若6AB =,APB ADB ∠=∠=60°,求四棱锥P ABCD -的体积。
的体积。
5、如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥;(II )设PD=AD=1,求棱锥D-PBC 的高.的高.6、如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点。
立体几何求体积专题精编版.doc
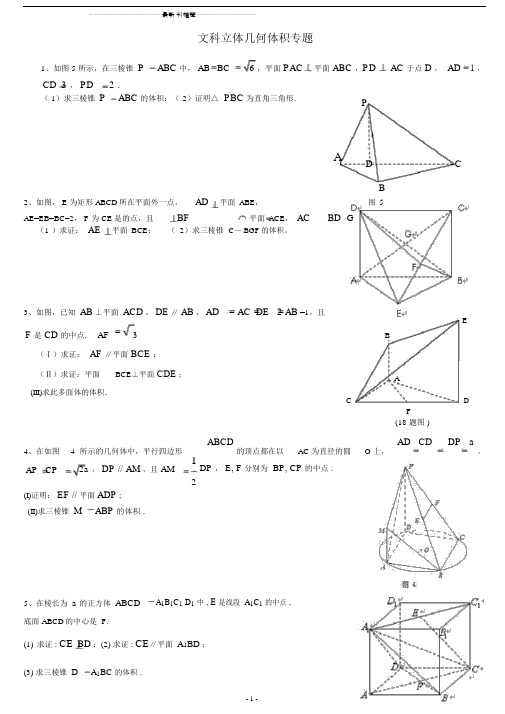
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯文科立体几何体积专题1、如图 5 所示,在三棱锥P ABC 中,AB BC 6 ,平面PAC 平面 ABC ,PD AC 于点 D , AD 1 ,CD 3 , PD 2 .( 1)求三棱锥P ABC 的体积;(2)证明△ PBC 为直角三角形.PAD CB2、如图, E 为矩形 ABCD所在平面外一点,AD平面ABE,图5AE=EB=BC=2, F 为 CE是的点,且BF平面ACE,AC BD G(1 )求证:AE平面BCE;(2)求三棱锥C— BGF的体积。
3、如图,已知AB⊥平面ACD,DE∥AB,AD AC DE 2 AB =1,且EF 是 CD 的中点.AF 3 B(Ⅰ)求证: AF ∥平面 BCE ;(Ⅱ)求证:平面BCE⊥平面CDE; A(III)求此多面体的体积.C DF(18 题图 )4、在如图 4 所示的几何体中,平行四边形ABCD的顶点都在以AC 为直径的圆O 上,AD CD DP a,AP CP 2a ,DP // AM,且 AM 1DP , E, F 分别为 BP, CP 的中点. 2(I)证明:EF //平面ADP ;(II)求三棱锥M ABP 的体积.5、在棱长为a的正方体ABCD A1B1C1 D1中,E是线段 A1C1的中点, 底面 ABCD的中心是 F.(1)求证 : CE BD;(2) 求证 : CE∥平面A1BD;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6、矩形 ABCD 中, 2AB AD ,E 是 AD 中点,沿 BE 将 ABE 折起到 A ' BE的位置,使 ''D , F 、 G 分别是 BE 、 CD 中点 .AC A ( 1)求证: A F ⊥ CD ;( 2)设 AB2,求四棱锥 A BCDE 的体积 .7 、 如 图 , 在 四 棱 锥P ABCD 中 , 底 面 是 边 长 为2 的 正 方 形 , 侧 面 PAD 底面 ABCD , 且A B C DP A P D2A ,D 若 E 、 F 分别为 PC 、 BD 的中点 .2( 1)求证: EF ∥平面 PAD ;( 2)求证:平面 PDC 平面 PAD .( 3)求四棱锥 P ABCD 的体积 V P ABCD .8、如图 , 在直三棱柱ABC A 1B 1C 1 中, AC 3 , BC 4, AB 5 , AA 1 4 ,点 D 是 AB 的中点,( 1)求证: AC BC 1 ;( 2)求证: AC 1 // 平面 CDB 1 ;( 3)求三棱锥 C 1 CDB 1 的体积。
立体几何体积表面积题型总结

立体几何体积表面积题型总结全文共四篇示例,供读者参考第一篇示例:立体几何体积和表面积是几何学中非常重要的概念,它们广泛应用于日常生活和各种工程领域。
在考试中,经常会出现与立体几何体积和表面积相关的题型,考查学生的综合能力和解题技巧。
本文将对关于立体几何体积表面积题型进行总结,希望能帮助读者更好地掌握相关知识。
在解立体几何体积表面积题型时,首先需要了解各种常见几何体的体积和表面积公式。
下面是一些常见几何体的体积和表面积公式:1. 立方体:- 体积公式:V = a³ (a为边长)- 表面积公式:S = 6a²了解以上公式是解立体几何体积表面积题目的基础,接下来需要根据具体题目的要求灵活运用这些公式。
在解题过程中,可以遵循以下一般步骤:1. 画图:根据题目绘制准确的图形,有助于理清思路和分析问题。
2. 确定参数:明确各个参数的含义,包括边长、半径、高等。
3. 应用公式:根据具体题目要求,选择合适的体积和表面积公式进行计算。
4. 计算验证:将得到的具体数值代入公式进行计算,并进行验证。
5. 总结解法:总结解题过程,确保计算结果正确且符合题目要求。
在解题过程中,有一些常见的考点和技巧也是需要注意的,下面列举一些常见的题型及解题技巧:1. 混合体积问题:有时题目会涉及到多种几何体的组合,需要将各个部分的体积分别计算,然后相加得到总体积。
2. 变换题型:有些题目需要根据给定条件进行变换,例如将一个正方体切割成若干小正方体,需要注意每个小正方体的边长与体积的关系。
3. 边长、半径的关系:根据题目给定的条件,需灵活利用边长、半径之间的关系来求解问题。
4. 知己知彼:要根据具体题目的特点选择合适的解题方法,不要死记硬背,要有灵活应对的能力。
5. 多维度思考:对于复杂的题目,可以通过多种角度进行思考,可以更快地找到解题思路。
第二篇示例:立体几何体积和表面积是几何学中非常重要的概念,它们广泛应用于工程、建筑、物理学和计算机图形学等领域。
立体几何形的体积计算知识点总结

立体几何形的体积计算知识点总结体积是立体几何形的一个重要属性,它用来描述一个物体所占的空间大小。
在几何学中,我们经常需要计算不同形状的物体的体积。
为了更好地理解和掌握立体几何形的体积计算,我们需要掌握一些基本的知识点。
本文将根据不同的几何形状,总结一些常用的体积计算公式和方法。
一、正方体的体积计算正方体是最简单的立体几何形之一,它的六个面都是正方形。
计算正方体的体积非常简单,只需要将正方体的边长乘以自身再乘以自身即可。
即体积=边长×边长×边长。
例如,一个边长为5厘米的正方体的体积为5×5×5=125立方厘米。
二、长方体的体积计算长方体是更常见的一种立体几何形,它的六个面中,相对的两个面是相等的长方形。
计算长方体的体积也非常简单,只需要将长方体的长、宽和高相乘即可。
即体积=长×宽×高。
例如,一个长10厘米,宽6厘米,高8厘米的长方体的体积为10×6×8=480立方厘米。
三、圆柱体的体积计算圆柱体是一个底面为圆形的立体几何形。
要计算圆柱体的体积,需要知道底面的半径和高。
计算公式为体积=底面积×高=π×半径的平方×高。
例如,一个底面半径为3厘米,高为6厘米的圆柱体的体积为3.14×3×3×6=169.56立方厘米。
四、球体的体积计算球体是一个所有点到球心的距离都相等的立体几何形。
计算球体的体积需要知道球的半径。
计算公式为体积=4/3×π×半径的立方。
例如,一个半径为4厘米的球体的体积为4/3×3.14×4×4×4=268.08立方厘米。
五、锥体的体积计算锥体是一个底面为圆形,顶点与底面圆心相连的立体几何形。
计算锥体的体积需要知道底面的半径和高。
计算公式为体积=1/3×底面积×高=1/3×π×半径的平方×高。
求立体几何形的体积的方法总结

求立体几何形的体积的方法总结立体几何形的体积计算方法总结立体几何形体积的计算是数学中的重要内容。
很多地方需要用到立体几何体积的计算方法,例如建筑、机械、化学等各个领域。
下面将对常见的几何体体积计算方法进行总结和介绍。
1. 直体的体积计算方法直体是指由两个平行的底面和沿着这两个底面的侧面组成的几何物体,如长方体、正方体、圆柱体、圆锥体等。
由于其底面和侧面的性质很稳定,直体的体积计算方法比较简单,一般采用公式计算即可。
如:(1)长方体的体积计算公式为V= lwh,其中l、w、h分别为长方体的长、宽和高。
(2)正方体的体积计算公式为V= a^3,其中a为正方体的边长。
(3)圆柱体的体积计算公式为V= πr^2h,其中r为圆柱体的底面半径,h为圆柱体的高。
(4)圆锥体的体积计算公式为V= 1/3 πr^2h,其中r为圆锥体的底面半径,h为圆锥的高。
以上公式计算的是标准形状的直体,如果是不规则形状的直体,可以将其划分为一些标准形状,然后分别计算,再将它们的体积相加。
2. 曲体的体积计算方法与直体不同,曲体是由曲面和两个端面(底面和顶面)组成的,如球体、棱锥、棱台、棒球棒等。
由于曲面的性质比较复杂,因此曲体的体积计算方法也相对较为复杂。
(1)球体的体积计算公式为V= 4/3 πr^3,其中r为球体的半径。
(2)棱锥的体积计算公式为V= 1/3 Sbh,其中S为底面的面积,b为底边长,h为高。
(3)棱台的体积计算公式为V= 1/3 h(S1+S2+√S1S2),其中S1、S2分别为上下底面的面积。
(4)棒球棒的体积计算需要将其分解为许多简单的几何图形,如圆台、圆柱、球等,然后分别计算它们的体积,再将其相加。
3. 复合体的体积计算方法复合体是由多个几何图形组成的,如汽车、火车等复杂的机械产品,通过将其分解成为多个简单的几何图形,每个几何图形计算体积,最后加和,来求出总体积。
总之,立体几何形的体积计算方法根据几何形状的不同而有所不同,有些体积计算公式比较简单,有些比较复杂。
习题范例解决立体几何中的体积问题

习题范例解决立体几何中的体积问题在立体几何的学习中,计算体积是一个重要的问题。
体积表示了一个立体物体所占据的空间大小,它在数学和实际应用中都有着广泛的应用。
为了更好地理解和解决立体几何中的体积问题,本文将通过一些习题范例来进行详细的解析。
1. 三棱柱的体积计算题目:一个三棱柱的底面是一个边长为5cm的等边三角形,高度为8cm。
求这个三棱柱的体积。
解析:首先计算底面的面积。
由于等边三角形的面积公式为 (边长)^2 * √3 / 4,代入数值计算得到底面面积为(5^2 * √3) / 4 = 10.83cm^2。
然后将底面面积乘以高度,即可得到体积。
计算结果为 10.83cm^2* 8cm = 86.64cm^3。
因此,这个三棱柱的体积为 86.64cm^3。
2. 圆柱的体积计算题目:一个圆柱的底面半径为4cm,高度为10cm。
求这个圆柱的体积。
解析:圆柱的面积公式为π * (半径)^2 * 高度。
代入数值进行计算,即可得到体积。
计算结果为π * 4cm^2 * 10cm = 125.66cm^3。
因此,这个圆柱的体积为 125.66cm^3。
3. 球的体积计算题目:一个球的半径为6cm。
求这个球的体积。
解析:球的体积公式为4/3 * π * (半径)^3。
代入数值进行计算,即可得到体积。
计算结果为4/3 * π * 6cm^3 = 904.78cm^3。
因此,这个球的体积为 904.78cm^3。
4. 锥体的体积计算题目:一个锥体的底面半径为3cm,高度为5cm。
求这个锥体的体积。
解析:锥体的体积公式为1/3 * π * (半径)^2 * 高度。
代入数值进行计算,即可得到体积。
计算结果为1/3 * π * 3cm^2 * 5cm = 15.71cm^3。
因此,这个锥体的体积为 15.71cm^3。
通过以上习题范例的解析,我们可以看到,计算立体几何中的体积问题需要根据不同的几何体选择相应的公式进行计算。
高考数学中的立体几何体积

高考数学中的立体几何体积在高考数学中,立体几何是我们必须要掌握的一项知识。
其中,计算各种立体几何的体积也是一项非常重要的技能。
那么,在立体几何中,我们应该如何计算体积呢?本文将详细探讨这个问题,帮助大家更好地掌握立体几何的体积计算知识。
1. 三棱锥体积的计算我们先来看一下三棱锥体积的计算。
三棱锥是指顶点为三角形顶点,底面为三角形的锥体。
计算三棱锥体积的公式为:$V =\frac{1}{3}S_hh$,其中$S_h$为底面积,$h$为高。
我们可以通过以下例题来更好地理解三棱锥体积的计算方法:如图所示,底面为边长为$3$的等边三角形,高为$4$,求此三棱锥的体积。
解:首先,我们需要求出三角形的面积$S$。
由于此三角形是等边三角形,因此可以使用海伦公式计算其面积:$$S=\sqrt{3}\times\frac{(3+3+3)}{2}\times\frac{(3+3-3)}{2}=3\sqrt{3}$$由此,我们可以得到该三棱锥的体积$V$:$$V=\frac{1}{3}S_hh=\frac{1}{3}\times3\sqrt{3}\times4=4\sqrt{3} $$因此,该三棱锥的体积为$4\sqrt{3}$。
2. 圆锥体积的计算我们接下来来看圆锥体积的计算。
圆锥是指顶点在圆锥轴上,底面为圆的锥体。
计算圆锥体积的公式为:$V = \frac{1}{3}\pir^2h$,其中$r$为底面半径,$h$为高。
以下是一个例题:如图所示,底面半径为$4$,高为$5$,求此圆锥的体积。
解:根据圆锥的体积公式,可以轻松计算出此圆锥的体积$V$:$$V=\frac{1}{3}\pir^2h=\frac{1}{3}\pi\times4^2\times5=\frac{80}{3}\pi$$因此,该圆锥的体积为$\frac{80}{3}\pi$。
3. 球体积的计算最后,我们来看一下球体积的计算。
球体积是指球体内部所填充的物质的容积。
立体几何体积计算练习题

立体几何体积计算练习题1. 正方体计算(1) 已知一个正方体的边长为5cm,计算其体积。
解答:正方体的体积计算公式为V = a³,其中a为正方体的边长。
代入已知数据可得,V = 5cm × 5cm × 5cm = 125cm³。
(2) 若正方体的体积为64cm³,求其边长。
解答:将正方体的体积计算公式改写为a³ = V。
代入已知数据可得,a³ = 64cm³。
对等式两边开立方根可得,a = ∛(64cm³) = ∛(4 × 4 × 4cm³) = 4cm。
因此,正方体的边长为4cm。
2. 长方体计算(1) 已知一个长方体的长、宽、高分别为8cm、6cm和4cm,计算其体积。
解答:长方体的体积计算公式为V = lwh,其中l、w和h分别为长方体的长、宽和高。
代入已知数据可得,V = 8cm × 6cm × 4cm = 192cm³。
(2) 若长方体的体积为360cm³,已知长和宽的比为2:3,求长方体的长、宽和高。
解答:设长和宽分别为2x和3x(其中x为比例系数),代入长方体的体积计算公式可得,(2x) × (3x) × h = 360cm³。
化简该方程可得,6x²h = 360cm³。
解方程可得,h = 360cm³ / (6x²)。
同时,已知长和宽的比为2:3,即有 (2x) / (3x) = 2/3。
解方程可得,x = 3。
代入h的表达式可得,h = 360cm³ / (6 × 3²) = 10cm。
因此,长方体的长为2x = 2 × 3 = 6cm,宽为3x = 3 × 3 = 9cm,高为10cm。
3. 圆柱体计算(1) 已知一个圆柱体的底面半径为4cm,高为10cm,计算其体积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 1
求立体几何体积方法归纳
一、分割法
如右图,多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且三角形ADE ,BCF 均 为等边三角形,EF//AB ,EF=2,则该多面 体的体积为: 二、补形法
四面体S —ABC 的三组对棱分别相等,且依次为25、13、5,求该四面体的体积.
练习:已知:长方体ABCD-A 1B 1C 1D 1 中,AB=4
,BC=2,
BB 1=3,求三棱锥 B 1- AD 1C 的体积
三、等积转换法
在边长为a 的正方体ABCD —
A 1
B 1
C 1
D 1中,M 、N 、P 分别是棱A 1B 1、 A 1D 1、A 1A 上的点,且满足A 1M= A 1B 1, A 1N=2ND 1,A 1P= A 1A ,如图,试求 三棱锥A 1—MNP 的体积.
强化练习
1、如图,在边长为a 的正方体 ABCD-A 1B 1C 1D 1
中,点E 为AB 上的任意一点,求三棱锥 A 1-DEB 1 的体积。
2、已知三棱锥P —ABC 中,PA ⊥ BC 、 ED ⊥BC 、ED ⊥PA , , PA=BC=a 且ED=b 求三棱锥的体积
3、已知ABCD-A1B1C1D1是棱长为a 的正方体,E 、F 分别 是棱AA1与CC1的中点,求四棱锥A1-EBFD1的体积?
B B 1 C
D
A C 1 D 1
A
1 E
F。
