matlab 解线性方程组的迭代法
matlab迭代法解线性方程组
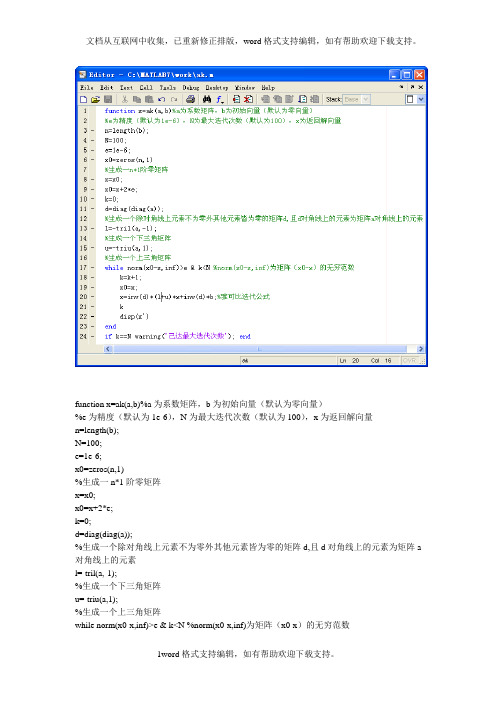
function x=ak(a,b)%a为系数矩阵,b为初始向量(默认为零向量)
%e为精度(默认为1e-6),N为最大迭代次数(默认为100),x为返回解向量
n=length(b);
N=100;
e=1e-6;
x0=zeros(n,1)
%生成一n*1阶零矩阵
x=x0;
x0=x+2*e;
k=0;
d=diag(diag(a));
%生成一个除对角线上元素不为零外其他元素皆为零的矩阵d,且d对角线上的元素为矩阵a 对角线上的元素
l=-tril(a,-1);
%生成一个下三角矩阵
u=-triu(a,1);
%生成一个上三角矩阵
while norm(x0-x,inf)>e & k<N %norm(x0-x,inf)为矩阵(x0-x)的无穷范数
k=k+1;
x0=x;
x=inv(d)*(l+u)*x+inv(d)*b;%雅可比迭代公式k
disp(x')
end
if k==N warning('已达最大迭代次数'); end
function X=BDD(f,x0,TOL)
%X用来存储迭代过程所有的根;
%f是符合不动点迭代要求的迭代方程;%x0设定的迭代初值;
%TOL允许的误差值;
x=feval(f,x0);
n=1;
X(:,n)=x;
while abs(x-x0)>TOL
x0=x;
x=feval(f,x0);
n=n+1;
X(:,n)=x;
end。
MATLAB方程的图形法迭代法直接法

5
迭代算法的步骤与技巧:
方程f(x)=0 (1)经过简单变形,化为xn+1= (xn), n=0,1,2... (2)*绘出y=x和y= (x)的图形,并观察 迭 第 (3)确定迭代初值x0,并代入程序进行迭代 代二 法 讲 (4)序列发散回到第1步;收敛获得求解
7
加速迭代法就是为了解决上述问题而产生的改进型 迭代法: 若迭代格式xn+1=(xn), n=0,1,2...,不收敛,则我们不 直接用(x)迭代,改用(x)与x的加权平均 h(x)= (x)+(1- )x 进行迭代,基于某个确定原则,比 如: =1/(1- '(xn) 改进后的加速迭代格式如下:
非线性是更一般的属性?
我们面对的大多数方程(组)都是非线性的。
2
定义:一些由实际问题列出的方程中常常包含三角 迭 第 函数、指数函数等,它们与n>=2代数方程一起统 代 二 称为非线性方程(组) 法讲 例如:3x-ex=0 ; xsinx=1 直
接方 法程 的 图 所以,求解这一类方程(组)更具现实意义: 形 法 计算机技术和数学软件技术的飞速发展为我们实现
隔离存在根的区间,区间逼近
二分法: 简单,但效率很高的一种算法
12
迭 代 法 直 接 法
线性方程组AX=B的求解
1
迭 代 法 直 接 法
第 二 讲 方 程 的 图 形 法
A=[0 1 -3 4;1 0 -2 3;3 2 0 -5;4 3 -5 0]; B=[-5;-4;12;5]; rank(A)==rank([A,B]) % ans=0 故原方程组无解 ans=1 有 唯一解 存在性 x=A\B %方法1:矩阵左除运算 x=inv(A)*B %方法2:逆矩阵求解法(须方阵) [L,U]=lu(A); %方法3:LU分解法 x=U\(L\B) [Q,R]=qr(A); %方法4:QR分解法 x=R\(Q\B) rref([A,B]) % 方法5:rref化行最简形 …p13~
JACOBI迭代法的matlab程序

对于大型线性代数方程组,常常用迭代法进行计算。迭代法有 存储空间小,程序简单等特点,在使用时,能保持悉数矩阵的稀疏 性不变。比较常用的迭代法有Gauss-Seidel迭代法,Jacobi迭代法, 和SOR方法。下面只介绍Jacobi迭代法。
已知线性方程组Ax=b,记A=(aij)2 0;-1 10 -2;0 -2 10]; • b=[3;7;6]; • tol=1e-6; • jacobi_fun(A,b,[0.1;0.1;0.1],tol,100)
函数调用及其结果显示
Thanks !
• A=D-L-U
• 其中,D=diag(a11,a22,…,ann)
设D非奇异,即aii≠0,i=1,2,3,…,n. 方程组Ax=b等价为
• 由此构造迭代公式
其中,迭代矩阵Bj和向量fj为
• 对线性方程组的Jacobi迭代计算求解,可以用matlab函数方便地实 现:
对线性方程组的Jacobi迭代计算求解,可 以用matlab函数方便地实现
jacobi迭代法matlab

jacobi迭代法matlabJacobi迭代法是一种常用的线性方程组求解方法,它是一种迭代法,通过不断迭代来逼近线性方程组的解。
Jacobi迭代法的基本思想是将线性方程组的系数矩阵分解为一个对角矩阵和一个非对角矩阵的和,然后通过迭代求解对角矩阵和非对角矩阵的乘积,最终得到线性方程组的解。
Jacobi迭代法的具体步骤如下:1. 将线性方程组的系数矩阵A分解为一个对角矩阵D和一个非对角矩阵R的和,即A=D+R。
2. 将线性方程组的右端向量b分解为一个对角矩阵D和一个非对角矩阵N的乘积,即b=Dx。
3. 对于任意的初始解向量x0,计算下一次迭代的解向量x1,即x1=D^(-1)(b-Rx0)。
4. 重复步骤3,直到达到预定的精度或迭代次数。
Jacobi迭代法的优点是简单易懂,易于实现,收敛速度较快。
但是,它的缺点也很明显,即收敛速度较慢,需要进行大量的迭代才能达到较高的精度。
在Matlab中,可以使用以下代码实现Jacobi迭代法:function [x,k]=jacobi(A,b,x0,tol,maxit)% Jacobi迭代法求解线性方程组Ax=b% 输入:系数矩阵A,右端向量b,初始解向量x0,精度tol,最大迭代次数maxit% 输出:解向量x,迭代次数kn=length(b); % 系数矩阵A的阶数D=diag(diag(A)); % 对角矩阵DR=A-D; % 非对角矩阵Rx=x0; % 初始解向量for k=1:maxitx1=D\(b-R*x); % 计算下一次迭代的解向量if norm(x1-x)<tol % 判断是否达到精度要求break;endx=x1; % 更新解向量end输出结果可以使用以下代码实现:A=[4 -1 0; -1 4 -1; 0 -1 4]; % 系数矩阵b=[15; 10; 10]; % 右端向量x0=[0; 0; 0]; % 初始解向量tol=1e-6; % 精度要求maxit=1000; % 最大迭代次数[x,k]=jacobi(A,b,x0,tol,maxit); % Jacobi迭代法求解线性方程组fprintf('解向量x=[%f; %f; %f]\n',x(1),x(2),x(3)); % 输出解向量fprintf('迭代次数k=%d\n',k); % 输出迭代次数以上就是Jacobi迭代法的主要内容,通过Matlab实现Jacobi迭代法可以更好地理解其基本思想和具体步骤。
matlab 解线性方程组的迭代法

小结
➢ 线性方程组求根方法的几何意义
➢ 线性方程组求根函数的理解与应用
设线性代数方程组为
展开为
若对角元素 逐一变量分离得方程组
即
此即为迭代公式
简单迭代解法的过程如下:
1 设定一组初值 2 第一次迭代:
得到
第k次迭代 第i个变量
3 第二次迭代: 得到
4 同样做法,得到第k+1次迭代:
迭代次数k的取值与精度要求有关,按下式判断:
若满足则停止迭代 为了便于编程,迭代公式可改写为:
matlab 解线性方程组的 迭代法
2020年4月22日星期三
第十讲 解线性方程组的迭代解法
内容提要
引言 简单迭代法 赛得尔迭代法 迭代解法的收敛性 MATLAB的线性方程组求解函数2 小结
1、引言
迭代解法的基本思想
根据给定方程组,设计出一个迭代公式,构造一 数组的序列 ,代入迭代公式,计算出 ,再代 入迭代公式,经过k次迭代运算后得到 ,若 收敛于某一极限数组xi,则xi就是方程组的近似解。
while(norm(x-x1)>eps) x1=x; x=(I-A)*x1+b; n = n + 1; if(n>=M) disp('Warning: 迭代次数太多,现
在退出!'); return;
end end
例:求解方程组
clear all; A =[ 1.0170 -0.0092 0.0095;
线性方程组求解的迭代法及Matlab的应用

线性方程组求解的迭代法及Matlab的应用2 定常迭代法 32.1 雅可比迭代法 42.2 高斯-赛德尔迭代法 42.3 超松弛迭代法 52.4 迭代的收敛性分析 62.5 实例 73 不定常迭代 93.1 最速下降法 93.2 共轭梯度法 103.3 实例 114 Matlab在定常迭代与不定常迭代中的应用 124.1 雅可比迭代法的程序 124.2 高斯-赛德尔迭代的程序 134.3 超松弛迭代的程序 134.4 最速下降法的程序 144.5 共轭梯度法的程序 144.6 Matlab实现的实例 154.6.1 定常迭代的收敛速度的比较 154.6.2 超松弛迭代法松弛因子的选择 164.6.3 不定常迭代的收敛速度的比较 18参考文献 20致谢 211 引言1.1 课题的目的和意义数值分析(numerical analysis)是研究分析用计算机求解数学计算问题的数值计算方法及其理论的学科,是数学的一个分支,它以数字计算机求解数学问题的理论和方法为研究对象。
为计算数学的主体部分。
它的主要内容有插值法,函数逼近,曲线拟和,数值积分,数值微分,解线性方程组的直接方法,解线性方程组的迭代法,非线性方程求根,常微分方程的数值解法。
数值分析这门学科有如下特点:面向计算机;有可靠的理论分析;要有好的计算复杂性;要有数值实验;要对算法进行误差分析。
:在许多工程实际应用中,超大规模的线性方程组的数值解法是时常要遇到的问题。
由于线性方程组的维数巨大,给具体的计算带来很大的问题——算法对计算机的内存需求大,算法的收敛速度慢以及计算舍人误差的累积扩张。
这些往往使理论上较好的算法无法真正的应用到工程实际中,因此寻求一种真正能实际应用的数值算法一直是人们关注的问题。
通常求解线性方程组一般可以分为直接解法和迭代解法。
现在流行的算法一般采用迭代的算法来求解线性方程组,这主要是为了加快求解的速度。
另外由于计算机的发展,在许多领域里涌现了一些新型的算法如神经网络,遗传算法,粒子群算法,模拟退火算法以及蚁群算法等。
迭代解法的matlab实现

解线性方程组b AX =的迭代法是从初始解出发,根据设计好的步骤用逐次求出的近似解逼近精确解.在第三章中介绍的解线性方程组的直接方法一般适合于A 为低阶稠密矩阵(指n 不大且元多为非零)的情况,而在工程技术和科学计算中常会遇到大型稀疏矩阵(指n 很大且零元较多)的方程组,迭代法在计算和存贮两方面都适合后一种情况.由于迭代法是通过逐次迭代来逼近方程组的解,所以收敛性和收敛速度是构造迭代法时应该注意的问题.另外,因为不同的系数矩阵具有不同的性态,所以大多数迭代方法都具有一定的适用范围.有时,某种方法对于一类方程组迭代收敛,而对另一类方程组迭代时就发散.因此,我们应该学会针对具有不同性质的线性方程组构造不同的迭代.4.1 迭代法和敛散性及其MATLAB 程序4.1.2 迭代法敛散性的判别及其MATLAB 程序根据定理4.1和谱半径定义,现提供一个名为pddpb.m 的M 文件,用于判别迭代公用谱半径判别迭代法产生的迭代序列的敛散性的MATLAB 主程序 输入的量:线性方程组b AX =的迭代公式(4.7)中的B ; 输出的量:矩阵B 的所有特征值和谱半径mH )(B ρ=及其有关迭代法产生的迭代序列的敛散性的相关信息.function H=ddpbj(B)H=eig(B);mH=norm(H,inf); if mH>=1disp('请注意:因为谱半径不小于1,所以迭代序列发散,谱半径mH 和B 的所有的特征值H 如下:')elsedisp('请注意:因为谱半径小于1,所以迭代序列收敛,谱半径mH 和B 的所有的特征值H 如下:')end mH4.1.3 与迭代法有关的MATLAB 命令(一) 提取(产生)对角矩阵和特征值可以用表4–1的MATLAB 命令提取对角矩阵和特征值.MATLAB 命令 功 能DX=diag(X) 若输入向量X ,则输出DX 是以X 为对角元的对角矩阵; 若输入矩阵X ,则输出DX 是以X 的对角元构成的向量;DX=diag(diag(X))输入矩阵X ,输出DX 是以X 的对角元构成的对角矩阵,可用于迭代法中从A 中提取D .lm=eig(A) 输入矩阵A ,输出lm 是A 的所有特征值.(二) 提取(产生)上(下)三角形矩阵第四章 解线性方程组的迭代法可以用表4–2的MATLAB 命令提取矩阵的上三角形矩阵和下三角形矩阵.MATLAB 命令 功 能U=triu(A) 输入矩阵A ,输出U 是A 的上三角形矩阵. L=tril(A) 输入矩阵A ,输出L 是A 的下三角形矩阵.U=triu(A,1) 输入矩阵A ,输出U 是A 的上三角形矩阵,但对角元为0,可用于迭代法中从A 中提取U .L=tril(A,-1)输入矩阵A ,输出L 是A 的下三角形矩阵,但对角元为0,可用于迭代法中从A 中提取L .(三)稀疏矩阵的处理对稀疏矩阵在存贮和运算上的特殊处理,是MA TLAB 进行大规模科学计算时的特点和优势之一.可以用表4–3的MATLAB 命令,输入稀疏矩阵的非零元(零元不必输入),即可进行运算.MATLAB 命令 功 能ZA=sparse(r,c,v,m,n)表示在第r 行、第c 列输入数值v ,矩阵共m 行n 列,输出ZA ,给出 (r , c ) 及v 为一稀疏矩阵.MA=full(ZA) 输入稀疏矩阵ZA ,输出为满矩阵MA (包含零元)4.2 雅可比(Jacobi )迭代及其MATLAB 程序4.2.2 雅可比迭代的收敛性及其MATLAB 程序判别雅可比迭代收敛性的MATLAB 主程序输入的量:线性方程组b AX =的系数矩阵A ; 输出的量:系数矩阵=A ()nn ija ⨯的kk nki j kja a a -=∑≠=1 ),,2,1(n k =的值和有关雅可比迭代收敛性的相关信息.[n m]=size(A); for j=1:ma(j)=sum(abs(A(:,j)))-2*(abs(A(j,j))); end for i=1:n if a(i)>=0disp('请注意:系数矩阵A 不是严格对角占优的,此雅可比迭代不一定收敛')return end end if a(i)<0disp('请注意:系数矩阵A 是严格对角占优的,此方程组有唯一解,且雅可比迭代收敛 ') end例4.2.2 用判别雅可比迭代收敛性的MATLAB 主程序,判别由下列方程组的雅可比迭代产生的序列是否收敛?(1)⎪⎩⎪⎨⎧=+--=-+-=--;2.45,3.8210,2.7210321321321x x x x x x x x x (2)⎪⎩⎪⎨⎧=+--=-+-=--.2.45.0,3.8210,2.7210321321321x x x x x x x x x 解 (1)首先保存名为jspb.m 的M 文件,然后在MATLAB 工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 5];a=jspb(A)运行后输出结果请注意:系数矩阵A 是严格对角占优的,此方程组有唯一解,且雅可比迭代收敛a =-8 -8 -1(2)在MATLAB 工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 0.5];a=jspb(A)运行后输出结果请注意:系数矩阵A 不是严格对角占优的,此雅可比迭代不一定收敛 a =-8.0000e+000 -8.0000e+000 3.5000e+0004.2.3 雅可比迭代的两种MATLAB 程序利用MATLAB 程序和雅可比迭代解线性方程组b AX =的常用的方法有两种,一种方法是根据雅可比迭代公式(4.11)、(4.12)式、定理4.3和公式(4.14)编写一个名为jacdd.m 的M 文件并保存,然后在MATLAB 工作窗口输入对应的命令,执行此文件;另一种方法是根据雅可比迭代的定义,利用提取对角矩阵和上、下三角矩阵的MATLAB 程序解线性方程组b AX =.下面我们分别介绍这两种方法.用雅可比迭代解线性方程组b AX =的MATLAB 主程序输入的量:线性方程组b AX =的系数矩阵A 和b , 初始向量X 0,范数的名称P = 1, 2, inf 或 'fro .',近似解X 的误差(精度)wucha 和迭代的最大次数max1;输出的量:系数矩阵=A ()nn ija ⨯的kk nki j kja a a -=∑≠=1 ),,2,1(n k =的值和有关雅可比迭代收敛性的相关信息及其b AX =的精确解jX 和近似解X .的M 文件如下:function X=jacdd(A,b,X0,P,wucha,max1) [n m]=size(A); for j=1:ma(j)=sum(abs(A(:,j)))-2*(abs(A(j,j))); end for i=1:n if a(i)>=0disp('请注意:系数矩阵A 不是严格对角占优的,此雅可比迭代不一定收敛')return end end if a(i)<0disp('请注意:系数矩阵A 是严格对角占优的,此方程组有唯一解,且雅可比迭代收敛 ') endfor k=1:max1kfor j=1:mX(j)=(b(j)-A(j,[1:j-1,j+1:m])*X0([1: j-1,j+1:m]))/A(j,j);endX,djwcX=norm(X'-X0,P); xdwcX=djwcX/(norm(X',P)+eps); X0=X';X1=A\b;if (djwcX<wucha)&(xdwcX<wucha)disp('请注意:雅可比迭代收敛,此方程组的精确解jX和近似解X如下:')returnendendif (djwcX>wucha)&(xdwcX>wucha)disp('请注意:雅可比迭代次数已经超过最大迭代次数max1 ')enda,X=X;jX=X1',例4.2.3用 范数和判别雅可比迭代的MATLAB主程序解例4.2.2 中的方程组,解的精度为0.001,分别取最大迭代次数max1=100,5,初始向量X0=(0 0 0)T,并比较它们的收敛速度.解(1)取最大迭代次数max1=100时.①首先保存名为jacdd.m的M文件,然后在MATLAB工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 5]; b=[7.2;8.3;4.2];X0=[0 0 0]'; X=jacdd(A,b,X0,inf,0.001,100)运行后输出结果请注意:系数矩阵A是严格对角占优的,此方程组有唯一解,且雅可比迭代收敛请注意:雅可比迭代收敛,此方程组的精确解jX和近似解X如下:a =-8 -8 -1jX =1.1000 1.2000 1.3000X =1.0994 1.1994 1.2993②在MATLAB工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 0.5]; b=[7.2;8.3;4.2]; X0=[0 0 0]';X=jacdd(A,b,X0,inf, 0.001,100)运行后输出结果请注意:系数矩阵A不是严格对角占优的,此雅可比迭代不一定收敛请注意:雅可比迭代收敛,此方程组的精确解jX和近似解X如下:a =-8.0000 -8.0000 3.5000jX =24.5000 24.6000 106.6000X =24.0738 24.1738 104.7974(2)取最大迭代次数max1=5时,①在MATLAB工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 5];b=[7.2;8.3;4.2]; X0=[0 0 0]'; X=jacdd(A,b,X0,inf,0.001,5)运行后输出结果请注意:系数矩阵A是严格对角占优的,此方程组有唯一解,雅可比迭代收敛请注意:雅可比迭代次数已经超过最大迭代次数max1a =-8 -8 -1jX =1.1000 1.2000 1.3000 X =1.0951 1.1951 1.2941②在MATLAB 工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 0.5]; b=[7.2;8.3;4.2]; X0=[0 0 0]'; X=jacdd(A,b,X0,inf, 0.001,5)运行后输出结果请注意:系数矩阵A 不是严格对角占优的,此雅可比迭代不一定收敛 请注意:雅可比迭代次数已经超过最大迭代次数max1 a =-8.0000 -8.0000 3.5000 jX =24.5000 24.6000 106.6000 X =5.5490 5.6490 27.6553由(1)和(2)可见,如果系数矩阵A 是严格对角占优的,则雅可比迭代收敛的速度快;如果系数矩阵A 不是严格对角占优的,则雅可比迭代收敛的速度慢.因此,kk nki j kj a a a -=∑≠=1 ),,2,1(n k =的值越小,雅可比迭代收敛的速度越快.(二)利用雅可比迭代定义编写的解线性方程组的MATLAB 程序利用雅可比迭代定义编写解线性方程组(4.5)的MATLAB 程序的一般步骤 步骤1 将线性方程组(4.5)的系数矩阵A 分解为U L D A --=,其中=D ⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn nn a a a a a a diag22112211),,(, -=L⎪⎪⎪⎪⎪⎭⎫⎝⎛-0001,2121n n n n a a aa -=U ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-000,1112nn n a a a . 在MATLAB 工作窗口输入程序>> A=[a11 a12 …a1n; a21 a22 …a2n;…; an1 an2 …ann;]; D=diag(A) U=triu(A,1), L=tril(A,-1)运行后即可输出U L D A ,,的; 步骤2 若对角矩阵D 非奇异(即),,1,0n i a ii =≠,则(4.5)化为 b D X U L D X 11)(--++=.若记b D f U L D B 1111),(--=+=.则方程组的迭代形式可写作1)(1)1(f X B Xk k +=+ )2,1,0( =k 可以利用下面的MATLAB 程序完成>>dD=det(D); if dD==0disp('请注意:因为对角矩阵D 奇异,所以此方程组无解.') elsedisp('请注意:因为对角矩阵D 非奇异,所以此方程组有解.') iD=inv(D); B1=iD*(L+U);f1=iD*b;for k=1:max1X= B1*X0+ f1; X0=X; djwcX=norm(X-X0,P);xdwcX=djwcX/(norm(X,P)+eps); X1=A\b;if (djwcX<wucha)&(xdwcX<wucha)disp('请注意:雅可比迭代收敛,此方程组的精确解jX和近似解X如下:')returnendendif (djwcX>wucha)|(xdwcX>wucha)disp('请注意:雅可比迭代次数已经超过最大迭代次数max1 ')endenda,X=X;jX=X1',4.3 高斯-塞德尔(Gauss-Seidel)迭代及其MATLAB程序4.3.3 高斯-塞德尔迭代两种MATLAB程序AX=的常用方法有两种,一利用MATLAB程序和高斯-塞德尔迭代解线性方程组b种方法是根据高斯-塞德尔迭代公式(4.16)、(4.17)、定理4.3和公式(4.14)编写一个名为gsdd.m的M文件并保存,然后在MATLAB工作窗口输入对应的命令,执行此文件;另一种方法是根据高斯-塞德尔迭代的定义,利用提取对角矩阵和上、下三角矩阵的AX=.下面我们分别介绍这两种方法.MATLAB程序解线性方程组b(一)高斯-塞德尔迭代定义的MATLAB程序1AX=的MATLAB主程序1 用高斯-塞德尔迭代定义解线性方程组bAX=的系数矩阵A和b, 初始向量X0,范数的名称P = 1, 2, 输入的量:线性方程组binf, 或'fro.',近似解X的误差(精度)wucha和迭代的最大次数max1.A()n n ij a⨯的对角元构成的对角矩阵D、A的上三角形矩阵输出的量:以系数矩阵=U,但对角元为0、A的下三角形矩阵L,但对角元为0和有关高斯-塞德尔迭代收敛性的AX=的精确解jX和近似解X.相关信息及其bD=diag(diag(A));U=-triu(A,1);L=-tril(A,-1); dD=det(D);if dD==0disp('请注意:因为对角矩阵D奇异,所以此方程组无解.')elsedisp('请注意:因为对角矩阵D非奇异,所以此方程组有解.')iD=inv(D-L); B2=iD*U;f2=iD*b;jX=A\b; X=X0; [n m]=size(A);for k=1:max1X1= B2*X+f2; djwcX=norm(X1-X,P);xdwcX=djwcX/(norm(X,P)+eps);if (djwcX<wucha)|(xdwcX<wucha)returnelsek,X1',k=k+1;X=X1;endendif (djwcX<wucha)|(xdwcX<wucha)disp('请注意:高斯-塞德尔迭代收敛,此A的分解矩阵D,U,L和方程组的精确解jX和近似解X如下:')elsedisp('请注意:高斯-塞德尔迭代发散,并且迭代次数已经超过最大迭代次数max1,方程组的精确解jX和迭代向量X如下:')X=X';jX=jX' end endX=X';D,U,L,jX=jX'例4.3.3 用高斯-塞德尔迭代定义的MATLAB 主程序解下列线性方程组,取初始值)0,0,0(),,()0(3)0(2)0(1=x x x ,要求当3)()1(10-∞+<-k k x x 时,迭代终止.(1)⎪⎩⎪⎨⎧=+--=-+-=--.2.45.0,3.8210,2.7210321321321x x x x x x x x x (2)⎪⎪⎩⎪⎪⎨⎧=++--=+-+=-+-=+-+.2132127,11613514,22382,575434321432143214321x x x x x x x x x x x x x x x x解 (1)首先保存名为gsdddy.m 的M 文件,然后在MATLAB 工作窗口输入程序>> A=[10 -1 -2;-1 10 -2;-1 -1 0.5]; b=[7.2;8.3;4.2]; X0=[0 0 0]'; X=gsdddy(A,b,X0,inf, 0.001,100)运行后输出结果请注意:因为对角矩阵D 非奇异,所以此方程组有解.请注意:高斯-塞德尔迭代收敛,此A 的分解矩阵D,U,L 和方程组的精确解jX 和近似解X 如下:此近似解与例4.2.3中的(1)中②的解X =(24.073 8, 24.173 8, 104.797 4)T比较,在相同的条件下, 高斯-塞德尔迭代比雅可比迭代得到的近似解的精度更高.(2)在MATLAB 工作窗口输入程序>> A=[3 4 -5 7;2 -8 3 -2;4 51 -13 16;7 -2 21 3];b=[5;2;-1;21]; X0=[0 0 0 0]';X=gsdddy(A,b,X0,inf,0.001,100)运行后输出结果请注意:因为对角矩阵D 非奇异,所以此方程组有解.请注意:高斯-塞德尔迭代发散,并且迭代次数已经超过最大迭代次数max1,方程组的精确解jX 和迭代向量X 如下:jX =0.1821 -0.2571 0.7286 1.3036X = 1.0e+142 *0.2883 0.1062 0.3622 -3.1374(二) 高斯-塞德尔迭代公式的MATLAB 程序2 根据高斯-塞德尔迭代公式(4.16)、(4.17)、定理4.3和公式(4.14),现提供名为用高斯-塞德尔迭代解线性方程组b AX =的MATLAB 主程序2 输入的量:线性方程组b AX =的系数矩阵A 和b , 初始向量X 0,范数的名称P = 1, 2, inf, 或 'fro.',近似解X 的误差(精度)wucha 和迭代的最大次数max1.输出的量:系数矩阵=A ()nn ija ⨯的kk nki j kja a a -=∑≠=1 ),,2,1(n k =的值和有关D =10.0000 0 0 0 10.0000 0 0 0 0.5000 U =0 1 2 0 0 2 0 0 0L =0 0 0 1 0 0 1 1 0 jX =24.5000 24.6000 106.6000 X =24.4996 24.5996 106.5984AX=的精确解jX和近似解X.高斯-塞德尔迭代收敛性的相关信息及其b[n m]=size(A);for j=1:ma(j)=sum(abs(A(:,j)))-2*(abs(A(j,j)));endfor i=1:nif a(i)>=0disp('请注意:系数矩阵A不是严格对角占优的,此高斯-塞德尔迭代不一定收敛')returnendendif a(i)<0disp('请注意:系数矩阵A是严格对角占优的,此方程组有唯一解,且高斯-塞德尔迭代收敛')endfor k=1:max1for j=1:mif j==1X(1)=(b(1)-A(1,2:m)*X0(2:m))/A(1,1)endif j==mX(m)=(b(m)-A(m,1:M1)*X(1:M1)')/A(m,m);endfor j=2:M1X(j)=(b(j)-A(j,1:j-1)*X(1:j-1) -A(j,j+1:m)*X(j+1:m))/A(j,j);endenddjwcX=norm(X'-X0,P);xdwcX=djwcX/(norm(X',P)+eps); X0=X';X1=A\b;if (djwcX<wucha)|(xdwcX<wucha)disp('请注意:高斯-塞德尔迭代收敛,此方程组的精确解jX和近似解X 如下:')returnendendif (djwcX>wucha)&(xdwcX>wucha)disp('请注意:高斯-塞德尔迭代次数已经超过最大迭代次数max1 ') enda,X=X;jX=X1',4.4 解方程组的超松弛迭代法及其MATLAB程序用雅可比迭代法和高斯-塞德尔迭代法解线性方程组时,有时收敛速度很慢,为了提高收敛速度,我们介绍超松弛迭代法,它是对高斯-塞德尔迭代的一种加速方法,适用于大型稀疏矩阵方程组的求解.4.4.2 超松弛迭代法收敛性及其MATLAB程序根据定理4.5和谱半径定义,现提供名为ddpbj.m的M文件,用于判别超松弛迭代用谱半径判别超松弛迭代法产生的迭代序列的敛散性的MATLAB主程序AX=的系数矩阵A和松弛因子om;输入的量:线性方程组b输出的量:矩阵])1([)(1D U L D B ωωωω-+-=-的所有特征值和谱半径mH)(ωρB =及其有关超松弛迭代法产生的迭代序列的敛散性的相关信息.D=diag(diag(A));U=-triu(A,1); L=-tril(A,-1); iD=inv(D-om*L); B2=iD*(om*U+(1-om)*D); H=eig(B2);mH=norm(H,inf); if mH>=1disp('请注意:因为谱半径不小于1,所以超松弛迭代序列发散,谱半径mH和B 的所有的特征值H 如下:') elsedisp('请注意:因为谱半径小于1,所以超松弛迭代序列收敛,谱半径mH和B 的所有的特征值H 如下:') end mH例4.4.1 当取ω=1.15,5时,判别用超松弛迭代法解下列方程组产生的迭代序列是否收敛?⎪⎪⎩⎪⎪⎨⎧-=+++-=---=+++=--+372364213824254321432143214321x x x x x x x x x x x x x x x x 解 (1)当取ω=1.15时,首先保存名为ddpbj.m 的M 文件,然后在MATLAB 工作窗口输入程序>> A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-1 3 2 7]; H=ddpbj(A,1.15)运行后输出结果请注意:因为谱半径小于1,所以超松弛迭代序列收敛,谱半径mH 和B 的所有的特征值H 如下:mH =0.1596 H =0.1049 + 0.1203i 0.1049 - 0.1203i -0.1295 + 0.0556i -0.1295 - 0.0556i (2)当取ω=5时,然后在MATLAB 工作窗口输入程序>> H=ddpbj(A, 5)运行后输出结果请注意:因为谱半径不小于1,所以超松弛迭代序列发散,谱半径mH 和B 的所有的特征值H 如下:mH =14.1082 H =-14.1082 -2.5107 0.5996 + 2.6206i 0.5996 - 2.6206i4.4.3 超松弛迭代法的MATLAB 程序用超松弛迭代法解线性方程组b AX =的MATLAB 主程序输入的量:线性方程组b AX =的系数矩阵A 和b , 初始向量X ,范数的名称P = 1, 2, inf, 或 'fro.',松弛因子om ,近似解X 的误差(精度)wucha 和迭代的最大次数max1.输出的量:谱半径mH ,以系数矩阵A 的对角元构成的对角矩阵D 、A 的上三角形矩阵U ,但对角元为0、A 的下三角形矩阵L ,但对角元为0, 迭代次数i ,有关超松弛迭代收敛性的相关信息及其b AX =的精确解jX 和近似解X .function X=cscdd (A,b,X,om,wucha,max1)D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1); jX=A\b;[n m]=size(A);iD=inv(D-om*L); B2=iD*(om*U+(1-om)*D);H=eig(B2);mH=norm(H,inf);for k=1:max1iD=inv(D-om*L); B2=iD*(om*U+(1-om)*D);f2= om*iD*b; X1= B2*X+f2;X=X1; djwcX=norm(X1-jX,inf); xdwcX=djwcX/(norm(X,inf)+eps);if (djwcX<wucha)|(xdwcX<wucha)disp('谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX,迭代次数i如下:')mH,D,U,L,jX=jX', i=k-1,returnif i> max1disp('迭代次数已经超过最大迭代次数max1,谱半径mH,方程组的精确解jX,迭代次数i如下:')mH,D,U,L,jX=jX', i=k-1,endendendif mH>=1disp('请注意:因为谱半径不小于1,所以超松弛迭代序列发散.')disp('谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX,迭代次数i和迭代序列X如下:')i=k-1,mH,D,U,L,jX,elsedisp('因为谱半径小于1,所以超松弛迭代序列收敛,近似解X如下:') end或function X=cscdd1 (A,b,X,om,wucha,max1)D=diag(diag(A));U=-triu(A,1);L=-tril(A,-1); jX=A\b;[n m]=size(A);iD=inv(D-om*L); B2=iD*(om*U+(1-om)*D);H=eig(B2);mH=norm(H,inf);for k=1:max1iD=inv(D-om*L); B2=iD*(om*U+(1-om)*D);f2= om*iD*b; X1= B2*X+f2; X=X1; djwcX=norm(X1-jX,inf);xdwcX=djwcX/(norm(X,inf)+eps);endif mH>=1disp('请注意:因为谱半径不小于1,所以超松弛迭代序列发散.谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX和近似解X如下:')elsedisp('请注意:因为谱半径小于1,所以超松弛迭代序列收敛.')if (djwcX<wucha)|(xdwcX<wucha)disp('谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX和近似解X 如下:')mH,D,U,L,jX=jX',elsedisp('迭代次数已经超过最大迭代次数max1,谱半径mH,方程组的精确解jX和迭代向量X如下:')mH,D,U,L,X=X1';jX=jX'returnendend例4.4.3用超松弛迭代法(取ω=1.15和5)解例4.4.1中的线性方程组.解(1)当取ω=1.15时,首先保存名为cscdd.m的M文件,然后在MATLAB工作窗口输入程序>> A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-1 3 2 7];b=[4;1;6;-3];X=[0 0 0 0]';X=cscdd (A,b,X,1.15,0.001,100),运行后输出结果谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX,迭代次数i如下:mH =0.1596D =5 0 0 00 8 0 00 0 -4 00 0 0 7U =0 -1 1 20 0 -1 -30 0 0 10 0 0 0L =0 0 0 0-2 0 0 0-1 2 0 01 -3 -2 0jX =0.4491 0.2096 -1.4850 -0.0299i =3因为谱半径小于1,所以超松弛迭代序列收敛,近似解X如下:X =0.44840.2100-1.4858-0.0303(2)当取ω=5时,保存名为cscdd.m的M文件,然后在MATLAB工作窗口输入程序>> A=[5 1 -1 -2;2 8 1 3;1 -2 -4 -1;-1 3 2 7];b=[4;1;6;-3];X=[0 0 0 0]';X=cscdd (A,b,X,5,0.001,100),运行后输出结果如下:请注意:因为谱半径不小于1,所以超松弛迭代序列发散.谱半径mH,A的分解矩阵D,U,L和方程组的精确解jX,迭代次数i和迭代序列X如下:i = mH =99 14.1082D =5 0 0 00 8 0 00 0 -4 00 0 0 7U =0 -1 1 20 0 -1 -30 0 0 10 0 0 0L =0 0 0 0-2 0 0 0-1 2 0 01 -3 -2 0jX = X =1.0e+114 *0.4491 -0.31220.2096 1.0497-1.4850 -3.7174-0.0299 3.9615。
基于Matlab的解线性方程组的几种迭代法的实现及比较

基于Matlab的解线性方程组的几种迭代法的实现及比较线性方程组的解法有很多种,其中一类常用的方法是迭代法。
迭代法根据一个初值逐步逼近方程组的解,在每一次迭代中利用现有的信息产生新的近似值,并不断地修正。
下面介绍基于Matlab的三种迭代法:雅可比迭代法、高斯-赛德尔迭代法和超松弛迭代法,并进行比较。
1. 雅可比迭代法雅可比迭代法是迭代法中最简单的一种方法。
对于线性方程组Ax=b,雅可比迭代法的迭代公式为:x_{i+1}(j)=1/a_{jj}(b_j-\\sum_{k=1,k\eq j}^n a_{jk}x_i(k))其中,i表示迭代次数,j表示未知数的下标,x_i表示第i次迭代的近似解,a_{jk}表示系数矩阵A的第j行第k列元素,b_j 表示方程组的常数项第j项。
在Matlab中,可以使用以下代码实现雅可比迭代:function [x,flag]=jacobi(A,b,X0,tol,kmax)n=length(b);x=X0;for k=1:kmaxfor i=1:nx(i)=(b(i)-A(i,:)*x+A(i,i)*x(i))/A(i,i);endif norm(A*x-b)<tolflag=1;returnendendflag=0;return其中,参数A为系数矩阵,b为常数项列向量,X0为初值列向量,tol为迭代误差容许值(默认为1e-6),kmax为最大迭代次数(默认为1000)。
函数返回值x为近似解列向量,flag表示是否满足容许误差要求。
2. 高斯-赛德尔迭代法高斯-赛德尔迭代法是雅可比迭代法的改进。
其基本思想是,每次迭代时,利用已经求出的新解中的信息来更新其他未知数的值。
迭代公式为:x_{i+1}(j)=(1/a_{jj})(b_j-\\sum_{k=1}^{j-1}a_{jk}x_{i+1}(k)-\\sum_{k=j+1}^n a_{jk}x_i(k))与雅可比迭代法相比,高斯-赛德尔迭代法的每一次迭代都利用了前面已求得的近似解,因此可以更快地收敛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迭代过程本质上就是计算极限的过程,一般不能 得到精确解。
迭代法的优点是程序简单,适合于大型方程组求 解,但缺点是要判断迭代是否收敛和收敛速度问题 。 1. 雅可比(Jacobi(1804-1851))迭代法(简单迭代法) 2. 赛得尔 (Seidel (1821 - 1896))迭代法
2、简单迭代法
while(norm(x-x1)>eps) x1=x; x=(I-A)*x1+b; n = n + 1; if(n>=M) disp('Warning: 迭代次数太多,现
在退出!'); return;
end end
例:求解方程组
clear all; A =[ 1.0170 -0.0092 0.0095;
遗传算法是一种基于自然选择的用于求解有约束和无约束 最优问题的方法。遗传算法反复修改包含若干个体的种群 。遗传算法在每一步中,随机从当前种群中选择若干个个 体作为父辈,并用它们产生下一代子辈。在若干代之后, 种群就朝着最优解“进化”。我们可以利用遗传算法去解决 各种最优化问题,包括目标函数是不连续、不可微、随机 或者高度非线性的问题。
若不满足收敛条件,适当调整方程次序或作一 定的线性组合,就可能满足收敛条件。
5、MATLAB的线性方程组求解函数 2
格式
solve('eqn1','eqn2',...,'eqnN','var1,var2,...,varN')
Matlab非线性方程组求解
格式
X=fsolve(FUN,X0)
说明: ① 求解方程形式F(X)=0 ② X、F可以是向量或矩阵 ③ X0 初值
clear all; A = [9 53 381;
53 381 3017; 381 3017 25317]; b=[76 489 3547]'; x0=zeros(3,1); [x,n]=gauseidel(A,b,x0,1e-4,10)
Warning: 迭代次数太多,可能不收敛 ! x=
-0.8037 3.3330 -0.2450 n = 200
实例:基于Matlab的透镜中心偏测量光轴拟合
光学中心偏测量仪作为精确测定和严格校正光学系统中心 偏误差的仪器,它可以指出透镜组中的各镜面相对于光轴的 中心偏移数值大小和方向。它的测量结果具有两个方面的 意义:其一是通过根据被测光学件各面的中心误差是否超出, 来判定光学件是否合格;其二是根据测量的结果来指导光学 系统的装校。
-0.0092 0.9903 0.0136; 0.0095 0.0136 0.9898]; b=[1 0 1]'; x0 = [0 0 0]'; [x,n]=richason(A,b,x0)
x= 0.9739 -0.0047 1.0010
n= 5
3、赛得尔迭代法
赛得尔迭代法与简单迭代法类似,只是迭代公式有 所改进。
简单迭代法
赛得尔迭代法
MATLAB程序设计
function [x,n]=gauseidel(A,b,x0,eps,M) if nargin==3
eps= 1.0e-6; M = 200; elseif nargin == 4 M = 200; elseif nargin<3 error return; end D=diag(diag(A)); %求A的对角矩阵 L=-tril(A,-1); %求A的下三角阵 U=-triu(A,1); %求A的上三角阵 。。。。。。
matlab 解线性方程组的 迭代法
2020年4月22日星期三
第十讲 解线性方程组的迭代解法
内容提要
引言 简单迭代法 赛得尔迭代法 迭代解法的收敛性 MATLAB的线性方程组求解函数2 小结
1、引言
迭代解法的基本思想
根据给定方程组,设计出一个迭代公式,构造一 数组的序列 ,代入迭代公式,计算出 ,再代 入迭代公式,经过k次迭代运算后得到 ,若 收敛于某一极限数组xi,则xi就是方程组的近似解。
G=(D-L)\U;
f=(D-L)\b;
x=G*x0+f;
n=1;
%迭代次数
while norm(x-x0)>=eps
x0=x;
x=G*x0+f;
n=n+1;
if(n>=M)
disp('Warning: 迭代次数太多,可能不
收敛!');
return;
end
end
例:线性代数方程组的迭代解法----赛得尔迭代法
MATLAB程序设计
function [x,n]=richason(A,b,x0,eps,M)
if(nargin == 3)
eps = 1.0e-6;
M = 200;
elseif(nargin == 4)
M = 200;
End I =eye(size(A)); x1=x0; x=(I-A)*x0+b; n=1; 。。。。。。
4、 迭代解法的收敛性
迭代解法的前提条件是迭代解出的近似解序列必须具 有收敛性。如果近似解序列是发散的, 迭代法则不能获得 解。
以下列初值进行简单迭代
k
X1
X2
X3
0
0
0
0
1
11
-14
-3
2
-69 81
66
3 -499 -374 -429
4 4851 -7149 -2124
迭代收敛条件:严格对角占优矩阵
设线性代数方程组为
展开为
若对角元素 逐一变量分离得方程组
即
此即为迭代公式
简单迭代解法的过程如下:
1 设定一组初值 2 第一次迭代:
得到Biblioteka 第k次迭代 第i个变量3 第二次迭代: 得到
4 同样做法,得到第k+1次迭代:
迭代次数k的取值与精度要求有关,按下式判断:
若满足则停止迭代 为了便于编程,迭代公式可改写为:
3)应用最小二乘法得到关于四参数的线性方程组。 得到各面球心的位置坐标后,按照一般直线拟合的方法,应使各球 心对优化轴距离的平方和最小,符合数学上的最小二乘法。N个 球心到优化轴距离的平方和:
扩展:基于MATLAB的非线性方程组遗传解法
胡斐,赵治国 (同济大学汽车学院,上海201804)
