特殊行列式与行列式计算方法总结
行列式的计算技巧和方法总结

计算技巧及方法总结一、 一般来说,对于二阶、三阶行列式,可以根据定义来做 1、二阶行列式2112221122211211a a a a a a a a -=2、三阶行列式333231232221131211a a a a a a a a a =.332112322311312213322113312312332211a a a a a a a a a a a a a a a a a a ---++ 例1计算三阶行列式601504321-解 =-601504321601⨯⨯)1(52-⨯+043⨯⨯+)1(03-⨯⨯-051⨯⨯-624⨯⨯-4810--=.58-=但是对于四阶或者以上的行列式,不建议采用定义,最常采用的是行列式的性质以及降价法来做。
但在此之前需要记忆一些常见行列式形式。
以便计算。
计算上三角形行列式nn nnn n a a a a a a a a a 221122211211000=下三角形行列式 nnn n a a a a a a 21222111000.2211nn a a a =对角行列式nn nnn n a a a a a a a a a221121222111000=二、用行列式的性质计算1、记住性质,这是计算行列式的前提将行列式D 的行与列互换后得到的行列式,称为D 的转置行列式,记为T D 或'D ,即若,212222111211nnn n n n a a a a a a a a a D=则 nnn n n n T a a a a a a a a a D212221212111=. 性质1 行列式与它的转置行列式相等, 即.T D D = 注 由性质1知道,行列式中的行与列具有相同的地位,行列式的行具有的性质,它的列也同样具有.性质2 交换行列式的两行(列),行列式变号.推论 若行列式中有两行(列)的对应元素相同,则此行列式为零. 性质3 用数k 乘行列式的某一行(列), 等于用数k 乘此行列式, 即.2121112112121112111kD a a a a a a a a a k a a a ka ka ka a a a D nnn n in i i n nnn n in i i n ===第i 行(列)乘以k ,记为k i ⨯γ(或k C i ⨯).推论1 行列式的某一行(列)中所有元素的公因子可以提到行列式符号的外面. 推论2 行列式中若有两行(列)元素成比例,则此行列式为零. 性质4 若行列式的某一行(列)的元素都是两数之和, 例如,nnn n in in i i i i n a a a c b c b c b a a a D21221111211+++=.则21212111211212111211D D a a a c c c a a a a a a b b b a a a D nnn n in i i n nn n n in i i n +=+=.性质5 将行列式的某一行(列)的所有元素都乘以数k 后加到另一行(列)对应位置的元素上, 行列式不变.注: 以数k 乘第j 行加到第i 行上,记作j i kr r +; 以数k 乘第j 列加到第i 列上,记作j i kc c +.2、利用“三角化”计算行列式 计算行列式时,常用行列式的性质,把它化为三角形行列式来计算. 例如化为上三角形行列式的步骤是:如果第一列第一个元素为0, 先将第一行与其它行交换使得第一列第一个元素不为0; 然后把第一行分别乘以适当的数加到其它各行,使得第一列除第一个元素外其余元素全为0;再用同样的方法处理除去第一行和第一列后余下的低一阶行列式,如此继续下去,直至使它成为上三角形行列式,这时主对角线上元素的乘积就是所求行列式的值.例2若21101321-=D , 则.213102011D D T =-=例3(1)01212111001211121---=--(第一、二行互换).(2)1211021101211121---=--(第二、三列互换) (3)072501111=(第一、二两行相等) (4)0337224112=---(第二、三列相等)例4(1)02222510211=--因为第三行是第一行的2倍. (2)075414153820141=---因为第一列与第二列成比例,即第二列是第一列的4倍.例5若121013201--=D , 则D 2121013201)2(121013402-=---=----又 D 412101320141240112204=--=--.例6 设,1333231232221131211=a a a a a a a a a 求.53531026333231232221131211a a a a a a a a a ---- 解 利用行列式性质,有33323123222113121153531026a a a a a a a a a ----=3332312322211312115353522a a a a a a a a a ---5)3(2⋅-⋅-=333231232221131211a a a a a a a a a 15)3(2⋅⋅-⋅-=.30=例7(1).110111311103111132+=++=(2)()1)2(1272305)2(11121272305211--+--++=----+122720521112730511---+--=. 例8 因为,12310403212213==++--+而15)40()29(02213123=+++=-+-.因此221312303212213-+-≠++--+.注: 一般来说下式是不成立的22211211222112112222212112121111b b b b a a a a b a b a b a b a +≠++++.例9(1)13201013113214113112----r r ,上式表示第一行乘以-1后加第二行上去, 其值不变.(2)33204103113214113113c c +--,上式表示第一列乘以1后加到第三列上去, 其值不变.例10计算行列式2150321263-=D . 解 先将第一行的公因子3提出来:,21503242132150321263-=-再计算.162354100430201541104702215421087042127189087042132150324213=⨯====----=-=D例11 计算.3351110243152113------=D解 21c c D→3315112043512131-------14125r r r r +-72160112064802131------32r r ↔72160648011202131----- 242384r r r r -+ 1510001080011202131---- 3445r r +.4025001080011202131=--- 例12计算.3111131111311113=D 解 注意到行列式的各列4个数之和都是6.故把第2,3,4行同时加到第1行,可提出公因子6,再由各行减去第一行化为上三角形行列式.D4321r r r r +++311113111131111163111131111316666= 141312r r r r r r --- .4820000200002011116=注:仿照上述方法可得到更一般的结果:.)]()1([1---+=n b a b n a abbbb b a b b b b a例13 计算.1111000000332211a a a a a a --- 解 根据行列式的特点,可将第1列加至第2列,然后将第2列加至第3列,再将第3列加至第4列,目的是使4D 中的零元素增多.4D12c c +1121000000033221a a a a a --23c c +1321000000003321a a a a -34c c +.44321000000000321321a a a a a a = 例14 计算.3610363234232dc b a c b a b a a dc b a cb a b a a dc b a cb a ba a d c baD ++++++++++++++++++=解 从第4行开始,后一行减前一行:Drr r r r r ---33412 .363023200c b a b a a c b a b a a c b a b a a d c b a +++++++++ 3423r r r r -- .20200ba a ab a a a cb a b a a dc b a +++++34r r -..0020004a ab a a cb a b a a dc ba =++++三、 行列式按行(列)展开(降阶法)1、行列式按一行(列)展开定义1 在n 阶行列式D 中,去掉元素ij a 所在的第i 行和第j 列后,余下的1-n 阶行列式,称为D 中元素ij a 的余子式, 记为ij M , 再记ij j i ij M A +-=)1(称ij A 为元素ij a 的代数余子式.引理(常用) 一个n 阶行列式D , 若其中第i 行所有元素除ij a 外都为零,则该行列式等于ij a 与它的代数余子式的乘积,即 ij ij A a D =定理1 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和, 即),,,2,1(2211n i A a A a A a D inin i i i i =+++= 或 ).,,2,1(2211n j A a A a A a D njnj j j j j =+++=推论 行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零, 即,,02211j i A a A a A a jn in j i j i ≠=+++或 .,02211j i A a A a A a nj ni j i j i ≠=+++2、用降价法计算行列式(常用)直接应用按行(列)展开法则计算行列式, 运算量较大, 尤其是高阶行列式. 因此, 计算行列式时,一般可先用行列式的性质将行列式中某一行(列)化为仅含有一个非零元素, 再按此行(列)展开,化为低一阶的行列式, 如此继续下去直到化为三阶或二阶行列式.3、拉普拉斯定理(一般少用)定义2 在n 阶行列式D 中,任意选定k 行k 列)1(n k ≤≤, 位于这些行和列交叉处的2k 个元素,按原来顺序构成一个k 阶行列式M , 称为D 的一个k 阶子式,划去这k 行k 列, 余下的元素按原来的顺序构成k n -阶行列式,在其前面冠以符号kkj j i i +++++- 11)1(,称为M 的代数余子式,其中k i i ,,1 为k 阶子式M 在D 中的行标,k j j j ,,,21 为M 在D 中的列标.注:行列式D 的k 阶子式与其代数余子式之间有类似行列式按行(列)展开的性质. 定理2 (拉普拉斯定理) 在n 阶行列式D 中, 任意取定k 行(列))11(-≤≤n k ,由这k 行(列)组成的所有k 阶子式与它们的代数余子式的乘积之和等于行列式D .例15求下列行列式的值:(1)214121312-- (2)120250723解 (1) 213142131)1(21122214121312-⨯+-⨯--⨯=--.272856)61(4)32()14(2-=--=--+--+-=(2) .3)45(312253120250723=-=⨯=例16计算行列式 .5021011321014321---=D解 521011321014321---=D 313422r r r r ++520711321014107----109211206527211417)1()1(2123223-=---⨯-=-++r r r r.241861926)1(122-=--=--⨯=+例17计算行列式 .0532004140013202527102135----=D解 53204140132021352)1(053200414001320252710213552-----=----=+D 53241413252---⋅-=1213)2(r r r r -++6627013210---.1080)1242(206627)2(10-=--=--⋅-=例18求证 21)1(11213112211132114321-+-=---n n x x xxx x x n xxn x n n.证 D3221143r r r r r r r r nn ----- 1111111111000011000111001111011110xxxx x x x ---- 11011100111101111111111)1(1xx x xn -----=+3221143r r r r r r r r nn ----- .)1(110000000100001000010000)1(211-++-=-----n n n x xxx x x x xx例19设,3142313150111253------=D D 中元素ij a 的余子式和代数余子式依次记作ij M 和ij A ,求14131211A A A A +++及41312111M M M M +++.解 注意到14131211A A A A +++等于用1,1,1,1代替D 的第1行所得的行列式,即314231315011111114131211-----=+++A A A A 3413r r r r +- 0011202250111111---11222511---=12c c + .4205201202511=-=--又按定义知,31413131501112514131211141312111-------=-+-=+++A A A A M M M M 34r r + 311501121)1(0010313150111251---=---- 312r r - .0311501501=-----例20 用拉普拉斯定理求行列式2100321003210032 的值. 解 按第一行和第二行展开..;2132132132=2132)1(21322121+++-⨯231)1(3123121+++-⨯+23)1(3233221+++-⨯+121+-=.11-=。
行列式的计算方法及一些特殊行列式的计算

~
D
x 一1 … 0
0
一
●
O D= 0
l O
O … 0 1 … 0
一
●
0
O …
_ .
。 2
■■
加
行 列 式 的 计 算 方 法 及 一 些 特 殊 行 列 式 的 计 算
陈 洁
( 湖北 工 业 大 学 理 学 院 , 湖北 武汉 摘
一
4 3 0 0 6 8 )
1 +a
引 I 1
1 l +a 2
● ● ●
0
1 1
● ● ●
递 推 法 是 根 据 行 列 式 的性 质 , 建 立 阶行 列 式 和 阶 行 列 式 的关 系.
4 3
●墨
1 2 3 … n
2
1
0 … 0 l … O
例5 . 计 算 行 列 式
X
O 例7 . 计算D = 3 n
一
要: 行 列 式 的 计 算 是 线 性 代 数 的 基 础 和 重要 内容 之
本 文 通过 一 些 具 体 的 例 子 , 介 绍 了 计 算 行 列 式 的 一般 方 法 7 2 . 一 些特 殊行 列 式 的计 算.
.
例3 . 计算行列式D =
●
1
● ●
关键 词 : 行 列式 降 阶 法 升 阶 法
一
1
1
、
1 . 化为“ 三 角形 ”
I
化为 “ 三角形 ” 是利 用行列式 的性质 , 把 所 求 行 列 式 的 主
对 角 线 下 方 的 元 素 全化 为零 .
3
关于求解行列式的几种特殊的方法

关于求解行列式的几种特殊的方法行列式是线性代数中一个重要的概念,它在计算机科学、物理学和工程学等领域都有广泛的应用。
在求解行列式的过程中,存在一些特殊的方法,可以帮助我们简化计算和提高效率。
本文将介绍几种常见的特殊方法,包括拉普拉斯展开、三角形展开和行列式性质的运用等。
1.拉普拉斯展开法拉普拉斯展开法是求解行列式的一种基本方法,适用于任意阶的矩阵。
其核心思想是通过分解矩阵,将复杂的行列式转化为多个较小规模的行列式的代数和。
具体步骤如下:1)选择一个行(列)展开,将行(列)按照一些特定的顺序展开。
2)对每一个元素a[i][j],构造一个以该元素为顶点的代数余子式M[i][j],即划去第i行和第j列后剩下的矩阵所构成的行列式。
3)计算每一个代数余子式的值M[i][j],并与对应的元素a[i][j]相乘,得到M[i][j]*a[i][j]。
4)将所有得到的乘积相加,该结果即为原行列式的值。
>例如,对于一个3阶矩阵A,可以选择按照第一行展开,则拉普拉斯展开为:>,A,=a11*M11-a12*M12+a13*M13>其中,M11,M12,M13分别是以元素a11,a12,a13为顶点的代数余子式。
拉普拉斯展开法的优点是适用于任意规模的矩阵,但是对于高阶矩阵来说,计算量较大,效率较低。
2.三角形展开法三角形展开法是求解上三角行列式的一种特殊方法,适用于上三角矩阵,即矩阵的主对角线以下的元素都为0。
该方法通过逐步消元来简化计算,减少了矩阵的规模。
具体步骤如下:1)将上三角矩阵A拆分为一个上三角矩阵B和下三角矩阵C的乘积,即A=BC。
2) 计算上三角矩阵B的主对角线上的元素的乘积,即B =b11*b22*...*bnn。
3)将下三角矩阵C的主对角线上的元素分别除以上一步得到的乘积,得到新的下三角矩阵C'。
4) 计算新的下三角矩阵C'的主对角线上的元素的乘积,即C' =c'11*c'22*...*c'nn。
行列式的计算技巧总结

行列式的计算技巧总结行列式是线性代数中的重要概念,它在计算中有着广泛的应用,如矩阵求逆、解线性方程组、判断矩阵的线性无关性等。
行列式的计算可以通过展开定理、性质和转置等多种方法进行。
下面是行列式计算的一些常见技巧总结。
1.行列式的定义和性质行列式是一个标量,用来描述一个矩阵的一些特性。
对于一个n阶方阵A,它的行列式记作det(A),A,或∆。
行列式具有以下性质:(1) det(A) = det(A^T) //行列互换,行列式不变(2) det(A·B) = det(A)·det(B) //两个矩阵相乘的行列式等于两个矩阵的行列式的乘积(3) 若矩阵A的其中一行(列)全为0,则det(A) = 0(4) 若矩阵A的两行(列)相同,则det(A) = 0(5) 若矩阵A的其中一行(列)成比例,即全部为c倍关系,则det(A) = c^n·det(A')(6) 若矩阵A的其中一行(列)都是两个矩阵B和C对应行(列)的和,则det(A) = det(B) + det(C)2.二阶和三阶行列式的计算二阶行列式的计算可以直接进行运算,即ad-bc。
三阶行列式的计算可以通过对角线和副对角线元素的乘积之和减去反对角线和主对角线元素的乘积之和,即a(ei-fh) - b(di-fg) + c(dh-eg)。
其中a、b、c、d、e、f、g、h、i是矩阵A的元素。
3.行列式的展开行列式的展开定理是行列式计算的重要工具。
对于n阶行列式,可以通过对任意一行(列)展开来计算行列式的值。
展开的时候,可以选择展开到其他行(列)上,也可以选择展开到其他元素,具体选择哪一行(列)或元素展开要根据实际情况决定。
展开后的行列式可以继续进行展开,直到变为二阶行列式,然后通过二阶行列式的计算结果反推回原行列式。
4.行列式的转置行列式的转置是行列式计算的另一个常用方法。
对于n阶行列式A,可以将其转置为A^T,然后利用性质(1) det(A) = det(A^T)进行计算。
(完整版)行列式的计算方法总结
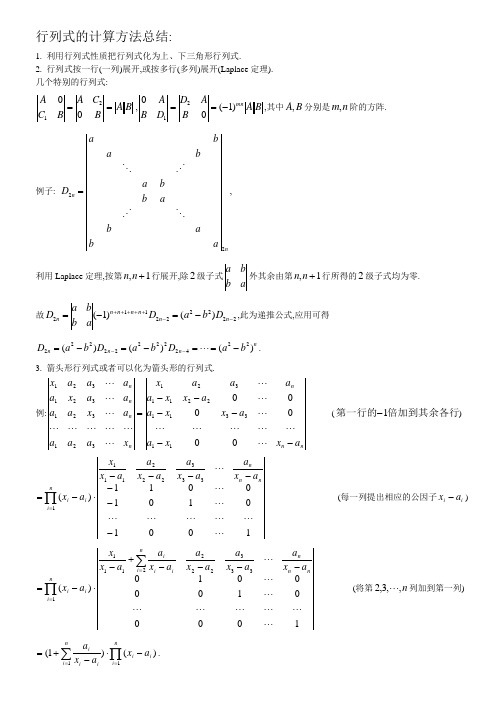
行列式的计算方法总结:1. 利用行列式性质把行列式化为上、下三角形行列式.2. 行列式按一行(一列)展开,或按多行(多列)展开(Laplace 定理). 几个特别的行列式:B A BC A BC A ==0021,B A BA D DB Amn )1(0021-==,其中B A ,分别是n m ,阶的方阵. 例子: nn abab ab b a b abaD 22=,利用Laplace 定理,按第1,+n n 行展开,除2级子式ab ba 外其余由第1,+n n 行所得的2级子式均为零. 故222222112)()1(--+++++-=-=n n n n n n n D b a D ab b a D ,此为递推公式,应用可得n n n n b a D b a D b a D )()()(224222222222-==-=-=-- .3. 箭头形行列式或者可以化为箭头形的行列式.例:nn n n n n n a x x a a x x a a x x a a a a x x a a a a x a a a a x a a a a x ------=0001133112211321321321321321 -----(倍加到其余各行第一行的1-) 100101010011)(3332221111-------⋅-=∏=nn n n i i i a x a a x a a x a a x x a x --------(每一列提出相应的公因子i i a x -) 1001000010)(33322221111nn n ni ii i n i i i a x a a x a a x a a x a a x x a x ----+-⋅-=∑∏== --------(将第n ,,3,2 列加到第一列)其它的例子:特点是除了主对角线,其余位置上的元素各行或各列都相同.n x a aa a a x a a a a a x a a a aa x a ++++ 321,nn n n a x a a a a a x a a a a a x a a a a a x ++++ 321321321321. 4. 逐行逐列相减法.行列式特点是每相邻两行(列)之间有许多元素相同.用逐行(列)相减可以化出零. 5. 升阶法(或加边法, 添加一行一列,利于计算,但同时保持行列式不变).例子:nn n n nnn n nn n n nn b a b a b a a b a b a b a a b a b a b a a b b b b a b a b a b a b a b a b a b a b a ++++-++++-++++----=++++++++++++10101010000011112122212212111121212221212111∑∑∑∑∑∑======+--+=---+--+=------=ni in i i i ni in ni i n i i i ni in n b b a na b b b b b a na a a ab b b 1112111121211110100000101111111010100111011101∑∑∑∑∑∑∑=≠======-+++=-++=nj nji i j i j ni i ni i ni i i ni i ni i a a b b a b a n b a 1111111)(1)1)(1(.例子:nnx a aaaa x a a a a a x a a a a a x a a a a a x a aaaa x a a a a a x a aa a a x a ++++=++++0001321321).1(00000000000010100010001000111213211321∑∑==+=+=----=ni in nni inx a x x x x x x x a a a a x a x x x x a a a a6. 利用范德蒙德行列式.计算行列式: n nn n nn nn n n nnx x x x x x x x x x x x x x x x D321223222122322213211111----=解: 令: nnnn nn n nn n n n nn n n ny x x x y x x x y x x x y x x x y x x x D211112112222212222212111111--------=,这是一个1+n 级范德蒙德行列式. 一方面,由范德蒙德行列式得)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ .可看做是关于y 的一个n 次多项式.另一方面,将1D 按最后一列展开,可得一个关于y 的多项式01111p y p y p y p D n n n n ++++=-- ,其中1-n y 的系数1-n p 与所求行列式D 的关系为1--=n p D .由)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ 来计算1-n y的系数1-n p 得:∑∏=≤<≤-⋅--=ni i ni j j in x x xp 111)(,故有∑∏=≤<≤-⋅-=-=ni i ni j j in x x xp D 111)(其它的例子:=+-+++-++-++------n n n n n n n n n n n n n n n n n n nn n n nb b a b a b a a b b a b a b a a b b a b a b a a 111121211111212222222122111121211111……每一行提公因子n i a ,nn n n n n n n n n n n n n nn n n a b a b a b a b a ba b a b a b a b a b a ba b a a a )()()()(1)()()()(1)()()()(1111112111122122222221111121111121++-++++++--+=).(1121∏≤<≤+-=n i j j j ii nn n n a b a b a a a7.利用数学归纳法证明行列式.(对行列式的级数归纳)证明当βα≠时,,1000001000100011βαβαβααββαβααββααββα--=+++++=++n n n D证明时,将n D 按第一行(或第一列)展开得21)(---+=n n n D D D αββα,利用归纳假设可得. 8. 利用递推公式.例子: 计算行列式,10000010001000βααββαβααββααββα+++++=n D 解: 按第一行展开得: 21)(---+=n n n D D D αββα,将此式化为:(1) )(211----=-n n n n D D D D αβα或 (2) )(211----=-n n n n D D D D βαβ 利用递推公式(1)得:n n n n n n n n D D D D D D D D βαβαβαβα=-==-=-=-------)()()(122322211 ,即n n n D D βα+=-1. (3)利用递推公式(2)得:n n n n n n n n D D D D D D D D αβαβαβαβ=-==-=-=-------)()()(122322211 ,即n n n D D αβ+=-1. (4)由(3)(4) 解得: ,,)1(,11⎪⎩⎪⎨⎧=+≠--=++βααβαβαβαn n n n n D其它的例子nn acb a ac b a c b a D00000000000=,按第一行展开可得21---=n n n bcD aD D ,此时令,,bc a ==+αββα则21)(---+=n n n D D D αββα,变形为211)(----=-n n n n D D D D αβα,此为递推公式.利用刚才的例子可求得结果. 这里,,bc a ==+αββα即βα,是方程02=+-bc ax x 的两个根.9. 分拆法.将行列式的其中一行或者一列拆成两个数的和,将行列式分解成两个容易求的行列式的和.例子:accccb ac c c bb ac c bbbac b b b b c a c accccb ac c c bb ac c bbbacb b b b a D n-+==210000V V acccb ac c b b a c b b b a b b b b c a accccb ac c c b b a c c b b b a c b b b b c +=-+=1V : 除第一行外,其余各行加上第一行的1-倍,所得行列式按第一列展开,2V 按第一列展开.11)(0000000--=----------=n b a c ba b c b c bc ba b c b c b b b a b c ba b b b b c V12)(--=n D c a V , 故11)()(---+-=n n n D c a b a c D ,由c b ,的对称性质,亦可得11)()(---+-=n n n D b a c a b D ,这两个式子中削去1-n D ,可得结论,bc c a b b a c D nn n ----=)()(.注: (1) 同一个行列式,可有多种计算方法.要利用行列式自身元素的特点,选择合适的计算方法. (2) 以上的各种方法并不是互相独立的,计算一个行列式时,有时需要综合运用以上方法,。
几种特殊类型行列式及其计算

1 行列式的定义及性质1.1 定义[3] n 级行列式111212122212n n n n nna a a a a a a a a等于所有取自不同行不同列的个n 元素的乘积1212n j j nj a a a (1)的代数和,这里12n j j j 是1,2,,n 的一个排列,每一项(1)都按下列规则带有符号:当12n j j j 是偶排列时,(1)带正号,当12n j j j 是奇排列时,(1)带有负号.这一定义可写成()()121212111212122212121n n nn j j j n j j nj j j j n n nna a a a a a a a a a a a τ=-∑这里12nj j j ∑表示对所有n 级排列求和.1.2 性质[4]性质1.2.1 行列互换,行列式的值不变.性质1.2.2 某行(列)的公因子可以提到行列式的符号外.性质1.2.3 如果某行(列)的所有元素都可以写成两项的和,则该行列式可以写成两行列式的和;这两个行列式的这一行(列)的元素分别为对应的两个加数之一,其余各行(列)与原行列式相同.性质1.2.4 两行(列)对应元素相同,行列式的值为零. 性质1.2.5 两行(列)对应元素成比例,行列式的值为零.性质1.2.6 某行(列)的倍数加到另一行(列)对应的元素上,行列式的值不变. 性质1.2.7 交换两行(列)的位置,行列式的值变号.2 行列式的分类及其计算方法2.1 箭形(爪形)行列式这类行列式的特征是除了第1行(列)或第n 行(列)及主(次)对角线上元素外的其他元素均为零,对这类行列式可以直接利用行列式性质将其化为上(下)三角形行列式来计算.即利用对角元素或次对角元素将一条边消为零.例1 计算n 阶行列式()1232311110010001n n na a D a a a a a =≠.解 将第一列减去第二列的21a 倍,第三列的31a 倍第n 列的1na 倍,得1223111110000000n n na a a a D a a ⎛⎫--- ⎪⎝⎭=1221nni i i i a a a ==⎛⎫=- ⎪⎝⎭∑∏. 2.2 两三角型行列式这类行列式的特征是对角线上方的元素都是c ,对角线下方的元素都是b 的行列式,初看,这一类型似乎并不具普遍性,但很多行列式均是由这类行列式变换而来,对这类行列式,当b c =时可以化为上面列举的爪形来计算,当b c ≠时则用拆行(列)法[9]来计算.例2 计算行列式123n n a c c c b a c c D bb ac bbba =. 解 当bc =时123n na b b b b a b b D bb a b bbba =. 将第2行到第行n 都减去第1行,则n D 化为以上所述的爪形,即112131000000n n a b b bb a a b D b a a bb a a b--=----.用上述特征1的方法,则有()11212131100000000ni i n n a bba abb a a b D b a a b b a a b=-----=----∑()()()()()11111n ni i i n i i a b b a b a b a b a b -+===-+----∑∏.当b c ≠时,用拆行(列)法[9],则112233000n nn x a a a x a a a b x a a b x a a D bb x a b b x a bbbx bbbb x b++==++-112233000nxa a x a a ab x a b x a ab b x b b x a bb bx bb b bb=+-()121100n n n x a ab a x a ax b D a b a b a x a a b-----=+----.化简得()()()()1211n n n n D b x a x a x a x b D --=---+-. ()1而若一开始将n x 拆为n a x a +-,则得()()()()1211n n n n D a x b x b x b x a D --=---+-. ()2由()()()()12n n x b x a ⨯--⨯-,得()()111nn n ij i j D a x b b x a a b ==⎡⎤=---⎢⎥-⎣⎦∏∏. 有一些行列式虽然不是两三角型的行列式,但是可以通过适当变换转化成两三角型行列式进行计算.例3 计算行列式()2n d b b bc x a aD n ca x a caax=≥. 解 将第一行a b ⨯,第一列ac⨯,得22n a da a a bc a x a a bc D aa x a a aaax=.即化为上()21-情形,计算得()()()()121n n n D d x a n ad bc x a --=-+---.而对于一些每行(列)上有公共因子但不能像上面一样在保持行列式不变的基础上提出公共因子的,则用升阶法[8]来简化.例4 计算行列式2112122122212111n n n n n n x x x x x x x x x x D x x x x x ++=+.解 将行列式升阶,得1221121221222121010101n nn n n n n x x x x x x x x D x x x x x x x x x x +=++. 将第i 行减去第一行的i x ()2,,i n =倍,得1212110001001n n nx x x x D x x -=--.这就化为了爪形,按上述特征1的方法计算可得212110100001001ni n i n x x x x D =+=∑ 211ni i x ==+∑.2.3 两条线型行列式这类行列式的特征是除了主(次)对角线或与其相邻的一条斜线所组成的任两条线加四个顶点中的某个点外,其他元素都为零,这类行列式可直接展开降阶,对两条线中某一条线元素全为0的,自然也直接展开降阶计算.例5 计算行列式112211n n n nna b a b D a b b a --=.解 按第一行展开可得()2213322111111111nn n n n n n nn n a b b a b a b D a b a b a b a a b +------=+-()112121n n n a a a b b b +=+-.例6 计算行列式111121111nnn n n n n nna b a b a b D c d c d c d ----=.解 方法1 直接展开可得()1111111112211111111010n n n n nn nn n n n n nna b a b a b a b D a c d b c d c d c d d c ----+----=+-()()11112111111111111111n n n n n n nn n n n n n a b a b a b a b a d b c c d c d c d c d -----+----=--()()21n n n n n a d b c D -=-.则()()()()()()2111121221nn n n n n n n n n n n n n i i i i n n i D a d b c D a d b c a d b c D a d b c ------==-=--==-∏.方法2 (拉普拉斯定理法[3]) 按第一行和第2n 行展开得()11121211211111n n n nn n n nnn n a b a b a b D c d c d c d --+++--=-()()21n n n n n a d b c D -=-. 其余的同法1.2.4 Hessenberg型行列式这类行列式的特征是除主(次)对角线及与其相邻的斜线,再加上第1或第n 行外,其他元素均为零,这类行列式都用累加消点法,即通常将第一行(列)元素化简到只有一个非零元素,以便于这一行或列的展开降阶计算.例7 计算行列式123111000022022011n n n D n nn n---=----.解 将各列加到第一列得()123120100022022000011n n n n n D n nn n+---=----. 按第一列展开得()100220122200011n n n D n n n n--+=----()()11!12n n -+=-.2.5 三对角型行列式形如n a bc abD cbca=的行列式,这类行列式的特征是除这三条斜线上元素外,其他元素均为零,这是一递推结构的行列式,所有主子式都有同样的结构,从而以最后一列展开,将所得的1n -阶行列式再展开即得递推公式. 对这类行列式用递推法[5].例8 计算行列式n a b c a bD cbca=.解 按第一列展开有12n n n D aD bcD --=-解特征方程20x ax bc -+=得12x x ==.则()()11121212,n n nx x D x x x x ++-=≠-.例9 计算行列式95499549n D =.解 按第一行展开得19200n n D D --+=.解特征方程得124,5x x ==.则1145n n n D a b --=+.分别使1,2n =得16,25,a b =-=则1154n n n D ++=-.2.6 各行(列)元素和相等的行列式这类行列式的特征是其所有行(列)对应元素相加后相等,对这类行列式,将其所有行(列)加到第一行(列)或第n 行(列),提取公因式后,再把每一行都减去第一行(列),即可使行列式中出现大量的零元素.例10 计算行列式111222111n nnna a a a a a D a a a ++=+.解 将第2行到第n 行都加到第1行,得11122211111n nnn nnna a a a a a a a a D a a a ++++++++++=+()2221111111n nnna a a a a a a a +=++++()1111010101n a a =+++()11n a a =+++.2.7 相邻两行(列)对应元素相差1的行列式这类行列式的特征是大部分以数字为元素且相邻两行(列)元素相差1的行列式,对这类行列式,自第一行(列)开始,前行(列)减去后行(列),或自第行n (列)开始,后行(列)减去前行(列),即可出现大量元素为1或1-的行列式,再进一步化简即出现大量的零元素.若相邻两行(列)元素相差倍数k ,则前(后)行(列)减去后(前)行(列)的k -倍,可使行列式出现大量的零元素.例11 计算行列式012211013221432340112310n n n n n n n D n n n n n ------=-----.解 依次用前行减去后行,可得111111111111111111111231n D n n n ------=-------.现将第1列加到第2列至第n 列,得10000120001220012220123241n D n n n nn ------=--------()()12121n n n --=--.例11 计算阶n 行列式221132214323423111111n n n n n n n n n n n a a a a a a a a a a a a D a a a a aa a a ----------=.解 这是相邻两行(列)相差倍数a ,可采用前行减去后行的a -倍的方法化简得231100000100000100000101nnnn n n a a a D a aa a a ----=-()11n n a -=-.2.8 德蒙德型行列式这类行列式的特征是有逐行(列)元素按方幂递增或递减,对这类行列式可以转化为德蒙德行列式来计算.例12 计算行列式1111111111222222111111111n n n n nn n nn n n n n nn n nn n n n n n a a b a b b a a b a b b D a b a a b a b b ----+--++++++=.解 将第i 行提出n i a ,得111122112211111111nnn nn i i nn n n n b b a a b b D a a a b b a a ++=++++⎛⎫ ⎪⎝⎭⎛⎫ ⎪=⎝⎭⎛⎫⎪⎝⎭∏()11iji j i j n a bb a ≤≤≤+=-∏.。
几种特殊类型行列式及其计算

几种特殊类型行列式及其计算特殊类型行列式是指其中元素满足一定的特殊规律或形式的行列式。
下面将介绍几种常见的特殊类型行列式及其计算方法。
1.对角行列式:对角行列式是指除了主对角线上的元素外,其余元素都为0的行列式。
对角行列式的计算非常简单,只需将主对角线上的元素相乘即可。
例如,行列式a00b00的值为a*b*c。
2.上三角行列式:上三角行列式是指除了主对角线及其上方的元素外,其余元素都为0的行列式。
上三角行列式的计算方法是将主对角线上的元素相乘。
例如,行列式120400的值为1*4*6=243.下三角行列式:下三角行列式是指除了主对角线及其下方的元素外,其余元素都为0的行列式。
下三角行列式的计算方法与上三角行列式相同,将主对角线上的元素相乘。
例如行列式708910111的值为7*9*12=7564.三角行列式:三角行列式是指一个矩阵的主对角线两侧的元素相同。
例如,行列式122334的值可以通过利用矩阵的对称性进行计算。
首先,将第二行减去第一行得到121134然后,再将第三行减去第一行的三倍得到12110-2-然后,再将第三行减去第二行的两倍得到121100-最后,将主对角线上的元素相乘,即1*1*(-2)=-2,即该行列式的值为-25.雅可比行列式:雅可比行列式是指一种特殊的三阶行列式形式。
∂(f1,f2,f3)---------∂(x,y,z)表示函数f1,f2,f3关于x,y,z的偏导数。
以上介绍了几种特殊类型的行列式及其计算方法。
了解不同类型的行列式有助于我们更好地理解和应用线性代数的相关理论和方法。
一类特殊行列式的计算公式

一类特殊行列式的计算公式在矩阵与行列式的计算中,常常会遇到一类特殊的行列式形式,它们有一些特殊的性质和计算公式。
在本篇文章中,我将介绍几种常见的特殊行列式,并给出它们的计算公式。
1.对称行列式对称行列式指的是行列式中的每一行都与其对应的列完全相同。
例如,以下是一个对称行列式的例子:```abcbcdcde```对称行列式有一个非常重要的性质,即它的值等于其中任意一个元素与该元素所在的余子式的乘积之和。
余子式是指将该元素所在的行列删去后的行列式。
以前述的对称行列式为例,假设我们要计算元素a的余子式:```deef```则根据上述性质,对称行列式的值可以表示为:abcbcdcde=a*,de,+b*,ef,+c*,dfef,,gh,,g```2.三角行列式三角行列式指的是行列式中的元素有一定的规律,每个元素下方都有一个或多个为0的元素。
以下是一个三角行列式的例子:```ab0c0000d```三角行列式的值等于对角线上的元素的乘积。
以前述的三角行列式为例,其计算公式为:```ab000d=a*0*0+0*0*0+0*b*0+0*0*d+c*0*0+0*0*d=0+0+0+0+0+0=0```3.对角行列式对角行列式指的是行列式中的非对角线上的元素全部为0,只有对角线上的元素不为0。
以下是一个对角行列式的例子:```a000b000c```对角行列式的值等于对角线上的元素的乘积。
以前述的对角行列式为例,其计算公式为:```a000b0=a*b*c```4.上三角行列式与下三角行列式上三角行列式指的是行列式中的非对角线上的元素全部为0,并且对角线以下的元素全为0。
以下是一个上三角行列式的例子:```abc0de00f```类似地,下三角行列式指的是行列式中的非对角线上的元素全部为0,并且对角线以上的元素全为0。
以下是一个下三角行列式的例子:```a00bc0def```对于上三角行列式和下三角行列式,它们的值等于对角线上的元素的乘积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊行列式及行列式计算方法总结一、 几类特殊行列式1. 上(下)三角行列式、对角行列式(教材P7例5、例6)2. 以副对角线为标准的行列式11112112,1221222,11,21,11,112,1(1)212,1100000000000000(1)n n n n n n n n n n n nnn n n n n nnn n n n n a a a a a a a a a a a a a a a a a a a a a a ---------===-L L L LL L MM M M M M M M M NL LLL 3. 分块行列式(教材P14例10)一般化结果:00n n m n n m n m m n m m nmA C A AB BC B ⨯⨯⨯⨯==⋅0(1)0n m n n m nmn n m mm nmm nA C A AB BC B ⨯⨯⨯⨯==-⋅4. 范德蒙行列式(教材P18例12) 注:4种特殊行列式的结果需牢记!以下几种行列式的特殊解法必须熟练掌握!!! 二、 低阶行列式计算二阶、三阶行列式——对角线法则 (教材P2、P3) 三、 高阶行列式的计算 【五种解题方法】1) 利用行列式定义直接计算特殊行列式;2) 利用行列式的性质将高阶行列式化成已知结果的特殊行列式;3) 利用行列式的行(列)扩展定理以及行列式的性质,将行列式降阶进行计算——适用于行列式的某一行或某一列中有很多零元素,并且非零元素的代数余子式很容易计算; 4) 递推法或数学归纳法; 5) 升阶法(又称加边法)【常见的化简行列式的方法】1. 利用行列式定义直接计算特殊行列式 例1 (2001年考研题)0001000200019990002000000002001D =L LM M M M M M L L L分析:该行列式的特点是每行每列只有一个元素,因此很容易联想到直接利用行列式定义进行计算。
解法一:定义法(1,2,...,2,1,)012...19990(1)2001!(1)2001!2001!n n n D τ--+++++=-=-=解法二:行列式性质法利用行列式性质2把最后一行依次与第n -1,n -2,…,2,1行交换(这里n =2001),即进行2000次换行以后,变成副对角行列式。
2001(20011)2001120011200002001000100200(1)(1)(1)2001!2001!019990002000000D ⨯---=-=--=L LL M M M M MML L解法三:分块法0001000200019990002000000002001D =L LM M M M M M L L L利用分块行列式的结果可以得到2000(2000-1)200010020=2001=2001(-1)2000!=200101999002000000D ⋅⋅L L MMM M M L L! 解法四:降阶定理展开按照每一行分别逐次展开,此处不再详细计算。
2. 利用行列式的性质将高阶行列式化成已知结果的特殊行列式 例21111111111111111a a D b b+-=+-分析:该行列式的特点是1很多,可以通过12r r -和34r r -来将行列式中的很多1化成0. 解:214143220011001100111111110110000110011111111110111100011001100r r r r r r a a a a a D ababb b b b ba aba b b------===----==-例33223111111322322222232233333333223444444a ab a b b a a b a b b D a a b a b b a a b a b b = ,(0)i a ≠ 分析:该类行列式特点是每行a 的次数递减,b 的次数增加。
特点与范德蒙行列式相似,因此可以利用行列式的性质将D 化成范德蒙行列式。
解:2311111123222222333312342333333323444444333331241234123433331234141()()()1()()()1()()()1()()()(,,,)()ji j i ij b bb a a a b b b a a a D a a a a b b b a a a b b b a a a b b b b a a a a V a a a a b b a a a a a a ≤<≤=⋅=⋅=⋅-∏练习:(11-12年 IT 专业期末考试题)若实数z y x ,,各不相等,则矩阵⎪⎪⎪⎪⎭⎫ ⎝⎛=222111z y x z y x M 的行列式=M __________ 3. 利用行列式的行(列)扩展定理以及行列式的性质,将行列式降阶进行计算 例400000000000n a b a b D a b ba=L L L L L L分析:该行列式特点是a 处于主对角线,b 在a 后的一个位置,最后一行中b 是第一个元素,a 是最后一个元素。
解:按第一列展开:1111111000000(1)(1)000000(1)(1)n n n n n n n na b b a b ab D a ba b aba a ab b a b ++-+-+=⋅-+-⋅=⋅+-⋅=+-L LL L OO L L练习:(11-12年期中考试题)xyy x x y x y x D n 00000000000000ΛΛΛΛΛΛΛ=4. 行(列)和相等的行列式 例5n a b b b a bD b b a=L L M M M ML分析:该行列式的特点是主对角线上元素为a ,其余位置上都是b 。
可将第2,3,…,n 列加到第1列上。
(类似题型:教材P12例8,P27 8(2)) 解:111110[(1)][(1)]110[(1)]()n n b b b b a b a b D a n b a n b b a a ba nb a b --=+-⋅=+-⋅-=+--L L L L M M M M M M M M L L 5. 箭头形(爪行)行列式 例601111200130100D n=L L L L L L分析:该类行列式特点是第一行、第一列及主对角上元素不为0,其余位置都为0.解此类行列式方法,是将行列式化成上三角行列式。
解:分别从第2,3,…,n 列提出因子2,3,…,n ,然后将第2,3,…,n 列分别乘以-1,再加到第1列上。
注:爪形行列式非常重要,很多看似复杂的行列式通过简单变化以后都可以化成爪形行列式进行计算! 练习:1) 教材习题P28: 8(6) 2) (11-12年期末考试题)23(1)2000300010000n a n n a a A n a na-----=-L L L L L L L3) (11-12年IT 期末考试题)nxn x xxa a a a x D n n n 00100002000011211ΛΛM M M M M ΛΛΛ-=-+例7123123123123n n n nx a a a a x a a D a a x a a a a x =L L L L L L分析:该类行列式特点是每一行只有主对角线上的元素与第一个元素不同。
解:1231122113311312112233112221221122000001100()()()101010011()()()01001(n n nn n nn n ni n i i in nn n i i x a a a a x x a D a x x a a x x a a a x a x a x a x a x a x a x a x a a a a x a x a x a x a x a x a x a =--=---------=-⋅----+---=-⋅--=-∑L L L L LLL L L L M M M M M LL L L M M M M L 11)[1]n nii i i ia x a ==+-∑∏6. 递推法或数学归纳法该方法用于行列式结构具有一定的对称性,教材P15例11就是递推法的经典例题。
利用同样的方法可以计算教材P27 8(4)。
7. 升阶法通常计算行列式都采用降阶的方法,是行列式从高阶降到低阶,但是对于某些行列式,可以通过加上一行或一列使得行列式变成特殊行列式,再进行计算。
例8 (教材P28 8(6))121+1111+1=111+n na a D a LL M M M M L , (0)i a ≠分析:该题有很多解法,这里重点介绍升阶法。
因为行列式中有很多1,因此可以增加一行1,使得行列式变成比较特殊或者好处理的行列式。
注意:行列式是方形的,因此在增加一行以后还要增加一列,以保持行列式的形状。
为了使行列式的值不改变,因此增加的列为1,0,0, 0例9 (教材P27 6(4))222244441111=a b c d D abcda b c d分析:此行列式可以应用性质6将行列式化为上三角行列式,也可以对比范德蒙行列式的形式,通过添加一行和一列把行列式变成范德蒙行列式以后再进行计算。
解法一:2433221213122222222222222222111100()()()0()()()111=()()()()()()100()()()()()()()(r a r r ar r ar c c c c b a c a d a D b b a c c a d d a b b a c c a d d a b a c a d a b cdb b ac c ad d a b a c a d a bc bd bb b ac c a b b ad d a b --------=---------+++=-----++-++-按第一列展开2222)()()()()()()()()()()()()()()b ac bd b b a c a d a c c a b b a d d a b b a a b a c a d b c b d c d a b c d +--=---+-++-+=------+++按第一行展开解法二:25322224444333341111()()()()()()()()()()1a b c d D a b c d a b c d x a x b x c x d b a c a d a c x x a b c d d x b x b d c ==----------3x 的系数是D -,因此D 等于3x 的系数的相反数,由此可计算得到结果。
