matlab求解热传导实例
一维非稳态导热方程求解 附Matlab程序
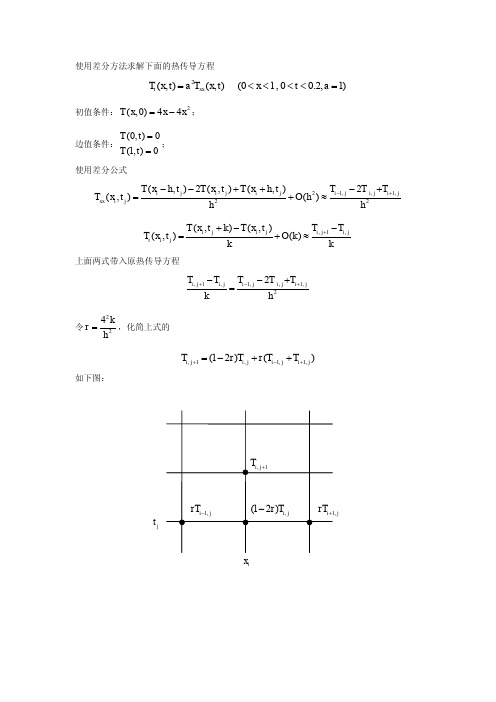
使用差分方法求解下面的热传导方程2(,)(,)(01,00.2,1)t xx T x t a T x t x t a =<<<<=初值条件:2(,0)44T x x x =-;边值条件:(0,)0(1,)0T t T t ==;使用差分公式1,,1,222(,)2(,)(,)2(,)()i j i j i j i j i j i jxx i j T x h t T x t T x h t T T T T x t O h h h -+--++-+=+≈,1,(,)(,)(,)()i j i j i j i jt i j T x t k T x t T T T x t O k kk++--=+≈上面两式带入原热传导方程,1,1,,1,22i j i ji j i j i jT T T T T kh +-+--+=令224kr h=,化简上式的,1,1,1,(12)()i j i j i j i j T r T r T T +-+=-++如下图:ix jt j编程MA TLAB 程序,运行结果如下1xtTfunction mypdesolution c=1;xspan=[0 1]; tspan=[0 0.2]; ngrid=[100 10]; f=@(x)4*x-4*x.^2; g1=@(t)0; g2=@(t)0;[T,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid); [x,t]=meshgrid(x,t); mesh(x,t,T); xlabel('x') ylabel('t') zlabel('T')function [U,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid) % 热传导方程:% Ut(x,t)=c^2*Uxx(x,t) a<x<b ts<t<tf % 初值条件: % u(x,0)=f(x)% 边值条件:% u(a,t)=g1(t)% u(b,t)=g2(t)%% 参数说明% c:方程中的系数% f:初值条件% g1,g2:边值条件% xspan=[a,b]:x的取值范围% tspan=[ts,tf]:t的取值范围% ngrid=[n,m]:网格数量,m为x网格点数量,n为t的网格点数量% U:方程的数值解% x,t:x和t的网格点n=ngrid(1);m=ngrid(2);h=range(xspan)/(m-1);x=linspace(xspan(1),xspan(2),m);k=range(tspan)/(n-1);t=linspace(tspan(1),tspan(2),n);r=c^2*k/h^2;if r>0.5error('为了保证算法的收敛,请增大步长h或减小步长k!')ends=1-2*r;U=zeros(ngrid);% 边界条件U(:,1)=g1(t);U(:,m)=g2(t);% 初值条件U(1,:)=f(x);% 差分计算for j=2:nfor i=2:m-1U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1));endend%%%%%%本文来自互联网%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%。
导热方程求解matlab

使用差分方法求解下面的热传导方程2(,)4(,)0100.2t xx T x t T x t x t =<<<<初值条件:2(,0)44T x x x =-边值条件:(0,)0(1,)0T t T t ==使用差分公式1,,1,222(,)2(,)(,)2(,)()i j i j i j i j i j i j xx i j T x h t T x t T x h t T T T T x t O h h h -+--++-+=+≈,1,(,)(,)(,)()i j i j i j i jt i j T x t k T x t T T T x t O k k k ++--=+≈上面两式带入原热传导方程,1,1,,1,22i j i ji j i j i jT T T T T k h +-+--+= 令224k r h=,化简上式的 ,1,1,1,(12)()i j i j i j i j T r T r T T +-+=-++ix jt j编程MATLAB 程序,运行结果如下x t Tfunction mypdesolutionc=1;xspan=[0 1];tspan=[0 0.2];ngrid=[100 10];f=@(x)4*x-4*x.^2;g1=@(t)0;g2=@(t)0;[T,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid);[x,t]=meshgrid(x,t);mesh(x,t,T);xlabel('x')ylabel('t')zlabel('T')function [U,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid)% 热传导方程:% Ut(x,t)=c^2*Uxx(x,t) a<x<b ts<t<tf% 初值条件:% u(x,0)=f(x)% 边值条件:% u(a,t)=g1(t)% u(b,t)=g2(t)%% 参数说明% c:方程中的系数% f:初值条件% g1,g2:边值条件% xspan=[a,b]:x的取值范围% tspan=[ts,tf]:t的取值范围% ngrid=[n,m]:网格数量,m为x网格点数量,n为t的网格点数量% U:方程的数值解% x,t:x和t的网格点n=ngrid(1);m=ngrid(2);h=range(xspan)/(m-1);x=linspace(xspan(1),xspan(2),m);k=range(tspan)/(n-1);t=linspace(tspan(1),tspan(2),n);r=c^2*k/h^2;if r>0.5error('为了保证算法的收敛,请增大步长h或减小步长k!')ends=1-2*r;U=zeros(ngrid);% 边界条件U(:,1)=g1(t);U(:,m)=g2(t);% 初值条件U(1,:)=f(x);% 差分计算for j=2:nfor i=2:m-1U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1));endend。
一维热传导方程数值解法及matlab实现分离变量法和有限差分法

一维热传导方程数值解法及matlab实现分离变量法和有限差分法一维热传导方程的Matlab解法:分离变量法和有限差分法。
问题描述:本实验旨在利用分离变量法和有限差分法解决热传导方程问题,并使用Matlab进行建模,构建图形,研究不同情况下采用何种方法从更深层次上理解热量分布与时间、空间分布关系。
实验原理:分离变量法:利用分离变量法,将热传导方程分解为两个方程,分别只包含变量x和变量t,然后将它们相乘并求和,得到一个无穷级数的解。
通过截取该级数的前n项,可以得到近似解。
有限差分法:利用有限差分法,将空间和时间分别离散化,将偏导数用差分代替,得到一个差分方程组。
通过迭代求解该方程组,可以得到近似解。
分离变量法实验:采用Matlab编写代码,利用分离变量法求解热传导方程。
首先设定x和t的范围,然后计算无穷级数的前n项,并将其绘制成三维图形。
代码如下:matlabx = 0:0.1*pi:pi;y = 0:0.04:1;x。
t] = meshgrid(x。
y);s = 0;m = length(j);for i = 1:ms = s + (200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t));endsurf(x。
t。
s);xlabel('x')。
XXX('t')。
zlabel('T');title('分离变量法(无穷)');axis([0 pi 0 1 0 100]);得到的三维热传导图形如下:有限差分法实验:采用Matlab编写代码,利用有限差分法求解热传导方程。
首先初始化一个矩阵,用于存储时间t和变量x。
然后计算稳定性系数S,并根据边界条件和初始条件,迭代求解差分方程组,并将其绘制成三维图形。
代码如下:matlabu = zeros(10.25);s = (1/25)/(pi/10)^2;fprintf('稳定性系数S为:\n');disp(s);for i = 2:9u(i。
matlab傅里叶谱方法求解热传导方程

文章标题:深度解析matlab傅里叶谱方法求解热传导方程在工程学和科学领域中,热传导方程是一个非常重要的偏微分方程,描述了物体内部温度分布随时间的变化。
而傅里叶谱方法是一种常用的数值求解方法,能够高效地对热传导方程进行求解。
本文将深入探讨matlab傅里叶谱方法在求解热传导方程中的应用,以及该方法在实际工程中的意义。
1. 热传导方程的基本概念热传导方程是描述物体内部温度分布随时间演化的方程。
一维情况下,热传导方程可以表示为:$$\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partialx^2}$$其中,$u(x,t)$是位置$x$和时间$t$的温度分布函数,$\alpha$是热扩散系数。
对于二维、三维情况,热传导方程的形式也可以相应拓展。
2. matlab傅里叶谱方法的基本原理傅里叶谱方法是一种基于傅里叶级数展开的数值求解方法。
它的基本思想是将热传导方程通过傅里叶变换转化为频域上的方程,再通过离散化的方式进行求解。
在matlab中,可以利用快速傅里叶变换(FFT)来高效地实现傅里叶谱方法。
该方法的优点是高精度、高效率,并且适用于多维情况。
3. matlab傅里叶谱方法的具体实现在matlab中,可以通过编写相应的程序来实现对热传导方程的求解。
首先需要将热传导方程进行离散化,得到一个离散的时间和空间网格。
然后利用傅里叶变换将热传导方程转化为频域上的方程,通过FFT算法高效地求解。
最后再利用逆傅里叶变换将频域上的解转化为时域的解。
通过这一系列步骤,就可以在matlab中实现对热传导方程的高效求解。
4. 实际工程中的应用与意义matlab傅里叶谱方法在实际工程中有着广泛的应用与意义。
例如在材料科学中,可以利用该方法对材料的热传导特性进行建模和仿真。
在电子工程领域,也可以利用该方法对电路元件的热特性进行分析和优化。
另外,在生物医学工程中,对人体组织的热传导特性进行研究也可以借助matlab傅里叶谱方法来实现。
三维adi导热的matlab编程

一、概述三维ADI(Alternating Direction Implicit)方法是一种常用的求解三维热传导方程的数值方法,其优点是可以克服显式差分方法的时间步长受限制的问题,同时保持计算效率。
在实际工程中,利用Matlab 编程实现三维ADI导热模型可以更好地模拟复杂热传导问题,具有广泛的应用价值。
二、三维ADI方法的基本原理1. 三维热传导方程的离散化三维热传导方程可以用差分形式表示为$$\frac{\partial T}{\partial t} = \alpha(\frac{\partial^2T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} +\frac{\partial^2 T}{\partial z^2})$$其中,$\alpha$为热传导系数,$T$为温度分布,$x$、$y$、$z$分别为空间坐标。
2. 三维ADI方法的求解步骤三维ADI方法的基本思想是将三维热传导方程按各个方向进行交替隐式求解,以避免显式差分方法的时间步长受限制。
第一步:在x方向进行隐式求解第二步:在y方向进行隐式求解第三步:在z方向进行隐式求解重复以上步骤直至收敛三、Matlab编程实现三维ADI导热模型1. 网格的离散化首先需要对求解区域进行网格化,建立离散化的空间网格。
可以利用Matlab中的meshgrid函数快速生成三维网格。
2. 设定初始条件和边界条件根据实际问题设定初始温度分布和边界条件,将问题转化为离散的矩阵形式。
需要根据网格的离散化程度确定时间步长和空间步长。
3. 三维ADI方法的编程实现利用Matlab编写三维ADI方法的求解函数,按照上文所述的求解步骤进行编程实现。
在每一步隐式求解时,可以利用循环结构逐步更新温度分布。
4. 收敛准则和计算效率在编程实现过程中,需要考虑收敛准则的设置和收敛性的检验,以及计算效率的优化。
可以利用Matlab提供的优化工具对代码进行优化,提高计算效率。
有限差分法matlab程序一维热传导

有限差分法matlab程序一维热传导一维热传导是一个常见的物理问题,涉及到热量在一个维度上的传递和分布。
在工程和科学领域中,研究和解决一维热传导问题对于优化系统设计和预测热现象非常重要。
本文将介绍如何使用有限差分法在MATLAB中模拟一维热传导过程。
有限差分法是一种常用的数值解法,用于近似求解微分方程。
它将连续的物理问题离散化,将连续的空间和时间划分为离散的网格点,并通过近似替代微分算子来计算离散点上的数值。
在一维热传导问题中,我们可以将传热方程离散化为差分方程,然后通过迭代计算来模拟热传导过程。
我们需要定义问题的边界条件和初始条件。
对于一维热传导问题,我们通常需要给定材料的热扩散系数、初始温度分布和边界条件。
假设我们研究的是一个长为L的细杆,材料的热扩散系数为α,初始温度分布为T(x,0),边界条件为T(0,t)和T(L,t)。
接下来,我们将空间离散化为N个网格点,时间离散化为M个时间步长。
我们可以使用等距网格,将杆的长度L划分为N个小段,每段的长度为Δx=L/N。
同样,时间也被划分为M个小步长,每个步长的长度为Δt。
这样,我们可以得到网格点的坐标x(i)和时间点的坐标t(j),其中i=1,2,...,N,j=1,2,...,M。
在有限差分法中,我们使用差分近似代替偏导数项。
对于一维热传导方程,我们可以使用向前差分近似代替时间导数项,使用中心差分近似代替空间导数项。
这样,我们可以得到差分方程:(T(i,j+1)-T(i,j))/Δt = α*(T(i+1,j)-2*T(i,j)+T(i-1,j))/Δx^2其中,T(i,j)表示在位置x(i)和时间t(j)的温度。
通过对差分方程进行重排和整理,我们可以得到递推公式:T(i,j+1) = T(i,j) + α*Δt*(T(i+1,j)-2*T(i,j)+T(i-1,j))/Δx^2现在,我们可以在MATLAB中实现这个递推公式。
首先,我们需要定义问题的参数和初始条件。
二维热传导方程数值解及matlab实现

在热传导学科中,二维热传导方程是一个非常重要的数学模型,用于描述二维热传导过程中温度分布随时间的变化规律。
通过对二维热传导方程的数值解及其在Matlab中的实现,可以更好地理解热传导过程及其在工程学、物理学和地球科学等领域的应用。
让我们来了解一下二维热传导方程的基本形式。
二维热传导方程通常可以表示为:$$\frac{\partial u}{\partial t} = \alpha \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) $$在这里,$u(x, y, t)$代表温度随空间坐标$(x, y)$和时间$t$的变化,$\alpha$代表热扩散系数。
方程右侧的两项分别表示温度在$x$方向和$y$方向的二阶导数。
通过数值方法对这个方程进行离散化处理,可以得到其数值解。
在进行数值解的求解过程中,一个常用的方法是有限差分法。
有限差分法将空间和时间进行离散化,将连续的问题转化为离散的问题。
通过将偏导数用差分的形式进行逼近,可以得到关于温度在不同空间点和时间点的离散方程,进而通过迭代求解得到数值解。
这里要注意,为了保证数值解的准确性和稳定性,需要对离散化步长进行合理的选择,并对边界条件和初始条件进行适当的处理。
那么,在Matlab中,我们如何实现二维热传导方程的数值解呢?我们可以通过定义空间网格和时间步长来进行离散化处理,然后利用循环结构和矩阵运算来进行迭代求解。
Matlab提供了丰富的矩阵运算和可视化工具,可以方便地实现对二维热传导方程数值解的求解和结果的可视化呈现。
我个人认为,二维热传导方程的数值解及其在Matlab中的实现,不仅仅是一个数学问题,更是一个工程问题。
通过对二维热传导方程的数值解,可以更好地理解热传导过程的规律,为工程实践中的热传导问题提供重要的参考依据。
通过Matlab的实现,可以更好地将数学模型与工程实践相结合,实现对热传导问题的仿真分析和优化设计。
二维热传导方程 matlab

二维热传导方程是描述二维热传导过程的数学模型,它在工程、物理、地球科学等领域都有重要应用。
在实际工程问题中,我们经常需要求解二维热传导方程,以预测物体表面的温度分布、热量传递速率等参数。
Matlab是一个强大的数学软件,通过Matlab我们可以很方便地求解二维热传导方程,并得到预期的结果。
一、二维热传导方程的基本形式二维热传导方程可以用偏微分方程的形式表示为:∂u/∂t = k(∂²u/∂x² + ∂²u/∂y²)其中,u(x, y, t)是温度分布随时间和空间的变化,k是热传导系数。
二、Matlab中求解二维热传导方程的方法在Matlab中,我们可以采用有限差分法(finite difference method)求解二维热传导方程。
有限差分法将偏微分方程离散化,转化为代数方程组,然后通过迭代求解得到数值解。
具体步骤如下:1. 离散化空间和时间变量,将连续的空间区域和时间区间分割成若干个小区间。
2. 利用二阶中心差分格式对二维热传导方程进行离散化,得到代数方程组。
3. 利用Matlab中的矩阵运算和迭代方法,求解代数方程组,得到数值解。
三、Matlab代码示例下面是一个简单的Matlab代码示例,用于求解二维热传导方程:```matlab定义参数和初始条件Lx = 1; Ly = 1; 区域大小Nx = 100; Ny = 100; 离散化网格数T = 1; 总时间Nt = 100; 时间步数k = 1; 热传导系数dx = Lx/Nx; dy = Ly/Ny;dt = T/Nt;x = 0:dx:Lx; y = 0:dy:Ly;[X, Y] = meshgrid(x, y);u = sin(pi*X).*sin(pi*Y); 初始温度分布迭代求解for n = 1:Ntun = u;for i = 2:Nx-1for j = 2:Ny-1u(i, j) = un(i, j) + k*dt/dx^2*(un(i+1, j)-2*un(i, j)+un(i-1, j)) + k*dt/dy^2*(un(i, j+1)-2*un(i, j)+un(i, j-1));endendend可视化结果figure;surf(X, Y, u);xlabel('x'); ylabel('y'); zlabel('Temperature');```以上代码首先定义了区域大小、离散化网格数、总时间、热传导系数等参数,然后利用有限差分法进行迭代求解,最后利用Matlab绘制了温度分布的三维图像。
