高一数学必修二直线和圆单元测试
直线和圆的方程单元测试

17.
(1)
(2) , 或
【分析】
(1)根据两条直线垂直的条件列方程,化简求得 .
(2)根据两条直线平行以及距离列方程,化简求得 .
(1)
由于 ,所以 .
(2)
依题意 ,则 ,
此时 ,即 ,故 .
由于两条直线的距离为 ,
所以 或 .
18.
(1) ;
(2) .
【分析】
(1)设出圆的标准方程,根据其过的点的坐标满足圆方程,列出等量关系,求解即可;
【详解】
解:由题知 , ,半径分别为 ,
根据两圆相交,可得圆心距大于两圆的半径之差而小于半径之和,
即 .
又 ,所以有 ,
,
再根据 ,
求得 ,
故选:B.
4.A
【分析】
设出直线的截距式方程,根据题意求出待定系数,可得结论.
【详解】
解:设直线 的方程为 ,则 的面积为 ①.
因为直线 过点 ,所以 ②.
联立①②,解得 , ,
(2)根据过 的圆的切线的斜率是否存在进行分类讨论,结合点到直线的距离公式求得切线方程.
(1)
由题意,设圆 的标准方程为: ,
圆 关于直线 对称,
圆 与 轴相切: …①
点 到 的距离为: ,
圆 被直线 截得的弦长为 , ,
结合①有: , ,
又 , , ,
圆 的标准方程为: .
(2)
当直线 的斜率不存在时, 满足题意
所以切线 的方程为 .
19.
(1)
(2) 或
【分析】
(1)将圆的一般方程化为标准方程,求出圆心,代入直线方程即可求解.
(2)设直线 的方程为: ,利用圆心到直线的距离即可求解.
(word完整版)高中数学必修二直线与方程及圆与方程测试题.docx
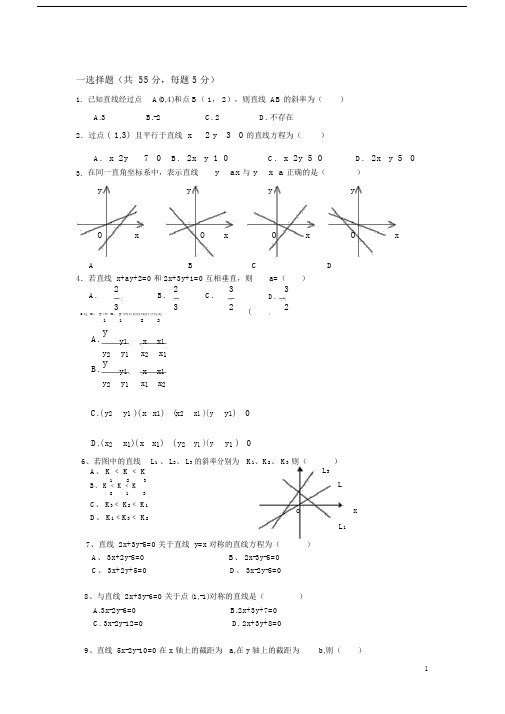
一选择题(共 55 分,每题 5 分)1. 已知直线经过点A(0,4)和点 B ( 1, 2),则直线 AB 的斜率为( )A.3B.-2C. 2D. 不存在2.过点 ( 1,3) 且平行于直线 x2 y3 0 的直线方程为()A . x 2y7 0 B . 2x y 1 0 C . x 2y 5 0 D . 2x y 5 0 3. 在同一直角坐标系中,表示直线y ax 与 yx a 正确的是()yyyyOxOxOxO xABCD4.若直线 x+ay+2=0 和 2x+3y+1=0 互相垂直,则a=()A .2B .2 C .33332D .(25.过 (x , y )和 (x , y )两点的直线的方程是)11 22A. yy 1 x x 1 y 2y 1 x 2 x 1 B.yy 1 x x 1 y 2 y 1x 1 x 2C.( y 2 y 1 )( x x 1) (x 2 x 1 )( y y 1) 0D.( x 2x 1)( x x 1) ( y 2 y 1 )( yy 1 ) 06、若图中的直线 L 1 、 L 2、 L 3 的斜率分别为 K 1、K 2、 K 3 则()A 、 K ﹤ K ﹤ KL 3123LB 、 K ﹤ K ﹤ K2 1 3C 、 K 3﹤ K 2﹤ K 1oxD 、 K 1﹤K 3﹤ K 2L 17、直线 2x+3y-5=0 关于直线 y=x 对称的直线方程为( )A 、 3x+2y-5=0B 、 2x-3y-5=0C 、 3x+2y+5=0D 、 3x-2y-5=08、与直线 2x+3y-6=0 关于点 (1,-1)对称的直线是()A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0A.a=2,b=5;B.a=2,b= 5 ;C.a= 2 ,b=5;D.a= 2 ,b= 5 .10、直线 2x-y=7 与直线 3x+2y-7=0 的交点是()A (3,-1)B (-1,3)C (-3,-1)D (3,1)11、过点 P(4,-1)且与直线 3x-4y+6=0垂直的直线方程是()A 4x+3y-13=0B 4x-3y-19=0C 3x-4y-16=0D 3x+4y-8=0二填空题(共20 分,每题 5 分)12.过点(1,2)且在两坐标轴上的截距相等的直线的方程_ __________;13 两直线 2x+3y- k=0 和 x- ky+12=0 的交点在y 轴上,则k 的值是14、两平行直线x 3y 4 0与 2x 6 y 9 0 的距离是。
高一数学必修二单元测验直线和圆

1、已知三点A (-2,-1)、B (x ,2)、C (1,0)共线,则x 为: ( )A 、7B 、-5C 、3D 、-12.直线)(0)11()3()12(R k k y k x k ∈==--+--,所经过的定点是( )A .(5,2)B .(2,3)C .(-21,3) D .(5,9) 3、若直线12++=k kx y 与直线221+-=x y 的交点位于第一象限,则实数k 的取值范围是( )A 、26-- kB 、061 k -C 、061 k -D 、21 k 4、过直线x+y-2=0和直线x-2y+1=0的交点且垂直于第二直线的直线方程为( )A 、+2y-3=0B 、2x+y-3=0C 、x+y-2=0D 、2x+y+2=05、以点A (-5,4)为圆心,且与x 轴相切的圆的方程是( )A 、25)4()5(22=-++y xB 、16)4()5(22=++-y xC 、16)4()5(22=-++y xD 、25)4()5(22=++-y x6、圆心在直线x=y 上且与x 轴相切于点(1,0)的圆的方程为: ( )A 、(x-1)2+y 2=1B 、(x-1)2+(y-1)2=1C 、(x+1)2+(y-1)2=1D 、(x+1)2+(y+1)2=17.过010531=--y x l :和012=++y x l :的交点,且平行于0523=-+y x l :的直线方程为_________.8.已知圆心在x 轴上,半径是5且以A (5,4)为中点的弦长是52,则这个圆的方程是_________.9、光线沿直线2x-y-3=0经两坐标轴反射后所在的直线是 .10、求过点(-1,2)且在两轴上截距相等的直线方程。
11、求过原点且与直线x=1及圆(x-1)2+(y-2)2=1相切的圆的方程。
12.已知圆C和y轴相切,圆心在直线0x上,且被直线x-y3=y=截得的弦长2,求圆C的方程.为7。
《直线和圆》单元测试题

《直线和圆》单元测试题一、选择题(每题2分,共40分)1.下面哪个选项是直线的性质? A. 无限延伸 B. 有一个起点和一个终点 C.由无数个点组成 D. 由两个点确定2.下面哪个选项是圆的性质? A. 无限延伸 B. 有一个起点和一个终点 C. 由无数个点组成 D. 由两个点确定3.下列直线中,哪一条与直线A平行? A. 直线B B. 直线C C. 直线D D.直线E4.下列直线中,哪一条与直线A垂直? A. 直线B B. 直线C C. 直线D D.直线E5.下列直线中,哪一条与直线A既不平行也不垂直? A. 直线B B. 直线C C.直线D D. 直线E6.在一个圆中,半径是r,直径是d,下列哪个等式成立? A. d = 2r B. r =d/2 C. d = r/2 D. r = d7.在一个圆中,半径是5cm,直径是10cm,周长是多少? A. 5cm B. 10cm C.15cm D. 20cm8.在一个圆中,半径是8cm,周长是多少? A. 4cm B. 8cm C. 16cm D. 32cm9.在一个圆中,半径是3cm,面积是多少? A. 3cm² B. 6cm² C. 9cm² D.12cm²10.在一个圆中,直径是6cm,面积是多少? A. 3cm² B. 6cm² C. 9cm² D.12cm²二、填空题(每题3分,共30分)11.直线的两个特点是________和________。
12.圆的两个特点是________和________。
13.直线A与直线B平行,则直线B与直线A________。
14.直线A与直线B垂直,则直线B与直线A________。
15.直径是半径的________。
16.圆心到圆上任一点的距离叫做________。
17.直线与圆的交点可能有________个。
18.圆的周长等于________。
高中数学第二章-直线与圆单元测试(提升卷)(原卷版)

第二章直线与圆单元过关检测能力提高B 版 学校:___________姓名:___________班级:___________考号:___________ 一、单选题 1.已知直线l 过点()1,2P -且与线段AB 的延长线有公共点,若()2,3A --,()3,0B ,则直线l 的斜率的取值范围是( )A .1,52⎡⎤-⎢⎥⎣⎦B .13,25⎛⎤- ⎥⎝⎦C .13,25⎛⎫- ⎪⎝⎭D .[)1,5,2⎛⎤-∞-+∞ ⎥⎝⎦2.已知,a b 满足21a b +=,则直线30ax y b ++=必过定点( )A .1,23⎛⎫- ⎪⎝⎭ B .11,26⎛⎫ ⎪⎝⎭ C .11,26⎛⎫- ⎪⎝⎭ D .12,3⎛⎫- ⎪⎝⎭3.若动点()()1122,,,A x y B x y 分别在直线1:70l x y +-=和2:50l x y +-=上移动,则AB 中点M 到原点距离的最小值为( )A .32B .23C .33D .424.圆22:4440C x y x y ++-+=关于直线20x y -+=对称的圆的方程是( )A .224x y +=B .22(2)(2)4-++=x yC .22(2)4x y -+=D .22(2)4x y ++=5.若对圆22(1)(1)1x y -+-=上任意一点(,)P x y ,34349x y a x y -++--的取值与x ,y 无关,则实数a 的取值范围是( )A .4a ≤B .46a -≤≤C .4a ≤或6a ≥D .6a ≥6.我们把顶角为36︒的等腰三角形称为黄金三角形......其作法如下:①作一个正方形ABCD ;②以AD 的中点E 为圆心,以EC 长为半径作圆,交AD 延长线于F ;③以D 为圆心,以DF 长为半径作⊙D ;④以A 为圆心,以AD 长为半径作⊙A 交⊙D 于G ,则ADG ∆为黄金三角形.根据上述作法,可以求出cos36︒=ABCD7.阿波罗尼斯是古希腊著名数学家,与欧几里得、阿基米德并称为亚历山大时期数学三巨匠,他对圆锥曲线有深刻而系统的研究,主要研究成果集中在他的代表作《圆锥曲线》一书,阿波罗尼斯圆是他的研究成果之一,指的是:已知动点M 与两定点Q 、P 的距离之比||||MQ MP λ=(0,1)λλ>≠,那么点M 的轨迹就是阿波罗尼斯圆.已知动点M 的轨迹是阿波罗尼斯圆,其方程为221x y +=,定点Q 为x 轴上一点,1,02P ⎛⎫- ⎪⎝⎭且2λ=,若点(1,1)B ,则2||||MP MB +的最小值为( ) ABCD8.数学家欧拉于1765年在他的著作《三角形的几何学》中首次提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半,这条直线被后人称之为三角形的欧拉线.已知ABC ∆的顶点为A (0,0),B (4,0),(C ,则该三角形的欧拉线方程为( )A0y --=B.0x -= C20y --=D.20x --=二、多选题9.下列说法错误的是( )A .“1a =-”是“直线210a x y -+=与直线20x ay --=互相垂直”的充要条件B .直线sin 20x y α++=的倾斜角θ的取值范围是30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭ C .过()11,x y ,()22,x y 两点的所有直线的方程为112121y y x x y y x x --=-- D .经过点(1,1)且在x 轴和y 轴上截距都相等的直线方程为20x y +-=10.已知圆22111:0M x y D x E y F ++++=与圆22222:0N x y D x E y F ++++=的圆心不重合,直线()()121212:0l D D x E E y F F -+-+-=.下列说法正确的是( )A .若两圆相交,则l 是两圆的公共弦所在直线B .直线l 过线段MN 的中点C .过直线l 上一点P (在两圆外)作两圆的切线,切点分别为A ,B ,则PA PB =D .直线l 与直线MN 相互垂直 11.以下四个命题表述正确的是( )A .直线()()34330m x y m m R ++-+=∈恒过定点()3,3--B .圆224x y +=上有且仅有3个点到直线:20l x y -+=的距离都等于1C .曲线22120C :x y x ++=与曲线222480C :x y x y m +--+=恰有三条公切线,则4m =D .已知圆22:4C x y +=,点P 为直线142x y +=上一动点,过点P 向圆C 引两条切线PA 、PB ,A 、B 为切点,则直线AB 经过定点(1,2) 12.已知圆22:5,,O x y A B +=为圆O 上的两个动点,且2,AB M =为弦AB 的中点()22,C a ,()22,2D a +.当,A B 在圆O 上运动时,始终有CMD ∠为锐角,则实数a 的可能取值为( ) A .-3B .-2C .0D .1三、填空题13.已知直线l :y x b =+被圆C :22(3)(2)6x y -+-=截得的弦长等于该圆的半径,则b =______.14.在平面直角坐标系中,若直线l 与圆221:1C x y +=和圆()()222:525249C x y -+-=都相切,且两个圆的圆心均在直线l 的下方,则直线l 的斜率为__________.15.如图,O 是坐标原点,圆O 的半径为1,点A (-1,0),B (1,0),点P ,Q 分别从点A ,B 同时出发,圆O 上按逆时针方向运动.若点P 的速度大小是点Q 的两倍,则在点P 运动一周的过程中,AP AQ ⋅的最大值是_______.16.以三角形边BC ,CA ,AB 为边向形外作正三角形BCA ',CAB ',ABC ',则AA ',BB ',CC '三线共点,该点称为ABC 的正等角中心.当ABC 的每个内角都小于120º时,正等角中心点P 满足以下性质:(1)120APB APC BPC ;(2)正等角中心是到该三角形三个顶点距离之和最小的点(也即费马点).由以上性质得222222(1)(1)(2)x y x y x y +-++++-+的最小值为_________四、解答题 17.已知P 是直线3480x y ++=上的动点,PA 、PB 是圆22:2210C x y x y +--+=的两条切线,A 、B 是切点.(1)求四边形PACB 面积的最小值;(2)直线上是否存在点P ,使60BPA ︒∠=?若存在,求出P 点的坐标;若不存在,说明理由.18.已知直线20x y -+=和圆22:8120C x y x +-+=,过直线上的一点()00,P x y 作两条直线PA ,PB与圆C 相切于A ,B 两点.(1)当P 点坐标为()2,4时,求以PC 为直径的圆的方程,并求直线AB 的方程;(2)设切线PA 与PB 的斜率分别为1k ,2k ,且127k k ⋅=-时,求点P 的坐标.19.已知()0,3A ,,B C 为222(0)x y r r +=>上三点.(1)求r 的值;(2)若直线BC 过点(0,2),求ABC 面积的最大值;(3)若D 为曲线22(1)4(3)x y y ++=≠-上的动点,且AD AB AC =+,试问直线AB 和直线AC 的斜率之积是否为定值?若是,求出该定值;若不是,说明理由.20.已知两个定点(0,4)A ,(0,1)B , 动点P 满足||2||PA PB =,设动点P 的轨迹为曲线E ,直线l :4y kx =-.(1)求曲线E 的轨迹方程;(2)若l 与曲线E 交于不同的C 、D 两点,且120COD ∠=︒ (O 为坐标原点),求直线l 的斜率; (3)若1k =,Q 是直线l 上的动点,过Q 作曲线E 的两条切线QM 、QN ,切点为M 、N ,探究:直线MN 是否过定点,若存在定点请写出坐标,若不存在则说明理由.21.如图,已知圆22:1O x y +=,点(),4P t 为直线4y =上一点,过点P 作圆O 的切线,切点分别为,M N .(Ⅰ)已知1t =,求切线的方程;(Ⅱ)直线MN 是否过定点?若是,求出定点坐标,若不是,请说明理由;(Ⅲ)若1t >,两条切线分别交y 轴于点,A B ,记四边形PMON 面积为1S ,三角形PAB 面积为2S ,求12S S ⋅的最小值.22.已知圆22:1O x y +=和点()1,4M --.(1)过点M 向圆O 引切线,求切线的方程;(2)求以点M 为圆心,且被直线212y x =-截得的弦长为8的圆M 的方程;(3)设P 为(2)中圆M 上任意一点,过点P 向圆O 引切线,切点为Q ,试探究:平面内是否存在一定点R ,使得PQ PR为定值?若存在,请求出定点R 的坐标,并指出相应的定值;若不存在,请说明理由.高考数学:试卷答题攻略一、“六先六后”,因人因卷制宜。
人教A版高中必修二试题直线与圆 单元测试.doc

直线与圆 单元测试一.选择题: 1.命题P :“m =-1” 命题Q :“直线mx +(2m -1)y +1=0和直线3x +my +3=0垂直”则 ( )A .P ⇒QB .Q P ⇒C .P ⇔QD .以上均不对 2.已知直线32:1+=x y l ,直线2l 与1l 关于直线x y -=对称,则直线2l 的斜率为( ) A .12 B .-12 C .2 D .-2 3.圆014222=+-++y x y x 关于直线),(022R b a by ax ∈=+-对称,则ab 的取值范围是( )A .]41,(-∞ B .]41,0( C .)0,41(-D .)41,(-∞4.在平面直角坐标系中,点A(1,2)、点B(5,0)到直线l 的距离分别为1和2,则符合条件的直线条数为A .4B .3C .2D .1 5.若函数1()axf x e b=-的图象在x =0处的切线l 与圆C:221x y +=相离,则P(a ,b)与圆C 的位置关系是 ( )A .在圆内B .在圆外C .在圆上D .不能确定 6.当x 、y 满足条件1<+y x 时,变量3-=y xu 的取值范围是( ) A .)31 31(,- B .)3 3(,- C .]31 31[,- D .)31 0(0) 31(,,Y - 7.方程04)(22=-++y x y x 表示的曲线是 ( )A.两条射线和一个圆B.一条直线和一个圆C.一条射线和一个半圆D.两条射线和一个半圆 8.如图,已知(4,0)A 、(0,4)B ,从点(2,0)P 射出的光线经直线AB 反向后再射到直线OB 上,最后经直线OB 反射后又回到P 点,则光线所经过的路程是( ) A . 210 B .6C .33D .259.定义{}⎩⎨⎧<≥=ba b ba ab a ,,,max ,设实数y x ,满足约束条件{},3,2max ,22y x y x z y x +-=⎩⎨⎧≤≤则z 的取值范围是( ) . A.[-5,8] B. [-5,6] C.[-3,6] D.[-8,8] 10.如图,阴影是集合22{(,)|(cos )(sin )4,0}P x y x y θθθπ=-+-=≤≤在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )A .π+B .116πC . 73π-D .2π+二.填空题:11.已知圆50)3()6(10)1()2(222221=+++=-+-y x C y x C :与圆:交于A 、B 两点,则AB 所在的直线方程是__________________12.已知点P(2,1)在圆C :2220x y ax y b ++-+=上,点P 关于直线10x y +-=的对称点也在圆C 上,则圆C 的圆心坐标为 、半径为 .13.如图,目标函数u=ax -y 的可行域为四边形OACB(含边界). 若点24(,)35C 是该目标函数的最优解,则a 的取值范围是14.已知定点)0,2(A ,P 点在圆122=+y x 上运动,AOP ∠的平分线交PA 于Q 点,其中O 为坐标原点,则Q 点的轨迹方程为 .15.已知AC BD 、为圆O :224x y +=的两条相互垂直的弦,两弦交点为(M ,则四边形ABCD 的面积的最大值为 .直线与圆 单元测试答题纸班级 姓名二、填空题(本大题共5小题,每小题4分,满分20分)11. 12. 13. 14. 15.三、解答题(本大题共4小题,满分40分.解答应写出文字说明.证明过程或演算步骤).16.已知过点A (0,1),且方向向量为22(1,):(2)(3)1a k l C x y =-+-=r e 的直线与,相交于M 、N 两点.(1)求实数k 的取值范围; (2)若O 为坐标原点,且12,OM ON k ⋅=u u u u r u u u r求的值.17.已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴;围成一个四边形,求使得这个四边形面积最小的k 值18.已知,a b 都是正数,△ABC 在平面直角坐标系x O y 内, 以两点A (a ,0 )和B (0,b )为顶点的正三角形,且它的第三个顶点C 在第一象限内.(1)若△ABC 能含于正方形D = { ( x , y ) | 0 x 1, 0 y 1}内, 试求变量 ,a b 的约束条件,并在直角坐标系a Ob 内画出这个约束条件表示的平面区域; (2)当(,)a b 在(1)所得的约束条件内移动时,求△ABC 面积S 的最大值,并求此时(,)a b 的值.19.如图,P 为圆O 外一点,PA 、PB 为圆的两条切线,A 、B 为切点,过P 的圆的割线交圆于点C 、D ,交AB 于Q 点,请建立适当的直角坐标系,利用解析几何法(坐标法)证明:PDPC PQ 112+= 直线与圆单元测试答案一、选择题(本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的). 题号 1 2 3 4 5 6 7 8 9 10 答案AAAAAAAAAB二、填空题(本大题共5小题,每小题4分,满分20分)11.2x+y=0 12.(0,1)r =2 13.]103,512[-- 14.943222=+⎪⎭⎫ ⎝⎛-y x 15.5三、解答题(本大题共4小题,满分40分.解答应写出文字说明.证明过程或演算步骤).16.解:(1)(1,),l a k =rQ 直线过点(0,1)且方向向量1l y kx ∴=+直线的方程为由22311,1k k -+<+得474733k -+<<1122(3)(,),(,)M x y N x y 设1y kx x =+22将代入方程(-2)+(y-3)=1得k x k x 22(1+)-4(1+)+7=0212227,11k x x x x k k ∴=++124(1+)+=2121212122(1)()18121k k OM ON x x y y k x x k x x k ∴⋅=+=++++=+=+u u u u r u u u r 4(1+)24,11k k k k∴==+4(1+)解得1,0,1k k =∆>∴=又当时……………………14分 17.1/818.(1)由题意知:顶点C 是分别以A 、B 为圆心,以|AB|为半径的两圆在第一象限的交点,由圆A: ( x –a )2 + y 2 = a 2 +b 2 , 圆B: x 2 + ( y – b )2 = a 2 + b 2 .解得 3a b x +=, 3a b y +=,∴C (23b a +,23b a + )△ABC 含于正方形D 内,即三顶点A ,B ,C 含于区域D 内时,∴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧≤+≤≤+≤≤≤≤≤.1230,1230,10,10b a b a b a 这就是 ( a , b )的约束条件. 其图形为右图的六边形, ∵a > 0 , b > 0 ,∴图中坐标轴上的点除外.(2)∵△ABC 是边长为22b a +的正三角形,∴ S = 43( a 2 + b 2)在(1)的条件下, 当S 取最大值等价于六边形图形中的点( a , b )到原点的距离最大,由六边形中P 、Q 、R 相应的OP 、OQ 、OR 的计算.OP 2 = OR 2 = 12+ ( 2 – 3)2 = 8 – 43,OQ 2 = 2(3 – 1)2 = 8 – 43. ∴ OP = OR =OQ ∴当 ( a , b ) = ( 1, 2 –3), 或(3– 1, 3– 1), 或( 2 –3, 1 )时, S max =23– 3.19.略。
高中数学-《直线与圆的位置关系》单元测试题

高中数学-《直线与圆的位置关系》单元测试题高中数学-《直线与圆的位置关系》单元测试题班级:__________姓名:__________成绩:__________ 一.选择题(每题5分,共12题,共60分)1.直线3x + 4y + 12 = 0 与圆(x + 1)^2 + (y + 1)^2 = 9的位置关系是A。
过圆心 B。
相切 C。
相离 D。
相交2.直线l将圆x^2 + y^2 - 2x - 4y = 0 平分,且与直线x + 2y = 0 垂直,则直线l的方程为A。
y = 2x B。
y = 2x - 2 C。
y = x + 1 D。
y = x - 13.若圆C半径为1,圆心在第一象限,且与直线4x - 3y = 0 和x轴都相切,则该圆的标准方程是A。
(x - 2)^2 + (y - 1)^2 = 1 B。
(x - 2)^2 + (y + 1)^2 = 1 C。
(x + 2)^2 + (y - 1)^2 = 1 D。
(x - 3)^2 + (y - 1)^2 = 14.若直线ax + by = 1与圆x^2 + y^2 = 1相交,则点P(a,b)的位置是A。
在圆上 B。
在圆外 C。
在圆内 D。
都有可能5.由直线y = x + 1上的一点向圆(x - 3)^2 + y^2 = 1引切线,则切线长的最小值为A。
1 B。
2 C。
3 D。
46.圆x^2 + y^2 + 2x + 4y - 3 = 0 上到直线l:x + y + 1 = 0的距离为2的点有A。
1个 B。
2个 C。
3个 D。
4个7.两圆x^2 + y^2 - 6x = 0 和x^2 + y^2 + 8y + 12 = 0 的位置关系是A。
相离 B。
外切 C。
相交 D。
内切8.两圆x + y = r,(x-3)+(y+1)=r外切,则正实数r的值是A。
10 B。
5 C。
2 D。
229.半径为6的圆与x轴相切,且与圆x+(y-3)^2=1内切,则此圆的方程是A。
高中数学第二章-直线与圆单元测试(基础卷)(解析版)

第二章直线与圆单元过关检测 基础A 卷解析版学校:___________姓名:___________班级:___________考号:___________一、单选题1.若圆22220x y x y m ++-+=m =( ) A .32-B .-1C .1D .32【答案】B 【分析】将圆的方程化为标准方程,即可求出半径的表达式,从而可求出m 的值. 【详解】由题意,圆的方程可化为()()22112x y m ++-=-,=1m =-. 故选:B. 【点睛】本题考查圆的方程,考查学生的计算求解能力,属于基础题. 2.若直线l 的倾斜角α满足203πα≤<,且2πα≠,则其斜率k 满足( ).A .0k <≤B .k >C .0k ≥,或k <D .0k ≥,或3k <-【答案】C 【分析】由直线的倾斜角的范围,得到斜率的范围,求解即可. 【详解】由02πα≤<,得tan 0α≥,由223ππα<<,tan α<,故0k ≥,或k <所以本题答案为C.【点睛】本题考查直线的倾斜角和斜率的关系,注意倾斜角的范围,正切函数在0,2π⎡⎫⎪⎢⎣⎭和,2ππ⎛⎫⎪⎝⎭上都是单调增函数.3.点(4,2)P -与圆224x y +=上任一点连线的中点的轨迹方程是( ) A .22(2)(1)1x y -++= B .22(2)(1)4x y -++= C .22(4)(2)4x y ++-= D .22(2)(1)1x y ++-= 【答案】A 【解析】试题分析:设圆上任一点为()00,Q x y ,PQ 中点为(),M x y ,根据中点坐标公式得,0024{22x x y y =-=+,因为()00,Q x y 在圆224x y +=上,所以22004x y +=,即()()2224224x y -++=,化为22(2)(1)1x y -++=,故选A.考点:1、圆的标准方程;2、“逆代法”求轨迹方程.【方法点晴】本题主要考查圆的标准方程、“逆代法”求轨迹方程,属于难题.求轨迹方程的常见方法有:①直接法,设出动点的坐标(),x y ,根据题意列出关于,x y 的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把,x y 分别用第三个变量表示,消去参数即可;④逆代法,将()()00{x g x y h x ==代入()00,0=f x y .本题就是利用方法④求M 的轨迹方程的.4.下列直线中,斜率为43-,且经过第一象限的是( ) A .3470x y ++= B .4370x y ++= C .43420x y +-= D .44420x y +-=【答案】C 【分析】 根据条件斜率为43-,且经过第一象限,依次讨论选项,即得解. 【详解】由直线的斜率为43-,故可排除A ,D 又B 中直线4370x y ++=在x,y 轴的截距分别为77,43--,故不经过第一象限,排除B 故选:C 【点睛】本题考查了直线的方程与图像,考查了学生概念理解,综合分析,数学运算的能力,属于基础题. 5.顺次连接点()4,3A -,()2,5B ,()3,2C ,()3,0D -所构成的图形是( ) A .平行四边形 B .直角梯形C .等腰梯形D .以上都不对【答案】A 【分析】由四个点的坐标可求出AB k ,BC k ,CD k ,AD k 根据斜率关系以及线段的长度,即可得结果. 【详解】因为()4,3A -,()2,5B ,()3,2C ,()3,0D -, 所以()531243AB k -==--,52323BC k -==--,()201333CD k -==--,()30343AD k -==----所以AB CD k k =,BC AD k k =, 所以四边形ABCD 是平行四边形. 故选:A 【点睛】本题主要考查了两直线平行的条件,考查了直线的斜率公式,属于基础题.6.经过点(0,1)P -作直线l ,若直线l 与连接(1,2),(2,1)A B -的线段总有公共点,则l 的倾斜角的取值范围是( ) A .0,4⎡⎤⎢⎥⎣⎦π B .3,44ππ⎡⎤⎢⎥⎣⎦ C .3,4ππ⎡⎫⎪⎢⎣⎭D .30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭【答案】D 【分析】结合图形利用,PA PB 的斜率得到直线l 的斜率的取值范围,从而可得直线l 的倾斜角的取值范围. 【详解】设直线l 的斜率为k ,倾斜角为α,1(2)101PA k ---==--,11102PB k --==-,由图可知,11k -≤≤,所以04πα≤≤或34παπ≤<. 故选:D 【点睛】关键点点睛:求直线倾斜角的取值范围的关键是求出直线的斜率的取值范围,结合图象,利用,PA PB 的斜率可得所要求的斜率的取值范围. 7.集合(){}22,4M x y x y =+≤,()()(){}222,11,0N x y x y r r =-+-≤>,且MN N =,则r 的取值范围是() A .()21 B .(]0,1C .(0,22-D .(]0,2 【答案】C 【分析】由题意知集合M 与N 中的两个圆内含或内切,由圆心距与半径差的关系可得结果. 【详解】由M N N ⋂=得N M ⊆,∴圆224x y +=与圆()()22211x y r -+-=内切或内含,∴22r -≥022r <≤故选C.【点睛】本题考查了圆与圆的位置关系,考查了集合间关系的转化,属于基础题.8.已知圆221:(2)(3)1C x y -+-=,圆222:(3)(4)9C x y -+-=,,M N 分别为圆12,C C 上的点,P 为x 轴上的动点,则||||PM PN +的最小值为( )A 17B 171C .622-D .524【答案】D 【分析】求出圆1C 关于x 轴的对称圆的圆心坐标A ,以及半径,然后求解圆A 与圆2C 的圆心距减去两个圆的半径和,即可求得||||PM PN +的最小值,得到答案. 【详解】如图所示,圆1C 关于x 轴的对称圆的圆心坐标3(2,)A -,半径为1, 圆2C 的圆心坐标为(3,4),,半径为3,由图象可知,当,,P M N 三点共线时,||||PM PN +取得最小值, 且||||PM PN +的最小值为圆3C 与圆2C 的圆心距减去两个圆的半径之和, 即22231(32)(34)4524AC --=-+---=-, 故选D .【点睛】本题主要考查了圆的对称圆的方程的求解,以及两个圆的位置关系的应用,其中解答中合理利用两个圆的位置关系是解答本题的关键,着重考查了数形结合法,以及推理与运算能力,属于基础题.评卷人 得分二、多选题9.过点(4,1)A 且在两坐标轴上截距相等的直线方程是( ) A .5x y += B .5x y -=C .40x y -=D .04=+y x【答案】AC 【分析】分两种情况求解,过原点时和不过原点时,结合所过点的坐标可求. 【详解】当直线过坐标原点时,直线方程为40x y -=;当直线不过坐标原点时,设直线方程为x y a +=,代入点(4,1)A 可得5a =, 即5x y +=.故选:AC. 【点睛】直线在两坐标轴上截距相等时,有两种情况:一是直线经过坐标原点;二是直线斜率为1-.10.(多选)已知直线l 经过点(3,4),且点(2,2),(4,2)A B --到直线l 的距离相等,则直线l 的方程可能为( )A .23180x y +-=B .220x y --=C .220x y ++=D .2360x y -+=【答案】AB 【分析】由题可知直线l 的斜率存在,所以设直线l 的方程为4(3)y k x -=-,然后利用点到直线的距离公式列方程,可求出直线的斜率,从而可得直线方程 【详解】当直线l 的斜率不存在时,显然不满足题意.当直线l 的斜率存在时,设直线l 的方程为4(3)y k x -=-,即430kx y k -+-=.=,所以2k =或23k =-, 所以直线l 的方程为220x y --=或23180x y +-=. 故选:AB 【点睛】此题考查直线方程的求法,考查点到直线的距离公式的应用,属于基础题11.已知圆22:4O x y +=和圆22:4240M x y x y +-+=+相交于A 、B 两点,下列说法正确的为( ) A .两圆有两条公切线 B .直线AB 的方程为22y x =+C .线段AB 的长为65D .圆O 上点E ,圆M 上点F ,EF 3【答案】AD 【分析】由圆与圆相交可判断A ;两圆方程作差可判断B ;利用垂径定理可判断C ;转化为圆心间的距离可判断D. 【详解】对于A ,因为两圆相交,所以两圆有两条公切线,故A 正确;对于B ,因为圆22:4O x y +=,圆22:4240M x y x y +-+=+, 两圆作差得4244x y -+=-即24y x =+, 所以直线AB 的方程为24y x =+,故B 错误; 对于C ,圆22:4O x y +=的圆心为()0,0,半径为2,则圆心到直线AB 的距离d ==, 所以2245452255AB,故C 错误; 对于D ,圆22:4240M x y x y +-+=+的圆心()2,1M -,半径为1,所以max 213EF OM =++=,故D 正确. 故选:AD.12.古希腊著名数学家阿波罗尼斯发现:平面内到两个定点A ,B 的距离之比为定值λ(1λ≠)的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系xOy 中,已知()4,2A -,()2,2B ,点P 满足2PA PB=,设点P 的轨迹为圆C ,下列结论正确的是( )A .圆C 的方程是()()224216x y -+-= B .过点A 向圆C 引切线,两条切线的夹角为3πC .过点A 作直线l ,若圆C 上恰有三个点到直线l 距离为2,该直线斜率为5±D .在直线2y =上存在异于A ,B 的两点D ,E ,使得2PDPE= 【答案】ABD 【分析】根据()4,2A -,()2,2B ,点P 满足2PA PB=,设点(),P x y ,求出其轨迹方程,然后再逐项运算验证.【详解】因为()4,2A -,()2,2B ,点P 满足2PA PB=,设点(),P x y ,则2=,化简得:228440x y x y +--+=,即 ()()224216x y -+-=,故A 正确;因为8,4AC R ==,所以1sin22R AC α==,则 26απ=,解得 3πα=,故B 正确;易知直线的斜率存在,设直线:420l kx y k -++=,因为圆C 上恰有三个点到直线l 距离为2,则圆心到直线的距离为:2d ==,解得15k =±,故C 错误; 假设存在异于A ,B 的两点(),2D m ,(),2E n2=,化简得:2222284124033m n n m x y x y --+++-+=,因为点P 的轨迹方程为:228440x y x y +--+=,所以22288341243m nn m -⎧=-⎪⎪⎨-+⎪=⎪⎩解得126m n =⎧⎨=⎩或 42m n =-⎧⎨=⎩(舍去),故存在 ()()12,2,6,2D E ,故D 正确;故选:ABD 【点睛】关键点点睛:本题关键是根据2PA PB=求出点P 的轨迹方程,进而再根据直线与圆的位置关系求解.三、填空题13.已知圆221:1C x y +=,圆222:(4)25C x y -+=,则两圆公切线的方程为________. 【答案】10x += 【分析】首先判断两圆的位置关系,根据位置关系再求两圆公切线方程. 【详解】解析圆221:1C x y +=,圆心为(0,0),半径为1;圆222:(4)25C x y -+=,圆心为(4,0),半径为5. 易知两圆内切,切点为(1,0)-,又两圆圆心都在x 轴上, 所以两圆公切线的方程为1x =-,即10x +=. 故答案为:10x += 【点睛】本题考查两圆的位置关系,公切线方程,属于基础题型.14.已知直线(34)30mx m y +-+=与直线230x my ++=互相垂直,则实数m 的值是______. 【答案】0或23【分析】利用直线垂直的性质得到2(34)0m m m +-=,解方程即得解. 【详解】∵直线(34)30mx m y +-+=和直线230x my ++=垂直,2(34)0m m m ∴+-=解得0m =或23. 故答案为:0或23.15.光线从点(1,4)射向y 轴,经过y 轴反射后过点(3,0),则反射光线所在的直线方程是________. 【答案】30x y +-=(或写成3y x =-+) 【解析】 【分析】光线从点(1,4)射向y 轴,即反射光线反向延长线经过(1,4)关于y 轴的对称点(1,4)-,则反射光线通过(1,4)-和(3,0)两个点,设直线方程求解即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学必修二直线和圆单元测试一、填空题130y +-=的倾斜角是 .2.直线l 经过A (2,1)、B (1,m 2)(m ∈R)两点,那么直线l 的倾斜角的取值围是 .3. 若圆2244100x y x y +---=上至少有三个不同点到直线l :0ax by +=的距离为则直线l 的倾斜角的取值围是 .4. 直线()00≠=++ab c by ax 截圆522=+y x 所得弦长等于4,则以|a |、|b |、|c |为边长的确定三角形一定是 .5. 已知直线1l 的方程为y x =,直线2l 的方程为0ax y -=(a 为实数).当直线1l 与直线2l 的夹角在(0,12π)之间变动时,a 的取值围是 . 6若直线1+=kx y 与圆122=+y x 相交于P 、Q 两点,且∠POQ =120°(其中O 为原点),则k 的值为 .7.如果点P 在平面区域22020210x y x y y -+⎧⎪+-⎨⎪-⎩≥≤≥上,点Q 在曲线22(2)1x y ++=上,那么PQ 的最小值为 .8.若曲线x 2+y 2+a 2x +(1–a 2)y –4=0关于直线y –x =0的对称曲线仍是其本身,则实数a = .9.已知圆22:1C x y +=,点A (-2,0)及点B (2,a ),从A 点观察B 点,要使视线不被圆C 挡住,则a 的取值围是 .10.在圆x 2+y 2=5x ,过点)23,25(有n 条弦的长度成等差数列,最小弦长为数列的首项a 1,最大弦长为a n ,若公差]31,61[∈d ,那么n 的取值集合为 .11.点P (a ,3)到直线0134=+-y x 的距离等于4,且在不等式032<-+y x 表示的平面区域,则点P 的坐标是 .12.将一画有直角坐标系的图纸折叠一次,使得点A (0,2)与点B (4,0)重合.若此时点C (7,3)与点D (m ,n )重合,则m +n 的值是 .13.已知圆22((2)16x y -+-=与y 轴交于A B ,两点,与x 轴的另一个交点为P ,则APB ∠= .14.设有一组圆224*:(1)(3)2()k C x k y k k k -++-=∈N .下列四个命题:A.存在一条定直线与所有的圆均相切 B.存在一条定直线与所有的圆均相交 C.存在一条定直线与所有的圆均不.相交 D.所有的圆均不.经过原点 其中真命题的代号是.(写出所有真命题的代号)二、解答题15.已知点A(2, 0), B(0, 6),坐标原点O 关于直线AB 的对称点为D, 延长BD 到P , 且|PD|=2|BD|.已知直线l :ax+10y+84-1083=0经过P , 求直线l 的倾斜角。
16.已知平面区域0240x y x y ≥⎧⎪≥⎨⎪+-≤⎩恰好被面积最小的圆222:()()C x a y b r -+-=及其部所覆盖.(1)试求圆C 的方程.(2)若斜率为1的直线l 与圆C 交于不同两点,.A B 满足CA CB ⊥,求直线l 的方程.17.如图所示,已知P (4,0)是圆x 2+y 2=36的一点,A 、B 是圆上两动点,且满足AP BP ⊥u u u r u u u r ,PQ PA PB =+u u u r u u u r u u u r,求点Q 的轨迹方程18.已知圆C :224x y +=.(1)直线l 过点()1,2P ,且与圆C 交于A 、B两点,若||AB =,求直线l 的方程; (2)过圆C 上一动点M 作平行于x 轴的直线m ,设m 与y 轴的交点为N ,若向量OQ OM ON =+u u u r u u u u r u u u r,求动点Q 的轨迹方程,并说明此轨迹是什么曲线.19.已知圆M :22(2)1x y +-=,设点,B C 是直线l :20x y -=上的两点,它们的横坐标分别是,4()t t t R +∈,点P 在线段BC 上,过P 点作圆M 的切线PA ,切点为A .(1)若0t =,MP =PA 的方程;(2)经过,,A P M 三点的圆的圆心是D ,求线段DO 长的最小值()L t .20.如图,已知:射线OA 为(0,0)y kx k x =>>,射线OB 为(0)y kx x =->,动点(,)P x y 在AOX ∠的部,PM OA ⊥于M ,PN OB ⊥于N ,四边形ONPM 的面积恰为k . (1)当k 为定值时,动点P 的纵坐标y 是横坐标x 的函数,求这个函数()y f x =的解析式;(2)根据k 的取值围,确定()y f x =的定义域.直线和圆单元测试1.32π 2.),2(]4,0[πππ⋃ 3.[5,1212ππ] 4.直角三角形 5.,1)∪(1)6.3± 7.328.22± 9.(-∞,,+∞) 10.{4,5,6,7} 11.)3,3(- 12.345 13.030 14.B D ,15.解:设D 点的坐标为(x 0, y 0),∵直线AB:1,26x y+=即3x+y —6=0, ∴000000113,3120360OD AB y k k x x y x y ⎧⎧=-=⎪⎪⎨⎨⎪⎪+-=+-=⎩⎩即. 解得x 0=,518 y 0=)56,518(56D 即,.由|PD|=2|BD|, 得λ=23-=PD BP . ∴由定比分点公式得x p =542554-=p y ,. 将P(542,554-)代入l 的方程, 得a=103. ∴k 1= -3. 故得直线l 的倾斜角为120° 16. 解:(1)由题意知此平面区域表示的是以(0,0),(4,0),(0,2)O P Q 构成的三角形及其部,且△OPQ 是直角三角形,所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),所以圆C 的方程是22(2)(1)5x y -+-=.(2)设直线l 的方程是:y x b =+.因为CA CB ⊥u u u r u u u r ,所以圆心C 到直线l,=解得:1b =-± 所以直线l 的方程是:1y x =-.17.解: 依题意知四边形PAQB 为矩形。
设AB 的中点为R ,坐标为(x ,y ),则在Rt △ABP中,|AR |=|PR |又因为R 是弦AB 的中点,依垂径定理 在Rt △OAR 中,|AR |2=|AO |2-|OR |2=36-(x 2+y 2)又|AR |=|PR |=22)4(y x +-所以有(x -4)2+y 2=36-(x 2+y 2),即x 2+y 2-4x -10=0因此点R 在一个圆上,而当R 在此圆上运动时,Q 点即在所求的轨迹上运动设Q (x ,y ),R (x 1,y 1),因为R 是PQ 的中点,所以x 1=2,241+=+y y x , 代入方程x 2+y 2-4x -10=0,得244)2()24(22+⋅-++x y x -10=0 整理得 x 2+y 2=56,这就是所求的轨迹方程18. 解(1)①当直线l 垂直于x 轴时,则此时直线方程为1=x ,l 与圆的两个交点坐标为()3,1和()3,1-,其距离为32,满足题意②若直线l 不垂直于x 轴,设其方程为()12-=-x k y ,即02=+--k y kx设圆心到此直线的距离为d ,则24232d -=,得1=d∴1|2|12++-=k k ,34k =, 故所求直线方程为3450x y -+=综上所述,所求直线为3450x y -+=或1=x (2)设点M 的坐标为()00,y x ,Q 点坐标为()y x ,则N 点坐标是()0,0y∵OQ OM ON =+u u u r u u u u r u u u r ,∴()()00,,2x y x y = 即x x =0,20y y =又∵42020=+y x ,∴4422=+y x 由已知,直线m //ox 轴,所以,0y ≠,∴Q 点的轨迹方程是221(0)164y x y +=≠ 19.解:(1)设(2,)(02).P a a a ≤≤(0,2),M MP Q解得1a =或15a =-(舍去).(2,1).P ∴ 由题意知切线PA 的斜率存在,设斜率为k .所以直线PA 的方程为1(2)y k x -=-,即210.kx y k --+=Q 直线PA 与圆M相切,1=,解得0k =或4.3k =-∴直线PA 的方程是1y =或43110.x y +-=(2)设(2,)(24).P a a t a t ≤≤+PA Q 与圆M 相切于点A ,.PA MA ∴⊥∴经过,,A P M 三点的圆的圆心D 是线段MP 的中点.(0,2),M D ∴Q 的坐标是(,1).2aa +设222225524().()(1)1().24455a DO f a f a a a a a =∴=++=++=++当225t >-,即45t >-时,2min 5()()1;2162t tf a f t ==++ 当22252t t ≤-≤+,即24455t -≤≤-时,min 24()();55f a f =-= 当2225t +<-,即245t <-时22min 515()(2)(2)(2)138242216t t t f a f t t =+=++++=++则45244()55245t L t t t >-=-≤≤-⎪<- 20.解:(1)设M(a ,ka ),N(b ,-kb ),(a>0,b>0)。
则|OM|=|ON|=。
由动点P 在∠AOx 的部,得0<y <kx . ∴,∴ONP OPN S S S ∆=+=四边形ONPM 12(|OM|·|PM|+|ON|·|PN|) =12[a (kx -y )+b (kx +y )]=12[k (a +b )x - (a -b )y ]=k ∴k (a +b )x -( a -b )y =2k ① 又由k PM = -1k =y ka x a --, k PN =1k =y kbx b+-, 分别解得21x ky a k +=+,21x kyb k-=+,代入①式消a 、b ,并化简得x 2-y 2=k 2+1。
∵y >0,∴y(2)由0<y <kx ,得 <k x⇔222222101x k x k k x⎧-->⎪⎨--<⎪⎩⇔222(1)1x k x k ⎧>⎪⎨-<+⎪⎩ ②(*) 当k=1时,不等式②为0<2恒成立,∴(*)⇔当0<k<1时,由不等式②得22211k x k +<-,x <,∴(*)⇔x <<当k>1时,由不等式②得22211k x k +>-,且22101k k+<-,∴(*)⇔x > 但垂足N 必须在射线OB 上,否则O 、N 、P 、M 四点不能组成四边形,所以还必须满足条件:1y x k <1x kx << (k>1).综上:当k=1时,定义域为{x|x>2};当0<k<1时,定义域为x <<};当k>1时,定义域为x <<。
