段广猛《面积问题之”水平宽铅锤高“模型的实战分析》

合集下载

详谈三角形面积问题之“宽高公式”

2018 年第 7—8 期（总第 187—188 期）
中国数学教育
ZHONGGUO SHUXUE JIAOYU
№7—8，2018 General，№187—188
详谈三角形面积问题之“宽高公式”
段广猛（江苏省高邮市赞化学校）
摘要：通过对三角形面积处理方法之一，即所谓“宽高公式”进行详细阐释，并展开实战分析，强化学生的割补意识，并分析割补策略，提升学生的解题技能，为课堂上的解题教学提供方向 .
· 92 ·
中国数学教育 2018 年第 7—8 期（总第 187—188 期）
角形的面积为S=源自1 2×水平宽
×
铅垂高，这个公
式不妨
称为“宽高公式”.
二、模型证明
如图8，过点 A 作 AG ⊥ Ox 于点 G ，交直线 BC 于
点
D
，则
S △ABC
=
1 2
OC·
AD
.
其中， OC 依然表示 B，C
B H
D
上的高线 AH ，则由 “ 底高公
OG
Cx
式”知
S △ABC
=
1 2
BC
·
AH
，要证
图6
S = △ABC
1 2
OC
·
AD，只要证
BC
·
AH
=
OC
·
AD
即可.
要证
乘积式成立，只要化成比例式，即
BC OC
=
AD AH
.
这个比
例式可以根据相似得到，即 △BCO ∽ △DAH. 而这两
y A
S △ABC
=
1 2
OC
·

铅锤高求三角形面积法

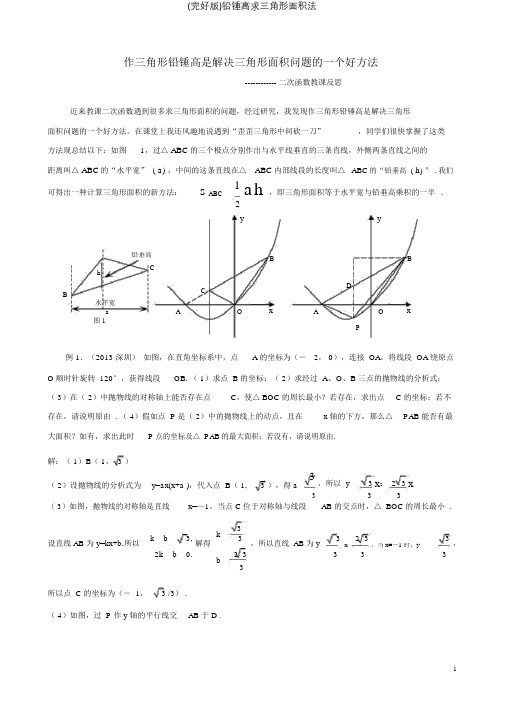
作三角形铅锤高是解决三角形面积问题的一个好方法------------ 二次函数教课反思近来教课二次函数遇到很多求三角形面积的问题，经过研究，我发现作三角形铅锤高是解决三角形面积问题的一个好方法。

在课堂上我还风趣地说遇到“歪歪三角形中间砍一刀” ，同学们很快掌握了这类方法现总结以下：如图1，过△ ABC 的三个极点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ ABC 的“水平宽” ( a ) ，中间的这条直线在△ ABC 内部线段的长度叫△ ABC 的“铅垂高 ( h ) ” . 我们可得出一种计算三角形面积的新方法：S ABC1ah ，即三角形面积等于水平宽与铅垂高乘积的一半.2yy铅垂高BBChCDB水平宽A O xA Oxa图 1P例 1．（2013 深圳）如图，在直角坐标系中，点A 的坐标为（－ 2， 0），连接 OA ，将线段 OA 绕原点O 顺时针旋转 120°，获得线段OB. （ 1）求点 B 的坐标；（ 2）求经过 A 、O 、B 三点的抛物线的分析式；（ 3）在（ 2）中抛物线的对称轴上能否存在点 C ，使△ BOC 的周长最小？若存在，求出点 C 的坐标；若不存在，请说明原由 . （ 4）假如点 P 是（ 2）中的抛物线上的动点，且在 x 轴的下方，那么△ PAB 能否有最大面积？如有，求出此时 P 点的坐标及△ PAB 的最大面积；若没有，请说明原由.解：（ 1）B （ 1， 3 ）（ 2）设抛物线的分析式为 y=ax(x+a )，代入点 B （ 1,3 ），得 a3，所以 y3 x 2 2 3 x33 3（ 3）如图，抛物线的对称轴是直线x=—1，当点 C 位于对称轴与线段AB 的交点时，△ BOC 的周长最小 .k 3k b3,33 2 3 3设直线 AB 为 y=kx+b.所以解得，所以直线 AB 为 y ，2k b 0.2 3 x，当 x=－1 时，yb3333所以点 C 的坐标为（－ 1， 3 /3） .（ 4）如图，过 P 作 y 轴的平行线交 AB 于 D .1 SPABSPADSPBD( y D y P )( x Bx A )21 3 x23 3 x 2 2 3 x 323 3 333 x 2 3 x 3 2 2 23 1392x82当 x=－ 1 时，△ PAB 的面积的最大值为9 3，此时 P 1 ,3 .28 24例 2．(2014 益阳 ) 如图 2，抛物线极点坐标为点 C( 1, 4), 交 x 轴于点 A( 3, 0) ，交 y 轴于点 B. (1)求抛物线和直线 AB 的分析式； (2)点 P 是抛物线 ( 在第一象限内 )上的一个动点，连接 PA ，PB ，当 P 点运动到极点C 时，求△ CAB 的铅垂高 CD 及 S CAB ；(3)能否存在一点 P ，使 S △ PAB =98若不存在，请说明原由 .S △ CAB ，若存在，求出 P 点的坐标；解： (1) 设抛物线的分析式为：y 1 a(x 1) 2 4 把 A （3,0）代入分析y 式求得 a1所以 y 1(x1) 2 4x 22x 3 设直线CAB 的解B析式为： y 2 kx b 由 y 1x 2 2x 3 求得 B 点的坐标为 (0,3) 把DA(3,0) ， B(0,3) 代入 y 2kx b 中1x解得：AO1k1, b3 所以 y 2x3图- 2(2) 因为 C 点坐标为 (１ ,4)所以当 x ＝１时， y 1＝ 4， y 2＝ 2 所以 CD ＝ 4- 2＝ 2S CAB13 2 3 (平方单位 ) 2(3) 假设存在吻合条件的点 P ，设 P 点的横坐标为 x ，△ PAB 的铅垂高为 h ，则h y 1y 2 ( x22x 3) ( x 3)x 291 3 ( x23x) 9 3化简3x 由 S = S得△ PAB8 △ CAB2 8得： 4x 212 x9 0解得， x3 将 x3代入 y 1 x 22x3 中，解得 P 点坐标为 ( 3 , 15 )2 22 4例 3．（ 2015 江津）如图，抛物线 yx 2 bxc 与 x 轴交于 A(1,0),B(- 3， 0) 两点，（ 1）求该抛物线的分析式；（ 2）设（ 1）中的抛物线交 y 轴于 C 点，在该抛物线的对称轴上能否存在点Q ，使得△ QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明原由 . （ 3）在（ 1）中的抛物线上的第二象限上能否存在一点 P ，使△ PBC 的面积最大？，若存在，求出点P 的坐标及△ PBC 的面积最大值 . 若没有，请说明原由 .解： (1) 将 A(1 ， 0) ， B( － 3，0) 代 yx2bx c 中得1 b ＝b 2c 0 ∴9 3b c 0 c3∴抛物线分析式为： yx 22x 3(2) 存在。

铅垂高水平宽面积公式

铅垂高水平宽面积公式
铅垂高水平宽面积的公式主要有以下三种：
一、公式1：面积= 泊松号 X 铅锤长度^²
①泊松号：指一个水体中水深和宽度的比值，根据泊松号表，可以确定水体深度和宽度的大小。

②铅锤长度：指用铅锤测定水体深度的时候，把铅锤垂直向下投放的距离，也就是两支铅锤的总长度。

二、公式2：面积= 2 X 垂膨泊松号 X 铅锤长度 X 面积系数
①垂膨泊松号：指水体中水深（投放铅锤时，从投放点到水体底部的距离）和宽度的比值，根据垂膨泊松号表，可以确定水体深度和宽度的大小。

②铅锤长度：与公式1中定义相同。

③面积系数：指水体宽度在铅锤投放时会发生变化而产生的影响，通过查阅相关资料可以确定面积系数的大小。

三、公式3：面积= 2 X 水柱体积 X 面积系数
①水柱体积：指用两支铅锤测量水体的时候，铅锤之间的柱体积，也就是一个整体的一个立方体的体积。

②面积系数：与公式2中定义相同。

专题13 宽高模型解决二次函数中的面积问题(解析版)

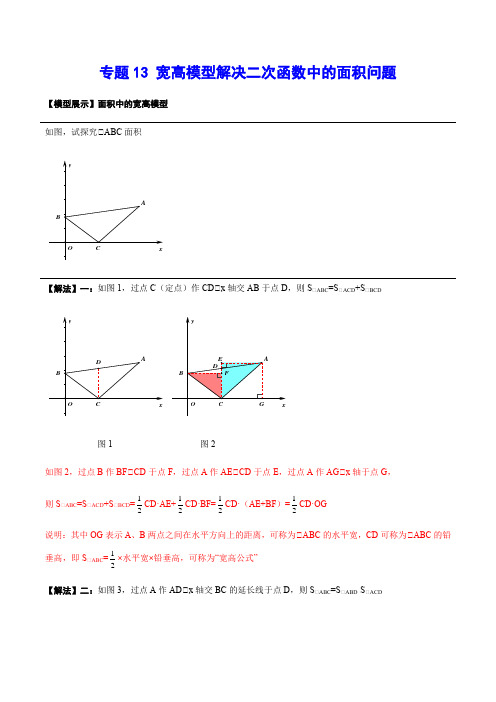
专题13 宽高模型解决二次函数中的面积问题【模型展示】面积中的宽高模型如图，试探究△ABC 面积【解法】一：如图1，过点C （定点）作CD△x 轴交AB 于点D ，则S △ABC =S △ACD +S △BCD图1 图2如图2，过点B 作BF△CD 于点F ，过点A 作AE△CD 于点E ，过点A 作AG△x 轴于点G ，则S △ABC =S △ACD +S △BCD =21CD·AE+21CD·BF=21CD·（AE+BF ）=21CD·OG 说明：其中OG 表示A 、B 两点之间在水平方向上的距离，可称为△ABC 的水平宽，CD 可称为△ABC 的铅垂高，即S △ABC =21×水平宽×铅垂高，可称为“宽高公式” 【解法】二：如图3，过点 A 作AD△x 轴交BC 的延长线于点D ，则S △ABC =S △ABD -S △ACD图3 图4如图4，过点B 作BH△AD 交于点H ，则S △ABC =S △ABD -S △ACD =21AD·BH -21AD·CG=21AD·（BH -CG ）=21AD·OC 说明：OC 是△ABC 的水平宽，AD 是△ABC 的铅垂高.【解法】三：如图5，过点B 作BD△y 轴交AC 于点D ，则S △ABC =S △ABD +S △BCD图5 图6如图6，过点C 作CH△BD 于点H ，过点A 作AG△x 轴于点G ，交BD 的延长线于点E ，则S △ABC =S △ABD +S △BCD =21BD·AE+21BD·CH=21BD·（AE+CH ）=21BD·AG 说明：BD 是△ABC 的水平宽，AG 是△ABC 的铅垂高.【解法】四：如图7，过点 A 作AE△y 轴于点E ，延长AE 交BC 反向延长线于点D ，则S △ABC =S △ACD -S △ABD图7 图8如图8，过点C 作CF△AD 交于点F ，则S △ABC =S △ACD -S △ABD =21AD·CF -21AD·BE=21AD·（CF -BE ）=21AD·OB 说明：AD 是△ABC 的水平宽，OB 是△ABC 的铅垂高.【模型总结】无论点A 、B 、C 三点的相对位置如何，“宽高模型”对图形面积求解总是适用，其证明方法、证明过程、最终结论都基本一致，利用大面积-小面积或割补法求解，体现出数学中“变中不变”的和谐统一之美。

20170103-初稿-段广猛-《用“倍半角模型”解题事半功倍》(1)(2)

用“倍半角模型”解题事半功倍段广猛（江苏省高邮市赞化学校）首先，一个问题如果是确定性的，那么就注定是可解的.其次，因果法是一种重要的思考问题的方式，“由因导果、执果索因”是分析问题、解决问题的重要途径.下面笔者借助平时教学中遇到过的一些问题，通过常规解法及“倍半角”解法，两相对比，让大家体会“倍半角”解题模型的优势.一、“倍半角模型”（一）问题的提出：首先介绍一下，什么是“倍半角模型”？如图1，在Rt△ABC 中，记∠A=β，则tan β=a b （不妨设a<b），当a、b 确定时，tan β及∠β都随之确定，那么2β及2β角也是确定的，从而tan 2β及tan2β的值也是确定的，既然是确定的，注定是可解的，那么如何求解呢？（二）由“倍β”到“半2β”：如图2，延长CA 至D，使AD=AB=c，连结BD，构造出等腰△ABD，则∠D=∠DBA=2β，从而构造出角2β，而且此2β角恰好在Rt△DBC 中，故可求出tan 2β=a b c +.上面这个过程不妨称为“由倍到半”的过程，简单易懂，但结论作用却很大，可以实现已知一个角的三角函数值，轻易求出这个角的一半所对应的三角函数值，从而此半角所在的直角三角形三边之比就可以确定下来，用于计算.（三）由“半β”到“倍2β”：如图3，作斜边AB 的垂直平分线交AC 于点E，连结BE，构造出等腰△ABE，则∠A=∠EBA=β，∠BEC=2β，从而构造出角2β，而且此2β角恰好在Rt△EBC 中，设CE=x，则AE=BE=b-x，在Rt△EBC 中，由勾股定理得222(b x)x a +=-，解之得222b a x b -=，故可求出tan2β=a x =222a b b a-（此公式不需要记忆）.上面这个过程不妨称为“由半到倍”的过程，计算稍显复杂，但结论作用却很大，可以实现已知一个角的三角函数值，轻易求出这个角的2倍所对应的三角函数值，从而此倍角所在的直角三角形三边之比就可以确定下来，用于计算.通过上面两个过程，可以看出，一般情况下，“由倍到半”容易，“由半到倍”稍复杂些，而且都是通过构造等腰三角形得出已知角的“半角”与“倍角”的，操作容易，作用极大.图2图1图3二、“特殊半角”的三角函数值下面通过几个“特殊半角”的三角函数值的求法，初步体验“倍半角模型”的重要作用.（一）15度角如何计算tan15°的值呢？由15°角容易联想到30°角，它们之间存在着“倍半”关系.如图4，先构造一个含30°角的Rt△ABC，设BC=1，CA=3,AB=2.延长CA至D，使AD=AB=2，连结BD，构造出等腰△ABD，则∠D=∠DBA=12∠BAC=15°，从而构造15°角，而且此15°角恰好在Rt△DBC中，故可求出tan15°=BCDC=123+=23-.值得一提的是，既然∠D=15°，那么∠DBC=75°，从而用图4还可以求出tan75°=DCBC=23+.实际上tan15°与tan75°互为倒数关系.另外，既然15°角构造出来了，如果继续同样地操作下去，还可以构造出7.5°角等，这个系列不妨称为“30°系列”，从而其三角函数值均可求，此处不再一一展开.（二）22.5度角同理，如何计算tan22.5°的值呢？由22.5°角容易联想到45°角，它们之间存在着“倍半”关系.如图5，先构造一个含40°角的Rt△ABC，设BC=1，CA=1,AB=2.延长CA至D，使AD=AB=2，连结BD，构造出等腰△ABD，则∠D=∠DBA=12∠BAC=22.5°，从而构造22.5°角，而且此22.5°角恰好在Rt△DBC中，故可求出tan22.5°=BCDC=121+=21-.值得一提的是，既然∠D=22.5°，那么∠DBC=67.5°，从而用图5还可以求出tan67.5°=DCBC=21+.实际上tan22.5°与tan67.5°互为倒数关系.另外，既然22.5°角构造出来了，如果继续同样地操作下去，还可以构造出11.25°角等，这个系列不妨称为“45°系列”，从而其三角函数值均可求，此处不再一一展开.还有一个有趣的角，值得一提，那就是18°角，如何计算sin18°的值呢？由18°角容易联想到36°角，它们之间存在着“倍半”关系.而36°角容易使人联想到“黄金三角形”，即顶角为36°的等腰三角形.如图6，先构造一个顶角为36°的等腰三角形△ABC，由“黄金三角形”的概念容易得出512BCAC-=，可设BC=512-，CA=BA=1.过A作AD图5图4⊥BC 于点D，由“三线合一”易知CD=12BC=514-，且∠CAD=12∠BAC=18°，从而构造18°角，而且此18°角恰好在Rt△CAD 中，故可求出sin18°=DC AC =514-.18°角的三角函数值求法，虽然没用到上述“倍半角模型”，但它们都体现出了数学解题中“联想机制”的重要作用.三、实战分析接下来，我将结合实际教学中遇到过的一些问题，通过常规解法及“倍半角”解法，两相对比，深入体会“倍半角”解题模型的巨大优势.例1.已知1tan 2α=，求tan tan 22αα及的值.简析：本题采用“构图法”结合“倍半角模型”解决，如图7-1，先构造出一个含α角的Rt△ABC，设BC=1，CA=2,AB=5.延长CA 至D，使AD=AB=5，连结BD，构造出等腰△ABD，则∠D=∠DBA=12∠BAC=2α，从而构造2α角，而且此2α角恰好在Rt△DBC 中，故可求出tan 2α=BC DC =1=525+2-.上述过程是“由倍到半”的过程.如图7-2，同理构造出一个含α角的Rt△ABC，设BC=1，CA=2,AB=5.作斜边AB 的垂直平分线交AC 于点E，连结BE，构造出等腰△ABE，则∠A=∠EBA=α，∠BEC=2α，从而构造出角2α，而且此2α角恰好在Rt△EBC 中，设CE=x，则AE=BE=2-x，在Rt△EBC 中，由勾股定理得2221(2x)x +=-，解之得34x =，故可求出tan2α=1x =43.上述过程是“由半到倍”的过程.图7-1图7-2例2.如图8，PA 、PB 切⊙O 于A 、B 两点，CD 切⊙O 于点E ，交PA 、PB 于C ，D ，若⊙O 的半径为r ，△PCD的周长等于3r ，则tan ∠APB的值是.常规解法：要求tan ∠APB 的值，需想办法将∠APB 构造在某一个直角三角形中，如图8-1，连结OA 、OB ，并延长PA 、BO 交于点F ，易知Rt△FAO∽Rt△FBP，且相似比为23FA FO AO FB FP BP ===，设FA=2x ，则FB=3x ，FO=3x-r，FP=2x+1.5r，故由23FO FP =可得：322 1.53x r x r -=+，解之得x=65r ,从而有：tan ∠APB=tan ∠FOA=1221255r FA x AO r r ===.“倍半角”解法：如图8-2，连结OA 、OB 、OP ，易知∠APB=2∠APO ，∠APB 因∠APO 的确定而确定，而且它们之间存在“倍半”关系，要求tan ∠APB 的值，只需要求tan ∠APO的值即可，显然tan ∠APO=23AO AP =，再构造如图8-3所示的“倍半角模型”，重新假设AO=2，AP=3，AQ=x，PQ=OQ=3-x，在Rt△AOQ 中由勾股定理得2222(3x)x +=-，解之得56x =，故可求出tan ∠APB=tan2∠APO=tan ∠AQO=2125AO AQ x ==.图8图8-1图8-2图8-3如图，在△ABC 中，∠C=90°，AC=8，AB=10，点P 在AC 上，AP=2，若⊙O 的圆心在线段BP 上，且⊙O 与AB、AC 都相切，试求⊙O 的半径.26．如图1，以△ABC 的边AB 为直径的⊙O 交边BC 于点E ，过点E 作⊙O 的切线交AC 于点D ，且ED ⊥A C．（1）试判断△ABC 的形状，并说明理由；（2）如图2，若线段AB 、DE 的延长线交于点F ，∠C =75°，CD =2﹣，求⊙O 的半径和BF 的长．图1图17．如图是利用四边形的不稳定性制作的菱形衣架．已知其中每个菱形的边长为13cm，135cos =∠ABC ，那么衣架两顶点A 、E 之间的距离为cm ．。

20170302-段广猛-《面积问题之”水平宽、铅锤高“模型的实战分析》

三角形面积问题之“宽高公式”的实战分析高邮市赞化学校段广猛《三角形面积问题之“宽高公式”的两种证明方法》一文中，主要介绍了三种情形下“宽高公式”模型的证明.如图1、图2、图3所示，12ABCS OC AD∆=⨯⨯，其中OC表示B、C两点在水平方向上的距离，简称这个三角形的“水平宽”；而AD表示点A到边BC在竖直方向上的距离，简称这个三角形的“铅锤高”.于是三角形的面积S=12⨯水平宽⨯铅锤高，这个公式不妨称为“宽高公式”.细心观察上面三种情形，操作方式都是过点A作平行于y轴的直线交边BC所在的直线于点D，则AD就是“铅锤高”；而B、C两点之间的水平距离，即线段OC就是“水平宽”.在实际应用中，笔者不建议学生固化思维，强记这里的结论而直接使用.一方面，这个公式课本上并没有直接出现，中考时能不能直接使用值得商榷；另一方面，对于图2的结论，大部分学生普遍可以接受，但是若是不知道这个公式推导的来龙去脉而强行直接使用，图1及图3的结论，多数学生是很难理解原理而导致不能正确使用.更何况，这三种情形下的推导过程也是相辅相成、思想统一的，都采用了“改斜归正”及“割补法”的思想，而这两种思想方法又是极其重要的解题原理，需要同学们认真深刻体会的，所以笔者强烈建议学生体会这里的推导原理，以达到灵活使用的目的.其实，掌握了原理，怎么割补三角形都可以，只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线都可以实现面积处理，仅仅是繁简程度不一而已，下文会一一提及.如图4、图5、图6所示，12ABC S BD AE ∆=⨯⨯，其中BD 表示点B 到边AC 在水平方向上的距离，简称这个三角形的“水平宽”；而AE 表示A、C 两点在竖直方向上的距离，简称这个三角形的“铅锤高”.于是依然有三角形的面积S=12⨯水平宽⨯铅锤高.这三张图的操作方式都是过点B 作平行于x 轴的直线交边AC 所在的直线于点D，则BD 就是“水平宽”；而A、C 两点之间的竖直距离，即线段AE 就是“铅锤高”.实际上，过点C 作平行于坐标轴的直线，无论是平行于x 轴，还是平行于y 轴，最终都可以实现对于此三角形的面积处理，有时是“割”，即“面积加法”；有时是“补”，即“面积减法”.由此可以看出，不用强记公式，只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线，无论是平行于x 轴，还是平行于y 轴，都可以实现面积处理.图7提供了一种方式，12ABC S CD AE ∆=⨯⨯.那么问题来了，割补方式千变万化，而且好像都可行，在解题实战中，难道就随意割补吗？非也！理论上是都可行，但计算量绝不相当！我们知道，“在变化中抓不变量”也是一种重要的思想方法，“以不变应万变”.此时再结合这个解题策略，就可以使计算过程“如履平地”.在三角形三个顶点中，一般情况下会有两个定点和一个动点，抓住这两个定点就是关键所在.如图8或图9所示，点B 和点C 是两个定点，而点A 是一个动点.这时，我们就应该过动点A 作平行于y 轴或者平行于x 轴的直线交直线BC 于点D，利用B、C 两个定点求出直线BC 的解析式，再设出动点A 的坐标，将横坐标或者纵坐标代入直线BC 的解析式，表示出点D 的坐标，进而容易表示出线段AD.在图9中，ABC ACD ABD S S S ∆∆∆=-=12AD CF ⋅11(CF )22AD BE AD BE -⋅=⋅-1(OE )2AD BE =⋅-12AD OB =⋅，因为B、C 都是定点，故OB 是常值，而且直线BC 的解析式易求，进而AD 的长度好表示.若是你“不信邪”，偏偏如图10所示那样“割补”，我想说“此路依然行得通”，但与前面的两种方法相比，一烦在“水平宽”BD 上，需要求出直线AC 的解析式，理论上肯定行得通，这条直线的解析式会因为点A 是动点而导致含有参数，计算量较大；二烦在“铅锤高”AE 上，也是因为点A 是动点而导致含有参数.“罪魁祸首”都在动点A 上，而“元凶”就是因为一开始过定点B 进行了“割补”.需要特别说明的是，这种方法并非是错误的，仅仅是计算量较大些，其操作依然是可行的.下面以2016年苏州中考压轴题第（2）问为例具体谈谈“宽高公式”的使用.（2016•苏州）如图11，直线l：y=-3x+3与x 轴、y 轴分别相交于A、B 两点，抛物线y=ax 2﹣2ax+a+4（a＜0）经过点B．（1）求该抛物线的函数表达式；（2）已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM、BM，设点M 的横坐标为m，△ABM 的面积为S，求S 与m 的函数表达式，并求出S 的最大值.对于第（1）小问，易知该抛物线的函数表达式为：y=-x 2+2x+3；对于第（2）小问，这是一个“两定一动型”三角形面积问题，“死咬”A、B 两定点“不松口”，过动点M 作平行于坐标轴的直线进行“割补”即可，这里提供两种方式.方式一：如图12所示，过动点M 作平行于y 轴的直线交边AB所在的直线于点N，则ABM MNB MNA S S S ∆∆∆=-=12MN OG ⋅11(OG )22MN AG MN AG -⋅=⋅-12MN OA =⋅.设M（t，-t 2+2t+3），其中t 的取值范围是0＜t＜3，则N（t，-3t+3），从而MN =M N y y -=（-t 2+2t+3）-（-3t+3）=-t 2+5t，而OA=1，故S=12（-t 2+5t）=-12t（t-5），当t=52时，S 有最大值为258.值得一提的是，上面的操作过程可总结如下：第一步：抓住两个定点A 和B，它们之间在水平方向上的距离OA 作为△ABM 的“水平宽”；第二步：过动点M 作平行于y 轴的直线交边AB 所在的直线于点N，则MN 作为△ABM 的“铅锤高”；第三步：将面积“往竖直线MN 上靠”，通过面积“减法”，得到所求三角形的面积为12ABM S MN OA ∆=⋅.方式二：如图13所示，过动点M 作平行于x 轴的直线交边AB 所在的直线于点N、交y 轴于点G，则ABM MNB MNA S S S ∆∆∆=+=12MN BG ⋅11(BG O )22MN OG MN G +⋅=⋅+12MN OB =⋅.设M（t，-t 2+2t+3），其中t 的取值范围是0＜t＜3，则N（223t t -，-t 2+2t+3），从而MN =M N x x -t -223t t -=253t t -+，而OB=3，故S=122533t t -+⋅⋅=-12t（t-5），当t=52时，S 有最大值为258.上面的操作过程可总结如下：第一步：抓住两个定点A 和B，它们之间在竖直方向上的距离OB 作为△ABM 的“铅锤高”；第二步：过动点M 作平行于x 轴的直线交边AB 所在的直线于点N，则MN 作为△ABM 的“水平宽”；第三步：将面积“往水平线MN 上靠”，通过面积“加法”，得到所求三角形的面积为12ABM S MN OB ∆=⋅.至此，这个“两定两动型”三角形面积问题，利用“宽高公式”得到了比较完美的解答.当然，关于面积处理，绝不仅仅只有“宽高公式”，还有很多其他的路可走，如“框图法”（亦可称“矩形大法”）、其他的割补法（如上题中连接OM 也是一种很好的分割处理手段）等等，但大多体现出来的思想方法都是“大同小异”的，即想方设法将所求“斜面积”“改斜归正”，使问题得以解决.后面若有机会，会专门成文，敬请期待！通过前面的《模型证明》及本文的《实战分析》，笔者认为根本不用记忆所谓的“宽高公式”，只要在处理面积的问题中，狠抓不动点不放手，过动点作平行于坐标轴的直线交这不动边所在的直线于一点，将三角形的面积进行“割”或“补”，即面积“加”或“减”，然后平移其中一条高线，即可转化为高线的“加”或“减”，就能够得出所谓的“宽高公式”！这道苏州中考真题中有一个限制条件“点M 在第一象限内”，很明显是为了简化起见.若是将这个条件去掉，即“点M 是抛物线上任意一动点”，那么△ABM 的面积为S 关于m 的函数表达式又如何求解呢？我想其他的方法就未必恰当了，这时“宽高法”的作用会更明显.图14及图15给出了两种情形，前者可看出此时方法过程跟原题一模一样；而后者可看出唯一的区别就是点N 位于了点M 的上方，此时MN=N M y y -，其他都没变化也就是这时候要分类了，分类的标准就是M、N“谁高谁低”，可分三类，也可分两类.甚至于，结合本人作品《巧用绝对值避开“繁琐的”分类讨论》一文，直接借用“绝对值”，y y 即可，最后解一个含绝对值的方程就可以了，在此不再一一赘述，将MN表示为M N有兴趣的同学可自行展开.同学们，研究之窗已向你们打开，还有什么道理不去认真钻研、琢磨呢！加油，中考必胜！最后来首打油诗结束本文，“横切竖切都可以，切法不一莫强求；关键抓住不动点，最好沿着动点切；切完之后即加减，加减之后即宽高！”。

“二次函数”面积最值问题的几种解法

“二次函数”面积最值问题的几种解法以微课堂公益课堂，奥数国家级教练与四位特级教师联手执教。

二次函数是初中数学的一个重点、难点，也是中考数学必考的一个知识点。

特别是在压轴题中，二次函数和几何综合出现的题型，才是最大的区分度。

而求三角形面积的最值问题，更是常见。

今天介绍二次函数考试题型种，面积最值问题的4种常用解法。

同学们只要熟练运用一两种解法，炉火纯青，在考试答题的时候，能够轻松答题，就好。

原题：在（1）中的抛物线上的第二象限是否存在一点P，使△PBC的面积最大？若存在，求出P点的坐标及△PBC的面积最大值，若没有，请说明理由。

考试题型，大多类似于此。

求面积最大值的动点坐标，并求出面积最大值。

一般解题思路和步骤是，设动点P的坐标，然后用代数式表达各线段的长。

通过公式计算，得出二次函数顶点式，则坐标和最值，即出。

解法一：补形，割形法。

方法要点是，把所求图像的面积适当的割补，转化成有利于面积表达的常规几何图形。

请看解题步骤。

解法二：铅锤定理，面积=铅锤高度×水平宽度÷2。

这是三角形面积表达方法的一种非常重要的定理。

铅锤定理，在教材上没有，但是大多数数学老师都会作为重点，在课堂上讲解。

因为，铅锤定理，在很多地方都用的到。

这里，也有铅锤定理的简单推导，建议大家认真体会。

解法二：铅锤定理，在求二次函数三角形面积最值问题，运用非常多。

设动点P的坐标，然后用代数式分别表达出铅锤高度和水平宽度，然后利用铅锤定理的计算公式，得出二次函数，必有最大值。

解法三：切线法。

这其实属于高中内容。

但是，基础好的同学也很容易理解，可以看看，提前了解一下。

解法四：三角函数法。

请大家认真看上面的解题步骤。

总之，从以上的四种解法可以得出一个规律。

过点P做辅助线，然后利用相关性质，找出各元素之间的关系。

设动点P的坐标，然后找出各线段的代数式，再通过面积计算公式，得出二次函数顶点式，求出三角形面积的最大值。

对于同学们中考数学来说，只要你熟练掌握解法一和解法二，那么二次函数几何综合题中，求三角形面积最大值问题，就非常简单了。

铅垂高与水平宽6种模型原理(一)

铅垂高与水平宽6种模型原理(一)铅垂高与水平宽6种模型模型定义铅垂高与水平宽6种模型是地图投影方式中比较常见的一种模型。

它将地球投影到一个长方形上，长方形的一条边为地球的赤道，另一条边则为某一子午线。

等角投影（兰伯特投影）等角投影是铅垂高与水平宽6种模型中最常见的一种投影方式。

它保持地球表面上的每一个角度都不变，因此被称为“等角投影”或“兰伯特投影”。

等积投影（面积投影）等积投影是铅垂高与水平宽6种模型中另一个常见的投影方式。

它可以保持地球表面上的任何一个区域面积不变，因此被称为“等积投影”或“面积投影”。

柱面投影柱面投影是将地球表面投影到一个圆柱体上，然后再展开到平面上。

在这种投影方式下，保持线段的直线性，但是面积的失真比较严重。

锥面投影锥面投影是将地球表面投影到一个圆锥体上，然后再展开到平面上。

在这种投影方式下，保持面积的相对大小，但是形状会发生畸变。

圆盘投影（正交投影）圆盘投影是将地球表面投影到一个圆盘上。

在这种投影方式下，保持在投影面上看到的所有角度和长度的比例都与球面地理上的原始值相同。

多层投影（高斯－克吕格投影）多层投影是将地球投影到多个圆锥面或圆柱面上，不同区域采用不同的投影方式。

这种方法可以同时保持角度和面积的几何关系。

以上是铅垂高与水平宽6种模型的详细解释。

选择不同的投影方式，需要根据实际需要和应用场景来进行选择。

模型特点在六种投影模型中，每种模型的特点和优劣并不一样。

以下列出各种模型的特点：•等角投影：保持角度不变，适用于航海等需要准确角度的应用。

•等积投影：保持面积不变，适用于地图上展示不同区域的面积大小比例。

•柱面投影：保持直线性，适用于航线和等经度线的展示。

•锥面投影：保持面积比例，适用于矩形地图的展示。

•圆盘投影（正交投影）：保持角度和长度比例不变，适用于卫星地图和渐进地图。

•多层投影：综合各种模型的优点，适用于展示大区域的地图。

模型应用各种铅垂高与水平宽模型在不同的应用场景中有着不同的应用。

铅垂高水平宽求三角形面积的原理

铅垂高水平宽求三角形面积的原理以铅垂高水平宽求三角形面积的原理为题，我们将从三角形的定义、铅垂线的概念以及如何利用这些概念来求解三角形面积等方面进行讨论。

让我们回顾一下三角形的定义。

三角形是由三条线段连接而成的图形，其中每条线段称为三角形的边，而三个顶点则是这些边的交点。

根据三角形的性质，我们可以将三角形分为不同的类型，例如等边三角形、等腰三角形、直角三角形等。

接下来，我们来介绍一下铅垂线的概念。

铅垂线是从一个点向一个平面垂直下落的线段。

在三角形中，我们可以通过顶点向对边引一条垂直线，这条垂直线即为铅垂线。

铅垂线与对边的交点称为垂足。

利用铅垂线，我们可以将三角形分割为两个直角三角形，从而简化问题的求解。

那么，如何利用铅垂高和水平宽来求解三角形的面积呢？我们可以利用三角形面积公式S = 1/2 * 底边长* 高来求解。

在这里，底边长即为水平宽，高即为铅垂高。

为了更好地理解这个公式，我们可以通过一个具体的例子来进行说明。

假设我们有一个三角形ABC，其中AB为底边，C为顶点，D为AB 的中点，AD为铅垂高，CD为水平宽。

我们最终的目标是求解三角形ABC的面积。

我们可以通过测量或已知条件得到底边AB的长度和铅垂高AD的长度。

接下来，我们可以利用铅垂线的性质，将三角形ABC分割为两个直角三角形ACD和BCD。

对于直角三角形ACD，我们可以利用三角形面积公式S = 1/2 * 底边长* 高来求解。

在这里，底边长即为水平宽CD的长度，高即为铅垂高AD的长度。

将这两个值代入公式中，即可计算出直角三角形ACD的面积。

同样地，对于直角三角形BCD，我们也可以利用三角形面积公式求解。

底边长为水平宽CD的长度，高为铅垂高AD的长度。

将这两个值代入公式中，即可计算出直角三角形BCD的面积。

我们将直角三角形ACD和BCD的面积相加，即可得到三角形ABC 的面积。

通过以上步骤，我们可以利用铅垂高和水平宽来求解三角形的面积。

这种方法可以简化计算过程，减少复杂度，提高求解效率。

面积问题之”水平宽、铅锤高“模型的实战分析

中考数学压轴题突破：铅锤法求二次函数面积

一、引言在中学生的学习生涯中，中考数学一直是备受关注的科目之一。

其中，二次函数是数学教学中的重要内容，而求二次函数面积更是中考数学中的一大难点。

然而，通过铅锤法求二次函数面积，可以帮助学生们更好地掌握这一难题。

本文将从深度和广度两方面展开讨论，帮助读者全面了解铅锤法求二次函数面积，在中考数学中取得突破。

二、铅锤法求解二次函数面积的基本原理铅锤法求解二次函数面积是一种通过几何实例来帮助学生理解二次函数的面积计算方法。

在求解二次函数面积时，首先可以将二次函数图像与x轴围成的图形，分割成若干个几何形状，如梯形、矩形等。

通过对这些几何形状进行面积计算，并进行累加，就可以得到二次函数图像与x轴围成的总面积。

这种方法能够直观地帮助学生理解二次函数的面积计算过程，从而提高他们的数学认知能力。

三、铅锤法求解二次函数面积的实际应用铅锤法求解二次函数面积不仅仅是一种理论计算方法，更适用于实际问题的求解。

当我们需要计算某个二次函数所表示的曲线与x轴围成的面积时，可以通过铅锤法将曲线分割成若干个几何形状，再进行面积计算，并进行累加，最终得到准确的面积结果。

这种方法在实际问题的求解中具有很强的适用性，且可以帮助学生将数学知识与实际问题相结合，提升解题能力。

四、铅锤法求解二次函数面积的个人观点与理解个人认为，铅锤法求解二次函数面积是一种非常有效的教学方法。

通过实际创造性的几何分割和面积累加，学生可以更直观地理解二次函数的面积计算方法，提高数学学习的趣味性和有效性。

在实际教学中，教师可以通过丰富的示例和实际问题，引导学生灵活运用铅锤法求解二次函数面积，从而提高他们的数学学习能力和解题思维。

五、总结与回顾本文从深度和广度两方面介绍了铅锤法求解二次函数面积的基本原理、实际应用和个人观点与理解。

我们可以通过铅锤法，帮助学生更好地理解和掌握二次函数面积的计算方法，提高他们的数学学习能力。

在中考数学的备战中，这一方法能够帮助学生更好地应对二次函数面积题型，取得更好的成绩。

第一节水平宽铅垂高面积处理

第一节水平宽铅垂高面积处理我们在做几何题的时候经常会遇到面积问题，尤其是三角形的面积，我们都知道三角形的面积等于底乘高的积的一半，但是在斜三角形中，一旦底与高不好表示，我们会采用割补法的策略。

特别地，在函数与几何的动点问题中，我们往往在动点处向坐标轴作平行线，利用“铅锤法”求出面积的表达式，下面我们就来看看斜三角形的面积处理模型．【例1】（2019•沈阳）如图，正比例函数11y k x =的图象与反比例函数22(0)k y x x=>的图象相交于点A ，点B 是反比例函数图象上一点，它的横坐标是3，连接OB ，AB ，则AOB ∆的面积是．【例2】（2020•南海区二模）如图所示，在矩形ABCD 中，8BA cm =，4BC cm =，点E 是CD 上的中点，P 、Q 均以1/cm s 的速度在矩形ABCD 边上匀速运动，其中动点P 从点A 出发沿A D C →→方向运动，动点Q 从点A 出发沿A B C →→方向运动，二者均达到点C 停止运动，设点Q 的运动时间为x ，PQE ∆的面积为y ，则下列能大致反应y 与x 函数关系的图象是( )A ．B ．C ．D ．【例3】（2020•重庆）如图，在平面直角坐标系中，已知抛物线2y x bx c =++与直线AB 相交于A ，B 两点，其中(3,4)A --，(0,1)B -．（1）求该抛物线的函数表达式；（2）点P 为直线AB 下方抛物线上的任意一点，连接PA ，PB ，求PAB ∆面积的最大值；【例4】（2020•宿迁）二次函数23y ax bx =++的图象与x 轴交于(2,0)A ，(6,0)B 两点，与y 轴交于点C ，顶点为E ．．（1）求这个二次函数的表达式，并写出点E 的坐标；（2）如图①，D 是该二次函数图象的对称轴上一个动点，当BD 的垂直平分线恰好经过点C 时，求点D 的坐标；（3）如图②，P 是该二次函数图象上的一个动点，连接OP ，取OP 中点Q ，连接QC ，QE ，CE ，当CEQ ∆的面积为12时，求点P 的坐标．【例5】（2020•深圳）如图1，抛物线23(0)y ax bx a =++≠与x 轴的交点(3,0)A -和(1,0)B ，与y 轴交于点C ，顶点为D ．（1）求该抛物线的解析式；（2）连接AD ，DC ，CB ，将OBC ∆沿x 轴以每秒1个单位长度的速度向左平移，得到△O B C '''，点O 、B 、C 的对应点分别为点O '、B '、C '，设平移时间为t 秒，当点O '与点A 重合时停止移动．记△O B C '''与四边形AOCD 重合部分的面积为S ，请直接写出S 与t 之间的函数关系式；【同步训练】1．（2020春•丛台区校级月考）如图，坐标系中四边形ABCD 的面积是( )A ．4B ．5．5C ．4．5D ．52．（2020•河南模拟）如图，矩形ABCD 的周长是28cm ，且AB 比BC 长2cm ．若点P 从点A 出发，以1/cm s 的速度沿A D C →→方向匀速运动，同时点Q 从点A 出发，以2/cm s 的速度沿A B C →→方向匀速运动，当一个点到达点C 时，另一个点也随之停止运动．若设运动时间为()t s ，APQ ∆的面积为2()S cm ，则2()S cm 与()t s 之间的函数图象大致是( )A ．B ．C ．D ．3．（2020•绵阳）如图，抛物线过点(0,1)A 和C ，顶点为D ，直线AC 与抛物线的对称轴BD的交点为B 0)，平行于y 轴的直线EF 与抛物线交于点E ，与直线AC 交于点F ，点FBDEF 为平行四边形．（1）求点F 的坐标及抛物线的解析式；（2）若点P 为抛物线上的动点，且在直线AC 上方，当PAB ∆面积最大时，求点P 的坐标及PAB ∆面积的最大值；4．（2020•菏泽）如图，抛物线26y ax bx =+-与x 轴相交于A ，B 两点，与y 轴相交于点C ，2OA =，4OB =，直线l 是抛物线的对称轴，在直线l 右侧的抛物线上有一动点D ，连接AD ，BD ，BC ，CD ．（1）求抛物线的函数表达式；（2）若点D 在x 轴的下方，当BCD ∆的面积是92时，求ABD ∆的面积；5．（2020•滁州模拟）在EFG==，正方形ABCD的边长为1，∠=︒，EG FG∆中，90G将正方形ABCD和EFG∆如图放置，AD与EF在一条直线上，点A与点E重合．现将正方形ABCD沿EF方向以每秒1个单位的速度匀速运动，当点A与点F重合时停止．在这个运动过程中，正方形ABCD和EFG∆重叠部分的面积S与运动时间t的函数图象大致是()A．B．C．D．第二节面积转化问题面积的问题中往往会出现需要转化的情况，常见的方法是底边成比例找点，利用平行线构造等高，利用相似转化面积之比等等，我们将通过下面的模型来加以说明．【例1】（2020•遂宁）如图，抛物线2(0)y ax bx c a =++≠的图象经过(1,0)A ，(3,0)B ，(0,6)C 三点．（1）求抛物线的解析式．（2）抛物线的顶点M 与对称轴l 上的点N 关于x 轴对称，直线AN 交抛物线于点D ，直线BE 交AD 于点E ，若直线BE 将ABD ∆的面积分为1:2两部分，求点E 的坐标．【例2】（2020•达州）如图，在平面直角坐标系xOy 中，已知直线122y x =-与x 轴交于点A ，与y 轴交于点B ，过A 、B 两点的抛物线2y ax bx c =++与x 轴交于另一点(1,0)C -．（1）求抛物线的解析式；（2）在抛物线上是否存在一点P ，使PAB OAB S S ∆∆=？若存在，请求出点P 的坐标，若不存在，请说明理由；【例3】（2020•成都）在平面直角坐标系xOy 中，已知抛物线2y ax bx c =++与x 轴交于(1,0)A -，(4,0)B 两点，与y 轴交于点(0,2)C -．（1）求抛物线的函数表达式；（2）如图1，点D 为第四象限抛物线上一点，连接AD ，BC 交于点E ，连接BD ，记BDE ∆的面积为1S ，ABE ∆的面积为2S ，求12S S 的最大值；【同步训练】1．（2020•齐齐哈尔）综合与探究在平面直角坐标系中，抛物线212y x bx c =++经过点(4,0)A -，点M 为抛物线的顶点，点B 在y 轴上，且OA OB =，直线AB 与抛物线在第一象限交于点(2,6)C ，如图①．（1）求抛物线的解析式；（2）直线AB 的函数解析式为 4y x =+ ，点M 的坐标为，cos ABO ∠= ；连接OC ，若过点O 的直线交线段AC 于点P ，将AOC ∆的面积分成1:2的两部分，则点P 的坐标为；2．（2020秋•碑林区校级期中）如图，抛物线2y x bx c =++经过点(3,12)和(2,3)--，与两坐标轴的交点分别为A ，B ，C ，它的对称轴为直线l ，顶点为D ．（1）求该抛物线的表达式和顶点D 的坐标；（2）直线AC 交抛物线的对称轴l 于点E ，在抛物线上是否存在点F ，使得BCF ∆与BCE ∆的面积相等，如果存在，请求出点F 的坐标；如果不存在，请说明理由．3．（2020•郴州）如图1，抛物线23(0)y ax bx a =++≠与x 轴交于(1,0)A -，(3,0)B ，与y 轴交于点C ．已知直线y kx n =+过B ，C 两点．（1）求抛物线和直线BC 的表达式；（2）点P 是抛物线上的一个动点．如图1，若点P 在第一象限内，连接PA ，交直线BC 于点D ．设PDC ∆的面积为1S ，ADC ∆的面积为2S ，求12S S 的最大值；第三节面积重叠问题动点问题是中考数学中的重难点部分，分类讨论在这类问题的处理中也是老生常谈了。

数学面积计算铅锤法使用技巧

数学面积计算铅锤法使用技巧
1. 嘿，你知道吗？在计算一些奇奇怪怪形状的面积时，铅锤法可太好用啦！比如说算那个歪七扭八的三角形的面积，用铅锤法就能轻松搞定呀！
2. 哇塞，数学面积计算铅锤法的使用技巧那可真是宝啊！就像给你一把钥匙，能打开各种复杂面积计算的大门。

比如碰到那个像迷宫一样复杂的图形，铅锤法一下就能找到答案呢，神奇吧！
3. 嘿呀，你想想，当你面对一个超级难搞的面积问题时，铅锤法就像救星一样出现啦！像那种看起来乱七八糟的多边形的面积，用它就能迎刃而解。

4. 哎呀呀，数学面积计算铅锤法真的绝了！跟你说，好比那个超级扭曲的图形，没它的话你可就头大了，但有了铅锤法，轻松搞定呀！
5. 哇哦，铅锤法在数学面积计算里那可太重要啦！就像有了秘密武器。

比如算那个形状奇怪得让人抓狂的图形，铅锤法能让你一下子豁然开朗。

6. 嘿，你可别小看这铅锤法哟！在面积计算中它可厉害着呢！就像面对那个弯弯绕绕的图案，铅锤法就能派上大用场啦！
7. 哇，铅锤法使用技巧是得好好掌握啊！否则遇到那些难搞的面积，不就傻眼了吗？就像那个看起来毫无头绪的形状，有技巧就能搞定哟！
8. 哎呀，数学面积计算铅锤法的魔力你可得分得清哟！比如看到那个稀奇古怪的轮廓，靠它就能算出面积呀！
9. 总之，铅锤法对于数学面积计算太重要啦！掌握了它的使用技巧，就能在各种复杂情况下游刃有余地算出面积。

管它是什么奇形怪状的图形，咱都不怕！。

对一道经典分割问题的探究

对一道经典分割问题的探究段广猛【摘要】操作与探究可以很好地训练学生的动手能力、空间想象能力、思维能力、分析与解决问题的能力. 文章对一类等腰三角形分割问题做较深入的研究与探索,解决怎样的三角形能分割成两个等腰三角形,以及如何分割等一般性问题,培养学生的分类意识,体现思维的有序性、灵活性和系统性.【期刊名称】《中国数学教育（初中版）》【年(卷),期】2018(000)012【总页数】4页(P51-53,57)【关键词】分割问题;动手操作;分类探究;画图能力【作者】段广猛【作者单位】江苏省高邮市赞化学校【正文语种】中文如果一个三角形恰好能够被分割成两个等腰三角形，那么这个三角形应该满足怎样的条件？并且如何分割呢？一、问题解决对于如此抽象的问题，笔者的解决方案按以下步骤逐一展开，此为思维的有序性. 1.大小假设如图1，在△ABC中，不妨设∠A≤∠B≤∠C，即∠A为最小角，∠C为最大角.2.总体策略逆向思考，反道而行；画出草图，精准分析.3.局部策略先通过观察做定性分析，缩小范围，再分类做定量研究.4.分类决策分三类解决问题：第一类是过最小角∠A的顶点分割；第二类是过较大角∠B的顶点分割；第三类是过最大角∠C的顶点分割.5.实施过程图2第一类：如图2，当过最小角∠A的顶点作分割线AD时，易得∠ADB＞∠C≥∠B≥∠BAC＞∠BAD.锁定△ABD，即∠ADB＞∠B＞∠BAD，故△ABD不可能为等腰三角形，可得结论1.结论1：对于任意三角形，过最小角的顶点都不能分割成两个等腰三角形.第二类：如图3，当过较大角∠B的顶点作分割线BD时，易得∠ADB＞∠C≥∠ABC≥∠A.锁定△ABD，则有∠ADB＞∠ABD，且∠ADB＞∠A.故要使△ABD为等腰三角形，只有一种可能，即∠ABD=∠A.图3图4接下来调整图形.如图4，∠ABD=∠A，继续观察做定性分析，锁定△BCD，易知∠C≥∠ABC＞∠CBD，故要使△BCD为等腰三角形，有两种情况，即∠C=∠CDB或∠CBD=∠CDB.情况1：如图5，当∠C=∠CDB时，设∠ABD=∠A=α，则∠C=∠CDB=2α，∠DBC=180°-4α，∠ABC=180°-3α..分析定量关系：由∠A≤∠ABC≤ ∠C及∠DBC ＞0°，则有解得36°≤α＜45°.有趣的是，此时还会发现∠C=2∠A，从而可以得到以下结论.结论2：当某三角形同时满足36°≤最小角α＜45°，且存在另一个角2α时，只需要过第三个角的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形. 情况2：如图6，当∠CBD=∠CDB时，设∠ABD=∠A=α，则∠CBD= ∠CDB=2α，∠C=180°-4α，∠ABC=3α..图6分析定量关系：由∠A≤∠ABC≤∠C，则有解得.有趣的是，此时还会发现∠ABC=3∠A，从而可以得到以下结论.结论3：当某三角形同时满足最小角，存在另一个角3α时，只需要过角3α的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.图7第三类：如图7，当过最大角∠C的顶点作分割线CD时，易得∠ADC＞∠B≥∠A.锁定△ACD，则有∠ADC＞∠A.故要使△ACD为等腰三角形，又分两种类型，即∠ACD=∠A或∠ACD=∠ADC.类型1：当∠ACD=∠A时，再锁定△BCD，继续观察做定性分析，但得不到任何有效信息来缩小范围.要使△BCD为等腰三角形，可能有三种情形，即∠BCD=∠B或∠BDC=∠B或∠BCD=∠BDC.情况1：如图8，当∠BCD=∠B时，设∠ACD=∠A=α，则∠BDC=2α，∠BCD=∠B=90°-α，所以∠ACB=90°，即△ACB为直角三角形.图8结论4：直角三角形一定可以分割成两个等腰三角形（只需沿着斜边的中线进行分割）.情况2：如图9，当∠BDC=∠B时，设∠ACD=∠A= α，则∠BDC= ∠B=2α，∠BCD=180°-4α，∠ACB=180°-3α.分析定量关系：由∠ABC≤∠ACB，且∠BCD ＞0°，则有解得α≤36°.有趣的是，此时还会发现∠B=2∠A，从而可以得到以下结论.结论5：当某三角形同时满足最小角α≤36°，且存在另一个角2α时，只需过第三个角的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.情况3：如图10，当∠BCD=∠BDC时，设∠ACD=∠A=α，则∠BCD=∠BDC=2α，∠B=180°-4α，∠ACB=3α.分析定量关系：由∠A≤∠B≤∠ACB，则有解得.有趣的是，此时还会发现∠ACB=3∠A，从而可以得到以下结论.结论6：当某三角形同时满足最小角α≤36°，且存在另一个角3α时，只需要过角3α的顶点分割出一个角α，这时原三角形将会被分割成两个等腰三角形.类型2：如图11，当∠ACD=∠ADC时，再锁定△BCD，继续观察做定性分析，易知∠BDC＞∠ACD，即∠BDC＞∠ADC，从而∠BDC＞90°.要使钝角△BCD为等腰三角形，只有一种可能，即∠BCD=∠B.图11图12如图12为调整后的图形，设∠A=α，则∠ACD=.分析定量关系：由∠A≤∠B，则有，解得α≤36°.有趣的是，此时有∠ACB=∠ACD+∠BCD=2∠B+∠B=3∠B，从而可以得到以下结论.结论7：当某三角形同时满足最小角α≤36°，且另两个角之间存在三倍关系时，可以过三倍角（即最大角）的顶点将原三角形分割成两个等腰三角形.6.整合结论为表述方便，可做如下规定：若某三角形有一个内角是另一个内角的二倍，则称此内角为“二倍角”；若某三角形有一个内角是另一个内角的三倍，则称此内角为“三倍角”.整合分析上述7个结论，进而解决以下两个关键性问题.问题1：哪些三角形可以被分割成两个等腰三角形？直角三角形都可以分割成两个等腰三角形（来源于结论4）；对于非直角三角形，只有当其存在二倍角或三倍角时，才有可能被分割成两个等腰三角形，具体如下.（1）当某个非直角三角形存在二倍角时，且其最小角α＜45°时，它可以被分割成两个等腰三角形（来源于结论2与结论5）；（2）当某个非直角三角形存在三倍角时，且其最小角α≤36°时，它可以被分割成两个等腰三角形（来源于结论3、结论6和结论7）.问题2：对于符合上述条件的三角形，如何分割？或者说分割策略有哪些？对于直角三角形，可以沿着斜边的中线，将其分割成两个等腰三角形；而对于非直角三角形，有以下分割策略.（1）最小角不分割，即不能过最小角的顶点分割（来源于结论1）；（2）二倍角不分割（来源于结论2与结论5）；（3）三倍角必分割（来源于结论3、结论6和结论7）.特别说明：（2）和（3）成立的前提是原三角形中有唯一的二倍角或者三倍角. 若该三角形中存在着两个二倍角或者三倍角，可以选择其中一个进行分割即可，其实这样的三角形有且只有两个，其内角分别为36°，72°，72°或，.这里的“收网行动”，充分体现了思维的整合性和灵活性，对于学生能力的要求较高，而且得到的结论是解决相关问题的重要“法宝”.二、实战分析万事俱备，只欠实战.下面笔者略举几例，来体悟上述所得结果在解题中的应用. 例1 如图13，试用一条直线将△ABC分割成两个等腰三角形，其中∠A=40°，∠B=20°.图13简析：首先，该直线必过△ABC的某个顶点，否则会割出一个四边形；其次，此△ABC的最小角∠B=20°＜36°，且∠C=3∠A，∠A=2∠B，即它既存在三倍角，又存在二倍角，故必可分割成两个等腰三角形.最小角不分割，即不能过最小角∠B分割；二倍角不分割，即不能过二倍角∠A分割；三倍角必分割，即必须过三倍角∠C来分割.由此，如图14及图15所示，此题有两种分割方案，问题得解.图14图15例2 给定一张等腰三角形纸片，剪一刀后被分成了两张等腰三角形纸片，求原等腰三角形纸片的各内角的度数.简析：（1）若此等腰三角形为等腰直角三角形，则可以沿着斜边的中线分割成两个等腰三角形.如图16，此时其各内角的度数分别为45°，45°和90°.图16（2）若此等腰三角形为非直角三角形，则其必然含有二倍角或者三倍角，具体可分以下四类.①当其顶角为底角的2倍时，设底角为α，顶角为2α，则有α+α+2α=180°，解得α=45°.此时它依然为等腰直角三角形，与前面重复.②当其底角为顶角的2倍时，设顶角为α，底角为2α，则有2α+2α+α=180°，解得α=36°.此时最小角α＜45°，故可以分割.如图17，其各内角的度数分别为36°，72°和72°，即为黄金三角形.③当其顶角为底角的3倍时，设底角为α，顶角为3α，则有α+α+3α=180°，解得α=36°.此时最小角α=36°，故可以分割.如图18，其各内角的度数分别为36°，36°和108°，仍为黄金三角形.④当其底角为顶角的3倍时，设顶角为α，底角为3α，则有3α+3α+α=180°，解得.此时最小角α＜36°，故可以分割.如图19，其各内角的度数分别为.图17图18图19综上所述：符合条件的等腰三角形有四种，其各内角的度数分别为45°，45°，90°或36°，72°，72°或36°，36°，108°或，问题得解.由实战分析可以看出，本文探索得出的结论对于解决相关的分割问题有极大的作用.但本文最大的价值还是体现在探索数学的乐趣中，这种过程性的享受与收获是笔者更愿意传递的信念与精神.【相关文献】[1]齐欣.融思维于探究[J].初中数学教与学，2016（9）：12-13.[2]郑岱勇.将三角形分割成两等腰三角形问题的教学探讨[J]. 福建基础教育研究，2014（11）：24-25.。

《面积问题之”水平宽、铅锤高“模型的实战分析》

勤奋是一种品质，优秀是一种习惯三角形面积问题之“宽高公式”的实战分析高邮市赞化学校段广猛《三角形面积问题之“宽高公式”的两种证明方法》一文中，主要介绍了三种情形下“宽高公式”模型的证明.1如图1、图2、图3所示，S ABC OC AD ，其中OC表示B、C两点在水平方向2上的距离，简称这个三角形的“水平宽”；而AD表示点A到边BC在竖直方向上的距离，简称这个三角形的“铅锤高”.于是三角形的面积S=水平宽铅锤高，这个公式不妨称为“宽高公式”.细心观察上面三种情形，操作方式都是过点A作平行于y轴的直线交边BC所在的直线于点D，则AD就是“铅锤高”；而B、C两点之间的水平距离，即线段OC就是“水平宽”. 在实际应用中，笔者不建议学生固化思维，强记这里的结论而直接使用.一方面，这个公式课本上并没有直接出现，中考时能不能直接使用值得商榷；另一方面，对于图2的勤奋是一种品质，优秀是一种习惯结论，大部分学生普遍可以接受，但是若是不知道这个公式推导的来龙去脉而强行直接使用，图1及图3的结论，多数学生是很难理解原理而导致不能正确使用.更何况，这三种情形下的推导过程也是相辅相成、思想统一的，都采用了“改斜归正” 及“割补法”的思想，而这两种思想方法又是极其重要的解题原理，需要同学们认真深刻体会的，所以笔者强烈建议学生体会这里的推导原理，以达到灵活使用的目的. 其实，掌握了原理，怎么割补三角形都可以，只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线都可以实现面积处理，仅仅是繁简程度不一而已，下文会一一提及.如图4、图5、图6所示，S ABC BD AE ，其中BD表示点B到边AC在水平方2向上的距离，简称这个三角形的“水平宽”；而AE表示A、C两点在竖直方向上的距离，简称这个三角形的“铅锤高”.于是依然有三角形的面积S=水平宽铅锤高.这三张图的操作方式都是过点B作平行于x轴的直线交边AC所在的直线于点D，则BD 就是“水平宽”；而A、C两点之间的竖直距离，即线段AE就是“铅锤高”.勤奋是一种品质，优秀是一种习惯 S ABC 那么问题来了，割补方式千变万化，而且好像都可行，在解题实战中，难道就随意割补吗？非也！理论上是都可行，但计算量绝不相当！我们知道，“在变化中抓不变量”也是一种重要的思想方法，“以不变应万变”.此时再结合这个解题策略，就可以使计算过程“如履平地”.在三角形三个顶点中，一般情况下会有两个定点和一个动点，抓住这两个定点就是关键所在.如图8或图9所示，点B 和点C 是两个定点，而点A 是一个动点.这时，我们就应实际上，过点 C 作平行于坐标轴的直线，无论是平行于 x 轴，还是平行于 y 轴，最终都可以实现对于此三角形的面积处理，有时是 “ 割 ” ，即 “ 面积加法 ” ；有时是 “ 补 ” ，即 “ 面积减法 ”. 由此可以看出，不用强记公式，只要过三角形的三个顶点中的任意一点作平行于坐标轴的直线，无论是平行于 x 轴，还是平行于 y 轴，都可以实现面积处理 . 图 7 提供了一种方式，12CD AE .勤奋是一种品质，优秀是一种习惯该过动点A作平行于y轴或者平行于x轴的直线交直线BC于点D，利用B、C两个定点求出直线BC的解析式，再设出动点A的坐标，将横坐标或者纵坐标代入直线BC的解析式，表示出点D的坐标，进而容易表示出线段AD.在图9中，S ABC S ACD S ABD = 1 AD CF2 AD BE AD(CF BE) AD(OE BE) AD OB，因为B、C都是定点，故OB是常值，而且直线BC的解析式易求，进而AD的长度好表示.若是你“不信邪”，偏偏如图10所示那样“割补”，我想说“此路依然行得通”，但与前面的两种方法相比，一烦在“水平宽”BD上，需要求出直线AC的解析式，理论上肯定行得通，这条直线的解析式会因为点A是动点而导致含有参数，计算量较大；二烦在“铅锤高”AE上，也是因为点A是动点而导致含有参数.“罪魁祸首”都在动点A上，而“元凶”就是因为一开始过定点B进行了“割补”.需要特别说明的是，这种方法并非是错误的，仅仅是计算量较大些，其操作依然是可行的.下面以2016年苏州中考压轴题第（2）问为例具体谈谈“宽高公式”的使用. （2016•苏州）如图11，直线l：y=-3x+3与x轴、y轴分别相交于A、B两点，抛物线y=ax2﹣2ax+a+4（a＜0）经过点B．（1）求该抛物线的函数表达式；勤奋是一种品质，优秀是一种习惯（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值.对于第（1）小问，易知该抛物线的函数表达式为：y=-x2+2x+3；对于第（2）小问，这是一个“两定一动型”三角形面积问题，“死咬”A、B两定点“不松口”，过动点M作平行于坐标轴的直线进行“割补”即可，这里提供两种方式.方式一：如图12所示，过动点M作平行于y轴的直线交边AB1所在的直线于点N，则S ABM S MNB S MNA=MN OG2MN AG MN(OG AG) MN OA.设M（t，-t2+2t+3），其中 t 的取值范围是 0＜t＜3，则N（t，-3t+3），从而MN= y M y N =（-t2+2t+3）-（-3t+3）=-t2+5t，而OA=1，故S=（-t2+5t）=-t（t-5），当 t=时，S 有最大值为.值得一提的是，上面的操作过程可总结如下：第一步：抓住两个定点A和B，它们之间在水平方向上的距离OA作为△ABM的“水平宽”；第二步：过动点M作平行于y轴的直线交边AB所在的直线于点N，则MN作为△ABM的“铅锤高”；第三步：将面积“往竖直线MN上靠”，通过面积“减法”，S ABM MN OA.得到所求三角形的面积为方式二：如图13所示，过动点M作平行于x轴的直线交边AB所在的直线于点N、交y勤奋是一种品质，优秀是一种习惯 S MNA =1MN BG MN OG 轴于点G ，则S ABM S MNBMN(BG O G ) 2 MN OB .设M （t ，-t 2+2t+3），其中 t 的取值范围是 0＜t ＜3，则 t 22t 2 t 2 2t t 2 5tN （，-t +2t+3），从而MN = x M x N t - = ， 3 3 3 而 OB=3，故 S= 1 t 2 5t 3=-1 t （t-5），当 t= 5 时，S 有23 2 2最大值为 .上面的操作过程可总结如下：第一步：抓住两个定点A 和B ，它们之间在竖直方向上的距离OB 作为△ABM 的“铅锤高”；第二步：过动点M 作平行于x 轴的直线交边AB 所在的直线于点N ，则MN 作为△ABM 的“水平宽”；第三步：将面积“往水平线MN 上靠”，通过面积“加法”，得到所求三角形的面积为 S ABM MN OB .至此，这个“两定两动型”三角形面积问题，利用“宽高公式”得到了比较完美的解答.当然，关于面积处理，绝不仅仅只有“宽高公式”，还有很多其他的路可走，如“框图法”（亦可称“矩形大法”）、其他的割补法（如上题中连接OM 也是一种很好的分割处理手段）等等，但大多体现出来的思想方法都是“大同小异”的，即想方设法将所求“斜面积”“改斜归正”，使问题得以解决.后面若有机会，会专门成文，敬请期待！通过前面的《模型证明》及本文的《实战分析》，笔者认为根本不用记忆所谓的“宽高公式”，只要在处理面积的问题中，狠抓不动点不放手，过动点作平行于坐标轴的直线交这不动边所在的直线于一点，将三角形的面积进行“割”或“补”，即面积“加”或“减”，然后平移其中一条高线，即可转化为高线的“加”或“减”，就能够得出所谓的“宽高公式”！这道苏州中考真题中有一个限制条件“点M 在第一象限内”，很明显是为了简化起见. 若是将这个条件去掉，即“点M 是抛物线上任意一动点”，那么△ABM 的面积为S 关于m 的函数表达式又如何求解呢？我想其他的方法就未必恰当了，这时“宽高法”的作用会更明显.图14及图15给出了两种情形，前者可看出此时方法过程跟原题一模一样；而后者可看出唯一的区别就是点N 位于了点M 的上方，此时MN= y N y M ，其他都没变化勤奋是一种品质，优秀是一种习惯也就是这时候要分类了，分类的标准就是M、N“谁高谁低”，可分三类，也可分两类. 甚至于，结合本人作品《巧用绝对值避开“繁琐的”分类讨论》一文，直接借用“绝对值”，将MN表示为 y M y N 即可，最后解一个含绝对值的方程就可以了，在此不再一一赘述，有兴趣的同学可自行展开.同学们，研究之窗已向你们打开，还有什么道理不去认真钻研、琢磨呢！加油，中考必胜！最后来首打油诗结束本文，“横切竖切都可以，切法不一莫强求；关键抓住不动点，最好沿着动点切；切完之后即加减，加减之后即宽高！”。

关注图形结构衍生通性通法--对一道“倍半角”问题的再思考

关注图形结构衍生通性通法--对一道“倍半角”问题的再思
考
段广猛
【期刊名称】《中国数学教育:初中版》
【年(卷),期】2022()11
【摘要】通过对一道“倍半角”问题的再思考,从图形结构特征分析,触发广泛联想,衍生相应的解题策略,突出通性通法,利用特殊化与一般化的研究路径,发挥教学机智,放眼长线发展,锤炼思维品质.
【总页数】6页(P59-64)
【作者】段广猛
【作者单位】江苏省苏州工业园区星湾学校
【正文语种】中文
【中图分类】G63
【相关文献】
1.渗透分类讨论注重通性通法r——对一节复习课的再思考
2.立足通性通法,兼顾巧解巧法——对一道公开课例题的解法分析与拓展
3.埋点布线构架体系关注通性通法——一次函数图像⑵教后设计及思考
4.渗透分类讨论注重通性通法——对一节复习课的再思考
5.关注通性通法适当灵活处理-——从一道向量问题看解题方法的发现与运用
因版权原因，仅展示原文概要，查看原文内容请购买。

三角形面积公式——之水平宽铅垂高

）之间的距离.2CH+（适合八年级）如图，已知边长为解析：不妨以B为原点，BC为x轴，BA为y轴建立平面直角坐标系，则点C坐标为（a，0），点D坐标为（a，a），∵E 为AD 的中点，∴点E 坐标为（12a ，a ）， ∵P 为CE 的中点，∴点P 坐标为（34a ，12a ），∵F 为BP 的中点，∴点F 坐标为（38a ，14a ）.过F 点作BC 的垂线交BD 于点G ，则点G 的横坐标为38a ，又直线BD 的解析式为y x =，∴点G 的纵坐标为38a ，∴△BDF 的铅垂高FG ＝38a －14a ＝18a ，∴S △BDF ＝2111122816BC FG a a a ==.公式应用2——左右垂线例2（适合八年级）如图，直线1y x =+与x 轴，y 轴分别交于点A ，B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，且∠BAC =90°.如果在第二象限内有一点P 1,2a ⎛⎫⎪⎝⎭，且△ABP 的面积与Rt △ABC 的面积相等，求a值.说明：本题常见解法有三，一是连结OP ，△的面积＝△AOB 面积+△BOP 面积－△AOP 积，然后用a 的代数式表示，与Rt △ABC 相等列方程求解；二是将点C 沿AB 翻折到C ’位置，则△ABC △ABC ’面积相等，若△ABP 的面积与Rt △ABC 相等，则可得PC ’//AB ，因此，可以由点A ，C 求C ’坐标，再根据AB 的斜率与点C ’的解析式，将点P 纵坐标代入，即可求a 的值三是考虑水平宽铅垂高公式来计算，但如果从A ，B ，P 三点向x 轴作垂线，较为复杂，不妨换个角度应用公式，即从A ，B ，P 向y 轴作垂线（即左右方向作垂线）解析：过线，则OB 而PE 度）由AB ＝3，OB ＝1，而P 的纵坐标为12，所以E 为AB 的中点，所以PE ＝-a +32，从而有11322122a ⎛⎫⨯⨯=⨯⨯-+ ⎪ ⎪⎝⎭ ，解得34a =-. 公式应用3——内外垂线从例2可以看到，三条垂线不一定作向x 轴，也可以作向y 轴，仿公式用即可.一般地，水平宽取的是最外的两条直线的距离，但这个做法不是绝对的，有12EF CG . 简单推导：S △ABC ＝S △ACG －S △BCG ＝1122CG EH CG FH -＝12EF CG . 说明：当取相邻两条垂线距离为水平宽时，第三条垂线将与第三边（AB ）的延长线相交，此时顶点（C ）到交点（G ）的距离为铅垂高（CG ）. 例3（适合九年级）如图所示，直线l ：y =3x +3与x 轴交于点A ，与y 轴交于点B ．把△AOB 沿y翻折，点A 落到点C ，抛物线过点B ，C 和D （3，0）．（1）求直线BD 和抛物线的解析式．（2）若BD 与抛物线的对称轴交于点M ，点N 在坐标轴上，以点N ，B ，D 为顶点的三角形与△MCD 相似，求所有满足条件的点N 的坐标．（3）在抛物线上是否存在点P ，使S △PBD =6？若存在，求出点P 的坐标；若不存在，说明理由．（4）点Q若存在，请直接写出点Q 解析：本题只解（3），由已知条件可以得抛物线解析式为243y x x =-+，BD 解析式为3y x =-+，由于问题中并未交待P 点在BD 的上方或下方，故要分类讨论：当P 在BD 下方时，如右上图，水平宽为OD ＝3，铅垂高为PE ＝224333x x x x x -++-=-；当P 在BD 上方时，P 可能在左，也可以在右，但两者本质相同，如右下图，此时依然取OD ＝3为水平宽，则铅垂高PE ＝223433x x x x x -+-+-=-+.两种情况合起来就是213362x x ⨯⨯-=，即234x x -=±.当234x x -=-时，方程无实数根，即P 在BD 下方时，不可能面积为6；当234x x -=时，解得121,4x x =-=，即当P （－1，8）或P （4，3）时，S △PBD =6.解后：从以上几例可以看到，形面积问题，尤其是在例3，可以将P对值）问题求解，可以有效回避原本点P在BD上方时，几何法要构造高等繁杂作法，使得问题解决简洁而快捷.。