电路分析基础下册习题课

合集下载

《电路分析基础》习题参考答案

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) SOW; (2) 300 V、25V,200V、75V; (3) R=12.50, R3=1000, R4=37.5021-2 V =8.S V, V =8.S V, V =0.S V, V =-12V, V =-19V, V =21.S V U =8V, U =12.5,A mB D 'AB B CU =-27.S VDA1-3 Li=204 V, E=205 V1-4 (1) V A=lOO V ,V=99V ,V c=97V ,V0=7V ,V E=S V ,V F=l V ,U A F=99V ,U c E=92V ,U8E=94V,8U BF=98V, u cA=-3 V; (2) V c=90V, V B=92V, V A=93V, V E=-2V, V F=-6V, V G=-7V, U A F=99V, u c E=92V, U B E=94V, U BF=98V, U C A =-3 V1-5 R=806.70, 1=0.27A1-6 1=4A ,11 =llA ,l2=19A1-7 (a) U=6V, (b) U=24 V, (c) R=SO, (d) 1=23.SA1-8 (1) i6=-1A; (2) u4=10V ,u6=3 V; (3) Pl =-2W发出，P2=6W吸收，P3=16W吸收，P4=-lOW发出，PS=-7W发出，PG=-3W发出1-9 l=lA, U5=134V, R=7.801-10 S断开：UAB=-4.SV, UA0=-12V, UB0=-7.2V; S闭合：12 V, 12 V, 0 V1-12 UAB=llV / 12=0.SA / 13=4.SA / R3=2.401-13 R1 =19.88k0, R2=20 kO1-14 RPl=11.110, RP2=1000第2章习题参考答案2-1 2.40, SA2-2 (1) 4V ,2V ,1 V; (2) 40mA ,20mA ,lOmA 2-3 1.50 ,2A ,1/3A2-4 60 I 3602-5 2A, lA2-6 lA2-7 2A2-8 lOA2-9 l1=1.4A, l2=1.6A, l3=0.2A2-10 11=OA I l2=-3A I p l =OW I P2=-l8W2-11 11 =-lA, l2=-2A I E3=10V2-12 11=6A, l2=-3A I l3=3A2-13 11 =2A, l2=1A ,l3=1A ,14 =2A, l5=1A2-14 URL =30V I 11=2.SA I l2=-35A I I L =7.SA2-15 U ab=6V, 11=1.SA, 12=-lA, 13=0.SA2-16 11 =6A, l2=-3A I l3=3A2-17 1=4/SA, l2=-3/4A ,l3=2A ,14=31/20A ,l5=-11/4A12-18 1=0.SA I l2=-0.25A12-19 l=1A32-20 1=-lA52-21 (1) l=0A, U ab=O V; (2) l5=1A, U ab=llV。

电路分析基础习题及答案

电路分析基础习题及答案电路分析是电气工程中非常重要的一门课程，它研究的是电路中电流、电压、功率等基本参数的计算和分析。

通过习题的练习，可以帮助学生更好地掌握电路分析的基础知识和解题方法。

本文将介绍一些电路分析的基础习题及其答案，希望对读者有所帮助。

1. 串联电阻电路假设有一个由三个电阻串联而成的电路，电阻值分别为R1、R2和R3。

求整个电路的总电阻。

解答：串联电路中，电流只有一条路径可以流通，所以电流在每个电阻上的大小是相等的。

根据欧姆定律，我们可以得到以下等式：U = I * R1U = I * R2U = I * R3其中U表示电压，I表示电流。

将这三个等式相加，可以得到总电阻的表达式：U = I * (R1 + R2 + R3)所以，总电阻为R1 + R2 + R3。

2. 并联电容电路假设有一个由两个电容并联而成的电路，电容值分别为C1和C2。

求整个电路的总电容。

解答：并联电路中，电压在每个电容上的大小是相等的。

根据电容器的充放电特性，我们可以得到以下等式：Q = C1 * UQ = C2 * U其中Q表示电容器上的电荷量，U表示电压。

将这两个等式相加，可以得到总电容的表达式：Q = (C1 + C2) * U所以，总电容为C1 + C2。

3. 交流电路中的电阻假设有一个由电阻R和电感L串联而成的交流电路，电源的电压为U，频率为f。

求电路中的电流大小。

解答：交流电路中，电流和电压的关系可以用欧姆定律和电感器的阻抗来表示。

电感器的阻抗公式为：Z = 2πfL其中Z表示电感器的阻抗，f表示频率，L表示电感。

根据欧姆定律，我们可以得到以下等式：U = I * (R + Z)将Z的表达式代入上式，可以得到：U = I * (R + 2πfL)所以，电流的大小为I = U / (R + 2πfL)。

通过以上习题的分析与解答，我们可以看到电路分析基础习题的解题思路和方法。

在实际应用中，电路分析是电气工程师必备的技能之一。

电路分析基础第四版课后习题第四章第五章第六章答案

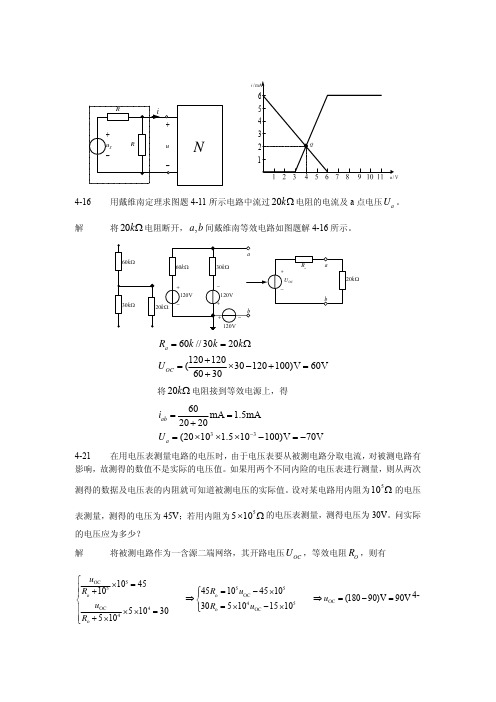
/i4-16 用戴维南定理求图题4-11所示电路中流过20k Ω电阻的电流及a 点电压。

a U 解将电阻断开，间戴维南等效电路如图题解4-16所示。

20k Ω,a bk Ω60//3020120120(30120100)V 60V6030a OCR k k k U ==Ω+=×−+=+ 将电阻接到等效电源上，得20k Ω3360mA 1.5mA2020(2010 1.510100)V 70V ab a i U −==+=×××−=− 4-21 在用电压表测量电路的电压时，由于电压表要从被测电路分取电流，对被测电路有影响，故测得的数值不是实际的电压值。

如果用两个不同内险的电压表进行测量，则从两次测得的数据及电压表的内阻就可知道被测电压的实际值。

设对某电路用内阻为的电压表测量，测得的电压为45V ；若用内阻为510Ω5510×Ω的电压表测量，测得电压为30V 。

问实际的电压应为多少？解将被测电路作为一含源二端网络，其开路电压，等效电阻OC U O R ，则有5OC 555o o OC OC 454OCo OC 4o 10451045104510(18090)V 90V 30510151051030510u R R u u u R u R ⎧×=⎪⎧+=−×⎪⎪⇒⇒=⎨⎨=×−×⎪⎪⎩××=⎪+×⎩−=4-28 求图题4-20所示电路的诺顿等效电路。

已知：12315,5,10,R R R =Ω=Ω=Ω。

10V,1A S S u i ==解对图题4-20所示电路，画出求短路电流和等效内阻的电路，如下图所示SC i对左图，因ab 间短路，故0,0i i α==，10A 0.5A 155SC i ==+ 对右图，由外加电源法，106ab R α=Ω− 4-30 电路如图题4-22所示。

电路分析基础第四版课后习题答案

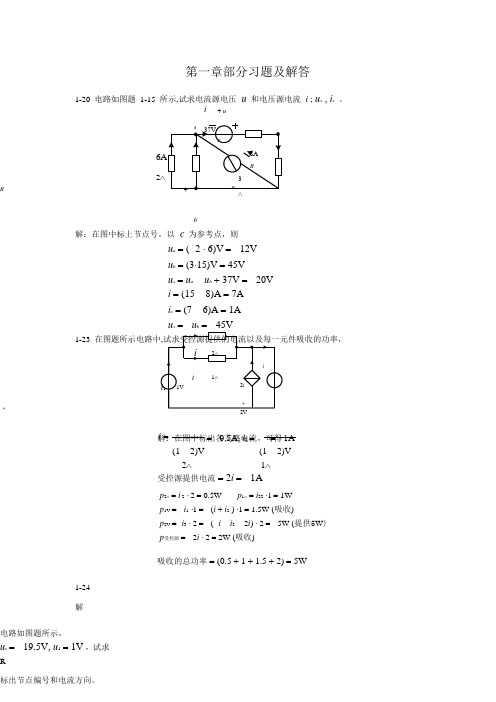
i = = 0.5A, i 2 = =1A 第一章部分习题及解答1-20 电路如图题 1-15 所示,试求电流源电压 u 和电压源电流 i ; u x , i x 。

i+ u2Rb解：在图中标上节点号，以 c 为参考点，则u a = ( 2 ⋅ 6)V = 12V u b = (3⋅15)V = 45V u x = u a u b + 37V = 20V i = (15 8)A = 7A i x = (7 6)A = 1A x b 1-23+解：在图中标出各支路电流，可得(1 2)V (1 2)V 2∧ 1∧受控源提供电流 = 2i = 1Ap 2∧ = i 2 ⋅ 2 = 0.5Wp 1∧ = i 22 ⋅1 = 1Wp 1V = i 1 ⋅1 = (i + i 2 ) ⋅1 = 1.5W (吸收)p 2V = i 3 ⋅ 2 = ( i i 2 2i ) ⋅ 2 = 5W (提供5W ) p 受控源 = 2i ⋅ 2 = 2W (吸收)吸收的总功率 = (0.5 + 1 + 1.5 + 2) = 5W1-24 解电路如图题所示，u s = 19.5V, u 1 = 1V ，试求R标出节点编号和电流方向。

ai +3∧u∧b+ui2∧4∧i+10ucRiiei1 =u11= 1A, u bc = u1 10u1 = 9Vu bc2u ab = i s ⋅ 3 = 10.5Vu ce = u cb + u ba + u s = (9 + 10.5 19.5) = 0V为确定R，需计算i4，u ce = u cd + u de = 0 ® u de = u cd = 10u1 = 10V故1-33 试用支路电流法求解图题所示电路中的支路电流i1, i2 , i3。

a 1∧ci+6Vb解求解三个未知量需要三个独立方程。

由KCL可得其中之一，即i1 + i2 + i3 = 5对不含电流源的两个网孔，列写KVL方程，得网孔badb网孔bdacb2i1 3i2 + 8 = 08 + 3i2 i3 + 6 = 0i 2 = = 4.5A, i s = i 1 + i 2 = 3.5Ai 3 = = 2.5A, i 4 = i s i 3 = ( 3.5 + 2.5)A = 1A整理得： ♦ 2i 1 2 = 8+ 3i ® ♦i 2 = 2A♥♥♣i 1 + i 2 + i 3 = 5 ♣i 1 = 1A ♠ ♠♠3i 2 i 3 = 2 ♠i 3 = 4A♦ i1 + 8i2 3i3 = 9 ® ♦i2 = 1A♥i3 = 1A® ♦♠(R +R)i M2 R1i M 1 R2i M 3 =u ♠♠♠==0♣i M 1 = 24 u® ♦(3 + 4)i M 3 = u ® ♦ ♥i M 3 i M 1 = 8♥ 第二章部分习题及解答2-1试用网孔电流法求图题所示电路中的电流i和电压u ab。

《电路分析基础》课程练习题及答案

电路分析基础第一章一、1、电路如图所示，其中电流为答( A )A 0.6 A B. 0.4 A C. 3.6 A D. 2.4 A2、电路如图示, 应为答( C )A. 0 VB. -16 VC. 0 VD. 4 V3、电路如图所示, 若、、均大于零，, 则电路的功率情况为答( B )A. 电阻吸收功率, 电压源与电流源供出功率B. 电阻与电流源吸收功率, 电压源供出功率C. 电阻与电压源吸收功率, 电流源供出功率D. 电阻吸收功率，供出功率无法确定UI S二、 1、图示电路中, 欲使支路电压之比，试确定电流源之值。

I SU解：由KCL 定律得：22328222U U U ++=V由KCL 定律得：0422=++U I U S1160-=S I A 或-5.46 A 2、用叠加定理求解图示电路中支路电流，可得：2 A 电流源单独作用时，2/3A;4 A 电流源单独作用时,-2A, 则两电源共同作用时-4/3A 。

3、图示电路ab端的戴维南等效电阻 4 ；开路电压22 V。

解：U=2*1=2 I=U+3U=8A Uab=U+2*I+4=22V Ro=4第二章一、1、图示电路中，7 V电压源吸收功率为答( C )A. 14 WB. -7 WC. -14 WD. 7 W2、图示电路在时开关闭合，时为答(D )精品文档A. B.C. D.3、图示桥式电路中,已知，欲使图中u=0，应满足的条件为答( A )A. B.C. D.二、1、试用叠加定理求图示电路中的电压。

4Ω解：4Ω电路可分为图1和图2单独作用图1U 1=-3v图2U 2=- 249+ ×（4×4）=-3V U=U 1+U 2=-6v 2、图示电路在换路前已达稳态。

当时开关断开，求的。

100u C解：Uc(0)=100vUc(∞)=40150×20=75v 10RC ==τUc （t ）=75+25ｅ-0.1t3、求：示网络ab 二端间的戴维南等效电路。

电路分析基础第四版课后习题第一章第二章第三章第四章答案

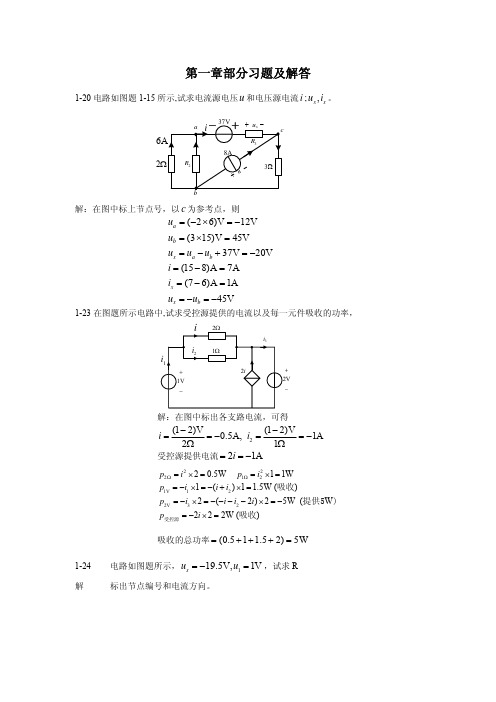
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ，列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示，试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向，
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2

《电路分析基础》习题及答案

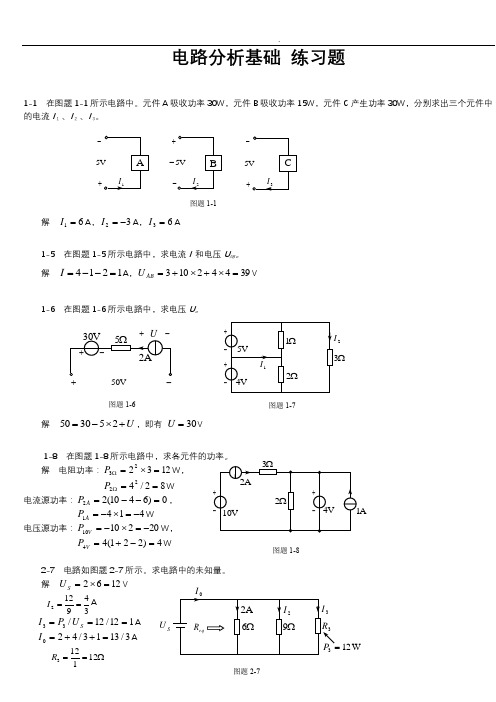
电路分析基础练习题1-1 在图题1-1所示电路中。

元件A 吸收功率30W ，元件B 吸收功率15W ，元件C 产生功率30W ，分别求出三个元件中的电流I 1 、I 2 、I 3。

解 61=I A ，32-=I A ，63=I A1-5 在图题1-5所示电路中，求电流I 和电压U AB 。

解 1214=--=I A ，39442103=⨯+⨯+=AB U V1-6 在图题1-6所示电路中，求电压U 。

解 U +⨯-=253050，即有 30=U V1-8 在图题1-8所示电路中，求各元件的功率。

解电阻功率：123223=⨯=ΩP W ，82/422==ΩP W电流源功率：0)6410(22=--=A P ，4141-=⨯-=A P W电压源功率：2021010-=⨯-=V P W ，4)221(44=-+=V P W2-7 电路如图题2-7所示。

求电路中的未知量。

解 1262=⨯=S U V349122==I A112/12/33===S U P I A3/1313/420=++=I AΩ==121123RΩ32-+-+V50A3U 3W123=PΩ===13363/13120I U R S eq2-9 电路如图题2-9所示。

求电路中的电流1I 。

解从图中可知，2Ω与3Ω并联，由分流公式，得1123553I I I =⨯=1113==I A所以，有131321+=+=I I I I 解得 5.01-=I A2-8 电路如图题2-8所示。

已知213I I =，求电路中的电阻R 。

解 KCL ：6021=+I I 213I I = 解得 451=I mA, 152=I mA. R 为6.615452.2=⨯=R k Ω解 (a)由于有短路线，Ω=6AB R , (b) 等效电阻为Ω=+=++=1.15.25.15.01//)1//11(1//1AB R2-12 电路如图题2-12所示。

电路分析基础(张永瑞)第三版-课后习题答案

Vc、Vd
Vd 6V，Va U oc
1 1 1 1 1 ( ) U V 6 0 oc c 3 4 12 3 12 1 U ( 1 1 )V 1 6 12 oc c 3 3 3 3
2U oc Vc 1.5 U oc 2Vc 42
10 4 7 A 11 2 2 3 1 A 3 6 3
画出戴维南等效电源接上电阻
R0 (1 1) // 2 3 // 6 3
U ab
当
Rx 6 Rx U oc R0 Rz 3 Rx
Rx 3 时，电压 U ab
9
时，电压
63 3V 33
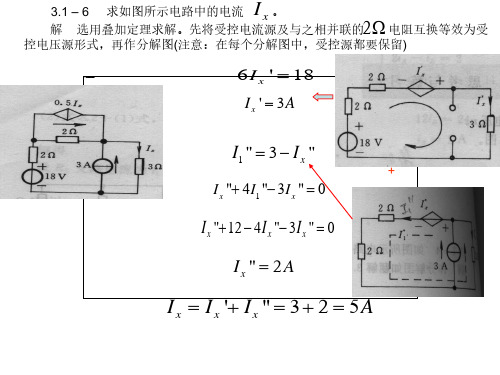
3.1 – 6 求如图所示电路中的电流 x。解选用叠加定理求解。先将受控电流源及与之相并联的2 电阻互换等效为受控电压源形式，再作分解图(注意：在每个分解图中，受控源都要保留)
I
6 I x ' 18
即解得
Ix ' 3A
I1 " 3 I x "
+
所以
I x " 4 I1 " 3I x " 0
所以等效电源内阻
R0
由最大功率传输定理可知，当
U 10 I
(b)
外加电源法求R0
RL R0 10
时其上可获得最大功率。此时
pL max
2 U oc 40 2 40W 4 R0 4 10
Vd 6 I1 0.5 A 12 12 Vc 21 I2 7A 3 3
由KCL求得
I sc I1 I 2 0.5 7 7.5 A
R0 U oc 15 2 I sc 7.5

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

有效值关系
波形图表示 U U I i Z Z 相量分析 I I I
1 2
U U U
1
2
相量图表示法
U I Z
U L UC arctan UR
Z R j ( X L X C ) Z
Z R 2 ( X L X C )2
2
2 2 Q UI sin I X I 无功功率(var) m Lm n X Cn
功 P Q Q 率复功率(VA) ~ * S UI 关 ZL= Zi* 最大功率传递定理系
2 i L C
视在功率(VA) S UI
P2 Q2
_
I 2
I3
jXL
R2
90 0
U R1 U C
45 0
I 1
U L
解用相量图分析 I I 10 2 101350 10450 I 10 A I 1 2 3 1 U U 200 5 10 U U 150V U

1 1 1 UN2 ( )U N 3 I S 6 jL4 jL4 R5

4.

图示电路， I 2 10 A、I 3 10 2 A、U 200V、R1 5、 R2 X L , 求：I1、X C、X L、R2。
+ U _
I1 R 1 + I 2 jX C UC
C2 25F
a
+
u
30 d
_ L2 10mH
iL2 C2 25F
b
解：
+
u
_ b
(1) u0=30V作用于电路，L1、 L2 短路， C1 、 C2开路。
L1 iC10 i0 a + C1 u0 30 c d L2
iL20
C2 _ b
i0= iL20 = u0/R =30/30=1A, iC10=0, uad0= ucb0 = u0 =30V (2) u1=120cos1000t V作用
7.07V ，电流有效值 I=________. 0.5A (b)电压有效值U=_______
i
60 (c)电压、电流间相位差 u– i =_________.

容性负载, |Z|=_________, 14.14 (d)该负载是______ =_________. 60 比较相位必须把正弦量化为标准正弦量的形式: 1 1 i (t ) cos(400 π t 150 180 ) cos(400 π t 30 ) 2 2 1 1 sin( 400 π t 30 90 ) sin( 400 π t 120 ) A 2 2 = u– i=60º –120º = –60º
I I I A AB CA I I I B BC AB
I I I C CA BC
P PAB PBC PCA
第八至十章（三）非正弦周期电流的电路
非正弦周期电流分析方法电路
基本概念：非正弦周期函数分解（直流分量、基波、高次谐波），平均值，有效值，平均功率电路的分解各次谐波电路的计算
i + u R L C
－
三相电路习题 1.三相对称电源线电压Ul=380V，对称负载阻抗 Z 10 ，若接成Y形，则线电流Il= 22 A，若接成Δ形，则线电流Il= 66 A。 2.三相四线制电路中，中性线的作用是（b ） a.使电源线电压对称 b.使不对称负载相电压对称 c.使不对称负载功率对称 d.使不对称负载电流对称
)
iR
－
2.
π 已知 : u 30 120cos1000t 60cos(2000t ) V. 4
L1 A1
C1 40mH A2 25F V1 L1 40mH i C1 i a C1 25F c c
求图示电路中各表读数(有效值)及电路吸收的功率。
30 d L2
V2
10mH A3
R1 C C C
U R2
I 3
U U U 2U 2 U U 75 2 U C R2 L C R2 R2 L
150 XC 15 10
75 2 R2 X L 7.5 10 2
5. 图示电路中,已知 X L X C R 2Ω 电流表A1的读数为3A,

3.
i1 + us1 –
is6
电路如图所示，试列写其相量形式的回路电流方程和节点电压方程。
L4 i2 R5
C2
C3 i3
回路法：
I 1 I S6
I 2 I S3

is3

1 1 ( j j L4 R5 ) I 3 ( j j L4 ) I 1 C2 C2
试问(1)A2和A3的读数为多少?
(2)并联等效阻抗Z为多少?
+
A1
A2
A3
U
-
L
R
C
6. R、L、C 串联电路的电感 L 增至原来的 4 倍时，谐振频率与原谐振频率之比为 ( C )。 (a) 4 (b) 2
1 (c) 2
7.在图示 RLC 并联正弦交流电路中，各支路电流有效值 I1＝I2＝I3＝1 A，当电压频率增加一倍而保持其有效值不变时， ) 各电流有效值应变为 ( 。 C (a) I 1＝2 A I 2＝2 A I 3＝2 A (b) I 1＝1 A I 2＝2 A I 3＝0.5 A (c) I 1＝1 A I 2＝0.5 A I 3＝2 A
+ . u i1 R i2 L i3 C
－
8.图示电路在频率 f = 1000 Hz 时发生谐振，且谐振时电流有效值I=0.2A ， XC = -314 ，电容上的电压为外加电压的 20 倍。 (1)求 R，L； (2) 若将频率 f 变为 500 Hz 而 R，L，C 及电源电压有效值不变，求电流 I，此时电路呈何性质？
R RI U
1 2 W Li 2
jL I U L
du 电容 i C dt
1 W Cu 2 2
jCU I C
纯电阻电路
电路结构式单一参数电路纯电感电路纯电容电路 R、L、C串联电路 G、C、L并联电路
三角函数表示
瞬时值关系
电压— 电流关系（大相量关系小相位）
( j L4 R5 ) I 2 U S1

is6
节点法：
U N1
+ us1 –
U N2
C2
C3பைடு நூலகம்
L4
U N3
R5
is3
U U N1 S1

1 1 jC 2U N 1 ( jC 2 )U N 2 U N 3 IS3 jL4 jL4
l p
四线制
Y形接法
负载三线制
Δ形接法
3U 30 ,I 对称， 0, P 3U I cos U 对称： I l p p N l l
四线制
3U 30 U l p
I A I B I C
不对称
相电压对称，相电流不对称
P PA PB P C
=0 o 初相位ψ，相位(ωt+ψ)，反相 =±180
同相
相位差

超前 > 0 滞后
<0
正弦交流电的表示方法
三角函数表示法波形图表示法
i I m sint
I 相量表示法 I
相量图表示法
正弦交流电路元件
电阻电感
u=iR
di uL dt
非正弦周期信号电路习题 A 1.图示电路中，电流 i1 (3 5sin t) i2 (3sin t 2sin3 t) A
则1 电阻两端电压 uR 的有效值为 ( a (a) (b) 30 V 13 V (c) 5 V
i1 L C R + uR i2
叠加
总有效值及平均功率的计算
1.
交流电路习题左图电路中，已知： + u( t ) 10sin( 400 π t 60 ) V u Z Z φ 1 i ( t ) cos( 400 π t 150 )A – 2 0.005s 400 rad/s , 频率 f=_____ 200Hz, 周期 T=_______. (a)电源电压角频率 =_________
2
ZL= RL + jXL可任意改变
Pmax
2 U oc 4 Ri
|ZL|可改变，不变
Pmax
|ZL| = |Zi| 2 cos U oc 2 | Z i | 2( Ri cos X i sin )
RC电路的电路的频频率特性
低通滤波电路
高通滤波电路串联谐振：条件，特点，应用并联谐振：条件，特点，应用
2.指出下列结果是否正确,若有错,试将其改正。
1. +
U –

I

j L + UL –

U (1) I R jω L
U ( 2) I R 2 (ω L)2
+ R UR –

(3) u uR uL
2 2 2 (5) U m UL UR