天然河道水面线试算简化方法_孙道宗
天然河道水面线计算的改进方法

天然河道水面线计算的一种改进方法发表日期:2008-03-14作者:文峰竹来源:水工网评论1条本文章系网络收集转载,不代表本站观点,如果有谬误或者任何侵犯权益的地方,请联系QQ 31184摘要:天然河道水面线的推算是水力学的经典问题,对于河道防洪、水库淹没有极其重要的意义。
在大量采用电算后,程序算法选取的欠妥时会导致计算成果与实际情况不相符合。
本文就天然水面线计算的基本公式出发,对常用的自下而上推算天然河道水面线的电算程序算法选择进行探讨,提出一种可行的预报—校正计算公式。
1、问题的由来天然河道水面线的推算是水力学的经典问题,对于河道防洪、水库淹没有极其重要的意义。
自上个世纪末以来,由于计算机的大量普及,天然河道水面线逐步由人工手算演变成程序电算,极大地提高了设计效率,把设计人员从繁琐、枯燥的数字计算中解放出来。
但在计算程序算法选取欠妥也会出现一些问题,造成计算成果与实际情况产生了较大的出入,尤其是在坡降较陡的山区河道,有些程序(例如原PC1500程序集中的水面线计算程序)计算的水面线非常低,与实际情况相去甚远。
本文就天然水面线计算的基本公式出发,对常用的自下而上推算天然河道水面线的电算程序算法选择进行探讨,提出一种可行的电算方法。
2、天然河道水面线基本方程的分析天然河道水面线计算在水利工程中均采用能量法,基本方程为:z1 +=z2 +++ ()…………①式中:Z1—上游断面的水位;Z2—下游断面的水位;v1—上游断面的流速;v2—下游断面的流速;α1—上游断面的动能校正系数;α2—下游断面的动能校正系数;—河道平均局部阻力系数;Δs—河段的长度;—河道平均流量;K—流量模数;将①式写成:z1 ++ -=z2 ++ …………②式中,对于从下游向上游推算情况,式右边项均为已知项,为定值。
令:f(z1)= z1 +()-…………③其中:=(K+ K)=(R+ R)对③式,当z1→z0(河床高程),、R→0,→R(定值),→定值,()→+∞,故f(z1)→+∞,即z1→z0为③式的一条渐近线;当z1→+∞,、R→+∞,→+∞,→0,()→0,即f(z1)= z1为③式的一条渐近线。
天然河道水面线计算的几种方法探讨

天然河道水面线计算的几种方法探讨摘要:介绍了明渠恒定均匀流法、天然河道水面线系统、HEC-RAS软件及SOBEK软件4种常用的水面线推算方法,并对不同河道进行了水面线推算,然后对计算结果进行了对比分析。
结果表明:对于坡度较小且沿程顺直、断面规整的河道,若下游起始水位对上游河道水位影响较小,则可用明渠恒定均匀流法进行水面线推算;若下游起始水位对上游河道水位影响较大,则可采用天然河道水面线系统进行水面线推算;对于断面不规整的缓流河道,水位推算结果大体呈天然河道水面线系统、HEC-RAS软件、SOBEK软件的趋势;对于急流河道,HEC-RAS软件推算的水位比SOBEK软件推算的水位偏高。
关键词:明渠恒定均匀流法;天然河道水面线系统;HEC-RAS软件;SOBEK 软件;水面线推算Abstract: nullah constant uniform flow method, four kinds of water lines in the natural channel surface line system, HEC-RAS software and SOBEK software projection methods, and different river water surface line projections, then the calculation results of the comparative analysis. The results show that: if the downstream starting water level on the upstream river water level downstream starting water level For a slope smaller and straight along regular cross-section of the river, upstream water level of rivers, the available the nullah constant uniform flow method, the water line projections; greater impact, you can use the natural channel surface line system for the water line projections; sectional irregular slow flow of the river, the water level projection results in a substantially natural channel surface line> HEC-RAS software> SOBEK software trend; rapids river HEC-RAS software projected water level than SOBEK software projected high water level.Keywords: nullah constant uniform flow method; natural channel surface line system; HEC-RAS software; SOBEK software; surface line projections前言水面线推算是河道整治的基础工作,其推算结果直接影响到河道断面的规划设计,进而影响到河道整治的工程量和工程造价。
01第一章--天然河道水面线推算

第一章天然河道水面线推算百图软件既可以处理一个糙率的单式断面天然河道,又可以处理二个或任意多个糙率的复式断面天然河道,也可以处理河道某处出现江心洲或分叉情况,还可以处理整条河道上,支流汇入或流出、过桥水头跌差等情况。
缓坡河道应从下游向上游推算,根据经验及《水力学》教材的介绍,当最下游断面的起始水位无法确定时,可用该断面附近的正常水深对应的水位作为起始水位。
陡坡河道应从上游向下游推算,根据经验,当最上游断面的起始水位无法确定时,可用该断面的临界水深或略小于临界水深对应的水位作为起始水位。
实际工程中,一条长距离的河道可能是缓、陡坡交替变化的情况,此时应先画出河底的纵断面图。
根据纵断面图,当人工能够分辨出缓、陡坡的分界点,可人工划分成单一的缓坡或陡坡分别进行推算。
当人工不能够分辨出缓、陡坡的分界点时,可假定该整条河道为缓坡,选择整条河道从下游向上游推算,若软件一直能进行推算,说明该段为缓坡;若软件不能进行推算,说明该段为陡坡。
软件运行终止的断面,即为缓、陡坡的分界点,按此方法判断出整条河道上的所有缓、陡坡的分界点,把整条河道划分成单一的缓坡或陡坡分别进行推算。
第一节 一个糙率天然河道水面线推算一、现状天然河道水面线推算根据下式,即华东水利学院编《水力学》(1999年版)式9.9,采用分段试算法,精确推算水位。
第一步、准备现状横断面数据文件数据文件为txt 格式,在excel 中整理数据时必须另存为文本文件(制表符分隔)类型的txt 文件。
原始横断面测量成果表的内容格式如下:横断测量成果表中,桩号允许带“+”或“-”,但不允许有其它非数字文本,程序通过加减号来识别桩号。
起点距即是累距,零点桩的起点距为0。
每个点的数据占一行,包括“起点距”、“高程”和“点注释”三项,中间用空⎪⎪ ⎭⎫⎝ ⎛ - + ∆ ++= + g v g v K lQ gv z gv z2 2 2 2 2 1 2 222 222211ξ α α格隔开,空格多少不受限制,其中“点注释”可以省略。
浅谈天然河道水面线推算要点及改进方法.doc

浅谈天然河道水面线推算要点及改进方法摘要:天然河道水面线推算是河道整治与建设工作的基础,是江河堤防工程设计的重要依据,在堤防工程建设和整治中发挥着重要的作用。
本文通过对天然河道水面线的推算的要点进行分析,并对水面线推算方法及改进进行探讨,以作实践参考。
关键词:天然河道;水面线推算;问题分析水面线推算是天然河道治理防洪规划和水利工程建设中的一个重要的工作内容,水面线推算的合理性和科学性对水利工程的效益产生直接影响。
然而,由于河道断面的不规则,河底坡降的不断变化,尤其是天然河道的水面线计算,是比较复杂的。
天然河道的水流一般是非恒定非均匀流,河道中各种水力要素随时间的变化相对缓慢,可以认为天然河道在一定时间内是恒定非均匀流。
在水利工程建设工作中,需要计算水面线时,经常计算不出结果或者计算的结果不合理,这时就需要我们掌握正确的水面线推算方法,根据天然河道恒定非均匀流水面线的计算公式,对天然河道水面线的计算前期的整理资料、划分河段、确定各参数进行计算,并指出水面线成果合理性和科学性。
一、天然河道水面线推算前期工作要点分析 1.1 准确收集地形资料准确的计算水面线,要依赖于较为完整的河道地形资料,计算前要对地形资料加以分析以适应水面线计算的要求。
横断面资料两岸高程应测到设计洪水位以上,水下部分应测完整,并要对断面资料加以分析,不是有效的过水面积如挖沙的深坑要进行断面修订。
纵断面资料应包括沿程高中低水位的同时水面线,以便了解水流沿程变化情况,还应沿河段进行洪水调查。
1.2 计算河段的划分水面线计算是逐段进行的,需要将计算河道划分为若干个计算断面,河道分段是否恰当直接影响水面线的计算成果,计算河段的划分应遵循以下原则:fan【】(1)每个计算河段内过水断面的形状、尺寸、糙率、比降等变化不应太大。
(2)在一个计算河段内上下游断面水位差不能过大,一般平原河流取0.2~1.0米,山区河流取1.0~3.0米。
(3)每个河段内没有支流流入或流出,若河道有支流存在,在支流汇入或分出的河段处,由于流量有变化,应在支流汇入或分出点前后加设断面,设的断面位置应使同一河段的流量沿程不变。
天然河道水面线计算中起推水位的确定 (优选.)

计 算 结 果 见 表 1 所 列 ,水 面 线 如 图 1 所 示 。
表 1 河 道 断 面 水 位 推 算 成 果 表 (一 )
桩号
0 100 200 300 400 500 600
3.74 3.74 4.67 5.03 5.37 5.69 6.00 6.30
起 推 水 位/m 3.80 4.00 4.50 3.80 4.00 4.50 4.65 4.62 4.81 5.02 5.01 5.11 5.36 5.35 5.41 5.68 5.68 5.71 5.99 5.99 6.01 6.30 6.30 6.31
研究与探索
Y A N J I U Y U T A N S U O
朱 忠 龙 :天 然 河 道 水 面 线 计 算 中 起 推 水 位 的 确 定
天然河道水面线计算中起推水位的确定
朱忠龙
(安徽省巢湖市水利规划设计院,安徽 巢湖 238000)
摘 要:河道水面线推算时,起推水位对上游断面水位的影响是 有 范 围 的 。 文 章 分 析 了 起 推 水 位 对 上 游 水 位 的 影 响 范 围 ,提 出 在 工程设计中,可将起推断面向下游延长一段距离,利用下游临界水位作为起推水位向上游推算设计河段的各断面水位 。 关 键 词 :天 然 河 道 ;水 面 线 ;起 推 水 位 ;临 界 水 位 中 图 分 类 号 :TV131.4;TV133 文 献 标 识 码 :A 文 章 编 号 :1673-5781(2014)04-0448-02
计 。 同 时 把 微 分 方 程 式 改 写 成 差 分 方 程 式 ,即 认 为 在
有 限 长 的 计 算 河 段 内 ,一 切 可 变 水 流 要 素 均 成 线 性 变
天然河道水面线计算
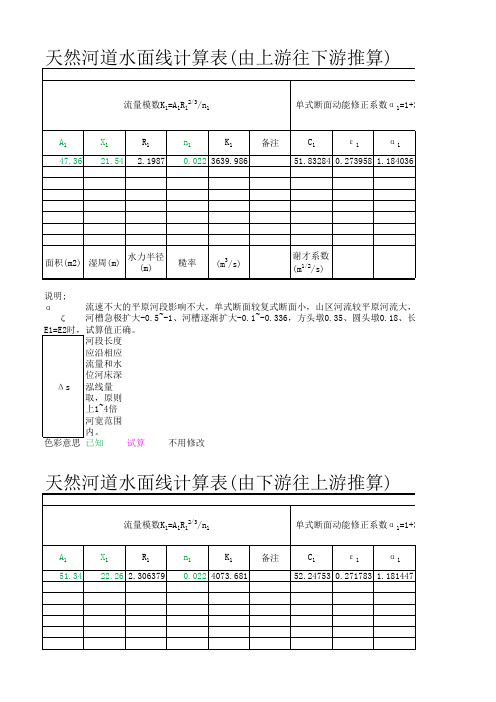
说明;αζ试算 不用修改
说明;αζ试算 不用修改
流速不大的平原河段影响不大,单式断面较复式断面小,山区河流较平原河流大,断
河槽急极扩大-0.5~-1、河槽逐渐扩大-0.1~-0.336,方头墩0.35、圆头墩0.18、长宽比均为4、如果长宽ε2-2ε3
ε2-2ε3
流速不大的平原河段影响不大,单式断面较复式断面小,山区河流较平原河流大,断
河槽急极扩大-0.5~-1、河槽逐渐扩大-0.1~-0.336,方头墩0.35、圆头墩0.18、长宽比均为4、如果长宽
大,断面特变水流近似堰流河段可达2.1左右,平原河流1.15~1.5,山区河流1.5~2.0。
墩0.18、长宽比均为4、如果长宽比大于4则值应有所增加,支流汇入时0.1,弯道时0.05.
)
α1α1大,断面特变水流近似堰流河段可达2.1左右,平原河流1.15~1.5,山区河流1.5~2.0。
墩0.18、长宽比均为4、如果长宽比大于4则值应有所增加,支流汇入时0.1,弯道时0.05.
)
1
+J2) 1
+J2)
j
= v12/(2g)
j
= v12/(2g)
1
=Z2+α2v22/(1
=Z2+α2v22/(2。
河道水面线计算

4.6 洪水水面线4.6.1计算公式⑴计算原理天然河道的洪水大多属于不稳定流,水面线的计算可以近似地视为稳定流量以简化计算。
稳定非均匀流按伯努利能量方程进行计算,即:j f h h g V Z g V Z +++=+2221112222αα式中:Z 2、Z 1为计算段上、下游断面水位;V 2、V 1为计算段上、下游断面平均流速,2α、1α为计算段上、下游断面的动能修正系数;h f 为沿程水头损失;h j 为局部水头损失。
在流量、控制断面水位和河段糙率确定后,即可由该式算出河道断面的水力要素。
⑵主要参数的确定根据一维水面线的计算公式,其关键在于沿程水头损失和局部水头损失的确定。
①动能修正系数αα是以总流的断面平均流速V 代替过水断面上各点的点流速V i 来计算断面的平均单位动能,为校正误差而引入的修正系数,理论上可按下式计算:A V dA V i A 33⎰=α式中:V i 为断面单元流速(m/s );V 为断面平均流速(m/s );A 为过水面积。
α是个大于1.0的数值,其值取决于断面上流速分布不均匀的程度,流速分布越不均匀,α值越大。
②沿程水头损失水流在流动过程中,由于克服河床的阻滞作用,边壁的低流速层对高流速层产生的阻力而消耗的能量,就是沿程阻力损失损失h f ,主要决定于均匀流的坡降,可表示为:23/42222AR L Q n L K Q L J h f === 式中:L 为计算段上下游断面间距(m ),K 为流量模数,R CA K =,一般采用2221111K K K +=,K 1、K 2是上下两断面的流量模数;C 为谢才系数,y R n C 1=,n 为糙率,y 可取1/4~1/6。
由上式可知,欲求h f ,主要是确定糙率n 值,工程河段天然河道糙率根据河道形态,河床组成及两岸植被情况结合,采用历史洪水反推糙率,未进行历史洪水调查段结合《天然河道糙率表》选定。
③局部水头损失局部水头损失即为河道的河床断面沿程不均匀引起的水头损失。
01第一章--天然河道水面线推算

第一章天然河道水面线推算百图软件既可以处理一个糙率的单式断面天然河道,又可以处理二个或任意多个糙率的复式断面天然河道,也可以处理河道某处出现江心洲或分叉情况,还可以处理整条河道上,支流汇入或流出、过桥水头跌差等情况。
缓坡河道应从下游向上游推算,根据经验及《水力学》教材的介绍,当最下游断面的起始水位无法确定时,可用该断面附近的正常水深对应的水位作为起始水位。
陡坡河道应从上游向下游推算,根据经验,当最上游断面的起始水位无法确定时,可用该断面的临界水深或略小于临界水深对应的水位作为起始水位。
实际工程中,一条长距离的河道可能是缓、陡坡交替变化的情况,此时应先画出河底的纵断面图。
根据纵断面图,当人工能够分辨出缓、陡坡的分界点,可人工划分成单一的缓坡或陡坡分别进行推算。
当人工不能够分辨出缓、陡坡的分界点时,可假定该整条河道为缓坡,选择整条河道从下游向上游推算,若软件一直能进行推算,说明该段为缓坡;若软件不能进行推算,说明该段为陡坡。
软件运行终止的断面,即为缓、陡坡的分界点,按此方法判断出整条河道上的所有缓、陡坡的分界点,把整条河道划分成单一的缓坡或陡坡分别进行推算。
第一节 一个糙率天然河道水面线推算一、现状天然河道水面线推算根据下式,即华东水利学院编《水力学》(1999年版)式9.9,采用分段试算法,精确推算水位。
第一步、准备现状横断面数据文件数据文件为txt 格式,在excel 中整理数据时必须另存为文本文件(制表符分隔)类型的txt 文件。
原始横断面测量成果表的内容格式如下:横断测量成果表中,桩号允许带“+”或“-”,但不允许有其它非数字文本,程序通过加减号来识别桩号。
起点距即是累距,零点桩的起点距为0。
每个点的数据占一行,包括“起点距”、“高程”和“点注释”三项,中间用空⎪⎪ ⎭⎫⎝ ⎛ - + ∆ ++= + g v g v K lQ gv z gv z2 2 2 2 2 1 2 222 222211ξ α α格隔开,空格多少不受限制,其中“点注释”可以省略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
■Z , 故 ■a -■b 要比 ■Z 更小得多 , 所以调
整值可按下式进行计算
■Z =■=H2 -H11
(9)
调整后 的上游 水位
Z1
=
Z
1 1
+ ■Z
, 用它在
Z 1 =f (A1)、Z 1 =f (R1 )曲线上查出的 A1 和 R1 ,
计算出 a1 及 b1 值后一定会满足 H1 =Z 1 +a1 -
SUN Dao-zong1 , XIAO Cuang-tong2
(1 .Jiangxi Province Hydraulic and Hydroelectric School ,Nanchang 330008 , China ; 2 .Jiangxi Province Jian County Hydropower Bureau , Jian 341300 , China)
124.400 3 750 3.96 0 .158 0.117 0 .041 124.441
-0 .0 12
124.388 3 720 3.95 0 .161 0.119 0 .042 124.430
-0 .0 01
说明 :1、第(4)项 , 待求水位
Z
第一行系第(15)项计算值
Z
1 1
+■Z
。
化 , 特令
a =(α2+g ζ)(QA )2
(3)
b =■2l(KQ )2 =■2l[ AnRQ2/ 3]
(4)
则公式(2)改写为
Z 1 +a1 -b1 =Z 2 +a2 +b2
(5)
设已 知项 为 H2 =Z 2 +a2 +b2 , 未知 H1 =
Z 1 +a1 -b1 , 若假设 Z 1 使算出的 H1 等于 H2 , 则
面面积 水力半
a
A(m) 径 R(m) (m)
b (m)
a -b (m)
H1 (m)
H1 (m)
调整值 ■Z (m)
初值
Z
1 1
确定
Z
11 1
A1
Z
1 1
(m) (m2) (m)
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15)
1 2
(K
2 1
+K
2 2
), 该项作为未知项(水力学上册
,
河海
大学编 , 1983 年 2 版)。
Z1
+ (α2+g ζ)(AQ1
)2
-
Q2 -K 2
■l= Z 2
+
(a2+g ζ)(AQ2 )2
(1)
(2)沿 程 水 头 损 失 项 采 用
hf
=
1 2
(J 1
+
J 2)■l=■2l(KQ1)2 +■2l(KQ2 )2 , 其中 ■2l(KQ1 )为未
水位关系曲线 , 河道 在 1 +500 、1 +000 之间为逐
渐扩散段 , 取 ζ=-0 .3 , 糙率 n =0 .0275 , 在下游 0 -20 处建坝 , 设计流量 Q =7 380 m3 s , 0 +000处
水位 为 122 .48 m , 试 推算上 游 0 +500 、1 +000 、
断面也有增量 ■A =B ■Z (B 为过水断面的水面
宽), 流速也有一个增量 ■V 即
■V
=■(QA )=-V·B
·■Z A
, 流速水头和局
部水头损失也产生一个增量 , 即
■a1 =-a1 2AB·■Z ≈-a1 ■Z
由于 a1 <0 , 则 ■a1 < ■Z , 同样 , 当所取
的计算段 ■l不太长时 , b 也是小于零 , ■b1 <
H2 -H1 =-0 .001 由结果可见计算准确 。
(2)其他各断 面的水位计算 同上 , 结 果见附
表。
5 结 论
上述推导及算例计算说明 , 按本文介绍的试算
方法 , 计算天然河道的水面线
,
简单明确 ,
初值
Z
1 1
的假定有规
律可循
,
即
Z
1 1
=H2
-(a 2
-b2
)(AA
2)2
1
,
而式中的
A1
b1 =H2 条件 。
应当注意应 用 ■Z =■进行调 整的前 提是
H2
-H
1 1
值较小
。
4 计算实例
河海 大 学 编 《水 力 学》 上册 第 330 页 实 例
(1983 年 2 版)。 某河道已测得 0 +000 、0 +500 、 1 +000 、1 +500 等测站过水断面面积 、水力半径和
第 29 卷 第 2 期 2003 年 6 月
江西水利科 技
JIANGXI HYDRAULIC SCIENCE & TECHNOLOGY
VoJlu.n2.920N0o3.2
天然河道水面线试算简化方法
孙道宗1 , 肖传通2
(1 .江西省水利水电学校 , 江西 南昌 330008 ;2 .江西省吉安县水电局 , 江西 吉安 343100)
计算 a2 =(α2+gζ)(AQ2 )2 =0 .466 m
b2
=
■2l[ A2
nQ R22
3]
2
=0
.368
m
a2 -b2 =0 .098 m
H2 =Z 2 +a2 +b2 =123 .314 m
②确定初值
Z
1 1
,
计算
a1
-b 1
及
H1
值
Z
11 1
=Z
2
+2b 2
=123
.216
m
由
Z
11 1
1 +000
124.172 4 800 2.79 0 .133 0.114 0 .019 124.191
+0 .0 23
1 +500 500 -0.3 124.195 4 920 2.80 0 .126 0.108 0 .018 124.213 124.429 +0.001 124.411 3860 124.400
2、第(7)、(8)两项 a 、b , 用于计算 H2(11)项及 Z 11(15)项为 a2 及 b2 用于计算(10)项 H1 则为 a1 及 b1 。
THE BRIEF METHED OF THE WATER SURFACE CURVE TRIAL CALCULATION OF NATURAL CANALS
知项(水力学上册 , 成都科技大学编 , 1982 年版)。 Z 1 + (α2+g ζ)(AQ1 )2 - ■2l(KQ1 )2 = Z 2 +
(α2+g ζ)(AQ2 )2 +■2l(KQ2 )2
(2)
上两式中 :Z 1 、A1 、K 1 —上游断 面的水位 、过水断
面面积 、流量模数 ;
Z 2 、A2 、K 2 —下游断面的水位 、过水断
1 +500三处断面的水位(流速系数 α=1 .1)。 (1)第一段 0 +500 处水位计算
①计算已知值(0 +000 断面)a2 -b2 及 H2 由 Z 2 =122 .48 查 Z =f(A)和 Z =f (R)曲线
图 0 +000 断面曲线得 A2 =2 560 m2 , R2 =2 .97 m
编辑 :张绍付
(4), 算出
a1
和
b1
值,
最后计算出
Z
1 1
+a 1
-b 1
=
H
1 1
显然算出 H11 不满足 H11 =H2 条件 , 需要进行
试算调整 。
3 初值 Z11 的调整及验证
将式
Z
1 1
+a 1
-b1
=H11
与
Z1
+a 1
-b 1
=H2
相减得
■Z +■a1 -■b1 =H2 -H11 =■
(8)
分析式(8), 当水位有一个增量 ■Z , 则过水
查
Z
=f (A)曲线图中
0
+500
断面曲
线得 A11 =2 460 m2
Z
1 1
=H2
-(a 2
-b2 )(AA21
)2
=123
.208
m
再由
Z
1 1
查
Z
=f (A得 A1 =2 450 m2 、R 1 =3 .14 m
计算 a1 =(a2+g ζ)(AQ1 )2 =0 .509 m
摘 要 :介绍 天然河道中流速水头不能忽略不计时水面线计算中确定一个较准确的水位初值的方法 . 关键词 :天然河道 ;水面线 ;试算 中图分类号 :TV131 .4 文献标识码 :A 文章编号 :1004 -4701(2003)02-0099 -03
目前《水力学》教科书中介绍的水面线计算都
面面积 、流量模数 ;
■l—上 、下游断面之间的流段长度 ;
α—流速改正系数 , 可取 α=1 .1 ;
ζ—流段的平均局部水头损失系数 。
公式(1)、(2)的右边均为已知值(即下游断面
为已知), 左边为未知待求值 , 只要确定 Z 1 , 则左
边各项均可求出 。
