高等数学 定积分的概念与性质
合集下载
高等数学 第5章 第一节 定积分的概念
定积分存在的两个充分条件:
定理1 设 f ( x) 在区间 [a, b]上连续, 则 f ( x)在区间 [a, b] 上可积. 定理2 设 f ( x)在区间 [a, b] 上有界， 且只有有限个间断点,则
f ( x)在区间 [a, b]上可积.
6
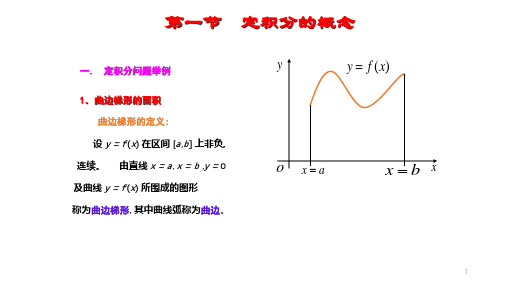
定积分的几何意义
y y f (x)
A
o xa xb x
lim
n
6n 2
3
10
1 i n
i
},
0,
n
A lim 0 i1
f ( i )xi
An
x xn1 nxn b
3
2. 变速直线运动的路程
设物体作直线运动,
已知速度 v v(t )是时间间隔 [T1 ,T2 ]上 的
连续函数, 且 v(t ) 0, 计算在这段时间内物体所经过的路程。
匀速直线运动：
路程=速度×时间.
(1) 分割
T1 t0 t1 ti1 ti tn T2 ,
v( i )
ti ti ti1
(i 1,2,, n)
(2) 近似代替
si v( i )t i
T1
i
T2
t t0 t1 t2 ti1 ti tn1 tn
(3) 求和 (4) 取极限
s
n i 1
s
i
n v(
i 1
i )t i
每 个小区间的长度 xi xi xi1 (i 1,2,n).
2
（2）近似代替
y Ai f (i )xi
(i 1,2,, n)
（3）求和
y f (x)
A1 A2
Ai
A
n i 1
Ai
n
高等数学-定积分的概念与性质
= σ=1 ( ) .
→0
其中()称为被积函数，()称为被积表达式，称为积分变量,
[, ]称为积分区间，称为积分下限，称为积分上限．
15
02 定积分的定义
注（1）定积分)( 是一个数值，它只与被积函数()
和积分区间[, ]有关，而与积分变量的符号无关，即
(2)近似（“以直代曲”）
在区间 [−1 , ] 上任取一点 ，以 ( ) 为高，
y
y=()
以 为底，作小矩形．小矩形的面积为
( ) ，用该结果近似代替[−1 , ]上的小
O
a
x i -1 ξ i x i
b
x
曲边梯形的面积 ，即
≈ ( ) （ = 1, 2, ⋯ , ）．
)(
=
)(
=
)( ．
（2）定积分存在，与区间的分法和每个小区间内 的取法无关.
Hale Waihona Puke （3）按照定积分的定义，记号)( 中的, 应满足关系
< ，为了研究的方便，我们补充规定：
① 当 =
② 当 >
时， = )( = )( 0；
在区间 [1,2] 内， 0 ≤ < 2 < 1 ，
则( )3 < .由性质5.5的推论1，得
2
1
>
2
1 ( )3 ．
28
极限，得 σ=1 ( ) .
→0
如果对于[, ]的任意分法及小区间[−1 , ]上点 的任意
取法，上述极限都存在，则称函数()在区间[, ]上可积，
高等数学PPT课件：定积分的概念与性质
(1) 任意 a x0 x1 x2 xn1 xn b xi xi xi1 ,(i 1,2, , n),
(2) 任取 i xi , f (i )xi (i 1,2, , n)
n
(3) 并作和 S f (i )xi i 1
(4) 记 max{ x1, x2 , , xn },
定积分的概念与性质
性质7(定积分中值定理）f ( x)在[a,b]上 连续,
至少存在一点 [a,b] 积分中值公式
ab f ( x)dx f ( )(b a) (a b).
证
m(b
a)
b
a
f
(
x
)
dx
M(b a)
m
b
1
a
b
a
f
(
x)dx
M
闭区间上连续函数介值定理: [a,b]
f
(
(a b)
平均值公式
27
定积分的概念与性质
b
a
f
(
x)dx
f ( )(b a)
(a
b)
积分中值公式的几何解释
y f ( ) •
y f (x)
O
a
•
bx
曲边梯形的面积 ==矩形的面积
28
定积分的概念与性质
b
a
f
(
x)dx
f ( )(b a)
(a
b)
例
求证
lim
n
na
n
sin xdx x
定积分
definite integral
定积分和不定积分是积分学的两个 主要组成部分.
不定积分侧重于基本积分法的训练, 而定积分则完整地体现了积分思想 ---一种认识问题、分析问题、解决问题的 思想方法.
(2) 任取 i xi , f (i )xi (i 1,2, , n)
n
(3) 并作和 S f (i )xi i 1
(4) 记 max{ x1, x2 , , xn },
定积分的概念与性质
性质7(定积分中值定理）f ( x)在[a,b]上 连续,
至少存在一点 [a,b] 积分中值公式
ab f ( x)dx f ( )(b a) (a b).
证
m(b
a)
b
a
f
(
x
)
dx
M(b a)
m
b
1
a
b
a
f
(
x)dx
M
闭区间上连续函数介值定理: [a,b]
f
(
(a b)
平均值公式
27
定积分的概念与性质
b
a
f
(
x)dx
f ( )(b a)
(a
b)
积分中值公式的几何解释
y f ( ) •
y f (x)
O
a
•
bx
曲边梯形的面积 ==矩形的面积
28
定积分的概念与性质
b
a
f
(
x)dx
f ( )(b a)
(a
b)
例
求证
lim
n
na
n
sin xdx x
定积分
definite integral
定积分和不定积分是积分学的两个 主要组成部分.
不定积分侧重于基本积分法的训练, 而定积分则完整地体现了积分思想 ---一种认识问题、分析问题、解决问题的 思想方法.
高等数学 第五章 定积分的概念及其性质
() a,( ) b, a (t) b,t [, ]
则有定积分换元公式：
b a f (x)dx
例1：计算定积分
(1)
4
cos(2
x
)dx
0
4
1
(2)
1 x2 dx
0
定积分的计算
解：(1)
4
cos(2
x
)dx
0
4
1
4
cos(2
x
)d
(2
x
)
20
4
4
令 t 2x ，则当 x 时，t
解：(2)、 y 1 x2
y2 x2 1( y 0)
如图
y
1S
o
1x
（2）
定积分的概念及性质 4、定积分的计算法则
法则1 常数因子可以提到积分号外.即
法则2 两个函数代数和的定积分等于它们定积分的代数和，即
法则3 (积分区间的可加性) 对任意的点c,若函数在区间
上均可积，则有
定积分的概念及性质
4
4
4
则当 x 0时，t ，有：
原式 1 2
4
4
cos
tdt
4
1 sin t 4 2 4
2 2
(2) 1 1 x2 dx 0
令 x sin t ，则当 x 1 时，t
2
则当 x 0时，t 0 ，有：
原式 2 1 sin2 td sin t 0
2
cos2
tdt
例2
求
1
0 (
x3
x
1)dx
．
解
1
(
x
3
x
1)dx
高等数学 第五章定积分习题课
∫
b
a
f ( x )dx ≤ ∫ g ( x )dx
a
b
⑧估值定理：设M 和 m 分别是函数 f ( x )在区间[a, b ]上的 估值定理： 最大值和最小值， 最大值和最小值，则
m (b − a ) ≤ ∫ f ( x )dx ≤ M (b − a )
a b
上连续, ⑨定积分中值定理：如果函数 f ( x ) 在闭区间[a, b ] 上连续 定积分中值定理： 则至少存在一点ξ ∈(a , b) ,使下式成立： 使下式成立： 使下式成立
b b b
b
a
b
b
∫
b
a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
⑤区间长： ∫ 1dx = b − a 区间长：
a
b
保号性： ⑥保号性：如果在区间[a, b ]上, f ( x ) ≥ 0 ，则∫ a f ( x )dx ≥ 0
b
⑦单调性：如果在区间 [a, b ] 上, f ( x ) ≤ g ( x ) 则 单调性：
b
∫
b
a
f ( x )dx = lim ∫ f ( x )dx −
t →b a
t
设 c ( a < c < b ) 为 f ( x ) 的瑕点，则有 的瑕点，
∫
b a
f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx
a c
c
b
= lim ∫ f ( x )dx + lim ∫ f ( x )dx − +
∫
b
a
f ′( x )dx = [ f ( x )] a = f (b) − f (a ) = a − b
积分的定义与基本性质
积分的定义与基本性质积分是高等数学中的一个重要概念，是微积分的核心内容之一。
积分的定义与基本性质是我们学习微积分的基础，下面我们来详细了解一下。
一、积分的定义积分是微积分中的一种重要概念，它是求解曲线下面的面积、求解函数的平均值、求解图形的重心等问题的工具。
积分的定义可以分为定积分和不定积分两种。
1. 定积分对于一个函数 f(x)，如果其在区间 [a,b] 内的任意一个小区间内都是有界的并且连续的，那么我们就可以在这个区间内求出这个函数的面积。
这时候，我们就可以使用积分的概念来求出该区间内 f(x) 函数的定积分。
具体而言，定积分的定义如下：若函数 f(x) 在区间 [a,b] 内连续，则将 [a,b] 分成 n 个等分，即：a = x0 < x1 < x2 < … < xn-1 < xn = b并令Δ xi = xi+1 - xi，Δ xi 是区间 [xi, xi+1] 的长度。
则若存在一个极限 I，满足当 n 趋近于无穷时，有：I = lim ∑f(xi*) * Δxin → ∞ i = 0其中，xi*是区间 [xi, xi+1] 内任意一点，上式中的极限值 I 就是 f(x) 在区间 [a,b] 内的定积分，可以表示为：∫b∫ f(x) dxa该式意思是对 f(x) 在 [a,b] 区间内的所有小区间的面积求和，得到的总面积就是该函数在该区间内的定积分。
2. 不定积分不定积分也叫原函数或者积分常数，是指函数的某一导函数。
具体而言：若函数 y = F(x) 的导数是 f(x)，则 f(x) 就是 y = F(x) 的不定积分，可以表示为：∫ f(x) dx = F(x) + C其中，C 是任意常数，称为积分常数。
二、积分的基本性质积分有许多基本性质，这些性质在进行积分运算的时候非常实用。
下面，我们来介绍一下积分的基本性质：1. 积分的线性性设 f(x) 和 g(x) 是区间 [a,b] 上的两个连续函数，k 是任意常数，则有：∫ (k f(x) + g(x)) dx = k ∫ f(x) dx + ∫ g(x) dx这条性质表明，积分运算具有线性性，可以将常数提出来进行运算。
高等数学定积分的概念及性质课件
2.可积的充分条件：
定理1.函数f (x)在[a,b]上连续，则f (x)在[a,b]可积。 定理2.函数f (x)在[a,b]上有界，且只有有限个间断点， 则f (x)在[a,b]可积。
(1) f (x) 0,
b
a f (x)dx A
定积分等于曲边梯形的面积
(2) f (x) 0,
n
A Ai i 1
2.取近似
y
f (i )
y f (x)
Ai
o
x0 x1 x2
x xi1 i
x
x x xn2 n1 n
2.取近似
任取i xi1, xi , Ai f (i )xi
n
A f (i )xi
i =1
3.取极限
y
分割越来越细（也就是插入的分点越来越多）
确定的常数I，则称f (x)在[a,b]上可积，称此极限I为函数
f (x)在区间[a,b]上的定积分, 记作 b f (x)dx，即 a
b
n
a
f (x)dx lim 0 i1
f (i )xi
积分上限 a,b称为积分区间
积分号
b
n
a
f (x)dx lim 0 i1
b
a f (x)dx A
定积分等于曲边梯形面积的相反数
(3) f (x)在区间a,b变号时,
b
a f (x)dx A1 A2 +A3 A4 A5
定积分等于各部分面积的代数和
例1 计算 b f (x)dx a
解：此曲边梯形是高为1,
底边长为b a的矩形
f (x) 0
b
a dx b a
定积分是高等数学中占有重要地位的
1
b a
g(x)dx
b
f (x)g(x)dx = f (ε)
a
但若
1
b a
g(x)dx
b
f (x)g(x)dx = Mf
a
则
b
(Mf − f (x))g(x)dx = 0
a
由 (Mf − f (x))g(x) 0 导出 (Mf − f (x))g(x) = 0
从而由
b a
g(x)dx
=
0，存在
ε
∈
(a,
−
h
x0 a
f (t)dt
−
f (x0)|
=|
x0 +h x0
f
(t)dt
−
h
x0 x0
+h
f
(x0
)dt
|
1 h
x0 +h
|f (t) − f (x0)|dt
x0
因为 f(x) 在 x0 连续，从而对 ε > 0，存在 δ > 0，当 |t − x0| δ 时， |f (t) − f (x0)| < ε，从而当 0 < h < δ 时，
1 h
x0 +h
|f (t) − f (x0)|dt < ε
x0
从而
lim
h→+0
x0 +h a
f
(t)dt
−
h
x0 a
f (t)dt
=
f (x0)
同样方法：
lim
h→−0
x0 −h a
f
(t)dt
−
h
x0 a
f (t)dt
=
高教社2024高等数学第五版教学课件-5.1 定积分的概念与性质
第五章 定积分
第一节 定积分的概念与性质
一、问题的提出
实例1 (求曲边梯形的面积)
由连续曲线 = ()(() ≥ 0)、
轴、直线 = 、 = 所围成的图形
称为曲边梯形。
用矩形面积近似取代曲边梯形面积
y
o
y
a
b
（四个小矩形）
x
o
a
b
x
（九个小矩形）
显然，小矩形越多，矩形总面积越接近曲边梯形面积．
→0
= max ∆
1≤≤
= σ=1 ± σ=1
=
→0
±
→0
性质1可以推广到有限个可积函数作和或者作差的情况.
性质2 被积函数的常数因子可提到积分号的外面，即
)(
总有下式成立：
)( = )( + )( .
例如，若 < < ，则
=
+
，
故 )( = )( − )(
= )( + )( .
证
因为 ≤ () ≤ ,由性质4得
≤ ≤ )( ,
又 = − ,
故( − ) ≤ ( ≤ )( − ).
性质6(积分中值定理)
∈
[, ]，使)(
设函数()在[, ]上连续，则至少存在一点
第一节 定积分的概念与性质
一、问题的提出
实例1 (求曲边梯形的面积)
由连续曲线 = ()(() ≥ 0)、
轴、直线 = 、 = 所围成的图形
称为曲边梯形。
用矩形面积近似取代曲边梯形面积
y
o
y
a
b
（四个小矩形）
x
o
a
b
x
（九个小矩形）
显然，小矩形越多，矩形总面积越接近曲边梯形面积．
→0
= max ∆
1≤≤
= σ=1 ± σ=1
=
→0
±
→0
性质1可以推广到有限个可积函数作和或者作差的情况.
性质2 被积函数的常数因子可提到积分号的外面，即
)(
总有下式成立：
)( = )( + )( .
例如，若 < < ，则
=
+
，
故 )( = )( − )(
= )( + )( .
证
因为 ≤ () ≤ ,由性质4得
≤ ≤ )( ,
又 = − ,
故( − ) ≤ ( ≤ )( − ).
性质6(积分中值定理)
∈
[, ]，使)(
设函数()在[, ]上连续，则至少存在一点
第五章 积分 5-1 定积分的概念与基本性质
性质 4 若 f (x) 是 [a, b] 上的连续函数, 则 | f (x) | 也是 [a, b] 上的连续函数, 从而可积, 且
b
b
|
a
f (x)d
x|
|
a
f (x)|d
x.
证明 由于 | f (x) | f (x) | f (x) |, 应用性质 3
b
b
b
a | f (x)|d x | a f (x) d x a | f (x)|d x,
43
4
1
1
1
2
7 1 sin 2
1 sin 2 x 1 sin 2
, 3
3
4
所以
21
3
4
4 7
d
x
3
4
dx 1 sin 2
x
3
4
2 3
d
x
.
18
《高等数学》课件 (第五章第一节)
推论 2 设 f R [a, b], 且在 [a, b] 上 f (x) 0, 则
b
a f ( x) d x 0.
性质 2 (积分对区间的可加性) 设 a c b, f R [a, b], 则 f R [a, c], f R [c, b],
且
b
c
b
f (x) d x f (x) d x f (x) d x.
a
a
c
一般, 当上式中三个积分都存在时, 无论 a, b, c 之间具有怎样 的大小关系, 等式都成立.
当 f (x) R [a, b] 时, 可在积分的定义中, 对 [a, b] 作特殊的分
划, 并取特殊的 i [x i 1, x i] , 计算和式. 如等分区间 [a, b], 并取 点 i 为 [x i 1, x i] 的右端点 x i 或左端点 x i 1 或中点.
b
b
|
a
f (x)d
x|
|
a
f (x)|d
x.
证明 由于 | f (x) | f (x) | f (x) |, 应用性质 3
b
b
b
a | f (x)|d x | a f (x) d x a | f (x)|d x,
43
4
1
1
1
2
7 1 sin 2
1 sin 2 x 1 sin 2
, 3
3
4
所以
21
3
4
4 7
d
x
3
4
dx 1 sin 2
x
3
4
2 3
d
x
.
18
《高等数学》课件 (第五章第一节)
推论 2 设 f R [a, b], 且在 [a, b] 上 f (x) 0, 则
b
a f ( x) d x 0.
性质 2 (积分对区间的可加性) 设 a c b, f R [a, b], 则 f R [a, c], f R [c, b],
且
b
c
b
f (x) d x f (x) d x f (x) d x.
a
a
c
一般, 当上式中三个积分都存在时, 无论 a, b, c 之间具有怎样 的大小关系, 等式都成立.
当 f (x) R [a, b] 时, 可在积分的定义中, 对 [a, b] 作特殊的分
划, 并取特殊的 i [x i 1, x i] , 计算和式. 如等分区间 [a, b], 并取 点 i 为 [x i 1, x i] 的右端点 x i 或左端点 x i 1 或中点.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dx
≤
e
⋅
(1
−
0
)
∫ 即 1 ≤ 1exdx ≤ e 0
b
∫a dx = b − a
2009年7月3日星期五
21
目录
上页
下页
返回
8. 积分中值定理
若 f (x) ∈ C[a ,b], 则至少存在一点 ξ ∈[a ,b], 使
∫b a
f
( x) dx
=
f
(ξ )(b − a)
证: 设 f (x) 在[a,b]上的最小值与最大值分别为 m, M ,
2009年7月3日星期五
13
目录
上页
下页
返回
定积分的几何意义:
f (x) > 0,
∫b a
f
(x)
dx
=
A
曲边梯形面积
f (x) < 0,
∫b a
f
( x) dx
=
−
A
曲边梯形面积的负值
y
A1
a
A2
A3
A5
A4
bx
∫b a
f
(x)
d
x
=
A1
−
A2
+
A3
−
A4
+
A5
各部分面积的代数和
2009年7月3日星期五
作以[xi−1 , xi ] 为底 , f (ξi )
y
为高的小矩形, 并以此小
梯形面积近似代替相应
窄曲边梯形面积 ΔAi , 得
o a x1 xi−1 xi b x
ξi
ΔAi ≈ f (ξi )Δxi (Δxi = xi − xi−1 ,) i = 1, 2, , n )
2009年7月3日星期五
6
上页
下页
返回
5.
∫
b a
f
(
x)
dx
=
∫c a
f
(
x)
dx
+
∫b c
f
(
x)
dx
证: 当 a < c < b 时,
a
因 f (x) 在 [a ,b] 上可积 ,
c
b
所以在分割区间时, 可以永远取 c 为分点 , 于是
∑ f (ξ i )Δxi = ∑ f (ξ i )Δxi + ∑ f (ξ i )Δxi
2009年7月3日星期五
7
目录
上页
下页
返回
2. 变速直线运动的路程
设某物体作直线运动, 已知速度 v = v(t) ∈C[T1 , T2 ], 且 v(t) ≥ 0, 求在运动时间内物体所经过的路程 s.
解决步骤: 1) 大化小. 在 [T1 , T2 ]中任意插入 n −1个分点, 将它分成
n 个小段 [ti−1 ,t i ] (i = 1, 2, , n), 在每个小段上物体经 过的路程为 Δ s i (i = 1, 2, , n)
23
目录
上页
下页
返回
内容小结
1. 定积分定义 —— 乘积和式的极限 2. 定积分的几何意义 3. 定积分存在的3个充分性条件 4. 定积分的8条基本性质
课后练习
习题5-1 1（2）（4）； 7； 8（利用定积分几何意义）； 9
2009年7月3日星期五
24
目录
上页
下页
返回
思考与练习
1. 用定积分表示下述极限 :
I
=
lim
n→∞
1 n
⎣⎡⎢sin
π
n
+ sin
2π
n
+
+
sin
(n
−1)π
n
⎤ ⎥⎦
∑ ∫ 解:
I
=
lim
1
n−1
sin
kπ
⋅π
=
1
n→∞ π k=0 n n π
π
sin x dx
0
0 π 2π
nn
∑ ∫ 或
I
=
lim
n−1
sin(π
⋅
k)
⋅1
=
1
sin
π
x
dx
n→∞ k =0
nn 0
(n−1)π π x
a = x0 < x1 < x2 < < xn = b , 令 Δx i = xi − xi−1 , 任取
n
ξ i ∈[xi , xi−1] , 只要 λ = 1m≤ia≤xn{Δxi} → 0时
∑ f (ξi ) Δxi
i=1
总趋于确定的极限 I ,则称此极限 I 为函数 f (x) 在区间
[a ,
[a, b]
[a, c]
[c, b]
令λ →0
∫b a
f
( x) dx
=
∫c a
f
(x)
dx
+
∫b c
f
(x)
dx
2009年7月3日星期五
17
目录
上页
下页
返回
当 a , b , c 的相对位置任意时, 例如 a < b < c ,
则有
a
b
c
∫c a
f
(
x)
dx
=
∫b a
f
(
x)
dx
+
∫c b
f
(
x)
−
x
⎤ ⎦
dx
= π ×12 − 1 ×1×1
o
1
x
42
=π−1 42
2009年7月3日星期五
15
目录
上页
下页
返回
三、定积分的性质 （设所列定积分都存在）
1.
∫b a
f
(
x)
dx
=
∫− a b
f
(
x)
dx
2.
∫
b
dx
a
=
b
−
a
∫a a
f
(
x)
dx
=
0
3.
∫b a
k
f
(
x)
dx
=
k
∫b a
f
(
x)
dx
14
目录
上页
下页
返回
∫ 例 2 求定积分
1
(
1 − (x − 1)2 − x)dx 的值.
0
∫ 解：
1
(
1 − (x − 1)2 − x)dx 表示圆 ( x − 1)2 + y2 = 1( y ≥ 0)
0
的一部分与直线 y = x 所围成的图形的面积， y = x
因此，
y
∫ 1⎡ 0⎣
1 − (x − 1)2
f
( x) d
x
=
n
lim ∑
λ→0 i=1
f
(ξ i
) Δxi
≥
0
推论1 若在 [a , b] 上 f (x) ≤ g(x), 则
∫b a
f
(
x)
dx
≤
∫
b a
g
(
x)
dx
2009年7月3日星期五
19
目录
上页
下页
返回
推论2
∫b a
f
(
x)
dx
∫≤ b a
f (x)
dx
(a < b)
证: ∵ − f (x) ≤ f (x) ≤ f (x)
= ξi2Δxi
= i2 n3
o
i 1x
∑ n
∑ f (ξi )Δxi
i=1
=1 n3
n
n i =1
i2
=
1 n3
⋅
1 6
n(n +1)(2n
+ 1)
=
1 (1+ 6
1)(2 n
+
1) n
∫ ∑ ∴
1 0
x2
dx
=
lim
λ →0
n i =1
ξ
i 2 Δxi
= lim 1 (1+ 1)(2 + 1)= 1 n→∞ 6 n n 3
n
2009年7月3日星期五
012
nn
25
目录
n−1 1 x
n
上页
下页
返回
思考: 如何用定积分表示下述极限
I
=
lim 1 n→∞ n
⎢⎣⎡sin
2π
n
+
+
sin
nπ
n
+
sin
(n
+ 1)π
n
⎤ ⎥⎦
提示:
∑ I = lim 1 n sin kπ ⋅π
n→∞ π k =1 n n
− lim 1 sin nπ + lim 1 sin (n +1)π
一、引 例 二、 定积分的定义 三、 定积分的性质
2009年7月3日星期五
4
目录
上页
下页
返回
一、引 例
矩形面积 = a h 梯形面积 = h (a + b)
2
1. 曲边梯形的面积
设曲边梯形是由连续曲线 y = f (x) ( f (x) ≥ 0)
及 x轴，以及两直线 x = a , x = b 所围成 , 求其面积 A .
则由性质7 可得
m
≤
b
1 −
a