制导组——仿真结果
制导系统引进新雷达探测设备仿真效果验证

制导系统引进新雷达探测设备仿真效果验证制导系统是现代军事作战中至关重要的一环,它可以提供精确的目标飞行轨迹信息,帮助武器系统迅速准确地发现、跟踪和攻击目标。
为了提升制导系统的性能,引进新雷达探测设备进行仿真效果验证是一种常见的方法。
本文将就制导系统引进新雷达探测设备的仿真效果验证进行详细探讨。
首先,制导系统引进新雷达探测设备的仿真效果验证具有重要意义。
新一代雷达探测设备通常具备更高的探测精度和更广的探测范围,这对于提升制导系统的作战效能至关重要。
然而,直接在实战中引入新设备可能存在一定的风险和成本。
因此,利用仿真方法进行验证,可以更直观地了解新设备对于制导系统性能的影响,减少实战风险,节省成本。
其次,制导系统引进新雷达探测设备的仿真效果验证需要基于真实场景进行。
仿真效果验证的目的是尽可能真实地模拟实际作战环境下的各种情况,以便更准确地评估新设备的性能。
为此,可以利用计算机仿真软件构建具有高度还原度的作战场景,包括地形、气候、目标特征等。
通过将新设备的雷达数据与实际情况进行对比,可以验证其探测性能是否符合预期。
第三,制导系统引进新雷达探测设备的仿真效果验证需要充分考虑各种复杂因素。
在真实作战环境中,各种复杂因素会对制导系统的性能产生影响,例如干扰、杂波、多路径效应等。
因此,在进行仿真效果验证时,需要将这些因素纳入考虑,并在仿真软件中对其进行模拟。
通过分析新设备在复杂环境下的性能表现,可以更全面地评估其适应性和稳定性。
第四,制导系统引进新雷达探测设备的仿真效果验证需要建立科学的评估指标体系。
制导系统的性能评估是一个复杂的过程,需要综合考虑多个指标,包括探测距离、抗干扰能力、目标分类准确率等。
在进行仿真效果验证时,需要根据实际需求,制定科学合理的评估指标体系,并将其纳入到仿真软件中进行量化分析。
通过对各种指标进行综合评估,可以客观地评估新设备的性能优劣。
最后,制导系统引进新雷达探测设备的仿真效果验证需要与实际测试相结合。
导弹制导系统设计与模拟仿真分数实现

导弹制导系统设计与模拟仿真分数实现导弹制导系统是现代军事装备中的重要组成部分,它可以实现对目标的精确打击。
而设计和模拟仿真则是制导系统研发的基础工作,通过设计和仿真可以评估系统性能,优化设计方案,并为真实试验提供指导。
导弹制导系统设计的核心是实现导弹对目标的准确定位和导引。
在设计过程中,需要考虑导弹与目标之间的距离、速度、方向等因素,以及导弹自身的机动性能和制导精度。
为了确保制导系统的效果,通常采用惯性导航、惯性制导以及引导头等多种技术手段相结合。
设计者需要根据实际情况选择适当的制导方案,并通过仿真验证其性能。
在实际的导弹制导系统设计过程中,可以使用计算机辅助设计软件进行模拟仿真。
这些软件提供了各种建模工具和仿真算法,可以根据设计要求建立仿真模型,并通过对模型进行仿真分析,评估系统性能。
通过模拟仿真可以探究系统的稳定性、精度、可靠性等关键指标,发现潜在问题,并针对性地优化系统设计。
与传统试验相比,模拟仿真具有成本低、效率高、可重复性强等优点。
导弹制导系统的设计和模拟仿真工作需要具备一定的专业知识和技能。
设计者需要具备对导弹动力学、控制理论和信号处理等方面的深入了解,以便能够合理选择模型参数和仿真算法。
此外,掌握仿真软件的使用方法也是必不可少的。
常见的仿真软件包括MATLAB/Simulink、ANSYS、SolidWorks等,它们提供了丰富的工具箱和模块,可以满足不同需求的仿真分析。
在导弹制导系统设计和模拟仿真过程中,需要进行一系列的工作。
首先,设计者需要收集和分析导弹系统的性能指标和需求,明确设计目标。
然后,基于系统的工作原理和运行方式,建立系统的数学模型或者计算机模型。
模型需要包括导弹的运动方程、传感器的输出模型、控制系统的模型等。
接下来,设计者需要设计和优化控制算法,以达到系统性能指标的要求。
最后,利用模拟仿真软件对模型进行仿真分析,评估系统的性能,并进行参数优化和方案比较。
导弹制导系统设计和模拟仿真是一项复杂且耗时的工作,需要设计者具备扎实的理论基础和实际经验。
制导炮弹姿态非线性模型预测控制仿真分析

V l3 o 1 o_5 N .
F b 2 1 e . 0 1
制 导 炮 弹 姿 态 非 线 性 模 型 预 测 控 制 仿 真 分 析
修 观 , 良明 王
( 京理T大学 能源与动力工程学院 , 苏 南京 209 ) 南 江 10 4
摘
要 : 实现 对 某制 导炮 弹攻 角 、 滑 角和 速度倾 斜 角指令 的快速 跟踪 控制 , 用具有 解析 控 为 侧 应
d vd d n o n u —o p o tol r n a i n rl o c n rle .Th o tl o n ni e r ii e i t a o tl o c n rle a d n n e —o p o tol r e u —o p o l a mo e n dl p e itv c n r l r o v rs h a ge o — ta k,sd —lp a d a k a g e b u t e eo iy r d cie o tol c n e t e n l — fatc e t i e si n b n n l a o t h v lct c mma d o o y a e o ma d f r t e n e —o p he n rl o n n i a o e p e itv o n s t b d r t c m n s o h i n rlo .T ine —o p o lne r m d l r d c ie
cm a d fa g ie r ete a cnrl rd s n i et l hd ui h o l er m dl o m n so u d po c l, ot l ei s s bi e s g te n n n a o e d j i oe g a s n i pe i i o t l e o i n a a t a cnrl a . h ot l ro eg ie r ete i rdc v cnr t d wt a nl i l o t w T ecnr l ft ud d po ci s te om h h yc ol oe h j l
军事科学导弹制导技术的模拟仿真快速原理验证

军事科学导弹制导技术的模拟仿真快速原理验证导弹制导技术是现代军事科学中的重要领域之一,对于提高战斗力和精确打击目标具有至关重要的作用。
而模拟仿真快速原理验证则是导弹制导技术研发过程中的一项重要环节。
本文将介绍导弹制导技术的模拟仿真快速原理验证的意义、方法和应用。
首先,模拟仿真快速原理验证在导弹制导技术研发中具有重要意义。
传统的导弹制导技术验证需要大量的试验和实际飞行测试,耗费时间和资源较多。
而基于模拟仿真的原理验证可以在虚拟环境中通过数学建模和计算机仿真,快速验证导弹制导技术的有效性和可行性,减少试验和测试的成本和周期,加快技术研发进程。
其次,模拟仿真快速原理验证的方法多样且灵活。
导弹制导技术的模拟仿真快速原理验证主要通过建立数学模型和开展计算机仿真来实现。
首先需要对导弹制导系统中的各个组成部分,如惯性导航系统、制导头、控制系统等进行建模。
接下来,根据实际场景和任务需求,进行相应的仿真验证,如导弹的飞行轨迹仿真、目标跟踪仿真等。
最后,分析仿真结果,评估制导技术的性能和可靠性。
模拟仿真快速原理验证能够模拟多种复杂的环境和飞行状态,实现对制导技术各个指标的检测和评估,为后期的实际试验提供有效的指导和辅助。
模拟仿真快速原理验证在导弹制导技术研发中有广泛的应用。
首先,在导弹制导系统的研制过程中,可以通过模拟仿真快速原理验证,评估不同算法和方案的性能,确定最优的方案。
其次,针对新型导弹系统的研发,可以通过模拟仿真快速原理验证,验证系统设计的合理性和有效性,确保系统在实际使用中达到预期的效果。
此外,模拟仿真还可以用于导弹防御系统的研发,通过模拟不同威胁和防御方案,评估导弹防御系统的可行性和应对能力。
通过模拟仿真快速原理验证,导弹制导技术的研发人员能够更好地掌握制导技术的基本原理和性能,提高制导系统的可靠性和精确性。
总之,导弹制导技术的模拟仿真快速原理验证是一项重要的科研工作,具有重要的意义、多样的方法和广泛的应用。
改进武器系统制导精度仿真对策研究

改进武器系统制导精度仿真对策研究摘要:在对武器制导系统研究过程中,精度仿真技术是一种必不可少的方法手段。
文中依据伴随系统理论,结合实际应用情况,在评定武器误差精度时,求出实验落点偏差。
实验结果显示,该仿真方法能够提升实验效率,改善武器系统制导精度。
标签:仿真对策;制导误差;武器系统引言在武器系统的检验过程中,检验方要对武器系统的性能进行考核,研究其是否能满足战术的标准要求,主要内容有制导精度、杀伤概率、安全性等[1],其中制导精度在系统性能中是非常重要的一项,因为制导精度的结果将直接影响系统武器的运行程度。
1.导弹制导系统仿真导弹制导控制体系研究方法:(1)理论分析。
在多种控制理论基础上,对系统进行优化设计。
(2)实体实验。
包含各种飞行试验、例行试验。
(3)仿真试验。
半实物仿真与数字仿真,在系统研究过程中,进行设计及性能试验。
导弹制导系统仿真的关键:仿真总体技术、专用仿真器、仿真精度方法、实时仿真技术、人机交互技术。
弹道系统设计成型后,必须定出导弹系统的射击精准度。
弹道系统的射击精度统计需拥有大量统计子样,大量统计子样是不可能靠实弹获取的。
武器系统飞行的仿真技术可以提供大量的仿真子样,称为模拟打靶,因此能够对武器系统中射击精准度进行统计。
2.制导精度分析(1)误差源分析飞行器的落点情况、制导精度都是导弹系统中非常重要的,对飞行器的性能进行研究,进而研究它的统计规律性。
一般来讲,对飞行器的飞行规律利用函数表示,然后进行分析研究。
影响命中精度误差的原因有很多,其中包括制导误差、再入误差、物理偏差等等。
分析所有的命中精度原因不太现实,只能对其中的主要误差源研究分析。
当找到了各种误差源的规律时,就可以利用弹道计算找出总的误差分布。
制导误差能够对飞行器落点精度产生影响,包括制导方法偏差和制导工具偏差。
①制导方法偏差,是由于存在干扰因素,加上制导方案的不完善造成的落点偏差。
通过对制导方案进行一系列研究改进,减少方法偏差在制导偏差中的比例。
三维末制导律设计与仿真

t a t o tif r t n o r e c ee ain,t e misl al lo h a f r e a il ,i me n h tt e / h t h u n o mai f ag t c lr t i w o t a o h si C l a s e d o t g t p d y t a s ta h e a r H g i a c a a to g rb sn s n etrq ai . u d n el w h ssrn o u t e s a d b t l y e u t KEYW ORDS: b sn s ;Mie o t l Ro u t e s x d c nr ;Di ia ie t e r o s p t h oy;Gu d n e lw s v i a c a
的鲁棒性能 , 但是要求对 目标的机动信 息进 行估 计。文献[ 3
—
5 中针对二维 导弹拦截 问题 , ] 基于 增益理论 设计 了
鲁 棒制 导律 , 其实质是系统 在满 足稳定性 的前提 下, 可能 尽 抑制 目标机动对制导系统输出的影 响, 但它着重 的鲁棒 稳定 性 和抗 干扰性 , 以牺牲 系统的 动态性能 为代价 的, 是 并且 这 些 制导律要求 导弹的推力在 整个拦截 过程 中可控 , 导 在 弹制导的末端 , 要求是难 以实 现的 , 该 因此不利 于工程 上的
实验2-利用SIMULINK进行制导弹道仿真
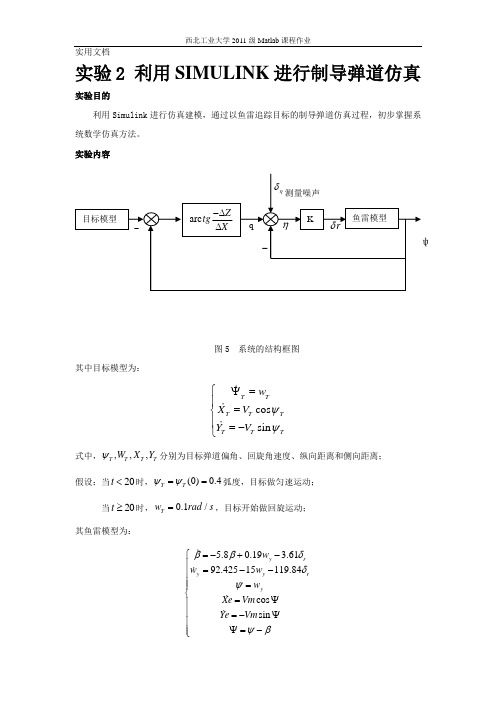
实验2 利用SIMULINK 进行制导弹道仿真 实验目的利用Simulink 进行仿真建模,通过以鱼雷追踪目标的制导弹道仿真过程,初步掌握系统数学仿真方法。
实验内容图5 系统的结构框图其中目标模型为:cos sin T T T T T T T T w X V Y V ψψ⎧ψ=⎪=⎨⎪=-⎩式中,,,,T T T T W X Y ψ分别为目标弹道偏角、回旋角速度、纵向距离和侧向距离;假设:当20t <时,(0)0.4T T ψψ==弧度,目标做匀速运动;当20t ≥时,0.1/T w rad s =,目标开始做回旋运动;其鱼雷模型为:5.80.19 3.6192.42515119.84cos sin y r y y ry w w w w Xe Vm Ye Vm ββδδψψβ⎧=-+-⎪=--⎪⎪=⎪⎨=ψ⎪⎪=-ψ⎪ψ=-⎪⎩式中,,,,,,,,y w r Vm Xe Ye βδψψ分别为鱼雷的侧滑角、回旋角速度、直舵角、航向角、弹道偏角、速度,地面坐标系中的X 轴和Z 轴坐标。
Vm=25m/s 。
鱼雷与目标的相对距离为,,T T X X Xe Y Z Ze ∆=-∆=-。
q 为地球视线角,q ηψ=-为雷体系中的提前角。
操舵规律,0.5,10r K K r δηδ=-=≤。
终端脱靶量定义为t f r =鱼雷模型仿真初值为:(0)(0)(0)(0)(0)(0)0.25/y w r Xe Ze Vm m s βδψ=======。
目标模型仿真初值为:(0)5/,(0)(0)1500,(0)0T T T T V m s X Z m w ====实验步骤由图5所示的系统控制结构图可知,该系统大致可以分为三个部分:目标模型,鱼雷模型以及观察模块。
1.根据目标模型和鱼雷模型的数学方程组,调用Simulink 工具箱模块库中的所需模块建立目标模型和鱼雷模型。
2.根据系统结构框图完成整个系统仿真模型的搭建,如图6 所示。
基于能量控制方法的航天器TAEM制导仿真

Ab ta t h up s f h r n l rae eg n g me t T E sr c :T ep ro eo et mia ae nr yma ae n ( A M)p aeg ia c st t e h s ud n ei o
基于能量控制方法 的航天器 T E 制导仿真 A M
童 中翔 1 董 小 龙 , 袁 新 威 。 李 伟 , 2 ,
(. 1 西北工业 大学, 西安,7 0 7 :2空军工程大学工程学院,西安,7 0 3 :3空军第 5飞行 学院,武威 ,7 3 0 ) 10 2 . 10 8 . 30 3
a p o c h s n t s p p rwh c a so e n r e ce a x m p e a d r a ie e dy a c p r a h p a e i hi a e i h tke ne r e ty v h l sa e a l e l s t n mi i n n z h
的基 于能量的制导方案具有 良 的制导效果。 好 关键词:再入航天器;末端能量管理;航向校准柱面;能量。 射程剖面;制导与控制
中 图分 类号 :V 4 . 48 2 文 献标 识码 :A
S u yo t d fTAEM a e Gu d n eBa e n Ene g n r l n Ph s i a c s d o r y Co t o l g i
sbp ae : - r h s, c us o h e h a n in n yid r(AC h e ad pef a u —h ss St n p ae a q i t n p a , ed g a g me tcl e H )p a r—n l u i i s i l n s n i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算机辅助设计课程设计任务报告基于“标准-3”的多拦截器协同反导建模与仿真授课教师:高长生、钟永健(助教)课题组成员:同学们写上哈尔滨工业大学航天学院航天工程系2011年9月- I -哈工大自主空间系统技术实验室技术报告目录第1章翻译组 (1)1.1 英文1/郭建 (1)1.1.1 自主导 (1)第2章体系组 (3)2.1 任务描述/鲁柱锋/赵航/张众正 (3)第3章拟合组 (4)3.1 任务描述/王飞/宋春林 (4)第4章制导组 (5)4.1 任务描述/赵曦/李涧青/张启龙 (5)第5章控制组 (14)5.1 任务描述/王田野/肖盈莹 (14)- II -目录第1章翻译组1.1英文1/郭建格式按照“gao首行缩2”、宋体、小四,1.1.1自主导格式按照“gao首行缩2”、宋体、小四,1.1.1.1惯性导航格式按照“gao首行缩2”、宋体、小四,各级标题由各小组统一定表1探测器的主要性能- 1 -哈工大自主空间系统技术实验室技术报告- 2 -5101520-50050卫星运行时间(h)位置矢量径向误差(m )5101520卫星运行时间(h)速度矢量径向误差(m /s )图3-15 利用迭代最小二乘方法的24小时导航误差历程第2章体系组第2章体系组2.1任务描述/鲁柱锋/赵航/张众正格式按照“gao首行缩2”、宋体、小四,各级标题由各小组统一定- 3 -哈工大自主空间系统技术实验室技术报告第3章拟合组3.1任务描述/王飞/宋春林格式按照“gao首行缩2”、宋体、小四,各级标题由各小组统一定- 4 -第4章制导组第4章制导组4.1任务描述EKV(Exoatmospheric Kill Vehicle)是美国MD(Missile Defense)系统下GBI(Group-Based Interceptor)的弹头部分,其主要用于拦截大气层外飞行的弹头目标。
EKV采取逆轨迎头碰撞方式实施拦截,即以目标弹头速度矢的反向正面迎击(交会角接近于零且末段拦截轨迹近似于目标弹道的逆向弹道) 。
它的优势在于:在大气层外,目标还没有机动,拦截相对容易;在大气层外将目标弹拦截,可以减少对己方的破坏;即使拦截不成功,还可在低空进行拦截,为后续拦截争取时间。
在不考虑助推段飞行偏差及中段调姿偏差的情况下,为定量分析和评估EKV对中远程弹道导弹的拦截性能或某机动弹头的中段突防性能,需进行EKV末段拦截弹道仿真。
由于EKV末制导时间较短(仅为20 ~25 s) ,最大轨控能力有限(约为4g ) ,且其拦截高程、空域受助推火箭投送能力及GB I 部署位置所限,因此需要对拦截仿真的初始状态进行必要的约束以保证仿真结果更贴近实际。
4.2EKV末段拦截弹道假设本文只对EKV末段拦截进行研究,即自红外导引头成功捕获目标到拦截结束。
假设拦截末段EKV处于理想拦截状态,具体如下:1.姿态稳定,红外导引头能持续跟踪目标;2.红外导引头无探测偏差;3.末制导系统理想工作,不考虑延迟等因素的影响;4.轨控加速度在最大能力范围内与指令加速度相等。
4.3EKV末段拦截弹道建模EKV末段拦截弹道仿真模型可包括拦截器结构模型、运动学与动力学模型、传感器测量模型以及制导控制模型等,如图1所示。
- 5 -- 6 -图1 动能拦截器制导控制系统仿真结构图在本文中,简化了动能拦截器制导控制系统模型,仅考虑运动学与动力学模型、数据处理和轨道运动控制。
4.3.1 来袭弹运动学模型EKV 末段拦截过程中,来袭弹尚未机动,即处于自由运动状态仅考虑地球引力作用,忽略柯氏及牵连惯性力的作用。
则来袭弹运动的微分方程为:(,,,,,)T tx ty tz tx ty tzT v v v a a a = 则:TAT Bu =+式中,00010000001000000100000000000000A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,00000000000000000000010000001001B ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,u 为地球引力加速度矢量00g ⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦。
第4章 制导组- 7 -4.3.2 动能拦截器动力学模型及其比例引导法来袭弹和拦截弹的相对运动分解到水平面和铅垂面。
则在铅垂面内相对运动方程及引导方程为(图2):co s()co s()sin ()sin ()cmm m cm c c cm cm cmm m cm c c cm c cm d D v v d td D v v d t d d N d t d t θεθεεθεθεθε⎧=---⎪⎪⎪=---⎨⎪⎪=⎪⎩式中,cm D 为拦截弹至来袭弹头的斜距,且指向来袭弹头为正;cmε为视线高低角;,m m v θ为来袭弹头速度及倾角;,c c v θ为拦截导弹的速度及倾角;N 为比例引导系数(以下计算过程中:N=7)。
图2 来袭弹和拦截弹运动状态铅垂面示意图水平面内的相对运动及导引模型同铅垂面,则不作具体讨论。
4.4 KEV 末段拦截弹道确定4.4.1 来袭弹初始状态确定来袭弹初始状态为末段拦截弹道初始时刻t0目标的运动状态。
首先根据来袭弹末段运动状态方程建立一条标准的目标自由段弹道,然后根据EKV 末段拦截对目标位置、高程的约束确定t0具体值。
t0确定后,目标初始状态- 8 -即确定。
4.4.2 EKV 初始位置确定由EKV 逆轨拦截(目标处于降弧段,EKV 处于弹道升弧段)的特点,t0时刻EKV 的位置可选在t0后某时刻目标自由段弹道某点。
具体位置应保证t0时刻与EKV 相对距离适中,由于两者相对速度在10km/s 以上,且EKV 末制导的时间在20s 左右,因此相对距离需选择在300km/s 左右。
相对距离确定后,EKV 初始位置000(),(),()m m m x t y t z t 可确定4.4.3 EKV 拦截弹道轨迹确定运用Runge-Kutta 积分法(如图3)解算来袭弹和拦截弹的运动微分方程可得出来袭弹和拦截弹运动轨迹。
并计算出每时刻来袭弹和拦截弹两者之间的距离,当其最小值Dmin 满足Dmin 小于最大允许脱靶量D ,即判定为EKV图3 Runge-Kutta 求解微分方程流程图第4章 制导组- 9 -4.5 仿真算例来袭弹弹道在考虑EKV 拦截高程、空域的基础上参考典型远程弹道导弹自由段运动参数,仿真起始时刻来袭弹、EKV 运动状态见表1(上排为EKV ,下排为来袭弹)(1)。
表1 末段拦截仿真参数由Runge-Kutta 解来袭弹自由段方程,并根据上表中初始状态即可绘制出来袭弹在t0时刻后弹道轨迹(假设不作规避动作,即无机动)。
5.86x(m)来袭弹弹道仿真轨迹y(m)z (m )图 4 来袭弹自由段仿真轨迹6x(m)动能拦截器弹道导弹拦截试验仿真y(m)z(m)图 5 EKV末制导拦截弹弹道轨迹仿真t(s)EKV拦截弹x方向加速度(m2/s)05001000150020002500t(s)EKV拦截弹y方向加速度(m2/s)图 6 EKV拦截弹X方向加速度变化图7 EKV拦截弹Y方向加速度变化0100020003000t(s)EKV拦截弹z方向加速度(m2/s)01020305t(s)D(m)图9 EKV拦截弹Z方向加速度变化图10来袭弹和拦截弹距离随时间变化- 10 -第4章 制导组- 11 -在图5和图6中,EKV 末制导命中来袭弹整个过程用时22.533s ,但两者之间的距离命中时为34m ,远远超出了最大脱靶量,由此可见此算法——即将整个运动过程投影到两个平面存在一定的问题。
若改变来袭弹和EKV 拦截弹的初始状态,如下表2,再仿真EKV 末段拦截过程,则得到如下轨迹,如图(11)。
表2 末段拦截仿真参数4x(m)动能拦截器弹道导弹拦截试验仿真y(m)z (m )图 11 EKV 末制导拦截仿真轨迹050010001500t(s)E K V 拦截弹x 方向加速度(m 2/s )050010001500t(s)E K V 拦截弹y 方向加速度(m 2/s )图 12 EKV 拦截弹X 方向加速度变化 图 13 EKV 拦截弹Y 方向加速度变化- 12 -50010001500t(s)E K V 拦截弹z 方向加速度(m 2/s )图 14 EKV 拦截弹Z 方向加速度变化此时,来袭弹与EKV 拦截弹最近的距离为10m ,相较于第一种初始状态,更加接近最大脱靶量。
则可看出,此种算法需要给定一个合适的初始状态以及比例引导系数N ,才能获得理想脱靶量。
由图(12)、图(13)和图(14)可看出,EKV 拦截弹在三个方向的加速度都十分大,高达15000km/s 2,远远超出了EKV 火箭推进器所能提供的最大推力。
若改变EKV 拦截弹比例引导系数N ,令N=20。
此时可得如下仿真结果:050010001500-2000-1000010002000t(s)E K V 拦截弹x 方向加速度(m 2/s )图 2 EKV 拦截弹X 方向加速度 图 15 EKV 拦截弹Y 方向加速度050010001500t(s)E K V 拦截弹y 方向加速度(m 2/s )第4章 制导组- 13 -7t(s)E K V 拦截弹z 方向加速度(m 2/s )图 16 EKV 拦截弹Z 方向加速度由上图可知,当调节比例引导系数N ,可以改变EKV 拦截弹运动过程中所需的加速度。
初步结论为比例引导系数越大,运动过程中需要的加速值越小。
4.6 结论本章建立了EKV 末制导拦截来袭弹弹道的模型,并给定初始量进行了仿真,所得结论不是很理想,原因在于所建立模型过程中将三维空间转化为两个二维平面中对各个数据量单独处理计算,忽略了两个平面间物理量之间的联系,从而使得最终计算出的脱靶量较大。
另一方面,从两组不同的初始状态数据可以看出,EKV 末制导拦截过程需要一个合适的初始状态,即合适的EKV 发射时机;同时对于不同的初始状态需要一个合适的比例引导系数来满足运动过程中所需的最大加速度。
第5章控制组5.1任务描述/王田野/肖盈莹格式按照“gao首行缩2”、宋体、小四,各级标题由各小组统一定- 14 -。
