《大学物理》第六章 恒定电流的磁场 (2)
合集下载
《大学物理课件》稳恒磁场
B 0I 2 r
0rR
B dl L
0
r2 R2
I
2 rB
0r 2
R2
I
B
0 Ir 2 R2
I
RR
r B
I . dB
dI B
B 的方向与 I 成右螺旋
0 r R,
r R,
B
0 Ir 2 R2
B 0I 2 r
I
R
0I B
2 R
oR r
第三节 磁场对电流和运动电荷的作用
一、安培力（载流导线在磁场中所受的宏观力）
2R
三．运动电荷的磁场。
电流激发的磁场可以视为所有运动电荷所激发的磁 场叠加,取载流导线上电流元 Idl ，其截面积为S ，
单度位为体v积,每内个作电定荷向带运电动为的q电。荷数为 n ，定向运动速
Idl
I
r
p
S
q
v
I
I dl
代入
dB 0 4
Idl r r3
0 4
nqsvdl r r3
在个运电动流电元荷中(有q， 电荷v)数在为rd处N的磁n感dV应，强则度一
r
r0
sin
r0 csc
r0
x 1
dB p y
所以
B 0
4
Ir0 csc2 d sin r02 csc2
0I 2 sin d
4 r0 1
Idz
z 2
dB
0 I 4 r0
(cos1
cos2 )
oz x 1
p
y
1， 2 分别是直电流
始点与终点处电流流向与
r
的夹角
讨论（1）若直导线视为“无限长”，
《恒定电流的磁场》课件
实验步骤
实验结果
将线圈放置在磁铁附近，连接电流表和导 线，观察并记录电流表的变化。
当磁铁穿过线圈时，线圈中会产生感应电 流，根据观察到的电流表变化，可以验证 法拉第电磁感应定律。
磁性材料的观察实验
磁性材料观察实验介绍
通过观察不同磁性材料的磁性表现， 了解磁性材料的性质和应用。
实验材料
不同种类的磁性材料、磁铁、导线等 。
实验步骤
将不同种类的磁性材料放置在磁铁附 近，连接导线，观察并记录材料的磁 性表现。
实验结果
根据观察到的磁性表现，可以了解不 同磁性材料的性质和应用，如永磁体 、电磁铁等。
THANKS
感谢观看
磁场的基本性质
磁场方向
磁场叠加原理
规定小磁针静止时北极所指的方向为 该点磁场的方向。
多个电流产生的磁场是各自产生的磁 场的矢量和。
磁场强度
描述磁场强弱的物理量，用符号H表 示，单位是安培/米（A/m）。
02 恒定电流产生的 磁场
安培环路定律
总结词
安培环路定律是描述磁场与电流之间 关系的物理定律。
详细描述
当导体在磁场中通以电流时，由于洛伦兹力的作用，电子受 到向一侧的偏移，导致导体两侧积累电荷，从而形成横向电 势差。霍尔效应广泛应用于电子学和半导体技术中，如磁传 感器、电机控制等。
磁阻效应
总结词
磁阻效应是指磁场对导体中电流的阻 碍作用，表现为电阻值的改变。
详细描述
当导体在磁场中时，磁场会对电子运 动产生洛伦兹力，导致电子轨道半径 增大，从而减小电流密度，增加电阻 。磁阻效应在磁记录、磁传感器等领 域有重要应用。
磁致伸缩效应
总结词
磁致伸缩效应是指磁场改变物质尺寸的现象。
大学物理恒定磁场PPT
磁场对通电导线的作用力
总结词
运动电荷在磁场中会受到洛伦兹力的作用，该力的大小与电荷的速度、电荷量以及磁场强度成正比。
详细描述
当电荷在磁场中运动时，电荷受到洛伦兹力的作用。洛伦兹力的大小与电荷的速度、电荷量以及磁场强度成正比，其方向由洛伦兹力公式确定。洛伦兹力在电场和磁场同时存在的情况下，会对电荷的运动轨迹产生影响。
总结词
磁通计、磁强计、铁磁物质、测量仪器等。
实验材料
将铁磁物质置于磁场中，使用磁通计和磁强计测量磁场的磁感应强度和磁场线分布。
实验步骤
通过测量数据可以得出磁场的分布情况，验证磁场的基本性质，如磁场线的闭合性、磁场的矢量性等。
实验结果
磁场的测量与观察实验
THANKS
感谢您的观看。
磁场可能改变数据存储介质中的信息，造成数据丢失或损坏。
磁场防护技术
为保护电子设备免受磁场干扰，需要采取相应的磁场防护技术。
磁场对电子设备的影响
利用磁感应强度传感器、磁通量计等设备，测量磁场的大小、方向和分布情况。
磁场测量技术
通过改变磁场源的电流、电压等参数，实现对磁场的控制和调节。
磁场控制技术
利用磁场在工业、医疗、军事等领域中实现各种应用，如磁悬浮技术、核磁共振成像等。
磁场对运动电荷的作用力
磁体在磁场中会受到磁力的作用，该力的大小与磁体的磁感应强度、磁体之间的距离以及磁体的体积成正比。
总结词
当两个磁体之间存在磁场时，它们之间会相互作用，产生磁力。磁力的大小与磁体的磁感应强度、磁体之间的距离以及磁体的体积成正比，其方向由库仑定律确定。磁力在磁场中起着重要的物理作用，如电磁感应、磁悬浮等。
在磁感应强度为B的磁场中，放入一个长度为L、面积为S的导体，当导体垂直于磁场方向放置时，导体受到的安培力F与B、L、S之间的关系为F=BIL。
03大学物理-电磁场-恒定电流产生的磁场
1. 真空磁导率：
ε 0 ≈ 8.85 ×10−12 C 2 ⋅ N −1 ⋅ m −2
介电常数 (电容率) 2. 相对介电常数 磁导率
4π ×10−7 ( µ = 0
2. 相对磁导率：
N T ⋅m ) 或 2 A A
（真空） εr = E （电介质） /E 0
3. 介电常数:
µr = B （磁介质） /B （真空） 0
H=
B
µ
∫∫
S
D ⋅ dS = ∑ q自
内
3. 稳恒磁场的安培环路定理： 磁场强度 H 沿任一闭合路径的线 积分，等于该闭合路径所包围传导 电流的代数和，与束缚电流以及闭 合路径之外的传导电流无关。
∫
L
H ⋅ dl = ∑ Ic
(内)
4
电流元 Idl 在某点产生的 dB 的方 向满足右手螺旋法则 毕奥-萨伐 尔定律 应用： 1. 将载流导体分割成无限个 电流元 Idl 2.
电场强度的 叠加原理
应用： 1. 将带电体分割成无限个 带电量为 dq 的电荷元 2.
确定（ r dq指向空间中 一点）
确定（ r Idl 指向空间中 一点）
3. 确定 dE 4. 若 dE 与 r 的方向相同， 直接积分 E = dE 若 dE 与 r 的方向不同， 进行对称性分析
= i 1= i 1
E = ∑ Ei = ∑
4πε 0 ri
qi
2
ri0
对于连续带电体： dE =
dq 0 r 2 4πε 0 r
E=∫
dq 0 r Q 4πε r 2 0
µ0 Idl × r 0 dB = 4π r2 µ0 Idl × r 0 B=∫ r2 4π L
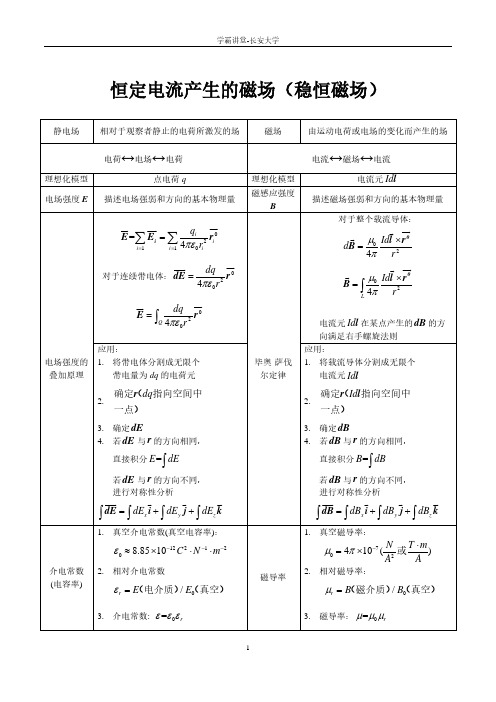
ε 0 ≈ 8.85 ×10−12 C 2 ⋅ N −1 ⋅ m −2
介电常数 (电容率) 2. 相对介电常数 磁导率
4π ×10−7 ( µ = 0
2. 相对磁导率：
N T ⋅m ) 或 2 A A
（真空） εr = E （电介质） /E 0
3. 介电常数:
µr = B （磁介质） /B （真空） 0
H=
B
µ
∫∫
S
D ⋅ dS = ∑ q自
内
3. 稳恒磁场的安培环路定理： 磁场强度 H 沿任一闭合路径的线 积分，等于该闭合路径所包围传导 电流的代数和，与束缚电流以及闭 合路径之外的传导电流无关。
∫
L
H ⋅ dl = ∑ Ic
(内)
4
电流元 Idl 在某点产生的 dB 的方 向满足右手螺旋法则 毕奥-萨伐 尔定律 应用： 1. 将载流导体分割成无限个 电流元 Idl 2.
电场强度的 叠加原理
应用： 1. 将带电体分割成无限个 带电量为 dq 的电荷元 2.
确定（ r dq指向空间中 一点）
确定（ r Idl 指向空间中 一点）
3. 确定 dE 4. 若 dE 与 r 的方向相同， 直接积分 E = dE 若 dE 与 r 的方向不同， 进行对称性分析
= i 1= i 1
E = ∑ Ei = ∑
4πε 0 ri
qi
2
ri0
对于连续带电体： dE =
dq 0 r 2 4πε 0 r
E=∫
dq 0 r Q 4πε r 2 0
µ0 Idl × r 0 dB = 4π r2 µ0 Idl × r 0 B=∫ r2 4π L
大学物理2习题答案
解 以螺绕环的环心为圆心，以环的平均半 径r 为半径的圆周为积分路径，根据磁介质 中的安培环路定理 l I Hd
L ( 内 )
得
H 2 π rN Inr 2 π I
Hn I
B H n I n N / 21 r 0 匝 / c m 1 0 0 0 匝 / m 0 r 0 r
L1
I L2 a 2a I
r
a
O
d FI d l B
该力对O点的磁力矩为
方向
x
x
d M r d F
2 μ I μ I 4 a 0 0 d M r I B d( x = 4 a x ) I d x = ( 1 ) d x 2 x 2 x
济南大学泉城学院
11.2 填空题
(2) 矩形截面的螺绕环尺寸见图，则在截面中点处的磁感应 强度为 ；通过截面S 的磁通量为 。
I Hdl
L 内
有
H d l N I 其 中 ， I 3 A
L
所以有
L 1
d l 3 6 1 8 A ; H d l 3 9 2 7 A ; H
L 2
L 3
d l 3 1 3 3 9 A ; H d l 3 A . H
L 4
济南大学泉城学院
济南大学泉城学院
第11章
恒定电流的磁场
11.1选择题
（1）有两条长直导线各载有5A的电流，分别沿x、y轴正 向流动。在 (40,20,0)cm处的 B 是[ ]。 z 解 视两长直导线为无限长。
沿x、y轴正向流动的电流分别用I1和I2表示。
则I1和I2在P点产生的磁感应强度分别为
I1
I2
大学物理第六章恒定电流
第6章 恒定电流前面讨论了静电现象及其规律。
从本章开始将研究与电荷运动有关的一些现象和规律。
本章主要讨论恒定电流，6.1 电流 电流密度6.1.1 电流1、电流的产生 我们知道，导体中存在着大量的自由电子，在静电平衡条件下，导体内部的场强为零，自由电子没有宏观的定向运动。
若导体内的场强不为零，自由电子将会在电场力的作用下，逆着电场方向运动。
我们把导体中电荷的定向运动称为电流。
2、产生电流的条件：①导体中要有可以自由运动的带电粒子(电子或离子)；②导体内电场强度不为零。
若导体内部的电场不随时间变化时，驱动电荷的电场力不随时间变化，因而导体中所形成的电流将不随时间变化，这种电流称为恒定电流（或稳恒电流）。
3、电流强度 电流的强弱用电流强度来描述。
设在时间t ∆内，通过任一横截面的电量是q ∆，则通过该截面的电流强度(简称电流)为q I t∆=∆ （6–1) 式（6–1)表示电流强度等于单位时间内通过导体任—截面的电量。
如果I 不随时间变化，这种电流称为恒定电流，又叫直流电。
如果加在导体两端的电势差随时间变化，电流强度也随时间变化，这时需用瞬时电流(0t ∆→时的电流强度)来表示：0lim t q dq I t dt∆→∆==∆ （6–2） 对于恒定电流，式(6–1)和式(6–2)是等价的。
在国际单位制中，电流强度的单位是安培(符号A)其大小为每秒钟内通过导体任一截面的电量为1库仑，即 111=库仑安培秒。
它是一个基本量。
电流强度是标量，所谓电流的方向只表示电荷在导体内移动的去向。
通常规定正电荷宏观定向运动的方向为电流的方向。
6.1.2 电流密度在粗细相同和材料均匀的导体两端加上恒定电势差后，；导体内存在恒定电场，从而形成恒定电流。
电流在导体任一截面上各点的分布是相同的。
如果在导体各处粗细不同，或材料不均匀(或是大块导体)，电流在导体截面上各点的分布将是不均匀的。
电流在导体截面上各点的分布情况可用电流密度j 来描述。
大学物理恒定磁场PPT课件
qv
（3） 当正电荷在某点的速度 v
方向于磁感应强度
B
的方向
之间F 的 夹qv角方为B向垂时直运，于所动v受电与磁荷场B在力组磁成场的F中平面受q.力vB sin 。
磁感强度 B 的定义
B 的方向: 小磁针平衡时N 极指示的方向为磁场的方向。
B 的大小:
B Fmax qv
单位：特斯拉
1( T ) 1 N (A m)-1
二、磁通量 磁场的高斯定理
静电场
定义
垂直通过某一曲面的磁感线的条数
中的电 通量
1、均匀磁场
B S BS cos
单位：韦伯（Wb）
en
s s
B
2、不均匀磁场
d B dS
B dS
B
S d S B dS
s
B
dS2 S2
dS1
1
B1
B2
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
2π
d2
d1
dx x
x Φ 0 Il ln d2
2 π d1
四、 毕奥—萨伐尔定律
一、毕奥—萨伐尔定律 1、 电流元 Idl产生的磁场
由毕奥和萨伐尔实验总结出：
dB
0
4π
Idl sin
r2
dB
0 4
Idl er
r2
r
dB
P* r Idl
dB
Idl
I
0 真空磁导率 0 4 107 N / A2
五、磁场中的高斯定律 B cos dS 0
B
S
ds
0
S
磁场中的高斯定律：
通过任意闭合曲面的磁通量等于零（磁
场是无源场） 。
大学物理稳恒磁场 ppt课件
2
NI R
B2
0 NI R2
2(R2 x2 )32
R
O1
O2
x
(1) 电流方向相同：
B B1 B2
0 NI
2R
[1
(R2
R3
x2
3
)2
]
8.51105 T
(2) 电流方向相反：
B B1 B2
0 NI
2R
[1 pp(t课R件2
R3
x
2
)
3 2
]
4.06 105 T
R 2 Indx R2 x2 3/2
B
dB 0nI
2
x2 x1
R2dx μ0nI ( R2 x2 3/2 2
x2 R2 x22
x1 ) R2 x12
B
0nI
2
cos2
ppt课件
cos1
27
讨论
B
0nI
2
cos2
cos1
I
在弧长为 dl 的线元内 流过的电流元为：
dI
dI I dl
真空的磁导率ppt课件
13
O
r P
Idl
dB
dB
Idl
P r
dB
I
电流元的磁感应线在垂直于电流元的平面内 是圆心在电流元轴线上的一系列同心圆。
磁感应线绕向与电流流向成右手螺旋关系
磁场叠加原理: B dB
oIdl rˆ
ppt课L件
L 4r 2
dB
μ0 4π
NI R
B2
0 NI R2
2(R2 x2 )32
R
O1
O2
x
(1) 电流方向相同：
B B1 B2
0 NI
2R
[1
(R2
R3
x2
3
)2
]
8.51105 T
(2) 电流方向相反：
B B1 B2
0 NI
2R
[1 pp(t课R件2
R3
x
2
)
3 2
]
4.06 105 T
R 2 Indx R2 x2 3/2
B
dB 0nI
2
x2 x1
R2dx μ0nI ( R2 x2 3/2 2
x2 R2 x22
x1 ) R2 x12
B
0nI
2
cos2
ppt课件
cos1
27
讨论
B
0nI
2
cos2
cos1
I
在弧长为 dl 的线元内 流过的电流元为：
dI
dI I dl
真空的磁导率ppt课件
13
O
r P
Idl
dB
dB
Idl
P r
dB
I
电流元的磁感应线在垂直于电流元的平面内 是圆心在电流元轴线上的一系列同心圆。
磁感应线绕向与电流流向成右手螺旋关系
磁场叠加原理: B dB
oIdl rˆ
ppt课L件
L 4r 2
dB
μ0 4π
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dBcos
B
900
dB cos
900
900 0I cosd 900 2 2 R
6-12解：
磁通量
dΦ BdS cos00
I1
l r1
r2
I2 r3
x
B
B2
B1
0I2 2x
0 I1 2 (d
x)
dS ldx
Φ dΦ r2 r3 r3
6-13解：
B内
0Ir 2R2
B
0I 2R
oR
r
dΦ BdS cos00 0Ir l dr 2R2
(1)质子作螺旋运动的半径； (2)螺距； (3)旋转频率。
结束 目录
已知：B =1.5 T v =1.0×107m/s
= 300
求：半径 R 螺距 h 旋转频率 n
解：
R
=
mv eB
=
m
vsin eB
1.67×10-27×1.0×107×0.5
dB
0dI
0
I b
dx
2x 2x
P （2）沿坐标轴投影积分，积分
B
2b
0
I b
dx
b 2x
o
θ
dB 0dI
0
I b
dy
y
θ
2d 2 ( y)2 x2
x
dB cos
0
I b
dy
x
2 ( y)2 x2 ( y)2 x2
6-10解：
（1）选坐标,取微小量
dB
0dI
0
I
R
Rd
θ
2R
2R
（2）沿坐标轴投影积分，积分
r2
dB
0
4π
Idl er r2
B dB 0
L
4π
I d l er L r2
毕奥－萨伐尔定律的应用
环形载流导线中心处的磁感强度
I
R
B 0I
2R
I
通电直导线外一点的磁感强度
B
0I
4πd
sin
2
sin
1
L
2
1 d
P
高为h的等边三角形的回路载有电流I，试求该三角形中心处 的磁感强度。
有限长直导线产生的磁场
= 0.5×105 T
结束 目录
6-17 一个电子射入B =(0.2 i+0.5 j )T 的非均匀磁场中，当电子速度为v =5×106j m/s时，求电子所受的磁力。
结束 目录
已知： v =5×106 j m/s
B =(0.2 i +0.5 j )T
求：F 解：
q = 1.6×10-19 C F = q v ×B
B
l
dx
=
2π0IRl 2
Rx 0
dx
=
4π0I l
=
4π×10-7×10×1 4π
= 1.0×10-6Wb
结束 目录
6-14 有一根很长的同轴电缆，由一圆 柱形导体和一同轴圆筒状导体组成，圆柱的
半径为R1，圆筒的内外半径分别为R1和 R2， 如图所示。在这两导体中，载有大小相等而
方向相反的电流 I ，电流均匀分布在各导体 的截面上。
安培环路定理
在真空中的恒定磁场内，磁感应强度B矢量沿
任何闭合曲线L的环流等于穿过闭合曲线回路所有
传导电流的代数和的0倍。
B dl L
0
Ii
i
B 0I
2πr
B
0rI 2 R2
B 0nI
磁场对载流导线的作用
安培定律
dF Idl B
9 10 12 13
6-9解： I
xb
（1）选坐标,取微小量
R
Φ 0 dΦ
无限长直载流导线与一个无限长薄电流板构成闭合回 路，电流板宽度为a，者相距为a（导线与板在同一平 面内），如右图所示．则导线与电流板间单位长度所 受作用力大小
B 0I
2πx
I
I
aa
dF dIlB I dxl 0I
a 2πx
6-22 彼此相距10cm的三根平行的 长直导线中各通有10A同方向的电流，试求 各导线上每1cm上的作用力的大和方向。
根导线载有电流 I1= I2= 20 A 电流流向如图所
示。求:
(1)两导线所在平面内与该两导线等距的一 点 A 处的磁感应强度；
(2)通过图中斜线所示面
积的磁通量.
(r1=r3=10cm, l =25cm)
I1 A. l I2
r1 r2 r3
结束 目录
解(1)：
B A =B 1A+B 2A
BA =
第六章 恒定电流的磁场
§6-2 §6-3
磁感应强度 毕奥-萨伐尔定律
dB 0 4
Idl sin
r2
§6-4 稳恒磁场的高斯定理与安培环路定理
B dl L
0
Ii
§6-5 带电粒子在电场和磁场中的运动
i
§6-6 磁场对载流导线的作用 dF Idl B
毕奥－萨伐尔定律
B
l
0 4
Idl sin
r
o
P
结束 目录
解：(1)
B0=
0 I 4a
=
4π×10-7×4.0 4×0.10
= 1.26×10-5 T
I
a
I
O
结束 目录
6-7 两根长直导线沿半径方向引到铁环 上A、B 两点，并与很远的电源相连，如图 所示。求：环中心的磁感应强度。
AI
O
BI
结束 目录
解：
π B
1=
4
I0 1 r2
l 1dl
I
P
结束 目录
解：
由对称性 By = 0
dI
=
d
π
I
dB=
0dI
2πR
=
0I
2π2R
d
y
..
.
. .
R
..
.d. l
d
. .
x
P dB
π
B =Bx = π2 dB cos
2
0 I
= 2π2R
π
π2 cos d
2
=
I
π0
2R
结束 目录
6-15 一个塑料圆盘，半径为 R，电荷 q 均匀分布在表面 ，圆盘绕通过圆心垂直盘
=
arc
tg
B 2P B 1P
=
45 0
结束 目录
6-5 如图所示的被折成钝角的长导线 中通有20A的电流。求：A点的磁感应强度。
设 d = 2cm, a =1200
Q
a
A
P
dOI
结束 目录
已知： I = 20A d =2cm 求：BA 解：
a = 120 0 Q
BA = BOP+B OQ BOP =0
=q (0.2 i +0.5 j )×( 5×106 j )
i jk = 1.6×10-19 × 0.2 0.5 0
0 5×106 0
= 1.6×10-13 k N
结束 目录
6-18 一电子以 1.0×106m/s 的速度 进入一均匀磁场，速度方向与磁场方向垂直。 已知电子在磁场中作半径为 0.1m 的圆周运 动 。求磁感应强度的大小和电子的旋转角速 度。
沿 y 轴方向的作用力
F2=4×102N。求磁感
z v1
应强度的1
y
结束 目录
已知： v1 = 2×106 i m/s q = 4×10-9 C
F2 = 4×102 j N 求：B
解： F = q v × B
B 沿 x 轴负方向
F = q vB
B
=
F qv
4×102 = 4×10-9×2×106
面的轴转动，角速度为ω 。求：圆盘中心处
的磁感应强度。
ω
R
q
结束 目录
解：
n
=
ω
2π
σ=πqR 2
ω
dq =σ 2πr dr
dI =n dq =nσ2πr dr
dB
=
0dI 2r
=
0nσπdr
B
=
R 0
0nσπdr
=
0nσπR
=
ω0 q
2πR
R r
dr
结束 目录
6-12 两平行直长导线相距d = 40 cm,每
2 0 I
2π(d
1
2
)
=
2 0 I1
πd
=
2×4π×10-7×20 π×40×10-2
= 4.0×10-5 T
结束 目录
解(2)：
Φ= S B .dS
= r 1+r 2 r1
2π 0xI1
+
0 I
2π(d
2
x
)
l dx
x dx dx
I1
l I2
=
π0I 1 l
ln
d r1 r1
r1 r2 r3
R3 R2
B 32πr = 0 I
I (πr 2
π(R
2 3
πR22)
R 2)2
π B
3
=
2
0I r
1
r 2 R22 R32 R22
r >R3
B4 =0
6-16 一带有电荷量为4.0×10-9 C的粒
子，在y~z平面内沿着和 y轴成450角的方向
以速度 v1=3×106 m/s运动，它受到均匀磁 场的作用力F1逆 x 轴方向；当这个粒子沿 x 轴方向以速度v2=2×106m/s运动时，它受到