高中数学概念最全的思维导图(精选.)
高中数学知识框架思维导图(整理版)
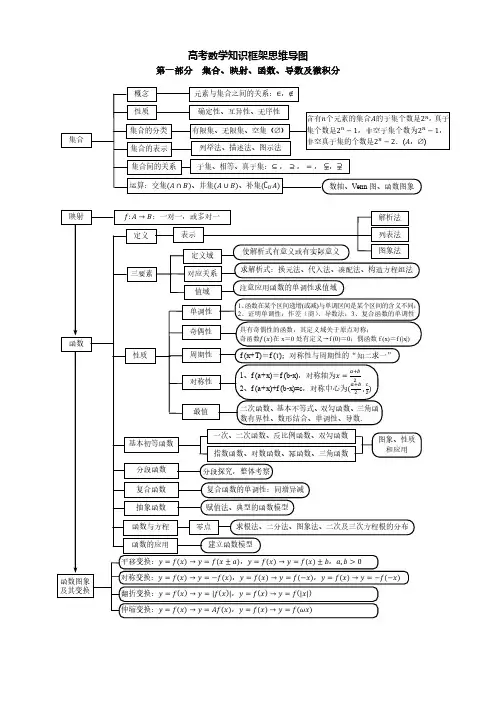
基本初等函数 指数函数、对数函数、幂函数、三角函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用 分段探究，整体考察 复合函数的单调性：同增异减 赋值法、典型的函数模型 零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换：������ = ������(������) → ������ = ������(������ ± ������)，������ = ������(������) → ������ = ������(������) ± ������，������, ������ > 0 函数图象 及其变换 对称变换：������ = ������(������) → ������ = −������(������)，������ = ������(������) → ������ = ������(−������)，������ = ������(������) → ������ = −������(−������) 翻折变换：������ = ������(������) → ������ = |������(������)|，������ = ������(������) → ������ = ������(|������|) 伸缩变换：������ = ������(������) → ������ = ������������(������)，������ = ������(������) → ������ = ������(������������)
������
第二部分
角的概念
三角函数与平面向量
弧长公式������ = ������������、扇形面积公式������ = ������������
2 1 π 2
高中数学知识框架思维导图
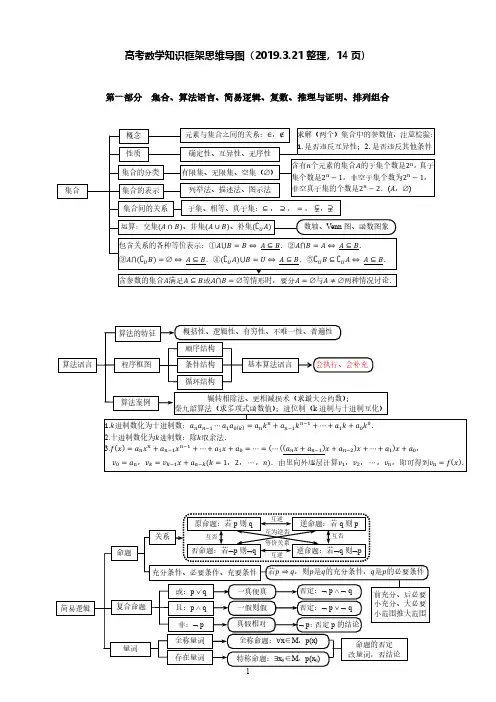
i．
①(1 ± i)2 = ±2i；
②1+i = i；1−i = −i；
1−i
1+i
③������ + ������i = i(������ − ������i)，
如3+4i = i(4−3i) = i；
4−3i 4−� = ������ + ������i、复平面内点 Z(������, ������)、向量���⃗⃗���⃗⃗���⃗��� = (������, ������)的一一对应关系； 复数模的几何意义：|������| = |������ + ������i| = √������2 + ������2 = |���⃗⃗���⃗⃗���⃗���|
2.对数的运算性质(������>0，且������ ≠1，������>0，������>0)：①log������(������ ∙ ������) = log������������ + log������������；
简易逻辑
命题
关系
原命题：若 p 则 q
互否
否命题：若p 则q
互逆
互为逆否 等价关系
互逆
逆命题：若 q 则 p
互否
逆命题：若q 则p
充分条件、必要条件、充要条件 若������ ⇒ ������，则������是������的充分条件，������是������的必要条件
复合命题 量词
或：p q 且：p q 非： p 全称量词 存在量词
2
映射
函数
函数图象 及其变换
第二部分 函数、导数及微积分
������: ������ → ������：一对一，或多对一
高一必修一数学指数函数思维导图
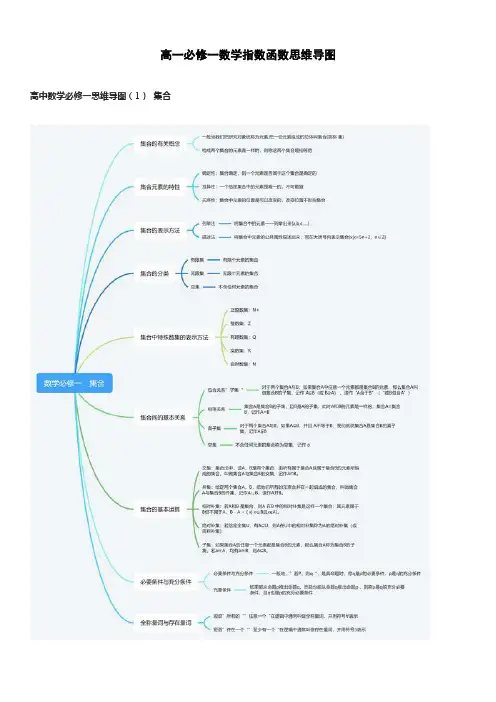
高一必修一数学指数函数思维导图高中数学必修一思维导图（1）集合
本章要求学生们初步理解集合的概念、相关特性以及表示方法，了解集合间的基本关系，掌握集合的基本运算。
高中数学必修一思维导图（2）一元二次函数、方程和不等式
本章首先要求学生们掌握等式性质与不等式性质以及推论，并运用解决简单问题。
其次掌握一元二次不等式的图像解法，通过图像找一元二次不等式解集。
高中数学必修一思维导图（3）函数的概念与性质
本章内容主要包括函数的概念及其表示、幂函数以及函数的基本性质三大内容，在对函数进行表示及研究其性质时，可以通过画图，用形象的方式去立即抽象的函数概念。
高中数学必修一思维导图（4）指数函数与对数函数
指数函数与对数函数时第四章主要讲的内容，同时也是两类重要的函数模型。
学生们需理解指数函数、对数函数的概念，理解指数函数、对数函数的单调性，掌握指数函数、对数函数图像通过的特殊点。
高中数学必修一思维导图（5）三角函数
第五章在学习三角函数之前，首先要对任意角和弧度制的概念进行一个初步的掌握，其次是把握三角函数的定义域、值域以及单调性。
最新高中数学知识点最全的思维导图
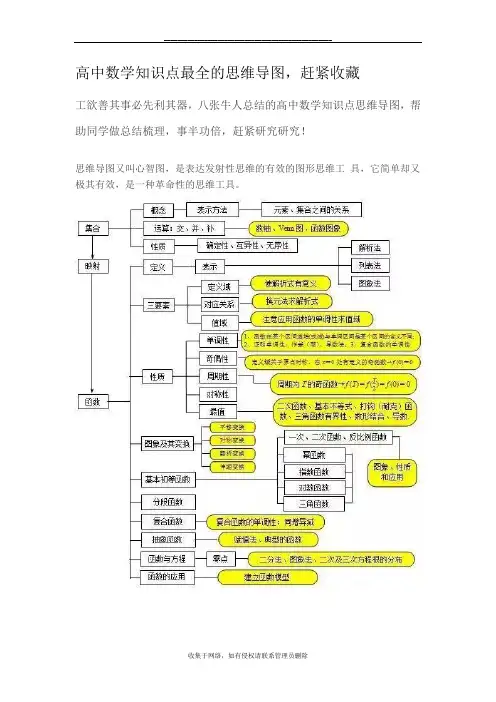
高中数学知识点最全的思维导图，赶紧收藏
工欲善其事必先利其器，八张牛人总结的高中数学知识点思维导图，帮助同学做总结梳理，事半功倍，赶紧研究研究！
思维导图又叫心智图，是表达发射性思维的有效的图形思维工具，它简单却又极其有效，是一种革命性的思维工具。
挂职锻炼学习心得
根据公司的统一安排，我到基建部挂职培训学习，协助项目经理负责工程建设前期管理工作。
回顾这一年来在基建部挂职锻炼学习，使我本人受益匪浅，对基建部的工作方式、内容、流程等都有了全新的认识，切实使我本人学习到知识，得到了锻炼，提高了能力，增长了才干，下面将我在基建部的学习感悟总结归纳如下：
一、学习工作情况
（一）认真努力学习，不断提高政治理论水平
我在挂职学习期间积极主动地向基建部的领导和同志学习，学习他们时刻按公司提出的“四个服务”的要求，始终坚持“以人为本、为客户解困、为企业服务”的工作理念，全面落实各项利民、惠民工作，对业务精益求精，对工作认真细致、一丝不苟，对生活严格要求、平易近人的工作作风。
他们这种严谨扎实的工作作风和超前谋划的意识深深感染和影响着我，通过他们的言传身教，使自己的工作作风得到进一步的转变。
（二）适应新环境，做好新工作
面对基建部不同的工作环境和任务，通过学习，我较快地适应了基建部的工作环境，熟悉了基建部工作内容和工作程序，掌握了一定的工作方法和技巧。
在较短的时间内便能独立地开展一定的本质工作，并取得了一定的工作成绩。
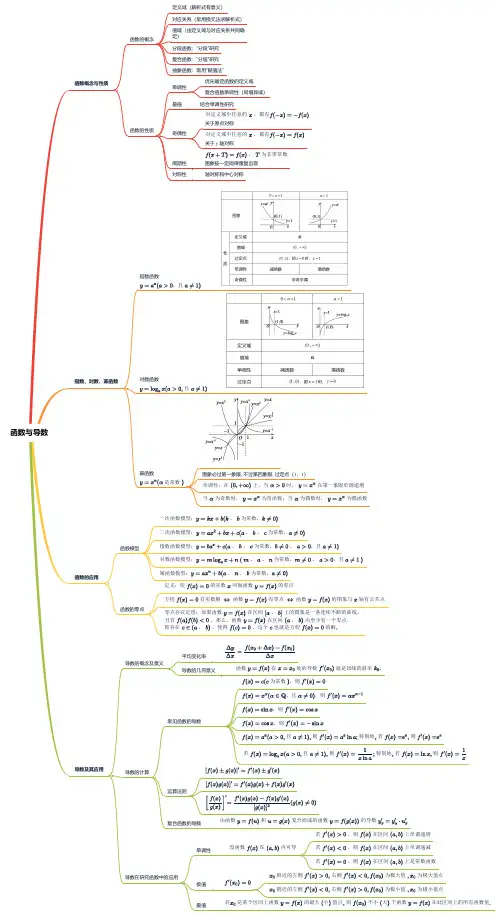
(2)函数与导数——高考数学一轮复习思维导图
新课程高中数学知识点思维导图
新课程高中数学知识点思维导图第一部分：集合、映射、函数、导数及微积分集合是由元素组成的整体，可以用数轴、Venn图或函数图象等方式表示。
集合具有确定性、互异性和无序性等特点。
定义域、值域、单调性、奇偶性、周期性和对称性等是函数的重要性质。
函数可以进行平移、对称、翻折和伸缩变换，最值是函数的重要特征。
对数函数、分段函数、复合函数和抽象函数等都是常见的函数类型。
函数与方程密切相关，函数在生活中有着广泛的应用。
导数是函数变化率的度量，基本初等函数的导数可以通过运用导数的运算法则求得。
导数的应用包括求极值和定积分等。
三角函数、复合函数的单调性、函数模型的建立等都是微积分的重要内容。
第二部分：三角函数与平面向量角的概念可以用弧度制或线度制表示，三角函数是角的重要性质之一。
同角三角函数之间有着密切的关系，诱导公式、和角、差角公式和二倍角公式等都是常用的公式。
三角函数的定义域、图象、对称性、最值、奇偶性、单调性和周期性等都是重要的性质。
正弦函数、余弦函数和正切函数的图象可以通过平移和伸缩变换得到，也可以用五点作图法进行绘制。
最小正周期是正弦函数和余弦函数的重要特征，对称轴和对称中心是正弦函数和余弦函数图象的重要点。
三角函数的化简、求值和证明都需要运用公式的变形和逆用。
平面向量是具有大小和方向的量，可以进行加减和数乘等运算。
向量的模、方向角和坐标等都是向量的重要性质。
向量的共线和垂直关系、平面向量的数量积和叉积等都是向量的重要概念。
概念：解析几何是一种通过运用坐标系和代数方法研究几何问题的数学分支。
线性运算：向量的加法和数乘运算。
基本定理：平面向量的基本定理包括平面向量的加法定理和数量积的几何意义。
平面向量：平面上具有大小和方向的量，可以用有向线段表示。
坐标表示：平面向量可以用坐标表示，其中x和y分别表示向量在x轴和y轴上的投影。
模：向量的大小，也称为模长或长度。
加、减、数乘几何意义：向量加法表示平移，向量减法表示连接两点的向量，数乘表示伸缩或反向。
高中数学知识框架思维导图(整理版)
柯西不等式
第四部分
位置关系
截距
解析几何
斜率公式、倾斜角的变化与斜率的变化: = tan ， =
倾斜角和斜率
重合
A1B2－A2B1＝0，C1B2－C2B1＝0
平行
A1B2－A2B1＝0，C1B2－C2B1≠0
相交
A1B2－A2B1≠0
垂直
直线的方程
z 的几何意义：
过可行域内一点（, ）
向直线 = ， = 作
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换： = () → = ( ± )， = () → = () ± ，, > 0
对称性
y＝Asin(x＋)＋b
化简、求值、
证明（恒等变形）
）
值域
图象
对称轴（正切函数除外）经过函数图象
的最高（或低）点且垂直 x 轴的直线，
对称中心是正余弦函数图象的零点，正
切函数的对称中心为( ，0)（k∈Z）.
最值
2
①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1
2+1 −1
高中数学思维导图大全
国
｀截式： y ＝妇干 b
＇，两点式:� V-VI-＝－X-— X1 芍( :¢:X动 五） y?-P1 芬寸
！截距式: :＋责＝ l （吐 0,b#o)
注意（1)截距百 :，可负，也可
1彝为o. (2)方程
各种形式的变化 和适用范围
宜 线
一般式：Ax+By+ C = O(AB-:f:. o)
的
两直线 行
序性
组合的分类
＾集 卜巳渠合的表示一 口
列举法，特征性质描述法、Veen图法 性质
(2)A云小(3)则A�B则A.::B或4=， 凡 (4)若A�B, B竺C，则AGC; (5)含有11. '个元素的集合有2“ 个子无宇 有2片－i 个真丁采：
(6)E心；的区别�E表示元素与集合关系
已表示集合与集合关系； (7)屿｛叶区别· 一 般地，a表示元压 ｛叶表示只有 一 个元素tr的菜合：
咖
(
5 l， 万
L1 5 ｀ 为方向向泣｝
la•司 lal• 2直线与平面的夹角6cosO=
恒|
（a 为直线方向向址，行为平面法向盘｝
I· 杭I 面角0:cos_0·=� 匠．开介 1 枫
飞，h，．为两平面 向优）．
倾斜角与斜卒
倾斜伽「包18OO)和斜率K气na的变化
！点斜式：，V － y0 ＝沁－X。)
,p) +b
描点法（五点作阻法— ） I 斗几何作图法
对称轴．（正切函数 除外）经过函数图 象的蚊扁氓t低）
点且垂直x轴的直线
对称中心是正余弦函
＿佟］象的零点，正切 函数的对称中心为 （一 .k.2it ，．0) (kGZ)
碑象可由正千玄曲线经过平移、伸缩得到，但耍注意先平移后伸缩与先伸缩后平移不同：
高中数学思维导图(新课标)
'
f x 与 f x 0 的区别
vt S ， at vt
'
0 0
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
导 数
导数概念
运动的平均速度 曲线的割线的斜率
'
0
k f
'
'
x
0
' '
； x
n
nx 1 x
定
映
A中元素在B中都有唯一的象；可一对一 （一一映射），也可多对一，但不可一对多 定义 函数的概念 表示 定义域
列表法 解析法 图象法 使解析式有意义及实际意义
第 二 部 分 映 射 、 函 数 、 导 数 、 定 积 分 与 微 积 分
射
三要素
区间 单调性 奇偶性 周期性 对称性
对应关系 值域
常用换元法求解析式 观察法、判别式法、分离常数法、单调性法、最值法、 重要不等式、三角法、图象法、线性规划等
函数的 基本性质
函 数
函数常见的
最值
几种变换
基本初等函数 分段函数 复合函数 抽象函数 函数与方程 函数的应用
平移变换、对称变换 翻折变换、伸缩变换
三角函数 单调性：同增异减 赋值法，典型的函数 零点 建立函数模型 求根法、二分法、图象法；一元二次方程根的分布 退出 上一页
函数的平均变化率
函数的瞬时变化率 运动的瞬时速度 曲线的切线的斜率
第一部分 第二部分 第三部分 第四部分 第五部分 第六部分
集合与简易逻辑 映射、函数、导数、定积分与微积分 三角函数与平面向量 数列 不等式 立体几何与空间向量
全套高中数学思维导图(清晰打印版)
高中数学选修 2-1 目录 第一章 常用逻辑用语 1.1 命题及其关系 1.2 充分条件与必要条件 1.3 简单的逻辑联结词 1.4 全称量词与存在量词 第二章 圆锥曲线与方程 2.1 曲线与方程 2.2 椭圆 2.3 双曲线 2.4 抛物线 第三章 空间向量与立体几何 3.1 空间向量及其运算 3.2 立体几何中的向量方法
两角和与差的正弦、余弦和正切公 式
简单的三角恒等变换
高中数学选修 1-2 目录 第一章 统计案例 1.1 回归分析的基本思想及其初 步应用 1.2 独立性检验的基本思想及其 初步应用 第二章 推理与证明 2.1 合情推理与演绎推理 2.2 直接证明与间接证明 第三章 数系的扩充与复数的引 入 3.1 数系的扩充和复数的概念 3.2 复数代数形式的四则运算 第四章 目录 第一章 解三角形 正弦定理和余弦定理 应用举例 实习作业 第二章 数列 数列的概念与简单表示法 等差数列 等差数列的前 n 项和 等比数列 等比数列的前 n 项和 第三章 不等式 不等关系与不等式 一元二次不等式及其解法 二元一次不等式(组)与简单的线 性规划问题 基本不等式
圆的方程 直线、圆的位置关系 空间直角坐标系
高中数学
思维导图
“我爱学习，学习使我妈快乐 我妈快乐，全家快乐！”
全套高中数学思维导图（清晰打印版）
高中数学必修一目录 第一章 集合与函数概念 集合 函数及其表示 函数的基本性质 第二章 基本初等函数(Ⅰ) 指数函数 对数函数 幂函数 第三章 函数的应用 函数与方程 函数模型及其应用
高中数学知识框架思维导图(整理版)
点斜式：y－y0＝k(x－x0)
注意：截距可正、
可负，也可为 0.
2 −1
注意各种形式的转化和运用范围.
x y
截距式： ＋ ＝1
a b
两直线的交点
距离
一般式：Ax＋By＋C＝0
两点间的距离公式|1 2 | = √(1 − 2 )2 + (1 − 2 )2 ．
2.
3.
分组求和法
2
=
1
−
−1)(2+1 −1)
2 −1
+1
1 1
1
= (
2 (+2)2
(−1) ∙4
4 2
(2−1)(2+1)
1ቤተ መጻሕፍቲ ባይዱ
2+1 −1
− (+2)2 )
= (−1) (
1
2−1
+
错位相加法: = ( + )−1 → = ( + ) −
复合函数
函数与方程
2
二次函数、基本不等式、双勾函数、三角函
数有界性、数形结合、单调性、导数.
基本初等函数
分段函数
, )
零点
求根法、二分法、图象法、二次及三次方程根的分布
建立函数模型
平移变换： = () → = ( ± )， = () → = () ± ，, > 0
与 的关系
1 ，
= 1，
= {
− −1 ， ≥ 2．
构造等差数列
an＋1 p an
= · ＋1 转为③
qn q qn－1
⑤an + 1＝pan＋qn
高中数学人教版(A版)必修思维导图
高中数学人教版（A版）必修必修一第一章 集合与函数概念1.1 集合1.2 函数及其表示1.3 函数的基本性质 第二章 基本初等函数（I ）2.1 指数函数2.2 对数函数2,3 幂函数第三章 函数的应用3.1 函数与方程3.2 函数模型及其应用必修二第一章 空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积第二章 点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质第三章 直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式第四章 圆与方程4.1 圆的方程4.2 直线、圆的位置关系4.3 空间直角坐标系必修三第一章 算法初步1.1 算法与程序框图1.2 基本算法语句 1.3 算法案例 第二章 统计2.1 随机抽样2.2 用样本估计总体 2.3 变量间的相关关系 第三章 概率3.1 随机事件的概率3.2 古典概型3.3 几何概型必修五第一章 解三角形1.3 正弦定理和余弦定理1.2 应用举例1.3 实习作业第二章 数列2.1 数列的概念与简单表示法2.2 等差数列2.3 等差数列的前n 项和2.4 等比数列2.5 等比数列的前n 项和第三章 不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法 3.3 二元一次不等式（组）与简单的线性规划问题3.4 基本不等式必修四第一章 三角函数1.1 任意角的弧度制1.2 任意角的三角函数1.3 三角函数的诱导公式1.4 三角函数的图像与性质1.5 函数y=Asin(wx+m)d 的图像1.6 三角函数模型的简单应用第二章 平面向量2.1 平面向量的实际背景及基本概念2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示2.4 平面向量的数量积2.5 平面向量的应用举例第三章 三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.2 简单的三角恒等变换。