结构动力学4对简谐和周期荷载的反应
结构动力学

第九章结构动力学§9.1概述一、结构动力计算的特点和内容前面各章讨论了结构在静力荷载作用下的计算问题。
它研究的是当结构处于静力平衡位置时,外荷载对结构的影响。
此时,荷载的大小、方向和作用点以及结构产生的内力、位移等均看作是不随时间t变化的。
本章将讨论结构在动力荷载作用下的计算问题。
所谓动力荷载,亦称为干扰力,是指大小、方向和作用位置等随时间t变化,并且使结构产生不容忽视的惯性力的荷载。
与静力计算所不同的是,结构在动力荷载作用下,其质量具有加速度,计算过程中必须考虑惯性力的作用。
结构的内力和位移是位置和时间t的函数,称为动内力和动位移,统称为结构的动力反应。
在实际工程中,绝大多数荷载都是随着时间变化的。
从工程实用角度来说,为了简化计算,往往将使结构产生的振动很小以至于惯性力可以略去不计的荷载视为静力荷载。
例如当人群缓慢行走在桥梁上时,桥梁不会产生明显的振动,这时人群的自重可以作为静力荷载考虑;当人群跑动通过时,桥梁将产生明显的振动,其上各质量将产生不容忽视的惯性力,因而,人群的自重必须作为动力荷载来考虑。
显然,区分静力荷载和动力荷载,主要是看其对结构产生的影响。
本章内容只将不仅随时间变化而且使结构产生较大动力反应的荷载作为动力荷载来考虑。
随着科学技术的迅速发展,研究动力荷载作用下结构的计算方法具有十分重要的工程意义。
在结构设计中,如何减小机器振动对现代化厂房的影响,如何减小风荷载及地震作用引起的高层建筑的动力反应等,都需要对动力荷载的作用进行深入的研究。
结构的动力反应与结构本身的动力特性和动力荷载的变化规律密切相关。
研究结构的自-192--193-由振动,得到的结构自振频率、振型和阻尼参数等正是反应结构动力特性的指标。
因此,研究结构的动力计算方法,需要分析结构的自由振动和动力荷载作用下的受迫振动两种情况,前者计算结构的动力特性,后者进一步计算结构的动力反应。
二、动力荷载的分类根据动力荷载的变化规律及其对结构作用的变化特点,将其分为以下几类:1、简谐性周期荷载 它是按简谐规律随时间连续变化其量值的荷载,可以用正弦或余弦函数表示,也称为简谐荷载,是工程中最常见的动力荷载。
结构动力学3-4

结构动力学
mu cu ku e
H (i j )
1 1 2 k i 1 ( ) [ 2 ( )] j n j n
u (t )
3.8 单自由度体系 对任意荷载的反应
总的稳态反应为:
j
p u (t ) H (i ) p e
Tp
0 Tp
p (t )dt p (t ) cos( j t )dt p (t ) sin( j t )dt n 1 ,2 ,3 , n 1 ,2 ,3 ,
4/71
0 Tp
0
3.7 单自由度体系对周期荷载的反应
当用Fourier级数展开法时,隐含假设周期函数是从-∞开 始 到 +∞ 。 初 始 条 件 (t=-∞) 的 影 响 到 t=0 时 已 完全消 失,仅需计算稳态解,即特解。 对应于每一简谐荷载项作用,体系的反应为:
对时域运动方程两边同时进行Fourier正变换,得 单自由度体系频域运动方程:
2 2U ( ) i 2 nU ( ) n U ( )
(t )e it dt iU ( ) u
(t )e it dt 2U ( ) u
p
1 2
...
τ
dτ du t 1脉 冲 引 起 的 反 应 du
t
du (t ) p ( )d h(t ) , t
2脉 冲 引 起 的 反 应以前所有脉冲作用下反应 的和:
du t τ时 刻 脉 冲 引 起 的 反 应
. . .
单位脉冲及单位脉冲反应函数
p (t ) P( )
结构动力学4

4.2 有阻尼体系的简谐振动
通解uc对应于有阻尼自由振动反应:
u c (t ) = e
−ζω n t
( A cos ω D t + B sin ω D t )
特解up可以设为如下形式 :
u p (t ) = C sin ωt + D cos ωt
p0 && & u + 2ζω n u + ω n u = sin ωt m
1 − (ω / ω n ) 2 C = u st [1 − (ω / ω n ) 2 ]2 + [2ζ (ω / ω n )]2 − 2ζω / ω n D = u st [1 − (ω / ω n ) 2 ]2 + [2ζ (ω / ω n )]2
运动方程的全解:u(t)=uc+up :
u(t ) = e
u (t ) = C sin ωt + D cos ωt = u 0 sin(ωt − ϕ )
u0 —稳态振动的振幅 φ —相角,反映体系振动位移与简谐荷载的相位关系
D 2 2 −1 u 0 = C + D , ϕ = tan (− ) C
u 0 = u st 1 [1 − (ω / ω n ) 2 ] 2 + [ 2ζ (ω / ω n )] 2
uc (t ) = A cos ωn t + B sin ωn t
ωn = k / m
c - complementary
4.1 无阻尼体系的简谐振动
&& mu + ku = p 0 sin ωt
特解—满足运动方程的解,记为up(t) ,是由动 荷载p0sinωt直接引起的振动解。 设特解为:u p (t ) = C sin ωt + D cos ωt
结构动力学4-2

N
而 ωn = K n / M n 。
Cn ζn = 2ω n M n
有阻尼体系振型坐标的运动方程可写为如下形式:
pn (t) && & qn qn (t) = , n = 1, 2,L, N Mn
2
上式即为有阻尼单自由度体系在外荷载作用下的标准运 动方程,可以采用在单自由度动力问题反应分析中的 有关方法进行计算。
n
m
4.3.3 有阻尼体系的振型叠加法
1、满足阻尼阵正交条件
{u (t )} = ∑ {φ}n qn (t )
n =1
N
运动方程化为N个解耦的关于振型坐标的运动方程:
&& & M n qn (t ) + Cn qn (t ) + Kn qn (t ) = pn (t ) n = 1, 2, L, N
Rdn—相应于n阶自振频率的动力放大系数, 或称振型反应的动力放大系数。
4.3.3 有阻尼体系的振型叠加法
1、满足阻尼阵正交条件
从以上分析可以看出,对于满足阻尼正交条件的结构体 系,当采用振型叠加法分析时,多自由度体系的动力反 应问题即转化为一系列单自由度体系的反应问题,并 可以考虑初始条件的影响。 此时在单自由度体系分析中采用的各种分析方法都可以 用于计算分析多自由体系的动力反应问题,使问题的 分析得到极大简化,因为求解N个独立的方程比求解一 个N阶联立的方程组要简便得多。
4.3.3 有阻尼体系的振型叠加法
2、不满足阻尼阵正交条件
采用振型展开:
{u} = ∑{φ}m qm (t )
m =1
L
其中L<N,比如:N=40000,而L=30 —100。 结构的运动方程为:
结构动力学

1. 振动方程及其通解 单自由度粘滞体系强迫运动微分方程为:
m y c y k y P(t )
可变形为:
(2 9)
(2 10)
P(t ) y 2 y y m
2
它是一个二阶常系数非奇次微分方程,通解为相应的 奇次微分方程通解与其一特解之和。
4.0
ξ= 0.1
3.0
2.0
ξ= 0.2 ξ= 0.3 ξ= 0.5 ξ= 1.0
1.0
0
1.0
2.0
η 3.0
•
βmax并不发生在共振θ/ω=η =1时, 而发生在 1 2 2 但因ξ一般很小,
max
1 1 2 2 2 1
1
(2 21)
(4)稳态振动——相位
简谐荷载 P(t)=F sinθt 作用的持时无限,式(2-15)右端按 固有频率振动的第一项很快衰减——瞬态振动; t→∞时,体系 反应仅存按激励率振动的第二项——稳态振动。
(2)特解 对于任意初始条件:
y(0) y0 , y(0) 0
(2 16a) (2 16b)
利用式(2-15)及其对时间的一阶导数方程,可解得:
注:式(2-26)也直接从无阻尼体系的振动反应求得。
静止初始条件下共振荷载反应(频率比等于1)
3. 简谐荷载 P(t )=F cosθt 的稳态反应
类同于简谐荷载 F sinθt 作用下的情形,仍设特解为:
y特 Asin t B cos t
(2 27)
将式(2-27)代入方程(2-10)并注意到 P(t)=F cosθt ,得
(2 24)
R(t )
结构动力学-第三章 单自由度体系 (Part 1)

结构动力学Dynamics of Structures 第三章单自由度体系Chapter 3 Single-Degree-of-Freedom SystemsPart 1华南理工大学土木工程系马海涛/陈太聪本章主要目的及内容目的:z 通过单自由度体系介绍动力学的基本概念z 若干实际问题的解内容:(1)无阻尼自由振动(2)有阻尼自由振动(3)对简谐荷载的反应(4)对周期荷载的反应(5)对任意荷载的反应(6)体系的阻尼和振动过程中的能量(7)隔振(震)原理(8)结构地震反应分析的反应谱法自由振动free vibration强迫振动forced vibration第三章单自由度体系SDOF Systems自由振动:结构受到扰动离开平衡位置以后,不再受任何外力影响的振动过程。
0mucu ku ++= 无阻尼自由振动单自由度系统的运动方程()mucu ku P t ++=00c muku =⇒+= 自由振动运动方程单自由度系统无阻尼自由振动的运动方程0muku += 初始扰动:00(0)(0)t t u u uu ==== 初始位移初始速度二阶齐次常微分方程Homogeneous second orderordinary differential equation无阻尼自由振动的数学模型000;(0),(0)t t muku u u uu ==+=== 初始条件Initial conditions2()0stC ms k e +=设解有以下形式()stu t Ce=代入方程得 C 和s 为待定常数。
因此,方程通解为:121212()n n i ti ts t s tu t C e C eC eC eωω−=+=+或模型求解0muku += 2ms k ⇒+=1,2n ks i mω⇒=±=±()cos sin n n u t A t B tωω=+三角函数形式通解()sin cos n n n n ut A t B t ωωωω=−+00(0)(0)t n t u A u uB u ω====== (0)()(0)cos sin n n nuu t u t tωωω=+(0)(0),nuA uB ω⇒==利用初始条件,我们有单自由度系统无阻尼自由振动问题的解其中n kmω=无阻尼自由振动为简谐运动Simple harmonic motion ωn 称为圆频率或角速度Angular frequency / velocity ()cos sin n n u t A t B tωω=+三角函数形式通解()sin cos n n n n ut A t B t ωωωω=−+振幅无阻尼自由振动问题解的图示(1)振幅–Amplitude of motion[]220(0)(0)n u u u ω⎡⎤=+⎢⎥⎣⎦基本参数(2)固有周期–Natural period of vibration2n nT πω=(3)固有频率–Natural frequency of vibration1n nf T =Hz (赫兹)固有频率s (秒)固有周期rad/s (弧度/秒)固有圆频率单位定义物理量名称2n nT πω=1n nf T =n k m ω=单自由度系统无阻尼自由振动系统参数§3.2 有阻尼自由振动0c uk u m u ++= 运动方程2()0stC ms cs k e ++=设解有以下形式()stu t Ce =代入方程得解为:221,222nc c s m m ω⎛⎞=−±−⎜⎟⎝⎠粘性阻尼模型2ms cs k ++=2c k s s m m++=22n c s s mω++=阻尼系数影响此项的取值进一步决定解的特征Critical damping and damping ration临界阻尼22022n cr n c c m m k c m ωω⎛⎞−=⇒⎜⎟⎝⎠===此时运动方程的解为12ns s ω==−()()n tu t A Bt e ω−=+0mucu ku ++= 验证—分别将两个解代入方程()n tu t Aeω−=()n tu t Bteω−=()22220n t nnnAem m m ωωωω−=−+=()2n t nnAem c k ωωω−−+左端=()()221n t nnnBem t c t kt ωωωω−⎡⎤−++−+⎣⎦左端=()2220n tnnnBec m t m k ωωωω−⎡⎤=−+−+=⎣⎦Critical damping and damping ration运动方程的解为()()n tu t A Bt e ω−=+()()(0)(1)(0)n tn u t u t ut e ωω−=++ (0)(0)n u AuA B ω==−+ 因此,解为根据初始条件,有()()n tn u t A Bt B eωω−=−++⎡⎤⎣⎦ 对应的速度表达式为(0)(0)(0)n A u B u uω==+ 或者(0)()(0)1(0)n t n uu t u t e u ωω−⎡⎤⎛⎞=++⎢⎥⎜⎟⎝⎠⎣⎦(0)()(0)1(0)n t n uu t u t e u ωω−⎡⎤⎛⎞=++⎢⎥⎜⎟⎝⎠⎣⎦ 解的特征由此项控制当阻尼大于临界阻尼时,0mucu ku ++= 220n n uu u ζωω++= 2n crc cm c ζω==其中,阻尼比1221120()s ts ts s u t C e C e<<=+临界阻尼可定义为:体系自由振动反应中不出现往复振动所需的最小阻尼值。
结构动力学 -单自由度体系的振动

13
§2.2 无阻尼自由振动
自由振动(free vibration) :无外界干扰的体系振动形 态称为自由振动(free vibration)。振动是由初始位 移或初始速度或两者共同影响下所引起的。 无阻尼自由振动:如果阻尼系数等于零,则这种自由 振动称为无阻尼自由振动(undamped free vibration)。 假设由于外界干扰,质点离开平衡位置,干扰消失后, 质点将围绕静力平衡点作自由振动。
或:m y ( t) c y ( t) k ( t) y m y g ( t) P e( f t) f
Peff (t ) :等效荷载,即在地面加速度yg (t )影响下,结构的响
应就和在外荷载p (t )作用下的响应一样,只是外荷载 p (t )
等于质量和地面加速度的乘积。
干扰力的大小只能影响振幅A的大小,而对结构自
振周期T的大小没影响。
(2)自振周期与质量平方根成正比,质量越大,则
周期越大;自振周期与刚度的平方根成反比,刚度
越大,则周期越小。要改变结构的自振周期,只有
改变结构的质量或刚度。
24
§2.2 无阻尼自由振动
k g
m
st
(3)把集中质点放在结构上产生最大位移的地方,则可
1、位移以静力平衡位置作为基准的,而这样确定的位移 即为动力响应。
2、在求总挠度和总应力时,要把动力分析的结果与静
力分析结果相加。
9
§2.1运动方程的建立
3、支座运动的影响 结构的动位移和动应力既可以由动荷载引起,也
可以由结构支座的运动而产生。 1)由地震引起建筑物基础的运动; 2)由建筑物的振动而引起安置在建筑物内的设备 基底的运动等等。
第3章简谐荷载反应
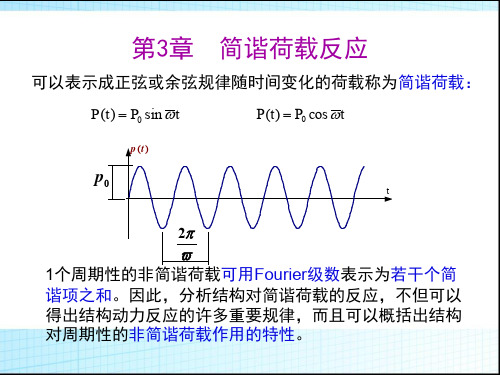
3 方程的通解:
v(t ) vc (t ) v p (t ) e t ( Asind t Bcos d t ) p0 1 2 (1 ) sint 2 cost (4) 2 2 2 k 1 2
方程的通解:
Sint:按体系自振频率振动的反应分量:瞬态反应。
p0 1 [ ] (0) 0 v(0) v 假设 2 k 1 简谐荷载作用下无阻尼体系的动力反应为: A 0, B
p0 1 v(t ) (sint sin t ) 2 k 1
⒋ 反应比:动力位移和静力位移的比值。即动力反应与同样的、 但静止作用的荷载所产生的位移的比值。 p0/k = Dst: 将荷载p0 静止地放在体系上所产生的位移;
v(t ) sint
p0 k
反应振幅:
1 2 (1 2 )2 ( 2 )2 (1 2 )2 ( 2 )2
2
2
2
p0 k
1 2
2 2
v(t ) vc (t ) v p (t ) e t ( Asind t Bcos d t ) p0 1 2 ( 1 ) sint 2 cost (4) 2 2 2 k 1 2
式中,常数A、B由初始条件确定。
第一项按自振频率d 振动,由初始条件确定的自由振动反 应。由于阻尼,这一项很快会衰减为零,即瞬态反应; 第二项按荷载频率 振动,即稳态反应,也称为强迫振动 反应。 ; 有些场合,如冲击荷载、地震等,应分析瞬态反应; 一般情况下,瞬态反应对结构强迫振动分析的意义不大, 这里主要讨论稳态反应的特性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
待定系数A、B由初值条件确定
A u(0)
B
u(0)
n
p0 k
/n 1 ( /n )2
u t0 u(0) ut0 u(0)
4.1 无阻尼体系的简谐振动
满足初始条件的解 :
瞬态反应
u(t)
u(0) cosnt
u(0)
n
p0 k
/ n 1 ( / n )2
sin nt
p0 k
1
1 ( / n )2
特解up可以设为如下形式 :
u p (t) C sin t D cost
u 2 nu n 2u
p0 m
sin t
(n2
2 )C
2 nD
p0 m
sin
t
2 nC
(n2
2)D
cost
0
4.2 有阻尼体系的简谐振动
1
(
n
)
2
C
(2
)D
n
ust
(2
)C
n
1
(
n
)2
D
运动方程:mu cu ku p0 sin t
初始条件:
u t0 u(0)
,ut0 u(0)
利用c=2mωnζ,并将运动方程两边同除m, 得到如下形式的运动方程:
u 2 nu n 2u
p0 m
sin t
4.2 有阻尼体系的简谐振动
通解uc对应于有阻尼自由振动反应:
uc (t) ent ( A cos Dt B sin Dt)
sin t
瞬态反应和稳态反应
稳态反应
4.1 无阻尼体系的简谐振动
稳态反应
:
u(t)
p0 k
1
1 ( / n )2
sin t
u0—稳态反应的振幅:
u0
p0 k
1
1 ( / n )2
ust—等效静位移,或静位移:
u st
p0 k
Rd—动力放大系数:
Rd
u0 u st
1
1 ( / n )2
4.1 无阻尼体系的简谐振动
0
C
u st
[1
(
1 ( /n )2 ]2
/n )2 [2 (
/n
)]2
D
u st
[1
(
2 /n / n )2 ]2 [2
(
/
n
)]2
运动方程的全解:u(t)=uc+up :
u(t) ent (AcosDt B sin Dt) C sin t D cost
4.2 有阻尼体系的简谐振动
4.2 有阻尼体系的简谐振动
(2)动力放大系数Rd(dynamic magnification factor) 振动的稳态解:
u(t) C sint D cost u0 sin(t )
u0 —稳态振动的振幅
φ —相角,反映体系振动位移与简谐荷载的相位关系
u0
C 2 D2 , tan1 ( D )
结构动力学
(2010)
结构动力学
第四章
单自由度体系对 简谐和周期荷载的反应
单自由度体系对简谐荷载作用下的反应是 结构动力学中的一个经典内容。
不仅工程中实际存在这种形式的荷载,而 且简谐荷载作用下单自由度体系的解提 供了了解结构动力特性和用于分析更复 杂荷载作用反应的手段和方法。
4.1 无阻尼体系的简谐振动
1 2
时, Rd
1 ,即体系不发生放大反应。
(2) 当
1 2
时, (Rd ) max
2
1,
1 2
(
n
) 峰值
1 2 2 。
(3)
当 /n
1 (共振时), Rd
1
2
。
(4) 当 / n 2 时, Rd 1 ,对任意 ζ 均成立。
4.2 有阻尼体系的简谐振动
(3)阻尼体系动力反应与荷载的相位关系
图4.3 有初始条件影响的动力反应时程
4.2 有阻尼体系的简谐振动
(1)共振反应(ω=ωn)
C
u st
[1
(
1 ( /n )2 ]2
/n )2 [2 (
/n
)]2
D
u st
[1
(
2 /n / n )2 ]2 [2
(
/
n
)]2
u(t)
ent ( AcosDt
B sin Dt)
ust
2
cost
C
u0 ust
1
[1 ( / n )2 ]2 [2 ( / n )]2
tan1 2 ( / n ) 1 ( / n )2
C
u
st
[1
(
/
1 n
( )2 ]2
/n )2 [2 (
/
n
)]2
D
u
st
[1
(
/
n )
2 /n 2 ]2 [2
(
/
n
)]2
namic magnification factor)
C
p0 k
1
1
( /
n
)2
,
mu ku p0 sint
D0
其构中自,振ω频/ω率n—之频比率;比,外荷载的激振频率与结
p—particular
4.1 无阻尼体系的简谐振动
全解=通解+特解
u(t) uc (t) up (t)
Acosnt B sin nt
p0 k
1
1 ( / n )2
sin t
为无阻尼自由振动:
uc (t) Acosnt B sin nt n k / m
c - complementary
4.1 无阻尼体系的简谐振动 mu ku p0 sint
特荷解载—p满0s足inω运t直动接方引程起的的解振,动记解为。up(t) ,是由动
设特解为:up (t) C sint D cost
C 0, D ust
2
满足零初始条件
A
1
2
ust
,
B 2
1
1 2
ust
运动解:
u(t)
ust
2
ent (cosDt
1
2
sinDt) cosnt
当ζ=0时 :
u(t)
u st 2
nt
c os n t
与无阻尼时的结果完全相同
(1)有阻尼体系的共振反应(ω=ωn) 图4.4 有阻尼体系共振反应时程
无阻尼体系动力放大系数
Rd
u0 u st
1
1 ( / n )2
①ω=0 ,Rd =1
②ω=ωn,Rd → ∞ 发生共振
③ω/ωn≥√2, Rd≤1
4.1 无阻尼体系的简谐振动
无阻尼体系共振时动力反应时程
共振时(ω=ωn):
u
p
(t)
u st 2
nt
c os n t
4.2 有阻尼体系的简谐振动
动力放大系数定义为 :
Rd
u0 u st
1
u0 ust [1 ( / n )2 ]2 [2 ( / n )]2
1
Rd [1 ( / n )2 ]2 [2 ( / n )]2
(2)动力放大系数Rd
Rd
1
[1 ( / n )2 ]2 [2 ( / n )]2
(2)动力放大系数Rd
(1) 当
运动方程:
mu ku p0 sint
其中:p0 —简谐荷载的幅值; ω —简谐荷载的圆频率。
初始条件 :
u t0 u(0) ,ut0 u(0)
4.1 无阻尼体系的简谐振动 mu ku p0 sint
运动方程是带有初值条件的二阶常微分方程, 全解=齐次方程的通解+特解
通解对应的方程是一个自由振动方程,其解uc
