(完整版)南邮电磁场第3章习题解答
电磁场与电磁波第三章作业题解答

第三章 恒定电流与恒定电场 作业习题解答3-1.半径为a 和b 的同心球,内球的电位为0u U =,外球的电位为0u =,两球之间介质的电导率为σ,试求这个球形电阻器的电阻。
解 设内球与外球之间的总电流为I ,而体电流密度矢量J V 在半径为r 的球面上大小相等,沿e r 方向,由此可写出电流密度矢量为24V r Ir =p J e 根据欧姆定律V =s J E 得到两球间的电场强度矢量24r Ir =ps E e由电场强度矢量,可计算两球间的电压,有2201444bbbrr aaa I IU d dr dr rr Ib aU ab πσπσπσ=⋅=⋅=-==⎰⎰⎰E l e e由此可得两球间的电阻为 014U b a R I ab-==ps 3-2.已知电流密度矢量22221022(A/m )V x y z y z x y x z J e e e =-+,试求:(1)穿过面积3x =,23y ≤≤,3.8 5.2z ≤≤,沿e x 方向的总电流;(2)在上述面积中心处电流密度的大小;(3)在上述面积上电流密度X 方向的分量J x 的平均值。
解 (1)根据电流I 与电流密度矢量J V 之间的通量关系()VS I d =⋅⎰⎰JS则穿过面积3x =,23y ≤≤,3.8 5.2z ≤≤,沿e x 方向的总电流为()33522222381022..x xy z x .I y z x y x z dydz =-+⋅⎰⎰ee e e()352223810399A ..y zdydz ==⎰⎰(2)面3x =,23y ≤≤,3.8 5.2z ≤≤中心处的坐标为3x =, 2.5y =, 4.5z = 代入J V 的表达式,得到2222222102210 2.5 4.523 2.523 4.5281.254581(A/m )V x y zx y z x y z y z x y x z J e e e e e e e e e =-+=⨯⨯-⨯⨯+⨯⨯=-+ 电流密度矢量的大小为2296.12(A/m )V V J J ==≈(3)面3x =,23y ≤≤,3.8 5.2z ≤≤上电流密度的平均值为()()()2399285A/m 325238x x I J S ..===-- 由此可以看出,由于电流密度矢量非均匀,X 方向平均电流密度的大小与该面中心处的电流密度大小不相等。
电磁场与电磁波:第三章作业答案
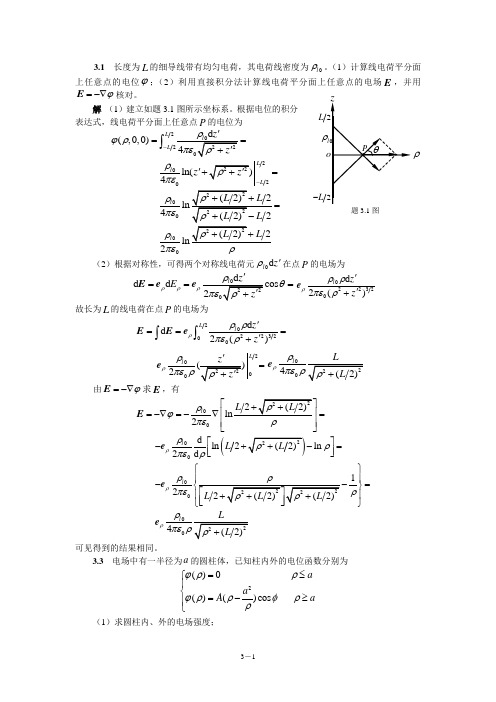
3.1 长度为L 的细导线带有均匀电荷,其电荷线密度为0l ρ。
(1)计算线电荷平分面上任意点的电位ϕ;(2)利用直接积分法计算线电荷平分面上任意点的电场E ,并用ϕ=-∇E 核对。
解 (1)建立如题3.1图所示坐标系。
根据电位的积分表达式,线电荷平分面上任意点P 的电位为2(,0,0)L L ϕρ-==⎰2ln(4L l L z ρπε-'+=04l ρπε=02l ρπε (2)根据对称性,可得两个对称线电荷元z l 'd 0ρ在点P 的电场为d d E ρρρθ'===Ee e 022320d 2()l z z ρρρπερ''+e故长为L 的线电荷在点P 的电场为2022320d d 2()L l z z ρρρπερ'==='+⎰⎰E E e20002L l ρρπερ'=e ρe 由ϕ=-∇E 求E ,有002l ρϕπε⎡⎢=-∇=-∇=⎢⎥⎣⎦E(00d ln 2ln 2d l L ρρρπερ⎡⎤-+-=⎢⎥⎣⎦e0012l ρρπερ⎧⎫⎪--=⎬⎪⎭e ρe可见得到的结果相同。
3.3 电场中有一半径为a 的圆柱体,已知柱内外的电位函数分别为2()0()()cos a a A aϕρρϕρρφρρ=≤⎧⎪⎨=-≥⎪⎩(1)求圆柱内、外的电场强度;L L -ρρ题3.1图(2)这个圆柱是什么材料制成的?表面有电荷分布吗?试求之。
解 (1)由ϕ=-∇E ,可得到a ρ<时, 0ϕ=-∇=Ea ρ>时, ϕ=-∇=E 22[()cos ][()cos ]a a A A ρφρφρφρρρφρ∂∂----=∂∂e e 2222(1)cos (1)sin a a A A ρφφφρρ-++-e e(2)该圆柱体为等位体,所以是由导体制成的,其表面有电荷分布,电荷面密度为0002cos S n a a A ρρρρεεεφ=====-e E e E3.4 已知0>y的空间中没有电荷,下列几个函数中哪些是可能的电位的解? (1)cosh y e x -; (2)x e y cos -;(3)cos sin e x x (4)z y x sin sin sin 。
电磁场与电磁波习题第3章概要

0
b1 1 Ir I 0 2 rdr 0 2 rdr 2 a 2 2 a 2 2 r
0 I 2 0 I 2 b Wm ln 16 4 a
d
0 I 2 0 I 2 b 1 2 LI Wm ln 2 16 4 a
2 4 U 0 4 U 0 P = IU = U0 1 1 1 1 a b a b
U0 U 1 1 1 R= = 4 U 0 I 4 a b 1 1 a b
3—3 一个半径为a的导体球作为电极深埋地下,土壤的电导率 为σ 。略去地面的影响,求电极的接地电阻。 解;当不考虑地面影响时,这个问题就相当于计算位于无限 大均匀导电媒质中的导体球的恒定电流问题。设导体球的电流 为I,则任意点的电流密度为
2
将M 0 2、L 0.1、a 0.02代入上式可得 m=2 0.1 0.02 2.512 10
2 4
A m
2
(M0为常数),求磁化电流的体密度和面密度。 解:磁化电流的体密度为
z2 3—19 球心在原点、半径为d的磁化介质球中,M ez M 0 2 a
3—26 空气绝缘的同轴线,内导体的半径为 a,外导体的内半 径为 b,通过的电流为I。设外导体壳的厚度很薄,因而其储存 的能量可以忽略不计。计算同轴线单位长度的储能,并由此求 单位长度的自感。
I 解:设内导体的电流均匀分布,则电流密度为: J 2 a
根据安培环路定律
C
H dl I
z2 J m M= ez M 0 2 a er ez e r r er M z M z Jm e =0 r z r r 0 0 Mz
电磁场与电磁波(第4版)第3章部分习题参考解答
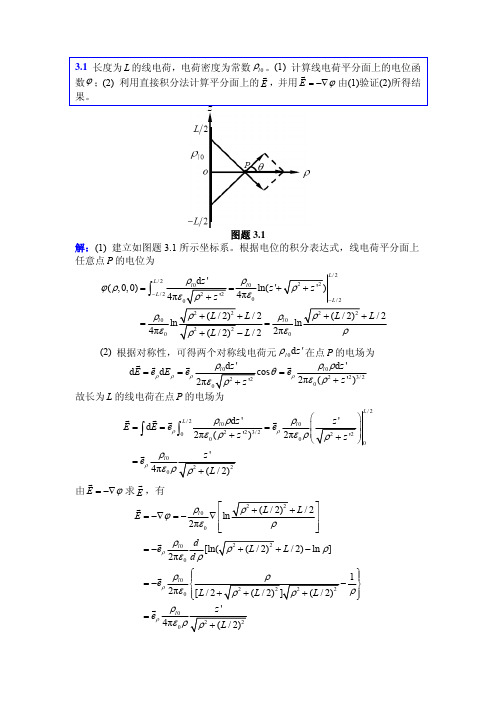
ε − ε 0 3 cos θ a E0 2 r ε + 2ε 0
(r ≥ a)
ϕ =0
ρ ( x)
ϕ = U0
0
d
图题 3.7
x
解:两导体板之间的电位满足泊松方程 ∇ 2ϕ = −
ρ d 2ϕ 1 ρ0 x ,故得 2 = − dx ε0 d ε0
解此方程,得
ϕ =−
ρ0 x3 + Ax + B 6ε 0 d
ρ 2 + ( L / 2) 2 + L / 2 ρl 0 ρ 2 + ( L / 2) 2 + L / 2 ρl 0 = ln ln ρ 4πε 0 ρ 2 + ( L / 2) 2 − L / 2 2πε 0
(2) 根据对称性,可得两个对称线电荷元 ρ l 0 dz ′ 在点 P 的电场为 G G ρl 0dz ' ρ l 0 ρ dz ' G G dE = eρ dEρ = eρ cos θ = eρ 2πε 0 ( ρ 2 + z '2 )3/ 2 2πε 0 ρ 2 + z '2 故长为 L 的线电荷在点 P 的电场为
G G G L/2 E = ∫ dE = eρ ∫
0
ρl 0 ρ dz ' z' G ρl 0 ⎛ e = ⎜ ρ 2 2 3/ 2 2 2 2πε 0 ( ρ + z ' ) 2πε 0 ρ ⎜ ⎝ ρ + z'
z'
2
⎞ ⎟ ⎟ ⎠0
L/2
G = eρ
ρl 0 4πε 0 ρ
ρ + ( L / 2) 2
3.8 试证明:同轴线单位长度的静电储能 We =
电磁学答案第3章

电磁学答案第3章第三章 静电场的电介质3.2.1 偶极矩为p →=q l →的电偶极子,处于场强为E 的外电场中,p →与E →的夹角为θ。
(1) 若是均匀的,θ为什么值时,电偶极子达到平衡?(2)如果E 是不均匀的,电偶极子能否达到平衡? 解: (1)偶极子受的力:F + =F _=qE因而F →+=-F →_∴偶极子受合力为零。
偶极子受的力矩T =p ⨯E即 T=qEsin θ当 T=0时,偶极子达到平衡,∴ pEsin θ=0p →≠0 E →≠0 ∴θ=0 , πθ=0这种平衡是稳定平衡。
θ=π是不稳定平衡。
(2) 当E →不是均匀电场时,偶极子除受力矩外还将受一个 力(作用在两个点电荷的电场力的合力)。
所以不能达到平衡。
3.2.2 两电偶极子1p→和2p →在同一直线上,所以它们之间距r比它们自己的线度大的很多。
证明:它们的相互作用力的大小为F=402123rp p πε,力的方向是:1p→与2p→同方向时互相吸引,反方向时互相排斥。
证: 已知当r >>l 时,偶极子在其延长线上一点的场强:E →=302rpπε→当 1p →与2p →同方向时,如图2p →所受的力的大小:+→F =E →q=r lr q p ∧+3201)2(2πε-→F = -E→q=r lr q p ∧--3201)2(2πε∴F→= +→F +-→F =r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =r l r l l r q p ∧⎥⎦⎤⎢⎣⎡---⋅3222322201)2()2(2262πε略去 422l 及 832l 等高级小量。
F→=-r r qlp ∧402146πε= -r r pp ∧402123πε当 1p →与2p →反方向时(如图),同理: F→= r l r l r q p ∧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--+323201)2(1)2(12πε =012πεq p ⨯r lr l l r ∧-+32223222)4()2(23略去高级小量得:F→=r rP P ∧402123πε3.2.3 一电偶极子处在外电场中,其电偶极矩为 ,其所在处的电场强度为 。
(完整word版)南京邮电大学电磁场与电磁波考试必背公式

电磁场与电磁波复习第一部分 知识点归纳 第一章 矢量分析1、三种常用的坐标系 (1)直角坐标系微分线元:dz a dy a dx a R d z y x →→→→++= 面积元:⎪⎩⎪⎨⎧===dxdy dS dxdz dS dydzdS zyx,体积元:dxdydz d =τ(2)柱坐标系长度元:⎪⎩⎪⎨⎧===dz dl rd dl drdl z r ϕϕ,面积元⎪⎩⎪⎨⎧======rdrdz dl dl dS drdz dl dl dS dz rd dl dl dS z z z r z r ϕϕϕϕ,体积元:dz rdrd d ϕτ=(3)球坐标系长度元:⎪⎩⎪⎨⎧===ϕθθϕθd r dl rd dl dr dl r sin ,面积元:⎪⎩⎪⎨⎧======θϕθϕθθθϕϕθθϕrdrd dl dl dS drd r dl dl dS d d r dl dl dS r r r sin sin 2,体积元:ϕθθτd drd r d sin 2=2、三种坐标系的坐标变量之间的关系 (1)直角坐标系与柱坐标系的关系⎪⎪⎩⎪⎪⎨⎧==+=⎪⎩⎪⎨⎧===z z x y y x r z z r y r x arctan,sin cos 22ϕϕϕ (2)直角坐标系与球坐标系的关系 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=⎪⎩⎪⎨⎧===z yz y x z z y x r r z r y r x arctan arccos ,cos sin sin cos sin 222222ϕθθϕθϕθ (3)柱坐标系与球坐标系的关系⎪⎪⎩⎪⎪⎨⎧=+=+=⎪⎩⎪⎨⎧===ϕϕθθϕϕθ22'22''arccos ,cos sin z r z zr r r z r r 3、梯度(1)直角坐标系中:z a y a x a grad z y x ∂∂+∂∂+∂∂=∇=→→→μμμμμ(2)柱坐标系中:za r a r a grad zr ∂∂+∂∂+∂∂=∇=→→→μϕμμμμϕ1 (3)球坐标系中: ϕμθθμμμμϕθ∂∂+∂∂+∂∂=∇=→→→sin 11r a r a r a grad r4.散度(1)直角坐标系中:z A y A x AA div z y X ∂∂+∂∂+∂∂=→ (2)柱坐标系中:zA A r rA r r A div zr ∂∂+∂∂+∂∂=→ϕϕ1)(1 (3)球坐标系中:ϕθθθθϕθ∂∂+∂∂+∂∂=→A r A r A r rr A div r sin 1)(sin sin 1)(1225、高斯散度定理:⎰⎰⎰→→→→=⋅∇=⋅ττττd A div d A S d A S,意义为:任意矢量场→A 的散度在场中任意体积内的体积分等于矢量场→A 在限定该体积的闭合面上的通量。
电磁场与电磁波理论_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年

电磁场与电磁波理论_南京邮电大学中国大学mooc课后章节答案期末考试题库2023年1.均匀平面波由空气垂直入射到理想介质平面,若入射波是左旋圆极化波,则反射波和折射波分别为()。
参考答案:右旋圆极化波,左旋圆极化波2.良导体趋肤效应是指场强以及电流密度主要分布在。
参考答案:导体表面3.均匀平面波的左旋圆极化波是指当我们将左手的大姆指指向电磁波的方向,其余四指指向电场矢量端点的方向。
参考答案:传播,旋转4.镜像法是指利用镜像电荷代替面或面的影响,利用原电荷和镜像电荷来计算场分布。
参考答案:导体,介质5.在静电场的__________,电位满足的是泊松方程;在静电场的__________,电位满足的是拉普拉斯方程。
参考答案:有源区,无源区6.均匀平面波是指电磁波的传播方向为直线,等相位面为,且在等相位面上各点的电磁场的大小和方向都是的。
参考答案:平面,相等7.均匀平面波是横电磁波,即没有方向的分量。
参考答案:纵向8.均匀平面波是横电磁波,该波的电场和磁场的的大小之比等于媒质的。
参考答案:波阻抗9.均匀平面波的右旋圆极化波是指当我们将右手的大姆指指向电磁波的方向,其余四指指向的是电场矢量的端点的方向。
参考答案:传播,旋转10.均匀平面波极化,磁场强度矢量的变化规律与电场强度矢量的变化规律是。
参考答案:一样11.镜象法的关键是要确定镜像电荷的__________、__________和__________,使场量原来所满足的方程及其边界条件保持不变。
大小,符号,位置12.利用分离变量法求解静电场边值问题时,最重要的就是确定既能满足_________又能满足_____________的每个分离函数的具体形式:三角函数、指数函数和线性函数。
参考答案:边界条件,拉普拉斯方程13.直接求解给定边界条件下一维电位分布所满足的二维常微分方程,称为__________。
参考答案:直接积分法14.关于导电媒质的复介电常数和复磁导率,说法正确的是:参考答案:复介电常数和复磁导率的实部分别对应导电媒质的介电常数和磁导率,虚部分别表示电损耗和磁损耗15.使用麦克斯韦积分方程推导时变电磁场的边界条件时,为得到法向分量的边界条件,需在界面附近取一个,为得到切向分量的边界条件,需在界面附近取一个。
电磁场与电磁波课后习题及答案三章习题解答

电磁场与电磁波课后习题及答案三章习题解答三章习题解答3.1 真空中半径为a 的⼀个球⾯,球的两极点处分别设置点电荷q 和q -,试计算球⾚道平⾯上电通密度的通量Φ(如题3.1图所⽰)。
解由点电荷q 和q -共同产⽣的电通密度为33[]4q R R π+-+-=-=R R D 22322232()(){}4[()][()]r z r z r z a r z a q r z a r z a π+-++-+-++e e e e 则球⾚道平⾯上电通密度的通量d d zz SSS Φ====??D S D e22322232()[]2d 4()()aq a ar r r a r a ππ--=++? 22121)0.293()aqaq q r a =-=-+ 3.2 1911年卢瑟福在实验中使⽤的是半径为a r 的球体原⼦模型,其球体内均匀分布有总电荷量为Ze -的电⼦云,在球⼼有⼀正电荷Ze (Z 是原⼦序数,e 是质⼦电荷量),通过实验得到球体内的电通量密度表达式为02314ra Ze r r r π??=-D e ,试证明之。
解位于球⼼的正电荷Ze 球体内产⽣的电通量密度为 124rZer π=D e 原⼦内电⼦云的电荷体密度为 333434a a Ze Zer r ρππ=-=- 电⼦云在原⼦内产⽣的电通量密度则为 32234344r ra r Ze rr r ρπππ==-D e e题3.1 图题3. 3图()a故原⼦内总的电通量密度为 122314ra Ze r r r π??=+=-D D D e 3.3 电荷均匀分布于两圆柱⾯间的区域中,体密度为30C m ρ, 两圆柱⾯半径分别为a 和b ,轴线相距为c )(a b c -<,如题3.3图()a 所⽰。
求空间各部分的电场。
解由于两圆柱⾯间的电荷不是轴对称分布,不能直接⽤⾼斯定律求解。
但可把半径为a 的⼩圆柱⾯内看作同时具有体密度分别为0ρ±的两种电荷分布,这样在半径为b 的整个圆柱体内具有体密度为0ρ的均匀电荷分布,⽽在半径为a 的整个圆柱体内则具有体密度为0ρ-的均匀电荷分布,如题3.3图()b 所⽰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章习题解答3.1 对于下列各种电位分布,分别求其对应的电场强度和体电荷密度:(1)()2,,x y z Ax Bx C Φ=++; (2)(),,x y z Axyz Φ=;(3)()2,,sin z A B z Φρϕρϕρ=+; (4)()2,,sin cos r Ar Φθϕθϕ=。
解:已知空间的电位分布,由E Φ=-∇r r 和20/Φρε∇=-可以分别计算出电场强度和体电荷密度。
(1) ()2x E e Ax B Φ=-∇=-+r r r0202εερA -=Φ∇-=(2) ()x y z E A e yz e xz e xy Φ=-∇=-++r r r r r020=Φ∇-=ερ(3) (2sin )cos z E e A Bz e A e B ρϕΦρϕρϕρ⎡⎤=-∇=-+++⎣⎦r r r r20004sin sin 3sin Bz Bz A A A ρεΦεϕϕεϕρρ⎛⎫⎛⎫=-∇=-+-=-+ ⎪ ⎪⎝⎭⎝⎭(4) ()2sin cos cos cos sin r E e Ar e Ar e Ar θϕΦθϕθϕϕ=-∇=-+-r r r r r200cos 2cos cos 6sin cos sin sin A A A θϕϕρεΦεθϕθθ⎛⎫=-∇=-+- ⎪⎝⎭3.5 如题3.5图所示上下不对称的鼓形封闭曲面,其上均匀分布着密度为0S ρ的面电荷。
试求球心处的电位。
解:上顶面在球心产生的电位为22001111100()()22S S d R d R d ρρΦεε=+-=- 下顶面在球心产生的电位为22002222200()()22S S d R d R d ρρΦεε=+-=- 侧面在球心产生的电位为030014π4πS S SSRRρρΦεε==⎰式中212124π2π()2π()2π()S R R R d R R d R d d =----=+。
因此球心总电位为1230S R ρΦΦΦΦε=++=3.6有02εε=和05εε=的两种介质分别分布在0z >和0z <的半无限大空间。
已知0z >时,201050x y z E e e e =-+r r r rV /m 。
试求0z <时的D r 。
解:由电场切向分量连续的边界条件可得1t 2t1212x xy y E E E E E E =⇒== 222010x y E E ⇒==-000520510x y z D D εε⇒<=⨯=-⨯代入电场法向方向分量满足的边界条件可得1n 2n1202250z z z D D D D D ε=⇒=⇒⨯= 200100z z D ε⇒<=于是有000010050100x y z z D e e e εεε<=-+r r r r3.9 如题3.9图所示,有一厚度为2d 的无限大平面层,其中充满了密度为()()0cos π/x x d ρρ=的体电荷。
若选择坐标原点为零电位参考点,试求平面层之内以及平面层以外各区域的电位和电场强度。
解:由对称性可知0y zΦΦ∂∂==∂∂,即222222222d d x y z x ΦΦΦΦΦ∂∂∂∇=++=∂∂∂。
设各区域中的电位和电场强度分别为1Φ,2Φ,3Φ和1E ρ,2E ρ,3E ρ。
由电位所满足的微分方程2012d πcos d x x d ρΦε⎛⎫=- ⎪⎝⎭222d 0d x Φ= 232d 0d x Φ= 解得011d πsin d πd x C x d ρΦε⎛⎫=-+ ⎪⎝⎭22d d C x Φ= 33d d C xΦ= 201112πcos πd x C x D d ρΦε⎛⎫=++ ⎪⎝⎭222C x D Φ=+ 333C x D Φ=+由于理想介质分界面没有面电荷,所以边界条件为d x =时 12ΦΦ= 12d d d d x xΦΦεε= d x -=时 13ΦΦ= 310d d d d x xΦΦεε=又根据对称性可知,在0=x 的平面上,电场强度是为零的,即0=x 时,1d /d 0x Φ=。
最后再选择零电位参考点使得0=x 时,()100Φ=。
联立解得0321===C C C 2012πd D ρε=- 202322πd D D ρε==-。
只要利用d d x Ee xΦ=-∇Φ=-r r r 就可以得到d x -<时, 20322πd ρΦε=- 33d 0d xE e xΦ=-=r r d x d ≤≤-时 2200122πcos ππd x d d ρρΦεε⎛⎫=- ⎪⎝⎭ 011d πsin d πx x d x E e e x d ρΦε⎛⎫=-= ⎪⎝⎭r r r d x >时, 20222πd ρΦε=- 22d 0d xE e xΦ=-=r r ✶ 选择不同的零电位参考点,得到的电位不同,但电场强度仍是相同的。
✶ 根据对称性只需求出0>x 的解,即1Φ和23ΦΦ=。
3.10 位于0x =和x d =处的两个无限大导电平面间充满了()01x d ρρ=+的体电荷。
若将0x =处的导电平板接地,而将x d =处的导电平板加上电压0U 。
试求板间的电位分布及电场强度为零的位置。
解:由于无限大导体极板之间电荷分布是只与x 有关,忽略边缘效应,可以认为电位分布也只与x 有关,且满足一维泊松方程2020d 1d x x d ρΦε⎛⎫=-+ ⎪⎝⎭ 其通解为 32001200()62x x x C x C d ρρΦεε=--++ 由(0)0Φ= ⇒ 02=C 而由0()d U Φ= ⇒ 000132ερd d U C +=因此板间电位分布为 3200000002()623U d x x x x d d ρρρΦεεε⎛⎫=--++ ⎪⎝⎭板间电场强度为 20000000223x U d E e x x d d ρρρΦεεε⎡⎤⎛⎫=-∇=+-+⎢⎥ ⎪⎝⎭⎣⎦r r r 从该式可以求出电场强度为零的位置为20000022000000000002423224 13U d d d U d b b ac x d d d d dρρρρεεεεερρρεε⎛⎫-±++ ⎪⎛⎫-±-⎝⎭===-±++ ⎪⎝⎭ 由于我们是讨论极板内电场强度,因此零点位置为000002213U d x d d d d ερρε⎛⎫=-+++ ⎪⎝⎭3.11 如题3.11图所示的平板电容器中,分别以两种不同的方式填充两种不同的介质1ε和2ε。
当两极板之间外加电压0U 时,试求电容器中电位和电场的分布以及电容器的电容。
解:对于图a :忽略边缘效应,可以认为电位分布也只与x 有关,均满足一维拉普拉斯方程。
且由介质分界面的边界条件可知,两种介质中的电位分布是相同的,其通解为Cx D Φ=+根据已知条件00x Φ==和02x dU Φ==,解得0D =和02U C d=,即平板电容器中的电位分布为2U x dΦ=根据E Φ=-∇r r ,可以得到平板电容器中的电场分布为 0d d 2x x U E e e x dΦΦ=-∇=-=-r r r r对0=x 平板上n x e e =r r,面电荷密度分别为()01n n 02 2 2S U y S d e D e E U y Sd ερεε⎧-∈⎪⎪=⋅=⋅=⎨⎪-∈⎪⎩r r r r 上下 总电量为 ()0012120222U U SQ S S U d d dεεεε=-⋅-=-+电容器的电容为 ()1202Q S C U dεε==+ 对于图b :忽略边缘效应,可以认为电位分布也只与x 有关,均满足一维拉普拉斯方程。
两种介质中的电位分布的通解可以分别设为111C x D Φ=+ 和 222C x D Φ=+根据已知条件100x Φ==和202x dU Φ==,以及分界面处的边界条件12x d x d ΦΦ===和12x dx dxxΦΦ==∂∂=∂∂可以解得20112U x dεΦεε=+ 和202012U x d U d εΦεε-=++根据E Φ=-∇r r,可以得到平板电容器中两种介质中的电场分布为0121112d d x x U E e e x d ΦεΦεε=-∇=-=-+r r r r 和 0212212d d x xU E e e x dΦεΦεε=-∇=-=-+r r r r 对0=x 平板上n x e e =r r,面电荷密度为 ()012n n 112 S x U e D e E e dεερεεε=⋅=⋅=-+r r r r r总电量为 121222S SQ S U d εερεε=⋅=-+ 电容器的电容为 120122Q SC U dεεεε==+3.12 已知在半径为a 的无限长圆柱形体内均匀分布着电荷密度为0ρ的体电荷。
圆柱体内外的介电常数分别为ε和0ε。
若取圆柱体的表面为零电位的参考面,试利用直接积分法求出圆柱体内外的电位和电场强度。
解:取定圆柱坐标系,使z 轴与圆柱体的中心轴线相重合,由电位和电场的对称性可知Φ与ϕ和z 无关。
圆柱体内外的电位1Φ和2Φ满足的微分方程分别为01d 1d d d ρΦρρρρε⎛⎫=- ⎪⎝⎭和 020d 1d d d ρΦρρρρε⎛⎫=- ⎪⎝⎭ 它们的通解可以分别表示式为 ()20111ln 4C D ρΦρρρε=-++ 和 222ln C D Φρ=+ 由轴线上的电位应为有限值可得10C =。
而由圆柱体的表面电位为零可得20104a D ρε-+= 和 22ln 0C a D += 即 2014D a ρε= 和 22ln D C a =- 于是有 ()()22014a ρΦρρε=-- 和 22ln C aρΦ= 代入圆柱体表面电位的法向导数的边界条件12r ar arrΦΦεε==∂∂=∂∂得到0202a C a ρε=-,即20202a C ρε=-。
最后得到圆柱体内外的电位分别为 ()()22014a ρΦρρε=- 和 2020ln 2a aρρΦε=- 而圆柱体内外的电场强度分别为 01110d d 2E e e ρρρρΦΦρε=-∇=-=r r r r 和 202220d d 2a E e e ρρρΦΦρερ=-∇=-=r r r r 3.13 如题3.13图所示,半径为a 的无限长导体圆柱,单位长度的带电量为l ρ。
其一半埋于介电常数为ε的介质中,一半露在空气中。
试求各处的电位和电场强度。
解:根据题意,空间中电位分布与ϕ和z 无关,均满足一维的拉普拉斯方程,即()()211222d 1d 0d d d 1d 0d d r r ΦΦρρρΦΦρρρ⎛⎫∇== ⎪⎝⎭⎛⎫∇== ⎪⎝⎭介质中空气中将上述两方程分别直接积分两次,得出通解为 111ln C D Φρ=-+ 和 222ln C D Φρ=-+ 根据不同介质分界面电位的连续性可知12C C C ==和12D D D ==,即 12ln C D ΦΦΦρ===+ 若设无限长导体圆柱上电位为0,也即()0a Φ=,可得ln D C a =-,即lnC aρΦ=导体圆柱的面电荷密度为 ()()0S CCεΦρεερ⎧-∂⎪=-=⎨-∂⎪⎩介质中空气中单位长度导体圆柱的电量为 0ππl C a C a ρεε=--即 0π()l C ρεε=-+于是得到导体圆柱外的电位和电场强度分别为0ln π()l a ρΦεερ=+ 和 0π()l E e ρρΦεερ=-∇=+r r3.14 如题3.14图所示同轴电容器,其中部分填充了介质ε,其余是空气。
