小学四年级奥数题库：几何计数问题(中等难度)_题型归纳

四年级奥数—几何中的计数问题

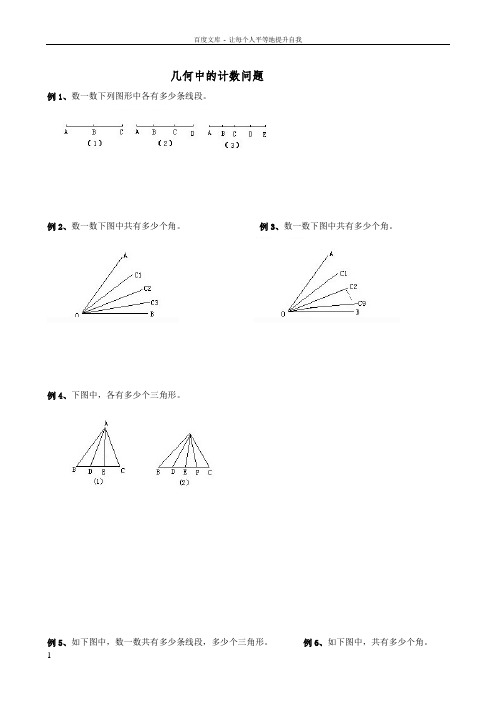
几何中的计数问题
例1、数一数下列图形中各有多少条线段。

例2、数一数下图中共有多少个角。

例3、数一数下图中共有多少个角。

例4、下图中，各有多少个三角形。

例5、如下图中，数一数共有多少条线段，多少个三角形。

例6、如下图中，共有多少个角。

例7、如下图，数一数共有多少个长方形。

例8、数一数下图中长方形的个数。

例9、数一数下面各图中所有正方形的个数。

例10、数一数下图中有多少个正方形。

例11、数一数下图三角形的个数。

例12、数一数下图中三角形的个数。

例13、数一数下图中三角形的个数。

例14、数一数下图中三角形的个数。

练：1、数一数下面各图中有多少条线段。

2、数一数下面各图中有多少个角。

3、数一数下面各图中，各有多少条线段。

4、数一数下面各图中，各有多少条线段，各有多少个三角形。

5、下面图中有多少个正方形。

6、下图中有多少个长方形。

7、下图中有多少个三角形。

8、下图中有多少个长方形。

9、下图中各有多少个三角形。

小学奥数几何计数(三) 精选练习例题含答案解析(附知识点拨及考点)

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．模块一、立体几何计数【例 1】用同样大小的正方体小木块堆成如下图的立体图形，那么一共用了__________块小正方体。

小学奥数全国推荐四年级奥数通用学案附带练习题解析答案33几何计数(一)

年级四年级学科奥数版本通用版课程标题几何计数（一）在几何中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等。

这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的。

通常采用一种简单原始的计数方法——枚举法。

具体而言，它是指把所要计数的对象一一列举出来，以保证枚举时无一重复、无一遗漏，然后计算其总数。

我们把直线上两点间的部分称为线段，这两个点称为线段的端点。

线段是组成三角形、正方形、长方形、多边形等图形最基本的元素。

因此，观察图形中的线段，探寻线段与线段之间、线段与其他图形之间的联系，对于了解图形、分析图形是很重要的。

数线段：如果一条线段上有n＋1个点（包括两个端点）（或含有n条“基本线段”），那么这n＋1个点把这条线段一共分成的线段总数为n＋（n－1）＋…＋2＋1条。

数角：数角与数线段相似，线段图形中的点类似于角图形中的边。

数三角形：可用数线段的方法（对应法）数如图所示的三角形，因为DE上有15条线段，每条线段的两端点与点A相连，可构成一个三角形，共有15个三角形。

同样一边在BC 上构成的三角形也有15个，所以图中共有30个三角形。

例1数出下图中有多少条线段。

A B CD分析与解：方法一：我们可以采用以线段左端点分类来数的方法。

以A点为左端点的线段有：AB、AC、AD 3条；以B点为左端点的线段有：BC、BD 2条；以C点为左端点的线段有：CD 1条。

所以，图中共有线段3＋2＋1＝6（条）。

方法二：把图中线段AB、BC、CD看做基本线段来数，那么，由1条基本线段构成的线段有：AB、BC、CD 3条；由2条基本线段构成的线段有：AC、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3＋2＋1＝6（条）线段。

例2 数出下图中总共有多少个角。

分析与解：在∠AOB 内有三条角分线1OC 、2OC 、3OC ，∠AOB 被这三条角分线分成4个基本角，那么∠AOB 内总共有多少个角呢？首先有OB C OC C OC C AOC 332211∠∠∠∠、、、这4个基本角，其次是由2个基本角组成的角有3个（即∠2AOC 、∠31OC C 、∠OB C 2），然后是由3个基本角组成的角有2个（即∠3AOC 、∠OB C 1），最后是由4个基本角组成的角有1个（即∠AOB ），所以∠AOB 内总共有角：4＋3＋2＋1＝10（个）。

4年级奥数培优讲义-15-图形计数-难版

几何中的计数问题包括：数线段、数角、数长方形、数正方形、数三角形、数综合图形等。

在几何图形的计数问题中，各种图形的基本概念及其相关性质是计数过程中寻找规律的基础。

掌握图形的规律和方法多种多样，常用的有按顺序数和分类数两种。

分类方法如：按点分类，按边分类，按块分类等等还要注意分类的合理性，只有当所分的类型包含所有情况并且相互不重叠，这样才有可能做到不重复、不遗漏。

【例1】★数一数图1中有多少条线段？【解析】第一种可以按端点进行分类，如图1中，线段最左边的端点是A ，即以A 为左端点的线段有AB 、AC 、AD 、AE 、AF 共五条；以B 为左端点的线段有BC 、BD 、BE 、BF 共四条；以C 为左端点的线段有CD 、CE 、CF ，共三条；以D 为左端点的线段有DE 、DF 共二条；以E 为左端点的线段有EF ，一条。

这些线段的和就是图形中线段的条数。

第二种可以按含基本线段多少的顺序去数。

在此题中最长的线段AF 上有四个分点，将AF 分成了5条小线段，这每条小线段就是基本线段。

首先有5条基本线段，其次是包含有两条基本线段的有4条，然后是包含有三条基本线段的有3条，包含有四条基本线段的有2条，包含有五条基本线段的有1条。

则线段AF上的线段条数可求。

5+4+3+2+1=15（条）典型例题知识梳理【例2】★数一数，右图中共有多少个角?【解析】我们规定：把相邻两条射线构成的角叫做基本角，我们可以这样分类数：由1个基本角构成的角有：∠AOB、∠BOC、∠COD、∠DOE、∠EOF共5个．由2个基本角构成的角有：∠AOC、∠BOD、∠COE、∠DOF共4个．由3个基本角构成的角有：∠AOD、∠BOE、∠COF共3个．由4个基本角构成的角有：∠AOE、∠BOF共2个．由5个基本角构成的角有：∠AOF共1个．角总数5+4+3+2+1=15(个)．【小试牛刀】数出图2中总共有多少个角？【解析】10个【例3】★数一数，右图中共有多少个三角形?你有什么好方法？【解析】1个三角形组成的：△AOB、△BOC、△COD、△DOE、△EOF共5个；2个三角形组成的：△AOC、△BOD、△COE、△DOF共4个；3个三角形组成的：△AOD、△BOE、△COF共3个；4个三角形组成的：△AOE、△BOF共2个；5个三角形组成的：△AOF共1个；共有5+4+3+2+1=15（个）.【例4】★★数一数：下面三个图中长方形分别有多少个？【解析】先数一数AB边上有多少条线段，每一条线段可以分别作为长方形的长，再数一数AD上有多少条线段，每一条线段可以分别作为长方形的宽，每一条长与一条宽搭配，就确定了一个长方形，这样就容易得出一共有多少个长方形了．先来看图(1)，AB边上包含着的10条线段中的每一条(想一想为什么)，都可与线段AD 对应，惟一确定一个长方形，所以图(1)中共有10×1=lO个长方形．再来看图(2)，与图(1)不同的是在AD上增加了一个分点，这样就有3条线段时，这3条线段分别与AB边上不同的线段构成长方形，所以图(2)中共有10×3=30个长方形．最后看图(3)，与上面的思路相同，由于AD边上有3+2+1=6条线段，所以图(3)中共有10×6=60个长方形．即：(1)(4+3+2+1)×1=10(个)；(2)(4+3+2+1)×(2+1)=30(个)；(3)(4+3+2+1)×(3+2+1)=60(个)．【小试牛刀】数一数图4中长方形的个数。

四年级奥数-几何计数

★) 下图中可以数出多少个三角形？
【例1补充】(★★★) 下图中可以数出多少个三角形？
【例2】 (★★★) 如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。那么橡皮筋如图木板上钉着20个钉子形成4行5列的正方形钉阵那么橡皮筋一共能套出个正方形。
【例3】 (★★★) 如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为1的三角形有多少个？
【例2补充】(★★★★) 下图的点可以连成多少个正方形？
1
【例4】 (★★) 在4×6的方格表中可以数出多少个长方形？多少个正方形？
【例5】 (★★) 在5×6的方格表中可以数出多少个如图所示的“ T ”字形？(“T”字形可旋转)
【例6】 (★★★) 下图中包含★的长方形共有多少个？ ★
【例7】 (★★★★) 在下图中只包含一个★的长方形有多少个？ ★ ★
2

四年级奥数题及答案：几何计数问题(中等难度)_题型归纳

四年级奥数题及答案：几何计数问题（中等难度）_题型归纳
几何计数问题：（中等难度）
图中共有______个三角形。

几何计数问题答案：以AB边上的线段为底边，以C为顶点共有三角形6个；
以AB边上的线段为底边，分别以G、H、F为顶点共有三角形3个；
以BD边上的线段为底边，以C为顶点的三角形共有6个。

所以，一共有15个三角形。

此题也可以用排列组合的方法来解，图中共有6条长线段，除三条直线共点的情况外（其中有3条线段共B点，有4条线段共C点），任取3条可以构成一个三角形，所以图中共有C_6^3-1-C_4^3=20-1-4=15（个）三角形。

分类枚举是一种很重要的解决计数问题的方法，按一定的规则恰当分类是关键。

做到既不重复，也不遗漏。

另外用排列组合解决计数问题也是小学奥数很重要的内容。

小学奥数几何计数(二) 精选练习例题含答案解析(附知识点拨及考点)

1.掌握计数常用方法；2.熟记一些计数公式及其推导方法；3.根据不同题目灵活运用计数方法进行计数．本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等，并渗透分类计数和用容斥原理的计数思想．一、几何计数在几何图形中，有许多有趣的计数问题，如计算线段的条数，满足某种条件的三角形的个数，若干个图分平面所成的区域数等等．这类问题看起来似乎没有什么规律可循，但是通过认真分析，还是可以找到一些处理方法的．常用的方法有枚举法、加法原理和乘法原理法以及递推法等．n 条直线最多将平面分成21223(2)2n n n ++++=++……个部分；n 个圆最多分平面的部分数为n (n -1)+2；n 个三角形将平面最多分成3n (n -1)+2部分；n 个四边形将平面最多分成4n (n -1)+2部分……在其它计数问题中，也经常用到枚举法、加法原理和乘法原理法以及递推法等．解题时需要仔细审题、综合所学知识点逐步求解．排列问题不仅与参加排列的事物有关，而且与各事物所在的先后顺序有关；组合问题与各事物所在的先后顺序无关，只与这两个组合中的元素有关．二、几何计数分类数线段：如果一条线段上有n +1个点(包括两个端点)（或含有n 个“基本线段”），那么这n +1个点把这条线段一共分成的线段总数为n +(n -1)+…+2+1条数角：数角与数线段相似，线段图形中的点类似于角图形中的边．数三角形：可用数线段的方法数如右图所示的三角形（对应法），因为DE 上有15条线段，每条线段的两端点与点A 相连，可构成一个三角形，共有15个三角形，同样一边在BC 上的三角形也有15个，所以图中共有30个三角形．ED CBA数长方形、平行四边形和正方形：一般的，对于任意长方形（平行四边形），若其横边上共有n 条线段，纵边上共有m 条线段，则图中共有长方形（平行四边形）mn 个．教学目标知识要点7-8-2.几何计数（二）例题精讲模块二、复杂的几何计数【例1】如下图在钉子板上有16个点，每相邻的两个点之间距离都相等，用绳子在上面围正方形，你可以得到个正方形．【考点】复杂的几何计数【难度】4星【题型】填空【关键词】学而思杯，2年级，第4题【解析】先看横着的正方形如下图⑴，可以得到94114++=个正方形，再看斜着的正方形如下图⑵可以得到4个正方形，如下图⑶可以得到2个正方形．这样一共可以得到144220++=个正方形．⑴⑵⑶<考点> 图形计数【答案】20个【巩固】如图，44⨯的方格纸上放了16枚棋子，以棋子为顶点的正方形有个．【解析】根据正方形的大小，分类数正方形．共能组成五种大小不同的正方形(如右图)．⨯的正方形：1个；⨯的正方形：4个；33⨯的正方形：9个；2211以11⨯正方形对角线为边长的正方形：4个；以12⨯长方形对角线为边长的正方形：2个．故可以组成9414220++++=(个)正方形．【巩固】下图是3×3点阵，同一行(列)相邻两个点的距离均为1。

四年级奥数提高班-第2讲几何计数

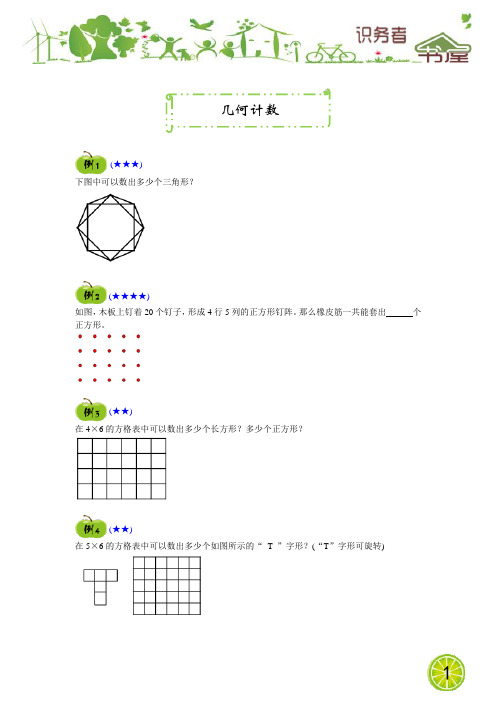
下图中可以数出多少个三角形？
如图，木板上钉着20个钉子，形成4行5列的正方形钉阵。

那么橡皮筋一共能套出个正方形。

在4×6的方格表中可以数出多少个长方形？多少个正方形？
在5×6的方格表中可以数出多少个如图所示的“T ”字形？(“T”字形可旋转)
几何计数
(★★★)
(★★★★)
(★★)
(★★)
(★★★)
下图中包含★的长方形共有多少个？
(★★★★)
在下图中只包含一个★的长方形有多少个？
(★★★★★)
如图，用9枚钉子钉成水平和竖直间隔都为1的正方阵。

用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。

其中面积为1的三角形有多少个？
本讲总结
枚举法——按照大小和位置
对应法——找到对应关系
容斥原理——不重不漏
和面积相关——熟悉公式
利用图形对称性
重点例题：例4，例6，例7。

小学奥数--几何计数25道

【题型】应用题【题目】用3根等长的火柴可以摆成一个等边三角形．如图19-1,用这样的等边三角形拼合成一个更大的等边三角形．如果这个大等边三角形昀每边由20根火柴组成，那么一共要用多少根火柴?【答案】630【解析】把大的等边三角形分为20“层”分别计算火柴的根数：最上一“层”只用了3根火柴；从上向下数第二层用了3×2＝6根火柴；从上向下数第三层用了3×3＝9根火柴；……从上向下数第20层用了3×20＝60根火柴．所以，总共要用火柴3×(1+2+3+…+20)＝630根．【难度】难度3【知识点】几何计数【题目】如图19-2，用长短相同的火柴棍摆成3×1996的方格网，其中每个小方格的边都由一根火柴棍组成，那么一共需用多少根火柴棍?【答案】13975【解析】横放需1996×4根，竖放需1997×3根，共需1996×4+1997×3＝13975根．【难度】难度2【知识点】几何计数【题目】图19-3是一个跳棋棋盘，请你计算出棋盘上共有多少个棋孔?【答案】【解析】把棋盘分割成一个平行四边形和四个小三角形，如下图．平行四边形中棋孔数为9×9＝81，每个小三角形中有10个棋孔，所以棋孔共有81+10×4＝121个．或直接数出有121个．【难度】难度3【知识点】几何计数【题目】如图19-4，在桌面上，用6个边长为l的正三角形可以拼成一个边长为1的正六边形．如果在桌面上要拼出一个边长为6的正六边形，那么，需要边长为1的正三角形多少个？【答案】【解析】如图AB＝6，组成△AOB需要边长为1的正三角形共：1+3+5+7+9+11＝36个，而拼成边长为6的正六边形需要6个△AOB，因此总共需要边长为1的正三角形36×6＝216个．【难度】难度4【知识点】几何计数【题目】如图19-5，其中的每条线段都是水平的或竖直的，边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米．求图中长方形的个数，以及所有长方形面积的和．【答案】100，10664【解析】确定好长方形的长和宽，长方形就唯一确定，而图中只需确定好横向线段，竖向线段，即可．于是横向线段有(1+2+3+4)＝10种选法，竖向线段也有(1+2+3+4)＝10种选法，则共有10×10＝100个长方形．这些长方形的面积和为：(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)＝124×86＝10664(平方厘米)．【难度】难度4【知识点】几何计数【题目】如图19-6，18个边长相等的正方形组成了一个3×6的方格表，其中包含“*”的长方形及正方形共有多少个?【答案】36【解析】我们把所求的长、正方形按占有的行数分为三类，每类的长、正方形的个数相等．其中只占有下面一行的有如下12种情况：于是共有12×3＝36个正、长方形包含“*”．【难度】难度4【知识点】几何计数【题目】图19-7是由若干个相同的小正方形组成的．那么，其中共有各种大小的正方形多少个?【答案】130【解析】每个4×4正方形中有：边长为1的正方形4×4个；边长为2的正方形3×3个；边长为3的正方形2×2个，边长为4的正方形1×1个．总共有4×4+3×3+2×2+1×1＝30个正方形．现在5个4×4的正方形，它们重叠部分是4个2×2的正方形．因此，图中正方形的个数是30×5－5×4＝130．【难度】难度4【知识点】几何计数【题目】图19-8中共有多少个三角形?【答案】22【解析】边长为1的正三角形，有16个．边长为2的正三角形，尖向上的有3个，尖向下的也有3个．因此共有16+3+3＝22个．【难度】难度2【知识点】几何计数【题目】图19-9是由18个大小相同的小正三角形拼成的四边形，其中某些相邻的小正三角形可以拼成较大的正三角形．那么，图中包含“*”的各种大小的正三角形一共有多少个?【答案】6【解析】设小正三角形的边长为1，分三类计算计数包含*的三角形中，边长为1的正三角形有1个；边长为2的正三角形有4个，边长为3的正三角形有1个；因此，图中包含“*”的所有大、小正三角形一共有1+4+1＝6个．【难度】难度2【知识点】几何计数【题目】如图19-10，AB，CD，EF，MN互相平行，则图中梯形个数与三角形个数的差是多少?【答案】20【解析】图中共有三角形(1+2+3+4)×4＝40个，梯形(1+2+3+4)×(1+2+4)＝60个，梯形比三角形多60－40＝20个．【难度】难度3【知识点】几何计数【题目】在图19-1l中，共有多少个不同的三角形?【答案】85【解析】下图中共有35个三角形，两个叠加成题中图形时，又多出5+5×2＝15个三角形，共计35×2+15＝85个三角形．【难度】难度5【知识点】几何计数【题目】如图19-12，一块木板上有13枚钉子．用橡皮筋套住其中的几枚钉子，可以构成三角形、正方形、梯形等等，如图19-13．那么，一共可以构成多少个不同的正方形?【答案】11【解析】按正方形的面积分类，设最小的正方形面积为1，面积为1的正方形有5个，如图a所示；面积为2的正方形有4个，如图b所示；面积为4的正方形有1个，如图c所示；还有1个面积比4大的正方形，如图d所示；于是，一共可以构成5+4+1+1＝11个不同的正方形．【难度】难度3【知识点】几何计数【题目】如图19-14，用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵．用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形．在这样得到的三角形中，面积等于1平方厘米的三角形共有多少个?【答案】32【解析】我们分三种情况来找面积为1平方厘米的三角形，这些三角形的底与高分别为1厘米或2厘米，利用正方形的对称性：(1)等腰直角三角形，如下图a所示有△AOC，△COE，△EOG，△GOA，△BOH，△DFB，△FHD，△HBF，共计8个，其中以AC，CF，FG，GA为底的各一个，以BF，DH为底的各两个．(2)直角三角形，如图b所示有△ACH，△CHD，△ACD，△DHA，△BEF，△BCE，△CEF，△CFB，△DEG，△DGH，△EGH，△EHD，△GAB，△GBF，△FAB，△FGA，共计16个，其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个．(3)钝角三角形，如图c所示有△ABE，△AHE，△ADE，△AFE，△CBG，△CFG，△CDG，△CHG共计8个，其中以AE、CG为边的各四个．于是，综上所述，共有面积为1平方厘米的三角形32个．【难度】难度4【知识点】几何计数【题目】如图19-15，木板上钉着12枚钉子，排成三行四列的长方阵．那么用橡皮筋共可套出多少个不同的三角形?【答案】200【解析】我们先任意选取三个点，那么第1个点有12个位置可以选择，第2个点有11个位置可以选择，第3个点有10个位置可以选择，但是每6种选法对应的都是同一个图形，如下图，ABC，ACB，BAC，BCA，CAB，CBA均是同一个图形．所以有12×11×10÷6＝220种选法，但是如果这3点在同一条直线上就无法构成三角形，其中每行有4种情况，共3×4；每列有1种情况，共1×4；2个边长为2的正方形的4条对角线，共4种情况．所以，可以套出220－3×4－1×4－4＝200个不同的三角形．【难度】难度2【知识点】几何计数【题目】如图19-16，正方形ACEG的边界上有A，B，C，D，E，F，G这7个点，其中B，D，F分别在边AC，CE，EG上．以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?【答案】12【解析】如果暂时不考虑点之间的排列位置关系，从7个点中任取4个点，则第一个点有7个位置可选，第二个点有6个位置可选，第三个点有5个位置可选，第四个点有4个位置可选，而不考虑先后，那么有4×3×2×1＝24种选法的实质是一样的，所有可能的组合数目应该是(7×6×5×4)÷24＝35．我们只要从中减去不能构成四边形的情形．对图19-16而言，任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边，而另一个则任意选取的时候，例如选定A、B、C3点，第4个点无论如何选取都不能构成四边形．正方形的4条边中有3条都存在这样的情况．而每次这种情况发生时，第4个顶点的选取有4种可能．所取的顶点只有4个，因此不可能出现同时选择了2条有3点共线的边的情况．那么需要排除的情况有4×3＝12种．所以，满足题意的四边形个数有35－12＝23个．【难度】难度4【知识点】几何计数【题目】数一数下列图形中各有多少条线段.【答案】15【解析】要想使数出的每一个图形中线段的总条数，不重复、不遗漏，就需要按照一定的顺序、按照一定的规律去观察、去数.这样才不至于杂乱无章、毫无头绪.我们可以按照两种顺序或两种规律去数.第一种：按照线段的端点顺序去数，如上图（1）中，线段最左边的端点是A，即以A为左端点的线段有AB、AC两条以B为左端点的线段有BC一条，所以上图（1）中共有线段2＋1＝3条.同样按照从左至右的顺序观察图（2）中，以A 为左端点的线段有AB、AC、AD三条，以B为左端点的线段有BC、BD两条，以C为左端点的线段有CD一条.所以上页图（2）中共有线段为3＋2＋1＝6条. 第二种：按照基本线段多少的顺序去数.所谓基本线段是指一条大线段中若有n 个分点，则这条大线段就被这n个分点分成n＋1条小线段，这每条小线段称为基本线段.如上页图（2）中，线段AD上有两个分点B、C，这时分点B、C把AD 分成AB、BC、CD三条基本线段，那么线段AD总共有多少条线段？首先有三条基本线段，其次是包含有二条基本线段的是：AC、BD二条，然后是包含有三条基本线段的是AD这样一条.所以线段AD上总共有线段3＋2＋1＝6条，又如上页图（3）中线段AE上有三个分点B、C、D，这样分点B、C、D把线段AE分为AB、BC、CD、DE四条基本线段，那么线段AE上总共有多少条线段？按照基本线段多少的顺序是：首先有4条基本线段，其次是包含有二条基本线段的有3条，然后是包含有三条基本线段的有2条，最后是包含有4条基本线段的有一条，所以线段AE上总共有线段是4＋3＋2＋1＝10条.解：①2＋1＝3（条）.② 3＋2＋1＝6（条）.③ 4＋3＋2＋1＝10（条）.小结：上述三例说明：要想不重复、不遗漏地数出所有线段，必须按照一定顺序有规律的去数，这个规律就是：线段的总条数等于从1开始的连续几个自然数的和，这个连续自然数的和的最大的加数是线段分点数加1或者是线段所有点数（包括线段的两个端点）减1.也就是基本线段的条数.例如右图中线段AF 上所有点数（包括两个端点A、F）共有6个，所以从1开始的连续自然数的和中最大的加数是6—1＝5，或者线段AF上的分点有4个（B、C、D、E）.所以从1开始的连续自然数的和中最大的加数是4＋1＝5.也就是线段AF上基本线段（AB、BC、CD、DE、EF）的条数是5.所以线段AF上总共有线段的条数是5＋4＋3＋2＋1＝15（条）.【难度】难度3【知识点】几何计数【题目】数出下图中总共有多少个角.【答案】10【解析】在∠AOB内有三条角分线OC1、OC2、OC3，∠AOB被这三条角分线分成4个基本角，那么∠AOB内总共有多少个角呢？首先有这4个基本角，其次是包含有2个基本角组成的角有3个（即∠AOC2、∠C1OC3、∠C2OB），然后是包含有3个基本角组成的角有2个（即∠AOC3、∠C1OB），最后是包含有4个基本角组成的角有1个（即∠AOB），所以∠AOB内总共有角：4＋3＋2＋1＝10（个）.解：4＋3＋2＋1＝10（个）.小结：数角的方法可以采用例1数线段的方法来数，就是角的总数等于从1开始的几个连续自然数的和，这个和里面的最大的加数是角分线的条数加1，也就是基本角的个数.【难度】难度3【知识点】几何计数【题目】数一数下图中总共有多少个角？【答案】55【解析】因为∠AOB内角分线OC1、OC2…OC9共有9条，即9+1=10个基本角. 所以总共有角：10+9+8+…+4+3+2+1=55（个）.【难度】难度3【知识点】几何计数【题目】如下图中，各个图形内各有多少个三角形？【答案】（1）6（2）10【解析】可以采用类似例1数线段的两种方法来数，如图（2）：第一种方法：先数以AB为一条边的三角形共有：△ABD、△ABE、△ABF、△ABC四个三角形.再数以AD为一条边的三角形共有：△ADE、△ADF、△ADC三个三角形.以AE为一条边的三角形共有：△AEF、△AEC二个三角形.最后以AF为一条边的三角形共有△AFC一个三角形.所以三角形的个数总共有4+3+2+1=10.第二种方法：先数图中小三角形共有：△ABD、△ADE、△AEF、△AFC四个三角形.再数由两个小三角形组合在一起的三角形共有：△ABE、△ADF、△AEC三个三角形，以三个小三角形组合在一起的三角形共有：△ABF、△ADC二个三角形，最后数以四个小三角形组合在一起的只有△ABC一个.所以图中三角形的个数总共有：4+3+2+1=10（个）.解：①3+2+1=6（个）② 4+3+2+1=10（个）.答：图（1）及图（2）中各有三角形分别是6个和10个.小结：计算三角形的总数也等于从1开始的几个连续自然数的和，其中最大的加数就是三角形一边上的分点数加1，也就是三角形这边上分成的基本线段的条数.【难度】难度3【知识点】几何计数【题目】如下图中，数一数共有多少条线段？共有多少个三角形？【答案】60,30【解析】分析在数的过程中应充分利用上几例总结的规律，明确数什么？怎么数？这样两个问题.数：就是要数出图中基本线段（基本三角形）的条数，算：就是以基本线段（基本三角形）条数为最大加数的从1开始的连续几个自然数的和.①要数多少条线段：先看线段AB、AD、AE、AF、AC、上各有2个分点，各分成3条基本线段，再看BC、MN、GH这3条线段上各有3个分点，各分成4条基本线段.所以图中总共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）.②要数有多少个三角形，先看在△AGH中，在GH上有3个分点，分成基本小三角形有4个.所以在△AGH中共有三角形4+3+2+1=10（个）.在△AMN与△ABC 中，三角形有同样的个数，所以在△ABC中三角形个数总共：（4+3+2+1）×3=10×3=30（个）.解：①在△ABC中共有线段是：（3+2+1）×5+（4+3+2+1）×3=30+30=60（条）②在△ABC中共有三角形是：（4+3+2+1）×3=10×3=30（个）.【难度】难度3【知识点】几何计数【题目】如右图中，共有多少个角？【答案】13【解析】分析本题虽然与上几例有区别，但仍可以采用上几例所总结的规律去解决. ∠1、∠2、∠3、∠4我们可视为4个基本角，由2个基本角组成的有：∠1与∠2、∠2与∠3、∠3与∠4、∠4与∠1，共4个角.由3个基本角组成的角有：∠1、∠2与∠3；∠2、∠3与∠4；∠3、∠4与∠1；∠4、∠1与∠2，共4个角，由4个基本角组成的角只有一个.所以图中总共有角是：4×3+1=13（个）.解：所以图中共有角是：4×3+1=13（个）.小结：由本题可以推出一般情况：若周角中含有n 个基本角，那么它上面角的总数是 n （n-1）+1.【难度】难度4【知识点】几何计数【题目】在图中(单位：厘米)：①一共有几个长方形?②所有这些长方形面积的和是多少?374218125【答案】100,12384【解析】①一共有(4321)(4321)100+++⨯+++=(个)长方形；②所求的和是[][]51281(512)(128)(81)(5128)(1281)(51281)2473(24)(47)(73)(247)(473)(2473)+++++++++++++++++++⨯+++++++++++++++++++ 1448612384=⨯=(平方厘米)。

小学奥数：几何计数一.专项练习及答案解析

7-8-1几何计数（一）教课目的掌握数常用方法；熟一些数公式及其推方法；依据不一样目灵巧运用数方法行数．本主要介了数的常用方法枚法、数法、形法、插板法、法等，并渗透分数和用容斥原理的数思想．知识重点一、几何计数在几何形中，有多风趣的数，如算段的条数，足某种条件的三角形的个数，若干个分平面所成的地区数等等．看起来仿佛没有什么律可循，可是通真分析，是能够找到一些理方法的．常用的方法有枚法、加法原理和乘法原理法以及推法等．n条直最多将平面分红223⋯⋯n(n2n2)个部分；n个2最多分平面的部分数n(n-1)+2；n个三角形将平面最多分红3n(n-1)+2部分；n个四形将平面最多分红4n(n-1)+2部分⋯⋯在其余数中，也常用到枚法、加法原理和乘法原理法以及推法等．解需要仔、合所学知点逐渐求解．摆列不与参加摆列的事物相关，并且与各事物所在的先后序相关；合与各事物所在的先后序没关，只与两个合中的元素相关．二、几何计数分类数段：假如一条段上有n+1个点(包含两个端点)（或含有n个“基本段”），那么n+1个点把条段一共分红的段数n+(n-1)+⋯+2+1条数角：数角与数段相像，段形中的点似于角形中的．数三角形：可用数段的方法数如右所示的三角形（法），因DE上有15条段，每条段的两头点与点A相，可构成一个三角形，共有15个三角形，同一在BC上的三角形也有15个，所以中共有30个三角形．数方形、平行四形和正方形：一般的，于随意方形（平行四形），若其横上共有n 条段，上共有条段，中共有方形（平行四形）个．m mn例题精讲模块一、简单的几何计数【例1】七个同的如右搁置，它有_______条称．7-8-1.几何计数（一）.题库题库版page1of10【考点】简单的几何计数【难度】1星【题型】填空【重点词】迎春杯，六年级，初赛，试题【分析】如图：6条．【答案】6条【例2】下边的表情图片中：，没有对称轴的个数为（）（A）3(B)4(C)5(D)6【考点】简单的几何计数【难度】2星【题型】选择【重点词】华杯赛，初赛，第1题【分析】经过观察可知，第1，2，5这三张图片是有对称轴的，其余的5张图片都没有对称轴，所以没有对称轴的个数为5，正确答案是C。