3章2伯努利方程
合集下载
第三章 流体的运动
x x
P1
s1
t+t
v1
y
v1 S 1 t = v2 S 2 t = V
y 得：
h1
t
s2
h2
v2 P2
A = （ P 1 - P 2） V
对于稳定流动来 说，由于在 x y 之间的 P1 流体的动能和重力势能 保持不变，所以机械能
x x
v1
s1
t+t
y
y
的增量仅由 x x 和 两段流体决定。
x x
P1
s1
t+t
v1
y
y
h1
t
s2
A = E 2 - E1
h2
v2 P2
1 2 1 2 （P1 P2 ） V V ( v 2 gh2 ) ( v1 gh1 ) 2 2
即：
1 1 2 2 P v1 gh1 P2 v 2 gh2 1 2 2
三
S2
连续性方程
1 v 1 S 1 t = 2 v 2 S 2 t
V2
S1
V1
2
1
1 v 1 S 1 = 2 v 2 S 2 即： v S = 常量 流体作稳定流动时，单位时间内流过同
一流管中任一截面的流体质量相等。
对于不可压缩的流体，由于它的密度不变 1v1S1= 2v2S2 即 : 1= 2 v 1S 1 = v 2S 2 说 明： (1)定义: 流量 Q = Sv (2)S与v 成反比。 (3)v 取截面S上流速的平均值。 (4)连续性方程的实质：流体在流动中质量守恒。 不可压缩流体的连续性方程
层与层之间的阻 力称为内摩擦力或粘 滞力。 ƒ = dv S dx
§1-2伯努利方程及其应用
§1-2伯努利方程及其应用
例1.3 如图1—5所示,液槽内离开液面h处开一小孔。液体密度为ρ, 液面上方是空气,它被液槽盖封闭住,其绝对压强为p,在液槽侧面小 孔处的压强为大气压强p0。当p>>p0时,试证明小孔处的液流速度 为： v2 = 2( p − p0 ) / ρ
解:将整个流体当作一个流管,用 v1和v分别表示水面处和 2 孔口处的流速。由连续性方程知 v 2 且因为S1>>S2,故 v 2 >> v1 可以近似地取 v1 = 0
第一章 流体的运动
§1-2伯努利方程及其应用
大 学 物 理
主讲教师：杨宏伟
第一章 流体的运动
§1-2伯努利方程及其应用
一 、 伯努利方程 伯努利方程是由瑞士物理学家伯努利 （D.Bernoulli）提出来的，是理想流体 作稳定流动时的基本方程，对于确定流 体内部各处的压力和流速都有很大的实 际意义,在水利、造船、航空航天等部门 有着广泛的应用。
第一章 流体的运动
§1-2伯努利方程及其应用
例1.2水管里的水在压强P=4×105Pa的作用下流入房 间，水管内直径为2.0cm,管内水的流速为4m/s。引入 到5m高处二层楼浴室的水管，内直径为1.0cm，试求浴 室内水的流速和压强（已知水的密度ρ=1000kg/m3）。 解：由连续性原理知
2
S1v1 = S 2 v2
A
B
将整个管子作流管，由连续性方 程 S1v1 = S 2 v2 以及伯努利方程 (1-5) 2
C
D E
p + 0.5 ρv = 恒量
图1—6 空吸作用 图1—6 空吸作用
第一章 流体的运动 由于 S1 >> S 2
《工程流体力学》第三章 流体运动研究方法及一维定常流基本方程
截面1-1和2-2：垂直于流动方向，为什么? 侧面1-2：平行于流动方向，为什么？
控制体：1-1-2-2，用I+III表示 在空间上：固定的
t时体系：1-1-2-2，t时刻占据控制体I+III的流体
t+dt时体系：1’-1’-2’-2’ dt时间后： t时体系沿流线运动到III+II
由质量守恒定律： t时体系内质量＝t+dt时体系内质量
定常流：空间中任一点参数随不随时间变化？ 不随
物理意义？
A1, r1, V1 —— 控制面1-1上的横截面积、气流密度、速度
物理意义？
A2, r2, V2 —— 控制面2-2上的横截面积、气流密度、速度
物理意义？
一维定常流连续方程：在一维定常流中，通过同一流管任 意截面上的流体质量流量、重量流量保持不变。
例1：已知平面非定常流中的流速分量为：ux=x+t, uy= -y+t, 求：流线方程和迹线方程。 解：流线微分方程：
其中t为常数 积分后：
最后得：
迹线微分方程：
其中t为变量
结论：非定常流中迹线与流线不同
—— 迹线方程 ——流线方程
例2：已知平面定常流中的流速分量为：ux=x, uy= -y, 求：流线方程和迹线方程。 解：由流线微分方程：
体系动量对时间变化率：
控制体 = t时体系 环境对控制体内流体作用力 = 环境对t时体系内流体作用力
牛顿第二定律： 某瞬时作用在体系上全部外力合力 =该瞬时体系动量对时间的变化率
分量形式：
作用在控制体内流体上的外力： 1)表面力：控制体外流体或固体壁面作用在控制面上力
作用在进口截面上切向力：0 作用在出口截面上切向力：0
控制体：1-1-2-2，用I+III表示 在空间上：固定的
t时体系：1-1-2-2，t时刻占据控制体I+III的流体
t+dt时体系：1’-1’-2’-2’ dt时间后： t时体系沿流线运动到III+II
由质量守恒定律： t时体系内质量＝t+dt时体系内质量
定常流：空间中任一点参数随不随时间变化？ 不随
物理意义？
A1, r1, V1 —— 控制面1-1上的横截面积、气流密度、速度
物理意义？
A2, r2, V2 —— 控制面2-2上的横截面积、气流密度、速度
物理意义？
一维定常流连续方程：在一维定常流中，通过同一流管任 意截面上的流体质量流量、重量流量保持不变。
例1：已知平面非定常流中的流速分量为：ux=x+t, uy= -y+t, 求：流线方程和迹线方程。 解：流线微分方程：
其中t为常数 积分后：
最后得：
迹线微分方程：
其中t为变量
结论：非定常流中迹线与流线不同
—— 迹线方程 ——流线方程
例2：已知平面定常流中的流速分量为：ux=x, uy= -y, 求：流线方程和迹线方程。 解：由流线微分方程：
体系动量对时间变化率：
控制体 = t时体系 环境对控制体内流体作用力 = 环境对t时体系内流体作用力
牛顿第二定律： 某瞬时作用在体系上全部外力合力 =该瞬时体系动量对时间的变化率
分量形式：
作用在控制体内流体上的外力： 1)表面力：控制体外流体或固体壁面作用在控制面上力
作用在进口截面上切向力：0 作用在出口截面上切向力：0
流体力学_第三章_伯努利方程及动量方程
4根线具有能量 意义： 总水头线 测压管水头线 水流轴线 基准面线
23
第三节 恒定总流的伯努利方程
例 用直径d=100mm的水管从水箱引水，水管水面与
管道出口断面中心高差H=4m，水位保持恒定，水头 损失hw=3m水柱，试求水管流量，并作出水头线 解：以0-0为基准面，列1-1、2-2断面的伯努利方程
第三节 恒定总流的伯努利方程
渐变流及其性质
渐变流
(u )u 0
渐变流的过流断面近于平 面，面上各点的速度方向 近于平行。 渐变流过流断面上的动压 强与静压强的分布规律相 同，即：
p z c g
1
第三节 恒定总流的伯努利方程
大小的变化 流速的变化 方向的变化
出现直线惯性力 压强沿流向变化
微小圆柱体的力平衡
p1dA ldA cos p2 dA l cos Z1 Z 2 p1 (Z1 Z 2 ) p2
Z1 p1 Z2 p2
4
第三节 恒定总流的伯努利方程
Z1 p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
40
2
,
2
第三节 恒定总流的伯努利方程
( a )( z2 z1 ) ( a )( z2 z1 ) ( a )
单位体积气体所受有效浮力
v1 2 gh d1 1 d 2
4
4
2 1
2 1
30
第三节 恒定总流的伯努利方程
Q v1
4
d
2 1
4
d
2 1
2 gh d1 d 1 2
23
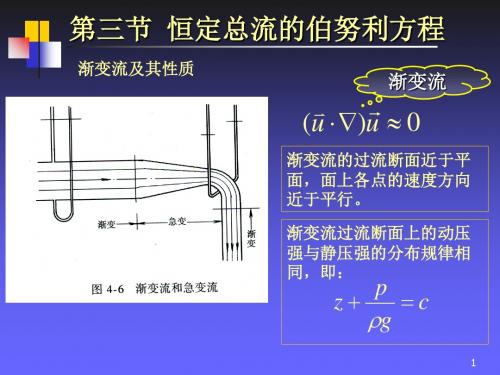
第三节 恒定总流的伯努利方程
例 用直径d=100mm的水管从水箱引水，水管水面与
管道出口断面中心高差H=4m，水位保持恒定，水头 损失hw=3m水柱，试求水管流量，并作出水头线 解：以0-0为基准面，列1-1、2-2断面的伯努利方程
第三节 恒定总流的伯努利方程
渐变流及其性质
渐变流
(u )u 0
渐变流的过流断面近于平 面，面上各点的速度方向 近于平行。 渐变流过流断面上的动压 强与静压强的分布规律相 同，即：
p z c g
1
第三节 恒定总流的伯努利方程
大小的变化 流速的变化 方向的变化
出现直线惯性力 压强沿流向变化
微小圆柱体的力平衡
p1dA ldA cos p2 dA l cos Z1 Z 2 p1 (Z1 Z 2 ) p2
Z1 p1 Z2 p2
4
第三节 恒定总流的伯努利方程
Z1 p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
40
2
,
2
第三节 恒定总流的伯努利方程
( a )( z2 z1 ) ( a )( z2 z1 ) ( a )
单位体积气体所受有效浮力
v1 2 gh d1 1 d 2
4
4
2 1
2 1
30
第三节 恒定总流的伯努利方程
Q v1
4
d
2 1
4
d
2 1
2 gh d1 d 1 2
大学物理教程第3章答案张文杰等主编中国农业大学出版社
思考题3.1 什么是连续性方程？答：假设以闭合外表内既无源，又无负源，那么根据质量守恒，进入该闭合外表的净流量等于闭合外表内物质的增加率，应用在稳定流动的流管中，我们得到连续性方程：ρ1A1v1=ρ2A2v2。
其中，ρ为密度,假设它在截面积 A处是均匀的； v为经过截面积A处的平均速度〔v与A垂直〕。
假设流体又是不可压缩的，连续性方程简化为A1v1=A2v2。
3.2 什么是伯努利方程？答：流体是稳定的，非黏性的，不可压缩的，伯努利方程给出同一流线任两点处的压强p，流速v，高度y满足p1+12ρv1²+ρgy1= p2+12ρv2²+ρgy2注意伯努利方程中每一项都是取的单位面积的内的量值。
方程指出：压力沿流线所作的功等于动能和势能的改变〔都指单位面积〕。
3.3 在定常流动中，流体是否可能加速运动？答：定常流动是指宏观上流体在空间某位置的流速保持不变，对某个流体质点而言，它在空间各点速度可能不同，也就是说，它可能是加速运动。
3.4 从水龙头徐徐流出的水流，下落时逐渐变细，为什么？答：据连续性原理知，，流速大处截面积小，所以下落时水的流速逐渐增大，面积逐渐减少变细。
3.5 两船平行前进时，假设靠的较近，极易碰撞，为什么？答：两船平行前进时，两条流线方向相同，，如果靠的较近，两船之间的流速将大于两船外侧的流速，这样两船都将受到一个指向对方的一个压力的作用，极易造成两船碰撞，稍有晃动，流线重合，船体就会相撞。
3.6 两条流线不能相交，为什么？答：如果两条流线相交，那么焦点处就会出现两个速度，这个结论是错误的，所以两条流线不能相交。
3.7 层流和湍流各有什么特点？引入雷诺数有哪些意义？答：流线是相互平行的流动称层流。
流体微团作复杂的无规那么的运动称为湍流。
无量纲的量雷诺数是层流向湍流过渡的一种标志。
以临界雷诺数为准，小于它为层流，大于它为湍流。
习题3.1 假设被测容器A内水的压强比大气压大很多时，可用图中的水银压强计。
第3章2 流体动力学基础-伯努利方程的应用
4
30
2
4
V2 A2 V1 A1
V12 p 1 0.198 H 2 1 1.5 2.72 4.22m水柱 2g V12 5.26m水柱 2g
列断面0-0和真空室断面1-1的能量方程
p0
V12 H1 H 2 2g p1
V12 H1 H 2 2.72 5.26 1.5 1.04m 2g 上述计算中没有考虑管道中的能量损失，而实际上若要用 射流泵产生上述真空，水箱应？ p1
p1
p真
0.2 13.6 2.72m水柱
出水口通大气，水池液面通大气，p2=p0=0。 对断面1-1、2-2列能量方程：
p1
V12 p2 V22 H2 2g 2g
A d 50 V22 V12 1 V12 1 V12 0.198V12 A2 d 2 75
27
A 2 p A pC V A 1 2 g AC
2 A
因为AA>AC，上式左端为正值，即PC<PA，而AC越小则PC值越 低。当PC比大气压还要低时，若在C处把管子开一小孔，管内 液体并不会漏出来，而外面的空气却反而会被大气压压进管子。 若在小孔上接一根管子，其下端浸在液箱中，则管内液面在大 气压的作用下会上升。 当
现取水流进入喷嘴前的A断面和水流流出喷嘴时的C断面列能 量方程（暂时不考虑能量损失）
pA
2 VA pC VC2 2g 2g
移项
p A pC
VC2 VA2 2g
p A pC
VA2 AA 1 2 g AC
30
2
4
V2 A2 V1 A1
V12 p 1 0.198 H 2 1 1.5 2.72 4.22m水柱 2g V12 5.26m水柱 2g
列断面0-0和真空室断面1-1的能量方程
p0
V12 H1 H 2 2g p1
V12 H1 H 2 2.72 5.26 1.5 1.04m 2g 上述计算中没有考虑管道中的能量损失，而实际上若要用 射流泵产生上述真空，水箱应？ p1
p1
p真
0.2 13.6 2.72m水柱
出水口通大气，水池液面通大气，p2=p0=0。 对断面1-1、2-2列能量方程：
p1
V12 p2 V22 H2 2g 2g
A d 50 V22 V12 1 V12 1 V12 0.198V12 A2 d 2 75
27
A 2 p A pC V A 1 2 g AC
2 A
因为AA>AC，上式左端为正值，即PC<PA，而AC越小则PC值越 低。当PC比大气压还要低时，若在C处把管子开一小孔，管内 液体并不会漏出来，而外面的空气却反而会被大气压压进管子。 若在小孔上接一根管子，其下端浸在液箱中，则管内液面在大 气压的作用下会上升。 当
现取水流进入喷嘴前的A断面和水流流出喷嘴时的C断面列能 量方程（暂时不考虑能量损失）
pA
2 VA pC VC2 2g 2g
移项
p A pC
VC2 VA2 2g
p A pC
VA2 AA 1 2 g AC
流体力学基本伯努力方程
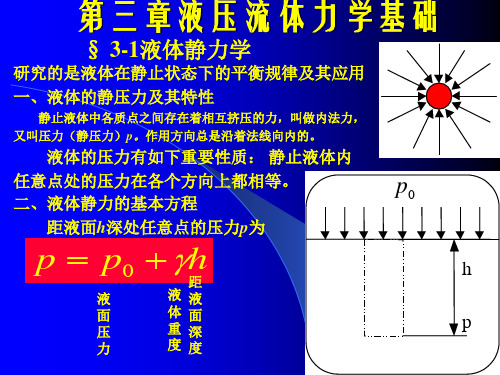
动能:Eu=mu2/2=Vρu2 /2 总能量: Vρgz+ pV+ Vρu2 /2 =C1
两边同除以Vρg，
动能-压力能：测速计 势能-动能：倒水，虹吸 动能-势能：喷泉
z+ p/ρg+ u2/2g=C
16
3.实际液体的伯努力方程1
z1
p1
g
u12 2g
(3-19)
z2
p2
g
u22 2g
s s s t
这就是理想液体的运动微分方程，也称液流的欧拉方程
13
2.理想液体的伯努力方程1
要在图3-10所示的一段微流 束上，寻找它各处的能量关 系 ， 将 式 (3-10) 的 两 边 各 乘 上ds，并从流线s上的截面1 积分到截面2，即
2
1
g
z s
1
p s
5. 如 图 所 示 ， 液 压 泵 输 出 的 流 量
A1
qp=0.5L/s，全部进入液压缸，液压 缸 大 腔 截 面 积 A1=2000mm2 ， 小 腔 截 面 积 A1=1000mm2 ， 进 、 回 油 管 直径d=10mm。求活塞的运动速度，
进、回油管中油液的流速。
qp
A2
v
d
21
当容器没有惯性加速度，即当液 体仅受重力作用时，则
j cos gz / s 质量力为 dsdAgz / s
这一微元体积的惯性力为
ma dAds du dAds u ds u dAds u u u
dt
s dt t
Q1
q A udA
在过流截面上各点的流速是不相等的。
流体力学第三章 (2)
（2）
即：圆管中水流处在紊流状态。 （2）
要保持层流，最大流速是0.03m/s。
问题：
1、怎样判别粘性流体的两种流态——层流和紊流？ 2、为何不能直接用临界流速作为判别流态（层 流和紊流）的标准？ 3、为什么用下临界雷诺数，而不用上临界雷诺数 作为层流与紊流的判别准则？
作业 P113
3
§4.3 不可压缩流体恒定圆管层流
粘性流体流动的两种流态
一、雷诺实验
1883年英国物理学家雷诺（Reynolds O.）通 过试验观察到液体中存在层流和紊流两种流态。
动画
二、两种流态的运动特征
1.层流 层流（laminar flow），亦称片流：是指流体质点 不相互混杂，流体作有序的成层流动。 特点： （1）有序性。水流呈层状流动，各层的质点互不 混掺，质点作有序的直线运动。 （2）粘性占主要作用，遵循牛顿内摩擦定律。 （3）能量损失与流速的一次方成正比。 （4）在流速较小且雷诺数Re较小时发生。
层流： 紊流：
三、层流、紊流的判别标准——临界雷诺数
临界雷诺数
Re c vc d
上临界雷诺数：层流→紊流时的临界雷诺数，它易受 外界干扰，数值不稳定。 下临界雷诺数：紊流→层流时的临界雷诺数，是流态 的判别标准，它只取决于水流边界的形状，即水流的 过水断面形状。
雷诺通过实验知：下临界雷诺数为一定值，而上临
3水力过渡区壁面管水力过渡区壁面管transitionregiontransitionregionwallwall介于水力光滑管区与水力粗糙管区之间的区域的介于水力光滑管区与水力粗糙管区之间的区域的紊流阻力受粘性和紊动同时作用这个区域称为过紊流阻力受粘性和紊动同时作用这个区域称为过三紊流核心区的流速分布三紊流核心区的流速分布流体切应力主要为紊流附加切应力流体切应力主要为紊流附加切应力圆管均匀流过流断面上切应力呈直线分布圆管均匀流过流断面上切应力呈直线分布根据实验管流混合长经验公式为根据实验管流混合长经验公式为11223311对数规律分布对数规律分布将223344代入代入11积分得到积分得到紊流速度分布式紊流速度分布式卡门常数卡门常数k04k04说明
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
截面上，z+p/ρ g=常数,则
A(zpg)dQ(zpg)Q
令u2udAV2VA
A2g
2g
V为截面平均速度
1 (u)3dA称为(动 通能 )量 修正系数 AA V
对圆管层流，α=2， 工程上的管流为紊流，α≈1
(z1p g 11V 2 1 g 2)Q 1(z2p g 22V 22 g 2)Q 2
用于测点速度.
沿流线伯努利方程
z0pg0 u20g2 z1pg1 u21g2
静压管和总压管
z0z1,u00,
u1 2gp0 gp1
伯努利方程应用
3、小孔定常出流
对0—0和1—1：
z0pga z1pga 1V 21g2
11,z0z1h V1 2gh 平均速 度
2
gzpV2 const单位：Pa
2
z
p
g
V2 2g
const
单位：mH2O
伯努利方程应用
1、静压管、总压管测速度
p u2 p 1 0
g 2g g
P0=Pa+ρ g(Δh+x)
P1=Pa+ρ g x
u1
2gp0p1
g
2gh
伯努利方程应用
2、 毕 托管 (Pitot Tube) 测流速
z1pg 11V 21 g 2z2pg 22V 22 g 2
V1A1 V2A2 V1 V2 A2 A1 (d D)2
V2
2g 1(d)4
(z1
z2
p1p2)
g
D
文丘里流量计
如果用水银压差计测压差则有
p1+ρ g(x+Δh)=p2+ρ g(z2-z1+x)+ρ ’gΔh
p1 gp2z1z2(,/1)h
QA2V2d 42
2g(,/1)h
1(d/D )4
考虑到流体的粘性影响及制造工艺等 因素，流量应乘上一个流量系数μ， 实验方法测定，一般取0.95-0.98。
文丘里效应
文丘里效应简单说就是，当空气从一个比较广大的空间流向比较 狭窄的端口时，在阻挡物的背风面上方端口附近气压相对较低， 产生的吸附作用使空气流动自然加速。这是美国著名建筑设计大 师赖特设计的一个房子，利用文丘里效应来冷却中间的空间。
则烟囱正常排烟时，P P
2
a2
但
P a2P a1agH
22
Z2Z1H
1
1
由 P P 得到
2
a2
P 1 P a 1 (a)g H 1 2 (V 1 2 V 2 2) 称为烟囱的自然抽力，通常为负值。
可见，H越大时，烟囱的自然抽力也越大。
总流伯努利方程的推广（流体对外界作功）
pg zV2 常数单位 Pa：
2
沿流线，(静压＋位压＋动压)守恒
几何意义： pgzV 22g常数单位 m2 ： H O
沿流线, (压力水头＋位置水头＋速度水头)＝总水头, 即：沿流线总水头守恒
伯努利方程
三种形式：
1) 能量形式 2) 压头形式 3) 水头形式
gz p V2 const 单位：J/kg
即沿流线 z 法 p g常 向数
曲率半径很大时，沿流线的法向，压强服从静压分布公式
缓变流和急变流的概念: 如果某处的流线的曲率半径非常大,则此处 的流动称为缓变流.否则称为急变流.
§3-7 总流的伯努利方程
总流：全部流束的总体
研究总流在截面1—1和2—2的部份，取某一流束，
速度和截面积为u1, dA1和u2，dA2。
uus gzs1ps
(u2/2)(g)z(p/)
s
s s
u2
p
( gz )0
s 2
u2
p
gz c
2
u2 z p c
2g g
伯努利方程
•伯努利方程的物理意义
能量意义： pgzV22 常数单位 J/： kg
沿流线，(压力能＋势能＋动能)守恒
其中，N为涡轮机的输出功，[J/kg]
§3-8 非定常的伯努利方程
非定常一元流动的运动方程：
u t u u sfs 1 p s
式 fs 中 g z s
或 u(gzpu2 )0
t s 2
Q1 Q2
z1pg1 1V 21g2 z2pg2 2V 22g2
z, p 通常在截面中心取值。
它与流线上的伯努利方程在形式上相同，如果计 算点速度就用流线形式，如果计算平均流速就用
此式。
总流伯努利方程应用举例
总流伯努利方程应用
1、文丘里流量计(Venturi Meter) 对截面1和2，总流伯努利方程
1、风机 (g1 zp 1V 2 1 2) P (g2 zp 2V 2 2 2)
其中，P为风机的静压头，[Pa]
2、水泵
(z1pg 1V 21 g 2)H(z2pg 2V 22 g 2)
其中，H为水泵的扬程，[mH2O]
3、涡轮机 (g1zp 1V 2 12)(g2zp 2V 2 22)N
总流伯努利方程应用
22
2、烟囱排烟原理 对截面1和2，总流伯努利方程
z1pg 11V 21 g 2z2pg 22V 22 g 2
1
1
V1A1 V2A2 V1 V2 A2 A1 (d D)2
V2
2g 1(d)4(z1ຫໍສະໝຸດ 2p1p2)g
D
设烟囱周围大气压为 Pa1，Pa2
§3-6 压强沿流线法向的变化
设流线某处的曲率半径为r 。
1 p
ar fr r
u2 arr,
frgco sg r z
u2
p
(gz )
r r
u2
p
(gz )
r r
当 r 时 , r(g z p)0,
伯努利方程
z1pg1 2u1g2 z2pg2 2ug 22
不可压缩连续方程 u1dA1=u2dA2 或 dQ1=dQ2
A 1(z1p g 12 u1 g 2)u1d1A A 2(z2p g 22 ug 2 2)u2d2A
总流的伯努利方程
设两截面处在缓变流中，在1—1和2—2
A(zpg)dQ(zpg)Q
令u2udAV2VA
A2g
2g
V为截面平均速度
1 (u)3dA称为(动 通能 )量 修正系数 AA V
对圆管层流，α=2， 工程上的管流为紊流，α≈1
(z1p g 11V 2 1 g 2)Q 1(z2p g 22V 22 g 2)Q 2
用于测点速度.
沿流线伯努利方程
z0pg0 u20g2 z1pg1 u21g2
静压管和总压管
z0z1,u00,
u1 2gp0 gp1
伯努利方程应用
3、小孔定常出流
对0—0和1—1：
z0pga z1pga 1V 21g2
11,z0z1h V1 2gh 平均速 度
2
gzpV2 const单位：Pa
2
z
p
g
V2 2g
const
单位：mH2O
伯努利方程应用
1、静压管、总压管测速度
p u2 p 1 0
g 2g g
P0=Pa+ρ g(Δh+x)
P1=Pa+ρ g x
u1
2gp0p1
g
2gh
伯努利方程应用
2、 毕 托管 (Pitot Tube) 测流速
z1pg 11V 21 g 2z2pg 22V 22 g 2
V1A1 V2A2 V1 V2 A2 A1 (d D)2
V2
2g 1(d)4
(z1
z2
p1p2)
g
D
文丘里流量计
如果用水银压差计测压差则有
p1+ρ g(x+Δh)=p2+ρ g(z2-z1+x)+ρ ’gΔh
p1 gp2z1z2(,/1)h
QA2V2d 42
2g(,/1)h
1(d/D )4
考虑到流体的粘性影响及制造工艺等 因素，流量应乘上一个流量系数μ， 实验方法测定，一般取0.95-0.98。
文丘里效应
文丘里效应简单说就是，当空气从一个比较广大的空间流向比较 狭窄的端口时，在阻挡物的背风面上方端口附近气压相对较低， 产生的吸附作用使空气流动自然加速。这是美国著名建筑设计大 师赖特设计的一个房子，利用文丘里效应来冷却中间的空间。
则烟囱正常排烟时，P P
2
a2
但
P a2P a1agH
22
Z2Z1H
1
1
由 P P 得到
2
a2
P 1 P a 1 (a)g H 1 2 (V 1 2 V 2 2) 称为烟囱的自然抽力，通常为负值。
可见，H越大时，烟囱的自然抽力也越大。
总流伯努利方程的推广（流体对外界作功）
pg zV2 常数单位 Pa：
2
沿流线，(静压＋位压＋动压)守恒
几何意义： pgzV 22g常数单位 m2 ： H O
沿流线, (压力水头＋位置水头＋速度水头)＝总水头, 即：沿流线总水头守恒
伯努利方程
三种形式：
1) 能量形式 2) 压头形式 3) 水头形式
gz p V2 const 单位：J/kg
即沿流线 z 法 p g常 向数
曲率半径很大时，沿流线的法向，压强服从静压分布公式
缓变流和急变流的概念: 如果某处的流线的曲率半径非常大,则此处 的流动称为缓变流.否则称为急变流.
§3-7 总流的伯努利方程
总流：全部流束的总体
研究总流在截面1—1和2—2的部份，取某一流束，
速度和截面积为u1, dA1和u2，dA2。
uus gzs1ps
(u2/2)(g)z(p/)
s
s s
u2
p
( gz )0
s 2
u2
p
gz c
2
u2 z p c
2g g
伯努利方程
•伯努利方程的物理意义
能量意义： pgzV22 常数单位 J/： kg
沿流线，(压力能＋势能＋动能)守恒
其中，N为涡轮机的输出功，[J/kg]
§3-8 非定常的伯努利方程
非定常一元流动的运动方程：
u t u u sfs 1 p s
式 fs 中 g z s
或 u(gzpu2 )0
t s 2
Q1 Q2
z1pg1 1V 21g2 z2pg2 2V 22g2
z, p 通常在截面中心取值。
它与流线上的伯努利方程在形式上相同，如果计 算点速度就用流线形式，如果计算平均流速就用
此式。
总流伯努利方程应用举例
总流伯努利方程应用
1、文丘里流量计(Venturi Meter) 对截面1和2，总流伯努利方程
1、风机 (g1 zp 1V 2 1 2) P (g2 zp 2V 2 2 2)
其中，P为风机的静压头，[Pa]
2、水泵
(z1pg 1V 21 g 2)H(z2pg 2V 22 g 2)
其中，H为水泵的扬程，[mH2O]
3、涡轮机 (g1zp 1V 2 12)(g2zp 2V 2 22)N
总流伯努利方程应用
22
2、烟囱排烟原理 对截面1和2，总流伯努利方程
z1pg 11V 21 g 2z2pg 22V 22 g 2
1
1
V1A1 V2A2 V1 V2 A2 A1 (d D)2
V2
2g 1(d)4(z1ຫໍສະໝຸດ 2p1p2)g
D
设烟囱周围大气压为 Pa1，Pa2
§3-6 压强沿流线法向的变化
设流线某处的曲率半径为r 。
1 p
ar fr r
u2 arr,
frgco sg r z
u2
p
(gz )
r r
u2
p
(gz )
r r
当 r 时 , r(g z p)0,
伯努利方程
z1pg1 2u1g2 z2pg2 2ug 22
不可压缩连续方程 u1dA1=u2dA2 或 dQ1=dQ2
A 1(z1p g 12 u1 g 2)u1d1A A 2(z2p g 22 ug 2 2)u2d2A
总流的伯努利方程
设两截面处在缓变流中，在1—1和2—2