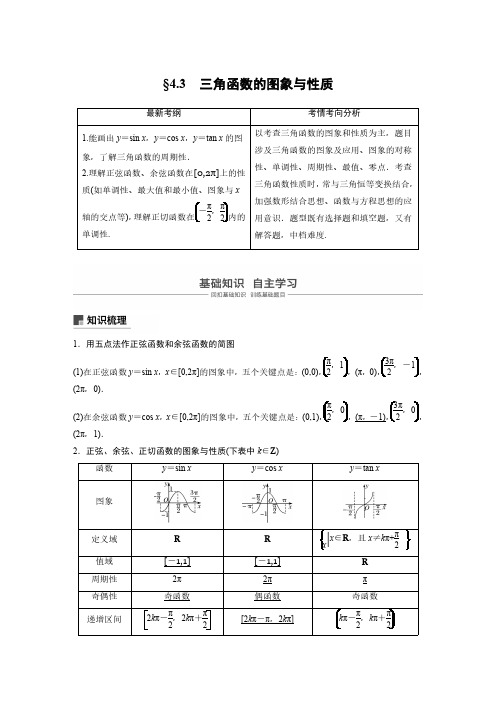
高三理科数学第一轮复习§3.3:三角函数的图象与性质
合集下载
高三数学一轮复习 第3章 三角函数第3课时 三角函数的图象和性质精品课件

解析: f(x)=1-cos24x-π2=12-12sin 4x, ∴T=24π=π2.
答案:
π 2
3.(2010·北京卷)已知函数f(x)=2cos 2x+sin2x-4cos x.
(1)求fπ3的值; (2)求f(x)的最大值和最小值.
解析: (1)fπ3=2cos23π+sin23π-4cosπ3 =-1+34-2=-94.
∴f(x)为奇函数,∴f(x)的图象关于原点对称.
答案: B
4.比较大小,sin-1π8________sin-1π0.
解析: 因为y=sin x在-π2,0上为增函数且-1π8>-1π0, 故sin-1π8>sin-1π0. 答案: >
5.函数y=sinx+π3,x∈0,π3的值域是________.
【变式训练】 3.(1)求函数y=sin π3-ห้องสมุดไป่ตู้x ,x∈[-π,π]的单调递减 区间;
(2)求y=3tanπ6-4x的周期及单调区间.
解析: (1)由 y=sinπ3-2x得 y=-sin2x-π3, 由-π2+2kπ≤2x-π3≤π2+2kπ 得 -1π2+kπ≤x≤152π+kπ,k∈Z. 又 x∈[-π,π], ∴-π≤x≤-172π,-1π2≤x≤152π,1112π≤x≤π. ∴函数 y=sinπ3-2x,x∈[-π,π]的单调递减区间为-π,-172π, -1π2,152π,1112π,π.
D.x|x≠kπ+34π,k∈Z,x∈R
解析: ∵x-π4≠kπ+2π,∴x≠kπ+34π,k∈Z. 答案: D
3.(2010·陕西卷)对于函数f(x)=2sin xcos x,下列选项中正确的是 ()
A.f(x)在π4,π2上是递增的 B.f(x)的图象关于原点对称 C.f(x)的最小正周期为2π D.f(x)的最大值为2 解析: ∵f(x)=2sin xcos x=sin 2x,
三角函数的图象与性质(高三一轮复习)

数学 N 必备知识 自主学习 关键能力 互动探究
— 27 —
(4)三角函数型函数奇偶性的判断除可以借助定义外,还可以借助其图象与性 质,如在y=Asin(ωx+φ)中代入x=0,若y=0,则为奇函数,若y为最大或最小值, 则为偶函数.若y=Asin(ωx+φ)为奇函数,则φ=kπ(k∈Z),若y=Asin(ωx+φ)为偶函 数,则φ=2π+kπ(k∈Z).
A.y=fx-π4为奇函数 B.y=fx-4π为偶函数 C.y=fx+4π-1为奇函数 D.y=fx+π4-1为偶函数
数学 N 必备知识 自主学习 关键能力 互动探究
— 21 —
(2)(2022·新高考Ⅰ卷)记函数f(x)=sin
ωx+π4
+b(ω>0)的最小正周期为T.若
2π 3
<T<π,且y=f(x)的图象关于点32π,2中心对称,则fπ2=( A )
— 10 —
数学 N 必备知识 自主学习 关键能力 互动探究
— 11 —
2.(易错题)(2023·宜昌检测)下列函数中,在其定义域上是偶函数的是( B )
A.y=sin x
B.y=sin x
C.y=tan x
D.y=cosx-π2
解析 对于A,∵y=sin x的定义域为R,sin(-x)=-sin x,∴y=sin x为奇函
数,A错误;对于B,∵y=
sin
x
的定义域为R,
sin-x
=
-sin
x
=
sin
x
,∴y=
sin x为偶函数,B正确;对于C,∵y=tan x的定义域为kπ-π2,kπ+2π(k∈Z),即定 义域关于原点对称,tan(-x)=-tan x,∴y=tan x为奇函数,C错误;对于D,∵y=
2014高考数学一轮复习课件3.3三角函数的图象与性质

调性、值域等是高考的热点内容,常与三角变换等知识交
汇,在考查三角函数图象与性质的同时,注重考查三角变换
的技能,及数形结合、转化与化归等数学思想.
创新探究之四
三角函数单调性的创新应用
π (2012· 课标全国卷)已知ω>0,函数f(x)=sin(ωx+ )在 4 π ( ,π )上单调递减,则ω的取值范围是( 2 1 5 A.[ , ] 2 4 1 C.(0, ] 2 1 3 B.[ , ] 2 4 D.(0,2] )
π π kπ 【解析】 由3x≠ +kπ,k∈Z得x≠ + , 2 6 3 k∈Z,.
【答案】
D
5π 2.函数f(x)=2cos(x+ )是( 2
)
A.最小正周期为2π 的奇函数 B.最小正周期为2π 的偶函数 C.最小正周期为2π 的非奇非偶函数 D.最小正周期为π 的偶函数
π 5 【解析】 f(x)=2cos(x+ π)=2cos(x+ )=-2sin 2 2 x,故f(x)是最小正周期为2π的奇函数.
π 【解析】 f(x)=sin(πx- )-1=-cos πx-1, 2 2π 因此函数f(x)是偶函数,周期T= =2. π
【答案】
B
1.若f(x)=Asin(ωx+φ)(A,ω≠0),则 π (1)f(x)为偶函数的充要条件是φ= +kπ(k∈Z); 2 (2)f(x)为奇函数的充要条件是φ=kπ(k∈Z). 2.对称性:正、余弦函数的图象既是轴对称图形,又 是中心对称图形且最值点在对称轴上,正切函数的图象只 是中心对称图形.
π 设函数f(x)=sin(ωx+φ)(ω>0,|φ|< ),给出以 2 下四个论断: ①它的最小正周期为π ; π ②它的图象关于直线x= 成轴对称图形; 12 π ③它的图象关于点( ,0)成中心对称图形; 3 π ④在区间[- ,0)上是增函数. 6 以其中两个论断作为条件,另两个论断作为结论, 写出你认为正确的一个命题________(用序号表示).
汇,在考查三角函数图象与性质的同时,注重考查三角变换
的技能,及数形结合、转化与化归等数学思想.
创新探究之四
三角函数单调性的创新应用
π (2012· 课标全国卷)已知ω>0,函数f(x)=sin(ωx+ )在 4 π ( ,π )上单调递减,则ω的取值范围是( 2 1 5 A.[ , ] 2 4 1 C.(0, ] 2 1 3 B.[ , ] 2 4 D.(0,2] )
π π kπ 【解析】 由3x≠ +kπ,k∈Z得x≠ + , 2 6 3 k∈Z,.
【答案】
D
5π 2.函数f(x)=2cos(x+ )是( 2
)
A.最小正周期为2π 的奇函数 B.最小正周期为2π 的偶函数 C.最小正周期为2π 的非奇非偶函数 D.最小正周期为π 的偶函数
π 5 【解析】 f(x)=2cos(x+ π)=2cos(x+ )=-2sin 2 2 x,故f(x)是最小正周期为2π的奇函数.
π 【解析】 f(x)=sin(πx- )-1=-cos πx-1, 2 2π 因此函数f(x)是偶函数,周期T= =2. π
【答案】
B
1.若f(x)=Asin(ωx+φ)(A,ω≠0),则 π (1)f(x)为偶函数的充要条件是φ= +kπ(k∈Z); 2 (2)f(x)为奇函数的充要条件是φ=kπ(k∈Z). 2.对称性:正、余弦函数的图象既是轴对称图形,又 是中心对称图形且最值点在对称轴上,正切函数的图象只 是中心对称图形.
π 设函数f(x)=sin(ωx+φ)(ω>0,|φ|< ),给出以 2 下四个论断: ①它的最小正周期为π ; π ②它的图象关于直线x= 成轴对称图形; 12 π ③它的图象关于点( ,0)成中心对称图形; 3 π ④在区间[- ,0)上是增函数. 6 以其中两个论断作为条件,另两个论断作为结论, 写出你认为正确的一个命题________(用序号表示).
高三数学一轮复习3.3三角函数的图象与性质课件

2 2 , ]上是增函数,故原点到 3 3 2 2 T 2 T 8 ,即 2 8 , , 的距离不超过 ,即 ,得T≥ 3 3 4 3 4 3 3 又ω>0,得0<ω≤ 3 . 因此ω的最大值为 3 . 4 4 答案: 3 4
方法三:因为f(x)在区间[
【互动探究】在本例(1)中函数不变,求函数在[-π,0]上 的单调递减区间. 【解析】方法一:x∈R时,y=sin( -2x)的减区间为[kπ ,kπ+ 5 ],k∈Z.令k=0得 5 ;令k=-1得 - x 12 12 12 12 13 7 ,故x∈[-π,0]时,y=sin( -2x)的减 - x - 3 12 12 区间为[-π,- 7 ],[ - ,0]. 12 12 3
6 3 2
3 6 3 7 , 6
所以y∈[- 3 ,2],所以ymax+ymin= 2 3. (2)选C.因为f(x)=1-2sin2x+2cos x=1-2(1-cos2x)+2cos x= 2cos2x+2cos x-1= 2(cos x ) 2 , 又因为x∈R,所以cos x∈[-1,1]. 所以当cos x= 1 时,f(x)有最小值,且f(x)min= 3 ;
第三节
三角函数的图象与性质
【知识梳理】 1.周期函数和最小正周期
非零常数 f(x+T)=f(x)
2.正弦函数、余弦函数、正切函数的图象和性质
函数
y=sinx
y=cosx
y=tanx
图象
定义域
值域
R __ [-1,1] ________
R __ [-1,1] ________
{x|x∈R且x≠ + _______________ 2 k π,k∈Z} _______________ R __
高考数学一轮复习第三章第五讲三角函数的图象与性质课件

由于 f(x)=tan 2x-π4的最小正周期为π2,故排除 D.故选 C.
答案:C
2.(考向 2)若函数 f(x)=sin ωx+4π(ω>0)在π2,π上单调递增, 则 ω 的取值范围是( )
A.12,54
B.12,34
C.0,
1 4
D.(0,2]
解析:∵函数 f(x)=sin ωx+π4(ω>0)在π2,π上单调递增, 则 ω·π2+π4≥-π2+2kπ,且 ω·π+π4≤π2+2kπ,k∈Z, 求得 4k-32≤ω≤2k+14,取 k=0,得-32≤ω≤14. ∵ω>0,∴可得 ω 的取值范围为0,41.故选 C. 答案:C
考点一 三角函数的定义域
1.(2023 年金牛区校级月考)函数 y=tan2x-π4的定义域为
()
A.xx≠kπ+π2,
k∈Z
B.xx≠k2π+ 83π,k∈Z
C.xx≠2kπ+π2,
k∈Z
D.xx≠2kπ+38π,
k∈Z
解析:由题意,得 2x-π4≠kπ+π2,k∈Z,解得 x≠k2π+83π,k∈Z, 故定义域为xx≠k2π+ 83π,k∈Z.故选 B.
正数;若 A<0,借助导公式 sin α=-sin (α±π)或 cos α=-cos (α±π)
将 A 化为正数. (2)根据 y=sin x 和 y=cos x 的单调区间列不等式求解.
[例 3]函数 f(x)=3sin 23π-2x的一个单调递减区间是(
)
A.71π2,1132π
B.1π2,71π2
2.正弦、余弦、正切函数的图象与性质(下表中 k∈Z)
函数
y=sin x
y=cos x
y=tan x
答案:C
2.(考向 2)若函数 f(x)=sin ωx+4π(ω>0)在π2,π上单调递增, 则 ω 的取值范围是( )
A.12,54
B.12,34
C.0,
1 4
D.(0,2]
解析:∵函数 f(x)=sin ωx+π4(ω>0)在π2,π上单调递增, 则 ω·π2+π4≥-π2+2kπ,且 ω·π+π4≤π2+2kπ,k∈Z, 求得 4k-32≤ω≤2k+14,取 k=0,得-32≤ω≤14. ∵ω>0,∴可得 ω 的取值范围为0,41.故选 C. 答案:C
考点一 三角函数的定义域
1.(2023 年金牛区校级月考)函数 y=tan2x-π4的定义域为
()
A.xx≠kπ+π2,
k∈Z
B.xx≠k2π+ 83π,k∈Z
C.xx≠2kπ+π2,
k∈Z
D.xx≠2kπ+38π,
k∈Z
解析:由题意,得 2x-π4≠kπ+π2,k∈Z,解得 x≠k2π+83π,k∈Z, 故定义域为xx≠k2π+ 83π,k∈Z.故选 B.
正数;若 A<0,借助导公式 sin α=-sin (α±π)或 cos α=-cos (α±π)
将 A 化为正数. (2)根据 y=sin x 和 y=cos x 的单调区间列不等式求解.
[例 3]函数 f(x)=3sin 23π-2x的一个单调递减区间是(
)
A.71π2,1132π
B.1π2,71π2
2.正弦、余弦、正切函数的图象与性质(下表中 k∈Z)
函数
y=sin x
y=cos x
y=tan x
高考第一轮复习数学三角函数的图象与性质三

探究创新
9.已知P1,cosx,Qcosx,1,x∈- , .
1求向量 和 的夹角θ的余弦用x表示的函数fx;
2求θ的最值.
解:1∵ · =2cosx,
| |·| |=1+cos2x,
∴fx=cosθ= .
2cosθ= = ,
x∈- , ,cosx∈ ,1.
∴2≤cosx+ ≤ , ≤fx≤1,即 ≤cosθ≤1.
解:定义域为R,又fx+f-x=lg1=0,
即f-x=-fx,∴fx为奇函数.
评述:定义域关于原点对称是函数具有奇偶性的必要但不充分条件.
例2求下列函数的单调区间:
1y= sin - ;2y=-|sinx+ |.
剖析:1要将原函数化为y=- sin x- 再求之.2可画出y=-|sinx+ |的图象.
3.判断y=-Asinωx+ ω>0的单调区间,只需求y=Asinωx+ 的相反区间即可,一般常用数形结合.而求y=Asin-ωx+ -ω<0单调区间时,则需要先将x的系数变为正的,再设法求之.读者考虑为什么
●教师下载中心
教学点睛
本节是图象和性质的综合应用的内容,例题讲解要突出数形结合思想、化归转化思想、分类讨论等数学思想方法,并注意三角知识的载体作用,注意和其他知识间的关联.
解析:显然fx为偶函数,结论①错.
对于结论②,当x=1000π时,x>2003,sin21000π=0,∴f1000π= - 1000π< ,因此结论②错.
又fx= - |x|+ =1- cos2x- |x|,-1≤cos2x≤1,
∴- ≤1- cos2x≤ .
故1- cos2x- |x|< ,即结论③错.
9.已知P1,cosx,Qcosx,1,x∈- , .
1求向量 和 的夹角θ的余弦用x表示的函数fx;
2求θ的最值.
解:1∵ · =2cosx,
| |·| |=1+cos2x,
∴fx=cosθ= .
2cosθ= = ,
x∈- , ,cosx∈ ,1.
∴2≤cosx+ ≤ , ≤fx≤1,即 ≤cosθ≤1.
解:定义域为R,又fx+f-x=lg1=0,
即f-x=-fx,∴fx为奇函数.
评述:定义域关于原点对称是函数具有奇偶性的必要但不充分条件.
例2求下列函数的单调区间:
1y= sin - ;2y=-|sinx+ |.
剖析:1要将原函数化为y=- sin x- 再求之.2可画出y=-|sinx+ |的图象.
3.判断y=-Asinωx+ ω>0的单调区间,只需求y=Asinωx+ 的相反区间即可,一般常用数形结合.而求y=Asin-ωx+ -ω<0单调区间时,则需要先将x的系数变为正的,再设法求之.读者考虑为什么
●教师下载中心
教学点睛
本节是图象和性质的综合应用的内容,例题讲解要突出数形结合思想、化归转化思想、分类讨论等数学思想方法,并注意三角知识的载体作用,注意和其他知识间的关联.
解析:显然fx为偶函数,结论①错.
对于结论②,当x=1000π时,x>2003,sin21000π=0,∴f1000π= - 1000π< ,因此结论②错.
又fx= - |x|+ =1- cos2x- |x|,-1≤cos2x≤1,
∴- ≤1- cos2x≤ .
故1- cos2x- |x|< ,即结论③错.
高考数学一轮复习讲义3三角函数的图象与性质
2x+π 3
B.y=2sin
2x-π 6
x+π C.y=2sin 2 3
2x-π D.y=2sin 3
答案 B
解析
函数 y=2sin
2x-π 6
的最小正周期 T=2π=π,
2
2×π-π 又 sin 3 6 =1,
∴函数 y=2sin
2x-π 6
的图象关于直线 x=π对称.
3
π-2x 6.函数 f(x)=4sin 3 的单调递减区间是______________________.
解析
当
x∈
0,π 2
时,2x-π∈
-π,5π 66
,
6
2x-π -1,1 sin 6 ∈ 2 ,
2x-π -3,3 故 3sin 6 ∈ 2 ,
2x-π
-3,3
即 y=3sin
6 的值域为 2 .
2x-3π
4.函数 y=-tan
4 的单调递减区间为________________.
π+kπ,5π+kπ 答案 8 2 8 2 (k∈Z)
2
2
递减区间 对称中心 对称轴方程
2kπ+π,2kπ+3π
2
2
(kπ,0)
x=kπ+π 2
[2kπ,2kπ+π] kπ+π,0 2 x=kπ
无 kπ,0 2
无
概念方法微思考 1.正(余)弦曲线相邻两条对称轴之间的距离是多少?相邻两个对称中心的距离呢? 提示 正(余)弦曲线相邻两条对称轴之间的距离是半个周期;相邻两个对称中心的距离也为 半个周期. 2.思考函数 f(x)=Asin(ωx+φ)(A≠0,ω≠0)是奇函数,偶函数的充要条件? 提示 (1)f(x)为偶函数的充要条件是φ=π+kπ(k∈Z);
高考数学一轮复习 第3章《三角函数》三角函数的图象课件

∴φ=-ωx0=-
2
(3
2)=
3
.
返回目录
解法四:(平移法)
由图象知,将y=5sin
2 3
x的图象沿x轴向左平移
2
个单
位,就得到本题图象.故所求函数解析式为
y=5sin〔 2 ( x+ )〕=5sin( 2 x+ ).
3
2
33
返回目录
考点三 三角函数图象的对称性
已知函数y=sin2x+acos2x= 1 a2 sin(2x+φ)(其中
3
(2)由此题两种解法可见,在由图象求解析式时,
“第一个零点”的确定是重要的,应尽量使A取正值.
(3)已知函数图象求函数
y=Asin(ωx+φ)(A>0,ω>0)的解析式时,常用的解题 方法是待定系数法,由图中的最大值或最小值确定A,由 周期确定ω,由适合解析式的点的坐标来确定φ,但由
返回目录
图象求得的y=Asin(ωx+φ)(A>0,ω>0)的解析式一般不唯 一,只有限定φ的取值范围,才能得出唯一解,否则φ的值不 确定,解析式也就不唯一.
学案3 三角函数的图象
考点分析
1. “五点法”作y=Asin(ωx+φ)(A>00,,ω,>,30)的,2简图
五点的取法是:设X=ωx+φ,由X取 2 2 来求相应的x值,及对应的y值,再描点作图.
2.变换作图法作y=Asin(ωx+φ)(A>0,ω>0)的 图象
(1)振幅变换:y=sinx→y=Asinx 返回目录
以“五点法”中的第一零点(
,0)作为突破口,要从图
象的升降情况找准第一零点的位置.要善于抓住特殊量和特
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
点拨
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
解析
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
第三章:三角函数与三角恒等变换 §3.3:三角函数的图象与性质
