5.4平移-人教版七年级数学下册练习
人教版七年级数学下册名校课堂练习5.4平移(含答案)
5.4 平移01课前预习要点感知1把一个图形整体沿着某一直线方向移动，会得到一个新的图形，这种移动就叫做________．预习练习1－1以下现象中属于平移的是()①温度计中，液柱的上升或下降；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上瓶装饮料的移动．A．①②B．①③C．②③D．②④1－2(朝阳中考)下列图形中，由如图经过一次平移得到的图形是()要点感知2平移的过程中，新图形中的每一点，都是由原图形中的某一点移动后得到的，这两点是________，连接各组对应点的线段________．画平移后的图形，是由平移的________和平移的________决定的．预习练习2－1将长度为5 cm的线段向上平移10 cm所得线段长度是()A．10 cm B．5 cmC．0 cm D．无法确定02当堂训练知识点1认识平移现象1．下列现象不属于平移的是()A．飞机起飞前在跑道上加速滑行B．汽车在笔直的公路上行驶C．游乐场的过山车在翻筋斗D．起重机将重物由地面竖直吊起到一定高度2．(赵县期末)在A、B、C、D四个选项中，能通过如图所示的图案平移得到的是()3．如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线()A．a户最长B．b户最长C．c户最长D．三户一样长4．如图，三角形A′B′C′是由三角形ABC沿射线AC方向平移2 cm得到，若AC＝3 cm，则A′C＝________．5．如图，三角形DEF是三角形ABC平移所得，观察图形：(1)点A的对应点是点________，点B的对应点是点________，点C的对应点是点；(2)线段AD，BE，CF叫做对应点间的连线，这三条线段之间有什么关系呢？知识点2画平移图形6．在5×5的方格纸中将图1中的图形N平移后的位置如图2所示，那么下面平移中正确的是()A．先向下移动1格，再向左移动1格B．先向下移动1格，再向左移动2格C．先向下移动2格，再向左移动1格D．先向下移动2格，再向左移动2格7．请在如图所示的方格中，将“箭头”向右平移3个单位长度．8．(甘肃模拟)如图所示，三角形ABC是通过平移三角形DEF得到的，已知ED和BA是对应线段，请在图中画出三角形DEF.03课后作业9．(曲靖期中)下面生活中的物体的运动情况可以看成平移的是()A．随风摆动的旗帜B．摆动的钟摆C．汽车玻璃上的雨刷的运动D．从楼顶自由下落的球(球不旋转)10．将左边的图案通过平移后可以得到的图案是()11．如图，在10×6的网格中，每个小方格的边长都是1个单位，将三角形ABC平移到三角形DEF的位置，下面正确的平移步骤是()A．先向左平移5个单位，再向下平移2个单位B．先向右平移5个单位，再向下平移2个单位C．先向左平移5个单位，再向上平移2个单位D．先向右平移5个单位，再向上平移2个单位12．(邵阳中考)某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是()A．甲种方案所用铁丝最长B．乙种方案所用铁丝最长C．丙种方案所用铁丝最长D．三种方案所用铁丝一样长13．(高邮模拟)如图，将三角形ABC平移到三角形A′B′C′的位置(点B′在AC边上)，若∠B＝55°，∠C＝100°，则∠AB′A′的度数为________．14．如图，三角形ABC经过一次平移到三角形DFE的位置，请回答下列问题：(1)点C的对应点是点________，∠D＝________，BC＝________；(2)连接CE，那么平移的方向就是________的方向，平移的距离就是线段________的长度，可量出约为________cm；(3)连接AD，BF，BE，与线段CE相等的线段有________．15．如图，方格中有一条美丽可爱的小金鱼．(1)若方格的边长为1，则小鱼的面积为________；(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程)．挑战自我16．(1)已知图1是将线段AB向右平移1个单位长度，图2是将线段AB折一下再向右平移1个单位长度，请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形；(2)若长方形的长为a，宽为b，请分别写出三个图形中除去阴影部分后剩下部分的面积；(3)如图4，在宽为10 m，长为40 m的长方形菜地上有一条弯曲的小路，小路宽度为1 m，求这块菜地的面积．参考答案课前预习要点感知1平移预习练习1－1D1－2 C要点感知2对应点平行且相等方向距离预习练习2－1 B当堂训练1．C 2.C 3.D 4.1 cm 5.(1)D E F(2)AD∥BE∥CF，AD＝BE＝CF. 6.C7.图略．8.图略．课后作业9．D10.A11.A12.D13.25°14.(1)E∠A FE(2)点C到点E CE2(3)AD，BF15.(1)16(2)图略．16.(1)图略．(2)三个图形中除去阴影部分后剩下部分的面积均为ab－b.(3)10×40－10×1＝390(m2)．。
(新人教版)数学七年级下册：5.4《平移》练习题及解析
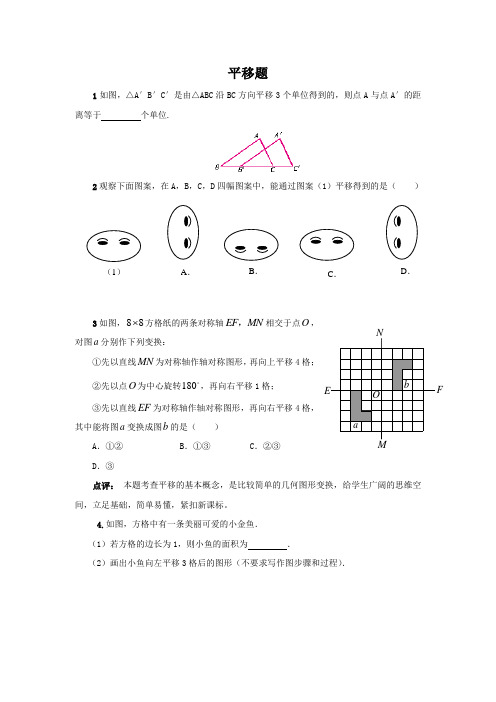
平移题
1如图，△A′B′C′是由△ABC沿BC方向平移3个单位得到的，则点A与点A′的距离等于个单位.
2观察下面图案，在A，B，C，D四幅图案中，能通过图案（1）平移得到的是（）
3如图， 方格纸的两条对称 轴 相交于点 ，对图 分别作下列变换：
①先以直线 为对称轴作轴对称图形，再向上平移4格；
②先以点 为中心旋转 ，再向右平移1格；
7分析：题中具体指明了平移的距离是2cm，在平移方向上只说明了“水平方向”，并未指明向左还是向右，故应分向左平移还是向右平移两种情况。作平移时可利用五个关键点平移后的位置进行。
解：平移后的图形如图2-2所示，有两种情况。
8分析：此题移动方向与距离均未知，只要求移动三条线段成一个三角形时最少需移动的格数，那么首先我们应该知道移动后组成三角形的大致形状，因平移不改变图形形状和大小，只是位置发生变化，故易知三角形形状应是“◣”，由此作为突破口去探索，显然若只移两条线段，单移任一条或两条向居中位置移动，最少格数是一样的，但三条就不同了，应让三条尽最大可能的少“拐弯”，观察图3-1，应在三条线段的“中间”画出最后所形成的三角形，如图3-2，可得出三条线段平移成一个三角形至少要平移9格。
(新人教版)七年级下册数学：5.4《平移》练习题及答案
平移练习题◆回顾归纳1．平移的要素：（1）平移的_________；（2）平移的_________．2．（1）平移：将一个图形沿某个方向_________叫平移．（2）平移的性质：对应点的连结线段_________且_________．3．平移作图方法：（1）找出已知图形上的关键点；（2）过这些点沿指定_______平移，使平移_______等于已知距离；（3）依次作出各个_______点，连结所平移后的点得平移图形．◆课堂测控知识点平移（1）将线段AB•向北偏东方向平移5cm，•则点A•平移方向_______，•平移距离为______．（2）1．经过平移后的图形与______形状和大小都不改变．2．下列物体运动中平移的是_________（填序号）．（1）打乒乓球的运动；（2）手表上指针的运动；（3）汽车在笔直公路上运动；（4）车轮的滚动．3．如图1所示的“田”字格可以看成由________平移得到的．图1 图2 图34．如图2所示，线段b向右平移3格，再向上平移______格，能与线段______重合．5．如图3所示，三角形ABC向下（右）平移_______格，再向右（下）平移_____得到三角形A′B′C′，图形的面积相等，形状不变．6．下列各组图形可以通过平移得到另一个图形的是（）A B C D7．（经典题）如图4所示，长方形ABCD中，对角线AC，BD交于点O．DE∥AC，CE ∥BC．那么三角形EDC可以看成什么三角形平移得到的，指出平移方向，并求出平移距离？图4◆课后测控1．将正方形ABCD向北偏东30°方向平移4cm，•则对角线交点O•向________•平移______cm．2．如图5所示，BC垂直于水平面，高5.196m，现要建造阶梯，•每级台阶不超过20cm，则至少要建_______级台阶（不足20cm，按一级台阶计算）图5 图6 图73．在5×5方格纸中将图6（1）中的图形N平移后的位置如图6（2）中所示，那么正确的平移方法是（）A．先向下移动1格，再向左移动1格B．先向下移动1格，再向左移动2格C．先向下移动2格，再向左移动1格D．先向下移动2格，再向左移动2格4．（互动探究题）如图7所示，在网格中，有三角形ABC，将A点平移到P点，画出三角形ABC平移后的图形．[解答]（1）将A点向_______（或向______）平移______格（或_____格）．（2）再向_____（或向_____）平移______格（或_______格），得点P．（3）同理B，C与A点平移次数方向距离一样，易得B′，C′．（4）连结PB′，PC′，B′C′得到三角形ABC平移后的三角形PB′C′．5．（经典题）如图所示，一块边长为8米的正方形土地，上面修了横竖各两条道路，宽都是1米，空白的部分种上各种花草，请利用平移的知识求出种花草的面积？◆拓展创新6．如图所示，在长方形ABCD中，AB=10cm，BC=6cm，试问将长方形ABCD•沿着AB方向平移多少才能使平移后的长方形与原来的长方形ABCD重叠部分的面积为24cm2？答案:回顾归纳1．（1）方向（2）距离2．（1）移动（2）平行或在同一条直线上，相等3．（2）方向；距离（3）对应课堂测控1．（1）北偏东；5cm （2）原图形 2．（3）3．小正方形包括中间四个小圆圈为基本图形4．2，c 5．3（或2），2（或3）6．C（点拨：A，B，D都不能通过平移得到）7．由三角形AOB，向右平移，平移距离为AD长．解题技巧：由平移图形的特征：大小，形状不变，猜想是△AOB．课后测控1．北偏东30°；4 2．26（点拨：519.620=26）3．C（点拨：或向左平移1格，再向下平移2格）4．（1）右；（下）；4；（5）（2）下；（右）；5；（4）（3），（4）图略5．将两条道路平移得到如图所示，则空白面积为（8-2）（8-2）=36（m2）思路点拨：运用平移思想方法是求这类面积问题最佳途径．6．设平行线段AE=x，A到E，E到F，则BE=AB-AE=10-x，因为BC=6，所以6（10-x）=24，•解得x=6，向右平移6cm．解题规律：扣住HEBC面积为24cm2，运用方程思想求解．。
人教版初一七年级下册数学课时练《5.4 平移》试题试卷 含答案
《5.4 平移》课时练一、选择题（共10小题）1．下列运动属于平移的是（）A．冷水加热过程中小气泡上升成为大气泡B．急刹车时汽车在地面上的滑动C．投篮时的篮球运动D．随风飘动的树叶在空中的运动2．将△ABC沿BC方向平移3个单位得△DEF．若△ABC的周长等于8，则四边形ABFD 的周长为（）A．14 B．12 C．10 D．83．如图，将△ABC沿BC方向平移3cm得到△DEF，若△ABC的周长为20cm，则四边形ABFD的周长为（）A．20cm B．22cm C．24cm D．26cm4．如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD 的周长是（）A．16 cm B．18 cm C．20 cm D．21 cm5．如图，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条小路（图中阴影部分），余下部分绿化，小路的宽为2m，则两条小路的总面积是（）m2A．108 B．104 C．100 D．986．如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A．2 B．4 C．8 D．167．如图是一块长方形ABCD的场地，长AB＝102m，宽AD＝51m，从A、B两处入口的中路宽都为1m，两小路汇合处路宽为2m，其余部分种植草坪，则草坪面积为（）A．5050m2B．5000m2C．4900m2D．4998m28．木匠有32米的木材，想要在花圃周围做边界，以下四种设计方案中，设计不合理的是（）A．B．C．D．9．如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，∠B＝90°，AB＝8，DH＝3，平移距离为4，求阴影部分的面积为（）A．20 B．24 C．25 D．2610．如图，在三角形ABC中，∠ABC＝90°，将三角形ABC沿AB方向平移AD的长度得到三角形DEF，已知EF＝8，BE＝3，CG＝3，则图中阴影部分的面积是（）A．12.5 B．19.5 C．32 D．45.5二、填空题（共5小题）11．如图，直径为2cm的圆O1平移3cm到圆O2，则图中阴影部分的面积为cm2．12．如图所示，在长为50米，宽为40米的长方形地块上，有纵横交错的几条小路（图中阴影部分），宽均为1米，其他部分均种植花草，则道路的面积是平方米．13．如图，△DEF是由△ABC沿直线BC向右平移得到，若BC＝6，当点E刚好移动到BC 的中点时，则CF＝．14．如图是用三角尺和直尺画平行线的示意图，将三角尺ABC沿着直尺PQ平移到三角尺A′B′C′的位置，就可以画出AB的平行线A′B′．若AC′＝9cm，A′C＝2cm，则直线AB平移的距离为cm．15．如图，将直角三角形ABC沿CB方向平移后，得到直角三角形DEF．已知AG＝3，BE ＝6，DE＝10，则阴影部分的面积为．三、解答题（共5小题）16．如图，平面直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为（3，2）．（1）填空：点A的坐标是，点B的坐标是；（2）将△ABC先向左平移3个单位长度，再向上平移1个单位长度，画出平移后的△A1B1C1；（3）求△ABC的面积．17．南湖公园有很多的长方形草地，草地里修了很多有趣的小路，如图三个图形都是长为50米，宽为30米的长方形草地，且小路的宽都是1米．（1）如图1，阴影部分为1米宽的小路（FF1＝EE1＝1），长方形除去阴影部分后剩余部分为草地，则草地的面积为；（2）如图2，有两条宽均为1米的小路（图中阴影部分），求草地的面积．（3）如图3，非阴影部分为1米宽的小路，沿着小路的中间从入口E处走到出口F处，所走的路线（图中虚线）长为．18．AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC＝80°．（1）若∠ABC＝50°，求∠BED的度数；（2）将线段BC沿DC方向平移，使得点B在点A的右侧，其他条件不变，若∠ABC＝120°，求∠BED的度数．19．如图所示，一块长为18m，宽为12m的草地上有一条宽为2m的曲折的小路，求这块草地的绿地面积．20．如图，已知两条射线BP∥CQ，动线段AD的两个端点A、D分别在射线BP、CQ上，且∠B＝∠ADC＝110°，F在线段AB上，AC平分∠DCF，CE平分∠BCF．（1）请判断AD与BC的位置关系，并说明理由；（2）求∠ACE的度数；（3）若平行移动AD，使∠BEC＝∠CAD，求∠CAD的度数．参考答案一、选择题（共10小题）1．B 2．A 3．D 4．C 5．C 6．A 7．B 8．A 9．D 10．B 二、填空题（共5小题）11．6．12．89．13．3．14．5.5．15．51．三、解答题（共5小题）16．解：（1）点A的坐标是：（4，﹣1），点B的坐标是：（5，3）；故答案为：（4，﹣1），（5，3）；（2）如图所示：△A1B1C1，即为所求；（3）．17．解：（1）将小路往左平移，直到E、F与A、B重合，则平移后的四边形EFF1E1是一个矩形，并且EF＝AB＝30，FF1＝EE1＝1，则草地的面积为：50×30﹣1×30＝1470（平方米）；故答案为：1470平方米；（2）小路往AB、AD边平移，直到小路与草地的边重合，则草地的面积为：（50﹣1）×（30﹣1）＝1421（平方米）；（3）将小路往AB、AD、DC边平移，直到小路与草地的边重合，则所走的路线（图中虚线）长为：30﹣1+50+30﹣1＝108（米）．故答案为：108米．18．解：（1）作EF∥AB，如图1，∵BE平分∠ABC，DE平分∠ADC，∴∠ABE＝∠ABC＝25°，∠EDC＝∠ADC＝40°，∵AB∥CD，∴EF∥CD，∵∠BEF＝∠ABE＝25°，∠FED＝∠EDC＝40°，∴∠BED＝25°+40°＝65°；（2）作EF∥AB，如图2，∵BE平分∠ABC，DE平分∠ADC，∴∠ABE＝∠ABC＝60°，∠EDC＝∠ADC＝40°，∵AB∥CD，∴EF∥CD，∵∠BEF＝180°﹣∠ABE＝120°，∠FED＝∠EDC＝40°，∴∠BED＝120°+40°＝160°．如图3，∵BE平分∠ABC，DE平分∠ADC，∴∠1＝∠ABC＝60°，∠EDC＝∠ADC＝40°，∵AB∥CD，∴∠2＝40°，∵∠1＝∠BED+∠2，∴∠BED＝60°﹣40°＝20°．如图4，∵BE平分∠ABC，DE平分∠ADC，∴∠ABE＝∠ABC＝60°，∠2＝∠ADC＝40°，∵AB∥CD，∴∠1＝∠ABE＝60°，∵∠3＝∠2＝40°，而∠1＝∠BED+∠2，∴∠BED＝60°﹣40°＝20°．综上所述，∠BED的度数为20°或160°．19．解：绿地的面积为：（18﹣2）×（12﹣2）＝160（m2），答：这块草地的绿地面积是160m2．20．解：（1）结论：AD∥BC．理由：∵BP∥CQ，∴∠DCB＝180°﹣∠B＝180°﹣110°＝70°，∵∠ADC+∠DCB＝110°+70°＝180°，∴AD∥BC．（2）∵AC平分∠DCF，CE平分∠BCF，∴∠ACF＝∠DCF，∠FCE＝∠FCB，∴∠ACE＝∠ACF+∠FCE＝∠DCF+∠FCB＝∠DCB＝×70°＝35°．（3）设∠ACD＝x，∵AB∥CD，∴∠BEC＝∠DCE＝35°+x，∵AD∥BC，∴∠DAC＝∠ACB＝70°﹣x，则有35°+x＝（70°﹣x），解得x＝28°，∴∠CAD＝70°﹣28°＝42°．。
人教版数学七年级下册《5.4平移》同步训练(含答案)
5.4 平移基础训练知识点1 平移的概念1.(2018山西吕梁柳林期末)下列运动属于平移的是( )A.荡秋千B.地球绕着太阳转C.风筝在空中随风飘动D.急刹车时，汽车在地面上的滑动2.(2018新疆期末)如图所示的小船通过平移后可得到的图案是( )知识点2 平移的性质3.(2018广东中山期末)如图，将三角形ABC沿BC方向平移得到三角形DEF,若BC=4，EC=1，则平移的距离为( )A.7B.6C.4D.34.(2018广西柳州柳北区三模)如图，三角形ADE是由三角形DBF沿BD所在直线平移得到的，AE，BF的延长线交于点C,若∠BFD=45°,则∠C的度数是( )A.43°B.44°C.45°D.46°5.如图，在四边形ABCD中，AD∥BC,若∠B与∠C互余，将AB，DC分别平移到EF 和EG的位置，则∠FEG的度数为 .6.如图，将周长为6cm的三角形ABC沿BC方向平移1cm得到三角形DEF，则四边形ABFD的周长为 .知识点3平移作图''';7.(1)如图，平移三角形ABC，使点A平移到点A'，画出平移后的三角形A B C(2)在(1)的条件下，指出点A,B,C 的对应点，并指出AB,BC,AC的对应线段和∠A，∠B, ∠C的对应角.知识点4平移的应用8.(2017江西新余一中期中)如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线( )A.a户最长B.6户最长C.c户最长D.一样长9.如图是“俄罗斯方块”游戏的一个画面，若使左上角的图形经平移插入到下面空白的A 处，应先向平移格，再向平移格.10.关注生活数学：某宾馆重新装修后考虑在大厅内的主楼梯上铺设地毯，已知主楼梯宽3m，其剖面图如图所示，请计算铺此楼梯，需要购买地毯多少平方米？参考答案：1.D解析：A,B,C项中的运动都不是沿某一直线方向移动，所以都不属于平移.故选D.2.B3.D解析：因为将三角形ABC沿BC方向平移得到三角形DEF，所以平移的距离为BE的长，因为BC=4,EC=1,所以BE=BC-EC=4-1=3.故选D.4.C解析：因为三角形ADE是由三角形DBF沿BD所在直线平移得到的，所以DF∥AE,因为AE，BF的延长线交于点C，所以DF∥AC，所以∠C=∠BFD=45°.故选C.5.90°解析：因为AB，DC分别平移到EF和EG的位置后，∠B的对应角是∠EFG，∠C的对应角是∠EGF, ∠B与∠C互余，所以∠EFG与∠EGF互余，所以∠EFG+∠EGF=90°.因为AD∥BC,所以∠AEF=∠EFG, ∠DEG=∠EGF,所以∠AEF+∠DEG=90°，所以∠FEG=180°-90°=90°.6. 8解析：∵三角形ABC沿BC方向平移1 cm得到三角形DEF，∴DF=AC,AD=CF =1cm.∵三角形ABC的周长为6 cm,∴AB+BC+AC=6cm,∴四边形ABFD的周长为AB+BF+DF+AD=AB+BC+CF+AC+AD=6+1+1=8(cm).7.(1)如图所示.(2)点A ，B ，C 的对应点分别是点A B C '''，，,线段AB,BC ，AC 的对应线段分别是A B B C A C ''''''，，，∠A,∠B ，∠ACB 的对应角分别A A B C A C B '''''''∠∠∠，，.名师点睛：因为平移后图形的大小和形状不会改变，只是位置改变，所以在画平移后的图形时，首先分析题目要求，找出平移的方向和距离，再分析已知图形，确定构成图形的关键点，然后根据平移的方向和距离平移每个关键点，最后顺次连接所作出的各个关键点.8.D解析：根据平移的性质，得电线的竖直长度一样，水平长度也一样，所以三户所用电线一样长，故选D.9.右 1 下 310.解析：由平移的性质，可知地毯的长为AB +BC = 1.2 +2.4= 3.6(m) ,3.6×3=10.8(m 2).故需要购买地毯10.8平方米.5.4 平移 提升训练1.(2018河北邯郸十一中课时作业)某数学兴趣小组开展动手操作活动，设计了如图所示的三种图形，现计划用铁丝按照图形制作相应的造型，则所用铁丝的长度关系是( )A.甲种方案所用铁丝最长B.乙种方案所用铁丝最长C.丙种方案所用铁丝最长D.三种方案所用铁丝一样长2.(2018山西忻州师院附中课时作业)如图，将三角形ABC 沿着BC 方向平移3cm 得到三角形DEF,AB=6cm,BC=9cm,DH=2cm,那么图中阴影部分的面积为cm 2.3.(2018湖北华中师大一附中课时作业)如图1，平移三角形ABD,使点D 沿BD 的延长线平移至点C ，得到三角形A B C '''，A B ''交AC 于点E ，AD 平分∠BAC.(1)猜想B EC '∠与A '∠之间的关系，并写出理由；(2)如果将三角形ABD 平移至如图2所示位置，得到三角形A B D ''',请问A D ''平分B A C '''∠吗？为什么？4.(2018陕西延安行知中学课时作业)联想与探索：如图1,将线段A 1A 2本向右平移1个单位长度至B 1B 2，得到封闭图形A 1A 2B 2B 1(即阴影部分)，在图2中，将折线A 1A 2A 3向右平移1个单位长度至B 1B 2B 3，得到封闭图形A 1A 2A 3B 3B 2B 1(即阴影部分).(1)在图3中，请你类似地画一条有两个折点的折线，同样向右平移1个单位长度，从而得到一个封闭图形，并用阴影表示；(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积(设长方形水平方向长均为a,竖直方向长均为b) ：S 1=，S 2=，S 3=;(3)如图4，在一块长方形草地上，有一条弯曲的小路(小路任何地方的水平宽度都是2个单位长度，长方形水平方向长为a,竖直方向长为b)，则空白部分表示的草地面积是多少？(4)如图5，若在(3)中的草地上又有一条横向的曲小路(小路任何地方的宽度都是1个单位长度），则空白部分表示的草地面积是多少？参考答案：1.D解析：由平移的性质,得三种方案所用铁丝的长度都是2a+2b.故选D.2.15解析： DEF ECH 2EF BC 9cm,DE AB 6cm,BE 3 cm HE DE DH 4cm EC BC BE 6cm11S =S S =DE EF EH EC 2211=6946=15(cm )22=====∴=-==-=∴--⨯⨯-⨯⨯阴影三角形三角形由平移的性质，知，， 名师点睛：将不规则图形的面积转化为两个三角形面积之差是解题的关键.3.解析：(1)(1)B EC=2A ''∠∠.理由如下：A B D ABD AD BAC BAD=DAC BAD=A AB A B BAC=B EC 11A =BAD=BAC=B EC B EC=2A 22'''∠'''∴∠∠∠∠'∴∠∠''''∴∠∠∠∠∠∠三角形是由三角形平移得到的，且平分，，，∥，，，即A DB A C.B A D =BAD AB A B BAC=B A C.11BAD=BAC B A D =B A C 22A DB A C'''''∠'''''∠∠'''∴∠∠'''''∠∠∴∠∠''''∴∠平分理由如下：，∥，，平分4.解析:(1)画图如下.(2)a(b-1) a(b-1) a(b-1)(3)因为小路任何地方的水平宽度都是2个单位长度, 所以空白部分表示的草地面积是b(a-2).(4)因为横向小路任何地方的宽度都是1个单位长度, 所以空白部分表示的草地面积是（a-2)(b-1).。
人教版七年级下册数学平移课时练习题(含答案)
人教版七年级下册数学5.4平移课时练习题（含答案）一、单选题1．“水是生命之源，滋润着世间万物”国家节水标志由水滴，手掌和地球变形而成．寓意：像对待掌上明珠一样，珍惜每一滴水!以下通过平移节水标志得到的图形是（）A．B．C．D．2．在下列现象中，属于平移的是（）A．月亮绕地球运动B．翻开书中的每一页纸张C．教室可移动黑板的左右移动D．投掷出去的铅球3．下列几种运动中属于平移的有（）①水平运输带上砖的运动；②笔直的铁路上行驶的动车（忽略车轮的转动）；③升降机上下做机械运动；④足球场上足球的运动．A．4种B．3种C．2种D．1种4．如图，在平面直角坐标系中，已知点A(2，1)，B(3，－1)，平移线段AB，使点B落在点B1（－1，－2）处，则点A的对应点A1的坐标为（）A．(0，－2)B．（－2，0）C．（0，－4）D．（－4，0）5．佳佳将坐标系中一图案横向拉长2倍，又向右平移2个单位长度，若想变回原来的图案，需要变化后的图案上各点坐标（）A．纵坐标不变，横坐标减2 B．纵坐标不变，横坐标先除以2，再均减2C．纵坐标不变，横坐标除以2 D．纵坐标不变，横坐标先减2，再均除以26．如图，ΔABC是直角三角形，它的直角边AB=6，BC=8，将ΔABC沿边BC的方向平移到ΔDEF 的位置，DE交AC于点G，BE=2，ΔCEG的面积为13.5，下列结论：①ΔABC平移的距离是4：②DG=1.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是（）A．①②B．②③C．③④D．②④7．如图所示，将三角形ABC平移得到三角形EFG，则图中共有平行线(含虚线)()A．3对B．4对C．5对D．6对8．如图，△ABC沿直线BC向右平移得到△DEF，已知EC=2，BF=8，则CF的长为（）A．3B．4C．5D．69．如图，将△ABC向右平移8个单位长度得到△DEF，且点B，E，C，F在同一条直线上，若EC＝4，则BC的长度是（）A．11B．12C．13D．1410．如图，在平面直角坐标系xOy中，将四边形ABCD先向上平移，再向左平移得到四边形A1B1C1D1，已知A1(−3,5),B1(−4,3),A(3,3)，则点B坐标为（）A．(1,2)B．(2,1)C．(1,4)D．(4,1)11．如图，在平面直角坐标系中，▱AOBC的顶点O与原点重合，顶点B在x轴正半轴上，顶点A 的坐标为(−1，2)．按以下步骤作图：先以点O为圆心，适当长为半径作弧，分别交边OA，OB于点D，E；再分别以点D，E为圆心，大于12DE的长为半径作弧，两弧在∠AOB内交于点F，作射线OF交AC边于点G．则点G的坐标为（）A．(3−√5，2)B．(√5，2)C．(√5−2，2)D．(√5−1，2) 12．如图，在数轴上，点A表示1，现将点A沿数轴做如下移动；第一次将点A向左移动3个单位长度到达点A1，第二次将点A向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点A3，按照这种移动规律移动下去，第n次移动到点A n，如果点A n与原点的距离不小于17，那么n的最小值是（）A．9B．10C．11D．12二、填空题13．如图，将△ABC沿直线BC方向平移3个单位得到△DEF，若BC=5，则BF=．14．如图，将△ABC沿BC方向平移至△DEF处.若EC＝2BE＝2，则CF的长为.15．在平面直角坐标系中，将点A(9，-7)向左平移2个单位长度，则平移后对应的点A‘的坐标是。
完整word人教版七年级数学下册5.4平移练习试题
完整word人教版七年级数学下册5.4平移练习试题人教版七年级数学下册平移练习试题平移题组1平移及其性质的应用1.以下现象属于平移的是( )①打气筒活塞的轮复运动；②电梯的上下运动；③钟摆的摆动；④转动的门；⑤汽车在一条笔直的马路上行走.A.③B.②③C.①②④D.①②⑤【解析】选D.①②⑤都是平移的现象，③④是旋转.2.图中的小船通过平移后可得到的图案是( )【解析】选B.根据平移定义可得：题图中的小船通过平移后可得到的图案是B.3.如图1，在△ABC和△DEF中，AB=AC=m，DE=DF=n，∠BAC=∠EDF，点D与点A重合，点E，F分别在AB，AC边上，将图1中的△DEF沿射线AC的方向平移，使点D与点C重合，得到图2，以下结论不正确的选项是()A.△DEF平移的距离是mB.图2中，CB平分∠ACEC.△DEF平移的距离是nD.图2中，EF∥BC【解析】选C.∵AB=AC=m，-1-/7∴△DEF平移的距离是m，故A正确，C错误.AB=AC，∴∠ACB=∠ABC.DE∥AB，∴∠EDB=∠ABC，∴∠ACB=∠ECB，∴CB平分∠ACE，故B正确.由平移的性质得到EF∥BC，故D正确.如图，直线m∥n，圆心在直线n上的☉A是由☉B平移得到的，那么图中两个阴影三角形的面积大小关系是()1<S21=S21>S2 D.不能确定【解析】选B.∵圆心在直线n上的☉A是由☉B平移得到的，∴两圆的半径相等，∴图中两个阴影三角形等底等高，S1=S2.如图，是一块电脑主板模型，每一个转角处都是直角，其数据如下图(单位：cm)，那么主板的周长是______cm.-2-/7【解析】由题意可得：主板的周长是：16+16+21+21+4+4=82(cm).答案：82【变式训练】某宾馆在重新装修后，考虑在大厅内的主楼梯上铺设地毯，2主楼梯宽为3m，其剖面如下图，那么需要购置地毯______m.【解析】由题意得：地毯的长为：1.2+2.4=3.6(m)，∴地毯的面积为×3=10.8(m2).答案：如图，长方形ABCD，AB=5cm，AD=8cm假设.将该长方形沿AD方向平移一段距离，得到长方形EFGH，试问：长方形ABFE与长方形DCGH的面积是否相等？(2)将长方形 ABCD平移多长距离，能使两长方形的重叠局部FCDE的面积是235cm？【解析】(1)面积相等：∵矩形EFGH是由矩形ABCD平移得到的，∴矩形ABCD的面积和矩形EFGH的面积相等，∴长方形ABFE与长方形DCGH的面积相等.(2)设AE=x，根据题意列出方程：5(8-x)=35，解得x=1，-3-/7∵A的对应点为E，∴平移距离为AE的长，故向右平移1cm，能使两长方形的重2叠局部FCDE的面积是35cm.【知识拓展】平移的其他性质如图，三角形ABC平移到三角形A′B′C′的位置，那么有：(1)A′B′∥AB，B′C′∥BC，C′A′∥CA.(2)A′B′=AB，B′C′=BC，C′A′=CA.∠A′=∠A，∠B′=∠B，∠C′=∠C.题组2平移作图及其应用定义：将一个图形L沿某个方向平移一段距离后，该图形在平面上留下的痕迹称之为图形L在该方向的拖影.如图，四边形ABB′A′是线段AB水平向右平移得到的拖影.那么将下面四个图形水平向右平移适当距离，其拖影是五边形的是()【解析】选A.只有三角形的拖影是五边形.如图，在10×6的网格中，每个小正方形的边长都是1个单位，将三角形ABC平移到三角形DEF的位置，下面正确的平移步骤是()-4-/7A.先向左平移5个单位，再向下平移2个单位B.先向右平移5个单位，再向下平移2个单位C.先向左平移5个单位，再向上平移2个单位D.先向右平移5个单位，再向上平移2个单位【解析】选A.根据网格结构，观察对应点A，D，点A向左平移5个单位，再向下平移2个单位即可到达点D的位置.所以平移的步骤是：先把△ABC向左平移5个单位，再向下平移2个单位.如图，线段AB和平移后的位置点C，作出线段AB平移后的图形.作法1：连接AC，再过点B作线段BD，使BD满足______，连接CD，那么CD为所作的图形.作法2：过点C作线段CD，使CD满足______且______，那么CD为所作的图形.再过点B作线段BD，使BD满足平行且等于AC，连接CD，那么CD为所作的图形.作法2：过点C作线段CD，使CD满足平行且等于AB，那么CD为所作的图形.答案：平行且等于AC平行等于AB【方法技巧】平移作图的技巧图形的平移是整体的平移，即图形上的任意一点或任意一条线段平移的方向和距离都是一致的，作出平移后的图形也就是作出关键点平移后的对应点，然后按照对应关系连接完成.2.直线型的平移作图也可以根据平移前后对应线段平行且相等进行作图.3.对于直线型的图形选择关键点时，以端点或交点作为关键点比拟适宜.能力提升如下图，一块长为60cm，宽为40cm的长方形地板，上面横竖各有两道宽-5-/7为5cm的花纹(图中阴影局部)，那么空白局部的面积是多少？【解析】(40-2×5)×(60-2×5)=30×50=1500(cm2).2答：空白局部的面积是1500cm.【母题变式】[变式一]如图1，在宽为20m，长为30m的长方形花园中，要修建两条同样宽的长方形道路，余下局部进行绿化.根据图中数据，计算绿化局部的面积为()图12222【解析】选B.利用“平移不改变图形的形状和大小〞，把两条长方形道路平移，平移到如下图的位置，绿化局部转化为长29m，宽19m的长方形，其面积为29×19=551(m2).[变式二]如图2，在长20米，宽10米的长方形草地内修建了宽2米的道路，那么草地的面积为________.-6-/7图2【解析】将道路分别向左、向上平移，得到草地为一个长方形，长方形的长为20-2=18(米)，宽为10-2=8(米)，那么草地面积为18×8=144平方米.答案：144平方米[变式三]如图3，在长32米，宽20米的矩形草坪上建有两条等宽的弯曲小路，把草坪分成了4局部，假设每条小路的宽度为2米，那么草坪的面积为______平方米.图3【解析】由平移的性质，草坪的长为32-2=30米，宽为20-2=18米，面积=30×18=540(平方米).答案：540-7-/7。
新人教版七年级数学下册同步练习5.4平移(练习卷+解析版)
18．（8 分）如图，在方格纸中，每个小正方形的边长均为 1 个单位长度有一个 △ABC，它的三个顶点均与小正方形的顶点重合． （1）将△ABC 向右平移 3 个单位长度，得到△DEF（A 与 D、B 与 E、C 与 F 对应），请在方格纸中画出△DEF； （2）在（1）的条件下，连接 AE 和 CE，请直接写出△ACE 的面积 S，并判断 B 是否在边 AE 上．
C、由图形可得其周长为：12cm，
D、由图形可得其周长为：12cm，
故最长的是 B．
故选：B．
3．下列生活现象中，属于平移的是（ ）
A．足球在草地上滚动
B．拉开抽屉
C．投影片的文字经投影转换到屏幕上
D．钟摆的摆动
解：A．足球在草地上滚动方向变化，不符合平移的定义，不属于平移
B．拉开抽屉符合平移的定义，属于平移；
解：∵将线段 DC 沿着 CB 的方向平移 7cm 得到线段 EF，
∴EF=DC=4cm，FC=7cm， ∵AB=AC，BC=12cm， ∴∠B=∠C，BF=5cm， ∴∠B=∠BFE， ∴BE=EF=4cm， ∴△EBF 的周长为：4+4+5=13（cm）． 故答案为：13． 14．如图，∠1=70°，直线 a 平移后得到直线 b，则∠2﹣∠3= 110 °．
A．12
B．24
C．21
人教版七年级下册数学 5
人教版七年级下册数学5.4平移 专题练习一.单选题（共 10 小题）1、如图，△ABC 中，∠ABC=90°沿BC 所在的直线向右平移得到△DEF ，下列结论中不一定成立的是（ ）A ．EC=CFB ．∠DEF=90°C ．AC ＝DFD ．AC ∥DF2、如图是一个基本图形，将其平移四次，把得到的新图形结合起来，能得到的图案是（ ）A ．B ．C ．D ．3、如图，在三角形ABC 中，90,3cm,4cm BAC AB AC ∠=︒==，把三角形ABC 沿着直线BC 向右平移2.5cm 后得到三角形DEF ，连接,AE AD ，有以下结论：①AC DF ∥；②AD CF ∥；③ 2.5cm CF =；④DE AC ⊥．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个4、如果存在一条线把一个图形分割成两个部分，使其中一个部分沿某个方向平移后能与另一个部分重合，那么我们把这个图形叫做平移重合图形．下列图形中，平移重合图形是( )A ．平行四边形B ．等腰梯形C ．正六边形D ．圆5、如图，将边长为5cm 的等边三角形ABC 沿边BC 向右平移3cm ，得到△DEF ，则四边形ADFB 的周长为（ ）cm ．A ．20B ．21C ．22D ．23 6、如图，面积为12cm 2的△ABC 沿BC 方向平移到△DEF 的位置，平移的距离是边BC 长的2倍，则图中四边形ACED 的面积为（ ）A ．24cm 2B ．36cm 2C ．48cm 2D ．无法确定7、如图，面积为2cm 2的△ABC ，沿BC 方向平移至△DEF 的位置，平移的距离是边BC 长的2倍，则图中的四边形ACED 的面积为（ ）A ．4cm 2B ．6cm 2C ．8cm 2D ．10cm 28、如图所示，三张正方形纸片①，②，③分别放置于长()a b +，宽()a c +的长方形中，正方形①，②，③的边长分别为a ，b ，c ，且a b c >>，则阴影部分周长为（ ）A ．42a c +B ．42a b +C ．4aD ．422a b c ++9、经过平移，ABC ∆移到DEF ∆的位置，如图，下列结论：①AD BE CF ==，且////AD BE CF ；②//AB DE ，//BC EF ，BC EF =；③AB DE =，BC EF =，AC DF =．正确的有( )A ．0个B ．1个C ．2个D ．3个10、如图，将△ABC 沿直线AB 向右平移后到达△BDE 的位置，连接CD 、CE ，若△ACD 的面积为6，则△BCE 的面积为（ ）A ．5B ．6C ．10D ．3二.填空题（共 8 小题）1、在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是_____．2、如图，△ABC 的面积为10，BC ＝4，现将△ABC 沿着射线BC 平移a 个单位（a ＞0），得到新的△A'B'C'，则△ABC 所扫过的面积为_____．3、如图，将直角△ABC 沿斜边AC 的方向平移到△DEF 的位置，DE 交BC 于点G ，BG=4，EF=10，则线段GC 的长 ______________．4、如图，若DEF ∆是由ABC ∆平移后得到的，已知点A 、D 之间的距离为1，2CE =，则BC =_______．5、如图，O 是正六边形ABCDEF 的中心，下列图形：△OCD ，△ODE ，△OEF ，△OAF ，△OAB ，其中可由△OBC 平移得到的有_________个．6、如图所示是一座楼房的楼梯，高1 m ，水平距离是2.8 m ．如果要在台阶上铺一种地毯，那么至少要买这种地毯________7、如图，在长为50米，宽为30米的长方形地块上，有纵横交错的几条小路，宽均为1米，其它部分均种植花草．则种植花草的面积______．8、如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B 到C 的方向平移到△DEF的位置，AB ＝10，DO ＝4，平移距离为6，则阴影部分面积为__三.解答题（共 6 小题）1、如图，平面内点A ，B 沿同一方向，平移相同距离分别得到点C ，D ，连接AB ，BC ，延长AC 到点E ，连接BE ，DE ，BC 恰好平分∠ABE ．(1)若∠ACB ＝100°，∠CBE ＝40°，求∠EBD 的度数；(2)若∠AED ＝∠ABC+∠EBD ，求证：BC//DE ．2、（1）动手操作如图1，在55⨯的网格中，将线段AB 向右平移，得到线段A B ''，连接AA '，BB '． ①线段AB 平移的距离是_________；②四边形ABB A ''的面积_________；（2）如图2，在55⨯的网格中，将折线ACB 向右平移3个单位长度，得到折线AC B '''．①画出平移后的折线AC B '''；②连接AA '，BB '，多边形ACBB C A '''的面积_________；（3）拓展延伸如图3，在一块长为a 米，宽为b 米的长方形草坪上，修建一条宽为m 米的小路（小路宽度处处相同），直接写出剩下的草坪面积_________．3、如图，在方格纸内将三角形ABC 经过平移后得到三角形111A B C ，图中标出了点A 的对应点1A ，解答下列问题．(1)在网格中画出三角形.111A B C .；(2)连接，1AA ，1BB ，则所得正方形.11AA B B .的面积是______，它的边长AB 是______．4、如图，在66⨯的正方形网格中，每个小正方形的边长为1，点A ，B ，C ，D ，E ，F ，P 均为格点（格点是指每个小正方形的顶点），请完成下列问题：(1)利用直尺画图：在图1中，过P 点画直线AB 的平行线和垂线；(2)平移图2中的三条线段AB 、CD 、EF 中的两条，使平移后三条线段首尾顺次相接组成一个三角形；（只画出一个三角形即可）(3)图2中所组成的三角形的面积为______．5、画图并填空：如图，在12⨯8 的方格纸中，每个小正方形的边长都为1 ，△ABC 的顶点都在方格纸的格点上，将△ABC 按照某方向经过一次平移后得到△A' B'C ' ，图中标出了点C 的对应点C ' ．（1）请画出△A' B'C ' ；（2）利用方格纸，在△ABC 中画出AC 边上的中线BD 和BC 边上的高AE ；（3）点F 为方格纸上的格点（异于点B ），若S ∆ACB = S ∆ACF ，则图中格点F 共有 个．（请在方格纸中标出点F ）6、平移和轴对称是数学中两种重要的图形运动．(1)平移①把笔尖放在数轴的原点处，先向负方向移动5个单位长度，再向正方向移动2个单位长度，这时笔尖的位置表示什么数？用算式表示以上过程及结果是（ ）．A ．(5)(2)7+++=+B ．(5)(2)3++-=+C ．(5)(2)3-++=-D ．(5)(2)7-+-=-②一机器人从原点O 开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳，当它跳2022次时，落在数轴上的点表示的数是________．(2)轴对称若对折纸条，表示-1的点与表示3的点重合，则表示2022的点与表示________的点重合．(3)若数轴上M ，N 两点对应的数分别表示为m ，n ，将点M 向正方向平移5个单位得到1M ，将点N 向负方向平移3个单位长度得到1N ，且1M ，1N 两点经对折后重合，对折的中间点表示的数为多少？（用含有m ，n 的式子表示）。
人教版七年级数学下册 5.4 平移 同步练习 试题 含答案
5.4 平移一．选择题（共8小题）1．下列现象中是平移的是（）A．将一张纸沿它的中线折叠B．电梯的上下移动C．飞碟的快速转动D．翻开书中的每一页纸张2．在下图所示的四个三角形中，能由△ABC经过平移得到的是（）A．B．C．D．3．下列现象属于平移的是（）①打气筒活塞的轮复运动，②电梯的上下运动，③钟摆的摆动，④转动的门，⑤汽车在一条笔直的马路上行走．A．③B．②③C．①②④D．①②⑤4．如图所示，共有3个方格块，现在要把上面的方格块与下面的两个方格块合成一个长方形的整体，则应将上面的方格块（）A．向右平移1格，向下3格B．向右平移1格，向下4格C．向右平移2格，向下4格D．向右平移2格，向下3格5．下列图形中，不能通过其中一个四边形平移得到的是（）A．B．C．D．6．下列四组图形中，平移其中一个三角形可以得到另一个三角形的一组图形是（）A．B．C．D．7．下列平移作图错误的是（）A．B．C．D．8．下列平移作图不正确的是（）A．B．C．D．二．填空题（共6小题）9．如图，将△ABC沿BC方向平移到△DEF，若A、D间的距离为1，CE＝2，则BF＝．10．如图，将周长为8的△ABC沿BC方向向右平移1.5个单位得到△DEF，则四边形ABFD的周长为．11．如图，△ABC平移后的图形是△A′B′C′，其中C与C′是对应点，请画出平移后的三角形△A′B′C′．（作图题）12．如图，在一块长为20m，为10m的长方形草地上，修建两条宽为2m的长方形小路，则这块草地的绿地面积（图中空白部分）为m213．如图，在△ABC中，∠B＝90°，BC＝5cm，AB＝12cm，则图中4个小直角三角形周长的和为．14．如图是一块长方形ABCD的场地，长AB＝a米，宽AD＝b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为米2．三．解答题（共6小题）15．如图，将三角形ABC水平向右平移得到三角形DEF，A，D两点的距离为1，CE＝2，∠A＝70°．根据题意完成下列各题：（1）AC和DF的数量关系为；AC和DF的位置关系为；（2）∠1＝度（3）BF＝．16．如图，已知直线AB∥CD，∠A＝∠C＝100°，E，F在CD上，且满足∠DBF＝∠ABD，BE平分∠CBF．（1）直线AD与BC有何位置关系？请说明理由；（2）求∠DBE的度数；（3）若平行移动AD，在平行移动AD的过程中，是否存在某种情况，使∠BEC＝∠ADB？若存在，求出∠ADB；若不存在，请说明理由．17．如图，将△ABC沿直线AB向右平移后到达△BDE的位置．（1）若AC＝6cm，则BE＝cm；（2）若∠CAB＝50°，∠BDE＝100°，求∠CBE的度数．18．如图，平面直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为（3，2）．（1）填空：点A的坐标是，点B的坐标是；（2）将△ABC先向左平移3个单位长度，再向上平移1个单位长度，画出平移后的△A1B1C1；（3）求△ABC的面积．19．如图，在正方形网格中有一个△ABC，按要求进行下列作图（只借助网格，需要写出结论）．（1）过点B画出AC的平行线；（2）画出三角形ABC向右平移5格，在向上平移2格后的△DEF；（3）若每一个网格的单位长度为a，求三角形ABC的面积．20．如图，凯瑞酒店准备进行装修，把楼梯铺上地毯．已知楼梯的宽度是2米，楼梯的总长度为8米，总高度为6米，已知这种地毯每平方米的售价是60元．请你帮老板算下，购买地毯多少钱？参考答案一．选择题（共8小题）1．B．2．C．3．D．4．C．5．D．6．A．7．C．8．C．二．填空题（共6小题）9．BF＝BE+EC+CF＝4．10．11．11．作法：（1）连接CC′，过点C作A′C′∥AC，且相等，再过点A′，作A′B′∥AB且相等，连接A′、B′、C′，△A′B′C′就是所画的三角形．12．144．13．3014．（ab﹣a﹣2b+2）．三．解答题（共6小题）15．解：（1）AC和DF的关系式为AC＝DF，AC∥DF．（2）∵三角形ABC水平向右平移得到三角形DEF，∴AB∥DE，∵∠A＝70°，∴∠1＝110（度）；（3）BF＝BE+CE+CF＝2+1+1＝4．故答案为：AC＝DF，AC∥DF；110；4；16．解：（1）直线AD与BC互相平行，理由：∵AB∥CD，∴∠A+∠ADC＝180°，又∵∠A＝∠C∴∠ADC+∠C＝180°，∴AD∥BC；（2）∵AB∥CD，∴∠ABC＝180°﹣∠C＝80°，∵∠DBF＝∠ABD，BE平分∠CBF，∴∠DBE＝∠ABF+∠CBF＝∠ABC＝40°；（3）存在．设∠ABD＝∠DBF＝∠BDC＝x°．∵AB∥CD，∴∠BEC＝∠ABE＝x°+40°；∵AB∥CD，∴∠ADC＝180°﹣∠A＝80°，∴∠ADB＝80°﹣x°．若∠BEC＝∠ADB，则x°+40°＝80°﹣x°，得x°＝20°．∴存在∠BEC＝∠ADB＝60°．17．解：（1）∵将△ABC沿直线AB向右平移得到△BDE，∴△ABC≌△BDE，∴BE＝AC＝6cm，故答案为：6；（2）由（1）知△ABC≌△BDE，∴∠DBE＝∠CAB＝50°、∠BDE＝∠ABC＝100°，∴∠CBE＝180°﹣∠ABC﹣∠DBE＝30°．18．解：（1）点A的坐标是：（4，﹣1），点B的坐标是：（5，3）；故答案为：（4，﹣1），（5，3）；（2）如图所示：△A1B1C1，即为所求；（3）．19．解：（1）如图，直线BP为所作．（2）如图，△DEF为所作；（3）三角形ABC的面积＝×3a×2a＝3a2．20．解：如图，利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为8米，6米，即可得地毯的长度为6+8＝14（米），地毯的面积为14×2＝28（平方米），故买地毯至少需要28×60＝1680（元）．购买地毯需要1680元．。
人教版数学七年级下册《5.4平移》基础训练（含答案）
人教版数学七年级下册5.4平移基础训练一、选择题1.下列运动属于平移的是( D )A.荡秋千B.地球绕着太阳转C.风筝在空中随风飘动D.急刹车时，汽车在地面上的滑动2. 下列各网格中的图形是用其图形中的一部分平移得到的是( C )A. B. C. D.3.如图，两个直角三角形重叠在一起，将其中一个三角形沿着BC边平移到△DEF 的位置，∠B=90°，AB=10，DH=2，平移距离为3，则阴影部分的面积为（ C ）A. 20B. 24C. 27D. 364.如图，三角形ADE是由三角形DBF沿BD所在直线平移得到的，AE，BF的延长线交于点C,若∠BFD=45°,则∠C的度数是( C )A.43°B.44°C.45°D.46°5. 两个三角形是通过平移得到的,下列说法错误的是( D )A. 平移过程中,两三角形周长不变B. 平移过程中,两三角形面积不变C. 平移过程中,两三角形的对应线段一定相等D. 平移过程中,两三角形的对应边必平行6.甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，能用其中一部分平移得到的是（ D ）A. B. C. D.7.如图，有a，b，c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线( D )A.a户最长B.6户最长C.c户最长D.一样长8. 如图,将四边形ABCD先向左平移3个单位,再向上平移2个单位,那么点A的对应点A'的坐标是( B )A. (6,1)B. (0,1)C. (0,-3)D. (6,-3)9.如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（ A ）A. 2B. 3C. 23D. 3210.如图，将三角形ABC沿BC方向平移得到三角形DEF,若BC=4，EC=1，则平移的距离为( D )A.7B.6C.4D.3二、填空题11.如图，在四边形ABCD中，AD∥BC,若∠B与∠C互余，将AB，DC分别平移到EF和EG的位置，则∠FEG的度数为 .【答案】90°12.如图，平移△ABC可得到△DEF，如果∠C=60°，AE=7cm，AB=4cm，那么∠F= ______ 度，DB= ______ cm．【答案】60；113.如图是“俄罗斯方块”游戏的一个画面，若使左上角的图形经平移插入到下面空白的A处，应先向平移格，再向平移格.【答案】右 1 下 314.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是cm2.【答案】16815.如图，矩形ABCD中，AB=5,BC=8，则矩形内部五个小矩形的周长之和为_________.【答案】26三、解答题''';16.(1)如图，平移三角形ABC，使点A平移到点A'，画出平移后的三角形A B C (2)在(1)的条件下，指出点A,B,C 的对应点，并指出AB,BC,AC的对应线段和∠A，∠B, ∠C的对应角.【答案】(1)如图所示.(2)点A ，B ，C 的对应点分别是点A B C '''，，,线段AB,BC ，AC 的对应线段分别是A B B C A C ''''''，，，∠A,∠B ，∠ACB 的对应角分别A A B C A C B '''''''∠∠∠，，. 17. 如图所示,已知在△ABC 中,BC =4 cm,把△ABC 沿BC 方向平移2 cm 得到△DEF.问:(1)图中与∠A 相等的角有多少个?(2)图中的平行线共有多少对?请分别写出来. (3)BE ∶BC ∶BF 的值是多少?(1) 【答案】共有3个,分别是∠D ,∠EMC ,∠AMD. (2) 【答案】两对,AB ∥DE ,AC ∥DF.(3) 【答案】∵△ABC 沿BC 方向平移2 cm, ∴BE =CF =2 cm . 又∵BC =4 cm, ∴BF =6 cm .∴BE ∶BC ∶BF =1∶2∶3.18.关注生活数学：某宾馆重新装修后考虑在大厅内的 主楼梯上铺设地毯，已知主楼梯宽3m ，其剖面图如图所示，请计算铺此楼梯，需要购买地毯多少平方米？解析：由平移的性质，可知地毯的长为AB +BC = 1.2 +2.4= 3.6(m) ,3.6×3=10.8(m2).故需要购买地毯10.8平方米.19. 如图,某住宅小区内有一长方形地块,想在长方形地块内修筑同样宽的两条小路,余下部分绿化,小路的宽为2 m,则绿化的面积为多少?【答案】如图所示,把两条小路平移到长方形地块ABCD的最上边和最左边,则余下部分EFCG是长方形.∵CF=32-2=30(m),CG=20-2=18(m),∴长方形EFCG的面积=30×18=540(m2). 答:绿化的面积为540m2.20.已知：如图，△ABC的面积为84，BC=21，现将△ABC沿直线BC向右平移a （0＜a＜21）个单位到△DEF的位置．（1）求BC边上的高；（2）若AB=10，①求线段DF的长；②连结AE，当△ABE时等腰三角形时，求a的值．【答案】解：（1）作AM⊥BC于M，∵△ABC的面积为84，×BC×AM=84，∴12解得，AM=8，即BC边上的高为8；（2）①在Rt△ABM中，BM=√AB2−AM2=6，∴CM=BC-BM=15，在Rt△ACM中，AC=√AM2+CM2=17，由平移的性质可知，DF=AC=17；②当AB=BE=10时，a=BE=10；当AB=AE=10时，BE=2BM=12，则a=BE=12；当EA=EB=a时，ME=a-6，在Rt△AME中，AM2+ME2=AE2，即82+（a-6）2=a2，，解得，a=253．则当△ABE时等腰三角形时，a的值为10或12或253。
2022-2023学年人教版七年级数学下册《5-4平移》同步练习题(附答案)
2022-2023学年人教版七年级数学下册《5.4平移》同步练习题（附答案）一．选择题1．如图是第七届世界军人运动会的吉祥物“兵兵”，将图中的“兵兵”通过平移可得到下列选项中的（）A．B．C．D．2．如图所示：某公园里有一处长方形风景欣赏区ABCD，AB长50米，BC宽25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小明同学在假期沿着小路的中间行走（图中虚线），则：小明同学所走的路径长约为（）米．（小路的宽度忽略不计）A．150米B．125米C．100米D．75米3．下列运动属于平移的是（）A．荡秋千B．地球绕着太阳转C．风车的转动D．急刹车时，汽车在地面上的滑动4．如图，将△ABC沿着某一方向平移一定的距离得到△DEF，则下列结论：①AD＝CF；②AC∥DF；③∠ABC＝∠DFE；④∠DAE＝∠AEB．其中正确的是（）A．仅①②B．仅①②④C．仅①②③D．①②③④5．如图，将直线CD向上平移到AB的位置，若∠1＝130°，则D的度数为（）A．130°B．50°C．45°D．35°6．如图，将△ABC向右平移acm（a＞0）得到△DEF，连接AD，若△ABC的周长是36cm，则四边形ABFD的周长是（）A．（36+a）cm B．（72+a）cm C．（36+2a）cm D．（72+2a）cm 7．如图，△ABC沿BC方向平移到△DEF的位置，若BE＝2cm，则平移的距离为（）A．1B．2C．3D．48．如图，将直角三角形ABC沿AB方向平移得到直角三角形DEF．已知BE＝4，EF＝8，CG＝3，则图中阴影部分的面积为（）A．16B．20C．26D．129．下列说法正确的个数是（）①同位角相等；②同旁内角互补，两直线平行；③若a∥b，b∥c，则a∥c；④直线外一点到这条直线的距离是指这一点到这条直线的垂线段；⑤在连接直线外一点与直线上各点的线段中，垂线段最短；⑥平移既改变图形的位置，也改变图形的形状与大小．A．2个B．3个C．4个D．5个10．如图，表示直线a平移得到直线b的两种画法，下列关于三角板平移的方向和移动的距离说法正确的是（）A．方向相同，距离相同B．方向不同，距离不同C．方向相同，距离不同D．方向不同，距离相同11．如图，直线m与∠AOB的一边射线OB相交，∠3＝120°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2﹣∠1＝．12．如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm2．13．在长为a（m），宽为b（m）一块长方形的草坪上修了一条宽2（m）的笔直小路，则余下草坪的面积可表示为m2；先为了增加美感，把这条小路改为宽恒为2（m）的弯曲小路（如图），则此时余下草坪的面积为m2．14．如图，在长20米，宽10米的长方形草地内修建了宽2米的道路，则道路的面积为．15．如图是一个会场的台阶的截面图，要在上面铺上地毯，则所需地毯的长度是．16．如图的网格纸中，每个小方格都是边长为1个单位的正方形，三角形ABC的三个顶点都在格点上．（每个小方格的顶点叫格点）（1）画出三角形ABC向上平移4个单位后的三角形A1B1C1；（2）画出三角形A1B1C1向左平移5个单位后的三角形A2B2C2；（3）经过（1）次平移线段AC划过的面积是．17．已知AB＝13，CD＝8，M和N分别为线段AB，CD的中点．（1）若BC重合，D在线段AB上，如图1，求MN的长度．（2）①如果将图1的线段CD沿着AB向右平移n个单位，求MN的长度与n的数量关系．②当n为多少的时，MN的长度为9．（3）如果AB保持长度和位置不变，点D保持图1的位置不变，改变DC的长度，将点C沿着直线AB向右移动m个单位，其余条件不变，①BN+BC；②MN﹣BC，请问以上两个式子哪一个式子的值是定值，定值是多少？18．在直角三角形ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，△ABC沿AB方向平移至△DEF，若AE＝8cm，DB＝2cm．（1）AC和DF的关系为．（2）∠BGF＝°．（3）求△ABC沿AB方向平移的距离．19．如图，AN∥DM，点B在AN上（点B与点A不重合），点C在DM上（点C与点D 不重合），∠DAB＝∠BCD．（1）那么AD∥BC吗？试说明理由；（2）若平行移动BC，保持∠ABC＝100°；点E、F在DC上，且满足∠F AC＝∠BAC，AE平分∠DAF．①小红发现可求出∠EAC的度数，请你帮助小红写出求∠EAC的度数的过程；②在平行移动BC的过程中，是否存在某种情况，使∠BCA＝∠DEA？若存在，请直接写出∠BCA的度数；若不存在，请说明理由．20．已知点C在射线OA上．（1）如图①，CD∥OE，若∠AOB＝90°，∠OCD＝120°，求∠BOE的度数；（2）在①中，将射线OE沿射线OB平移得O′E'（如图②），若∠AOB＝α，探究∠OCD 与∠BO′E′的关系（用含α的代数式表示）；（3）在②中，过点O′作OB的垂线，与∠OCD的平分线交于点P（如图③），若∠CPO′＝90°，探究∠AOB与∠BO′E′的关系．参考答案一．选择题1．解：将图中的“兵兵”通过平移可得到图为：故选：C．2．解：由平移的性质可知，由于小路的宽度忽略不计，因此说行走的路程为AD+AB+BC＝25+50+25＝100（米），故选：C．3．解：A、荡秋千，不符合题意；B、地球绕着太阳转，不符合题意；C、风车的转动，不符合题意；D、急刹车时，汽车在地面上的滑动，属于平移变换，符合题意；故选：D．4．解：∵△ABC沿着某一方向平移一定的距离得到△DEF，∴①AD∥CF，正确；②AC＝DF，正确；③∠ABC＝∠DEF，故原命题错误；④∠DAE＝∠AEB，正确．所以，正确的有①②④．故选：B．5．解：∵∠1和∠2是邻补角，∴∠1+∠2＝180°，∵∠1＝130°，∴∠2＝180°﹣∠1＝50°，∵AB∥CD，∴∠D＝∠2＝50°，故选：B．6．解：∵将周长为36cm的△ABC沿边BC向右平移a个单位得到△DEF，∴AD＝a，BF＝BC+CF＝BC+a，DF＝AC，又∵AB+BC+AC＝36cm，∴四边形ABFD的周长＝AD+AB+BF+DF＝a+AB+BC+a+AC＝（36+2a）（cm）．故选：C．7．解：△ABC沿BC方向平移到△DEF的位置，若BE＝2cm，则平移的距离为2cm，故选：B．8．解：由平移的性质可知，S△ABC＝S△DEF，EF＝BC＝8，∵CG＝3，∴BG＝BC﹣CG＝5，∴S阴＝S梯形EFGB＝（5+8）×4＝26，故选：C．9．解：①同位角相等，错误，只有两直线平行，才有同位角相等；②同旁内角互补，两直线平行，正确；③若a∥b，b∥c，则a∥c，正确；④直线外一点到这条直线的距离是指这一点到这条直线的垂线段的长度，故本小题错误；⑤在连接直线外一点与直线上各点的线段中，垂线段最短，正确；⑥平移只改变图形的位置，不改变图形的形状与大小，故本小题错误；综上所述，正确的有②③⑤共3个．故选：B．10．解：由图和平移可得：三角板平移的方向不同，距离不同，故选：B．二．填空题11．解：作OC∥m，如图，∵直线m向上平移直线m得到直线n，∴m∥n，∴OC∥n，∴∠1＝∠BOC，∠2+∠AOC＝180°，∠AOC＝∠3﹣∠1，∴∠2+∠3﹣∠1＝180°，∴∠2﹣∠1＝180°﹣120°＝60°，故答案为：60°．12．解：由题意，阴影部分是矩形，长为5﹣2＝3（cm），宽为3﹣1＝2（cm），∴阴影部分的面积＝2×3＝6（cm2），故答案为6．13．解：余下草坪的长方形长仍为a，宽为（b﹣2），则面积为a（b﹣2）＝ab﹣2a；长方形的长为a，宽为b﹣2．余下草坪的面积为：a（b﹣2）＝ab﹣2a，故答案为：（ab﹣2a），（ab﹣2a）．14．解：将道路分别向左、向上平移，得到草地为一个长方形，长方形的长为20﹣2＝18（米），宽为10﹣2＝8（米），则草地面积为18×8＝144米2．∴道路的面积为20×10﹣144＝56米2故答案为：56米2．15．解：楼梯的长为5m，高为2.5m，则所需地毯的长度是5+2.5＝7.5（m）．故答案为：7.5m．三．解答题16．解：（1）如图，A1B1C1即为所求；（2）如图，△A2B2C2即为所求；（3）经过（1）次平移线段AC划过的面积＝4×4＝16．故答案为：16．17．解：（1）∵M和N分别为线段AB，CD的中点，∴AM＝BM＝AB，CN＝DN＝CD，∵MN＝BM﹣CN＝AB﹣CD，∵AB＝13，CD＝8，∴MN＝﹣＝；（2）①∵线段CD沿着AB向右平移n个单位，∴BC＝n，∵MN＝BM﹣BN＝AB﹣（CN﹣BC）＝AB﹣CD+BC，∵AB＝13，CD＝8，∴MN＝+n；②∵MN＝9，∴+n＝9，∴n＝；（3）∵点C沿着直线AB向右移动m个单位，∴BC＝m，∵点D保持位置不变，∴CD＝8+m，∵N是CD的中点，∴CN＝DN＝CD＝（8+m）＝4+m，∴BN＝CN﹣BC＝4+m﹣m＝4﹣m，当0＜m≤8时，∴BN+BC＝4﹣m+m＝4，MN﹣BC＝（BM﹣BN）﹣BC＝AB﹣BN﹣BC＝﹣（4﹣m）﹣m＝；∴BN+BC是定值4，MN﹣BC是定值；当m＞8时，N点在B点右侧，∵BN＝BC﹣CN＝m﹣4﹣m＝m﹣4，MN＝BM+BN＝+m﹣4＝m+，∴BN+BC＝m﹣4+m＝m﹣4，MN﹣BC＝m+﹣m＝，∴BN+BC不是定值，MN﹣BC是定值；综上所述：无论m取何值，MN﹣BC的值都是定值．18．解：（1）∵△ABC沿AB方向平移至△DEF，∴AC＝DF，AC∥DF，故答案为：AC＝DF，AC∥DF；（2）由平移的性质得出AC∥DF，∴∠ACB＝∠DGB＝90°，∴∠BGF＝180°﹣90°＝90°，故答案为：90；（3）由平移得AD＝BE，AE＝8cm，DB＝2cm，∴AD＝BE＝＝3（cm），∴平移的距离为3cm；19．（1）解：结论：AD∥BC．理由：∵AB∥CD，∴∠D+∠DAB＝180°，∵∠DAB＝∠BCD，∴∠D+∠BCD＝180°，∴AD∥BC．（2）①∵AD∥BC，∴∠DAB+∠ABC＝180°，∵∠ABC＝100°，∴∠DAB＝80°，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠EAC＝∠DAF+∠F AB＝（∠DAF+∠F AB）＝40°．②存在．理由：∵AD∥BC，∴∠DAC＝∠ACB，∵CD∥AB，∴∠DEA＝∠EAB，∵∠ACB＝∠DEA，∴∠DAC＝∠EAB，∴∠DAE＝∠CAB，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠DAE＝∠EAF＝∠F AC＝∠CAB＝20°，∴∠ACB＝∠DAC＝60°．20．解：（1）∵CD∥OE，∴∠AOE＝∠OCD＝120°，∴∠BOE＝360°﹣∠AOE﹣∠AOB＝360°﹣90°﹣120°＝150°；（2）∠OCD+∠BO′E′＝360°﹣α．证明：如图②，过O点作OF∥CD，∵CD∥O′E′，∴OF∥O′E′，∴∠AOF＝180°﹣∠OCD，∠BOF＝∠E′O′O＝180°﹣∠BO′E′，∴∠AOB＝∠AOF+∠BOF＝180°﹣∠OCD+180°﹣∠BO′E′＝360°﹣（∠OCD+∠BO′E′）＝α，∴∠OCD+∠BO′E′＝360°﹣α；（3）∠AOB＝∠BO′E′．证明：∵∠CPO′＝90°，∴PO′⊥CP，∵PO′⊥OB，∴CP∥OB，∴∠PCO+∠AOB＝180°，∴2∠PCO＝360°﹣2∠AOB，∵CP是∠OCD的平分线，∴∠OCD＝2∠PCO＝360°﹣2∠AOB，∵由（2）知，∠OCD+∠BO′E′＝360°﹣α＝360°﹣∠AOB，∴360°﹣2∠AOB+∠BO′E′＝360°﹣∠AOB，∴∠AOB＝∠BO′E′．。
数学人教版七年级下册同步训练：5.4 平移(有答案)
数学人教版七年级下册同步训练：5.4 平移一、单选题1.下列说法不正确的是（ ）A.平移不改变图形的形状和大小B.平移中图形上每个点移动的距离可以不同C.经过平移，图形的对应线段、对应角分别相等D.经过平移，图形的对应点所连线段平行(或在同一直线上)且相等2.下列运动属于平移的是( )A.荡秋千B.急刹车时,汽车在地面上的滑动C.地球绕着太阳转D.风筝在空中随风飘动3.下列四个图形中，可以由图通过平移得到的是（ ）A. B. C. D.4.如图，将ABC △沿着由点B 到点C 的方向平移到DEF △，己知7,6,4AB BC EC ===，那么平移的距离为（ ）A. 1B. 2C. 3D. 65.甲、乙两支同样的温度计如图所示放置，如果向左平移甲温度计，使其度数20正对着乙温度计的度数-10，那么此时甲温度计的度数-5正对着乙温度计的度数是（ ）A.5B.15C.25D.306.如图，在俄罗斯方块游戏中，出现一小方块拼图向下运动，通过平移运动拼成一个完整的图案，最终所有图案消失，则对小方块进行的操作为（ ）A.向右平移1格再向下B.向右平移3格再向下C.向右平移2格再向下D.以上答案均可7.如图，ADE △是由DBF △沿BD 所在的直线平移得到的,,AE BF 的延长线交于点C 若45BFD ∠=︒,则C ∠的度数是（ ）A.43︒B.44︒C.45︒D.46︒二、填空题8.如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字路，余下部分绿化，道路的宽为2m ，则绿化的面积为 2m .9.如图，直角三角形ABC 的周长为2018，在其内部有5个小直角三角形，且这5个小直角三角形都有一条边与BC 平行，则这5个小直角三角形周长的和为_.10.如图，边长为10的正方形ABCD 沿AD 方向平移a 个单位，重叠部分面积为20，则a = .11.如图，已知三角形ABC 平移后得到三角形A B C '''.102BAC ∠=︒,16cm BC =,则B A C '''∠= ，B C ''= ，与BB '平行的线段是 .三、解答题12.如图，在边长为1的小正方形组成的网格中，将ABC △向右平移5个单位长度，再向上平移4个单位长度，得到123A B C △.1.在网格中画出123A B C △，2.求ABC △的面积.13.己知，90AOB ∠=︒，点C 在射线OA 上，//CD OE1.如图1，若120OCD ∠=︒，求BOE ∠的度数;2.把90AOB ∠=︒改为120AOB ∠=︒，射线OE 沿射线OB 平移，得O E '，其他条件不变(如图2所示)，探究OCD ∠与BO E '∠的数量关系;3.在2.的条件下，作PO OB '⊥，垂足为O '，与OCD ∠的平分线CP 交于点P ，若BO E α'∠=，请用含α的式子表示CPO '∠ (请直接写出答案).参考答案1.答案：B平移中图形上每个点移动的距离相同，故B 错误.2.答案：BA,荡秋千和C:地球绕着太阳转属于中心旋转,D 属于不规则运动。
(新人教版)数学七年级下册：5.4《平移》练习题及答案
平移练习题1 如图1，在长方形ABCD 中，横向阴影部分是长方形，另一阴影部分是平行四边形，根据图中标明的数据，其中空白部分的面积是多少？2 如图2，某商场重新装修后，准备在大厅的主楼梯上铺设一种红色的地毯，已知这种地毯的批发价为每平方米40元，已知主楼梯道的宽为3米，其侧面如图2所示，则买地毯至少需要多少元？3 如图3，在四边形ABCD 中，AD ∥BC ，AB ＝CD ，AD ＜BC ，则∠B 与∠C 的数量关系怎样？试说明你的理由.4如图4，在△ABC 中，E 、F 分别为AB 、AC 上的点，且BE ＝CF ，则FE ＜BC 吗？为什么？图1c 图3ECBDADFBACE图4 M5 A 、B 两城市之间有一条国道，国道的宽为a ，现要在国道修建一座垂直于国道的立交桥，使通过A 、B 两城市路程最近，请你设计建桥的位置，并说明理论依据.6某医院用一个边长为1米的正方形材料制作一个红十字会的大型的“十字”标志.如图1，在正方形的四个角上挖去四个相同的小正方形即制作而成，则这个“十”字标志的周长为_________米.7在宽为20m ，长为30m 的矩形地面上，修筑同样宽的二条道路，余下的部分作为蔬菜地，根据图中数据，计算蔬菜地面积为_________.8有一种叫“俄罗斯方块”的电脑游戏，游戏规则是这样的：通过平移等变换，使所给的各种各样的方块排满每一横行，每排满一行，便消去一行，得100分；同时排满2行，得300分；依此类推.假如现在在电脑屏幕上显示的图形如图5所示，电脑给出的三个方块分别是甲、乙、丙，在只考虑平移的情况下，应如何平移甲、乙、丙三个方块，才能消去1行，得到100分？甲参考答案1简析利用“平移不改变图形的形状和大小”这一性质可使本题迅速解决.由图形可知，四个空白四边形经过平移可以组成一个长方形，其长为（a－c），宽为（b－c），所以面积为：（a－c）（b－c）＝ab－ac－bc+c2.说明这里通过平移的知识，避免了对图形的分割，使求解简洁、方便.2简析我们可以利用平移的知识分别将楼梯水平方向的线段沿竖直方向平移到BC上，竖直方向的线段沿水平方向平移到AC上，于是铺地毯的横向线段的长度之和就等于横向直角边的长度，纵向线段的长度之和就等于纵向直角长度，所以地毯的总长度至少为 5.6米+2.8米＝8.4米，此总面积为8.4米×3米＝25.2平方米，所以购买地毯至少需要25.8平方米×40元/平方米＝1018元.说明这道若要通过逐步计算，你会觉得比较复杂的，而运用了平移的知识，则问题就显得这么简单，因此，同学们在学习平移知识时一定要用心去体会.3简析由于∠B与∠C的位置较散，故考虑将∠B与∠C变换到同一个三角形中来.而AD∥BC，AD＜BC，故将线段AB沿着AD的方向平移AD长，即点B平移到点E，此时有DE＝AB，DE∥AB，所以∠DEC＝∠B，于是，在△DEC中，因为DE＝DC，所以∠DEC＝∠C，故∠B＝∠C.说明本题从平移的角度来思考问题，使问题简洁获解.4简析由于已知条件中的线段BE、CF和结论中的线段FE、BC比较散，所以我们可以考虑运用平移的知识将这四条线段相对集中，即将EF平移到BM，则此时BE平移到MF，这样只要说明BC＞BM即可，而由于CF＝BE＝MF，再考虑到MF与CF的对称关系，作∠MFC的平分线交BC于点D，易得DM＝DC，因为BD+DM＞BM，所以BC＞EF，即FE＜BC.说明若已知条件中出现相互平行且相等的线段自然要想到利用平移知识解决问题，若条件中并没有出现这些问题，我们要想利用平移的知识求解，则可通过平移使有关线段或角相对集中，从而可降低求解的难度.5简析不妨设国道的两边分别为l1、l2，桥为MN，那么从A到B要走的路线就是A→M →N→B了，如图5，而MN＝a＝定值，于是要使路径最短，只要AM+BN最短即可.此时两线段应在同一平行方向上，若设想先过桥，即平移MN于AC，从C到B应是余下的路程，连结BC的线段即为最短的，此时不难说明线段BC与国道边缘l2的交点N就是修桥的位置.说明本题是设计建桥的位置，却隐含了平移的知识，体现了数学知识与社会生活的紧密联系，既能使我们在具体情况中分析、解决问题，又很好地培养和锻炼了同学们的发散思维能力.6分析：将这个“十字”标志的水平线段向上平移或向下平移，正好组成正方形的水平两条边；将这个“十字”标志的竖直线段向左能够移或向右平移，可以正好组成正方形的竖直两条.这样这个“十字”标志的周长正好等于大正方形的周长.而这个图1大正方形的周长为4米，所以应填4.7分析：把两条道路平移到边上去，如图3所示，则四块空白部分（即蔬菜地）可组成长（30－1）=29（m），宽（20－1）=19（m）的矩形，所以29×19=551(m2).即蔬菜地的面积为551m2.图37要给如图4所示的楼梯铺上地毯，数据如图所示，问共需地毯多长？分析：由于台阶级数未知，每级台阶的宽和高也未知，故直接求解不易.若采用平移的方法，把台阶宽都移到水平线上，台阶高都移到铅垂线上，这样所铺地毯的总米数就等于整个台阶的水平宽度和铅垂高度之和.即共 4需地毯的米数为8+4=12（米）8分析：甲方块左移2小格，下移1小格至屏幕左下角；乙方块右移1小格，下移6小格；丙方块下移6小格至屏幕图5 右下角.这样就排满1行，得到100分.。
人教版数学七年级下册5.4平移试题试卷含答案
5.4 平移5.4.1 平移的概念1．下列现象中，不属于平移的是（ ）A．滑雪运动员在平坦的雪地上滑行B．钟摆的摆动C．大楼上上下下迎送来客的电梯D．火车在笔直的铁轨上飞驰而过2．下列现象中属于平移的是（ ）A．升降电梯从一楼升到五楼B．闹钟的秒针运动C．树叶从树上随风飘落D．汽车方向盘的转动3．把“笑脸”进行平移，能得到的图形是（ ）A．B．C．D．4．下列运动属于平移的是（ ）A．荡秋千B．地球绕着太阳转C．风车的转动D．急刹车时，汽车在地面上的滑动5．如图为一只小牛，将图中的小牛进行平移，得到的小牛可能是下列选项中的（ ）A．B．C．D．参考答案及解析5.4 平移5.4.1 平移的概念1．【答案】B【解析】A，滑雪运动员在平坦的雪地上滑雪，属于平移；B，钟摆的摆动，不属于平移；C，大楼上上下下迎送来客的电梯，属于平移；D，火车在笔直的铁轨上飞驰而过，属于平移．故选B．2．【答案】A【解析】A，升降电梯从一楼升到五楼，符合平移的特点，是平移，；B，闹钟的秒针运动是旋转，不是平移；C，树叶从树上随风飘落不符合平移的特点，不是平移；D，方向盘的转动是旋转，不是平移．故选A．3．【答案】D【解析】观察可知，图形进行平移能得到图形D．故选D．4．【答案】D【解析】A，荡秋千，属于旋转变换；B，地球绕着太阳转，属于旋转变换；C，风车的转动，属于旋转变换；D，急刹车时，汽车在地面上的滑动，属于平移变换．故选D．5．【答案】B【解析】观察可知，得到的小牛可能是B．故选B ．5.4.2 平移的性质1．如图，将三角形ABC 沿OM 方向平移一定的距离得到三角形A B C '''，则下列结论中不正确的是（ ）A ．//AA BB ''B ．AA BB ''=C ．ACB A B C '''∠=∠D ．BC B C ''=2．如图，若三角形ABC 是由三角形DEF 经过平移后得到的，则平移的距离（ ）A ．线段BC 的长度B ．线段BE 的长度C ．线段EC 的长度D ．线段EF 的长度3．如图，ABC ∆沿BC 方向平移到DEF ∆的位置，若2cm BE =，则平移的距离为（ ）A ．1B ．2C ．3D ．44．如图，DEF ∆是由ABC ∆通过平移得到，且点B 、E ，C 、F 在同一条直线上，如果14BF =，6EC =．那么这次平移的距离是 __________．5．如图，三角形ABC 中，2cm AB =，3cm AC =， 3.5cm BC =，将三角形ABC 沿BC 方向平移2cm，连接AD，则四边形ACFD的周长是__________．纠错笔记________________________________________________________________________5.4.2 平移的性质1．【答案】C【解析】由平移的性质，可得A ，B ，D 正确，ACB A C B ∠=∠'''，A C B ∠'''和A B C ∠'''大小关系不确定，故C 错误，故选C ．2．【答案】B【解析】三角形ABC 是由三角形DEF 经过平移后得到的，则平移的距离为线段BE 的长度，故选B ．3．【答案】B【解析】ABC ∆沿BC 方向平移到DEF ∆的位置，点B 平移到E ，若2cm BE =，则平移的距离为2cm ，故选B ．4．【答案】4【解析】DEF ∆ 是由ABC ∆通过平移得到，BE CF ∴=，1()2BE BF EC ∴=-，14BF = ，6EC =，1(146)42BE ∴=-=．故答案为：4．5．【答案】10cm【解析】 三角形ABC 沿BCA 方向平移2cm 得到DEF ∆，2cm AD CF ∴==，3cm DF AC ==，∴四边形ACFD 的周长232310(cm)=+++=．故答案为10cm ．参考答案及解析5.4.3 平移的应用1．如图，将Rt ABC △沿着点B 到点C 的方向平移到DEF △的位置，已知6AB =，2HD =，3CF =，则图中阴影部分的面积为（ ）A ．12B ．15C ．18D ．242．如图，将直线CD 向上平移到AB 的位置，若1130∠=︒，则D 的度数为（ ）A ．130︒B ．50︒C ．45︒D ．35︒3．如图，学校课外生物小组的试验园地的形状是长()35AB 米、宽20米的矩形，为便于管理，要在中间开辟一横两纵共三条等宽的小道，则小道的宽为多少米？若设小道的宽为x 米，则种植面积（单位：平方米）为（ ）A ．2352035202x x x ⨯--+B ．352035220x x ⨯--⨯C ．(352)(20)x x --D ．(35)(202)x x --4．如图，将长为5cm ，宽为3cm 的长方形ABCD 先向右平移2cm ，再向下平移1cm ，得到长方形A B C D ''''，则阴影部分的面积为__________2cm ．5．平移ABC ∆，使点A 移动到点A '，画出平移后的△A B C '''（不写作法，保留作图痕迹）．________________________________________________________________________纠错笔记5.4.3 平移的应用1．【答案】B【解析】由平移，可知ABC ∆的面积与DEF ∆的面积相等，∴阴影部分面积与梯形ABEH 的面积相等，由平移的性质得，6DE AB ==，3BE CF ==，6AB = ，2DH =，624HE DE DH ∴=-=-=，∴阴影部分的面积为1(46)3152⨯+⨯=．故选B ．2．【答案】B【解析】如图1130∠=︒ ，12180+∠=︒，2180150∴∠=︒-∠=︒，AB CD ，250D ∴∠=∠=︒，故选B ．3．【答案】C【解析】依题意，得：(352)(20)x x --，故选C ．4．【答案】18【解析】由题意，空白部分是矩形，长为523(cm)-=，宽为312(cm)-=，∴阴影部分的面积为：253222318(cm )⨯⨯-⨯⨯=，故答案为：18．5．【答案】如图，△A B C '''即为所作：参考答案及解析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.4平移
一、选择题
1.下列运动过程属于平移的是（）
A.荡秋千
B.摇动水井上的轱辘
C.小火车在笔直的铁轨上行进
D.宇宙中的行星运行
2.给出以下现象：①风扇的转动；②打气筒打气时，活塞的运动；③钟摆的摆动；④传送带上，瓶装饮料的移动.其中属于平移的是（）
A.①②
B.①③
C.②③
D.②④
3.如图所示是“胡巴”的五个图案，②，③，④，⑤哪一个图案可以通过平移图案①得到（）
A.②
B.③
D.⑤
4.下列运动是平移的是（）.
（1）推拉窗户；（2）电风扇的运动；
（3）升降机的上下移动；（4）钟表的时针运动；
（5）汽车在笔直的高速路上行驶.
A.（3）（5）
B.（2）（4）
C.（1）（3）（5）
D.（1）（3）（4）
5.如图，哪一个选项的右边图形可由左边图形平移得到（）
6.如图，直线a∥b，直线c与直线a，b分别交于点D，E，射线DF⊥直线c，则图中与∠1互余的角有（）
A.4个
C.2个
D.1个
7.将左图的图案通过平移后可以得到的图案是（）
8.如图，将直径为2cm的半圆水平向左平移2cm，则半圆所扫过的面积（阴影部分）为（）
A.πcm2
B.4cm2
2
9.如图，O是正六边形ABCDEF的对角线的交点，下列三角形中可由三角形OBC平移得到的是（）
A.三角形OCD
B.三角形OAB
C.三角形OAF
D.三角形OEF
10.下列图形中可由平移得到的是（）
二、填空题
11.如图，AB∥CD，直线EF分别交AB，CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于 .
12.如图，△ABC经过一次平移到△DFE的位置，请回答下列问题：
（3）连接AD，BF，BE，与线段CE相等的线段有 .
13.如图所示，由三角形ABC平移得到的三角形有个.
14.如图是某公园里一处矩形风景欣赏区ABCD，长AB=50m，宽BC=25m，为方便游人观赏，公园特意修建了如图的小路（图中非阴影部分），小路的宽均为1m，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为.
15.如图：直角△ABC中，AC=5，BC=12，AB=13，则内部五个小直角三角形的周长为________．
三、解答题
16.如图，将阴影小正方形在网格中平移到小正方形A的位置.
（1）画出平移后的阴影小正方形；
（2）写出三种平移方法（图中每个小正方形的边长都是1cm）；
（3）画出（2）中平移时经过的区域（涂上阴影），你能求出平移过程中阴影小正方形所经过区域（包括原来的）的面积吗？
17.如图所示，四幅汽车标志设计中，能通过平移得到的是（）
18.如图，有一个由4个三角形组成的图形，通过平移，你能用它组成什么图案？试一试，把你的图案与同学们交流一下．
19.如图，每个小正方形的边长为1，每个小方格的顶点叫格点.
（1）画出△ABC的AB边上的中线CD；
（2）画出△ABC向右平移4个单位长度后得到的△A1B1C1；
（3）图中AC与A1C1的关系是：；
（4）S△ABC的面积是 .
20.如图，将直角三角形ABC沿射线BC的方向平移得到三角形DEF.AB=8，BE=5，GE=5，求阴影部分的面积.
答案：
1~10.CDBCC AABCB
11.30°.
12.（1）E ，∠A，EF ；（2）点C 到点E 的方向，CE ，1.5；（3）AD 、BF.
13.5
14.98m.
15.30.
16.解：（1）如图：
（2）如图，方法有很多种，答案不唯一，
图（1）将阴影小正方形先向右平移2cm ，再向下平移2cm ；
图（2）将阴影小正方形向右下方45°方向平移2cm ；
图（3）将阴影小正方形先向右平移1cm ，再向下平移2cm ，最后向右平移1cm ；
（3）如图（答案不唯一），
∵小正方形的边长都为1cm ，
∴每个小正方形的面积都是1cm2.
图（1）中平移经过区域的面积是5×1=5（cm2）；
图（2）中平移经过区域的面积是3×1+21
×1×1×4=5（cm2）；
图（3）中平移经过区域的面积是5×1=5（cm2）. 17.A.
解：B 、C 、D 都不能由“基本图案”经过平移得到，而A 是由一个圆作为基本图形平移得到. 平移的性质
故选A.
18.解：组成的图案如下：（答案不唯一）
19.解：（1）如图所示.
（2）如图所示.
（3）根据平移的性质得出，AC 与A1C1的关系是：平行且相等；
（4）S△ABC=7×5-21×6×2-2×1-21×3×1-21
×7×5=8.
20.解：∵直角三角形ABC 沿BC 的方向平移到三角形DEF ，
∴S△ABC=S△DEF.
∵S 四边形ABEG=S△ABC -S△CEG，S 四边形CGDF=S△DEF -S△CEG，
∴S 四边形ABEG=S 四边形CGDF.
∵四边形ABEG 可以看作是以AB 、EG 为两底，BE 为高的直角梯形，AB=8，BE=5，GE=5，
∴S 四边形ABEG=21×(8+5)×5=2
65， ∴S 四边形CGDF=S 四边形ABEG=2
65，
65
即图中阴影部分的面积为
.
2。