串联谐振电路
串联lc谐振电路

串联LC谐振电路一、什么是LC谐振电路LC谐振电路是由电感(L)和电容(C)组成的一种特殊类型的电路,它在特定频率下能够产生共振现象。
串联LC谐振电路是指电感和电容按照一定的方式串联连接起来,形成一个电路环路。
二、串联LC谐振电路的工作原理串联LC谐振电路的工作原理可以通过以下几个方面来解释:1. 电感和电容的特性电感是由线圈或线圈组成的元件,当通过电流时,会产生磁场。
电容则是由两个导体之间的绝缘介质隔开而构成的元件,它能够存储电荷。
在LC谐振电路中,电感和电容的特性起到关键作用。
2. 谐振频率的选择串联LC谐振电路的谐振频率由电感和电容的参数决定,可以通过以下公式计算得出:f = 1 / (2 * π * √(L * C))其中,f为谐振频率,π为圆周率,L为电感值,C为电容值。
3. 谐振现象的产生当输入信号的频率等于谐振频率时,串联LC谐振电路会出现谐振现象。
此时,电流通过电感和电容时,存在相位差,并且两者的阻抗大小相等,形成共振。
三、串联LC谐振电路的应用串联LC谐振电路在实际应用中有着广泛的用途,下面介绍几个常见的应用场景:1. 无线通信系统在无线通信系统中,频率选择电路(或称作射频滤波器)常采用串联LC谐振电路。
通过调整电感和电容的参数,可以选择性地将特定频率范围内的信号通过,其余频率的信号则被滤除,实现信号的选择性放大。
2. 照明电路在某些照明电路中,串联LC谐振电路可以用于提高电路的功率因数(PF)以及减少谐波。
通过在负载电路中串联一个谐振电路,可以减轻电网的负担,提高电能的利用效率。
3. 调谐电路串联LC谐振电路还可以用于构建调谐电路,实现频率的调节。
通过调整电容或电感的值,可以改变电路的谐振频率,使其适应不同的应用需求。
四、串联LC谐振电路的设计与优化在进行串联LC谐振电路的设计与优化时,需要考虑以下几个因素:1. 负载要求根据具体的应用需求,需要确定负载电路的参数,以及谐振频率和谐振电流的要求。
串联谐振电路
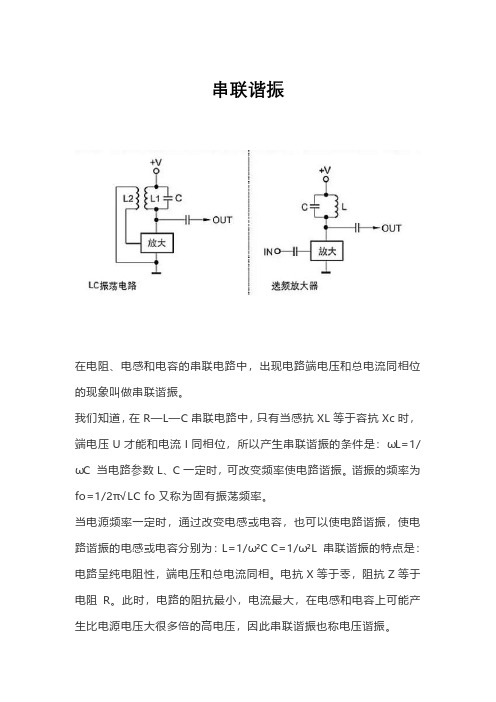
串联谐振
在电阻、电感和电容的串联电路中,出现电路端电压和总电流同相位的现象叫做串联谐振。
我们知道,在R—L—C串联电路中,只有当感抗XL等于容抗Xc时,端电压U才能和电流I同相位,所以产生串联谐振的条件是:ωL=1/ωC 当电路参数L、C一定时,可改变频率使电路谐振。
谐振的频率为fo=1/2π√LC fo又称为固有振荡频率。
当电源频率一定时,通过改变电感或电容,也可以使电路谐振,使电路谐振的电感或电容分别为:L=1/ω²C C=1/ω²L 串联谐振的特点是:电路呈纯电阻性,端电压和总电流同相。
电抗X等于零,阻抗Z等于电阻R。
此时,电路的阻抗最小,电流最大,在电感和电容上可能产生比电源电压大很多倍的高电压,因此串联谐振也称电压谐振。
串联谐振时,电感电压UL或电容电压UC与端电压U之比,叫做电路的品质因数,用符号Q表示,即Q=UL/U=UC/U=ωL/R
由于谐振时电感及电容两端电压是电源电压的Q倍,所以收音机的谐振回路可利用这一点来选择某一频率的信号。
但在电力工程上,由于串联谐振会出现过电压、大电流,以致损坏电气设备,所以要注意避免串联谐振。
串联并联谐振电路频率计算公式

串联并联谐振电路频率计算公式一、串联谐振电路频率计算公式。
1. 公式推导。
- 对于串联谐振电路,其阻抗Z = R + j(X_L - X_C),其中R为电阻,X_L=ω L为电感的感抗(ω = 2π f,L为电感值),X_C=(1)/(ω C)为电容的容抗,C为电容值。
- 在串联谐振时,X_L = X_C,即ω L=(1)/(ω C)。
- 解这个等式求ω,得到ω=(1)/(√(LC)),由于f = (ω)/(2π),所以串联谐振频率f_0=(1)/(2π√(LC))。
2. 示例。
- 已知一个串联电路中,电感L = 10mH,电容C = 1μ F。
- 根据串联谐振频率公式f_0=(1)/(2π√(LC)),将L = 10×10^- 3H,C = 1×10^-6F代入公式。
- 先计算√(LC)=√(10×10^-3)×1×10^{-6}=√(10^-8) = 10^-4。
- 则f_0=(1)/(2π×10^-4)≈1591.55Hz。
二、并联谐振电路频率计算公式。
1. 公式推导(对于理想情况,即忽略电阻R时)- 对于并联谐振电路,当R很小可忽略时,其导纳Y = jω C+(1)/(jω L)。
- 在并联谐振时,导纳Y的虚部为0,即jω C+(1)/(jω L)=0。
- 化简可得ω C=(1)/(ω L),解得ω=(1)/(√(LC)),所以并联谐振频率f_0=(1)/(2π√(LC)),这与串联谐振频率公式形式相同(在理想情况下)。
2. 考虑电阻R时的公式(以电感L与电阻R串联后再与电容C并联的电路为例)- 导纳Y=(1)/(R + jω L)+jω C。
- 在谐振时,Y的虚部为0。
- 经过复杂的复数运算(这里省略详细步骤),可得谐振频率f_0=(1)/(2π)√(frac{1){LC}-frac{R^2}{L^2}},当Rllω L时,就近似为f_0=(1)/(2π√(LC))。
RLC串联谐振电路

RLC 串联谐振电路 一、知识要求:理解RLC 串联电路谐振的含义;理解谐振的条件、谐振角频率、频率;理解谐振电路的特点,会画矢量图。
二、知识提要:在RLC 串联电路中,当总电压与总电流同相位时,电路呈阻性的状态称为串联谐振。
(1)、串联谐振的条件:C L C L X X U U ==即(2)、谐振角频率与频率:由LCf LC:C L πωωω21110===谐振频率得(3)、谐振时的相量图:(4)、串联谐振电路的特点: ①.电路阻抗最小:Z=R②、电路中电流电大:I 0=U/R③、总电压与总电流同相位,电路呈阻性④、电阻两端电压等于总电压,电感与电容两端电压相等,相位相反,且为总电压的Q 倍,。
即:U L =U C =I 0X L =I 0X C =L X R U=U RX L =QU 式中:Q 叫做电路的品质因数,其值为:CRf R L f R X R X Q C L 00212ππ====>>1(由于一般串联谐振电路中的R 很小,所以Q 值总大于1,其数值约为几十,有的可达几百。
所以串联谐振时,电感和电容元件两端可能会产生比总电压高出Q 倍的高电压,又因为U L =U C ,所以串联谐振又叫电压谐振。
) (5)、串联谐振电路的应用:适用于信号源内阻较低的交流电路。
常被用来做选频电路。
三、例题解析:1、在RLC 串联回路中,电源电压为5mV ,试求回路谐振时的频率、谐振时元件L 和C 上的电压以及回路的品质因数。
解:RLC 串联回路的谐振频率为Uc∙LCf π210=谐振回路的品质因数为 RLf Q 02π=谐振时元件L 和C 上的电压为 mV 5mV 5C L CLR Q U U === 2、 在RLC 串联电路中,已知L =100mH ,R =3.4Ω,电路在输入信号频率为400Hz 时发生谐振,求电容C 的电容量和回路的品质因数。
解:电容C 的电容量为F 58.14.6310141)2(120μπ≈==L f C 回路的品质因数为 744.31.040028.620≈⨯⨯==R L f Q π3、已知某收音机输入回路的电感L=260μH,当电容调到100PF 时发生串联谐振,求电路的谐振频率,若要收听频率为640KHz 的电台广播,电容C 应为多大。
串联谐振_实验报告

一、实验目的1. 理解串联谐振电路的基本原理和特性。
2. 掌握串联谐振电路的谐振频率、品质因数和通频带的测量方法。
3. 通过实验验证理论分析,加深对串联谐振电路的理解。
二、实验原理串联谐振电路由电感L、电容C和电阻R组成,按照其原件的连接形式可分为串联谐振和并联谐振。
本实验主要研究串联谐振电路的特性。
1. 谐振频率:串联谐振电路的谐振频率f0由以下公式给出:f0 = 1 / (2π√(LC))其中,f0为谐振频率,L为电感,C为电容。
2. 品质因数Q:串联谐振电路的品质因数Q表示电路的选频性能,由以下公式给出:Q = 1 / (R√(LC))其中,Q为品质因数,R为电阻,L为电感,C为电容。
3. 通频带:通频带B为谐振曲线两侧电流有效值下降到最大电流的1/√2时对应的频率范围,由以下公式给出:B = f2 - f1其中,f1为下限截止频率,f2为上限截止频率。
三、实验仪器与设备1. 信号发生器:提供不同频率的正弦交流信号。
2. 数字多用表:测量电压、电流和电阻。
3. 电感器、电容器和电阻器:构成串联谐振电路。
4. 电路连接线:连接实验仪器和设备。
四、实验步骤1. 按照实验电路图连接电路,确保连接正确无误。
2. 将信号发生器的输出端连接到串联谐振电路的输入端。
3. 将数字多用表分别连接到电感、电容和电阻的相应位置,用于测量电压、电流和电阻。
4. 设置信号发生器的输出频率为f0,即谐振频率,观察并记录电路中的电压、电流和电阻的数值。
5. 改变信号发生器的输出频率,分别在谐振频率两侧的频率点测量电路中的电压、电流和电阻的数值。
6. 根据实验数据绘制幅频特性曲线,分析谐振频率、品质因数和通频带的特性。
7. 通过实验验证理论分析,总结实验结果。
五、实验结果与分析1. 谐振频率:实验结果显示,当信号发生器的输出频率为f0时,电路中的电压、电流和电阻的数值达到最大值,验证了谐振频率的理论分析。
2. 品质因数Q:实验结果显示,随着电阻的增大,品质因数Q减小,与理论分析一致。
串联谐振电路实验报告

串联谐振电路实验报告串联谐振电路实验报告引言:电路实验是电子工程专业学生的基础实践课程之一。
其中,串联谐振电路实验是一项非常重要的实验,它能帮助学生深入理解谐振电路的工作原理和特性。
本文将对串联谐振电路实验进行详细的介绍和分析。
一、实验目的串联谐振电路实验的主要目的是通过实际操作,观察和分析串联谐振电路的频率特性、幅度特性和相位特性,加深对谐振电路的理论知识的理解。
二、实验原理串联谐振电路由电感L、电容C和电阻R串联而成。
当电路中的电感和电容选择合适的数值,并且电路工作在谐振频率附近时,电路会表现出特殊的谐振现象。
在谐振频率附近,电路的阻抗最小,电流最大。
这种谐振现象可以通过实验来验证。
三、实验装置与步骤实验所需的装置主要有信号发生器、示波器、电感、电容和电阻等。
实验步骤如下:1. 搭建串联谐振电路,将信号发生器连接到电路的输入端,示波器连接到电路的输出端。
2. 设置信号发生器的频率为可变频率,初始值设置为较低的频率。
3. 调节信号发生器的频率,观察示波器上的波形变化。
4. 当示波器上的波形达到最大振幅时,记录此时的频率,即为谐振频率。
5. 重复步骤3和4,改变电路中的电感和电容数值,观察谐振频率的变化。
四、实验结果与分析在实验中,我们调整了电路中的电感和电容数值,并观察了谐振频率的变化。
实验结果表明,电路中的电感和电容数值越大,谐振频率越低。
这是因为电感和电容的数值决定了电路的固有频率。
另外,我们还观察了电路的幅度特性和相位特性。
在谐振频率附近,电路的幅度特性表现为电流最大,而在谐振频率两侧,电路的幅度逐渐减小。
相位特性则表现为在谐振频率附近,电路的输入信号和输出信号的相位差最小,而在谐振频率两侧,相位差逐渐增大。
五、实验误差与改进在实验过程中,我们注意到了一些误差。
首先,由于实际电路元件的参数可能存在一定的误差,所以实验结果与理论值可能会有一定的偏差。
其次,实验中的测量误差和仪器误差也会对实验结果产生影响。
串联谐振计算

串联谐振计算
串联谐振电路是一种电路,其中电容和电感器按照一定的方式排列,使得电路在特定频率下具有最大电压振幅。
以下是串联谐振电路的计算公式:
1. 谐振频率:f=(1/2π√(LC))
其中,L为电感值,C为电容值
2. 谐振电阻:R=(√L/C)
其中,R为谐振电阻值
3. 谐振电压:V=Vp(R/(R+Rl))
其中,V为谐振电压值,Vp为电压源峰值,Rl为负载电阻
需要注意的是,以上公式均为理论计算值,在实际应用中需要考虑电路元件的实际参数误差和其它因素的影响,因此实际测量值可能会与理论计算值有所差异。
RLC串联谐振电路应用

品质因数计算公式
品质因数的影响因素
品质因数受到电阻、电感和电容的影 响,电阻越大,品质因数越低;电感 和电容越大,品质因数越高。
Q=ωL/R,其中ω是角频率,L是电感, R是电阻。
02
RLC串联谐振电路的应用 场景
信号源发生器
信号源发生器
RLC串联谐振电路可以用于产生特定频率的信号,如振荡器或信号源。通过调 整电感(L)和电容(C)的值,可以获得所需的频率,用于各种电子设备和系 统的信号源。
测量仪器
• 测量仪器:RLC串联谐振电路在 各种测量仪器中具有广泛应用, 如示波器、频谱分析仪和网络分 析仪等。这些仪器利用RLC电路 的谐振特性来测量信号的频率、 幅度和相位等参数,为科学研究 和技术开发提供准确的数据。
03
RLC串联谐振选择性
RLC串联谐振电路在某一特定频率下呈现零阻抗,而在其他频率下呈现
智能化
随着物联网和人工智能技术的融合,RLC串联谐振电路将 与传感器、执行器等智能器件集成,实现智能化控制和远 程监控。
技术展望
新材料的应用
随着新材料技术的不断发展,新型的电介质、磁性材料等将在 RLC串联谐振电路中得到应用,以提高其性能和稳定性。
先进封装技术
采用先进的封装技术,如三维集成和薄膜封装等,可实现RLC串联 谐振电路的高密度集成和微型化。
组成
RLC串联谐振电路由一个电阻器、一个电感器和两个电容器 组成。
工作原理
原理概述
RLC串联谐振电路在某一特定频率下呈现纯阻性, 此时电路的阻抗最小,电流最大。
电流最大值公式
当角频率ω=√(L/C)时,电路的阻抗最小,电流最 大。
频率计算公式
谐振频率f=1/√(2πLC)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
串联谐振电路
学号: 姓名: 成绩:
1、实验目的
1. 加深对串联谐振电路条件及特性的理解。
2. 掌握谐振频率的测量方法。
3. 理解电路品质因数Q和通频带的物理意义及测量方
法。
4. 测定RLC串联谐振电路的频率特性曲线。
5. 深刻理解和掌握串联谐振的意义及作用。
6. 掌握电路板的焊接技术以及信号发生器、交流毫伏
表等仪器的使用。
7. 掌握Multisim软件中的Function Generator、
Voltmeter、Bode Plotter等仪表的使用,以AC Analysis
等SPICE仿真分析方法。
8. 用Origin绘图软件绘图。
2、实验原理
RLC串联电路如图7.1所示,改变电路参数L、C或电源频率时,都可能使电路发生谐振。
该电路的阻抗是电源角频率的函数
(7-1)
当时,电路中的电流与激励电压同相,电路处于谐振状态。
谐振角频率,谐振频率。
谐振频率仅与元件的数值有关,而与电阻和激励电源的角频率无关,
当时,电路呈容性,阻抗角<0;当时,电路呈感性,阻抗角>0。
1.电路处于谐振状态时的特性:
(1) 回路阻抗,为最小值,整个回路相当于一个纯电阻电
路。
(2) 回路电路I0的数值最大,
(3) 电阻的电压U R的数值最大,
(4) 电感上的电压U L与电容上的电压U C数值相等,相位相
差。
2.电路的品质因数Q和通频带B
电路发生谐振时,电感上的电压(或电容上的电压)与激励电压之比称为电路的品质因数Q,即
(7-2)
定义回路电流下降到峰值的0.707时所对应的频率为截止频率,介于两截止频率间的频率范围为通频带。
(7-3)
3.谐振曲线
电路中电压与电流随频率变化的特性称频率特性,它们随频率变化的曲线称频率特性曲线,也称谐振曲线。
在固定的条件下:
改变电源角频率,可得到图7.2响应电压随电源角频率变化的谐振曲线,回路电流与电阻电压成正比。
从图中可以看到,U R的最大值在谐振角频率ω0处,此时U C=U L=Q U。
U C的最大值在ω<ω0处, U L的最大值在ω>ω0处。
图7.3则表示经过归一化处理后不同值时的电流频率特性曲线。
从图中可以看:值愈大,曲线尖峰值愈峻端,其选择性就愈好,但电路的通过的信号频带越窄,即通频带越窄。
3、实验内容
1. Multisim仿真
(1) 创建电路:从元器件库中选择可变电阻、电容、电感创建如图电路。
(2) 当电阻R= 100、200、300时,用Multisim软件仿真串联谐振电路的谐振曲线,在同一张图中画出
谐振曲线,说明R对Q值、带宽的影响。
从图中可以直观的看出,随着R值的减小,B值逐渐减小,由
Q值逐渐增大,即说明R值越小,选择性越好,通频带越,
窄。
而且,谐振频率与电阻阻值没有关系。
(3) 利用谐振的特点设计选频网络,在串联谐振电路(R=100Ω L=4.7mH C=100nF)上输入频率为
3.5kHz、占空比为30%、脉冲幅度为5V的方波电压
信号,用Multisim软件测试谐振电路输入信号和
输出信号(电阻上电压)的频谱、测试输入信号
和输出信号波形。
输入频谱
输出频谱
从傅里叶频谱中,可以看出在谐振频率附近处,输出电压最大,体现了谐振电路的选频特性。
时域输入输出波形
根据串联谐振电路的选频特性,谐振频率附近的正弦信号才可以通过,于是这部分正弦信号叠加产生了图示波形。
2. 测量元件值并计算理论值。
R L=38Ω R1=100Ω L=4.7mH C=112nF
则 R=128Ω
=43585.5 rad/s
=7.67 kHz
=1.48
=5.17 kHz
3. 在电路板上焊接如图所示电路,信号电压有效值设
置为1V。
4. 用两种不同方法测量电路的f0值。
方法一维持信号源的输出幅值不变,令信号源的频率有小逐渐变大,当U R读数最大时的频率。
测得。
方法二将输入输出信号接入示波器,并设定在X-Y模式。
当椭圆变成一条直线时,电路发生谐振。
测得。
分析:方法一测得的f o=8.80kHz,方法二测得的f o=7.45kHz,理论值是f o=7.67kHz,三者的值存在着误差。
误差的原
因:(1)可能由于仪器本身的误差;(2)测量过程中数据记录的误差;(3)电容电感本身有阻值,这些阻值带来的误差;(4)由于信号发生器上的频率不稳定,导致读数
的误差等原因。
5. 电路响应的谐振曲线的测量
频率电压电压电压
0.565182300
1134512390
22801762630
46297383420
7112938304400
7.5114843004340
7.67115044504300
8114547104210
8.5112550804050
9109354003860
10110158703450
1284464802700
1470769202130用Origin软件绘图得如下图:
从上图可测得,实际谐振频率
左右,-3dB带宽
:。
上图所显示的谐振曲线只能说能看个大概,很是不理想,分析如下:
1. 记录的数据虽然在谐振频率附近有所增加,但整体还
是太少了,共
计记录了13组数据,应该记录至少30组数据才能精确的画出谐振曲
2. 电感L的谐振曲线在图中总是在上升,主要原因是所取
频率的范围
太小了,所取频率的最大值还没达到电感L的谐振频率。
电容C的谐振曲线相对较为理想,谐振频率是最小的,能很好的察到最大值。
四.实验结论
电路处于串联谐振时,回路阻抗最小,电流最大,电阻两端的电压最大。
而且,串联谐振电路具有选频特性,能够筛选
出通频带内的信号。
电阻值越小,选择性越好,通频带越
窄。
