多重共线性检验与修正
计量经济学实验五 多重共线性的检验与修正 完成版
习题1.下表给出了中国商品进口额Y 、国内生产总值GDP 、消费者价格指数CPI 。
年份 商品进口额 (亿元)国内生产总值(亿元)居民消费价格指数(1985=100)1985 1257.8 8964.4 1001986 1498.3 10202.2 106.5 1987 1614.2 11962.5 114.3 1988 2055.1 14928.3 135.8 1989 2199.9 16909.2 160.2 1990 2574.3 18547.9 165.2 1991 3398.7 21617.8 170.8 1992 4443.3 26638.1 181.7 1993 5986.2 34634.4 208.4 1994 9960.1 46759.4 258.6 1995 11048.1 58478.1 302.8 1996 11557.4 67884.6 327.9 1997 11806.5 74462.6 337.1 1998 11626.1 78345.2 334.4 1999 13736.4 82067.5 329.7 2000 18638.8 89468.1 331.0 2001 20159.2 97314.8 333.3 2002 24430.3 105172.3 330.6 200334195.6117251.9334.6资料来源:《中国统计年鉴》,中国统计出版社2000年、2004年。
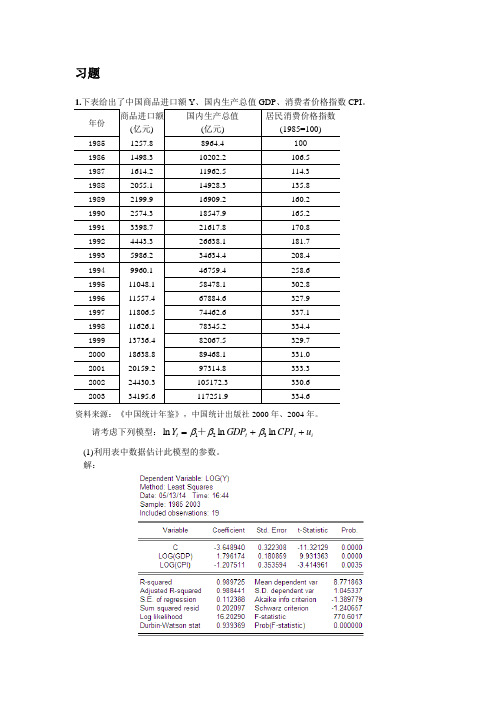
请考虑下列模型:i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
解:ln 3.6489 1.796ln 1.2075ln t t t Y GDP CPI =--+t= (-11.32) (9.93) (-3.415)20.988770.6.0.1124R F S E ===(2)你认为数据中有多重共线性吗?多重共线性的检验 1)综合统计检验法若 在OLS 法下:R 2与F 值较大,但t 检验值较小,则可能存在多重共线性。
第四章 多重共线性

2
( x2 i x3 i ) 2 x [1 2 x3 i
2 2i
2
2 2 x2 i (1 r23 )
ˆ Var( 3 ) 同样可得
2
2 2 x3 i (1 r23 )
ˆ ˆ Cov( 2 , 3 )
r23 2
2 2 2 (1 r23 ) x2 i x3 i
1 X X 21 X 31
1 X 22 X 32
1 X 2n X 3n
nX 3 X 2 i X 3 i 2 X 3 i
X 2 i
2 X 2 i X 2 i X 3 i
X 3 i n nX 2 2 X 2 i X 3 i nX 2 X 2 i 2 X 3 i nX 3 X 2 i X 3 i
其中vi为随机变量,则称解释变量X2、X3、 …、 Xk 之间存在着不完全的多重共线性。 注意:解释变量之间不存在线性关系,并非不存在 非线性关系,当解释变量之间存在非线性关 系时,并不违反古典假定。
5
二、产生多重共线性的背景
多重共线性产生的经济背景主要有几种情形:
1.经济变量之间具有相同的变化趋势。
10
n X X nX 2 nX 3 n 0
nX 2 X
2 2i
nX 3 X 2 i X 3 i
2 X 3 i
X 2 i X 3 i nX 2
2 2 X 2 i nX 2
X 2 i x2 i X 2 X 3 i x3 i X 3
nX 3
X 2 i X 3 i nX 2 X 3
这里r23是X2,X3的相关系数。
16
EViews计量经济学实验报告-多重共线性的诊断与修正的讨论

实验题目 多重共线性的诊断与修正一、实验目的与要求:要求目的:1、对多元线性回归模型的多重共线性的诊断;2、对多元线性回归模型的多重共线性的修正。
二、实验内容根据书上第四章引子“农业的发展反而会减少财政收入”,1978-2007年的财政收入,农业增加值,工业增加值,建筑业增加值等数据,运用EV 软件,做回归分析,判断是否存在多重共线性,以及修正。
三、实验过程:(实践过程、实践所有参数与指标、理论依据说明等)(一)模型设定及其估计经分析,影响财政收入的主要因素,除了农业增加值,工业增加值,建筑业增加值以外,还可能与总人口等因素有关。
研究“农业的发展反而会减少财政收入”这个问题。
设定如下形式的计量经济模型:i Y =1β+2β2X +3β3X +4β4X +5β5X +6β6X +7β7X +i μ其中,i Y 为财政收入CS/亿元;2X 为农业增加值NZ/亿元;3X 为工业增加值GZ/亿元;4X 为建筑业增加值JZZ/亿元;5X 为总人口TPOP/万人;6X 为最终消费CUM/亿元;7X 为受灾面积SZM/千公顷。
图1: 1978~2007年财政收入及其影响因素数据年份财政收入CS/亿元 农业增加值NZ/亿元 工业增加值GZ/亿元 建筑业增加值JZZ/亿元总人口TPOP/万人最终消费CUM/亿元受灾面积SZM/千公顷 1978 1132.3 1027.5 1607 138.2 96259 2239.1 50790 1979 1146.4 1270.2 1769.7 143.8 97542 2633.7 39370 1980 1159.9 1371.6 1996.5 195.5 98705 3007.9 44526 1981 1175.8 1559.5 2048.4 207.1 100072 3361.5 39790 1982 1212.3 1777.4 2162.3 220.7 101654 3714.8 33130 1983 1367 1978.4 2375.6 270.6 103008 4126.4 34710 1984 1642.9 2316.1 2789 316.7 104357 4846.3 31890 1985 2004.8 2564.4 3448.7 417.9 105851 5986.3 44365 1986 2122 2788.7 3967 525.7 107507 6821.8 47140 1987 2199.4 3233 4585.8 665.8 109300 7804.6 42090 1988 2357.2 3865.4 5777.2 810 111026 9839.5 50870 1989 2664.9 4265.9 6484 794 112704 11164.2 46991 1990 2937.1 5062 6858 859.4 114333 12090.5 38474 1991 3149.48 5342.2 8087.1 1015.1 115823 14091.9 55472 1992 3483.37 5866.6 10284.5 1415 117171 17203.3 51333 1993 4348.95 6963.8 14188 2266.5 118517 21899.9 48829 1994 5218.1 9572.7 19480.7 2964.7 119850 29242.2 55043 19956242.2 12135.8 24950.6 3728.8 12112136748.2458211996 7407.99 14015.4 29447.6 4387.4 122389 43919.5 46989 1997 8651.14 14441.9 32921.4 4621.6 123626 48140.6 53429 1998 9875.95 14817.6 34018.4 4985.8 124761 51588.2 50145 1999 11444.08 14770 35861.5 5172.1 125786 55636.9 49981 2000 13395.23 14944.7 40036 5522.3 126743 61516 54688 2001 16386.04 15781.3 43580.6 5931.7 127627 66878.3 52215 2002 18903.64 16537 47431.3 6465.5 128453 71691.2 47119 2003 21715.25 17381.7 54945.5 7490.8 129227 77449.5 54506 2004 26396.47 21412.7 65210 8694.3 129988 87032.9 37106 2005 31649.29 22420 76912.9 10133.8 130756 96918.1 38818 2006 38760.2 24040 91310.9 11851.1 131448 110595.3 41091 2007 51321.78 28095 107367.2 14014.1 132129 128444.6 48992利用EV 软件,生成i Y 、2X 、3X 、4X 、5X 、6X 、7X 等数据,采用这些数据对模型进行OLS 回归。
4.4 多重共线性的补救措施

• 如果模型出现了严重的多重共线性,就应采取 必要的措施进行补救。然而,由于经济系统的 复杂性,要将多重共线性消除干净几乎是不可 能的,只能选择合适的方法减弱多重共线性对 模型的影响。目前,常用的方法有以下几种: • 一、增加样本容量
• 在计量经济模型中,如果变量样本数据太少,很 容易产生多重共线性。在这种情况下,增加样本容量, 将有助于减弱,甚至消除多重共线性。
• 本章实例参见教材P85~P88.
8
3
三、逐步回归法
• 1.目的:寻找最优回归方程——使R2较 大,F显著;每个回归系数显著 • 2.种类 • (1)逐个剔除法 • (2)逐个引入法 • (3)有进有出法 • 3.准则:一次只能引入或剔除一个自变 量,直至模型中所有自变量均显著 4
• 4、基本做法:
将应变量 Y 的每一个解释变量Xi (i=1,2, …,k)分别进行回归,对每一个回归方程根据 经济理论和统计检验进行综合分析判断,从中挑出一 个最优的基本回归方程,在此基础上,再逐一引入其 它解释变量,重新作回归,逐步扩大模型的规模,直 至从综合情况看,出现最好的模型估计形式。 5、变量取舍标准:在引进新解释变量的回归方程中: (1)如果新解释变量在符合经济意义的前提下,能使 拟合优度R2有所提高,并且,每个参数统计检验显著, 则采纳改变量。 (2)如果新解释变量不能改善拟合优度,同时,对 其它参数无明显影响,则可舍弃该变量。 (3)如果新解释变量能使拟合优度有所改善, R2 有所提高,但对其它参数的符号和数值有明显影响, 统计检验也不显著,则可以断定新解两个变量中,舍去 对应变量影响较小,经济意义相对次要的一个,保留 影响较大,经济意义相对重要的一个。 5
五、将时间序列数据与界面数据相结合
第五 多重共线性(共54张PPT)

▪ 但是应注意:
▪ 如果研究的目的仅在于预测被解释变量Y,而各个解释变量X之间的 多重共线性关系的性质在未来将继续保持,这时虽然无法精确估计 个别的回归系数,但可估计这些系数的某些线性组合,因此多重共 线性可能并不是严重问题。
第三节 多重共线性的检验
多重共线性检验的任务是:
1)检验多重共线性是否存在;
4、变量的显著性检验失去意义
存在多重共线性时
参数估计值的方差与标准差变大
容易使通过样本计算的t值小于临界值, 误导作出参数为0的推断
可能将重要的解释变量排除在模型之外
5、模型的预测功能失效
▪ 变大的方差容易使区间预测的“区间”变大,使预测
失去意义。
▪其次,由于参数估计量的方差变大,因而对样本值的 反映十分敏感,即当样本观测值稍有变化时,模型参数 就有很大差异,致使模型难以应用。
2)估计多重共线性的范围,即判断哪些变量之间存在
共线性。
一、 检验多重共线性是否存在
1.简单相关系数检验法
利用解释变量之间的线性相关程度去判断是否存在严重多重 共线性的一种简便方法。
一般而言,如果每两个解释变量的简单相关系数比较高,如 大于0.8,则可认为存在着较严重的多重共线性。
注意 较高的简单相关系数只是多重共线性存在的充分条件, 而不是必要条件。特别是在多于两个解释变量的回归模型中, 有时较低的简单相关系数也可能存在多重共线性。因此并不 能简单地依据相关系数进行多重共线性的准确判断。
如果拟合优度变化显著,则说明新引入的变量是一个独立的解释 变量;
如果拟合优度变化很不显著,则说明新引入的变量不是一个独立 的解释变量,它可以用其他变量的线性组合代替,也就是说它与其 他变量之间存在多重共线性。
多重共线性修正

则 zi=β0+β2Inx2i+ui 这时方程就成为了一元线性回归模型, 显然已不存在多重共线性。
第三类: 第三类:减少参数估计量的方法
多重共线性的主要后果是参数估计量 具有较大的方差,所以采取适当方法减小 参数估计量的方差,虽然没有消除模型中 的多重共线性,但确能消除多重共线性造 成的后果。
且从理论上可以证明,存在k>0,使得的ˆ (k ) β ˆ 均方误差比 β 的均方误差小。因此,用岭回 归来估计偏回归系数比用普通最小二乘法估 计要稳定得多。这样就消除了多重共线性对 参数估计的危害。
确定岭回归系数K值
确定k值需要使用搜索法。在0到1区间 内,按照一定的间隔(如0.01等)取k值,观 ˆ (k ) = X T X + kI −1 X T Y 察岭回归估计量β 随 k值变化的情况,当k从0慢慢变大时,开 ˆ 始岭回归估计量 β (k )的变动剧烈,以后慢慢 趋于稳定。选择岭回归系数应满足的条件是 : (1)所有的岭回归估计量大小和符号符合经 济理论 ˆ (2)所有的岭回归估计量β (k ) 趋于稳定
多重共线性的修正
多重共线性修正方法的汇总:
第一类:删除引起共线性解释变量 第二类:重新设定模型 第三类:减少参数估计量的方法 第四类:其他
第一类: 第一类:删除引起共线性解释变量
找出引起多重共线性的解释变量,将 它排除出去,是最为有效的克服多重共线 性问题的方法。 这类方法以逐步回归法为代表,得到 了最广泛的应用。
ˆ β (k ) = X T X + kI
其中k称为岭参数。
(
)
−1
计量经济学第四章 多重共线性

x2i
3 2
x3i
x3i
参数的估计值为:
ˆ2
x32i x2i yi x2i x3i x3i yi
(
x22i )(
x32i ) (
x2i
x 3i
)2
x32i
2
x3i yi x32i 2 2
x32i x32i
x2i x3i x22i
x2i x3i
ˆ1 Y ˆ2 X 2 ˆ3 X 3
ˆ2
x32i x2i yi x2i x3i x3i yi ( x22i )( x32i ) ( x2i x3i )2
ˆ3
x22i x3i yi x2i x3i x2i yi •
(
x22i )(
x32i ) (
x2i
x 3i
)
2
x2i yi x3i yi
x2i x3i x32i
4.2多重共线性的后果
如果X1和X2完全线性相关,则存在非0的λ使得:
1 2 X 2i 3 X 3i 0
则有:
1 2 X 2 3 X 3 0
2 X 2i X 2 3 X3i X3 0
X 2i X3i X 2iYi
X
2 3i
X
3iYi
VAR
COV
(βˆ )
2
(XX)1
2
N X 2i
X 3i
X2i
X
2 2i
X 2i X 3i
计量经济第六章多重共线性

• 2、数据采集的范围有限,或采集 的样本量小于模型的自变量个数。
• 如在罕见疾病的研究过程中,由于病 情罕见、病因又相当复杂,而只能在 少数的患者身上采集大量的变量信息。
3、模型中采用滞后变量
在计量经济模型中,往往需要引入 滞后变量来反映真实的经济关系。 例如,消费=f(当期收入, 前期收入) 显然,两期收入间有较强的线性相 关性。
up
三、方差膨胀因子法
• 自变量间的共线性程度越大时,VIF值也随之 增大。所以也可利用方差膨胀因子来检验 多重共线性问题。 • 一般来说,当VIF >10时,表明 涉及的两个 变量存在高度线性相关,模型存在不完全 多重共线性。
P111 【经典实例】
• 计算得到的方差膨胀因子值分别为
VIF1 =10000,VIF2 =10000,VIF3 =9.6525,VIF4 =11.5875
2 2 2 1
同理易得
ˆ ) Var( 2
• EVIEWS遇到完全多重共线性时,会 显示 • Near singular matrix,无法进行估 计
2、不完全多重共线性下的后果
(1)估计量的方差增大 2 2 x 2 ˆ) 由于 Var ( 1 2 x12x2 (x1 x2 )2
• 可以看出,除了 VIF3 10 ,其余的方 差膨胀因子值均大于10,表明模型中 存在较严重的多重共线性问题。
up
第三节 多重共线性的修正 一、改变模型的形式 二、删除自变量 三、减少参数估计量的方差 四、其它方法 习题
up
• 一、改变模型的形式
• (一)变换模型的函数形式
• 例如将线性回归模型转化为对数模 型或者多项式模型。 • (二)改变模型的自变量的形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多重共线性检验与修正
数据来源:《中国统计年鉴2014》12-10、4-3、12-4、12-5、12-8、
Eviews操作:
1、基本操作:
(1)录入数据:命令:data y l m f a ir
(y代表粮食产量,l代表第一产业劳动力数量,m代表农业机械总动力,f代表化肥施用量,a代表农作物总播种面积,ir为有效灌溉面积/农作总播种面积得出的灌溉率)
(2)做线性回归:命令:LS y c l m f a ir
2、检验多重共线性
(1)方差膨胀因子判断法
在生成的线性回归eq01中,view—coefficient diagnostics—variance inflation factors
看生成表格中的Centered VIF,发现L、M、F、A、IR的方差膨胀因子都很大,说明存在严重多重共线性。
(eg:L的Centered VIF指以L为因变量,M、A、F、IR为自变量所做出的辅助回归的判定系数R²,然后1/1-R²得出的值。
)
(由课本内容可知,当完全不共线性时,VIF=1;完全共线性时,VIF=正无穷)(2)相关系数矩阵判断法
命令:cor l m f a ir
这个是通过看各个解释变量之间的相关系数来判断是否存在多重共线性的。
可以看到大多数解释变量之间两两相关系数都大于0.9。
相关系数极大说明解释变量之间存在很高的相关性,因而也就很可能存在共线性。
3、修正多重共线性
(1)逐步回归排除引起共线性的变量
①菜单栏操作
在生成的线性回归eq01中,Estimate—Method—STEPLS
接下来会出现两个框框,上面的框框是固定住不做逐步回归的变量,一般设定为y和c
下面的框框是需要进行逐步回归选择是否剔除的变量,这里填入l m f a ir 然后出来一个新的表格,这个表格已经自动选择了可以保留的变量l a f,剔除了m ir
②命令栏操作
命令:STEPLS y c @ l m f a ir
这条命令其实和菜单栏操作的意思一样,stepls代表采用逐步回归方法,@前的y、c代表固定不做逐步回归的变量,@后的l、m、f、a、ir代表要做逐步回归的变量
出来的结果和菜单栏操作的结果是一样的。
(注:当然,固定保留的变量你也可以根据自己的需要进行选择,只不过一般是固定保留y和c)
做完逐步回归后,按照保留下来的变量,重新做线性回归就可以得到不存在多重共线性的新模型了。
(2)岭回归法减小参数估计量方差
这个方法没法在Eviews做。
